Similar presentations:
Дифференциальные уравнения Колмогорова. Анализ типовых моделей систем ТО. Полумарковские процессы. (Лекция 4)
1. Моделирование систем и процессов
Лекция 4.Дифференциальные уравнения Колмогорова
Анализ типовых моделей систем ТО
Полумарковские процессы
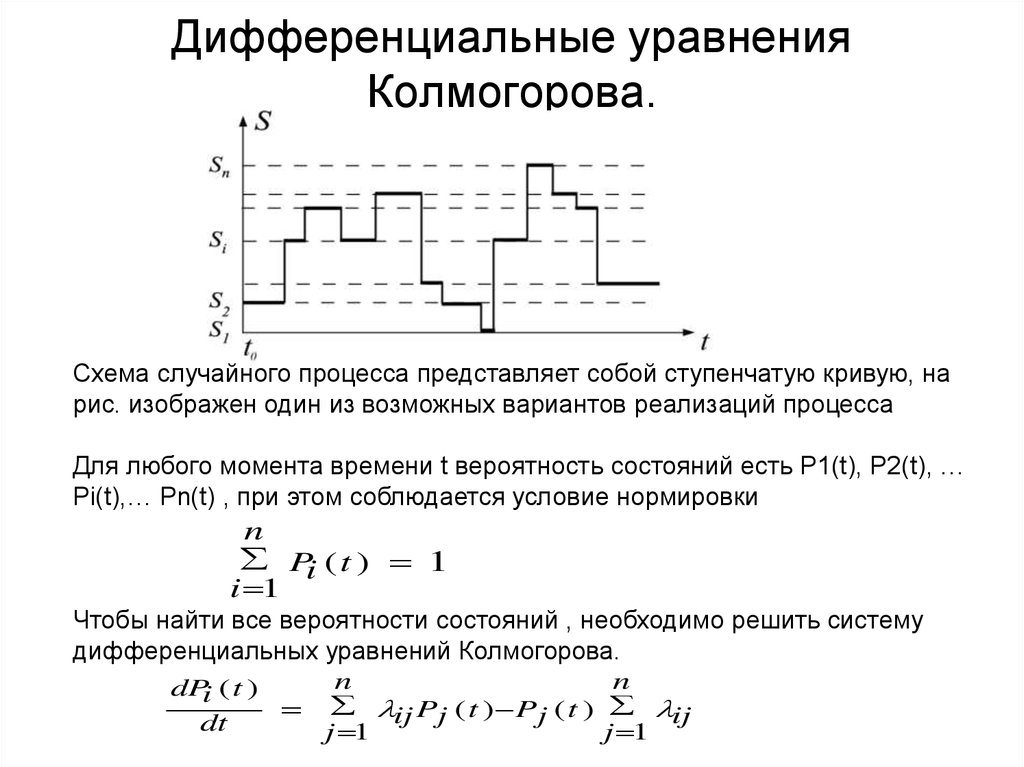
2. Дифференциальные уравнения Колмогорова.
Схема случайного процесса представляет собой ступенчатую кривую, нарис. изображен один из возможных вариантов реализаций процесса
Для любого момента времени t вероятность состояний есть P1(t), P2(t), …
Pi(t),… Pn(t) , при этом соблюдается условие нормировки
n
Pi ( t ) 1
i 1
Чтобы найти все вероятности состояний , необходимо решить систему
дифференциальных уравнений Колмогорова.
n
n
dPi ( t )
ij Pj ( t ) Pj ( t ) ij
dt
j 1
j 1
3. Система дифференциальных уравнений А.Н. Колмогорова
dPi ( t ) N ( t ) ( t ) Naij
a ji P j ( t )
Pi
j 1
j 1
dt
(1)
Для однородных систем система уравнений (1) превращается
в систему дифференциальных уравнений с постоянными
коэффициентами (2), при aij ( t ) aij const
N
dPi ( t ) N
aij Pi ( t ) a ji P j ( t )
dt
j 1
j 1
(2)
dPi ( t ) 0
При tlim
система дифференциальных
dt
уравнений (2) вырождается в систему алгебраических
уравнений (3)
N
N
aij Pi aij P j 0
j 1
j 1
(3)
4. Правила составления системы дифференциальных уравнений
1.2.
3.
4.
Производная
вероятности пребывания системы в состоянии
ei равна алгебраической сумме, число слагаемых которой равно
числу ребер на графе состояний, соединяющих ei состояние с
другими состояниями.
Если ребро направлено в состояние ei, то слагаемое берется со
знаком «плюс»; если направлено из состояния ei – со знаком
«минус».
Каждое слагаемое равно произведению вероятности того
состояния, из которого направлено ребро, на интенсивность
потока событий, переводящего систему по данному
направлению.
Число отрицательных слагаемых равно числу ребер
направленных из состояния ei , число положительных – числу
ребер, направленных в состояние ei.
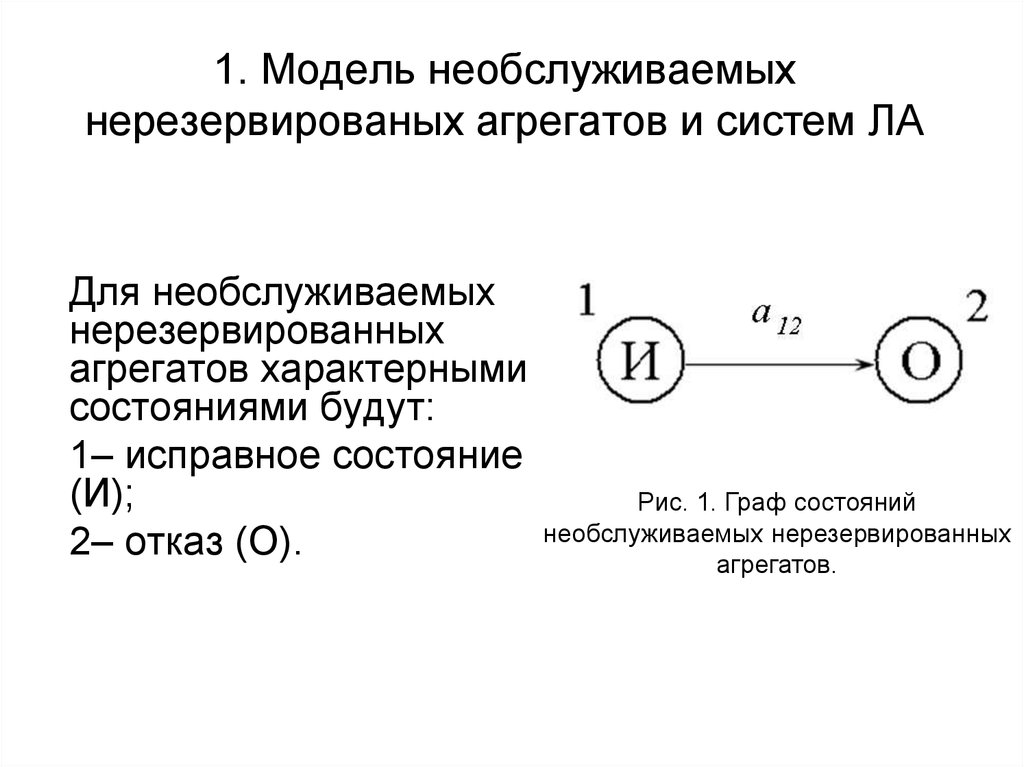
5. 1. Модель необслуживаемых нерезервированых агрегатов и систем ЛА
Для необслуживаемыхнерезервированных
агрегатов характерными
состояниями будут:
1– исправное состояние
(И);
2– отказ (О).
Рис. 1. Граф состояний
необслуживаемых нерезервированных
агрегатов.
6.
Поведение агрегатов описывается системойдифференциальных уравнений:
dP1( t )
a12 P1( t ) где a12 - интенсивность
dt
отказов необслуживаемого агрегата
dP2 ( t )
a12 P1( t )
dt
От системы дифференциальных уравнений перейдем к
системе алгебраических уравнений
SP1( s ) P1( 0 ) P1( s )
SP2 ( s ) P2 ( 0 ) P1( s )
7.
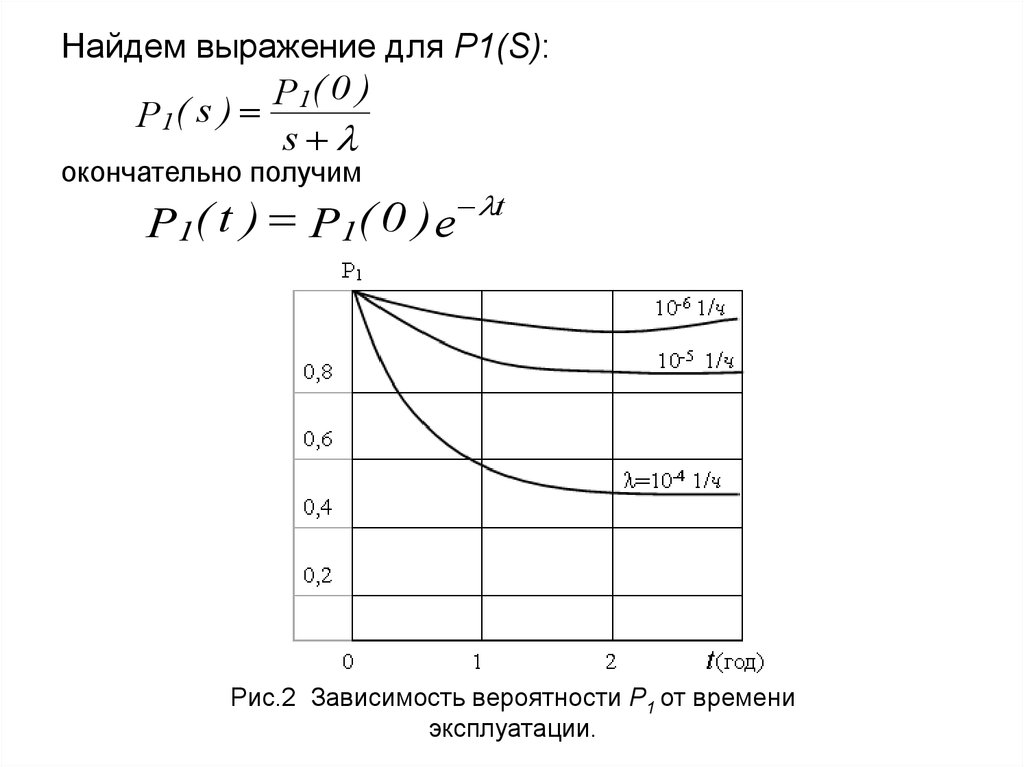
Найдем выражение для P1(S):P
1( 0 )
P1( s )
s
окончательно получим
P1( t ) P1( 0 ) e
t
Рис.2 Зависимость вероятности P1 от времени
эксплуатации.
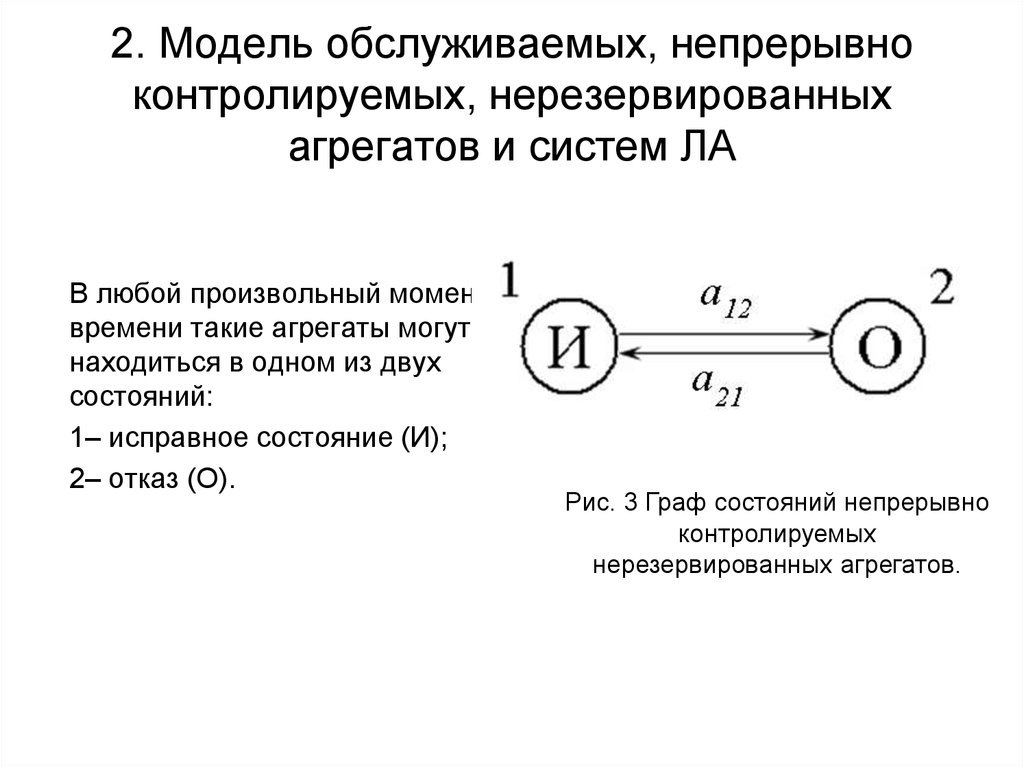
8. 2. Модель обслуживаемых, непрерывно контролируемых, нерезервированных агрегатов и систем ЛА
В любой произвольный моментвремени такие агрегаты могут
находиться в одном из двух
состояний:
1– исправное состояние (И);
2– отказ (О).
Рис. 3 Граф состояний непрерывно
контролируемых
нерезервированных агрегатов.
9.
Система дифференциальных уравнений для этоймодели будет:
dP1( t )
a12 P1( t ) a21 P2 ( t )
dt
dP2 ( t )
a21 P2 ( t ) a12 P1( t )
dt
где
НП
НП
T устр
a12 нп a 21 1
нп
Т устр
- параметр потока отказов непрерывно контролируемых
нерезервированных агрегатов;
- среднее время устранения отказов;
- интенсивность восстановления.
Получить выражение для вероятности P1(t) нахождения
агрегата в состоянии готовности;
a21 a12
НП НП t
a12 a21 t
t
e
e
P1
a12 a21 a12 a21
НП НП
10.
В стационарном режиме эксплуатации (t ) системауравнений выражается в систему алгебраических
уравнений:
a12 P1 a21 P2 0
a12 P1 a21 P2 0
из которой, с учетом условий нормирования P1+P2=1,
получим
P1
НП
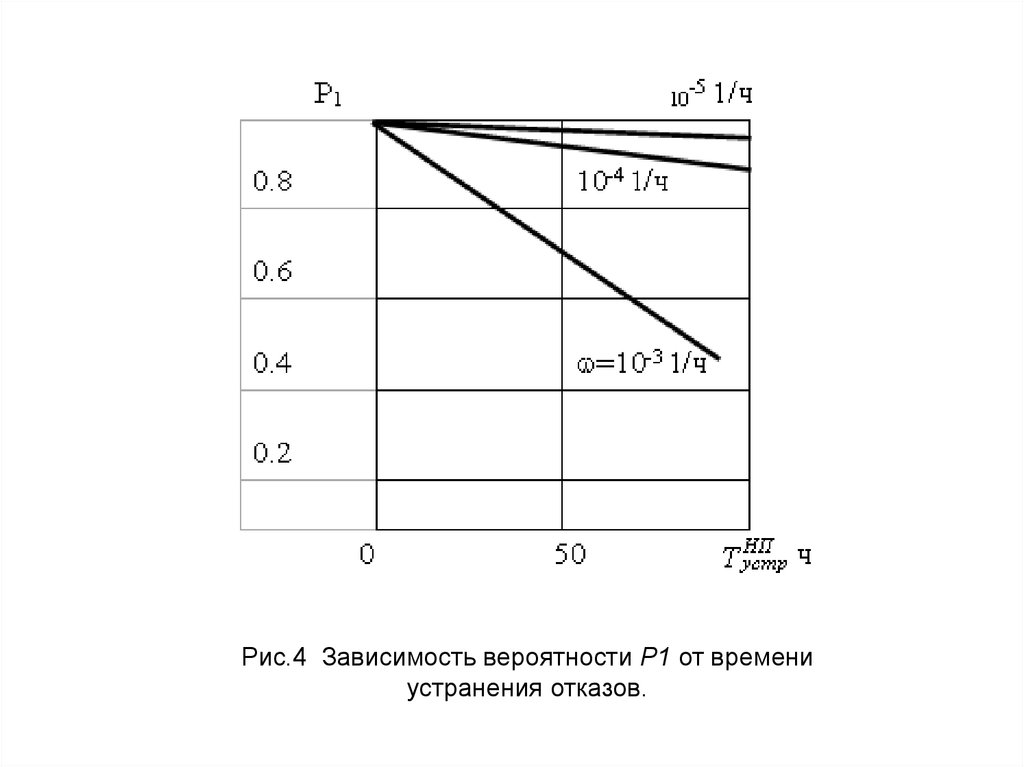
11.
Рис.4 Зависимость вероятности P1 от времениустранения отказов.
12. 3. Модель нерезервированных агрегатов и систем с регламентированным ТО
В любой произвольный моментвремени такие агрегаты могут
находиться в одном из двух
состояний:
1- исправное состояние (И);
2- регламентированное ТО (ТО);
3– скрытый отказ (СО/ТО)
Рис.5 Граф состояний непрерывно
контролируемых
нерезервированных агрегатов.
13.
Система дифференциальных уравнений для этоймодели будет:
dP1( t )
a12 a13 P1( t ) a21 P2 ( t )
dt
dP2 ( t )
a12 P1( t ) a21 P2 ( t ) a32 P3 ( t )
dt
dP3 ( t )
a13 P1( t ) a32 P3 ( t )
dt
a12 ТО
a
где
= τ ТО
1
21
ТО
1
a13 МТО
a
32
МТО ТО
1
МТО
1 1
- параметр потока отказов нерезервированных агрегатов с РТО,
ТО - продолжительность РТО, в ходе которого устраняются все отказы и
выполняются профилактические работы и проверки,
МТО - периодичность ТО.
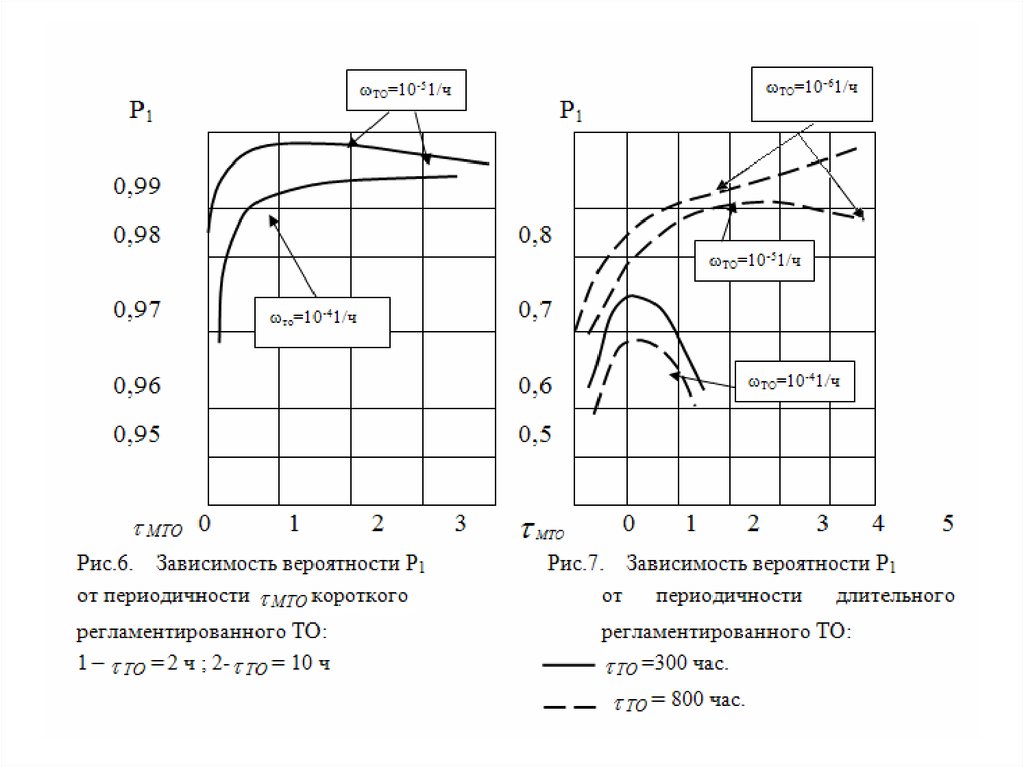
14.
Получим следующие выражения для P1, P2 и P3:ТО
TO MTO
ТО TO МТО e
P1
МТО
P2
1 TO MTO TO TO
P3
MTO
e
ТО МТО
TO ТО МТО e
MTO
ТО МТО 1
ТО
ТО МТО
ТО ТО МТО e
МТО
1
TO МТО
1
15.
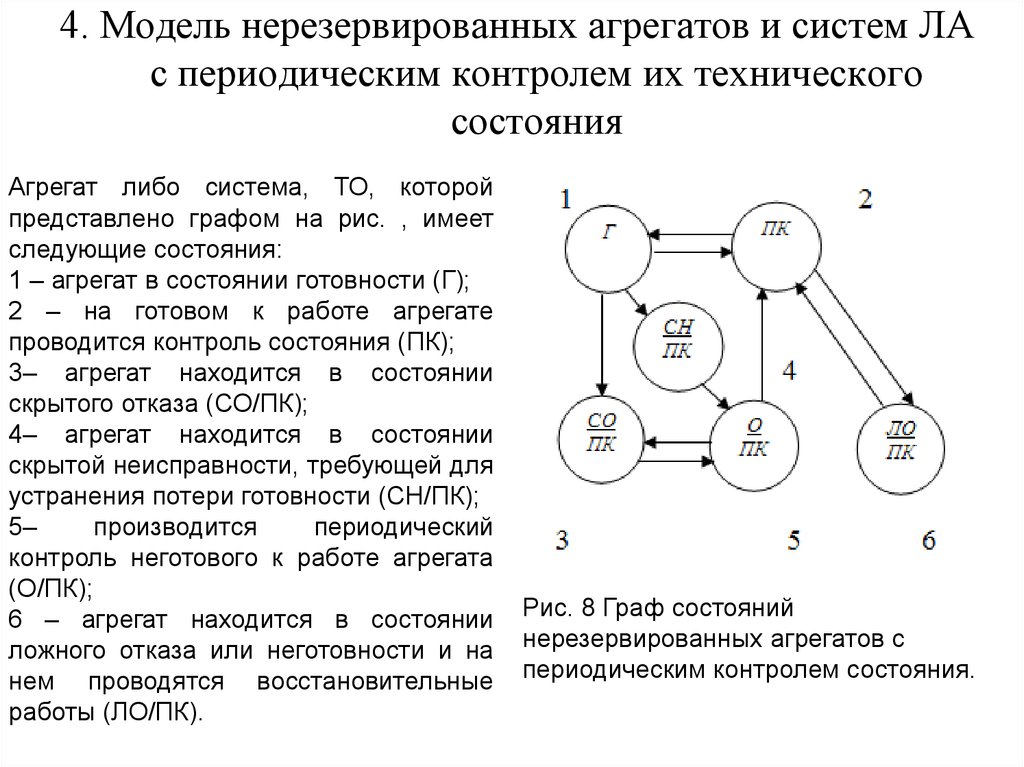
16. 4. Модель нерезервированных агрегатов и систем ЛА с периодическим контролем их технического состояния
Агрегат либо система, ТО, которойпредставлено графом на рис. , имеет
следующие состояния:
1 – агрегат в состоянии готовности (Г);
2 – на готовом к работе агрегате
проводится контроль состояния (ПК);
3– агрегат находится в состоянии
скрытого отказа (СО/ПК);
4– агрегат находится в состоянии
скрытой неисправности, требующей для
устранения потери готовности (СН/ПК);
5–
производится
периодический
контроль неготового к работе агрегата
(О/ПК);
6 – агрегат находится в состоянии
ложного отказа или неготовности и на
нем проводятся восстановительные
работы (ЛО/ПК).
Рис. 8 Граф состояний
нерезервированных агрегатов с
периодическим контролем состояния.
17.
В рассматриваемой модели ТО возможны следующиепереходы:
1-2 – перевод из состояния готовности на периодический контроль;
1-3 – отказ агрегата;
1-4 – неисправность;
2-1 – перевод агрегата после контроля в состояние готовности;
2-6 – ложный отказ;
3-5 – перевод отказавшего агрегата на контроль;
4-5 – перевод неисправного агрегата на контроль;
5-2 – перевод агрегата на подтверждающий контроль
5-3 – переход в состояние скрытого отказа из-за ложного пропуска
отказа;
6-2 – перевод агрегата на подтверждающий контроль.
18.
Система дифференциальных уравнений для рассматриваемого графасостояний (рис.8) имеет следующий вид
dP1 t
a12 a13 a14 P1 t a21 P2 t
dt
dP2 t
a12 P1 t a21 a26 P2 t a52 P5 t a62 P6 t
dt
dP3
a13 P1 t a35 P3 t a53 P5 t
dt
dP4 t
a14 P1 t a45 P4 t
dt
dP5 t
a35 P3 t a45 P4 t a52 a53 P5 t
dt
dP6 t
a26 P2 t a62 P6 t
dt
19.
Для исследования стационарного режима ТО ЛА необходимоперейти от системы диф. уравнений к системе алгебраических
уравнений:
a12 a13 a14 P1 a 21 P 2 0
a12 P1 a21 a26 P2 a52 P5 a62 P6 0
a13 P1 a35 P3 a53 P5 0
a24 P1 a45 P4 0
a35 P3 a45 P4 a52 a53 P5 0
a26 P2 a62 P6 0
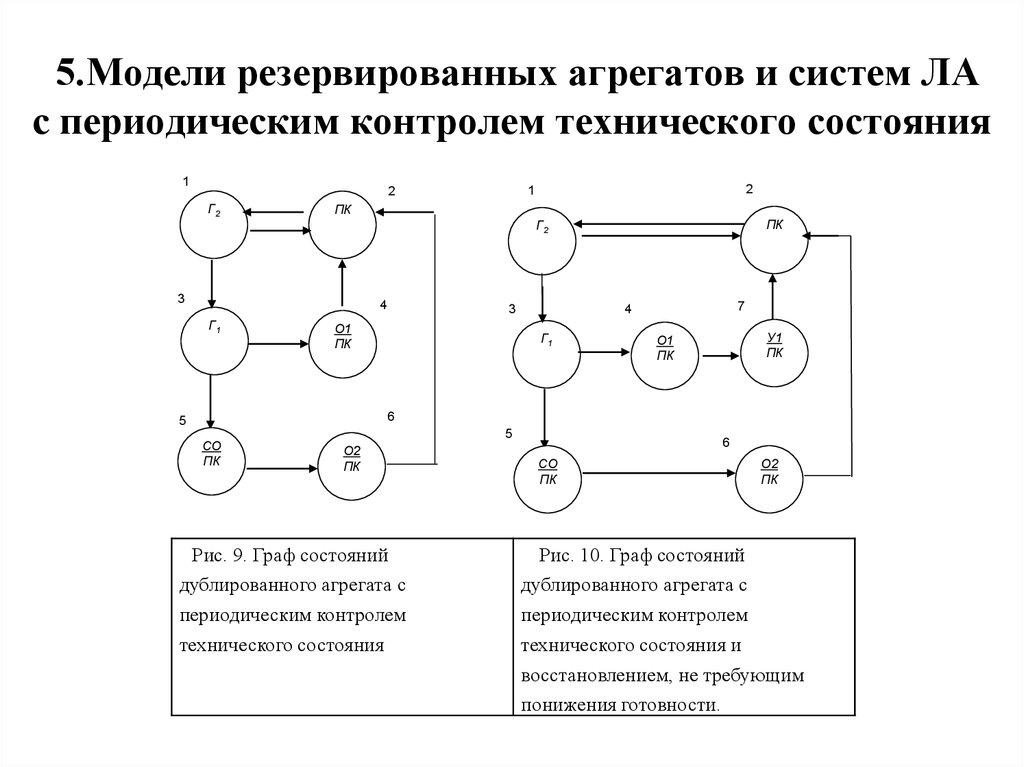
20. 5.Модели резервированных агрегатов и систем ЛА с периодическим контролем технического состояния
12
1
2
Г2
ПК
ПК
Г2
3
4
Г1
3
О1
ПК
7
4
Г1
У1
ПК
О1
ПК
6
5
СО
ПК
5
О2
ПК
Рис. 9. Граф состояний
дублированного агрегата с
периодическим контролем
технического состояния
6
СО
ПК
О2
ПК
Рис. 10. Граф состояний
дублированного агрегата с
периодическим контролем
технического состояния и
восстановлением, не требующим
понижения готовности.
21. Состояния графа рис.9 приведены ниже:
• 1 – два канала (основной и резервный) находятся в готовности (Г2);• 2 - проводится периодический контроль на агрегате с двумя
работоспособными каналами (ПК);
• 3– агрегат находится в готовности с одним работоспособным каналом
(Г1)
• 4– проводится контроль работоспособности (периодический) на
агрегате с одним работоспособным каналом и устранение отказа
(01/ПК);
• 5– скрытый отказ агрегата (отказ и второго канала) (СО/ПК);
• 6 – проводится периодический контроль неработоспособного агрегата
(с двумя отказавшими каналами) и устранение отказов;
22. Возможные переходы дублированных агрегатов с периодическим контролем технического состояния:
• 1-2 – перевод агрегата с обоими работоспособными каналамина контроль;
• 1-3 – отказ одного канала;
• 2-1 – перевод агрегата после контроля в состояние готовности;
• 3-4 – перевод агрегата с одним отказавшим каналом на
контроль;
• 3-5 – отказ второго канала агрегата;
• 4-2 – перевод агрегата на подтверждающий контроль после
устранения отказа;
• 5-6 – перевод агрегата с двумя отказавшими каналами на
контроль;
• 6-2 – перевод агрегата на подтверждающий контроль после
устранения отказов.
23.
Система дифференциальных уравнений дляориентированного графа рис.9 имеет вид:
dP1 t
a12 a13 P1 t a21 P2 t
dt
dP2 t
a12 P1 t a21 P2 t a42 P4 t a62 P6 t
dt
dP3 t
a13 P1 t a34 a35 P3 t
dt
dP4 t
a34 P3 t a42 P4 t
dt
dP5 t
a35 P3 t a56 P5 t
dt
dP6 t
a56 P5 t a62 P6 t
dt
24. Перейдя к системе алгебраических уравнений, найдем:
a12 a13 P1 a21 P2 0a12 P1 a21 P2 a42 P4 a62 P6 0
a13 P1 a34 a35 P3 0
a35 P3 a56 P5 0
a34 P3 a42 P4 0
a56 P5 a62 P6 0
6
Pi 1
i 1
25. Полумарковские процессы эксплуатации
Случайный процесс, при котором переходы междусостояниями являются марковскими, а время нахождения в
любом из состояний описывается произвольной функцией
распределения (кроме экспоненциальной), называют
полумарковским процессом.
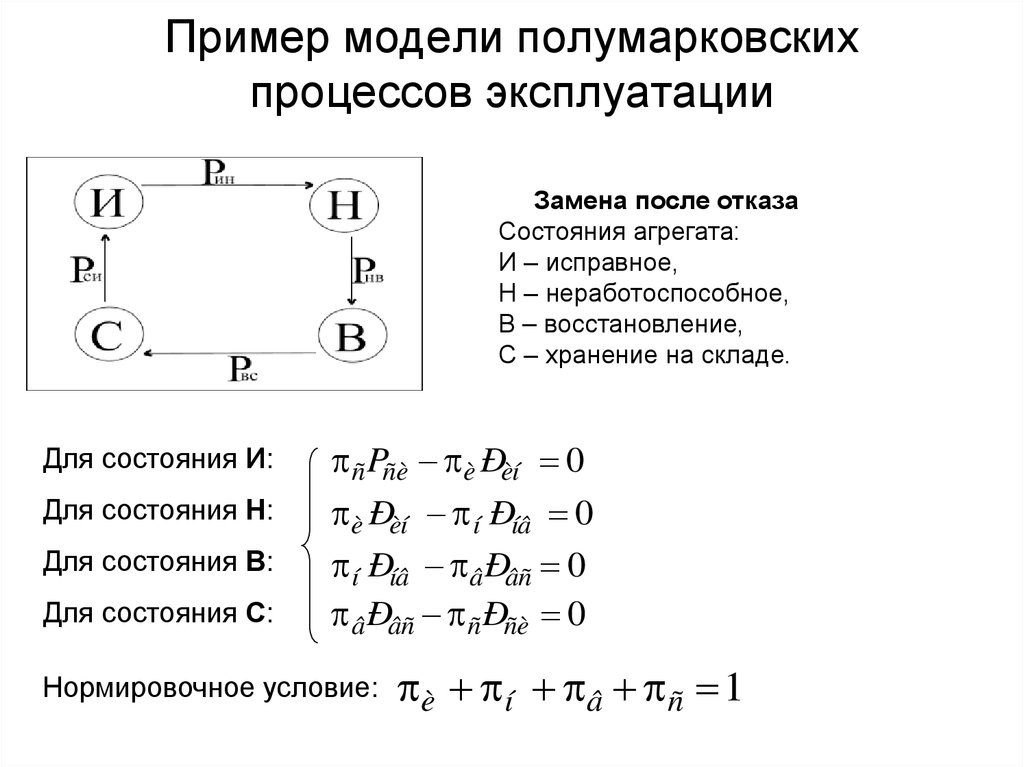
26. Пример модели полумарковских процессов эксплуатации
Замена после отказаСостояния агрегата:
И – исправное,
Н – неработоспособное,
В – восстановление,
С – хранение на складе.
Для состояния И:
Для состояния Н:
Для состояния В:
Для состояния С:
ñ Pñè è Ðèí 0
è Ðèí í Ðíâ 0
í Ðíâ â Ðâñ 0
â Ðâñ ñ Ðñè 0
Нормировочное условие:
è í â ñ 1
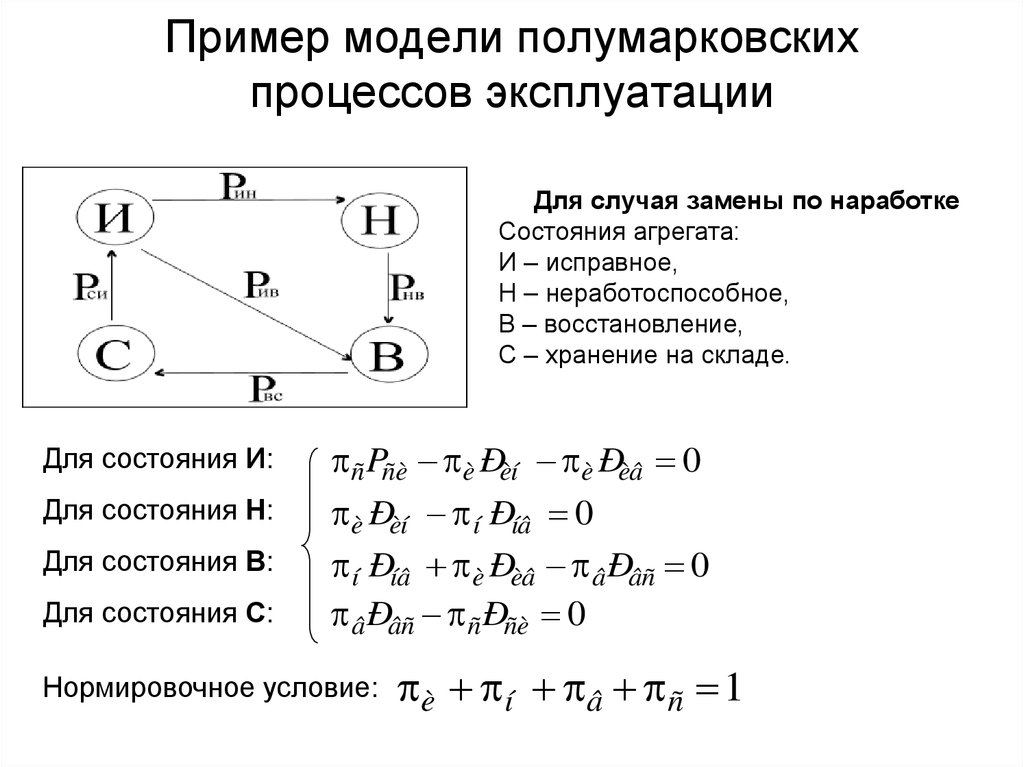
27. Пример модели полумарковских процессов эксплуатации
Для случая замены по наработкеСостояния агрегата:
И – исправное,
Н – неработоспособное,
В – восстановление,
С – хранение на складе.
Для состояния И:
Для состояния Н:
Для состояния В:
Для состояния С:
ñ Pñè è Ðèí è Ðèâ 0
è Ðèí í Ðíâ 0
í Ðíâ è Ðèâ â Ðâñ 0
â Ðâñ ñ Ðñè 0
Нормировочное условие:
è í â ñ 1
28. Пример модели полумарковских процессов эксплуатации
Профилактическая замена принепрерывном контроле параметра
Состояния агрегата:
И – исправное,
З – профилактическая замена,
В – восстановление,
С – хранение на складе.
Для состояния И:
Для состояния С:
Для состояния В:
Для состояния З:
с Рси и Риз 0
в Рвс с Рси 0
з Рзв в Рвс 0
и Риз з Рзв 0
Нормировочное условие:
è c â ç 1
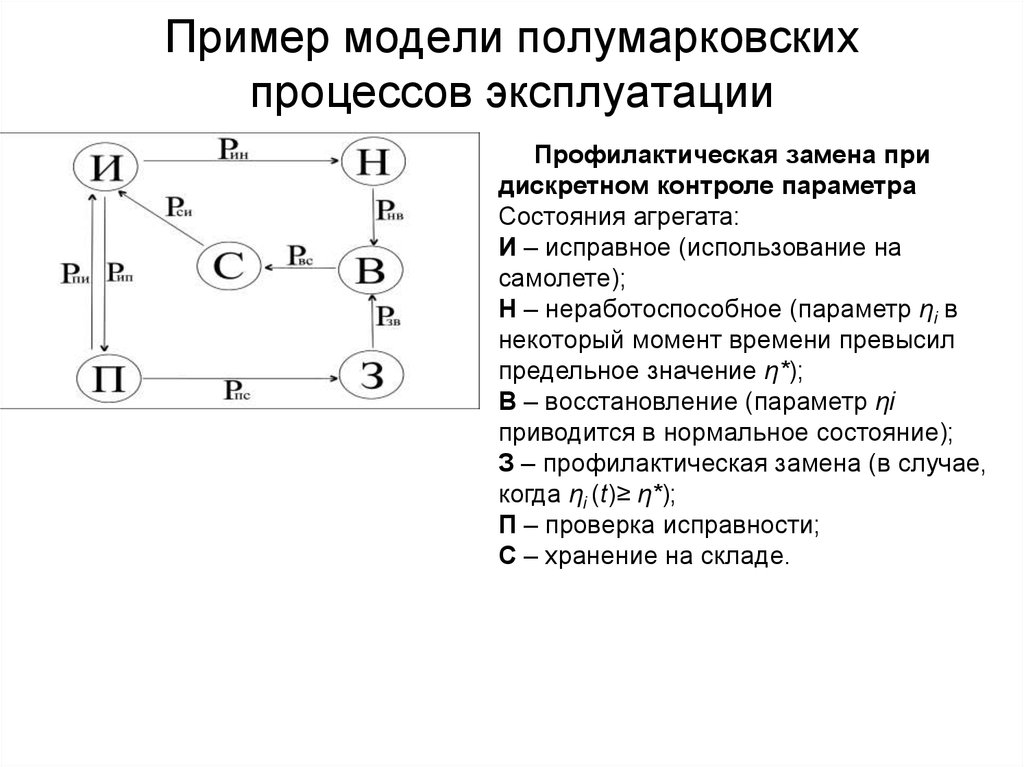
29. Пример модели полумарковских процессов эксплуатации
Профилактическая замена придискретном контроле параметра
Состояния агрегата:
И – исправное (использование на
самолете);
Н – неработоспособное (параметр ηi в
некоторый момент времени превысил
предельное значение η*);
В – восстановление (параметр ηi
приводится в нормальное состояние);
З – профилактическая замена (в случае,
когда ηi (t)≥ η*);
П – проверка исправности;
С – хранение на складе.
30. Пример модели полумарковских процессов эксплуатации
Для состояния И:Для состояния Н:
Для состояния В:
Для состояния С:
Для состояния З:
Для состояния П:
п Рпи с Рси и Рип и Рин 0
и Рин н Рнв 0
н Рнв з Рзв в Рвс 0
в Рвс с Рси 0
п Рпз з Рзв 0
и Рип п Рпи п Рпз 0
Нормировочное условие:
è í â ñ ç ï 1
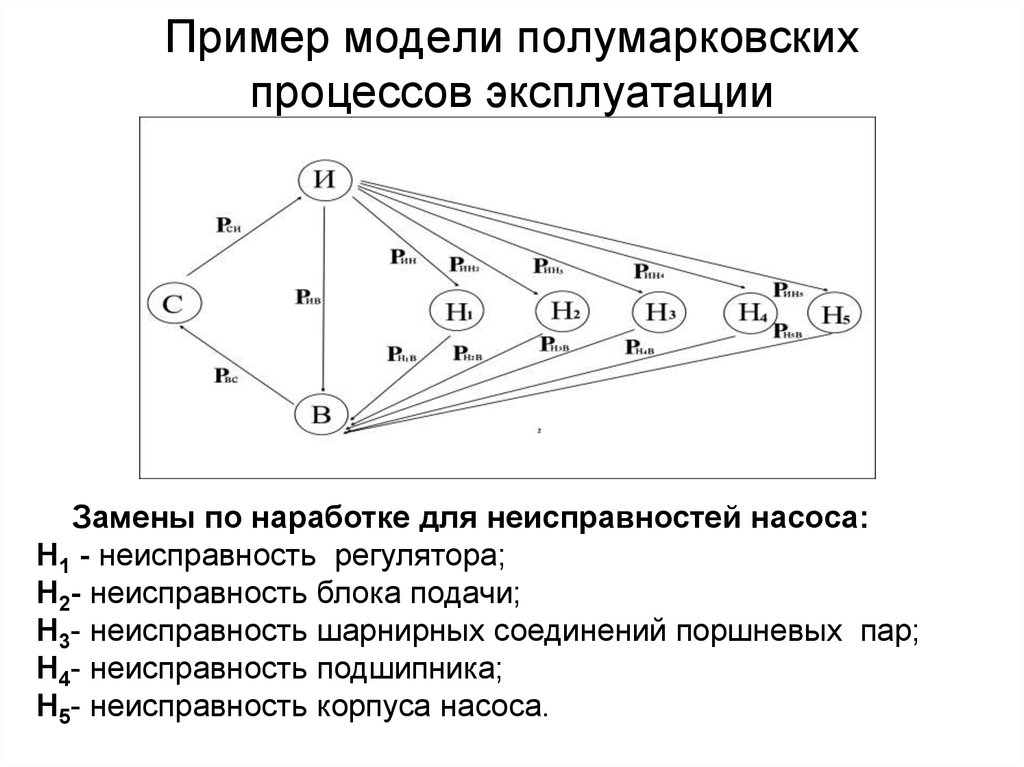
31. Пример модели полумарковских процессов эксплуатации
Замены по наработке для неисправностей насоса:Н1 - неисправность регулятора;
Н2- неисправность блока подачи;
Н3- неисправность шарнирных соединений поршневых пар;
Н4- неисправность подшипника;
Н5- неисправность корпуса насоса.



















 mathematics
mathematics








