Similar presentations:
Дифференциальные уравнения-4
1. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ-4
2. 5. Линейные ДУ I порядка.
Общий вид линейного ДУ I порядка:
A( x) y B( x) y C ( x) 0
А(х), В(х) и С(х)- заданные функции,
причем A( x) 0
3.
A( x) y B( x) y C ( x) 0B( x)
C ( x)
y
y
0
A( x)
A( x)
p (x )
q (x )
y p ( x) y q ( x)
: A( x) 0
4.
Существуетнесколько
(по
существу
равносильных) приёмов решения линейного ДУ.
Рассмотрим метод Иоганна
Бернулли
(Bernoulli)швейцарский
математик
1667-1748.
5.
Метод И.Бернулли основан на простом замечании,что любую величину h (переменную или
постоянную) можно представить в форме
произведения двух сомножителей: h=uv [u=u(x),
v=v(x)], причем один из них можно выбрать по
своему желанию, но отличным от нуля.
6.
tan x uvНапример:
можем взять
u ex
или
u ln x
или
u arcsin x
или
u 1 x2
соответственно этому придется взять
v e x tan x
tan x
v
ln x
tan x
v
arcsin x
v
tan x
1 x2
7. Пример 1. Найти общее решение ДУ:
3y y x
x
q(x)
p (x )
Это линейное ДУ вида
y p( x) y q ( x)
Представим (неизвестное нам!) общее решение
ДУ в виде:
y u v
8.
Найдём производную:y (uv) u v uv
Подставим её в уравнение:
3
u v u v uv x
x
3
v (u u ) u v x
x
(*)
Используем своё право выбора u, взяв его таким,
чтобы выражение в скобках было равно нулю.
9.
3u u 0
x
3
u u
x
du 3
u
dx x
du 3
dx
u
x
du
3
u x dx
10.
ln u 3 ln x CПоскольку в качестве u нам надо взять какое-нибудь
одно из решений ДУ, то положим С=0.
ln u 3 ln x
ln u ln x
u x3
3
11.
Подставляя u x 3 в уравнение (*) и учитывая, что3
u u 0
x
x3 v x
dv 1
2
dx x
dx
dv 2
x
, получим:
u v x
dx
dv x 2
1
v C
x
12.
Общее решение ДУ:1
y u v x C
x
3
или
y u v x 2 Cx3
Ответ.
Общее решение ДУ:
y x Cx
2
3
13. Изложим приём в общем виде:
y p( x) y q ( x)Представим (неизвестное нам!) общее решение
ДУ в виде:
y u v
14.
Найдём производную:y (uv) u v uv
Подставим её в уравнение:
u v u v p( x)uv q( x)
v (u p( x)u ) u v q( x)
(**)
Используем своё право выбора u, взяв его таким,
чтобы выражение в скобках было равно нулю.
15.
u p( x)u 0u p ( x) u
du
p( x) u
dx
du
p( x) dx
u
du
u p( x) dx
16.
ln u ln ep ( x ) dx
C
Поскольку в качестве u нам надо взять какое-нибудь
одно из решений ДУ, то положим С=0.
ln u ln e
p ( x ) dx
u e
p ( x ) dx
A(x )
u A(x)
17.
Подставляя u A(x) в уравнение (**) и учитывая,что
u p( x)u 0
, получим:
u v q(x)
A( x) v q( x)
q ( x)
dv A( x) dx
dv q( x)
dx A( x)
q ( x)
v
dx
A( x)
q ( x)
dv
dx
A( x)
B( x) C
v B( x) C
18.
Общее решение ДУ:y u v A( x) B( x) C
Ответ. Общее решение ДУ: y A( x) B( x) C
19. Пример 2. Найти общее решение ДУ:
2y y tan x cos x
Решение:
p (x )
q(x)
y u v
y (uv) u v uv
u v u v u v tan x cos 2 x
2
v (u u tan x) u v cos x
20.
1) u u tan x 0u u tan x
du
u tan x
dx
du
tan x dx
u
du
u tan x dx
ln u ln cos x C
C 0
ln u ln cos x
u cos x
21.
2) u v cos 2 x2
v cos x cos x
dv
cos x
dx
dv cos x dx
v sin x C
dv cos x dx
3) Общее решение ДУ: y u v (sin x C ) cos x
Ответ. Общее решение ДУ:
y (sin x C ) cos x
22. Пример 3. Найти общее решение ДУ:
y2
x2
2 y 1 x e
x
Решение:
y p( x) y q ( x)
Нужно привести к виду
y
2
x2
2 y 1 x e
x
x
y 2x y 1 x e x
p (x )
2
q(x)
x2
23.
y u vy (uv) u v uv
u v u v 2x u v (1 x ) e x
x2
2
v (u 2 x u) u v 1 x e x
2
x2
24.
1) u 2 x u 0u 2 x u
du
2x u
dx
du
2 x dx
u
du
u 2 x dx
ln u x 2 C
C 0
ln u ln e
u e
x2
x2
25.
2) u v 1 x e x2
x2
v e 1 x e x
x2
2
dv
x 1 x2
dx
x2
dv x 1 x 2 dx
2
dv
x
1
x
dx
3
dv
x
x
dx
x2 x4
v
C
2 4
2
4
x
x
x
C
3) Общее решение ДУ: y u v e
2 4
2
Ответ. Общее решение ДУ:
2
4
x
x
x
y e C
2 4
2
26.
Пример 4.Решить задачу Коши:
2
y y x 4
x
Решение:
2
4
y y x
x
p (x )
q(x)
4
, если y(1)=
3
27.
y u vy (uv) u v uv
2
4
u v uv uv x
x
2
v (u u ) u v x 4
x
28.
21) u u 0
x
2
u u
x
du 2
u
dx x
du 2
dx
u
x
du
2
u x dx
ln u 2 ln x C
C 0
ln u ln x
u x
2
2
29.
2) u v x 4v x 2 x 4
dv
2
x
dx
2
dv
x
dx
x3
v C
3
dv x dx
2
3) Общее решение ДУ:
3
x
2
y u v x C
3
30.
Найдем частное решение ДУ:4
Подставим начальные условия y (1)
3
общее решение ДУ и вычислим С:
3
x
2
y x C
3
4 2 13
1 C
3
3
4 1
C
3 3
C 1
в
- общее решение
3
x
2
y x 1
3
или
5
x
y x2
3
частное решение
31. Пример 5. Найти общее решение ДУ:
yy
2
x y
Решение:
Нужно привести к виду
x p ( y ) x q ( y )
Иногда нужно решать линейные ДУ относительно х:
у принимаем за независимую переменную, а х- за
искомую функцию.
32.
yy
x y2
dy
y
dx x y 2
dx x y 2
dy
y
x
x y
y
1
x x y
y
33.
1x x y
y
p( y)
q( y )
x u v
x (uv) u v uv
1
u v u v u v y
y
1
v (u u ) u v y
y
34.
11) u u 0
y
1
u u
y
du 1
u
dy y
du dy
u
y
du
dy
u y
ln u ln y C
C 0
ln u ln y
u y
35.
2) u v ydv dy
v y y
dv
1
dy
v y C
dv dy
3) Общее решение ДУ:
x u v y y C
Ответ. Общее решение ДУ:
x y y C






















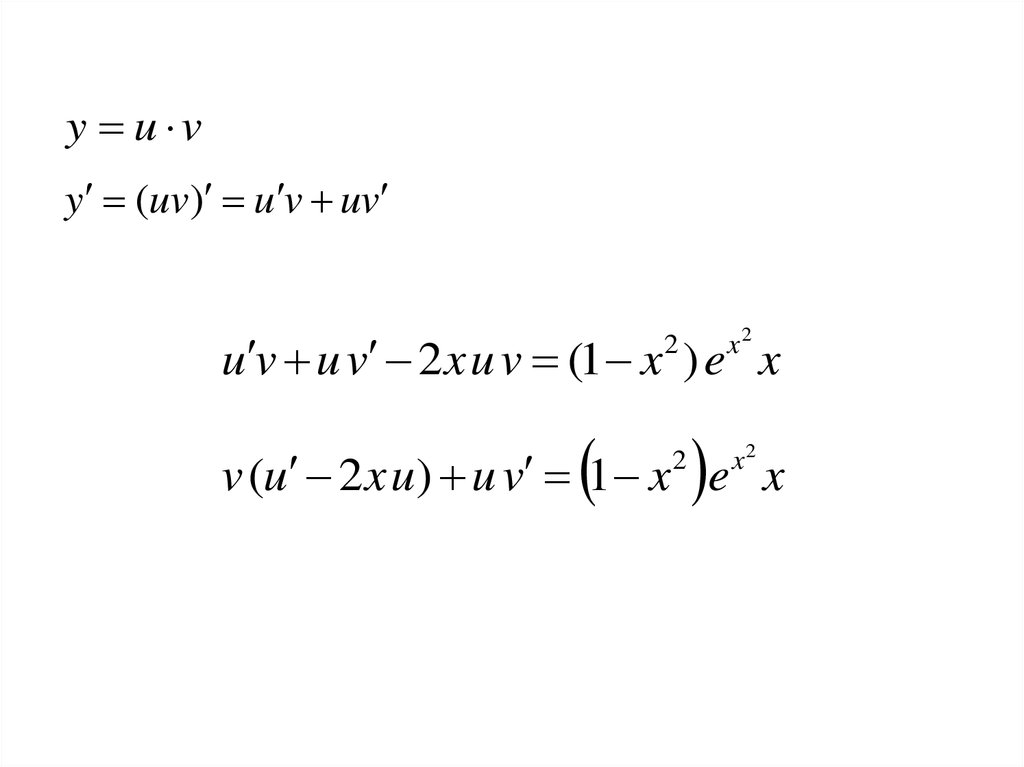








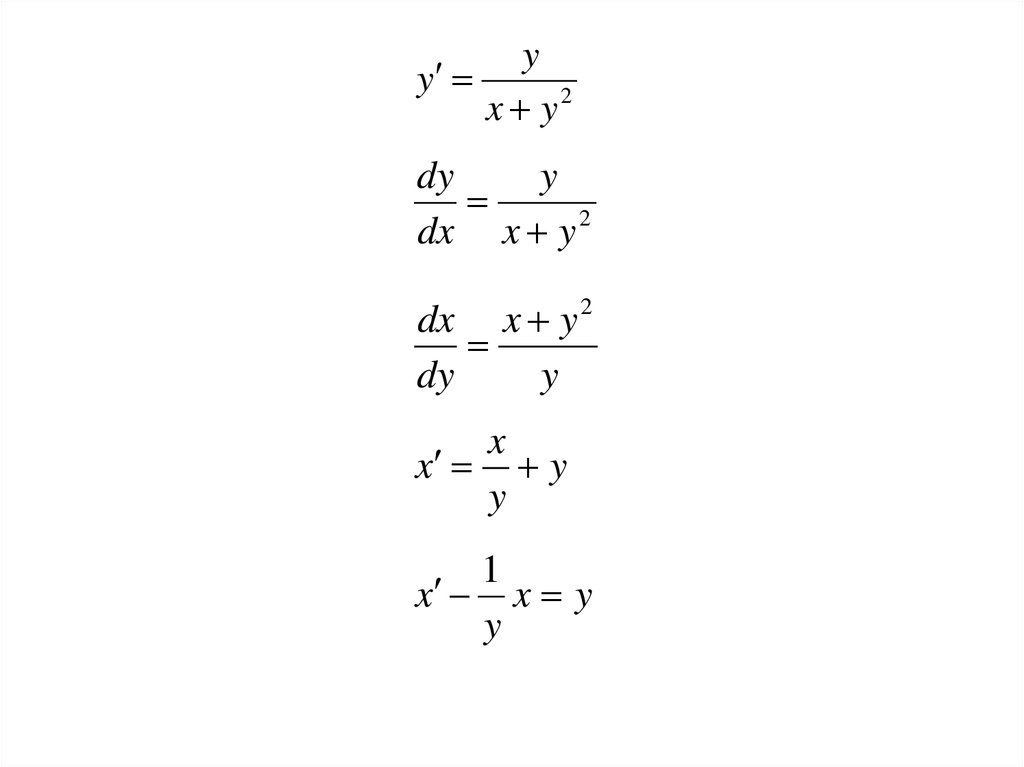
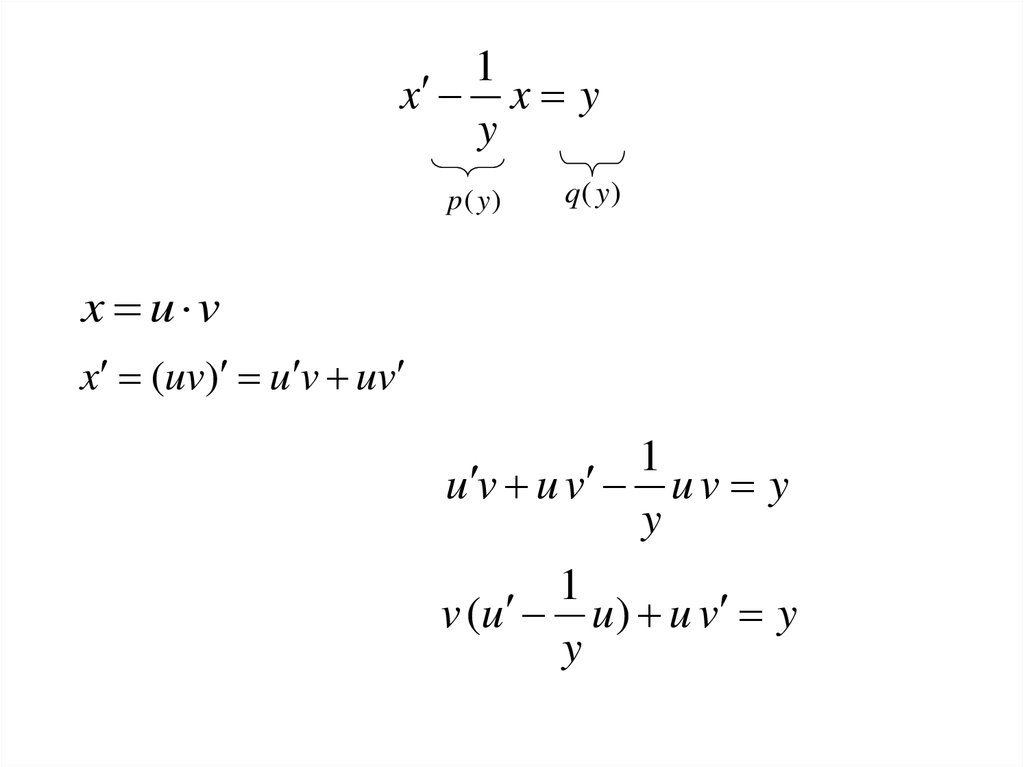
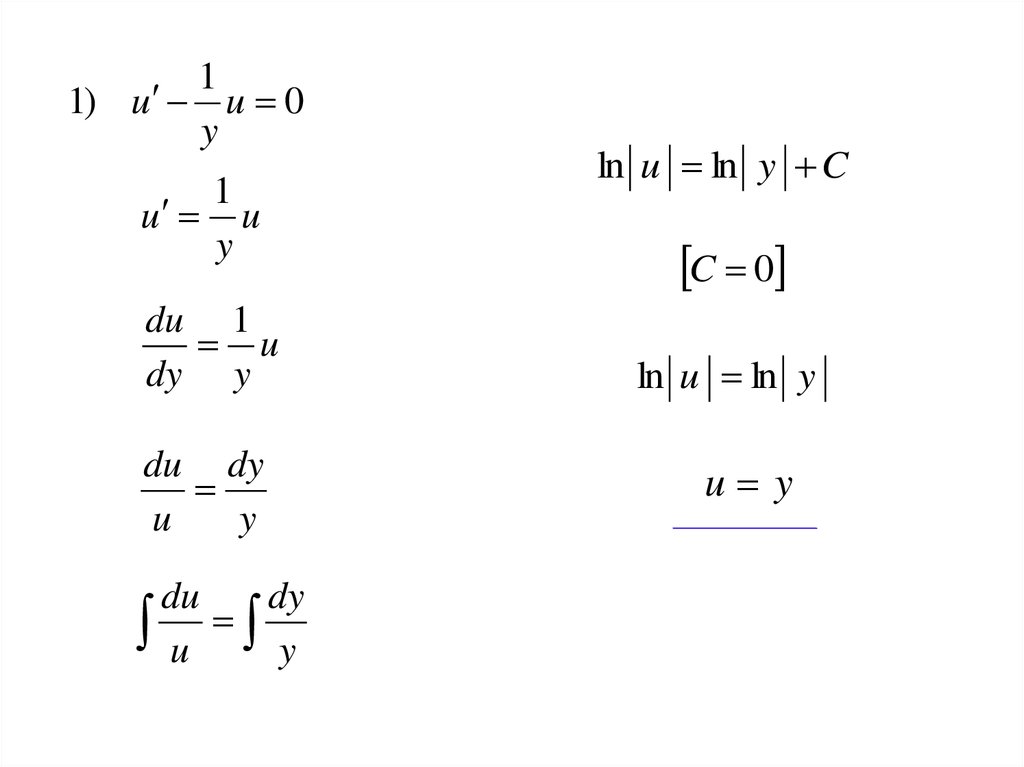

 mathematics
mathematics








