Similar presentations:
Определение дифференциального уравнения, его порядка и его решения
1. Определение дифференциального уравнения, его порядка и его решения
Дифференциальным уравнением называетсяуравнение, связывающее независимую переменную
x, неизвестную функцию y(x) и ее производные.
Порядком дифференциального уравнения
называется порядок старшей производной, входящей
в это уравнение.
Это дифференциальное уравнение третьего порядка.
2. В общем случае дифференциальное уравнение порядка n имеет следующий вид:
Дифференциальное уравнение порядка n,разрешенное относительно старшей производной:
y
(n)
( n 1 )
f ( x,y,y ,y , ,y
)
Решением дифференциального уравнения
называется функция, которая при подстановке в
это уравнение вместе со своими производными
обращает его в тождество.
3. Пример
Дифференциальное уравнение:Его решение: y cos2 x
Проверка:
Подставим функцию y cos2 x в уравнение
y 2sin 2 x,
y 4cos2 x
4cos2 x 4cos2 x 0
0 0
4. Дифференциальные уравнения первого порядка
F( x,y,y ) 0или
y f ( x,y )
Например,
xy x 2e y 3 0
y
y
sin x
x
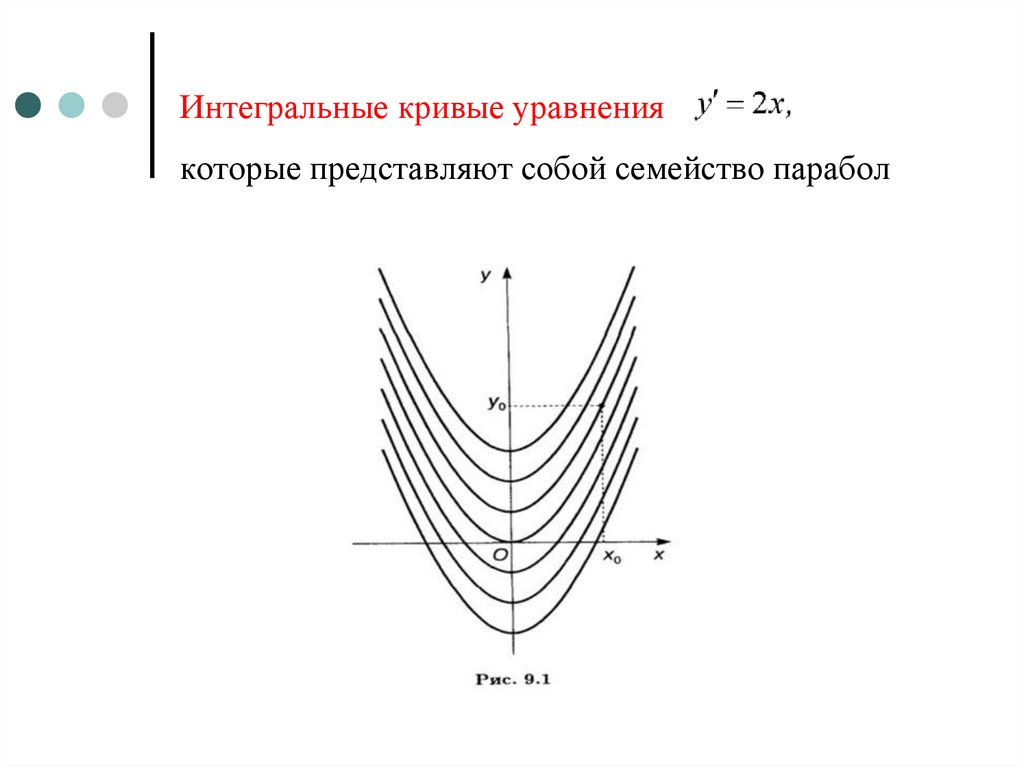
5. График решения дифференциального уравнения называется его интегральной кривой.
Пример.y 2 x,
Мы знаем, что y
dy
, подставим в уравнение:
dx
dy
2 x, умножим обе части уравнения на dx:
dx
dy 2 x dx, проинтегрируем это уравнение:
y x 2 C , где С - произвольная
dy
2
x
dx,
постоянная.
6. Интегральные кривые уравнения
которые представляют собой семейство парабол7.
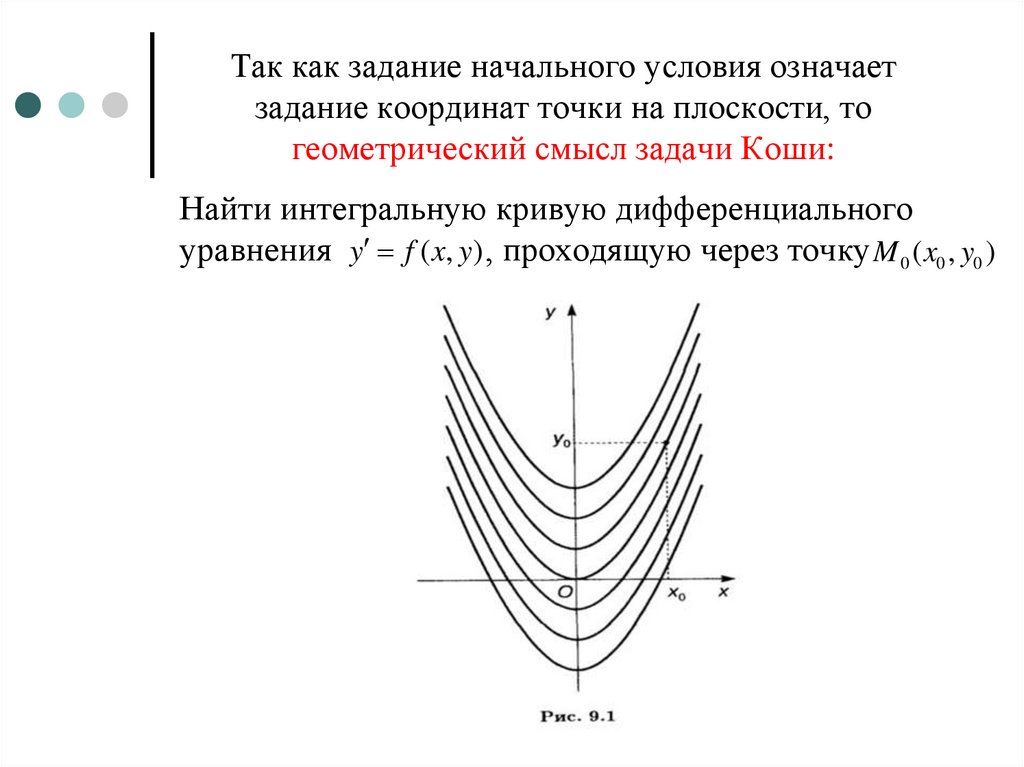
8. Так как задание начального условия означает задание координат точки на плоскости, то геометрический смысл задачи Коши:
Найти интегральную кривую дифференциальногоуравнения y f ( x, y) , проходящую через точку M 0 ( x0 , y0 )
9. Рассмотренные задачи показали, что дифференциальные уравнения первого порядка имеют бесчисленное множество решений.
Эти решения задаются формулой: y ( x,C ) , гдеС - произвольная постоянная. Это - общее решение
дифференциального уравнения первого порядка.
Частное решение - это решение, получающееся из
общего при определенном значении C.
Чтобы из множества решений выделить одно,
задают начальное условие:
y x x0 y0
Начальное условие во многих физических задачах является
математической записью начального состояния процесса.
10. Теорема Коши. Теорема о существовании и единственности решения задачи Коши.
Если в дифференциальном уравнениифункция f ( x, y ) непрерывна в некоторой области
D, содержащей точку
, то существует
решение этого уравнения, удовлетворяющее
начальному условию
.
Если, кроме того, непрерывна и частная
производная f , то это решение единственно.
y
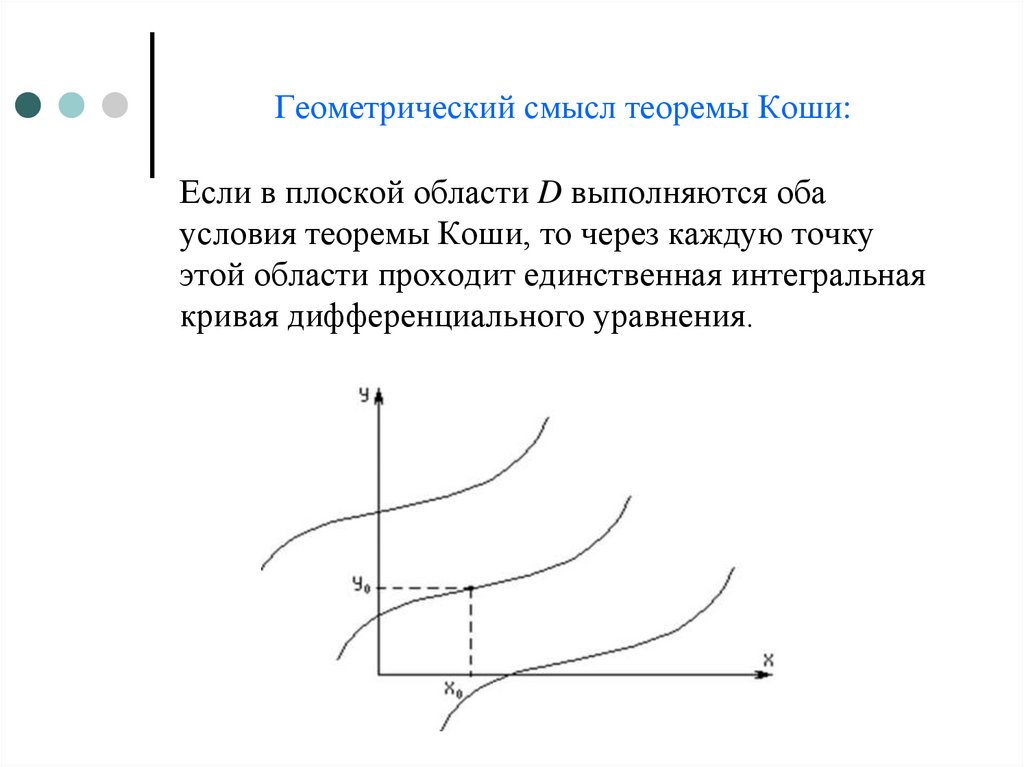
11. Геометрический смысл теоремы Коши:
Если в плоской области D выполняются обаусловия теоремы Коши, то через каждую точку
этой области проходит единственная интегральная
кривая дифференциального уравнения.
12. Общим решением дифференциального уравнения первого порядка (1)
называется функция, зависящая от x и
произвольной постоянной С и удовлетворяющая
следующим двум условиям:
1). Эта функция является решением
дифференциального уравнения (1) при любых
значениях произвольной постоянной C.
2). Из этой функции
можно получить
частное решение y ( x,C0 ), удовлетворяющее
начальному условию
, определив с помощью
этого условия значение произвольной постоянной С.
13. Дифференциальные уравнения с разделяющимися переменными
Уравнением с разделяющимися переменныминазывается уравнение вида
y f ( x) g ( y )
(1)
Или
X ( x )Y( y )dx X 1( x )Y1( y )dy 0
(2)
14. (1) Разделив обе части уравнения (1) на и умножив на dx, будем иметь
ydy
dx
dy
f ( x) g ( y )
dx
(1)
Разделив обе части уравнения (1) на g ( y ) и
умножив на dx, будем иметь
dy
f ( x)dx
g ( y)
dy
g ( y) f ( x)dx C
15.
16. Решить уравнение
y tg 1 x y ady 1
tg x y a
dx
tg 1 xdy ( y a)dx
Разделяем переменные
dy
tg xdx
y a
dy
y a tg xdx
a const
17. Вычисляем интегралы
ln | y a | ln | cos x | ln | C |Используем свойства логарифмов
C
ln | y a | ln
cos x
| y a |
C
cos x
y a
y a
C
cos x , но С - любое число, поэтому
C
cos x
y
C
a
cos x
18.
19. Решить задачу Коши:
y sin x y ln y,y
x
Сначала найдем общее решение.
2
e
20. Для этого подставим , умножим уравнение
Для этого подставим ydy
, умножим уравнение
dx
на dx и разделим переменные:
dy
dx
y ln y sin x
dy
dx
y ln y sin x
x
ln | ln y | ln | tg | ln | C |
2
x
ln y C tg
2
x
ln | ln y | ln | C tg |
2
y e
C tg
x
2
21. Вычисление
dxsin x
1 способ - универсальная тригонометрическая
x
подстановка tg t
2
x
2dt
arctg t , x 2arctg t , dx
2
1 t2 ,
Тогда
sin x
2tg
1 tg
Значит
x
2
или
2 x
sin x
2t
1 t2
2
2dt
2
dx
dt
x
1
t
ln
|
t
|
C
ln
|tg
| C
sin x 2t t
2
1 t2
dx
x
ln
|
tg
| C
sin x
2
22. Второй способ вычисления
xd
dx
dx
2
sin x x x x x
2sin cos
sin cos
2
2
2
2
x
d
2
x
x
cos 2
d (tg )
2
2 ln | tg x | C
x
x
2
sin
tg
2
2
x
cos
2
23. Продолжим решение задачи Коши.
Общее решение нашлиy e
Есть начальное условие
y
e e
C tg
x
C tg
x
2
e
2
y e
4
tg
x
2
e eC C 1
y e
tg
x
2
- частное решение
или решение задачи Коши
24. Однородные дифференциальные уравнения первого порядка
дифференциальное уравнение видаy
y f
x
называется однородным дифференциальным
уравнением первого порядка.
25. Примеры.
yy f
x
Примеры.
2
1.
x
y
y sin 5 2
x
y
2.
xy y ln
3.
y
x y
x y
y
x
26. Как решаются однородные дифференциальные уравнения первого порядка?
При помощи подстановкиy
u или y ux ,
x
где u – новая неизвестная функция.
Получим уравнение с разделяющимися
переменными.
Можно также применить подстановку x uy.
27. Пример. Найти общее решение однородного дифференциального уравнения первого порядка.
yx
y e
Полагаем
y
x
, тогда y ux и y u x u
u x u eu u
u x eu
28. Получили уравнение с разделяющимися переменными
Подставим udu
,
dx
e u du
dx
x
u
e
du
dx
x
e u ln| x | C
e
y
x
ln| x | C
- общий интеграл
29.
30. Решение
yx y
x y
Разделим числитель и знаменатель на x
y
x
y
y
1
x
1
,
y ux ,
u x u
- однородное
y u x u ,
1 u
1 u
1 u2
u x
1 u
1 u
dx
du
1 u2
x
1 u
dx
du
x
1 u2
31.
Продолжение решения1 u
dx
du
1 u2
x
u
dx
1
du
1 u 2 1 u 2 x
du
1 d (1 u 2 ) dx
1 u 2 2 1 u 2 x
1
arctg u ln(1 u 2 ) ln | x | ln | C |
2
y
arctg ln C x 2 y 2
x
32. Линейные дифференциальные уравнения первого порядка. Уравнение Бернулли
Линейное уравнение первого порядка – этоуравнение вида
y P( x) y Q( x)
(или уравнение, которое можно привести к такому виду)
Примеры:
y 2 xy xe
x2
xy 2 y 2 x 4
33. Метод Бернулли решения линейного уравнения
Применяем подстановку:y uv
где u и v – новые неизвестные функции от x .
Подставим в данное уравнение y P ( x) y Q( x)
y uv, y u v uv
Получим
Пусть
u P( x)u v v u Q( x)
u P ( x)u 0, тогда
v u Q (x )
34. Пример
Найти общее решение.u v uv 2 xuv xe
u v u (v 2 xv) xe
1. v 2 xv 0
x2
x2
2.
u v xe
x2
35. Решаем сначала первое уравнение:
1.2.
dv
2 xv
dx
dv
2 xdx
v
dv
v 2 xdx
ln | v | x 2 ln | C |
v Ce
x2
, пусть C 1
v e
x2
u v xe
u e
x2
x2
xe
x2
u x
x2
u C
2
Так как y uv ,
x2
x2
y C e
2
36. Решить задачу Коши.
y y tg x sec x, y x 0 037. Решение
Найдем сначала общее решениеy y tg x sec x
y uv, y u v uv
u v uv uvtg x
u v u (v vtg x)
1.
v vtg x 0
dv
v tg xdx
1
v
cos x
1
cos x
1
cos x
2.
u v
1
cos x
u 1
u x C
x C
- общее решение
y
cos x
38. Найдем частное решение (решение задачи Коши)
- общее решение, y x 0 0 - начальноеусловие.
0 C
0
C 0
cos0
x
y
- частное решение или
cos x
решение задачи Коши.
39. Уравнение Бернулли
1.y P( x) y Q( x) y
0 и 1
Пример
y
4
y x y
x
Ответ:
4 1
y x ln | x | C
2
2
40.
41. Понятие об особом решении
Рассмотрим уравнение y 3 3 y 2dy
33 y2
dx
dy
3
y
2
3dx
2
3
y dy 3 dx
1
3
y x C
y ( x C )3 - общее решение
42.
43. При разделении переменных исключили случай
y 0Проверим дополнительно, является ли
решением.
Проверка.
Левая часть: y 0. Правая часть: 3 y 2 3 02 0
является решением уравнения.
- особое решение.
Через точки особого решения проходят два
решения.
44. Свойства особого решения.
1. Как и всякое решение оно удовлетворяетдифференциальному уравнению.
2. Рассмотрим условие теоремы Коши для уравнения
y f ( x, y) в точках особого решения.
, f ( x, y ) 3 3 y 2
1
df
2 3
2
3 y
имеет точки разрыва при y 0 .
3 y
dy
3
df
В точках особого решения dy имеет разрыв, т.е.
нарушается условие единственности теоремы Коши.
45. Особым решением называется такое решение дифференциального уравнение, которое во всех своих точках не удовлетворяет свойству
единственности, т.е.в любой окрестности каждой точки особого
решения существуют по крайней мере две
интегральные кривые, проходящие через эту точку.










































 mathematics
mathematics








