Similar presentations:
Расчет надежности систем с восстановлением
1. НЭКИС
РАСЧЕТ НАДЕЖНОСТИ СИСТЕМ СВОССТАНОВЛЕНИЕМ
1
2.
Восстановление – процесс перевода объекта вработоспособное состояние из неработоспособного состояния.
Восстанавливаемый объект – объект, для которого в
рассматриваемой ситуации проведение восстановления
работоспособного состояния предусмотрено в нормативно –
технической
и
(или)
конструкторской
(проектной)
документации. Применительно к ИС это могут быть дисплей,
блоки питания, множительная техника и т.д..
Невосстанавливаемый объект – объект, для которого в
рассматриваемой ситуации проведение восстановления
работоспособного состояния не предусмотрено в нормативно
– технической и (или) конструкторской (проектной)
документации. Применительно к ИС это могут быть все
микросхемы,
материнские
платы,
сетевые
карты,
видеоадаптеры, накопители на жестких дисках и т.д.
2
3. Показатели надежности восстанавливаемых объектов
Средняя наработка на отказ объекта (наработка на отказ)определяется:
n
T
t
i 1
i
n(t )
,
где ti наработка между
отказов за время
t.
(
i
-м отказами, суммарное число
3
4. Время восстановления. Пояснение.
Время восстановления – это время, затраченное наобнаружение, поиск причины отказа и устранения
последствий отказа. Опыт показывает, что в сложных
системах поиск отказавшего элемента 70-90% времени
восстановления приходится на поиск отказавшего элемента.
4
5.
Среднее время восстановления - это математическоеожидание времени восстановления работоспособного
состояния объекта после отказа:
1 n
Tв i ,
n i 1
где
- число восстановлений, равное числу отказов; время, затраченное на восстановление (обнаружение, поиск
причины и устранение отказа), в часах.
1 n
Tв i ,
n i 1
5
6.
В случае, если интенсивность восстановлений постоянна,то есть (t ) const
, вероятность восстановления за
заданное время подчиняется экспоненциальному закону.
Используя свойство этого распределения можно записать:
1
TB .
Для
восстанавливаемого
объекта
вводится
характеристика надежности–коэффициент готовности:
n
KГ
t
i 1
n
i
n
t t
i 1
i
i 1
,
B
i
6
7.
Если известно время жизни, тоT
KГ 0 ,
T0 TB
T0 , TB
-
среднее время между отказами (математическое
ожидание) и среднее время восстановления. Для
показательного
распределения
времен
отказов
и
восстановлений можно записать:
1
T0 ,
1
TB ,
где , - интенсивности отказов и восстановлений.
7
8.
TKГ 0
,
T0 TB
Коэффициент оперативной готовности
K ОГ K Г P (t P ),
где K Г
- коэффициент готовности; вероятность
безотказной работы объекта в течение времени,
необходимого
для
безотказного
использования
по
назначению.
8
9. Марковский случайный процесс с дискретными состояниями и непрерывным временем
Сложные, в большинстве случаев, ИС являютсявосстанавливаемыми системами. Для математического
описания процессов функционирования ИС с точки зрения
надежности, развивающихся в форме случайного процесса,
может быть с успехом применен математический аппарат,
разработанный в теории вероятностей для так называемых
марковских случайных процессов. Поясним понятие
марковского случайного процесса.
9
10.
Пусть имеется некоторая физическая система S, состояниекоторой меняется с течением времени (под системой можно
понимать что угодно: АСУ, АСУ ТП и т. д.). Например, отказ
любого элемента ИС может произойти в любой момент
времени; окончание ремонта (восстановление) этого
элемента также может произойти в любой момент времени.
10
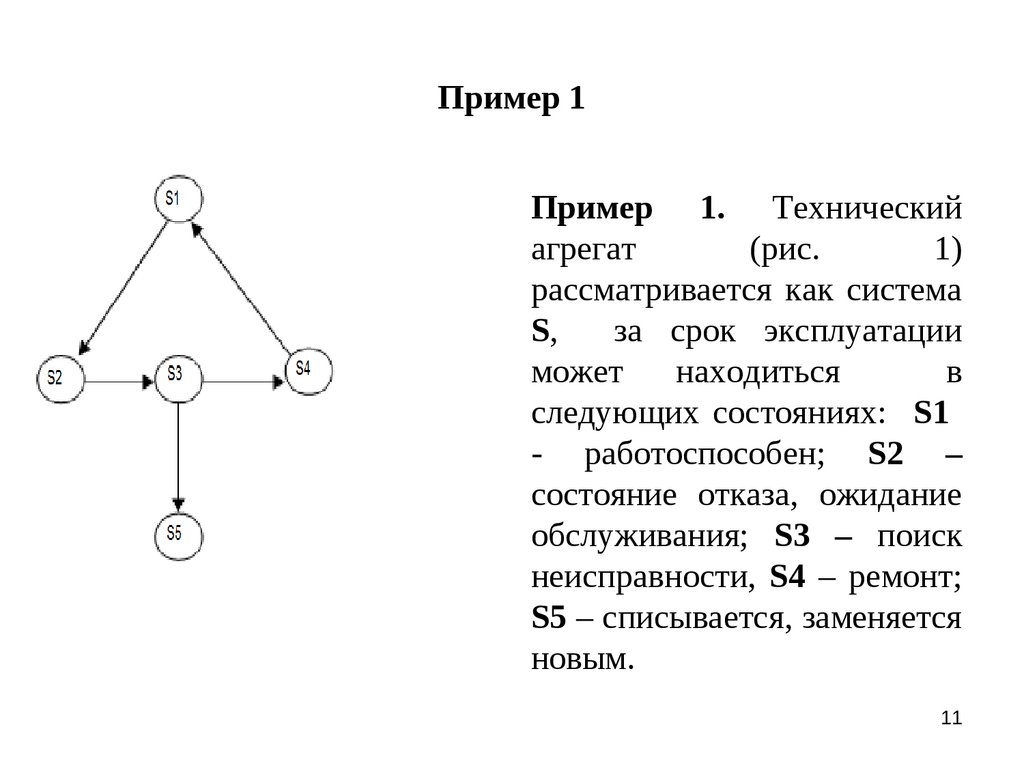
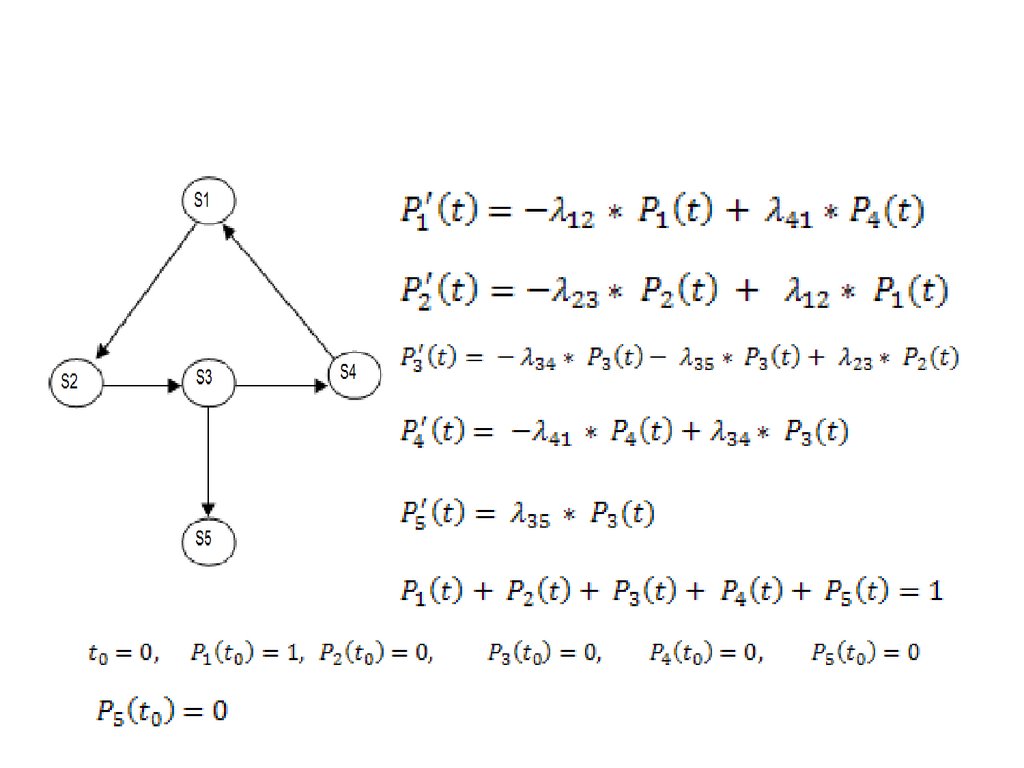
11. Пример 1
Пример 1. Техническийагрегат
(рис.
1)
рассматривается как система
S,
за срок эксплуатации
может
находиться
в
следующих состояниях: S1
- работоспособен; S2 –
состояние отказа, ожидание
обслуживания; S3 – поиск
неисправности, S4 – ремонт;
S5 – списывается, заменяется
новым.
11
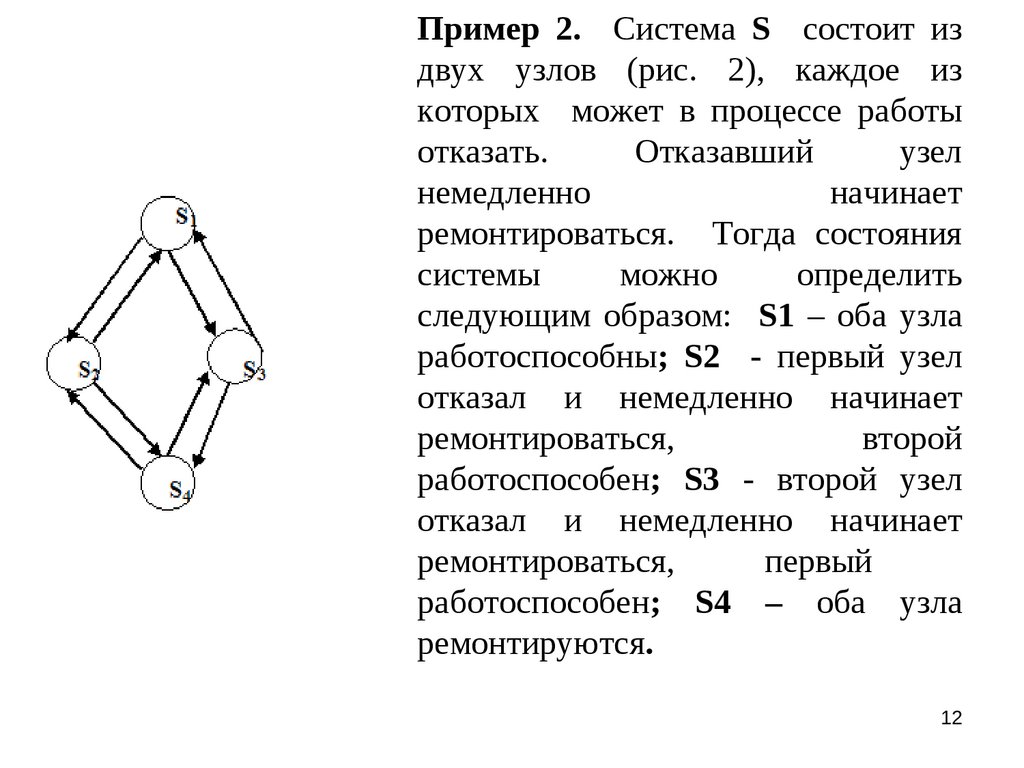
12.
Пример 2. Система S состоит издвух узлов (рис. 2), каждое из
которых может в процессе работы
отказать.
Отказавший
узел
немедленно
начинает
ремонтироваться. Тогда состояния
системы
можно
определить
следующим образом: S1 – оба узла
работоспособны; S2 - первый узел
отказал и немедленно начинает
ремонтироваться,
второй
работоспособен; S3 - второй узел
отказал и немедленно начинает
ремонтироваться,
первый
работоспособен; S4 – оба узла
ремонтируются.
12
13.
Для описания таких процессов в ряде случаев можетбыть с успехом применена схема марковского процесса с
дискретными состояниями и непрерывным временем, который
мы будем для краткости называть непрерывной цепью
Маркова. Случайный процесс, протекающий в системе S,
называется марковским процессом, если он обладает
следующим свойством: для каждого момента времени
вероятность любого состояния системы в будущем зависит
только от ее состояния в настоящем и не зависит от того, когда
и каким образом система пришла в это состояние (т.е. как
развивался процесс в прошлом). Ясно, что в примере 1 и 2 в
первом приближении характеристики работы системы в
будущем (частота отказов, потребность в ремонте) зависят от
состояния устройства в настоящий момент и не зависят от того,
когда и как устройство достигло своего настоящего состояния.
13
14.
Пусть система S в процессе эксплуатации можетнаходиться в состояниях S1, S2, …, Sn. Переход системы S из
состояния в состояние может осуществляться в любой
момент времени.
14
15.
Обозначим Pi (t) - вероятность того, что в моментвремени t система будет находиться в состоянии Si
(i=1, . . .,n). Очевидно, для любого момента t сумма
вероятностей состояний равна единице:
так как события, состоящие в том, что в момент t система
находится в состояниях S1,S2,..,Sn, несовместны и образуют
полную группу.
15
16.
Поставим задачу – определить для любого tвероятности состояний:
p1 (t ), p2 (t ), ... , pn (t ).
16
17.
Для того, чтобы найти эти вероятности, необходимознать характеристики процесса. В случае процесса с
непрерывным временем
нам не придется задавать
определенные, отличные от нуля, переходные вероятности
pi j
; вероятность перехода системы из состояния в
состояние в точно в момент времени t будет равна нулю (т.
к. вероятность любого отдельного значения непрерывной
случайной величины).
17
18.
Пусть система S в момент времени находится всостоянии Si . Рассмотрим элементарный промежуток
времени t , примыкающий к моменту:
0
t
t + t
18
19.
Назовем плотностью вероятности перехода пределотношения вероятности перехода системы за время t из
состояния Si в состояние Sj к длине промежутка t:
i j
lim
t 0
Pij ( t )
t
,
Pij ( –t )вероятность того, что система, находившаяся
где
в момент в состоянии Si за время перейдет из него в
состояние Sj (плотность вероятностей перехода определяется
только для j i).
19
20.
Из формулы следует, что при малом t вероятностьперехода pi j ( t ) равна с (точностью до бесконечно малых
t :
высшего порядков) равна
ij
pi j ( t ) i j t.
20
21.
Если все плотности вероятностей перехода i j независят от
(т. е. от того, в какой момент начинается
элементарный участок t ), марковский процесс называют
однородным; если эти плотности представляют собой какие i j (t ) , процесс называется
то функции времени
неоднородным. При пользовании сокращенным названием
«непрерывная марковская цепь» мы также будем различать
однородные и неоднородные цепи.
t
21
22.
Предположим, что нам известны плотностивероятностей перехода для всех пар состояний Si , Sj .
Такой граф, с проставленными у стрелок плотностями
вероятностей перехода, мы будем называть размеченным
графом состояний.
Оказывается, зная размеченный граф состояний,
можно определить вероятности состояний:
p1 (t ), p2 (t ), ... , pn (t ),
А именно, эти вероятности удовлетворяют
определенного вида дифференциальным уравнениям, так
называемым уравнениям Колмогорова
22
23.
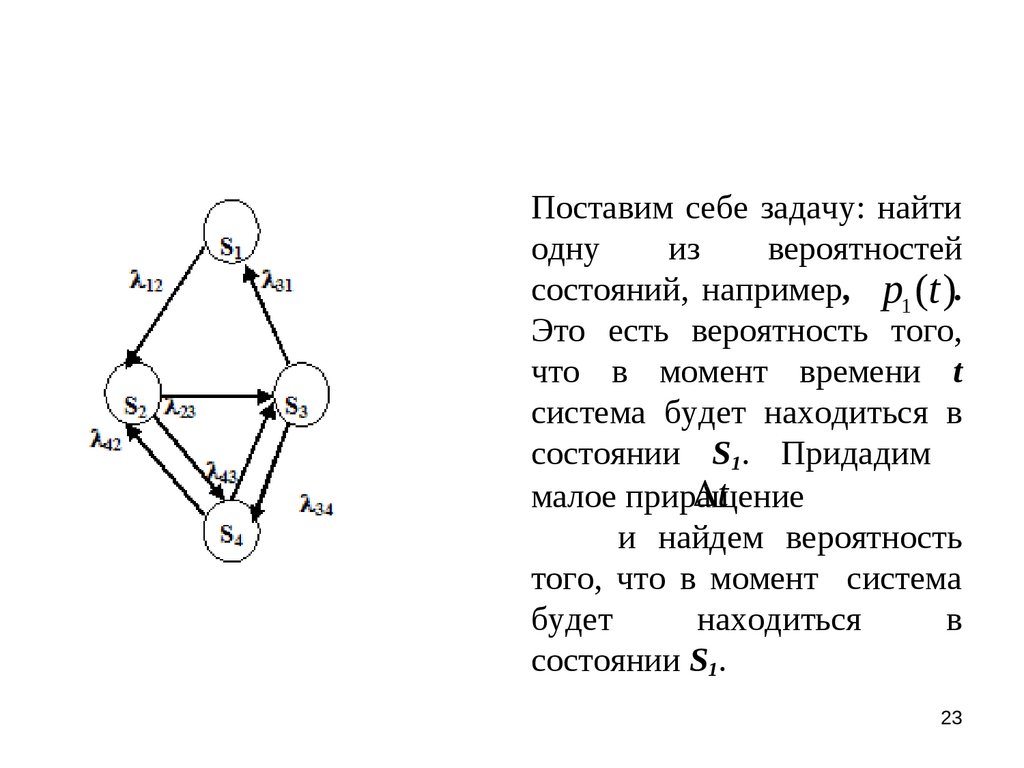
Поставим себе задачу: найтиодну
из
вероятностей
состояний, например, p1 (t ).
Это есть вероятность того,
что в момент времени t
система будет находиться в
состоянии S1. Придадим
t
малое приращение
и найдем вероятность
того, что в момент система
будет
находиться
в
состоянии S1.
23
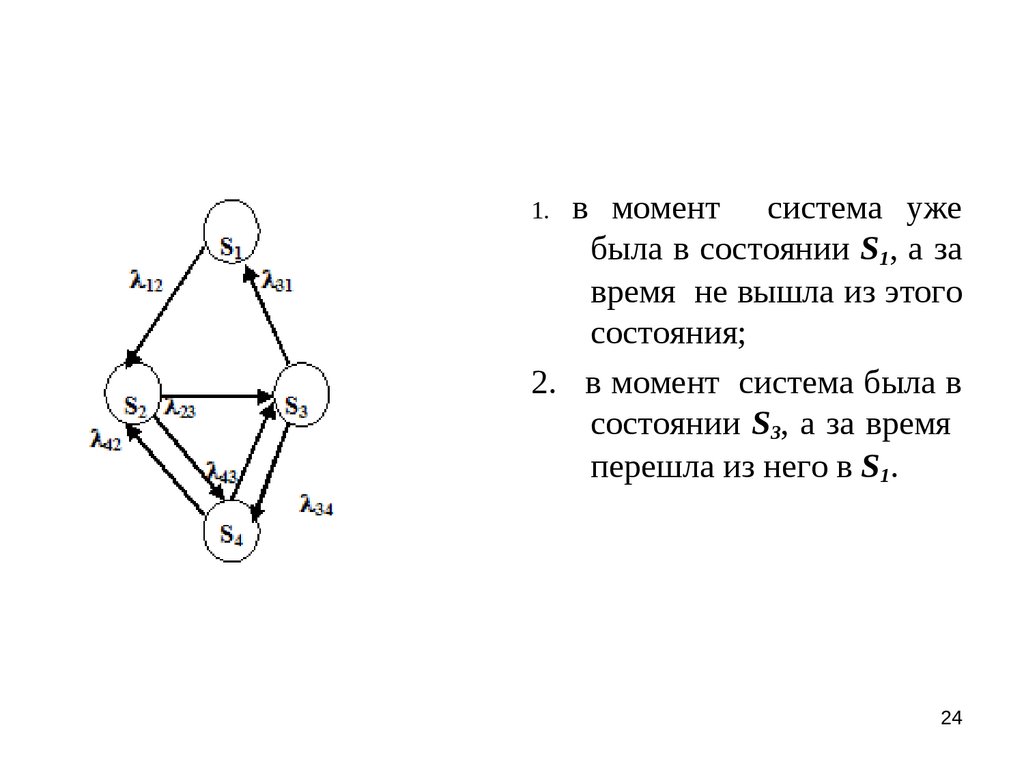
24.
в момент система ужебыла в состоянии S1, а за
время не вышла из этого
состояния;
2. в момент система была в
состоянии S3, а за время
перешла из него в S1.
1.
24
25.
Вероятностьпервого
варианта
найдем
как
произведение
вероятности того, что в момент
система была в состоянии S1, на
условную вероятность того, что
будучи в состоянии S1, система не
перейдет из него в S2. Эта условная
вероятность (с точностью до малых
высшего порядков) равна
1 12 t
25
26.
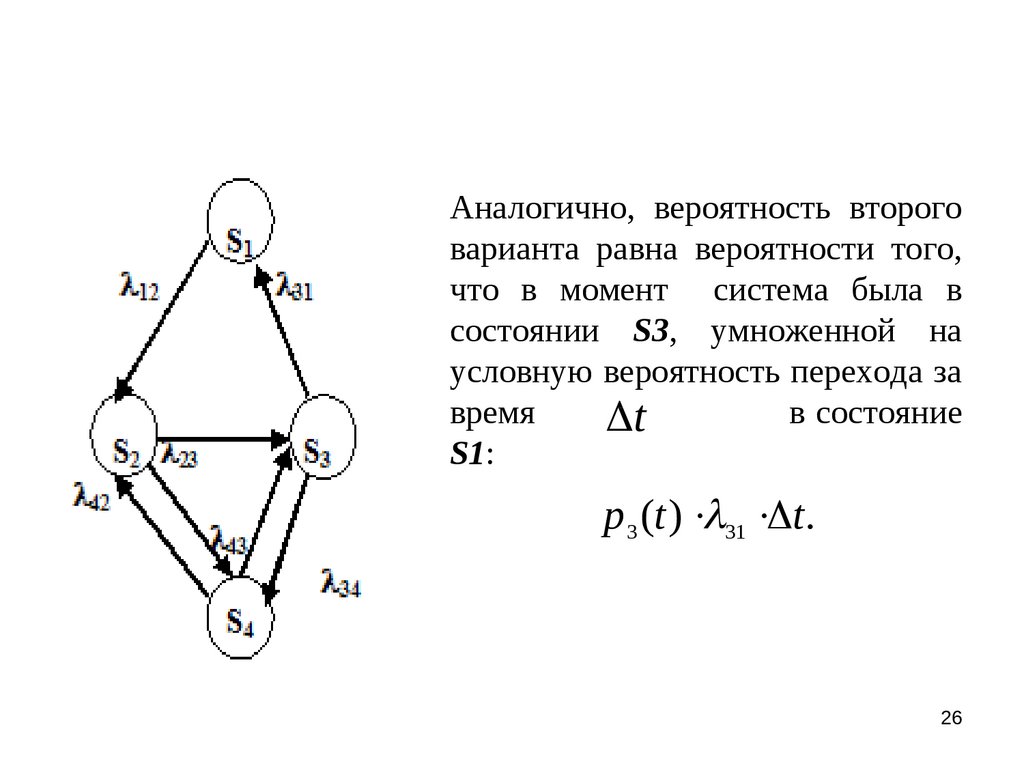
Аналогично, вероятность второговарианта равна вероятности того,
что в момент система была в
состоянии S3, умноженной на
условную вероятность перехода за
время
в состояние
t
S1:
p 3 (t ) 31 t.
26
27.
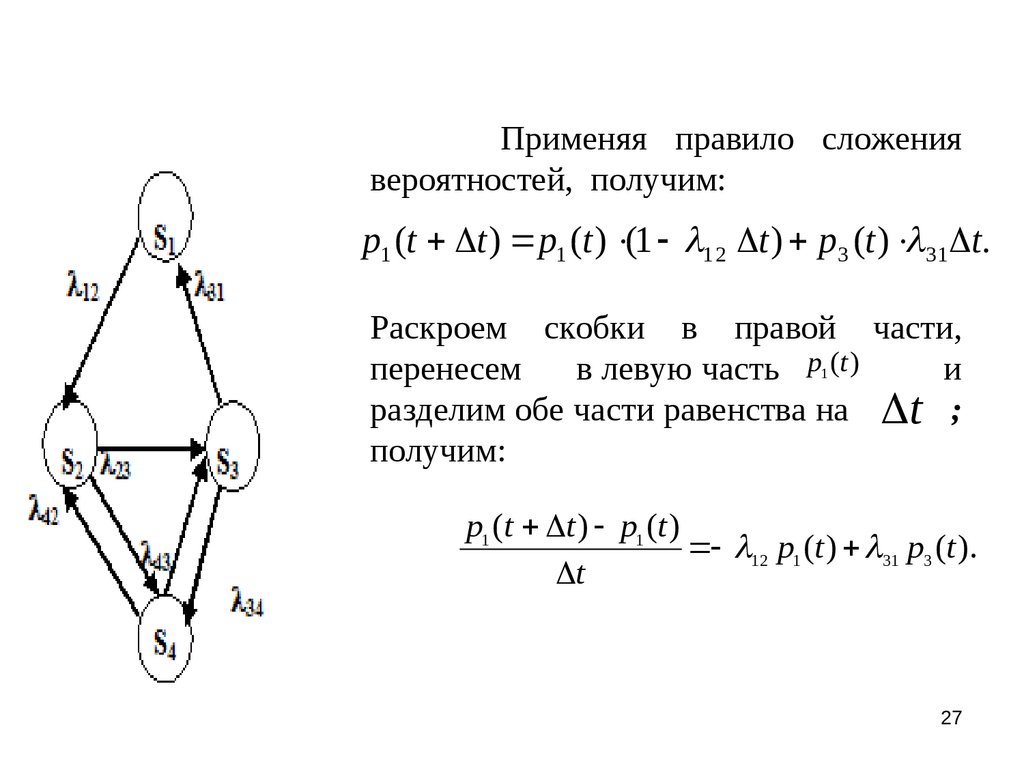
Применяя правило сложениявероятностей, получим:
p1 (t t ) p1 (t ) (1 1 2 t ) p 3 (t ) 31 t.
Раскроем скобки в правой части,
перенесем
в левую часть p1 (t )
и
разделим обе части равенства на t ;
получим:
p1 (t t ) p1 (t )
12 p1 (t ) 31 p3 (t ).
t
27
28.
Теперь устремимt
и перейдем к пределу:
к нулю
p1 (t t ) p1 (t )
lim
12 p1 (t ) 31 p3 (t ).
t 0
t
Левая часть не что иное, как
p1 (t ) :
производная функции
28
29.
Аналогичные дифференциальныеуравнения могут быть выведены и
для
остальных
вероятностей
состояния:
p2 (t ), p3 (t ), p4 (t ).
29
30.
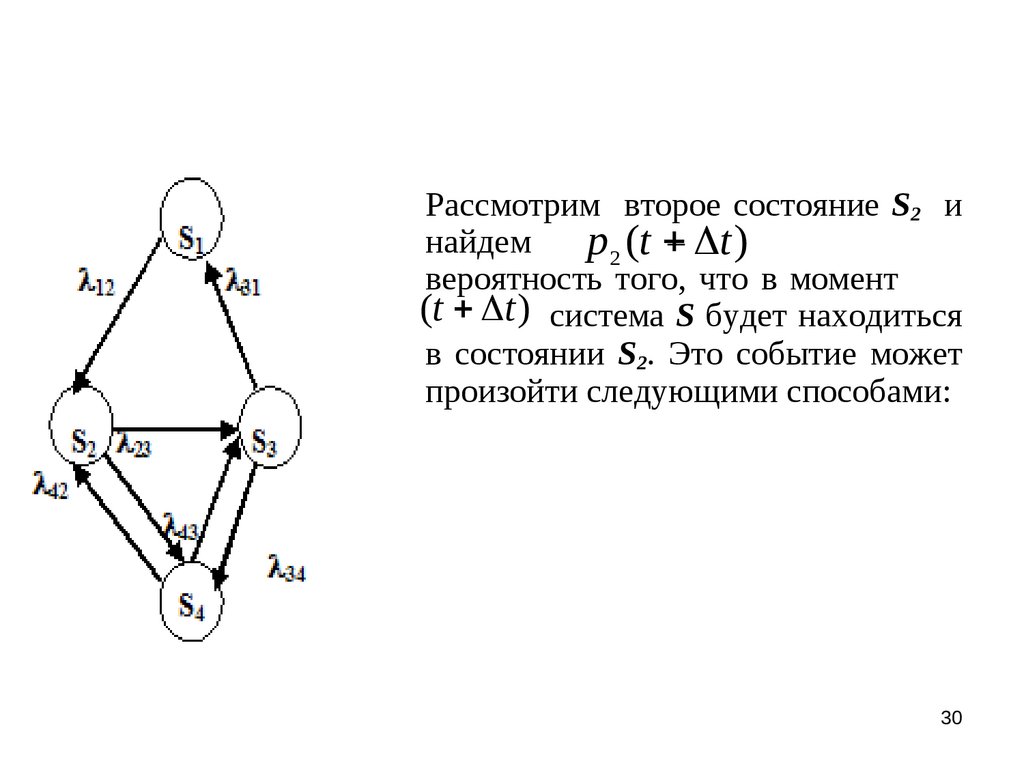
Рассмотрим второе состояние S2 инайдем
p2 (t – t )
вероятность того, что в момент
(t t ) система S будет находиться
в состоянии S2. Это событие может
произойти следующими способами:
30
31.
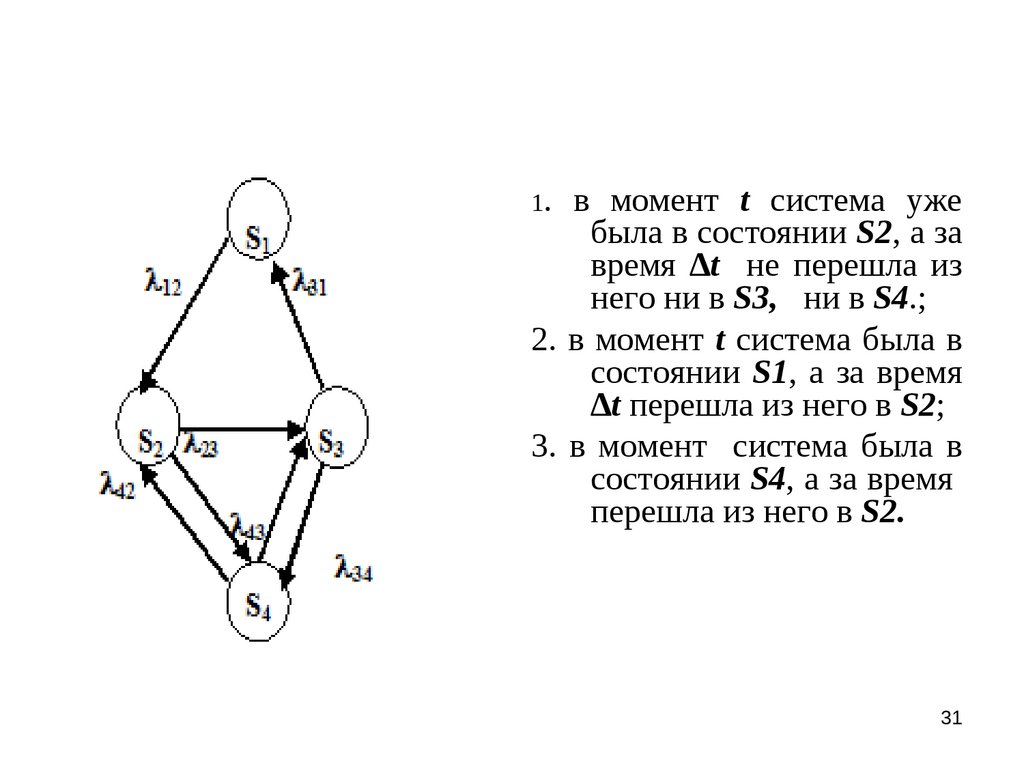
1.в момент t система уже
была в состоянии S2, а за
время ∆t не перешла из
него ни в S3, ни в S4.;
2. в момент t система была в
состоянии S1, а за время
∆t перешла из него в S2;
3. в момент система была в
состоянии S4, а за время
перешла из него в S2.
31
32.
Вероятность первоговарианта вычисляется так:
умножается на условную
вероятность того, что система
за не перейдет ни в S3, ни в
S4.
Так
как
события,
состоящие в переходе за
время
из S2 в S3 и из
t S2 в
S4
,
несовместны,
то
вероятность того,
что
осуществится один из этих
переходов, равна сумме их
вероятностей, т. е.
2 3 t 2 4 t
(с точностью до бесконечно
малых высших порядков).
32
33.
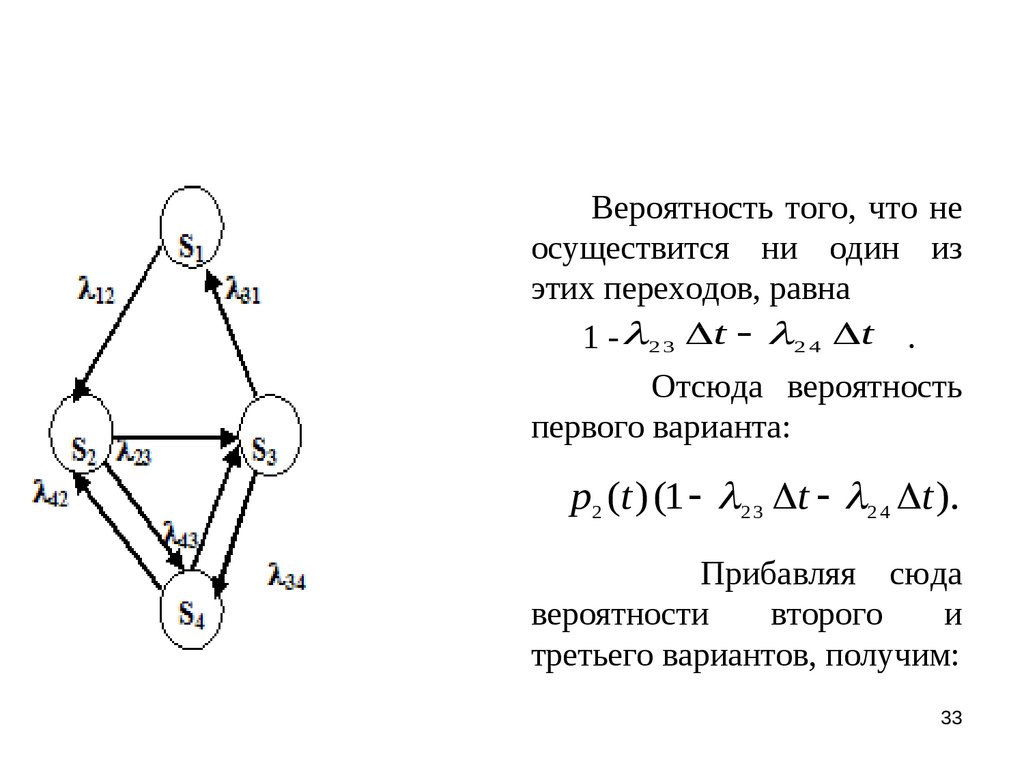
Вероятность того, что неосуществится ни один из
этих переходов, равна
1 - 2 3 t 2 4 t .
Отсюда вероятность
первого варианта:
p2 (t ) (1 2 3 t 2 4 t ).
Прибавляя сюда
вероятности
второго
и
третьего вариантов, получим:
33
34.
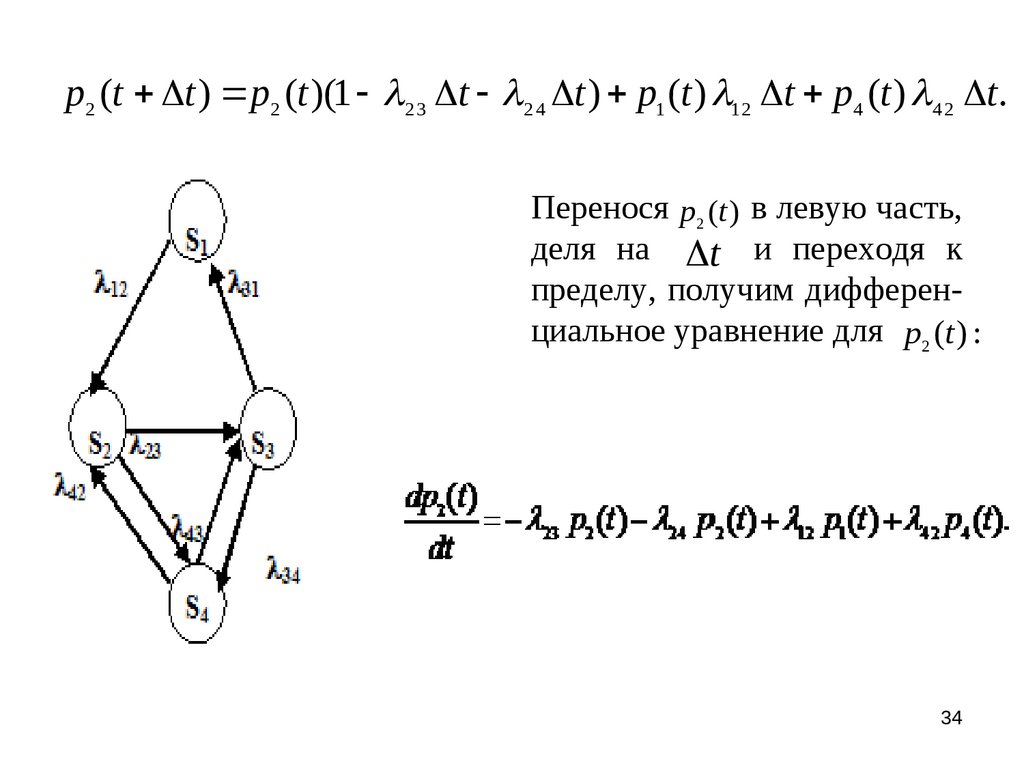
p2 (t t ) p2 (t )(1 2 3 t 2 4 t ) p1 (t ) 12 t p4 (t ) 4 2 t.Перенося p2 (t ) в левую часть,
деля на t и переходя к
пределу, получим дифференциальное уравнение для p2 (t ) :
34
35.
Рассуждая аналогично длясостояний
S3 ,
S4 ,
получим
в
результате
систему дифферен-циальных
уравнений:
35
36.
dp1 (t )12 p1 (t ) 31 p3 (t ) ,
dt
dp2 (t )
2 3 p2 (t ) 2 4 p2 (t ) 12 p1 (t ) 4 2 p4 (t ) ,
dt
dp3 (t )
31 p3 (t ) 3 4 p3 (t ) 2 3 p2 (t ),
dt
dp4 (t )
4 2 p4 (t ) 2 4 p2 (t ) 3 4 p3 (t ) .
dt
p1 (t ) p2 (t ) p3 (t ) p4 (t ) 1
36
37.
Эти уравнения для вероятностей состояний иназываются уравнениями Колмогорова. Интегрирование этой
системы уравнений даст нам искомые вероятности состояний
как функции времени. Начальные условия берутся в
зависимости от того, каково было начальное состояние S.
Например, если в начальный момент времени ( t 0) система
S находилась в состоянии S1, то надо принять начальные
условия:
t 0 p1 (0) 1, p2 (0) 0, p3 (0) 0, p4 (t ) 0.
37
38.
Заметим, что всех четырех уравнений дляp1 (t ), p2 (t ), p3 (t ), p4 (t )
можно было бы и не писать; действительно для всех , и
любую из вероятностей
можно выразить через три
остальные. Например,
можно выразить через
p4 (t )
остальные в виде
p1 (t ) p2 (t ) p3 (t ) p4 (t ) 1
p4 (t ) 1 [ p1 (t ) p2 (t ) p3 (t )]
38
39. Правило записи уравнений Колмогорова
В левой части каждого уравнения стоит производнаявероятности состояния, а правая часть содержит столько
членов, сколько стрелок связано с данным состоянием.
Если стрелка направлена из состояния, соответствующий
член имеет знак «минус»; если в состояние – знак «плюс».
Каждый член равен произведению плотности вероятности
перехода, соответствующей данной стрелке, умноженной
на вероятность того состояния, из которого исходит
стрелка.
39
40.
41. НЭКИС
РАСЧЕТ НАДЕЖНОСТИ СИСТЕМ СВОССТАНОВЛЕНИЕМ.
МАРКОВСКИЕ ПРОЦЕССЫ.
ПРЕДЕЛЬНЫЕ ВЕРОЯТНОСТИ.
41
42.
Некоторые цепи Маркова, удовлетворяющиеопределенным условиям имеют предельные вероятности равные
константам. Пусть некая ИС с дискретными состояниями:
S1 , S2 , . . ., Sn,
в которой протекает марковский случайный процесс с
непрерывным временем (непрерывная цепь Маркова).
Предположим, что все интенсивности потоков событий,
переводящих систему из состояние, постоянны:
другими словами, все потоки событий – простейшие
const
,
i
j
(стационарные пуассоновские) потоки.
42
43.
Записавсистему
дифференциальных
уравнений
Колмогорова для вероятностей состояний и проинтегрировав
эти уравнения при заданных начальных условиях, мы
получим вероятности состояний, как функции времени, т.е. n
функций:
p1(t), p2(t), . . ., pn(t)
при любых t дающих в сумме единицу:
.
n
pi 1
i 1
43
44.
Поставим теперь следующий вопрос: что будетпроисходить с системой S при t ? Будут ли функции p1(t),
p2(t), . . ., pn(t) стремиться к каким-то пределам? Эти пределы,
если
они
существуют,
называются
предельными
вероятностями состояний.
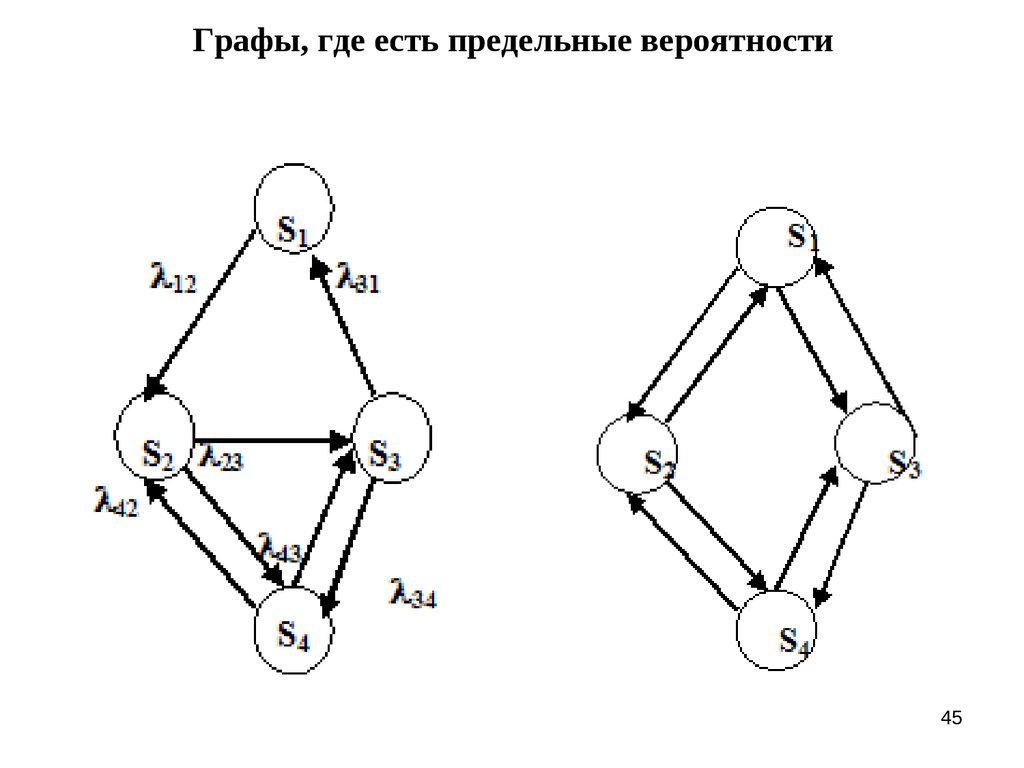
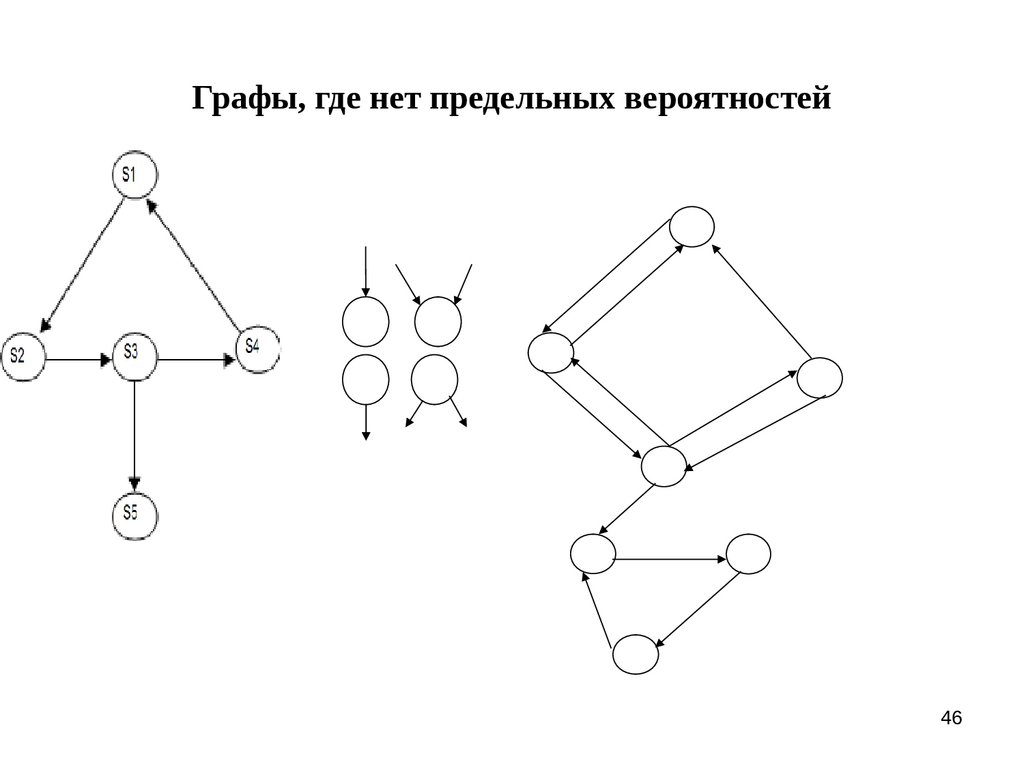
Можно доказать следующее общее положение. Если
число состояний системы S конечно и из каждого состояния
можно перейти (за то или иное число шагов) в каждое
другое, то предельные вероятности состояний существуют и
не зависят от начального состояния системы.
44
45. Графы, где есть предельные вероятности
4546. Графы, где нет предельных вероятностей
4647.
Предположим, что поставленное условие выполнено,и предельные вероятности существуют:
(t ) pi
p
i
t
lim
(i 1,2,..., n) .
47
48.
Предельные вероятности мы будем обозначать теми жебуквами p1, p2, . . ., pn , что и сами вероятности состояний,
понимая под ними на этот раз не переменные величины
(функции времени), а постоянные числа.
Очевидно, предельные вероятности состояний, так же
как и допредельные, в сумме должны давать единицу:
n
pi 1
i 1
48
49.
Таким образом, при t в системе S устанавливаетсянекоторый предельный стационарный режим: он состоит в
том, что система случайным образом меняет свои состояния,
но вероятность каждого из них уже не зависит от времени:
каждое из состояний осуществляется с некоторой
постоянной вероятностью.
49
50.
Например, если у системы S состояния: S1, S2, S3,причем их предельные вероятности равны 0.2, 0.3 и 0.5 это
означает, что после перехода к установившемуся режиму
система S в среднем две десятых времени будет находиться в
состоянии S1, три десятых – в состоянии S2, и половину
времени – в состоянии S3.
Например, если вероятность отказа системы равна
Рп=0.00001, то простой системы за 4 года составит:
Тп = 4*365*24*Рп = 0.3504 (ч.)
Для вычисления предельных вероятностей состояний
p1, p2, . . ., pn
в системе уравнений Колмогорова,
описывающих вероятности состояний, нужно положить все
левые части (производные) равными нулю и решить систему
линейных уравнений.
50
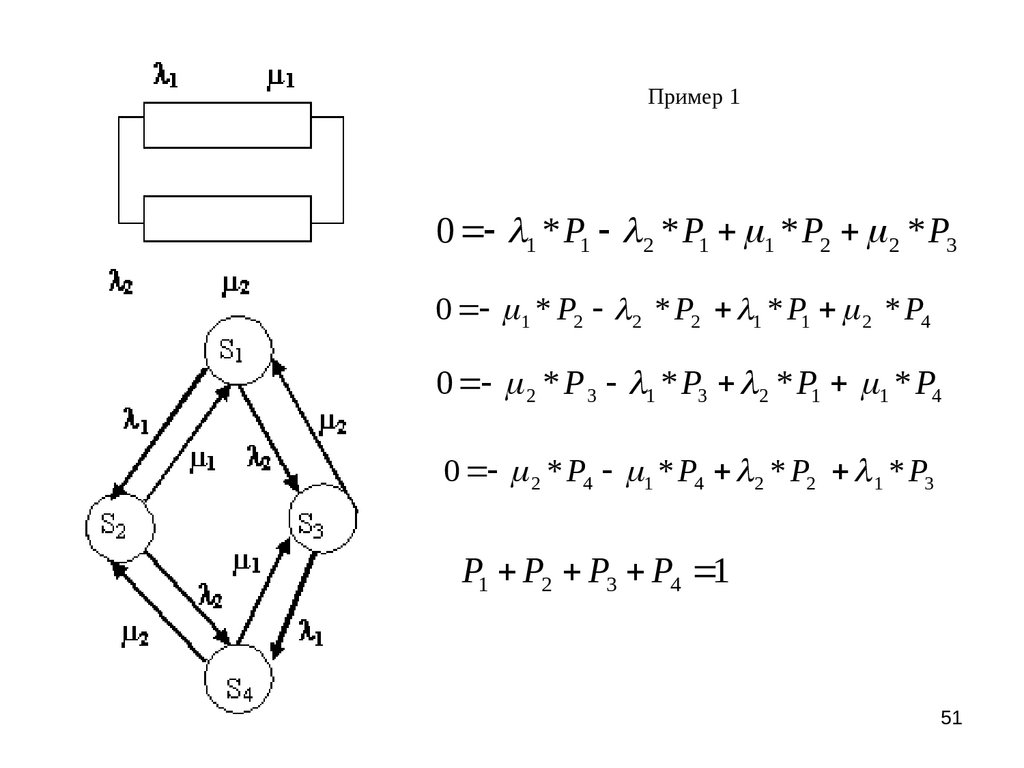
51. Пример 1
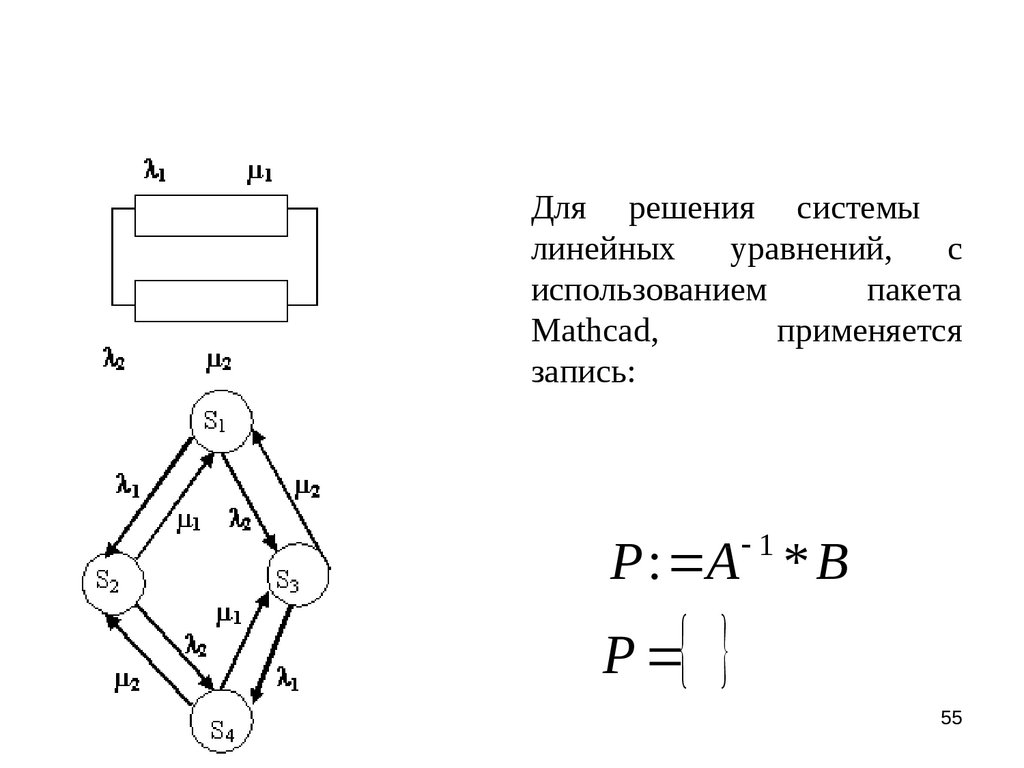
0 1 * P1 2 * P1 1 * P2 2 * P30 1 * P2 2 * P2 1 * P1 2 * P4
0 2 * P 3 1 * P3 2 * P1 1 * P4
0 2 * P4 1 * P4 2 * P2 1 * P3
P1 P2 P3 P4 1
51
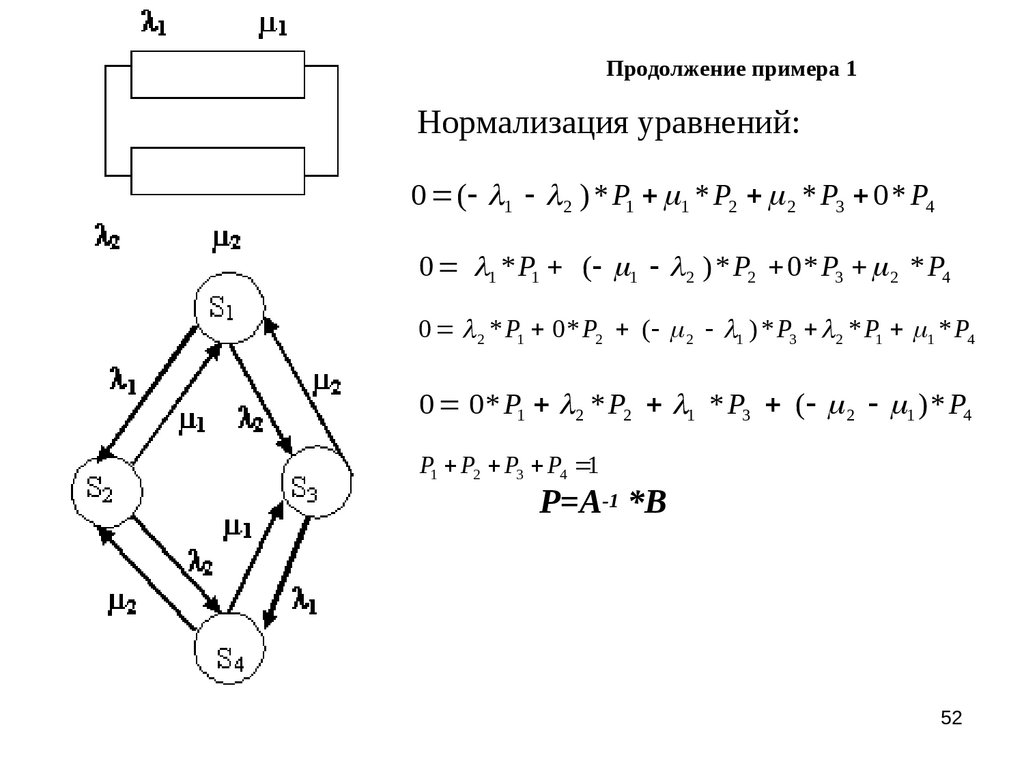
52. Продолжение примера 1
Нормализация уравнений:0 ( 1 2 ) * P1 1 * P2 2 * P3 0 * P4
0 1 * P1 ( 1 2 ) * P2 0 * P3 2 * P4
0 2 * P1 0 * P2 ( 2 1 ) * P3 2 * P1 1 * P4
0 0 * P1 2 * P2 1 * P3 ( 2 1 ) * P4
P1 P2 P3 P4 1
P=A-1 *B
52
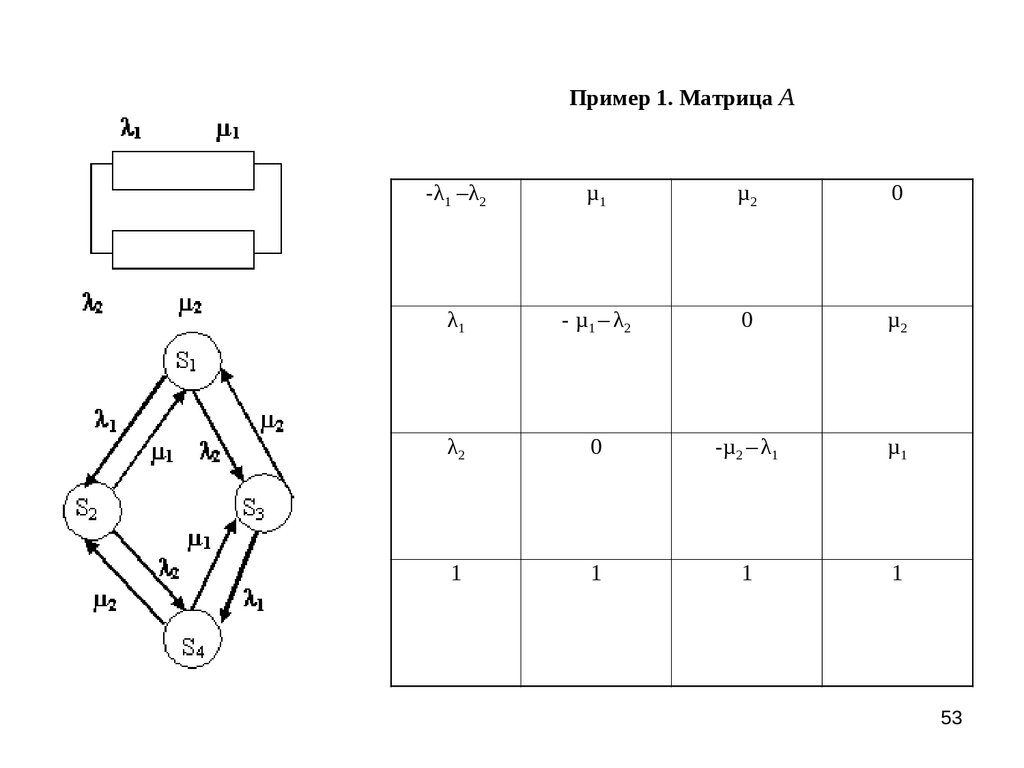
53. Пример 1. Матрица А
-λ1 –λ2µ1
µ2
0
λ1
- µ1 – λ2
0
µ2
λ2
0
-µ2 – λ1
µ1
1
1
1
1
53
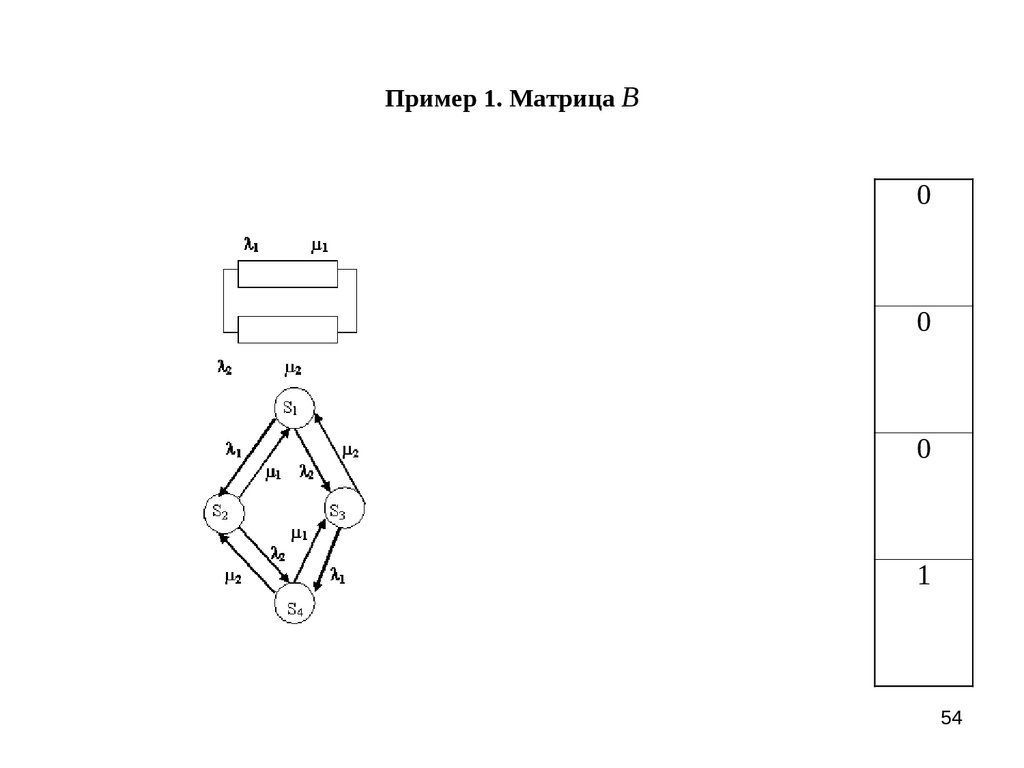
54. Пример 1. Матрица B
00
0
1
54
55.
Для решения системылинейных
уравнений,
с
использованием
пакета
Mathcad,
применяется
запись:
1
P : A * B
P
55
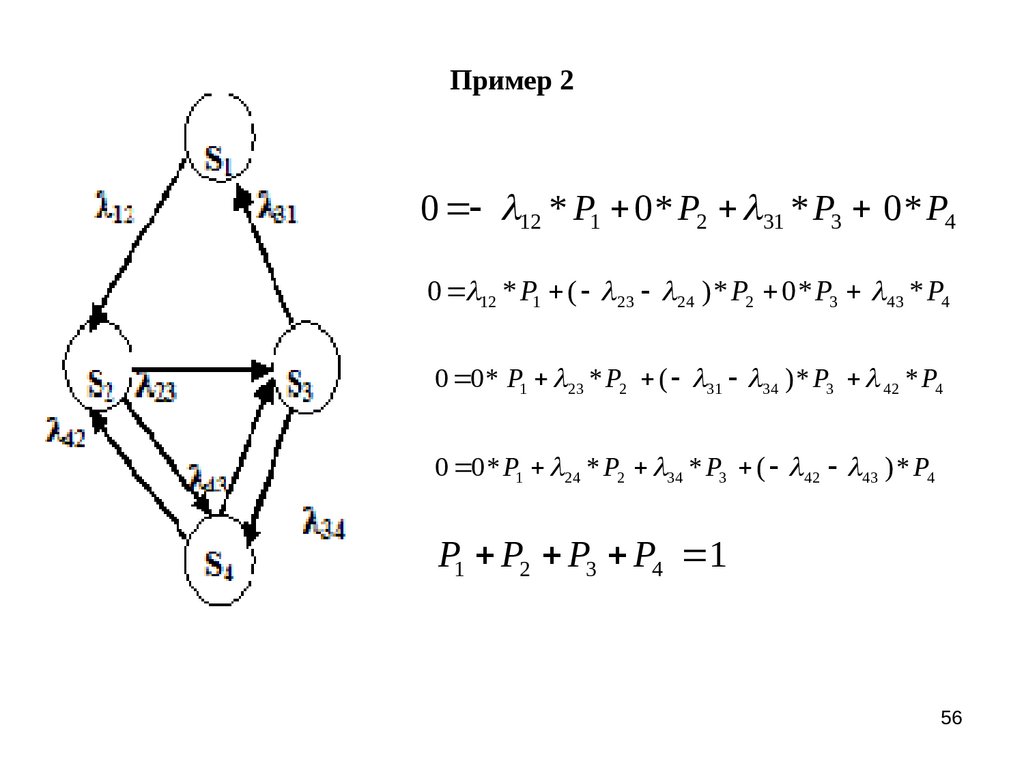
56. Пример 2
0 12 * P1 0 * P2 31 * P3 0 * P40 12 * P1 ( 23 24 ) * P2 0 * P3 43 * P4
0 0 * P1 23 * P2 ( 31 34 ) * P3 42 * P4
0 0 * P1 24 * P2 34 * P3 ( 42 43 ) * P4
P1 P2 P3 P4 1
56
57. Процесс «гибели и размножения»
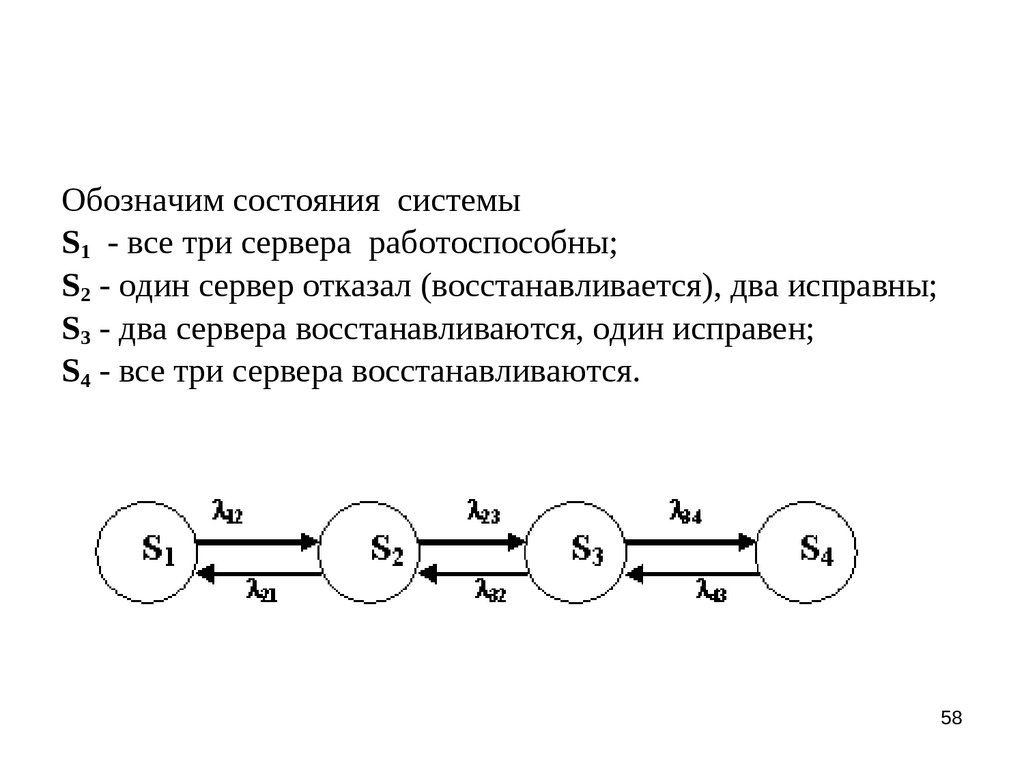
Рассмотрим пример. Пусть система управленияпредприятия на верхнем уровне управления включает три
одинаковых сервера, каждый из которых может отказывать;
отказавший сервер немедленно начинает восстанавливаться.
Обозначим соcтояния системы
57
58.
Обозначим соcтояния системыS1 - все три сервера работоспособны;
S2 - один сервер отказал (восстанавливается), два исправны;
S3 - два сервера восстанавливаются, один исправен;
S4 - все три сервера восстанавливаются.
58
59.
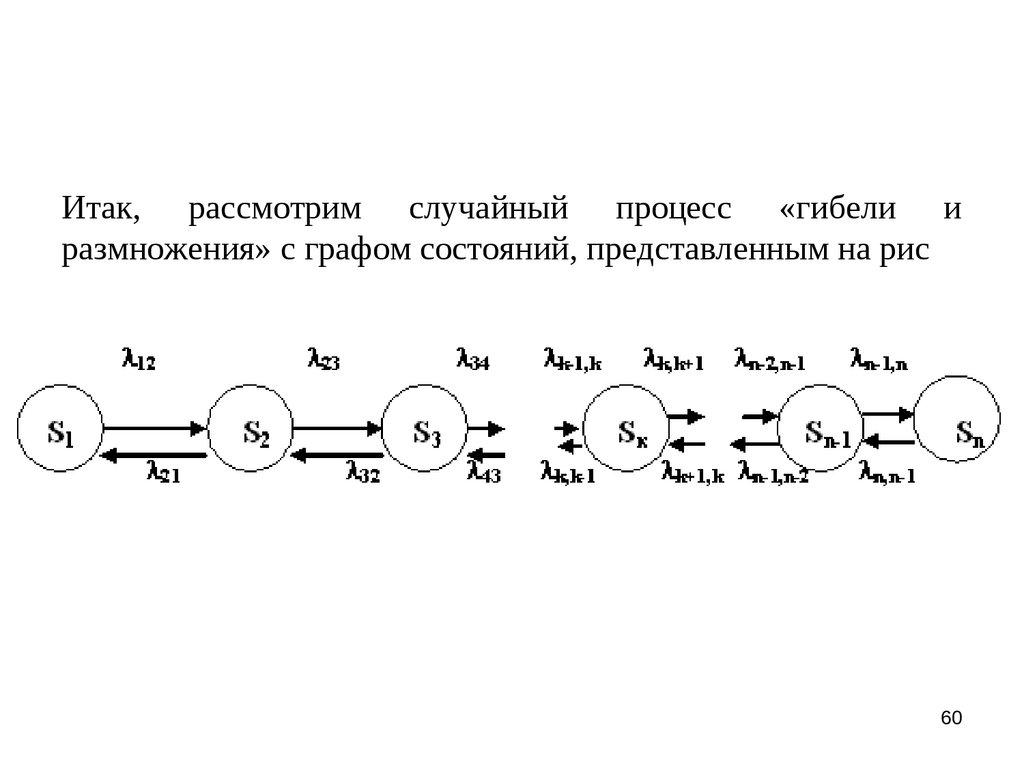
Марковская непрерывная цепь называется«процессом гибели и размножения», если ее граф состояний
имеет вид, представленный на рисунке, т.е. все состояния
можно вытянуть в одну цепочку, в которой каждое из
средних состояний (S2, . . . , Sn-1) связано прямой и обратной
связью с каждым из соседних состояний, а крайние
состояния (S1, . . . ,Sn) – только с одним соседним
состоянием.
59
60.
Итак, рассмотрим случайный процесс «гибели иразмножения» с графом состояний, представленным на рис
60
61.
Напишемуравнения для предельных
состояний. Для первого состояния S1 имеем:
вероятностей
12 P1 21 p2 0.
Отсюда следует
61
62.
Для второго состояния S2 можем записать:23 p2 21 p2 12 p1 32 p3 0.
Но, в силу
, можно сократить справа и
слева равные друг другу члены 12 p1 и 21 p2 ; получим:
23 p2 32 p3 ,
и далее, совершенно аналогично,
34 p3 43 p4 ,
.. .
62
63.
Одним словом, для схемы “гибели и размножения” члены,соответствующие стоящим друг над другом стрелкам, равны
между собой:
k 1, k pk 1 k , k 1 pk ,
где k принимает все значения от 2 до n.
63
64.
p1 , p2 , p3 , ... , pnИтак, предельные вероятности состояний
в любой схеме “гибели и размножения” удовлетворяют
уравнениям:
12 p1 21 p2 ,
23 p2 32 p3 ,
34 . p. 3. . 43 p4
и нормировочному условию:
n 1, n pn 1 n , n 1 pn
p1 p2 p3 ... pn 1
64
65.
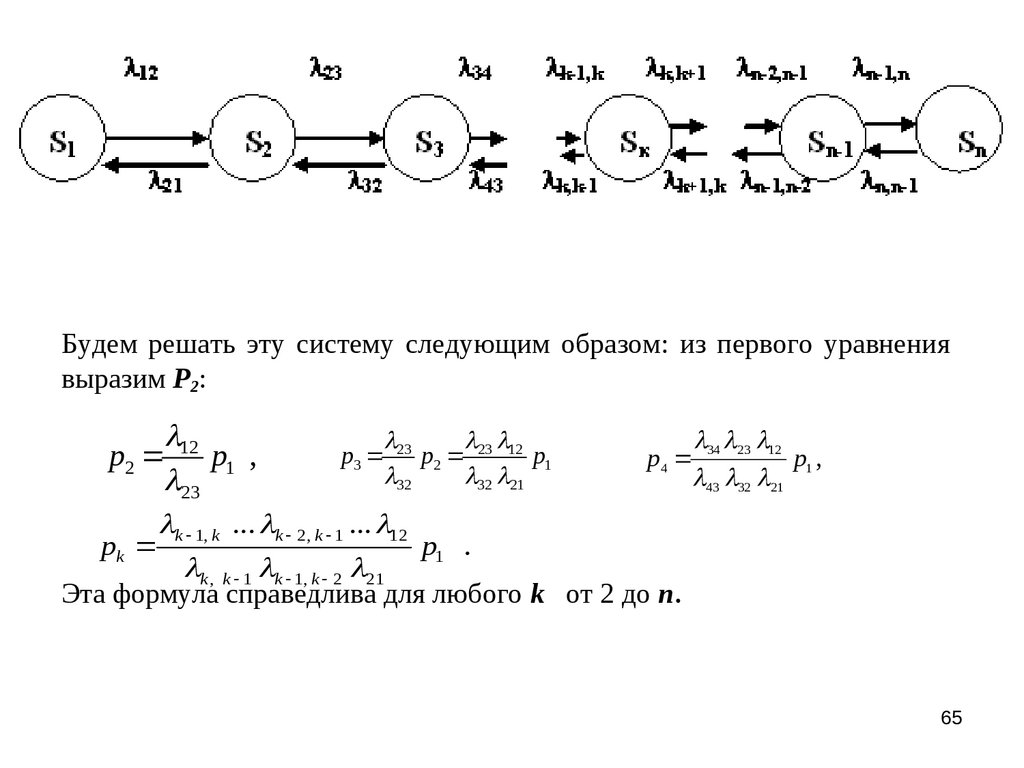
Будем решать эту систему следующим образом: из первого уравнениявыразим P2:
p3 23 p2 23 12 p1
p2 12 p1 ,
32
32 21
23
k 1, k ... k 2, k 1 ... 12
pk
p1 .
k , k 1 k 1, k 2 21
p4 34 23 12 p1 ,
43 32 21
Эта формула справедлива для любого k от 2 до n.
65
66.
Обратим внимание на ее структуру. В числителе стоитпроизведение всех плотностей вероятности перехода
(интенсивностей) , стоящих у стрелок, направленных слева
направо, с начала и вплоть до той, которая идет в состояние
Sk ; в знаменателе – произведение всех интенсивностей ,
стоящих у стрелок, идущих справа налево, опять – таки, с
начала и вплоть до стрелки, исходящей из состояния Sk .
При k = n в числителе будет стоять произведение
интенсивностей , стоящих у всех стрелок, идущих слева
направо, а в знаменателе – у всех стрелок, идущих справа
налево.
66
67.
Подставим эти выражения в нормировочное условие: P1 + P2 +P3 + …+ Pn = 1. Получим:
k 1, k k 2, k 1 ... 12
23 12
12
p1
p1
p1 ...
p1
21
32 21
k , k 1 k 1, k 2 ... 21
откуда n 1, n 2 , n 1
...
... 12
n , n 1 n 1, n 2 ... 21
p1 1,
1
p1
.
k 1, k k 2, k 1 ... 12
n 1, n ... 12
12 23 12
1
...
...
21 23 21
k , k 1 k 1, k 2 ... 21
n , n 1 ... 21
67
68.
Остальные вероятности выражаются через P1:p2 12 p1 ,
21
23 12
p3
p1 ,
32 21
.....
... 12
pk k 1, k
p1 ,
k , k 1 ... 21
... 12
pn n 1, n
p1 .
n , n 1 ... 21
Таким образом, задача «гибели и размножения» решена в
общем виде: найдены предельные вероятности состояний.
68
69. Пример
Пример. Рассмотрим пример, приведенный в самомначале данного раздела. Система управления включает три
одинаковых сервера; поток отказов – простейший, среднее
время безотказной работы каждого сервера равна T0.
Отказавший сервер сразу начинает восстанавливаться;
среднее время ремонта (восстановления) узла равно Тв; закон
распределения этого времени, т.е поток восстановлений –
простейший. Система работоспособна, если работоспособны
два любых сервера из трех. Рассчитать простой системы из–
за отказов серверов за 4 года непрерывной и круглосуточной
эксплуатации.
69
70.
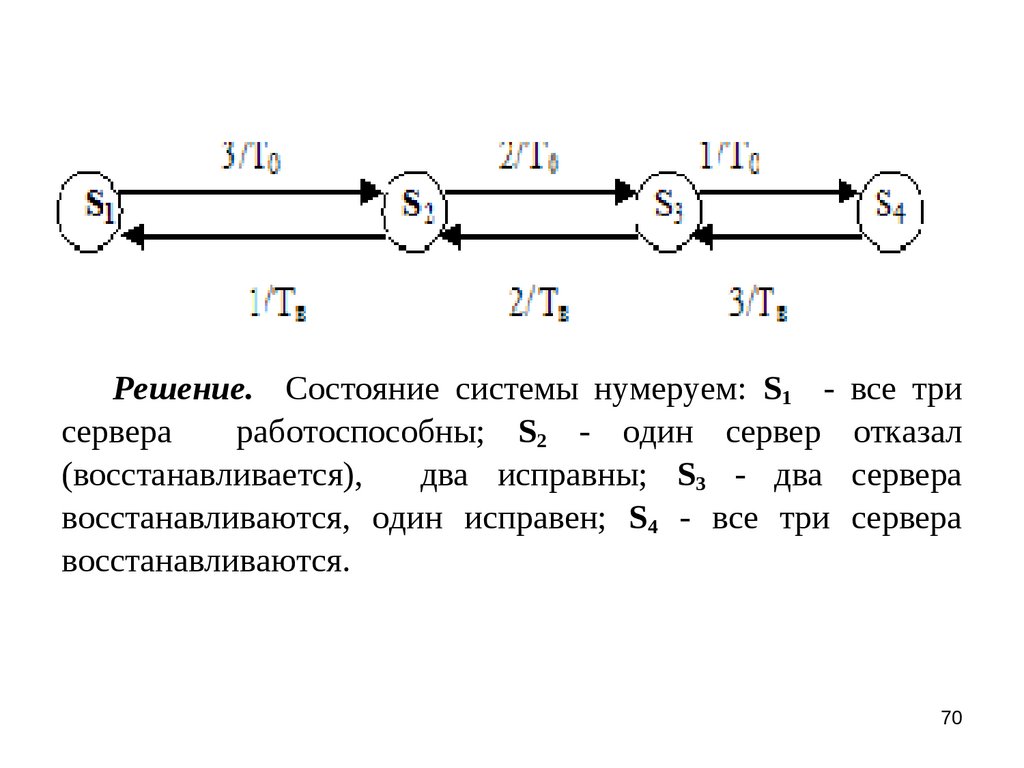
Решение. Состояние системы нумеруем: S1 сервераработоспособны; S2 - один сервер
(восстанавливается),
два исправны; S3 - два
восстанавливаются, один исправен; S4 - все три
восстанавливаются.
все три
отказал
сервера
сервера
70
71.
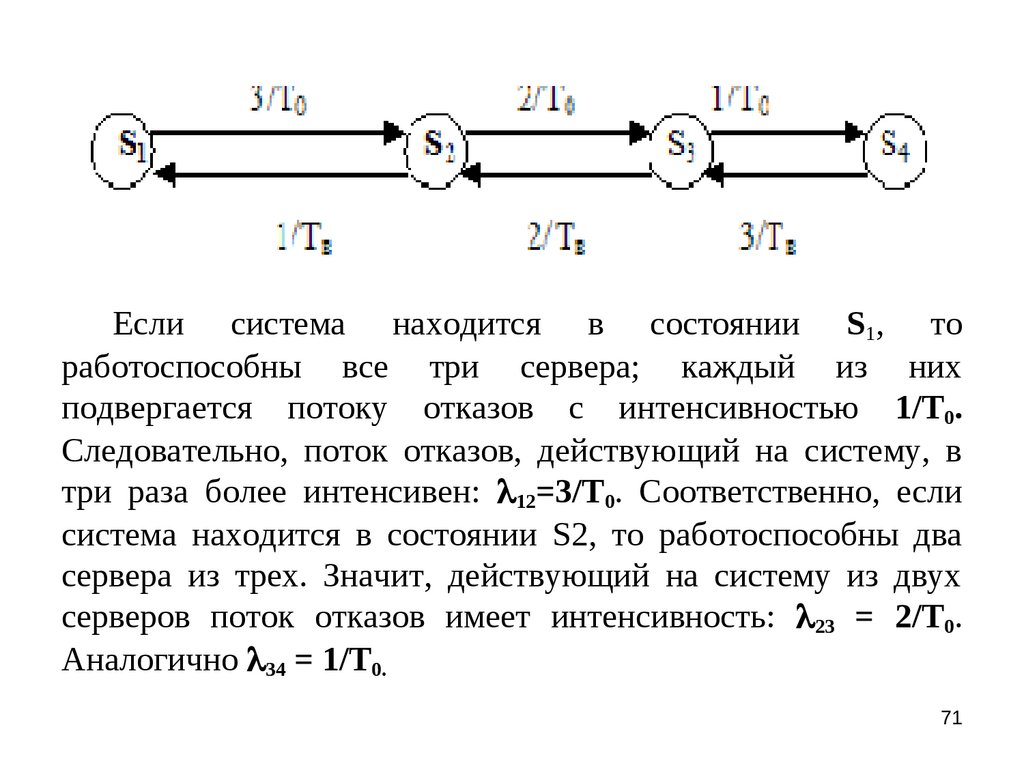
Если система находится в состоянии S1, тоработоспособны все три сервера; каждый из них
подвергается потоку отказов с интенсивностью 1/T0.
Следовательно, поток отказов, действующий на систему, в
три раза более интенсивен: 12=3/T0. Соответственно, если
система находится в состоянии S2, то работоспособны два
сервера из трех. Значит, действующий на систему из двух
серверов поток отказов имеет интенсивность: 23 = 2/T0.
Аналогично 34 = 1/T0.
71
72.
По стрелкам влево система переходит послевосстановления работоспособности отказавшего сервера.
Среднее время восстановления сервера Tв, следовательно
интенсивность потока восстановлений, действующего на
один восстанавливаемый сервер, равна =1/Tв ( 21 =1/Tв),
на два восстанавливаемых сервера - = 2/Tв ( 32 = 2/Tв), на
три - = 3/Tв ( 43 = 3/Tв).
72
73.
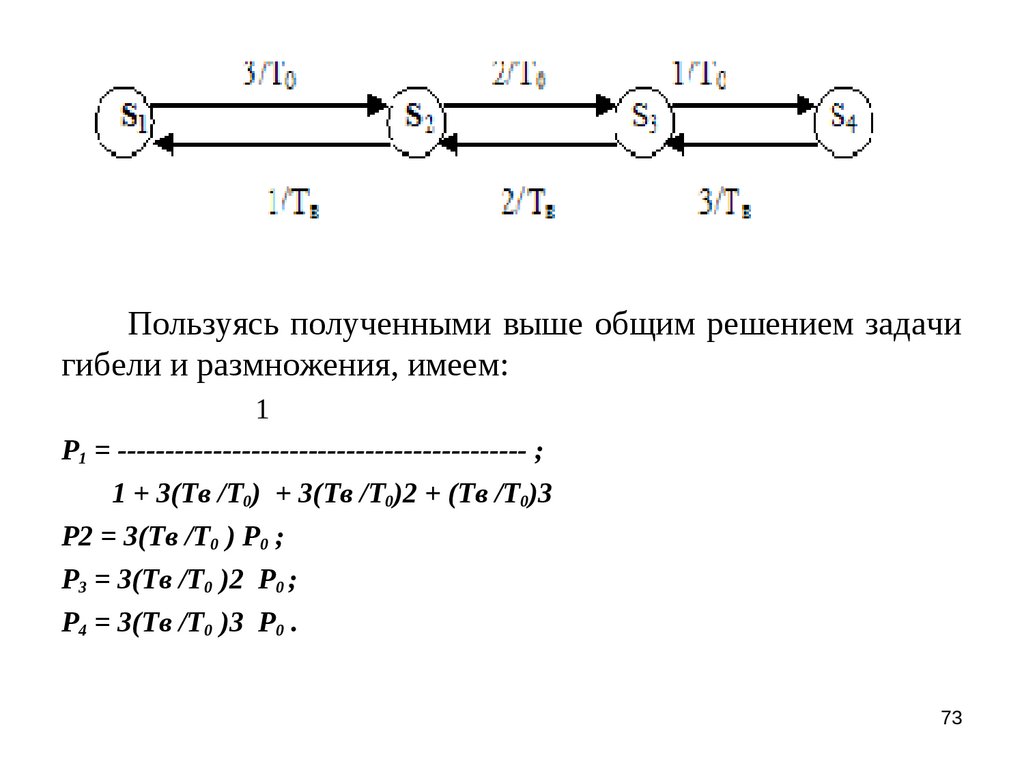
Пользуясь полученными выше общим решением задачигибели и размножения, имеем:
1
P1 = ------------------------------------------- ;
1 + 3(Tв /T0) + 3(Tв /T0)2 + (Tв /T0)3
P2 = 3(Tв /T0 ) P0 ;
P3 = 3(Tв /T0 )2 P0 ;
P4 = 3(Tв /T0 )3 P0 .
73
74.
Найденные предельные вероятности представляютсобой среднее относительное время пребывания системы в
данном состоянии. Вероятность отказа системы определяется
суммой P3 + P4 (простой системы, если отказали 2 или 3
сервера). Среднее время пребывания системы в
неработоспособном состоянии Tн за время T можно
рассчитать:
Tн = T ( P3 + P4 )
74
75.
Зададимся конкретными значениями: T0 - 40000 ч..Отказавший сервер направляется немедленно направляется в
фирменный сервисный центр (фирменные сервера Compaq,
Intel оснащаются, как правило своими фирменными
комплектующими). Пусть среднее время восстановление
сервера составляет Tв – 48 ч. Подставляем заданные
значения в полученные выше формулы:
P1 = 0.996408623
75
76.
P2 = 0,003587071P3 = 1,43483E-06
P4 = 1,72179E-09
T = (4 года)*(365 дней)*(24 часа) = 35040 ч.
Tн = T*( P3 + P4 ) = 9 (минут).
Таким образом, за 4 года непрерывной эксплуатации
системы простой из–за отказа двух и более серверов
составит не более 9 минут.
По зарубежным источникам, допустимое время простоя
ответственных ИС (систем связи, банковских систем и т.д.)
не должно превышать в год 5 минут (вероятность
безотказной работы 0.99999) .
76
77. Конец
7778.
7879.
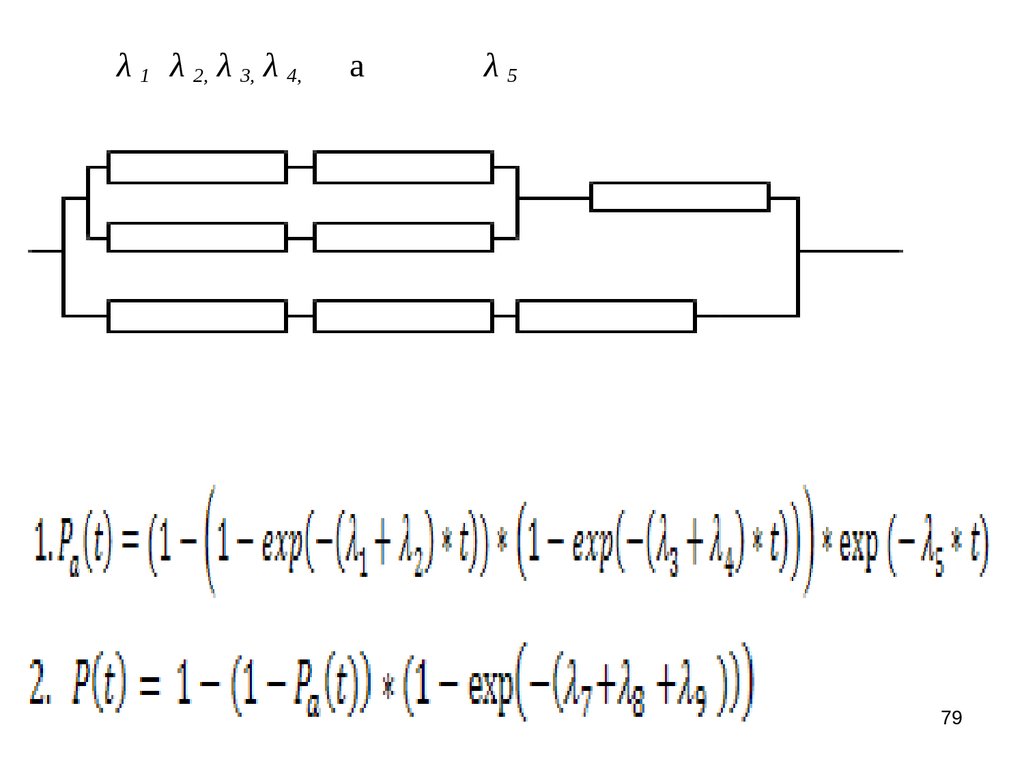
λ 1 λ 2, λ 3, λ 4,a
λ5
λ7 , λ8 , λ 9
79
80.
8081. Задача.
Наработка до отказа измерительного комплексаподчинена экспоненциальному закону с интенсивностью
отказов λ = 1,5*10-4 ч-1, среднее время восстановления
составляет 1,5 ч. Процесс измерений составляет 2,5 ч.
Определить количественные характеристики
надежности устройства P(t), Кг, Ког, T0 в течение года.
Решение. 1. По формуле P ( t ) = exp (-λ t ) определяем
Р(365*24) = EXP(-λ*365*24)=0,877.
2. Т0 = 1/ λ = 1/(1,5 *10 -5) = 6667 ч.
3. Кг = µ/(µ + λ)=(1/Тв)/(1/Тв + λ )=0,9998.
4. Ког = Кг * P(2,5)=0,9994.
81























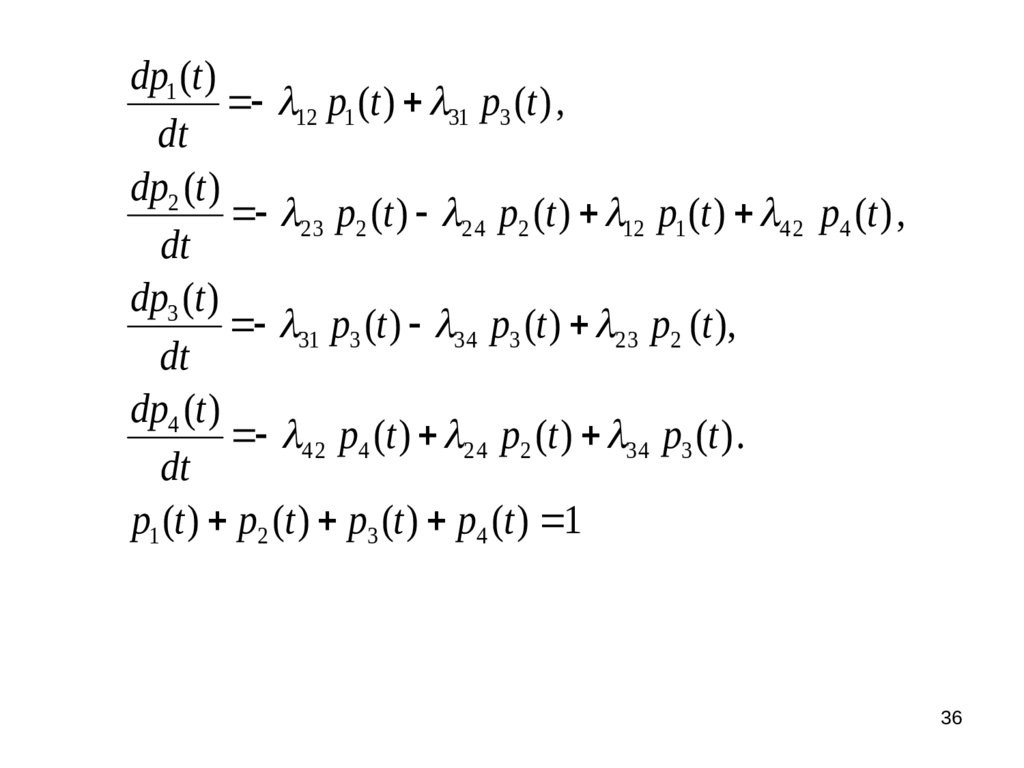






























 mathematics
mathematics








