Расчет показателей надежности систем с нелинейной схемой расчета надежности. Практика 3

1.

Практика 4
МОТН
Расчет показателей надежности
систем с нелинейной схемой
расчета надежности

2.

Расчет показателей надежности
нелинейных схем
Оценка вероятности безотказной работы системы,
имеющей сложную структурную схему
надежности, например, в виде мостиковых схем,
производится методами
• перебора состояний
• разложением относительно особого элемента
• минимальных путей и сечений
• логико-вероятностными методами

3.

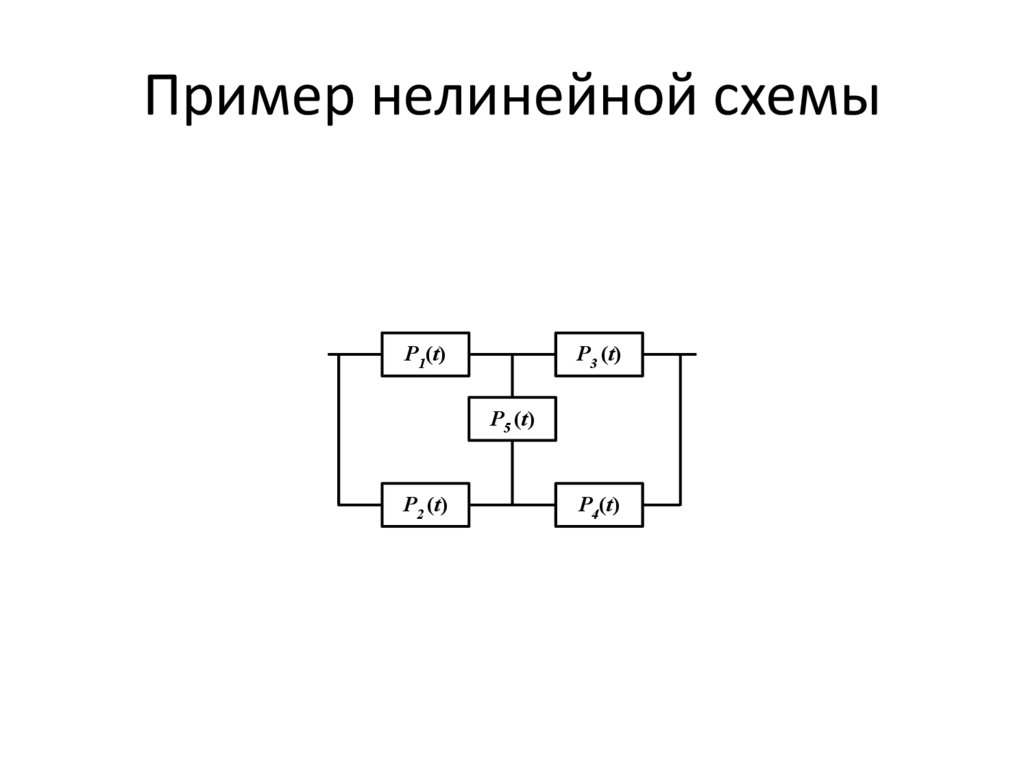
Пример нелинейной схемы
P1(t)
P3 (t)
P5 (t)
P2 (t)
P4(t)

4.

Расчет показателей надежности
нелинейных схем
Рассчитываемые показатели надежности
системы
• ВБР - P(tзад)
• средняя наработка системы- T
Исходные данные для расчета
ВБР отдельных элементов pi(tзад) + qi(tзад) =1
Период эксплуатации – нормальный
Закон распределения наработки элементов экспоненциальный

5.

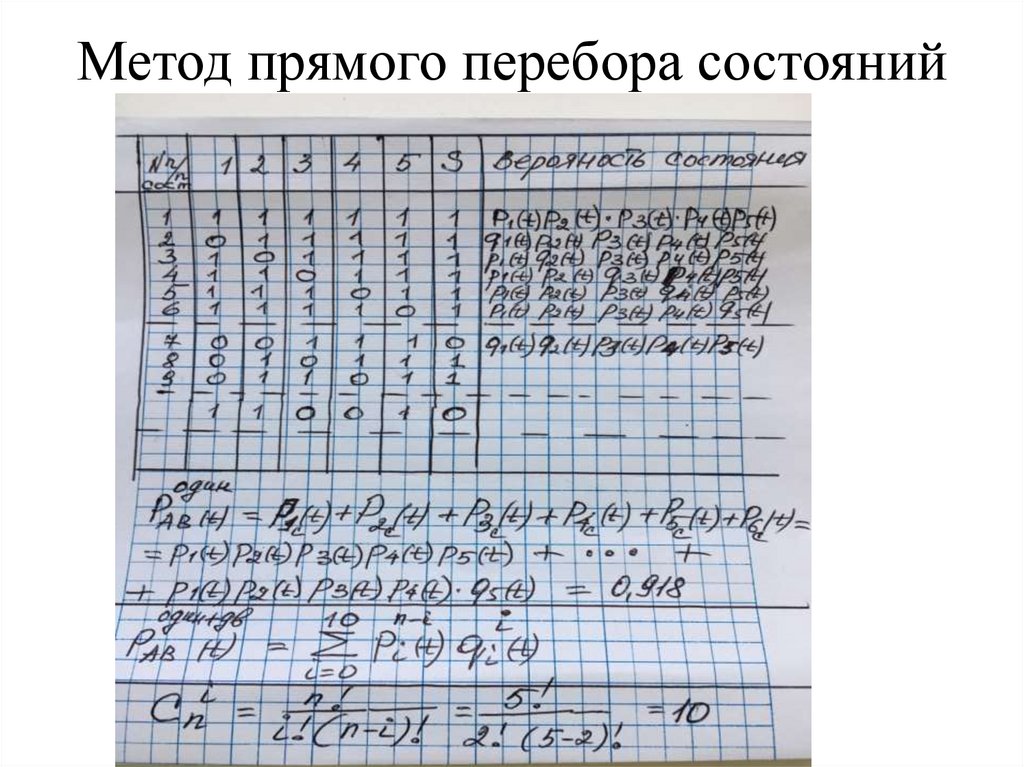
Метод прямого перебора состояний или
метод гипотез
• Перебираются возможные состояния элементов и кодируются « 1»
(работоспособное состояние) и «0» (неработоспособное)
• отказы элементов независимые и случайные
• По состоянию элементов и схеме надежности определяется
состояние системы: работоспособное -1 или неработоспособное -0
• Коды состояний элементов и системы заносятся в таблицу
• В графе таблицы «Состояния системы-S» формируются
• 2 непересекающихся множества:
набор «1» характеризует работоспособные состояния системы
набор « 0»- неработоспособные состояния системы
• Каждое состояние характеризуется определенным набором элементов
• Вероятность каждого состояния определяется произведением
• вероятностей состояний элементов:работоспособен/неработоспособен

6.

Метод прямого перебора состояний
или метод гипотез

7.

Метод прямого перебора состояний
• P АВ-один (t)=0.918
• При 2-х отказах – число состояний 10, из
них неработоспособных 2,
работоспособных 8
• P АВ-двойн (t)=8*р(t)³*g(t)²=8*0,9³*0,1²=0.0583
• P АВ (t) = P один(t)+ P двойн(t)=0.9763

8.

Метод прямого перебора состояний
или метод гипотез
• эффективен только при малом количестве
элементов, поскольку число состояний
системы из n элементов составляет . N 2 n
• Если в таблицу состояний включать только
сочетания, отвечающие работоспособному
(или только неработоспособному) состоянию
системы в целом, то расчет может быть
упрощен.
• При равнонадежных элементах расчет
упрощается

9.

Метод разложения относительно особого
элемента
• Метод разложения относительно особого
элемента характеризуется наибольшей
точностью расчета показателей
• Особым элементом является тот элемент
системы, исключение которого позволяет описать
ее последовательно-параллельной схемой
надежности.

10.

Метод разложения относительно
особого элемента
если в системе имеется два особых элемента с вероятностями
безотказной работы p1 (t ) и p2 (t ) , то в системе возможны следующие
состояния H i с вероятностью их появления P( H i ) :
состояние H 1 – особые элементы исправны
P ( H1 ) = p1 (t ) p2 (t ) ;
состояние H 2 – особые элементы неисправны
P ( H 2 ) = [1 p1 (t )] [1 p 2 (t )] ;
состояние H 3 – первый особый элемент исправен, второй –
неисправен
P( H 3 ) = p1 (t ) [1 p 2 (t )] ;
состояние H 4 – второй особый элемент исправен, первый –
неисправен,
P ( H 4 ) [1 p1 (t )] p 2 (t ).

11.

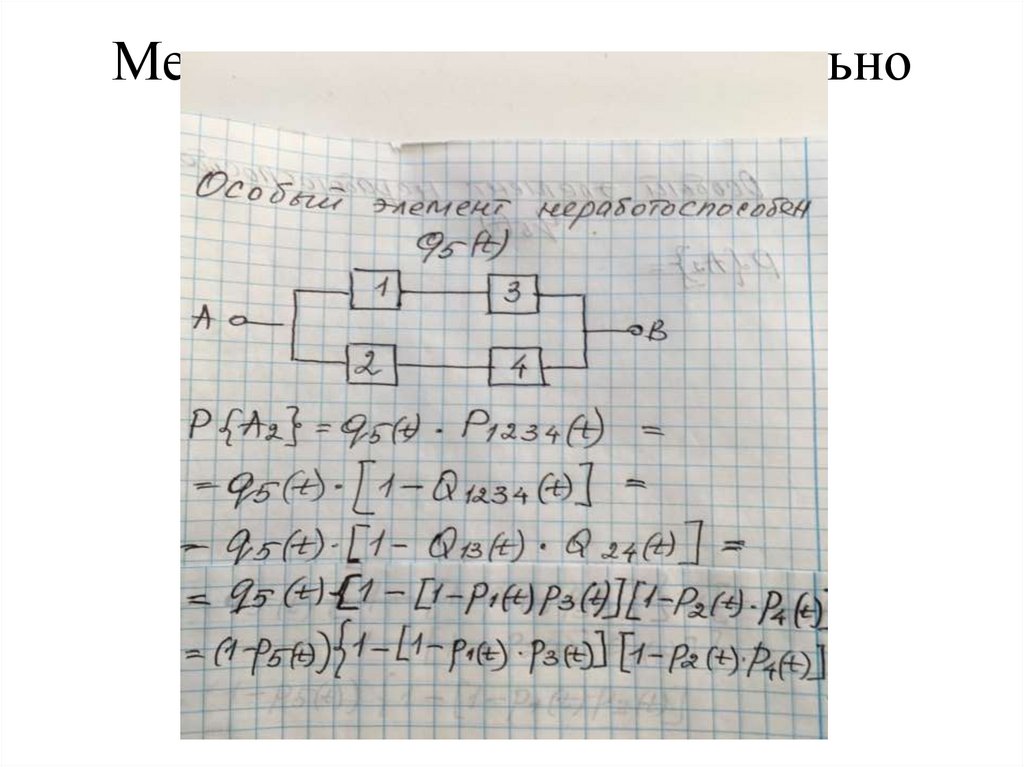
Метод разложения относительно
особого элемента
Так, в структурной схеме расчета надежности, приведенной на
рис. 4.6, можно выделить в качестве особого элемент e5 , который
может находиться в работоспособном состоянии с вероятностью
p5 (t ) и в неработоспособном состоянии с вероятностью q5 (t ) .
Вероятность безотказной работы такой системы определится по
формуле
P{ A} P{ A1} P{ A2 }
p5 (t ) {1 [1 p1 (t )][1 p2 (t )]}{1 [1 p3 (t )][1 p4 (t )]}
[1 p5 (t )]{1 [1 p1 (t ) p3 (t )][1 p2 (t ) p4 (t )]}.
(4.31)

12.

Метод разложения относительно
особого элемента

13.

Метод разложения относительно
особого элемента

14.

Метод разложения относительно
особого элемента
Для получения числового значения вероятности безотказной
работы системы P{A} все элементы примем равнонадежными с
вероятностями безотказной работы к моменту времени t , равными
pi (t ) 0,9 . тогда вероятность работоспособного состояния системы
к этому моменту времени будет равна P{ A} 0,978.
Для упрощения расчетов целесообразно проводить декомпозицию
системы таким образом, чтобы в выделяемой подсистеме было не
более двух или трех особых элементов.

15.

Метод минимальных путей и
сечений
• используют для получения граничных значений показателей
надежности.
• При оценке вероятности безотказной работы системы «сверху»
используют метод «путей», т.е. определяют минимальные наборы
работоспособных элементов (путей), обеспечивающих
работоспособное состояние системы в целом.
• При оценке вероятности безотказной работы системы «снизу»
определяется набор минимальных сечений
• При формировании пути производят подбор вариантов соединения
элементов, обеспечивающих наличие цепи, при неработоспособном
состоянии остальных элементов системы. Набор элементов образует
минимальный путь, если исключение любого элемента из набора
приводит к отказу пути; следовательно, в пределах одного пути
элементы образуют последовательное соединение, все пути находятся
в параллельном соединении.

16.

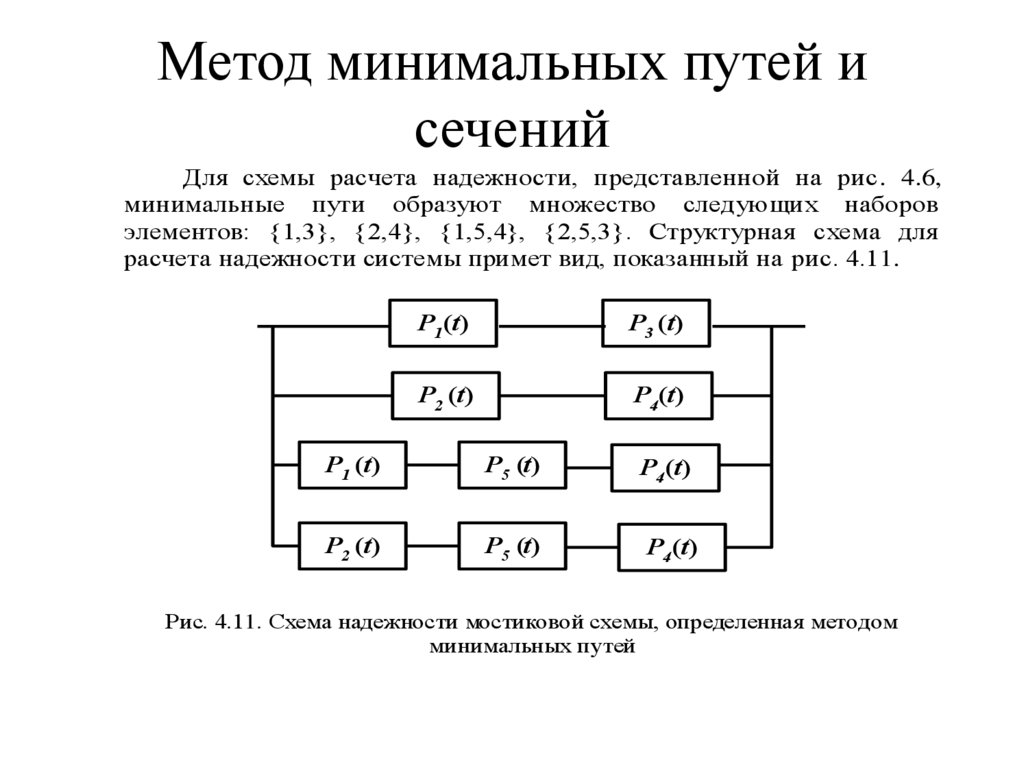
Метод минимальных путей и
сечений
Для схемы расчета надежности, представленной на рис. 4.6,
минимальные пути образуют множество следующих наборов
элементов: {1,3}, {2,4}, {1,5,4}, {2,5,3}. Структурная схема для
расчета надежности системы примет вид, показанный на рис. 4.11.
P1(t)
P3 (t)
P2 (t)
P4(t)
P1 (t)
P5 (t)
P4(t)
P2 (t)
P5 (t)
P4(t)
Рис. 4.11. Схема надежности мостиковой схемы, определенная методом
минимальных путей

17.

Метод минимальных путей и
сечений
Для оценки безотказности системы «сверху» используется
формула
PB (t ) 1 Q13 (t ) Q24 (t ) Q154 (t ) Q253 (t )
1 {1 p1 (t ) p3 (t )} {1 p2 (t ) p 4 (t )}
(4.33)
{1 p1 (t ) p5 (t ) p4 (t )} {1 p2 (t ) p5 (t ) p3 (t )}.
Если вероятность безотказной работы каждого элемента
системы равна pi (t ) 0,9 , то оптимистичная оценка вероятности
безотказной работы системы равна PB (t ) 0,997.

18.

Метод минимальных путей и
сечений
• При оценке вероятности безотказной работы системы «снизу»
определяется набор минимальных сечений, каждое из которых
составлено из минимального количества элементов, перевод которых
из работоспособного состояния в неработоспособное состояние,
вызывает отказ системы.
• При правильном выборе элементов сечения переход любого элемента
в работоспособное состояние восстанавливает работоспособное
состояние системы.
• Таким образом, в пределах сечения элементы соединены параллельно,
т.к. для работы системы достаточно наличия работоспособного
состояния любого из элементов сечения, а сечения образуют
последовательное соединение.

19.

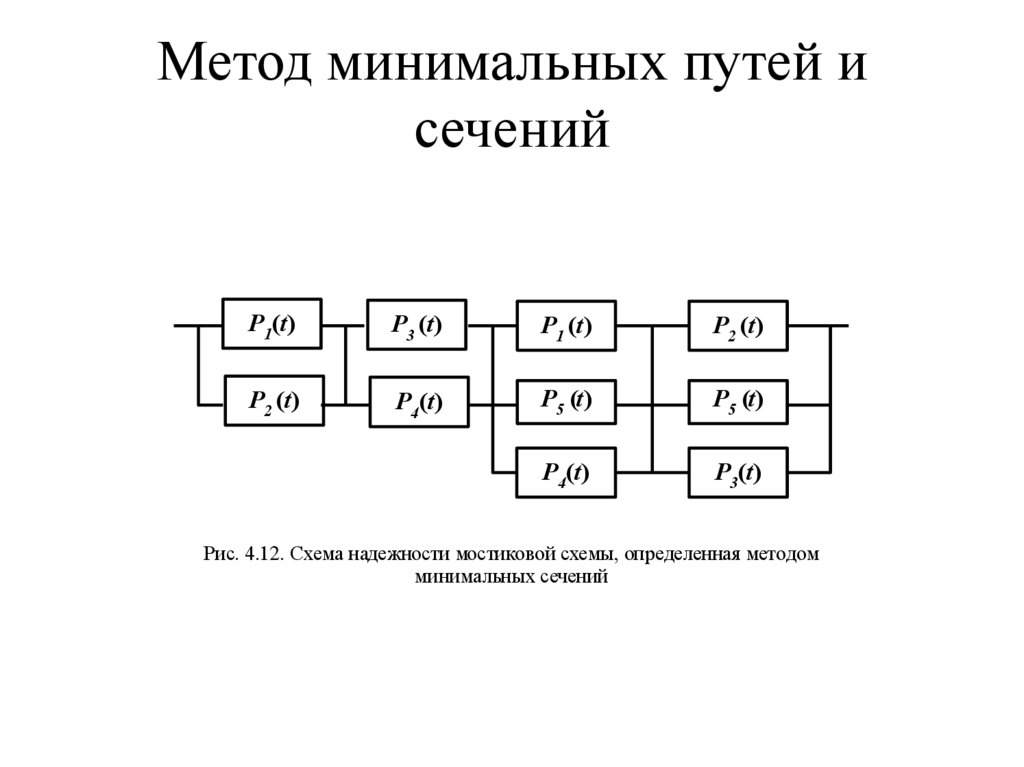
Метод минимальных путей и
сечений
• Для схемы, представленной на рисунке, минимальные
сечения образуют следующие наборы множеств
элементов: {1,2}, {3,4}, {1,5,4}, {2,5,3}.
• в пределах сечения элементы соединены параллельно,
т.к. для работы системы достаточно наличия
работоспособного состояния любого из элементов
сечения
• сечения образуют последовательное соединение.

20.

Метод минимальных путей и
сечений
P1(t)
P3 (t)
P1 (t)
P2 (t)
P2 (t)
P4(t)
P5 (t)
P5 (t)
P4(t)
P3(t)
Рис. 4.12. Схема надежности мостиковой схемы, определенная методом
минимальных сечений

21.

Метод минимальных путей и
сечений
Оценка безотказности «снизу» может быть получена по
формуле
PH (t ) p12 (t ) p34 (t ) p154 (t ) p 253 (t )
{1 [1 p1 (t )][1 p 2 (t )]}{1 [1 p3 (t )][1 p 4 (t )]}
{1 [1 p1 (t )][1 p5 (t )][1 p 4 (t )]}
(4.34)
{1 [1 p 2 (t )][1 p5 (t )][1 p3 (t )]}.
При pi (t ) 0,9 оценка вероятности безотказной работы «снизу»
равна PH (t ) 0,978, что совпадает с вероятностью безотказной
работы системы, полученной методом разложения относительно
особого элемента.

22.

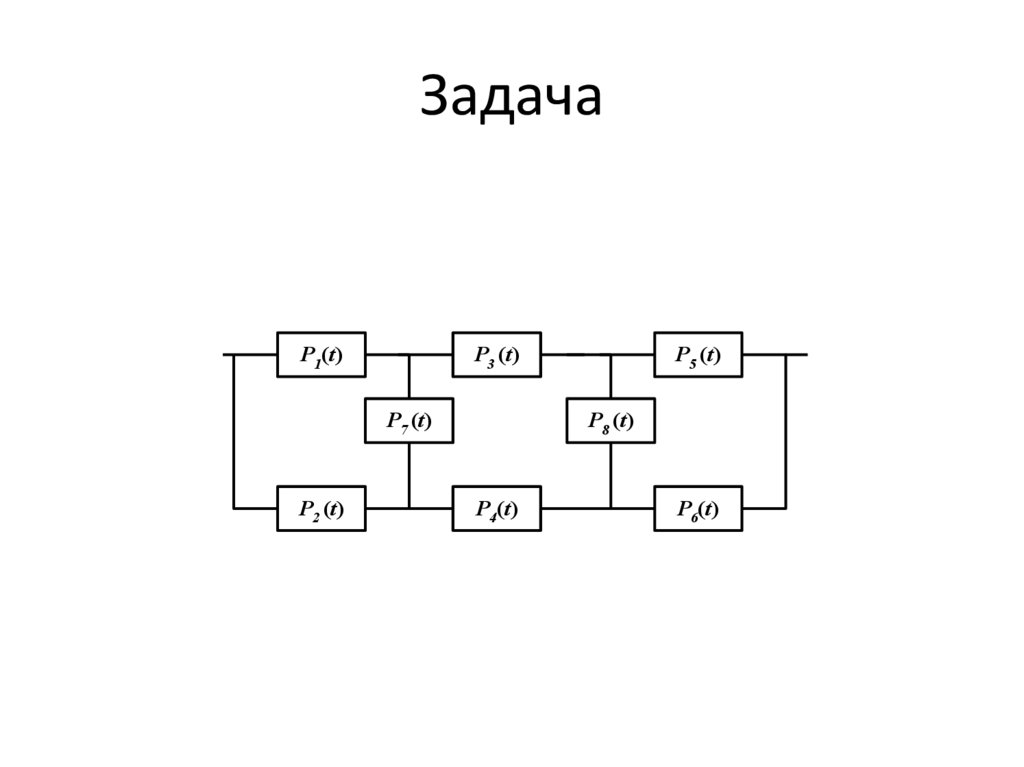
Задача
P1(t)
P3 (t)
P7 (t)
P2 (t)
P5 (t)
P8 (t)
P4(t)
P6(t)

23.

Метод гипотез или прямого перебора

24.

25.

Метод разложения относительно особого элемента

26.

27.

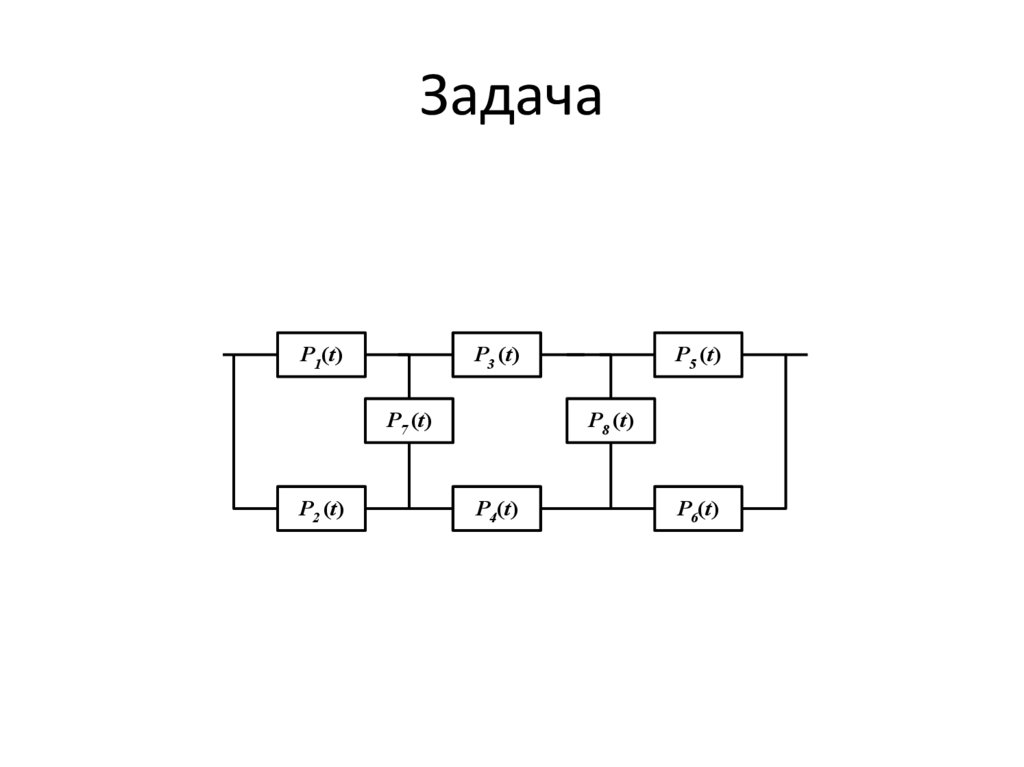
Задача
P1(t)
P3 (t)
P7 (t)
P2 (t)
P5 (t)
P8 (t)
P4(t)
P6(t)

28.

Метод минимальных путей и сечений

29.

Задача для самостоятельного решения – решить тремя методами:
метод гипотез
метод разложения относительно особого элемента
метод минимальных путей и сечений

30.

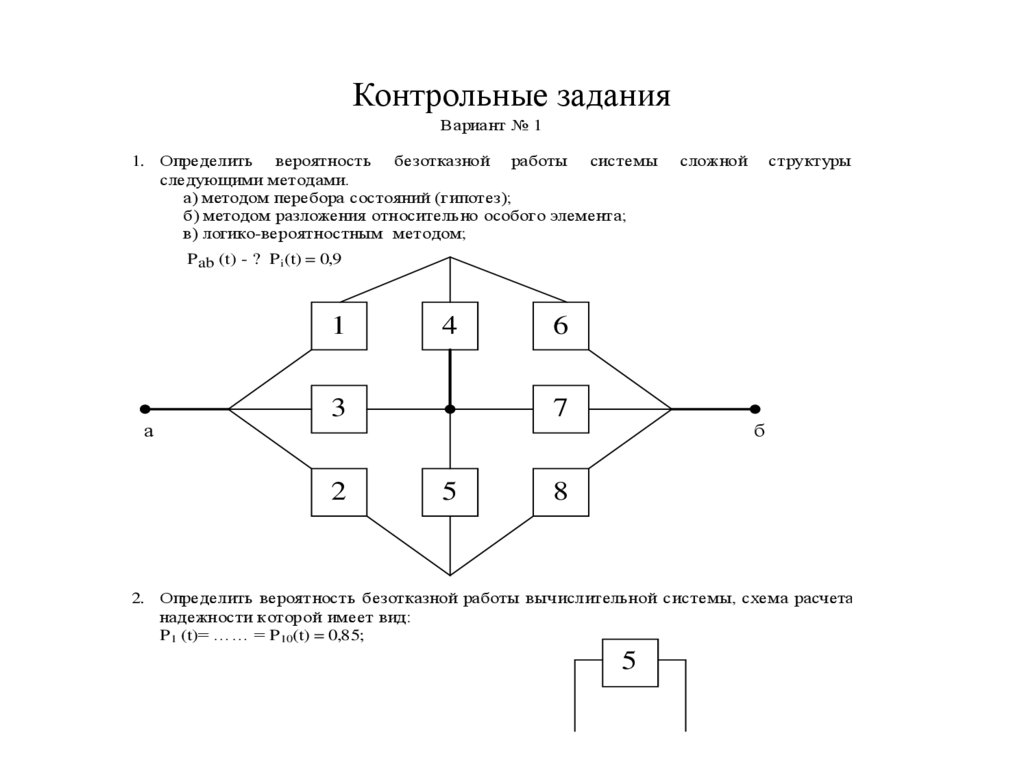
Контрольные задания
Вариа нт № 1
1. Определить вероятность безотказной работы системы
следующими методами.
а) методом перебора состояний (гипотез);
б) методом разложения относительно особого элемента;
в) логико-вероятностным методом;
сложной
структуры
P ab (t) - ? P i(t) = 0,9
1
а
4
3
2
6
7
5
б
8
2. Определить вероят ность безотказной работы выч ислительной с истемы, схема расчета
надежности которой имеет вид:
P 1 (t)= …… = P 10(t) = 0,85;
5

31.

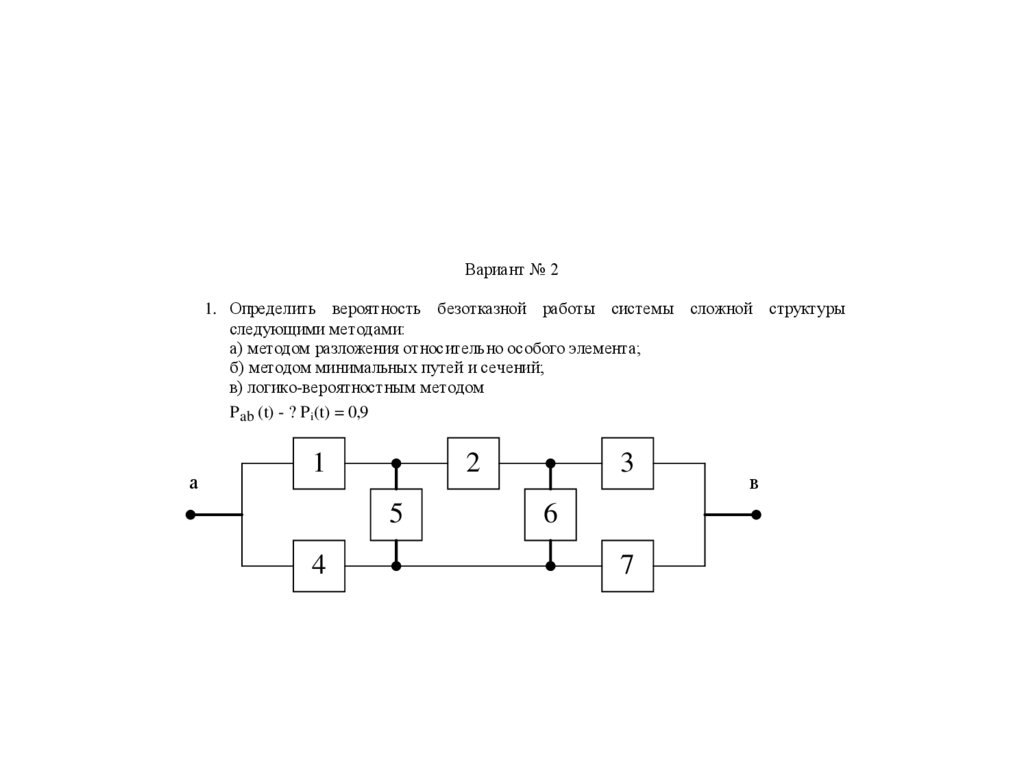
Вариант № 2
1. Определить вероятность безотказной работы системы сложной структуры
следующими методами:
а) методом разложения относительно особого элемента;
б) методом минимальных путей и сечений;
в) логико-вероятностным методом
P ab (t) - ? P i(t) = 0,9
а
1
2
5
4
3
6
7
в

32.

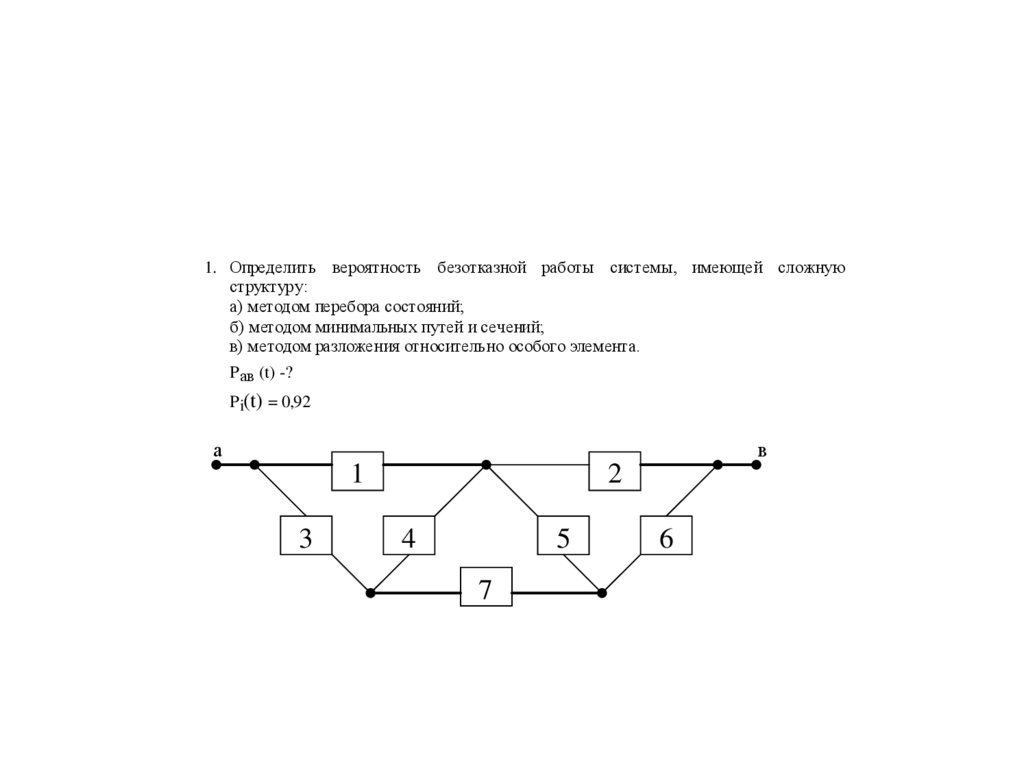
1. Определить вероятность безотказной работы системы, имеющей сложную
структуру:
а) методом перебора состояний;
б) методом минимальных путей и сечений;
в) методом разложения относительно особого элемента.
P ав (t) -?
P i(t) = 0,92
а
в
1
3
2
4
5
7
6

33.

Задание
• Варианты 5,7,12,19,25 можно заменить более
простым (по желанию)
• Решить зачетную задачу тремя методами:
• 1. Метод гипотез или перебора состояний
(составить таблицу состояний с учетом
одиночных отказов)
• 2. метод разложения относительно особого
элемента
• 3. Метод путей и сечений (найти диапазон
ВБР)