Случайные процессы

1.

Случайные процессы

2.

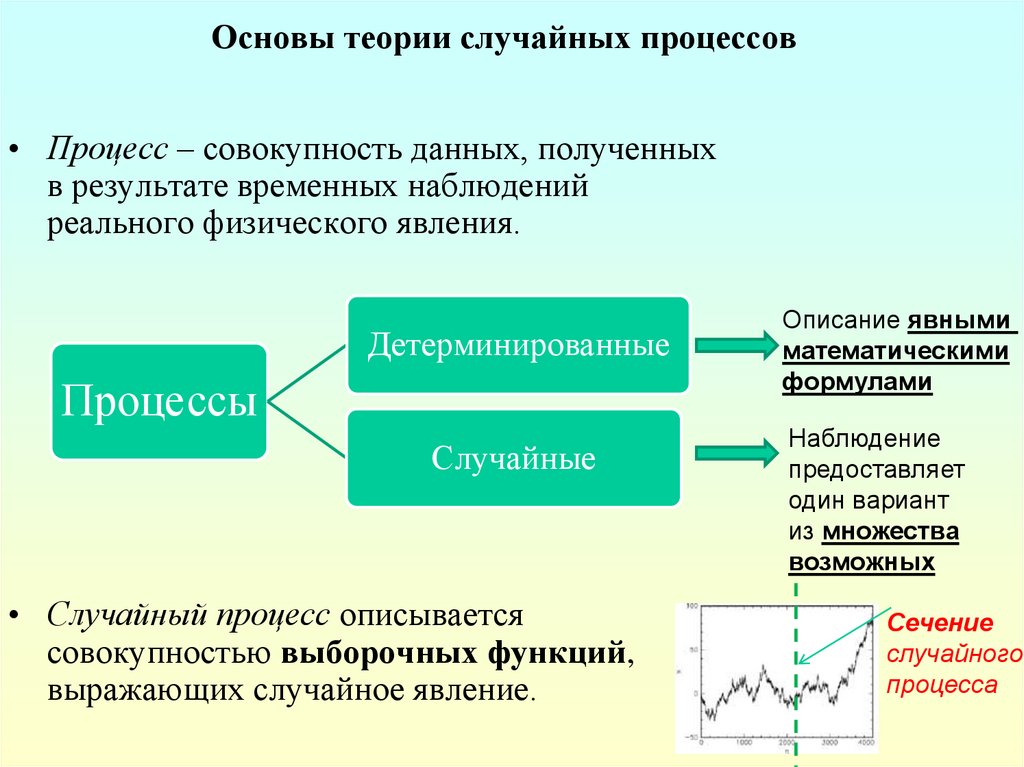
Основы теории случайных процессов
• Процесс – совокупность данных, полученных
в результате временных наблюдений
реального физического явления.
Детерминированные
Процессы
Случайные
• Случайный процесс описывается
совокупностью выборочных функций,
выражающих случайное явление.
Описание явными
математическими
формулами
Наблюдение
предоставляет
один вариант
из множества
возможных
Сечение
случайного
процесса

3.

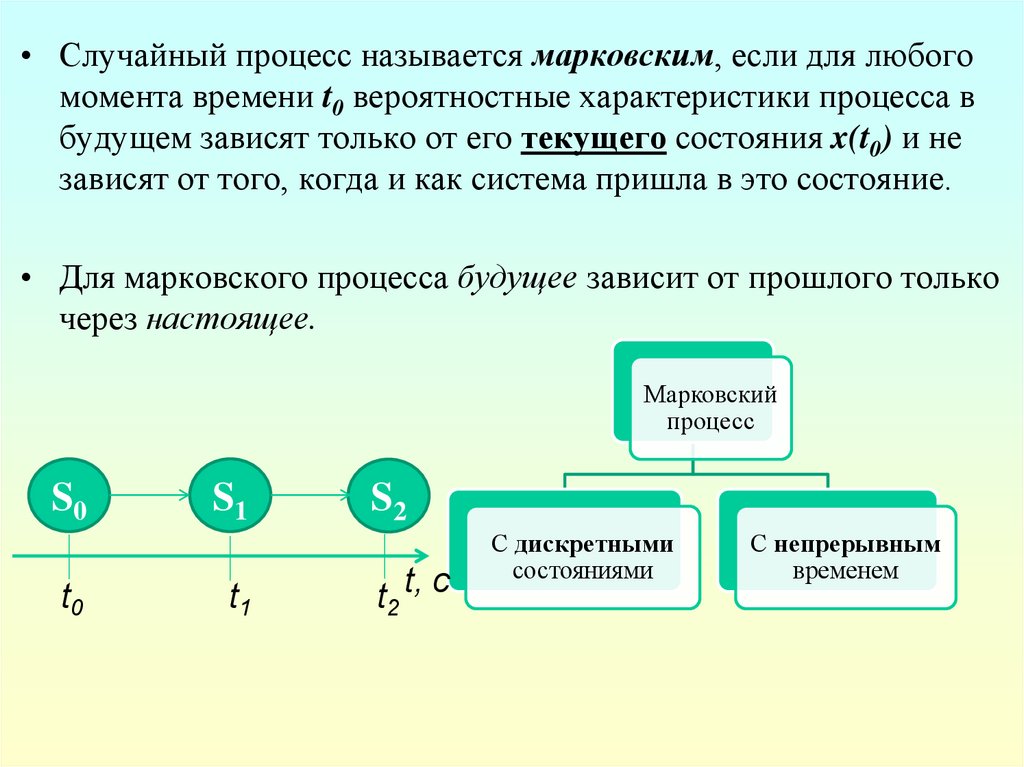
• Случайный процесс называется марковским, если для любого
момента времени t0 вероятностные характеристики процесса в
будущем зависят только от его текущего состояния x(t0) и не
зависят от того, когда и как система пришла в это состояние.
• Для марковского процесса будущее зависит от прошлого только
через настоящее.
Марковский
процесс
S0
t0
S1
t1
S2
t2 t, с
С дискретными
состояниями
С непрерывным
временем

4.

Граф состояний:
S0
S2
S1
S3
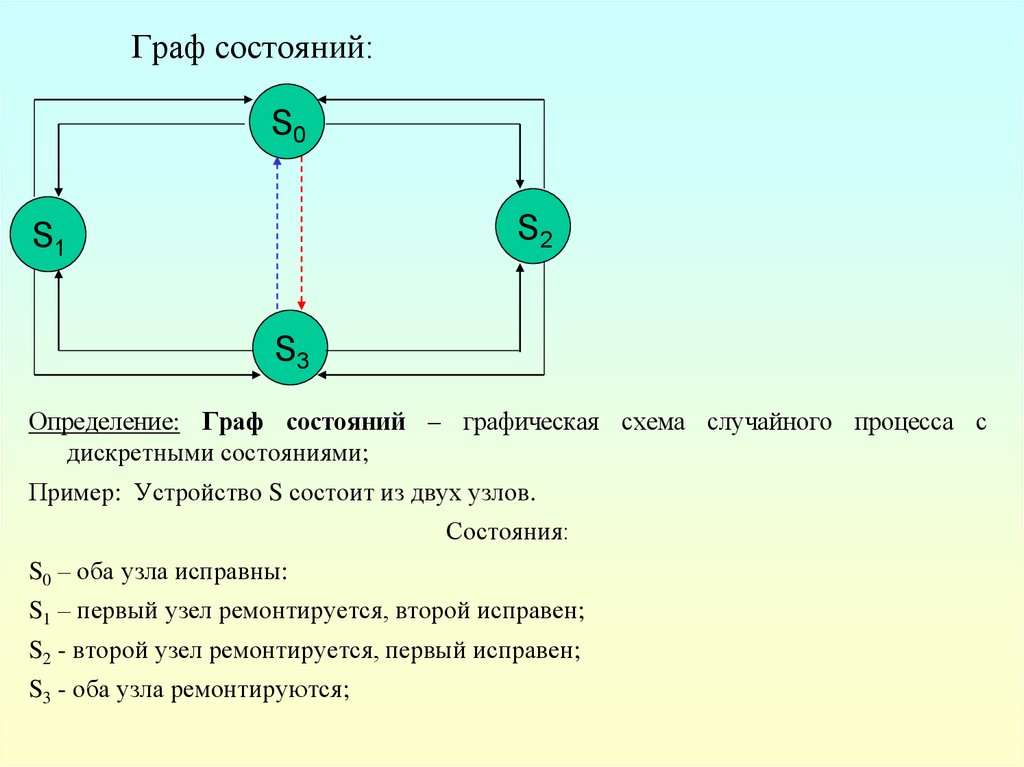
Определение: Граф состояний – графическая схема случайного процесса с
дискретными состояниями;
Пример: Устройство S состоит из двух узлов.
Состояния:
S0 – оба узла исправны:
S1 – первый узел ремонтируется, второй исправен;
S2 - второй узел ремонтируется, первый исправен;
S3 - оба узла ремонтируются;

5.

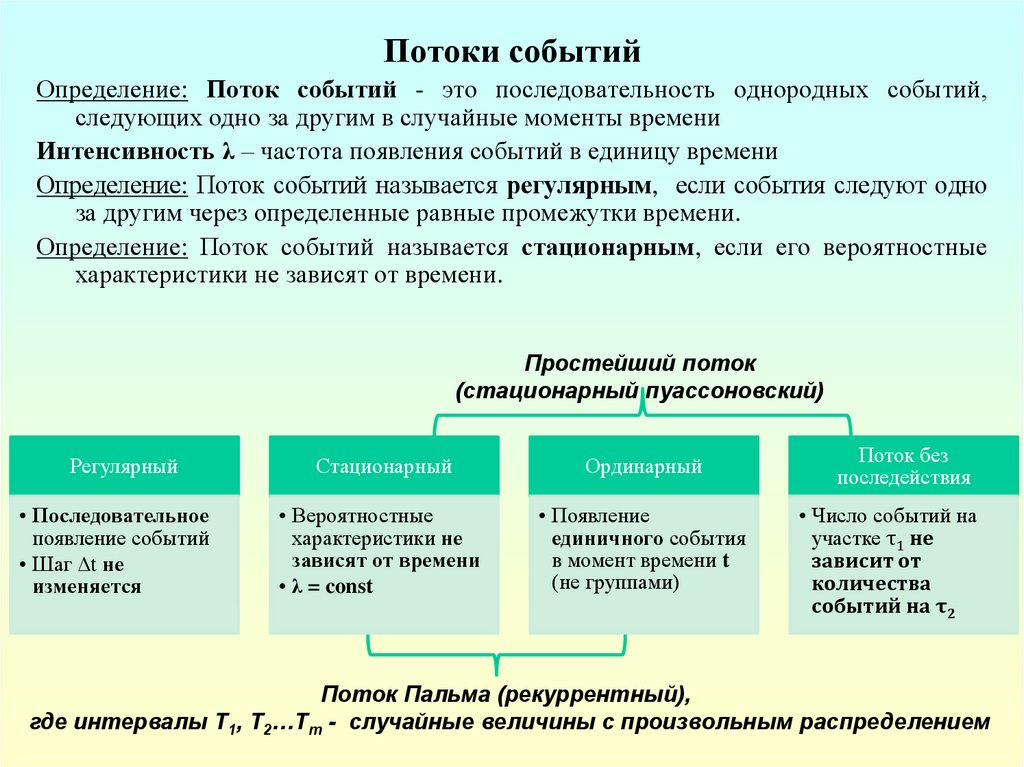
Потоки событий
Определение: Поток событий - это последовательность однородных событий,
следующих одно за другим в случайныe моменты времени
Интенсивность λ – частота появления событий в единицу времени
Определение: Поток событий называется регулярным, если события следуют одно
за другим через определенные равные промежутки времени.
Определение: Поток событий называется стационарным, если его вероятностные
характеристики не зависят от времени.
Простейший поток
(стационарный пуассоновский)
Регулярный
• Последовательное
появление событий
• Шаг ∆t не
изменяется
Стационарный
Ординарный
• Вероятностные
характеристики не
зависят от времени
• λ = const
• Появление
единичного события
в момент времени t
(не группами)
Поток без
последействия
• Число событий на
участке τ1 не
зависит от
количества
событий на τ2
Поток Пальма (рекуррентный),
где интервалы T1, T2…Tm - случайные величины с произвольным распределением

6.

Определение: Поток событий называется потоком без
последействия, если для любых двух непересекающихся
участков времени τ1 и τ2 число событий, попадающих на один
из них, не зависит от числа событий, попадающих на другие.
Определение: Поток событий называется ординарным, если
вероятность попадания на малый участок времени t0 двух и
более событий пренебрежимо мала по сравнению с
вероятностью попадания одного события.

7.

Случайные процессы
Простейший поток событий называется
(стационарным пуассоновским), если он:
Стационарен;
Ординарен;
Не имеет последействия;
простейшим
Теорема: При наложении (суперпозиции) достаточно большого
числа n независимых, стационарных и ординарных потоков с
интенсивностями λi (i=1,2..n) получается поток, близкий к
простейшему с интенсивностью:
n
i 1 i

8.

Случайные процессы
Рассмотрим
простейший
поток
событий
как
неограниченную
последовательность
случайных
точек:
T
t
0
Число m событий, попадающих
распределено по закону Пуассона:
на
( )
Pm ( )
e
m!
отрезок
m
(1)
τ,

9.

Случайные процессы
Математическое ожидание равно дисперсии:
a=σ2=λτ
Вероятность того, что за время τ не произойдет ни одного
события (m=0):
P0 ( ) e
( 2)
Найдем распределение интервала времени Т между
произвольными
двумя
соседними
событиями
простейшего потока.

10.

Случайные процессы
Вероятность того, что на участке времени длиной t не
появится ни одного из последующих событий, равна:
P(T t ) e
(3)
Вероятность противоположного события, т.е. функция
распределения случайной величины T:
F (t ) P(T t ) 1 e
( 4)
Плотность вероятности случайной величины есть
производная ее функции распределения:
(t ) F (t ) e
(5)

11.

Случайные процессы
Распределение, задаваемое функцией распределения (4)
или плотностью вероятности (5) называется
показательным (или экспоненциальным)
Таким образом, интервал времени между двумя
соседними
произвольными
событиями
имеет
показательное
распределение,
для
которого
математическое
ожидание
равно
среднему
квадратическому отклонению случайной величины:
a=σ=1/λ

12.

Случайные процессы
Важнейшее свойство показательного распределения:
Если промежуток времени, распределенный по
показательному закону, уже длился некоторое время τ
то это никак не влияет на закон распределения
оставшейся части промежутка (T- τ). Он будет таким
же, как и закон распределения всего промежутка Т.
Для простейшего потока с интенсивностью λ вероятность
попадания на элементарный отрезок времени Δt хотя
бы одного события:
P t P(T t ) 1 e t
t
( 6)

13.

Основоположник
теории массового обслуживания
Андре́й Никола́евич
Колмого́ров (1903—1987)
Профессор МГУ с 1931 года.
Один из крупнейших
математиков XX века.
Один из основоположников
современной теории
вероятностей.
Создатель теории случайных
процессов и теории массового
обслуживания.

14.

Случайные процессы
Уравнения Колмогорова
Рассмотрим пример из Лекции №2.
Пусть λij – интенсивность простейшего потока событий,
под воздействием которых происходит переход
системы из состояния Si в состояние Sj.
Вероятностью i-го состояния называется вероятность
pi(t) того, что в момент t система будет находиться в
состоянии Si.
i 3
t : p (t ) 1
i 0 i

15.

Случайные процессы
Рассмотрим систему в момент t и зададим малый
промежуток времени Δt.
Найдем вероятность p0(t+Δt) того, что система в момент
(t+ Δt) будет находиться в состоянии S0.
Это достигается разными способами:
1) Система в момент t с вероятностью po(t) находилась в
состоянии S0 , и за время Δt не вышла из него.
(λ01+λ02) – интенсивность суммарного простейшего
потока, выводящего систему из состояния S0.
PΔt≈ (λ01+λ02)Δt вероятность выхода системы из
состояния S0.

16.

Случайные процессы
По теореме умножения вероятностей:
p0(t)(1-(λ01+λ02)Δt) - вероятность того, что система
находилась в состоянии S0 и за время Δt не вышла из
него.
2) Система в момент t с вероятностью p1(t) (или p2(t))
находилась в состоянии S1 (или S2) и за время Δt
перешла в состояние S0.
λ10Δt – вероятность перехода системы из состояния S1
в состояние S0.
λ20Δt – вероятность перехода системы из состояния S2
в состояние S0.

17.

Случайные процессы
По теореме умножения вероятностей:
p1(t)λ10Δt - вероятность того, что система находилась в
состоянии S1 и за время Δt перешла в состояние S0.
p2(t)λ20Δt - вероятность того, что система находилась в
состоянии S2 и за время Δt перешла в состояние S0.
По теореме сложения вероятностей:
p0(t+ λ20Δt)= p1(t)λ10Δt+p2(t)λ20Δt+p0(t)(1-(λ01+λ02)Δt).
Отсюда,
p0 (t t ) p0 (t )
p1 (t ) 10 p2 (t ) 20 p0 (t )( 01 02 )
t

18.

Случайные процессы
При Δt 0 получаем дифференциальное уравнение 1го
порядка:
p0 ' (t ) 10 p1 (t ) 20 p2 (t ) ( 01 02 ) p0 (t )
Рассуждая аналогично для других состояний системы S
получаем систему дифференциальных уравнений
Колмогорова для вероятностей системы:
p0 ' (t ) 10 p1 (t ) 20 p2 (t ) ( 01 02 ) p0 (t )
p ' (t ) p (t ) p (t ) ( ) p (t )
( 7)
1
01 0
31 3
10
13
1
p2 ' (t ) 02 p0 (t ) 32 p3 (t ) ( 20 23 ) p2 (t )
p3 ' (t ) 13 p1 (t ) 23 p2 (t ) ( 31 32 ) p3 (t )

19.

Случайные процессы
Правило составления уравнений Колмогорова:
В левой части каждого уравнения стоит
производная вероятности i-го состояния. В правой части сумма произведений вероятностей всех состояний (из
которых есть дуги в i-е состояние) на интенсивности
соответствующих потоков событий, минус суммарная
интенсивность всех потоков, выводящих систему из
данного состояния, умноженная на вероятность i-го
состояния.
Для решения системы (7) необходимо добавить
3
условие: i
p (t ) 1
i 0 i

20.

Случайные процессы
Зададим начальные условия для системы
дифференциальных уравнений (7):
При t=0 p0(0)=1,
p1(0)=p2(0)=p3(0)=0
(предположим, что при t=0 система была исправна,
т.е. находилась в состоянии S0.).
Решение уравнений Колмогорова позволяют найти
все вероятности состояний системы как функции времени.
Особый интерес – предельные (финальные)
вероятности системы (при Δt ).

21.

Случайные процессы
Предельная вероятность состояния Sj. системы S
показывает среднее время пребывания системы в этом
состоянии (в долевом отношении).
Предельные вероятности постоянны в системе
(7) p'0(t)= p'1(t)= p'2(t)=p'3(t)=0.
Получаем СЛАУ, описывающих стационарный
режим:
(
(
(
(
01
)p p p
10
)p p p
20
)p p p
31
)p p p
02
13
23
32
0
1
2
3
10
01
02
13
1
0
0
1
20
31
3
32
23
2
3
2

22.

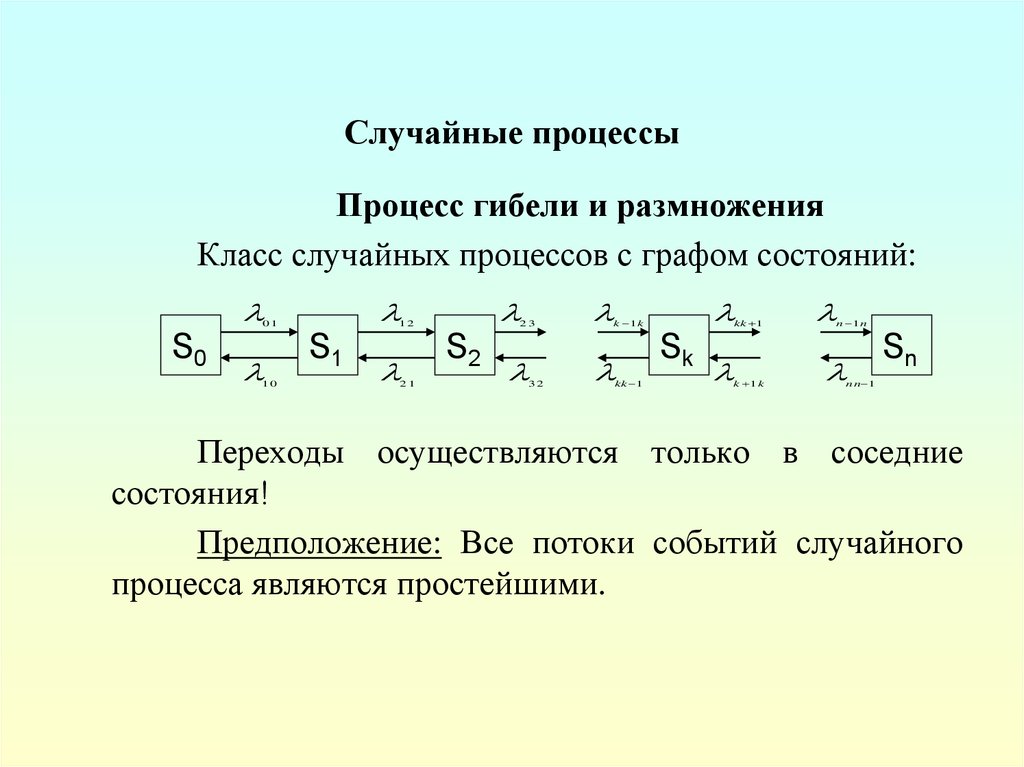
Случайные процессы
Процесс гибели и размножения
Класс случайных процессов с графом состояний:
01
S0
10
12
S1
21
23
S2
32
k 1 k
kk 1
kk 1
Sk
k 1 k
n 1 n
Sn
n n 1
Переходы осуществляются только в соседние
состояния!
Предположение: Все потоки событий случайного
процесса являются простейшими.

23.

Случайные процессы
СЛАУ для предельных вероятностей:
p p
p p
........................
p p
........................
p p
01
0
10
1
12
1
21
2
k 1 k
k 1
kk 1
k
n 1 n
n 1
nn 1
n
Нормировочное условие: p0+p1+…+pn=1

24.

Случайные процессы
Решение СЛАУ:
p (1
...
12
01
n 1 n ....
12
01
10
21
10
nn 1....
21
10
0
p p; p
p;
01
1
12
0
10
) ;
01
01
2
0
21
10
1
p
p;
n 1 n ....
n
nn 1....
12
01
0
21
10
Числители в коэффициентах при p0 представляют
произведение всех интенсивностей потоков слева направо до
состояния Sk (k=I, 2, ..., п), а знаменатели- произведение всех
интенсивностей потоков справа налево до состояния Sk (k=I, 2, ..., п).

25.

Случайные процессы
Пример:
Задан граф состояний системы S:
1
S0
4
2
S1
3
S2
Найти предельные
вероятности системы S.
Решение:
1
2 1
1 2 1 1
p
0
.
706
0
.
176
p
0.706 0.118
p0 (1
) 0.706 1
2
4
3 4
4 3 4
Таким образом, в стационарном режиме система S
находится в состоянии S0 – 70,6% времени; в состоянии
S1 – 17,6% времени; в состоянии S2 – 11,8% времени.

26.

2
1
1
3
4
0,5
2
2
4
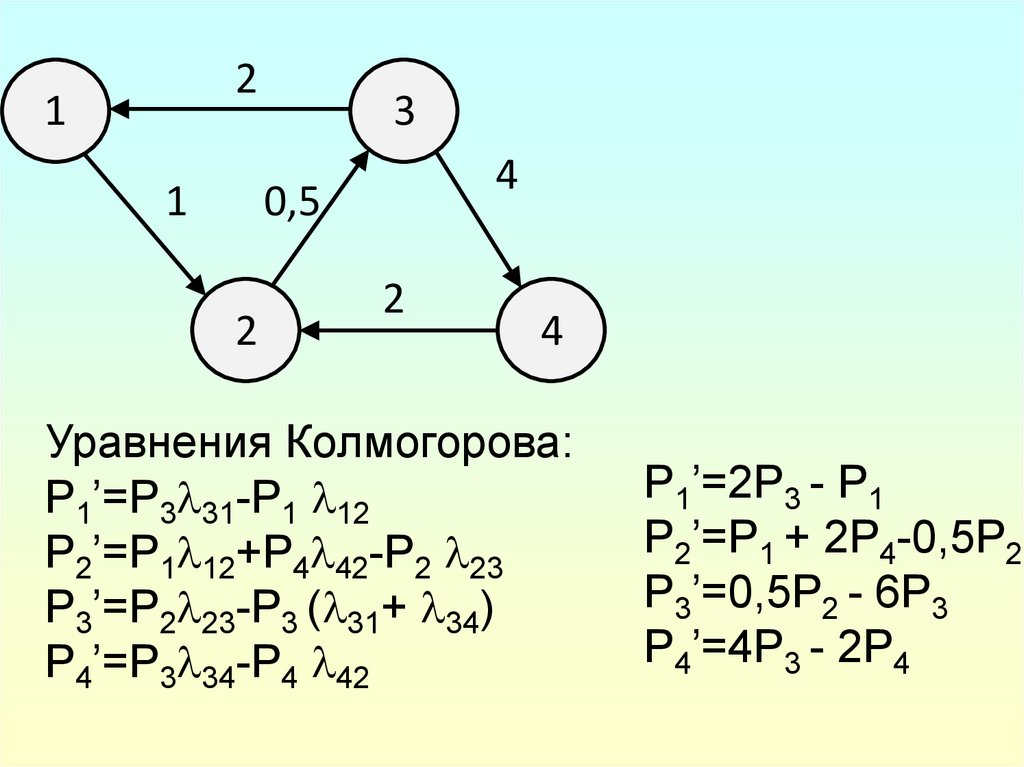
Уравнения Колмогорова:
P1’=P3 31-P1 12
P2’=P1 12+P4 42-P2 23
P3’=P2 23-P3 ( 31+ 34)
P4’=P3 34-P4 42
P1’=2P3 - P1
P2’=P1 + 2P4-0,5P2
P3’=0,5P2 - 6P3
P4’=4P3 - 2P4

27.

Уравнения Колмогорова
для стационарного режима:
P1’=2P3 - P1
=0
P2’=P1 + 2P4-0,5P2=0
P3’=0,5P2 - 6P3
=0
P4’=4P3 - 2P4
=0
Уравнения Колмогорова
в матричном виде
P1
P2
P3
P4
1
-1
0
2
0
2
1
-0,5
0
2
3
0
0,5
-6
0
4
0
0
4
-2

28.

Заменим одну строку матрицы на условие нормировки, добавим столбец
свободных членов, все элементы которого равны 0 кроме ячейки напротив
строки с условием нормировки. Решим систему уравнений и получаем
стационарные вероятности.
1
2
3
4
P1
-1
1
0
1
P2
0
-0,5
0,5
1
P3
2
0
-6
1
P4
0
2
0
1
0
0
0
1
Ответ
P1=0,118
P2=0,706
P3=0,059
P4=0,118