Similar presentations:
Взаимное положение прямой и плоскости, двух плоскостей
1. Начертательная геометрия Семинар №5 Взаимное положение прямой и плоскости, двух плоскостей . Подготовили: Данилова У.Б.,
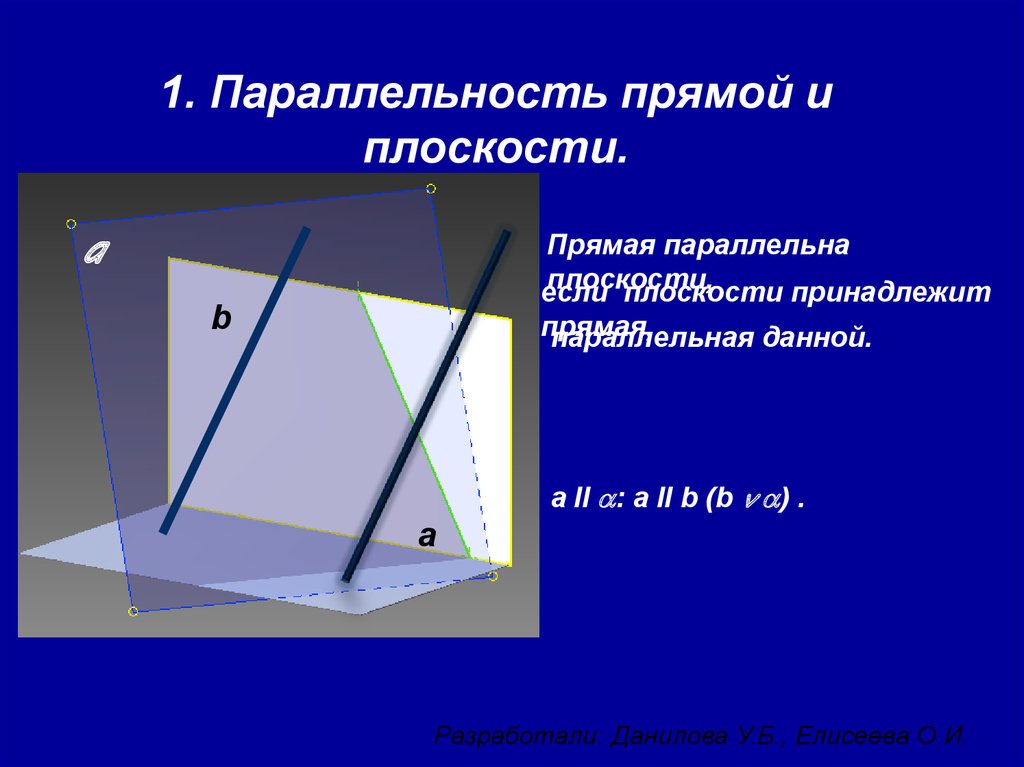
Разработали: Данилова У.Б., Елисеева О.И.2. 1. Параллельность прямой и плоскости.
aПрямая параллельна
плоскости,
если
плоскости принадлежит
b
прямая,
параллельная данной.
a II a: a II b (b v a) .
a
Разработали: Данилова У.Б., Елисеева О.И.
3.
Задача 35. Построить проекции горизонтальнойпрямой , проходящей через точку А параллельно
плоскости, заданной прямыми а и b.
h’’ab
1’’
2’’
h’’A
2’
1. Задаем горизонталь в
плоскости, заданной прямыми a
и b.
2. Через точку А проводим
горизонталь, параллельную
заданной.
1’
Разработали: Данилова У.Б., Елисеева О.И.
4.
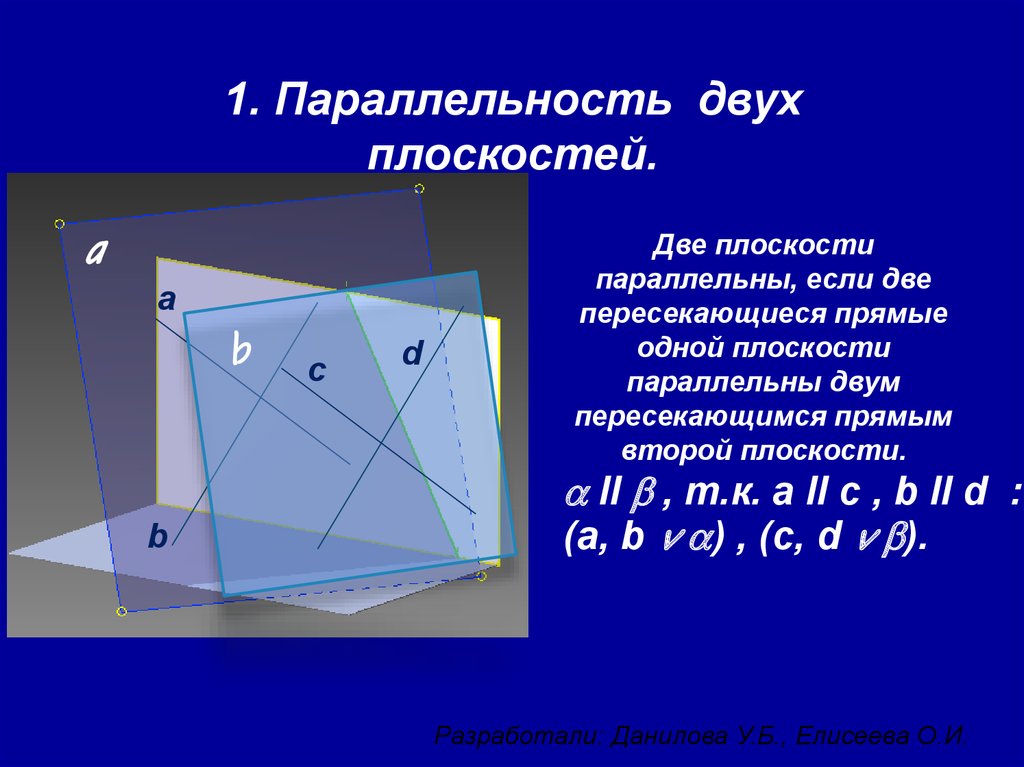
1. Параллельность двухплоскостей.
a
c
b
d
Две плоскости
параллельны, если две
пересекающиеся прямые
одной плоскости
параллельны двум
пересекающимся прямым
второй плоскости.
a II b , т.к. a II c , b II d :
(a, b v a) , (c, d v b).
Разработали: Данилова У.Б., Елисеева О.И.
5. Задача 37а. Построить проекции плоскости, проходящей через точку А, параллельно плоскости, заданной на чертеже. Плоскости
задать горизонталью и фронталью.2’’
fА’’
f’’
1.
hА’’
1’’
h’’
2.
3.
f’
2’
1’
h’
f А’
hА’
4.
Решение.
a-Плоскость общего
положения, заданная
треугольником BCD.
Задаем горизонталь в
плоскости ВCD .
Задаем фронталь в
плоскости ВCD.
Через точку А проводим
горизонталь и фронталь,
параллельно найденным:
hA” II h” , fA” II f”,
hA’ II h’, fA’ II f’.
Разработали: Данилова У.Б., Елисеева О.И.
6.
Задача 37б. Построить проекции плоскости,проходящей через точку А, параллельно плоскости,
заданной на чертеже. Плоскости задать следами.
1.
f0b
2.
1’’
h”A
3.
1’
4.
h’A
h0b
5.
6.
Решение.
a-Плоскость общего положения,
заданная следами.
Если α II β, то следы плоскости b
должны быть параллельными
следам плоскости a
Чтобы точка А (см. задачу 26 б)
принадлежала плоскости β
соответствующие проекции
точки А должны принадлежать
проекциям прямой,
принадлежащей плоскости.
Задаем горизонталь, проходящую
через точку А, h’ II hoα
Находим фронтальный след
горизонтали точку 1.
Через точку 1’’ проводим
фронтальный след плоскости β.
Разработали: Данилова У.Б., Елисеева О.И.
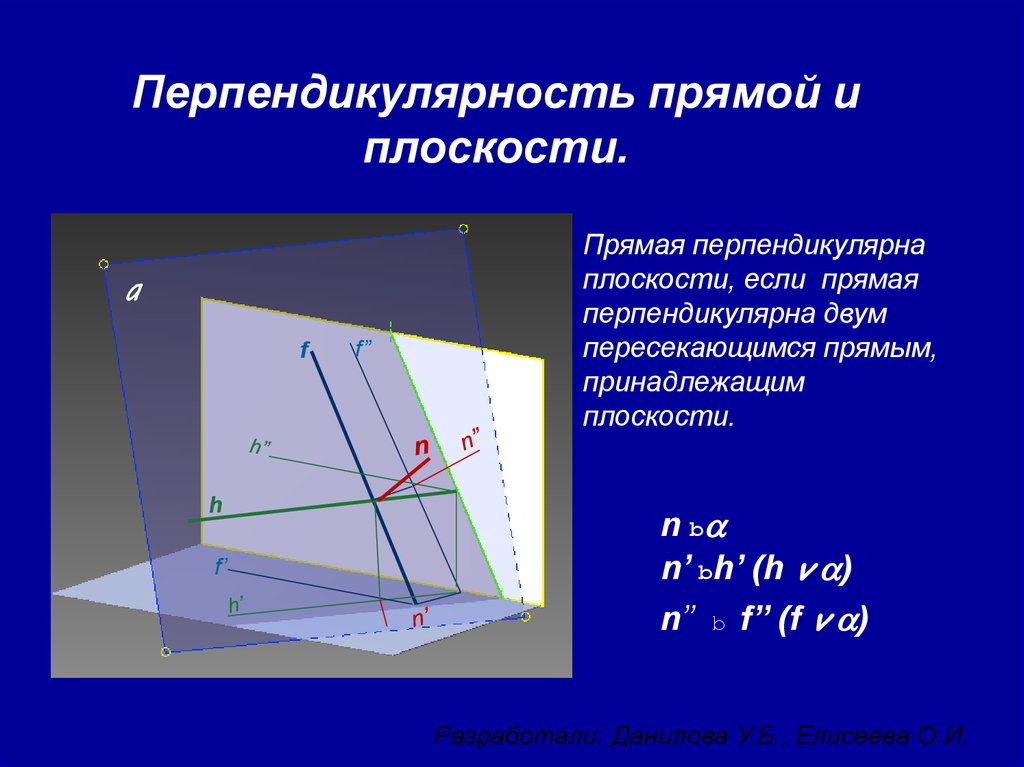
7. Перпендикулярность прямой и плоскости.
ff’
f’’
Прямая перпендикулярна
плоскости, если прямая
перпендикулярна двум
пересекающимся прямым,
принадлежащим
плоскости.
n ba
n’ bh’ (h v a)
n’’ b f’’ (f v a)
Разработали: Данилова У.Б., Елисеева О.И.
8. Перпендикулярность плоскостей.
ff’’
Плоскости
перпендикулярны, если
одна из плоскостей
содержит в себе нормаль
ко второй плоскости.
a
b
b
n
b
a, n v b
f’
Разработали: Данилова У.Б., Елисеева О.И.
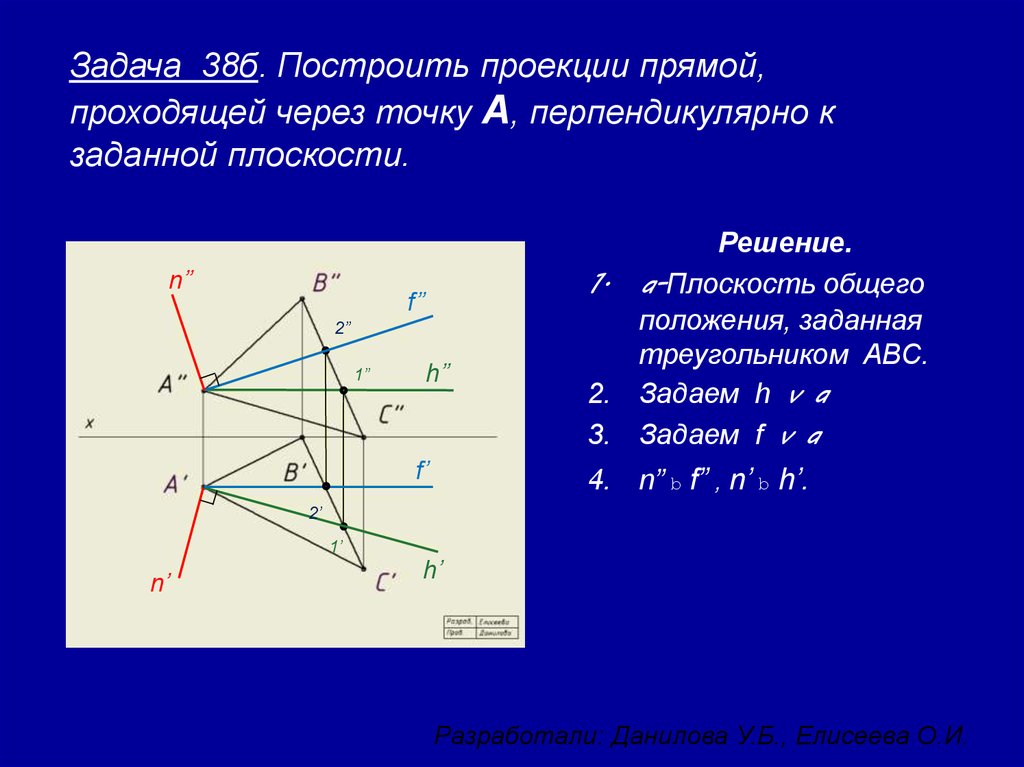
9. Задача 38б. Построить проекции прямой, проходящей через точку А, перпендикулярно к заданной плоскости.
n’’f’’
2’’
1’’
h’’
f’
Решение.
1. a-Плоскость общего
положения, заданная
треугольником ABC.
2. Задаем h v a
3. Задаем f v a
4. n” b f” , n’ b h’.
2’
1’
n’
h’
Разработали: Данилова У.Б., Елисеева О.И.
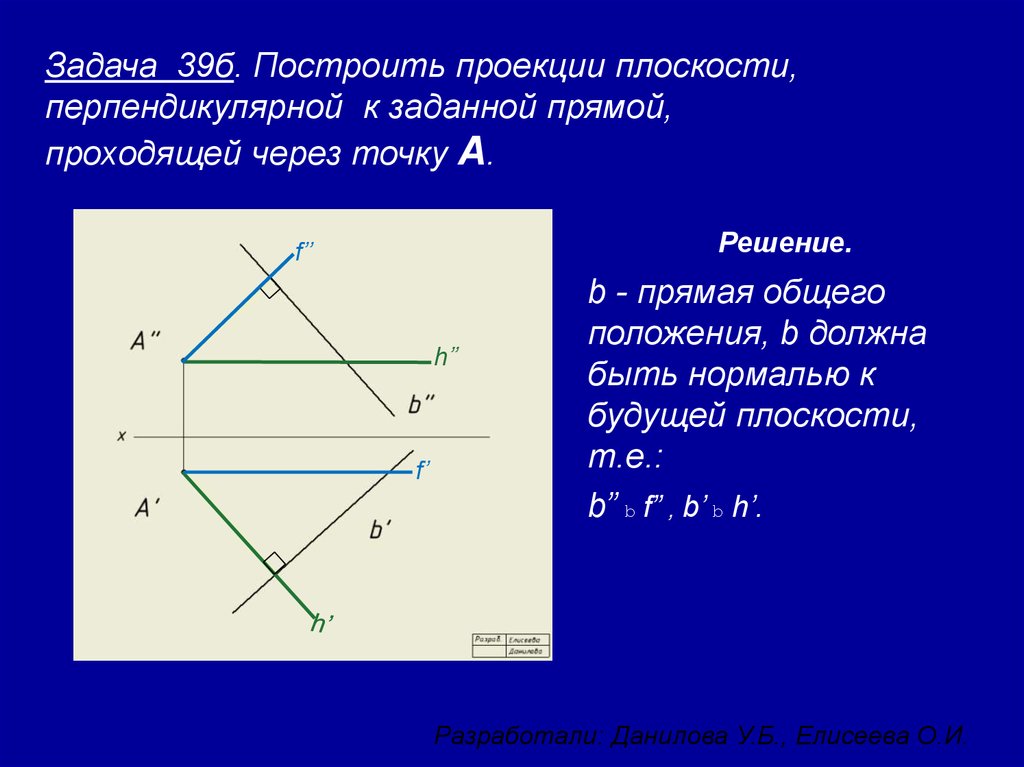
10. Задача 39б. Построить проекции плоскости, перпендикулярной к заданной прямой, проходящей через точку А.
Решение.f’’
h’’
f’
b - прямая общего
положения, b должна
быть нормалью к
будущей плоскости,
т.е.:
b” b f” , b’ b h’.
Разработали: Данилова У.Б., Елисеева О.И.
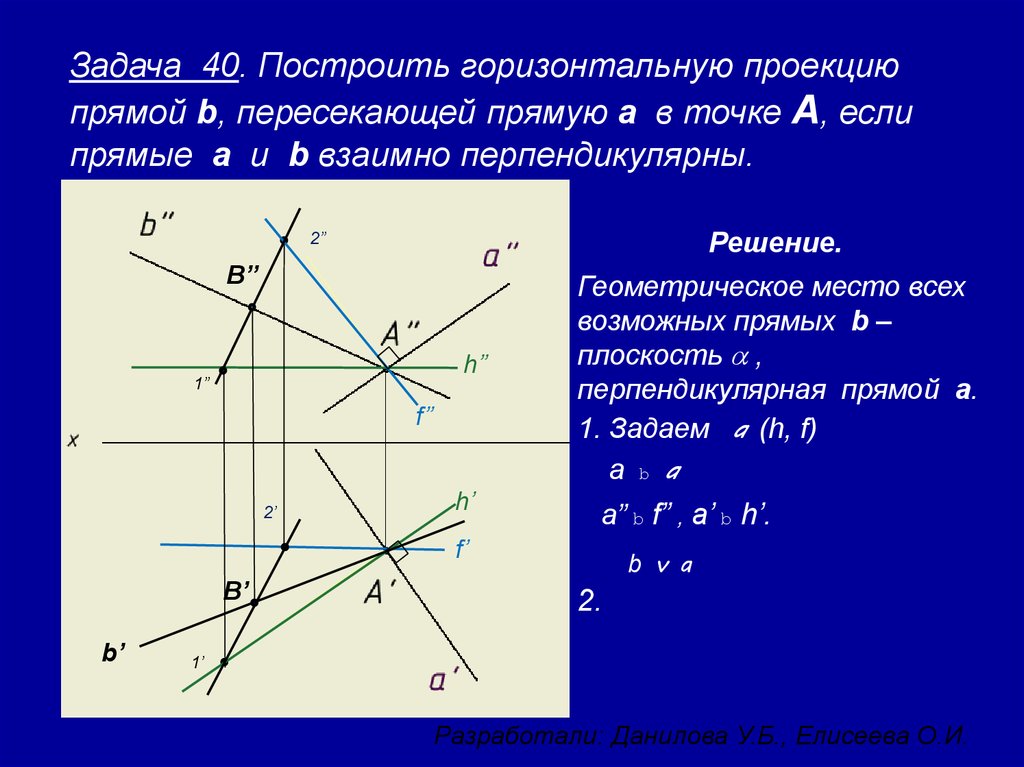
11. Задача 40. Построить горизонтальную проекцию прямой b, пересекающей прямую a в точке А, если прямые a и b взаимно
перпендикулярны.Решение.
2’’
В’’
h’’
1’’
f’’
2’
h’
Геометрическое место всех
возможных прямых b –
плоскость a ,
перпендикулярная прямой a.
1. Задаем a (h, f)
a b a
a” b f” , a’ b h’.
f’
В’
b’
b v a
2.
1’
Разработали: Данилова У.Б., Елисеева О.И.





 drafting
drafting








