Задание плоскости на чертеже. Взаимное положение прямой и плоскости, двух плоскостей. Проекции многогранников

1. ЛЕКЦИЯ 2 Задание плоскости на чертеже. Взаимное положение прямой и плоскости, двух плоскостей. Проекции многогранников.

ЛЕКЦИЯ 2
Начертательная геометрия
1 семестр
для студентов ф-та ИУ
Задание плоскости на чертеже.
Взаимное положение прямой и плоскости, двух плоскостей.
Проекции многогранников.
Подготовили:
доценты кафедры РК-1 Сенченкова Л.С., Палий Н.В.

2.

3. Задание плоскости на
чертеже

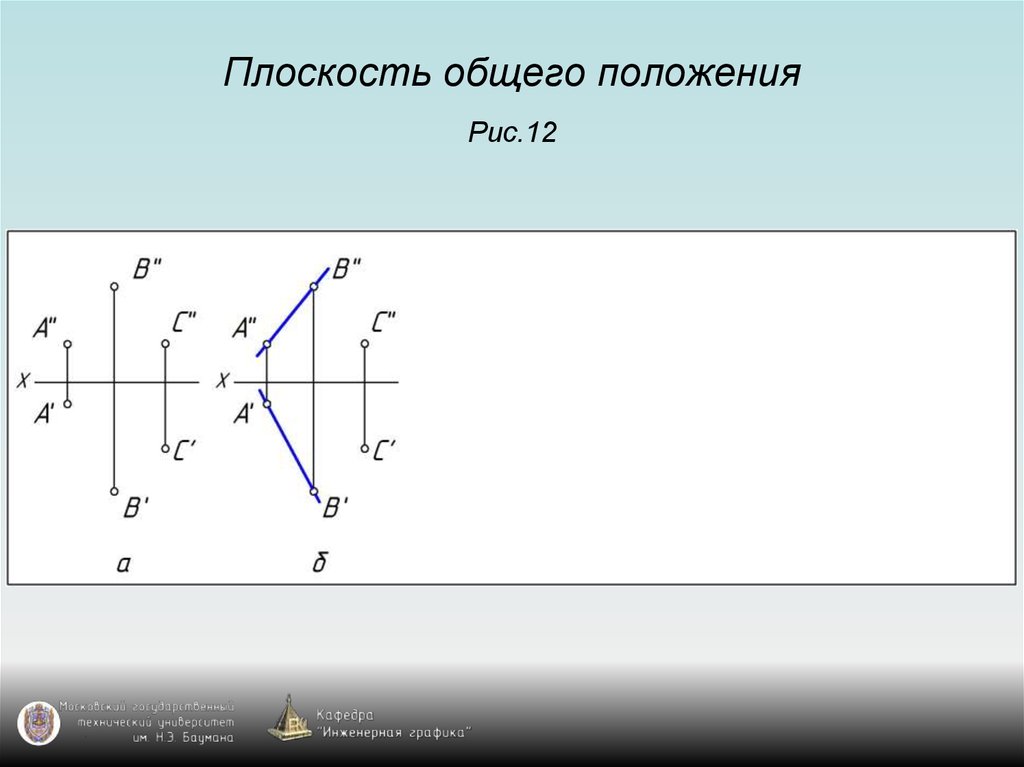
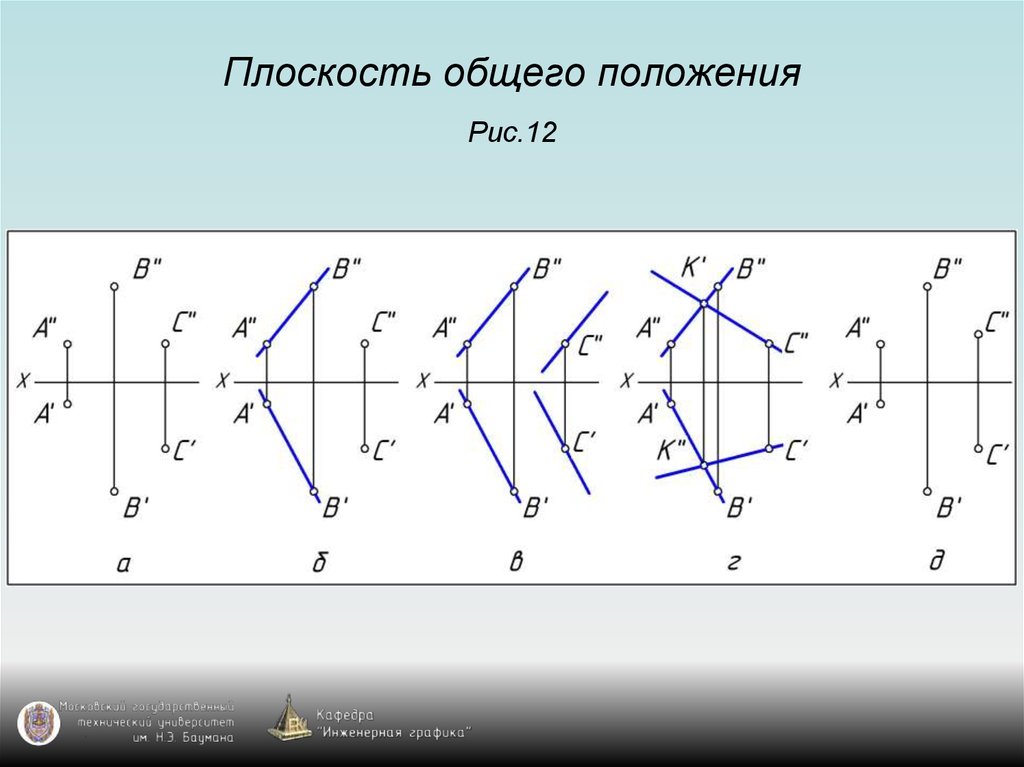
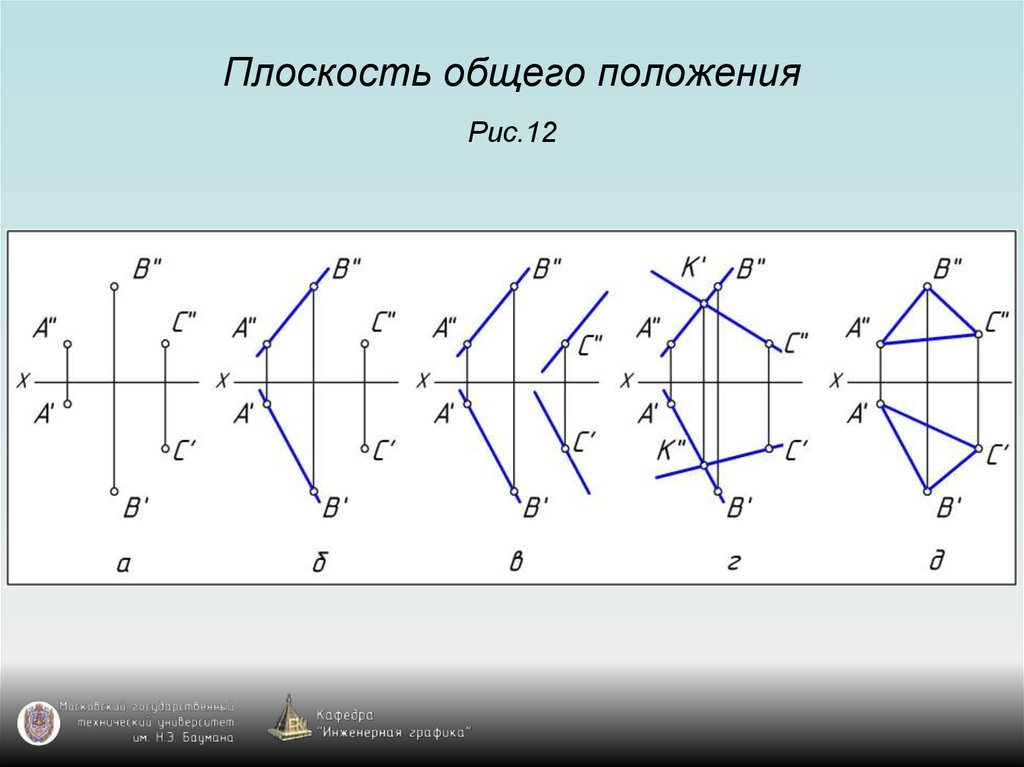
3. Плоскость общего положения Рис.12

4. Плоскость общего положения Рис.12

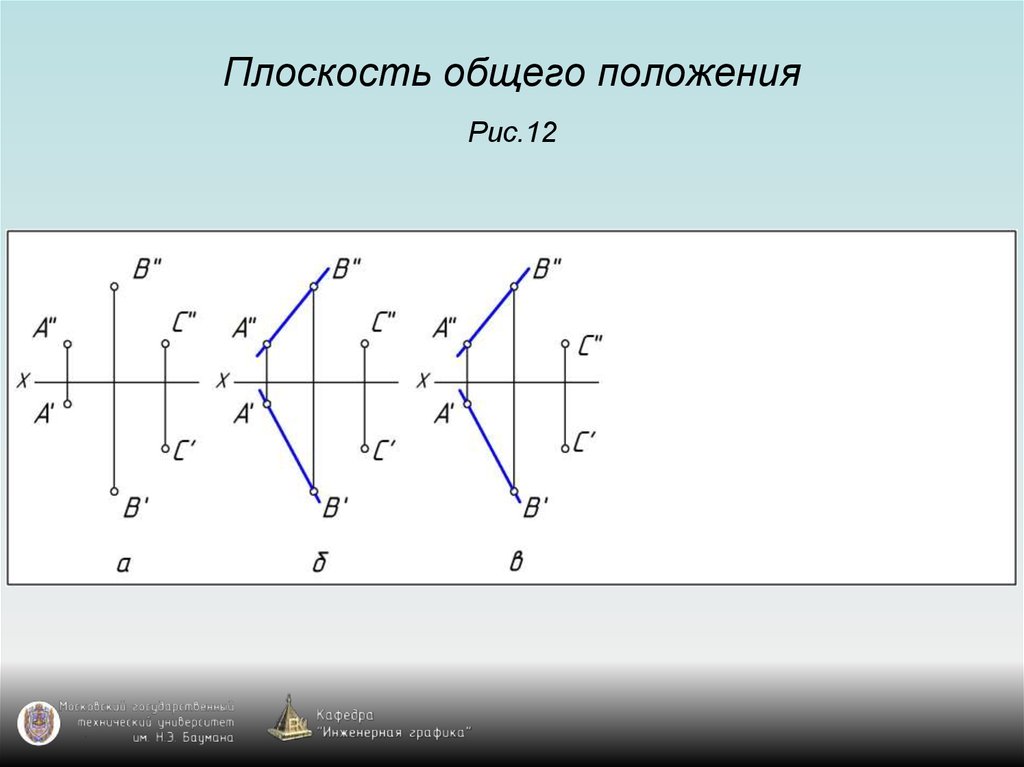
5. Плоскость общего положения Рис.12

6. Плоскость общего положения Рис.12

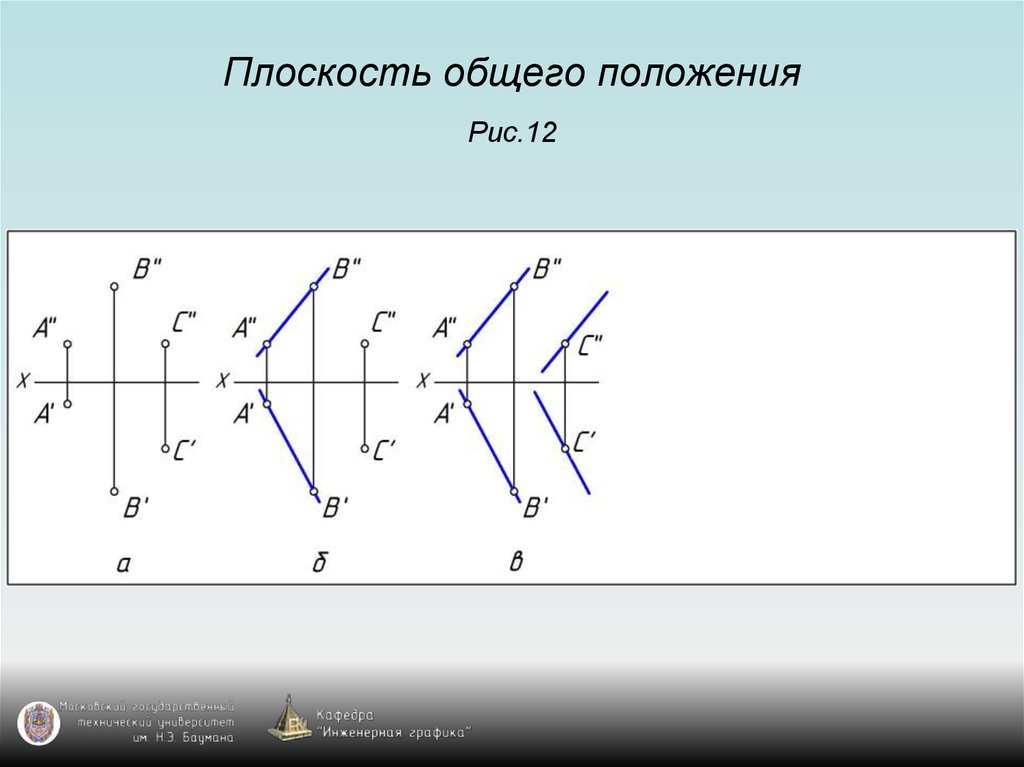
7. Плоскость общего положения Рис.12

8. Плоскость общего положения Рис.12

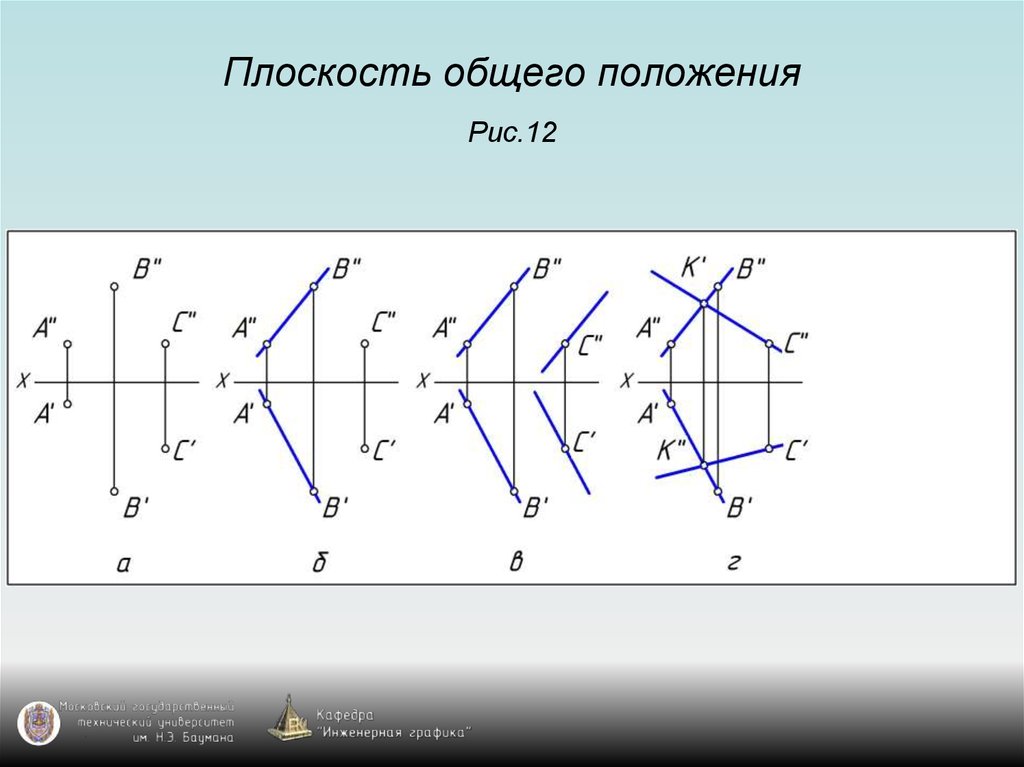
9. Плоскость общего положения Рис.12

10. Плоскость общего положения Рис.12

11. Плоскость общего положения Рис.12

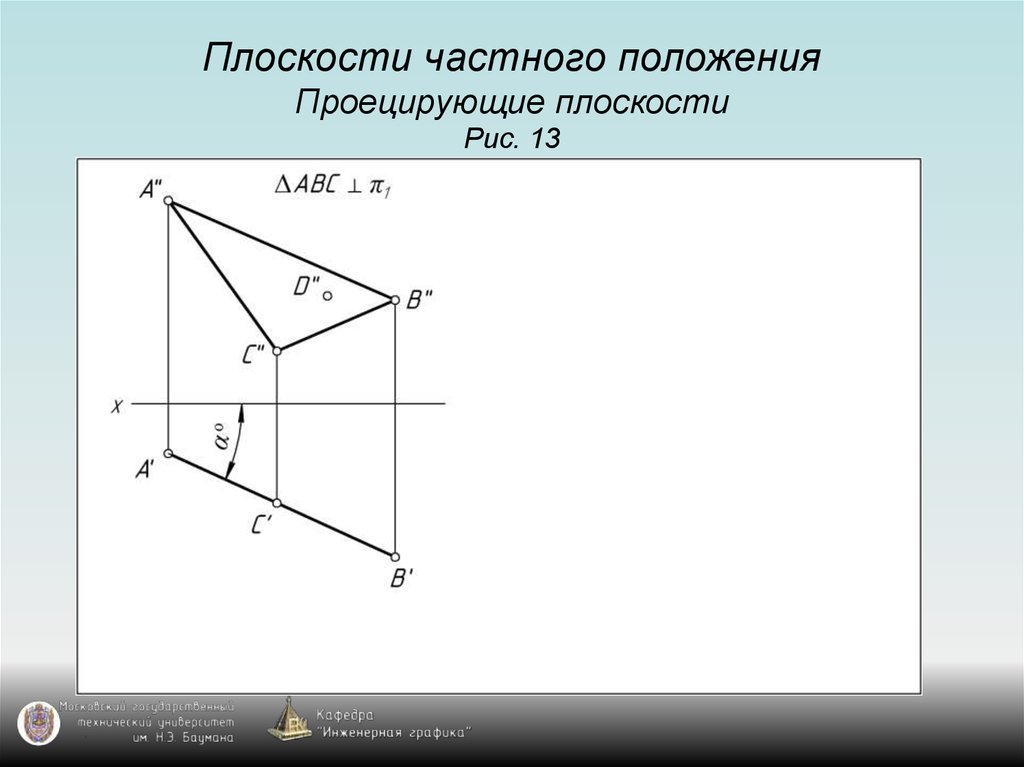
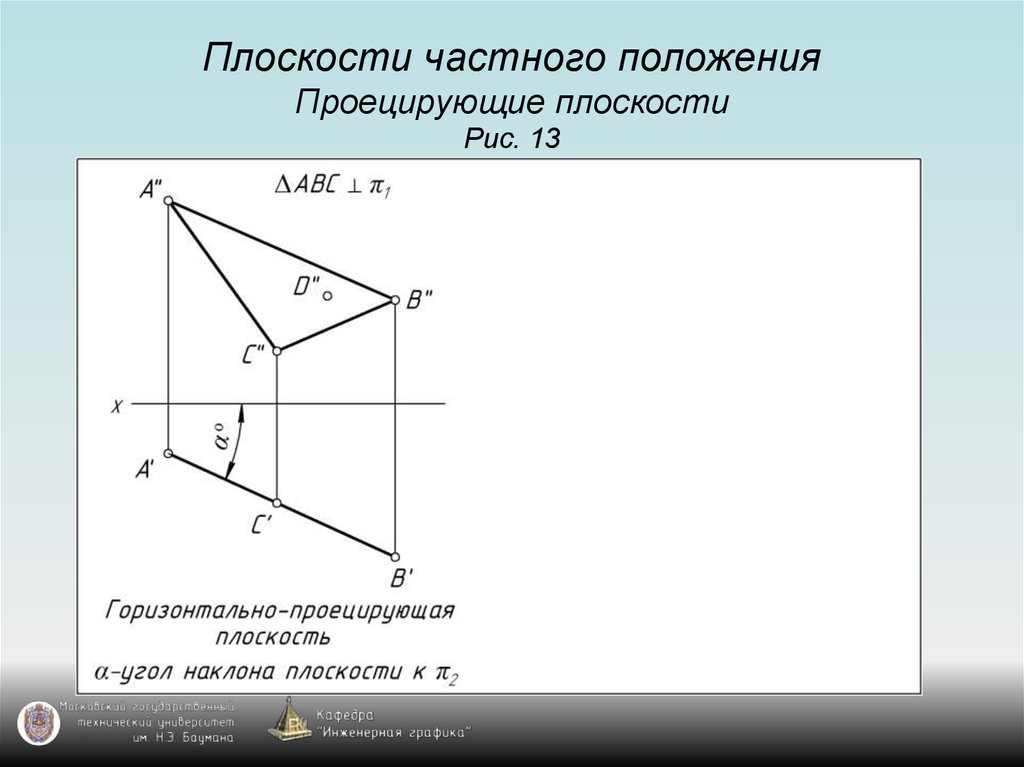
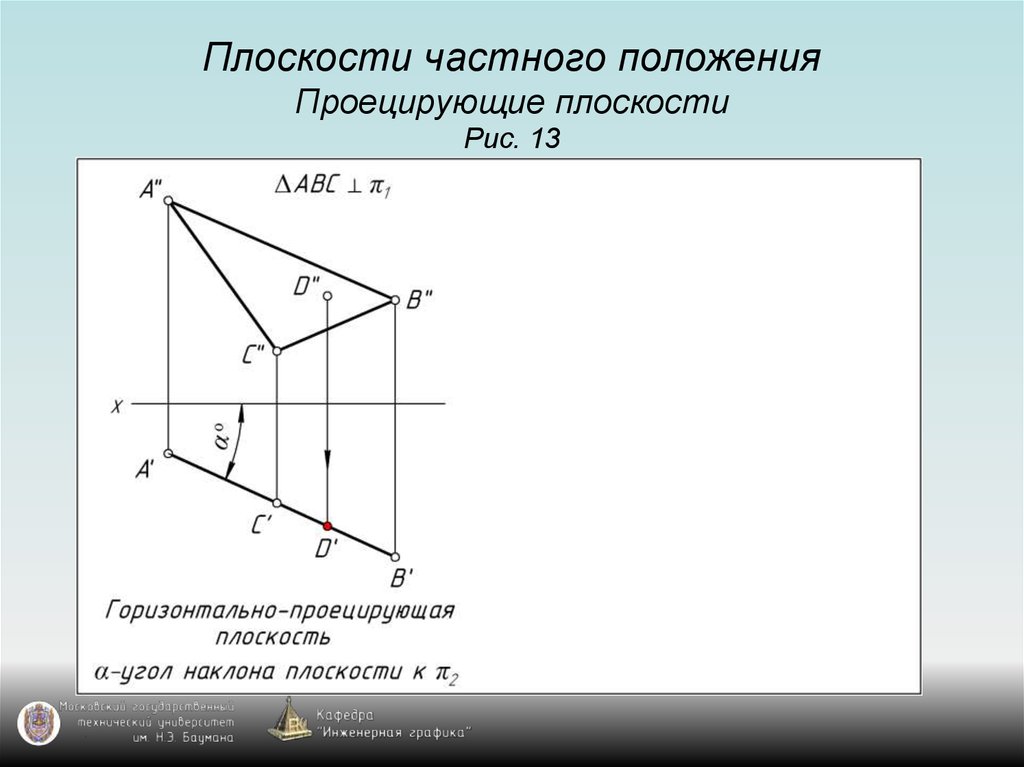
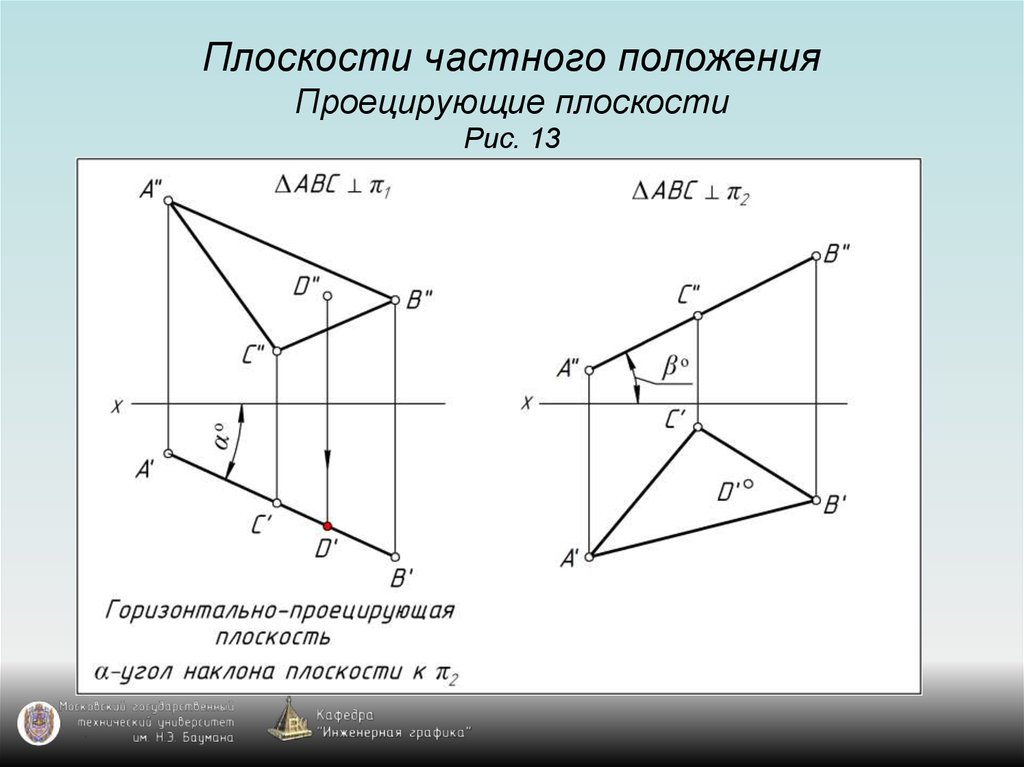
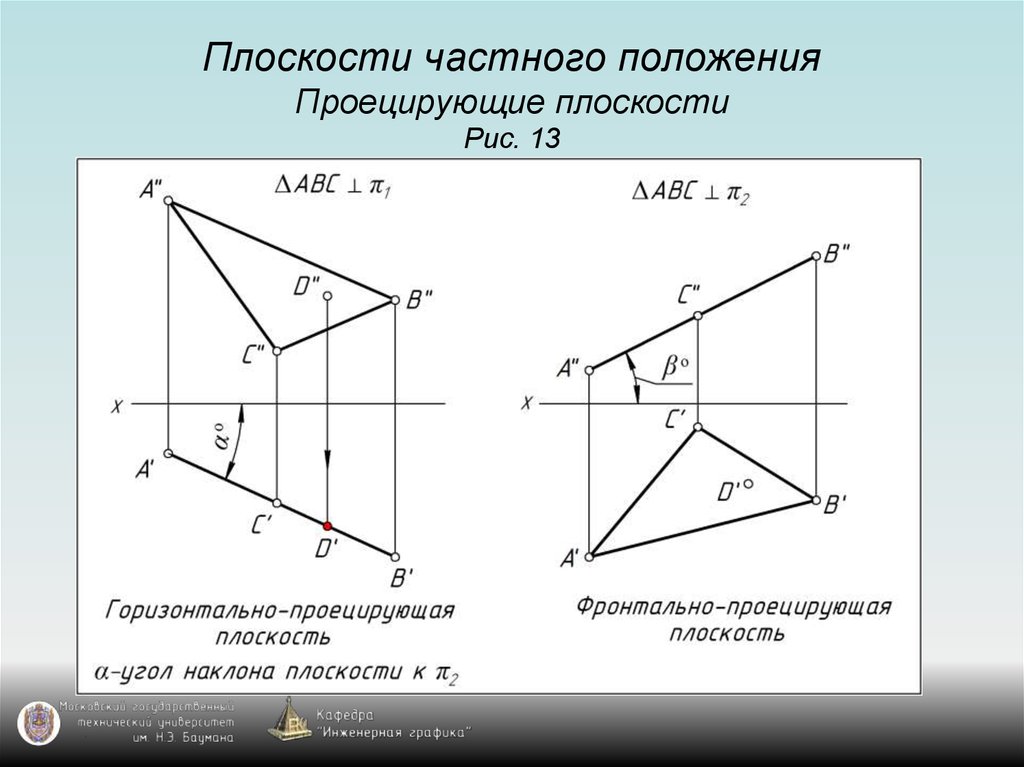
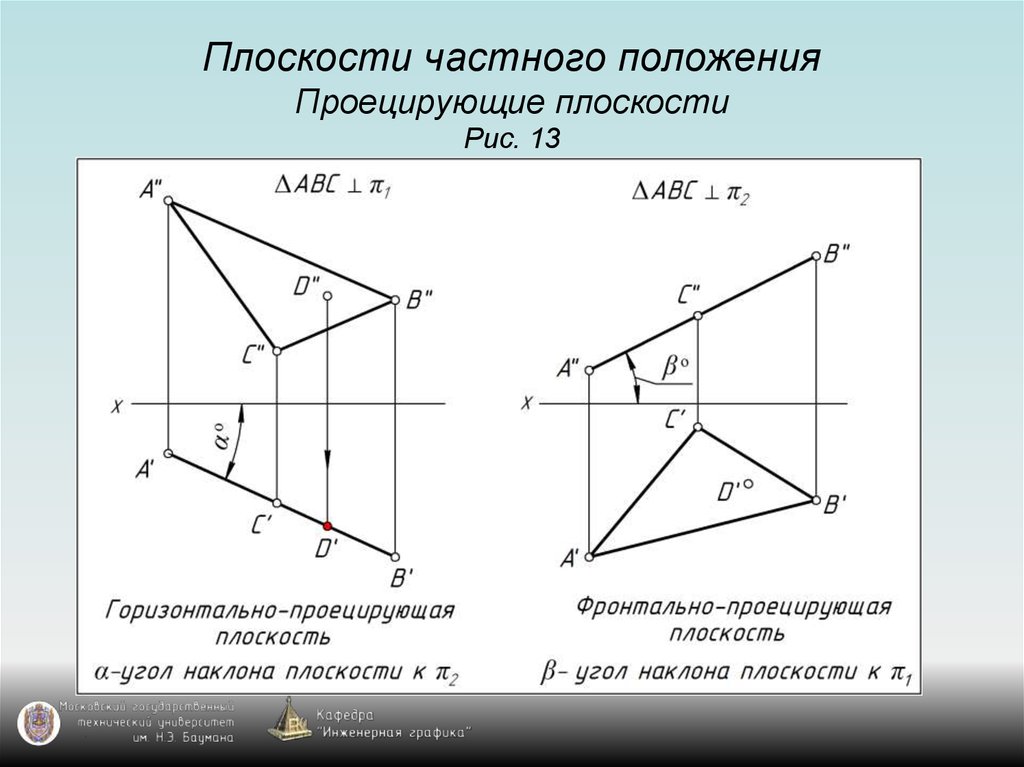
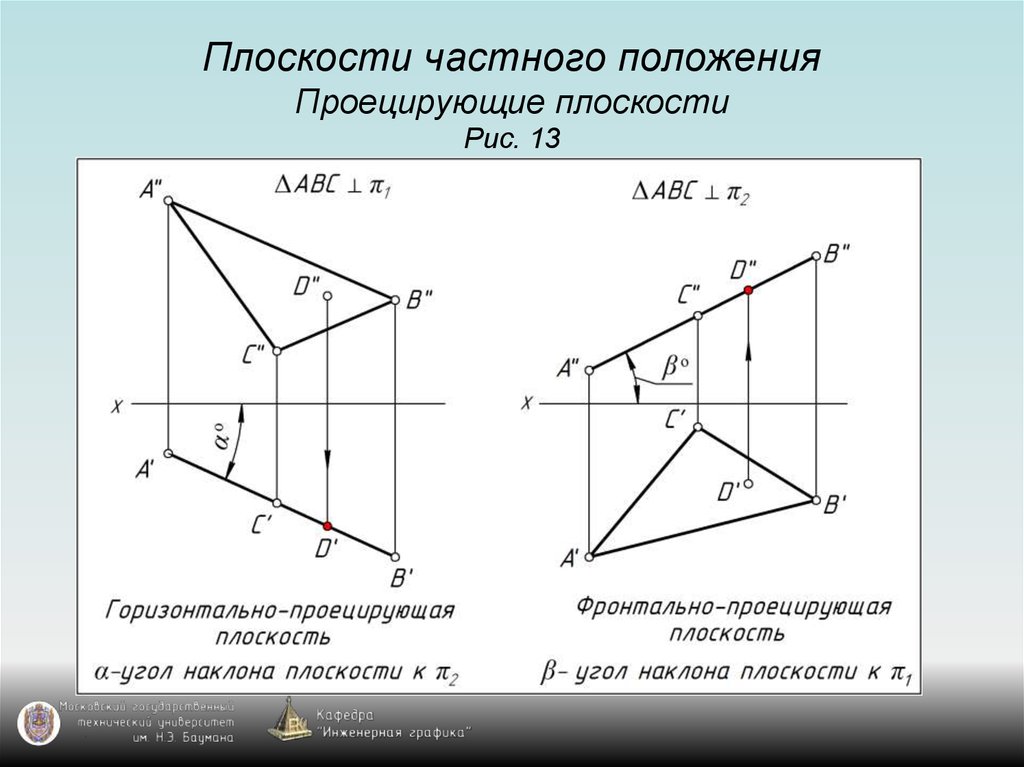
12. Плоскости частного положения Проецирующие плоскости Рис. 13

13. Плоскости частного положения Проецирующие плоскости Рис. 13

14. Плоскости частного положения Проецирующие плоскости Рис. 13

15. Плоскости частного положения Проецирующие плоскости Рис. 13

16. Плоскости частного положения Проецирующие плоскости Рис. 13

17. Плоскости частного положения Проецирующие плоскости Рис. 13

18. Плоскости частного положения Проецирующие плоскости Рис. 13

19. Плоскости частного положения Проецирующие плоскости Рис. 13

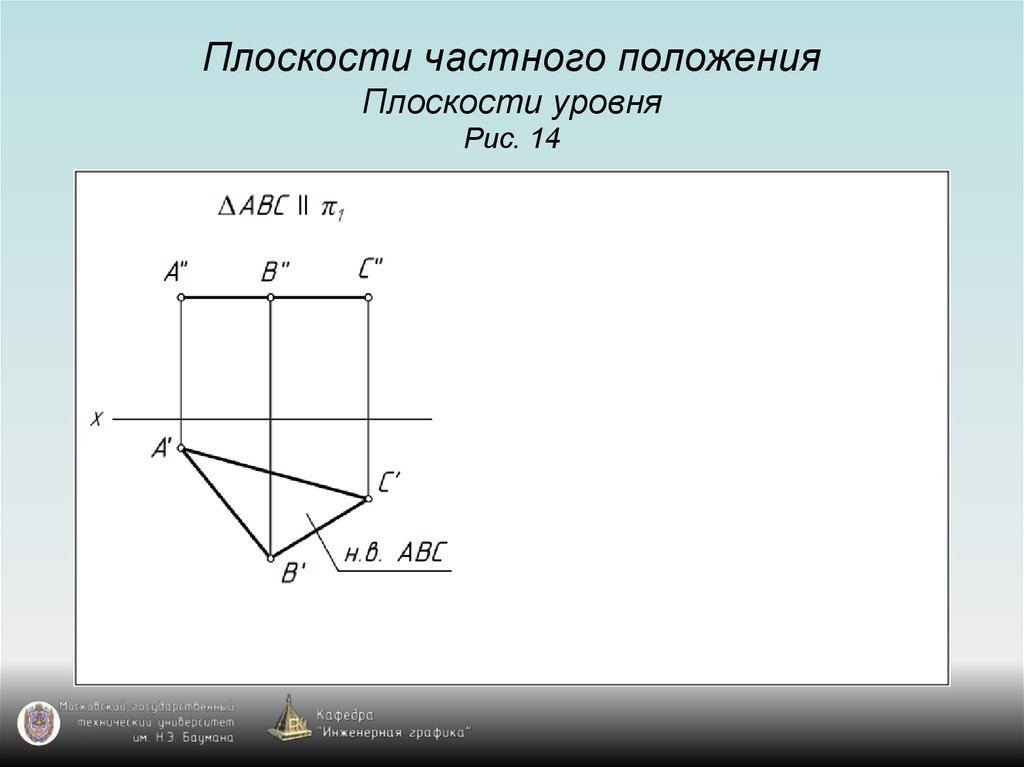
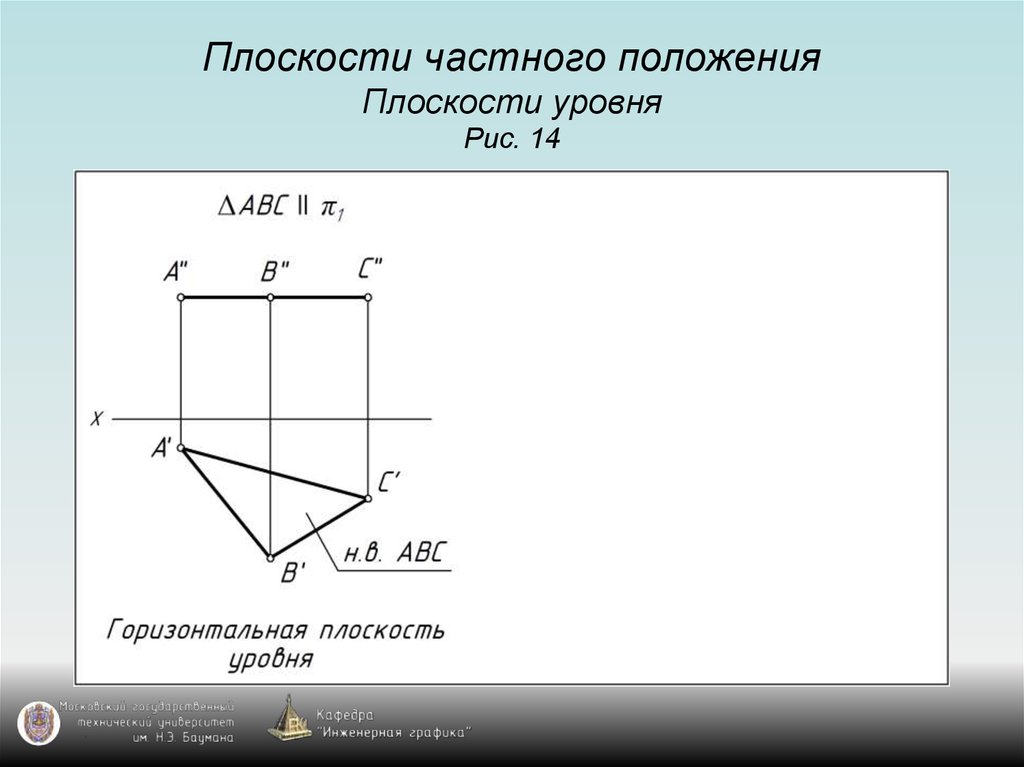
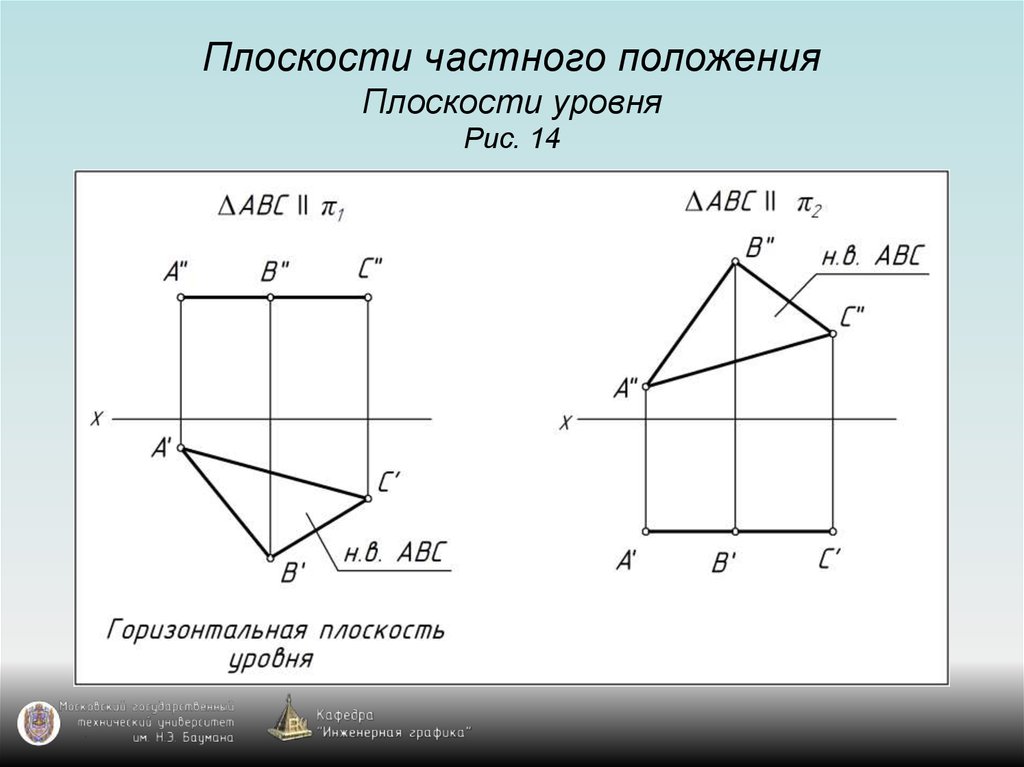
20. Плоскости частного положения Плоскости уровня Рис. 14

21. Плоскости частного положения Плоскости уровня Рис. 14

22. Плоскости частного положения Плоскости уровня Рис. 14

23. Плоскости частного положения Плоскости уровня Рис. 14

24. Построение проекций точек и прямых, принадлежащих плоскости

Отметим:
• Прямая задаётся двумя точками или точкой и
направлением.
• Если две точки прямой принадлежат
плоскости, то прямая принадлежит этой
плоскости, т.е. все точки такой прямой
принадлежат данной плоскости.

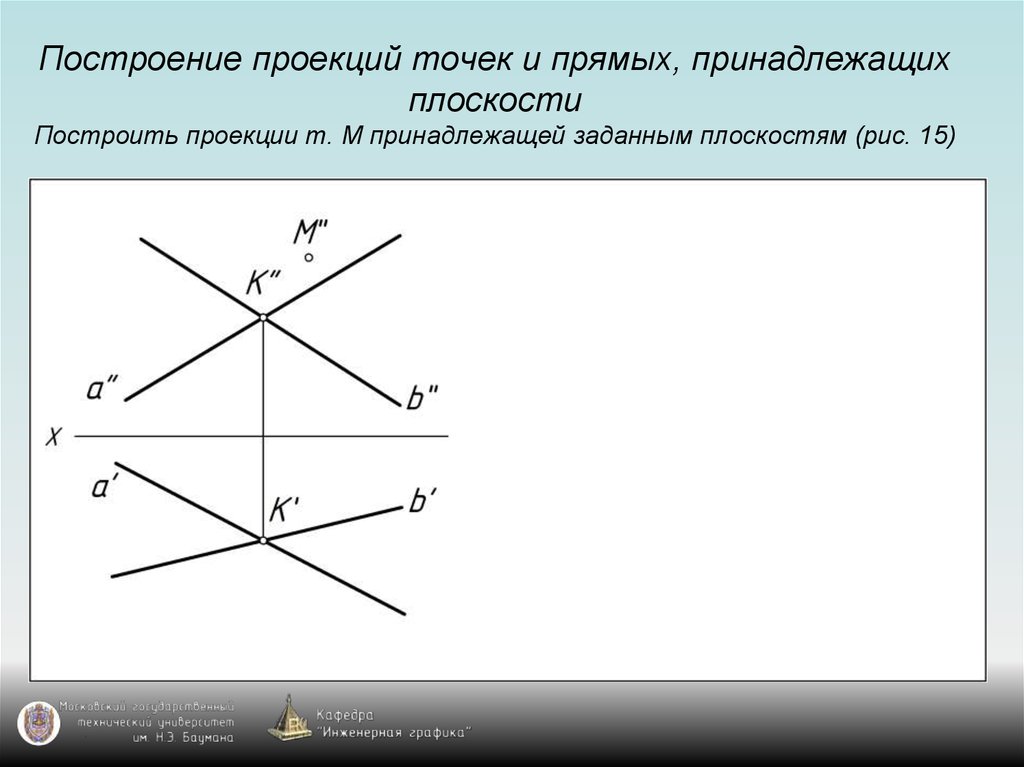
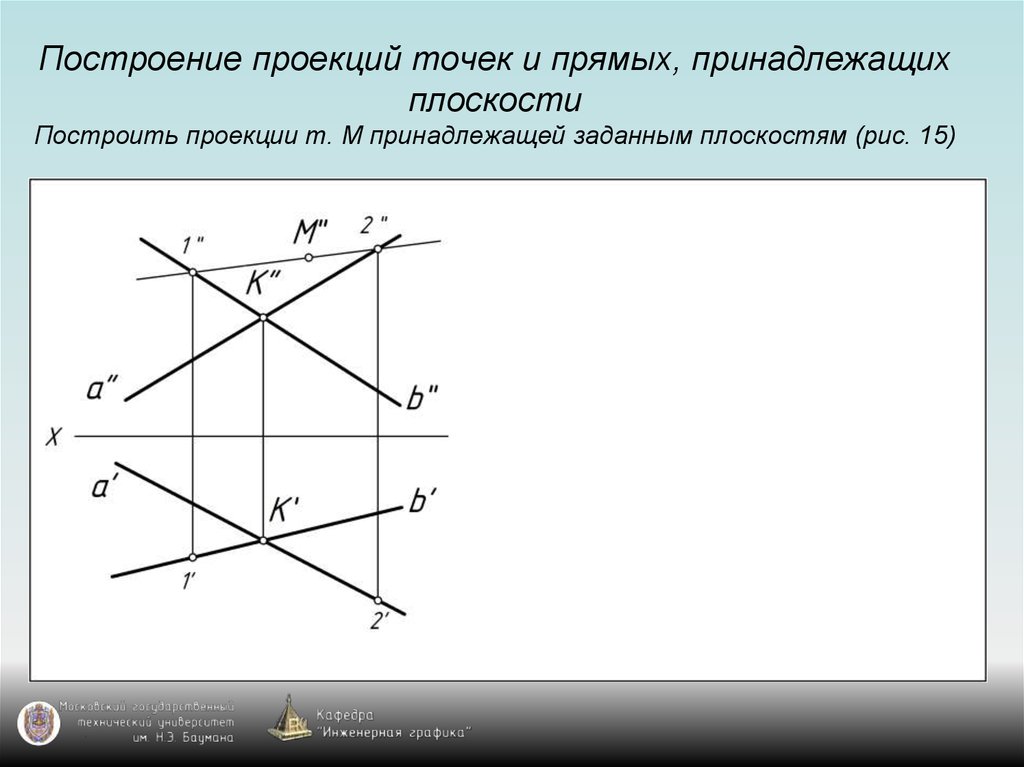
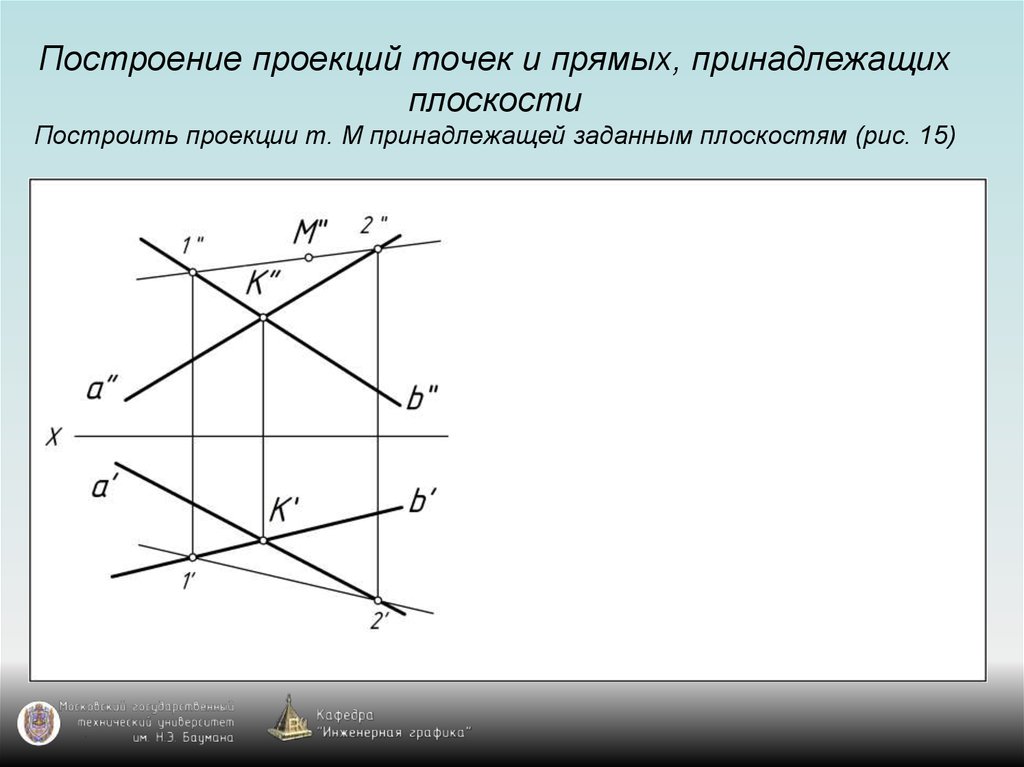
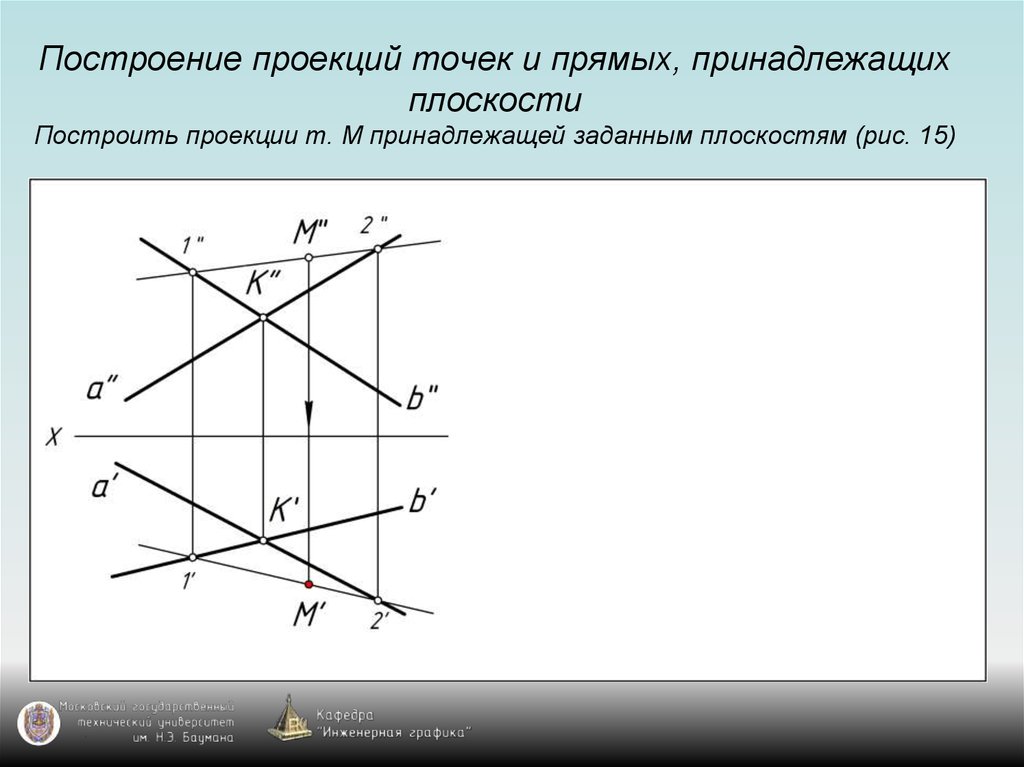
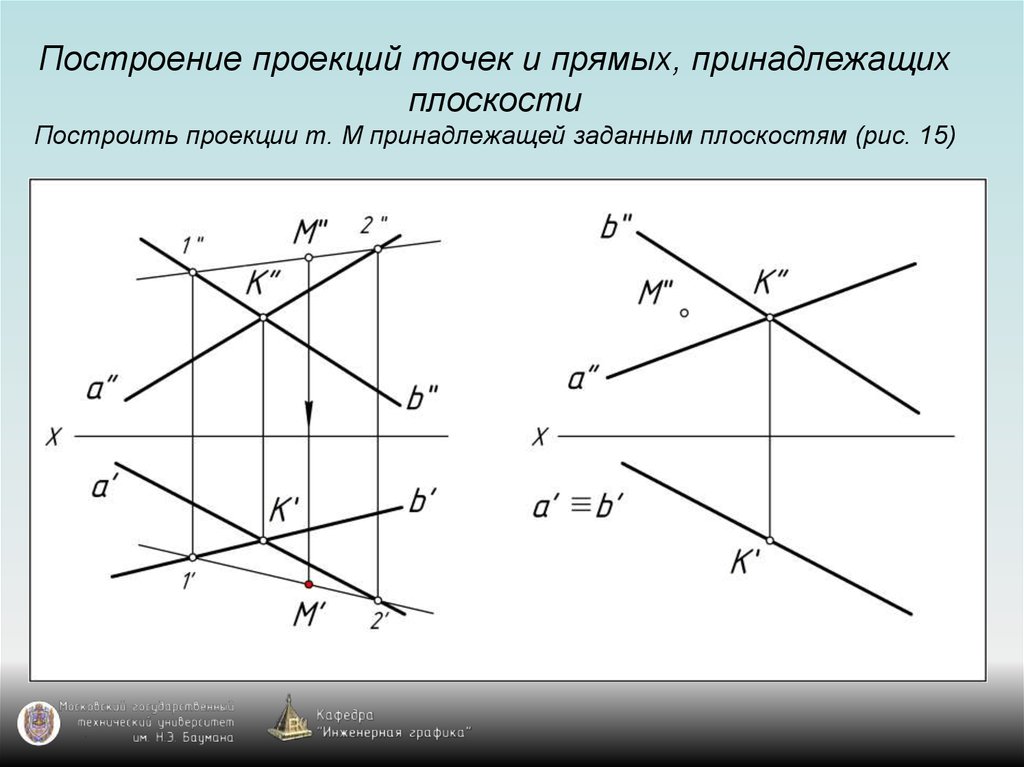
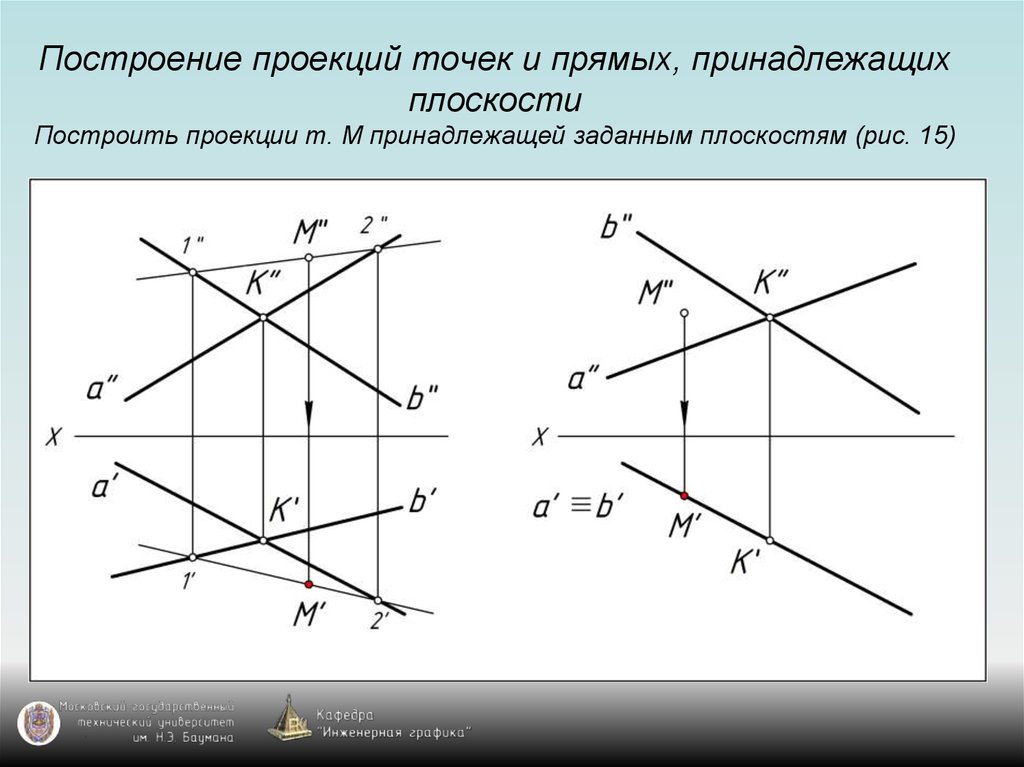
25. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

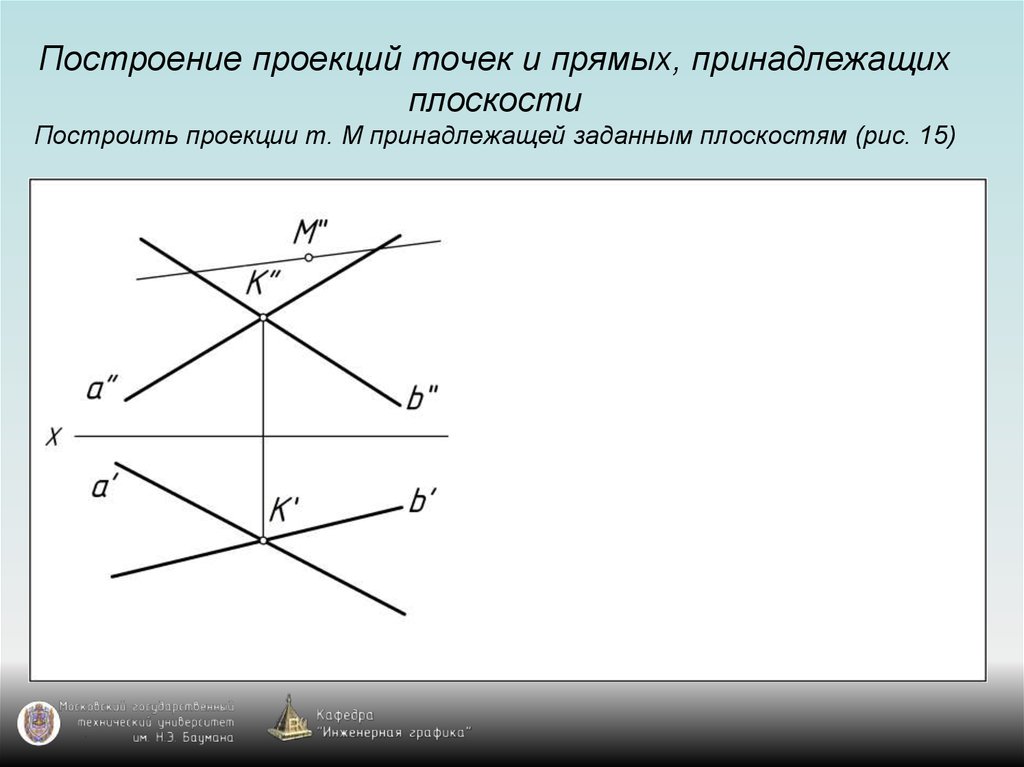
26. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

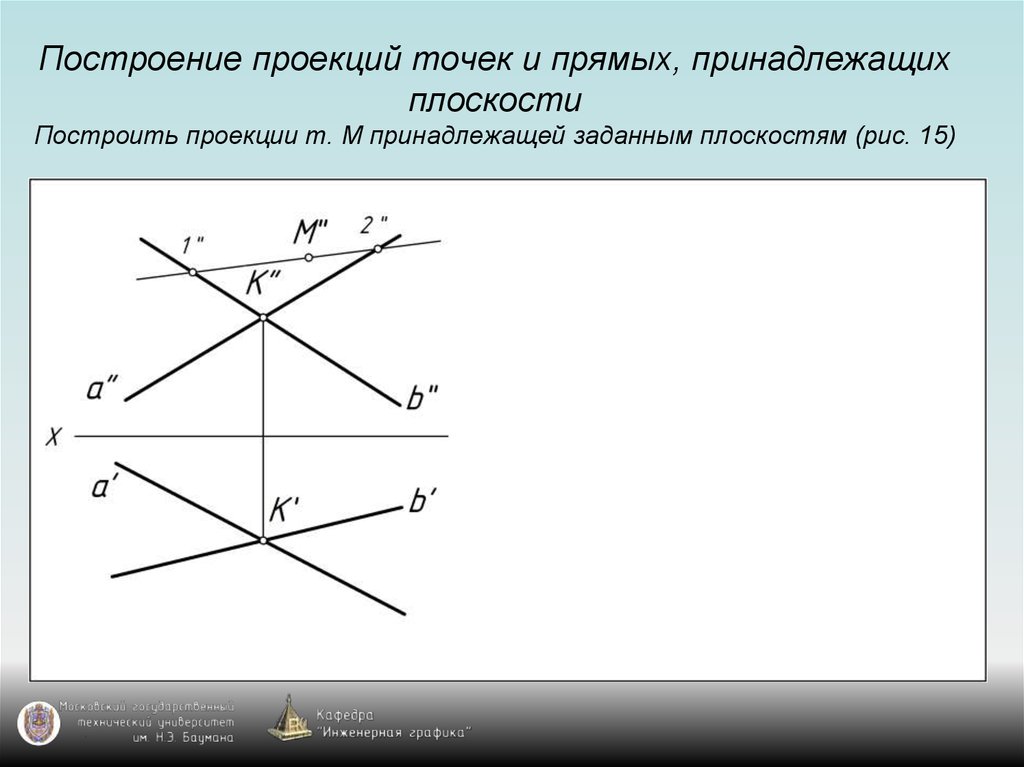
27. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

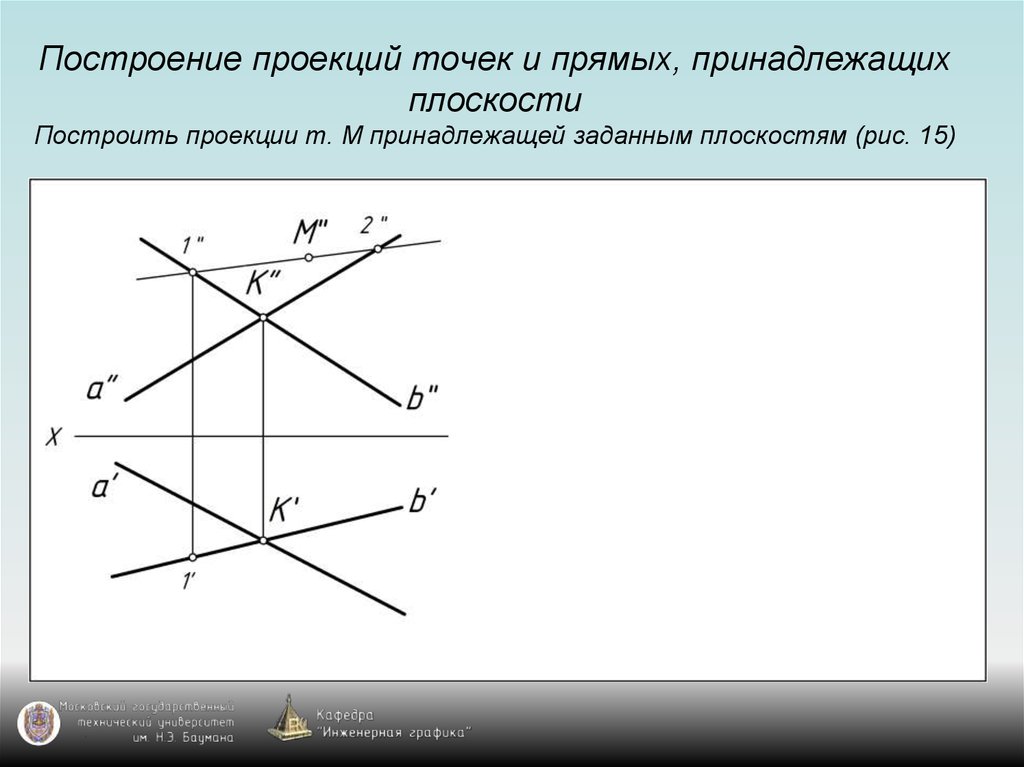
28. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

29. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

30. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

31. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

32. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

33. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

34. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

35. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

36. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

37. Построение проекций точек и прямых, принадлежащих плоскости Построить проекции т. М принадлежащей заданным плоскостям (рис. 15)

38. Общее правило построения проекции точки, принадлежащей плоскости

Для построения проекции точки, принадлежащей
плоскости общего положения, надо воспользоваться
проекциями прямой, принадлежащей заданной плоскости
и проходящей через точку (используем свойство
принадлежности).

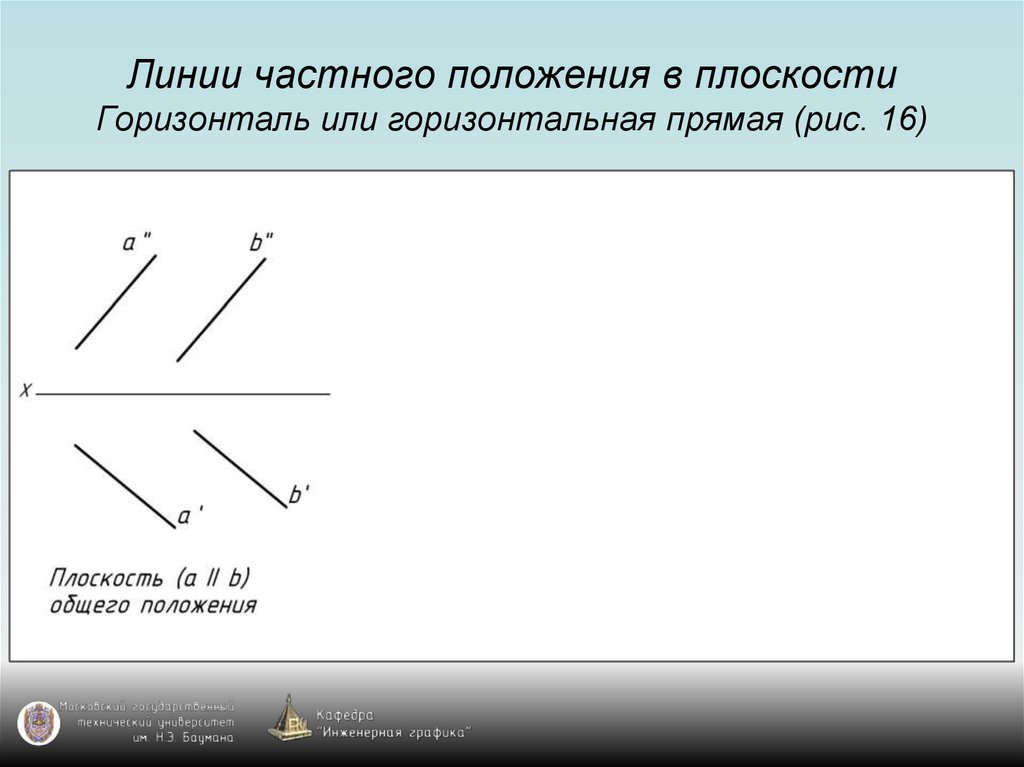
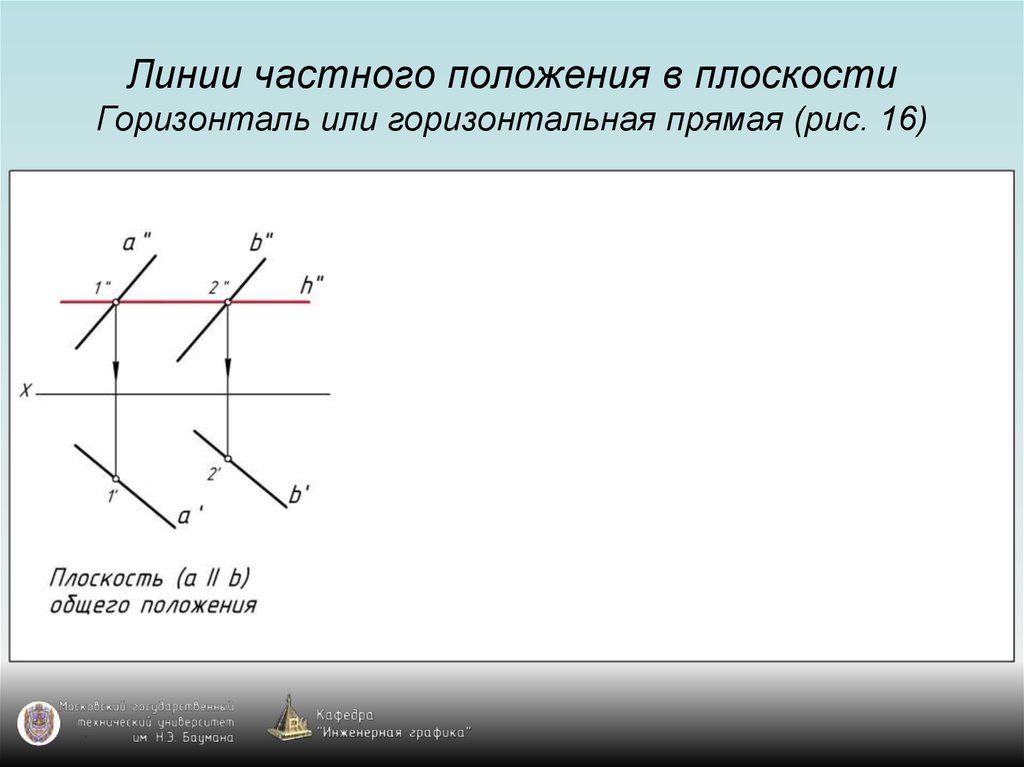
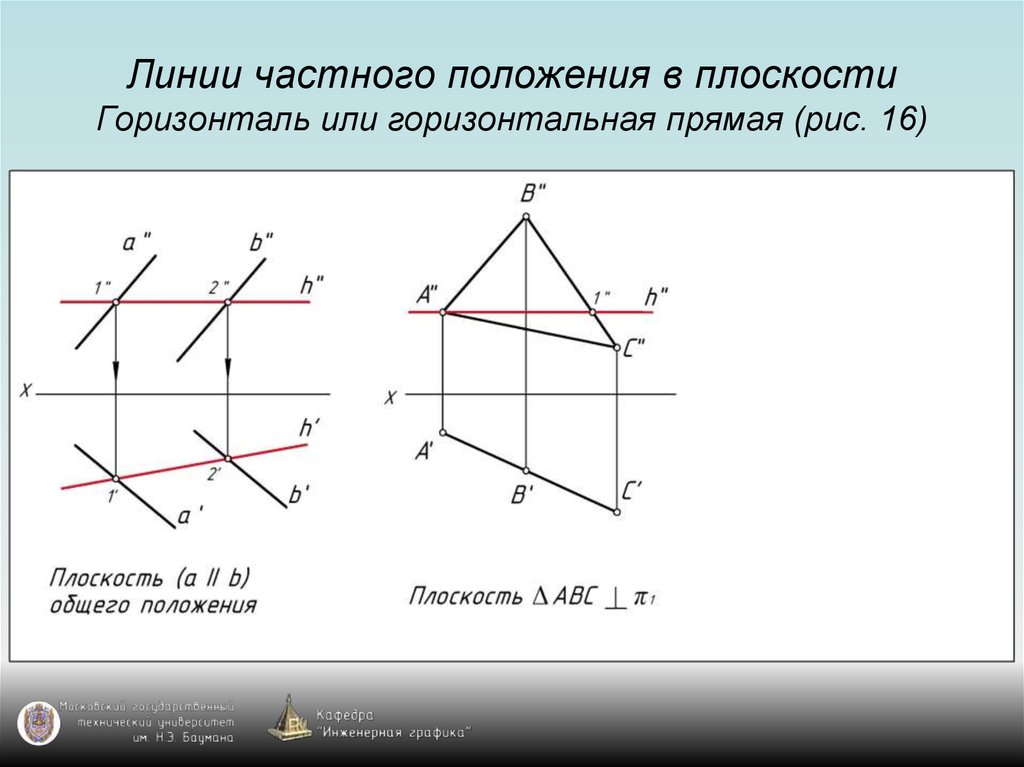
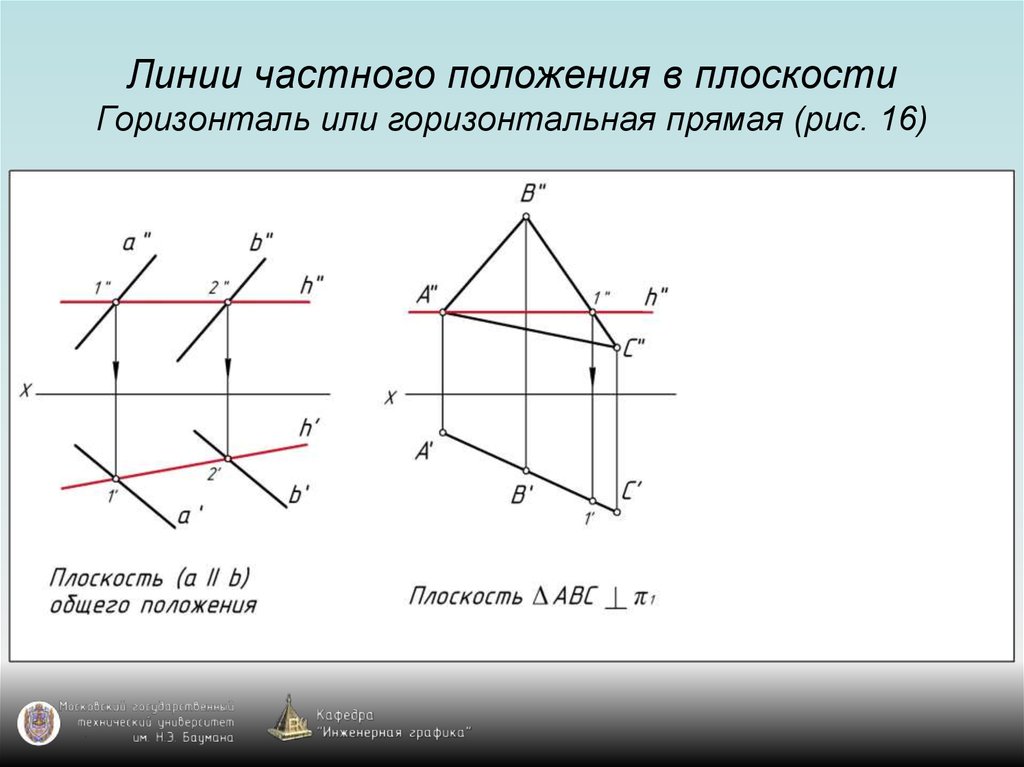
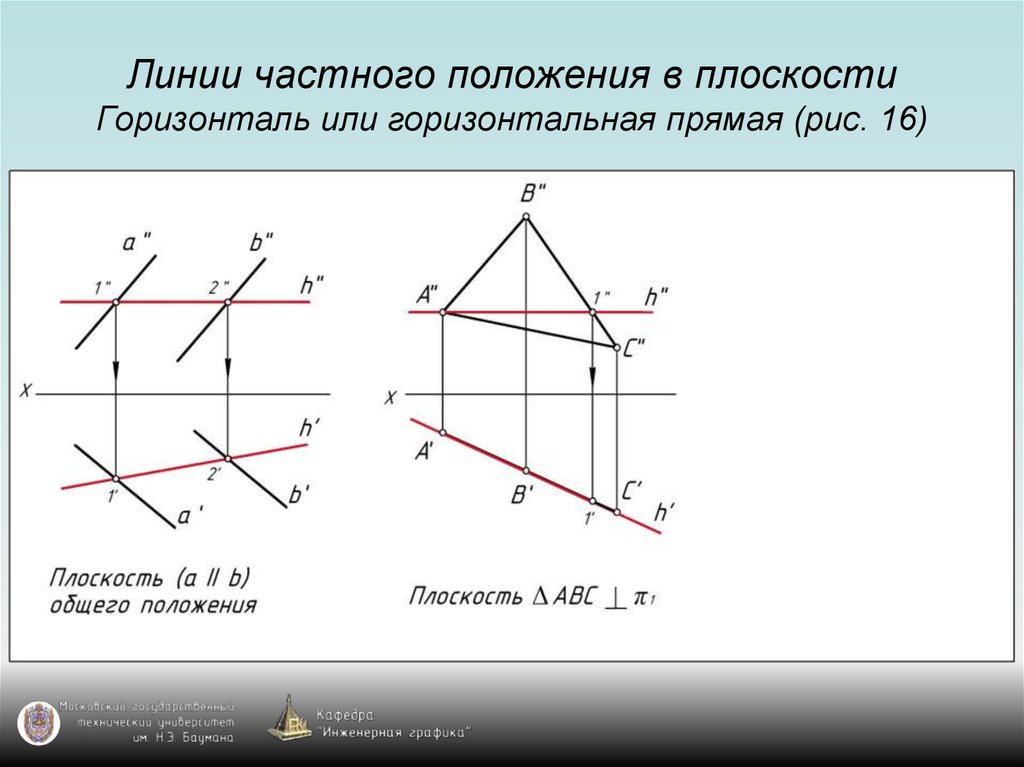
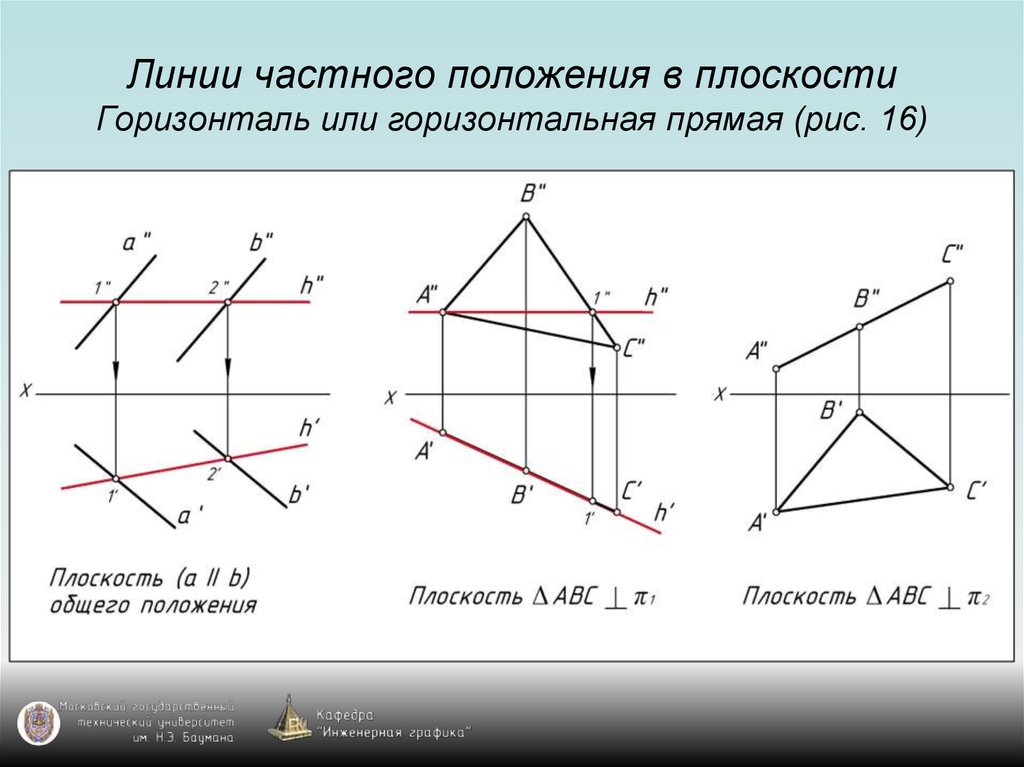
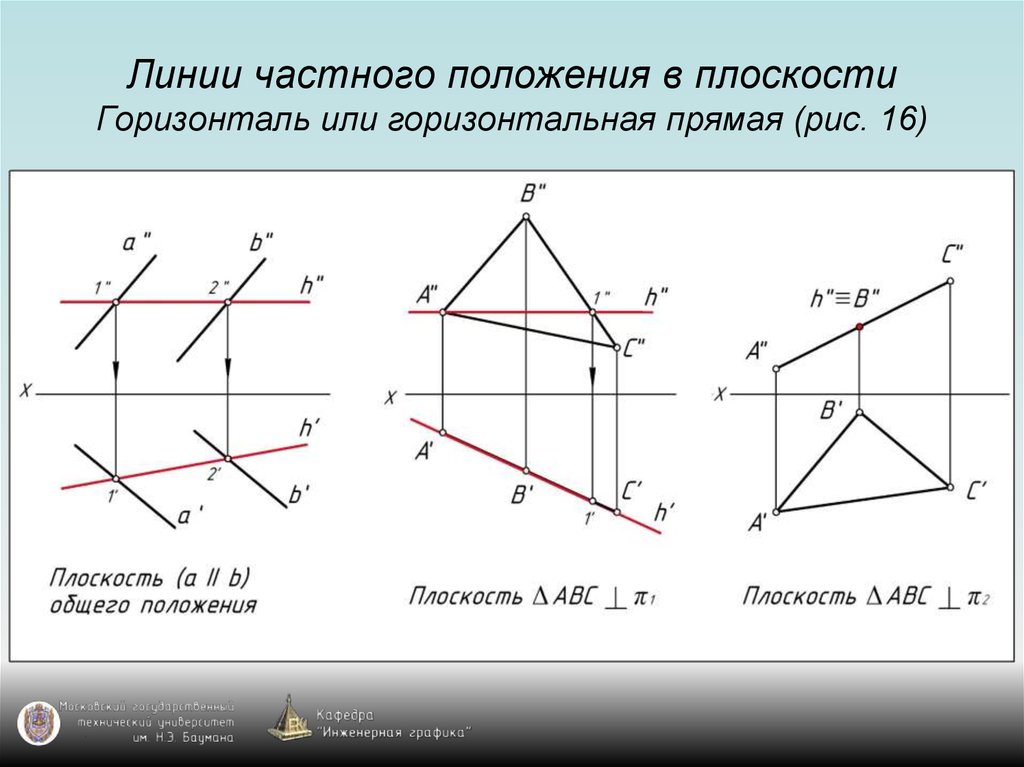
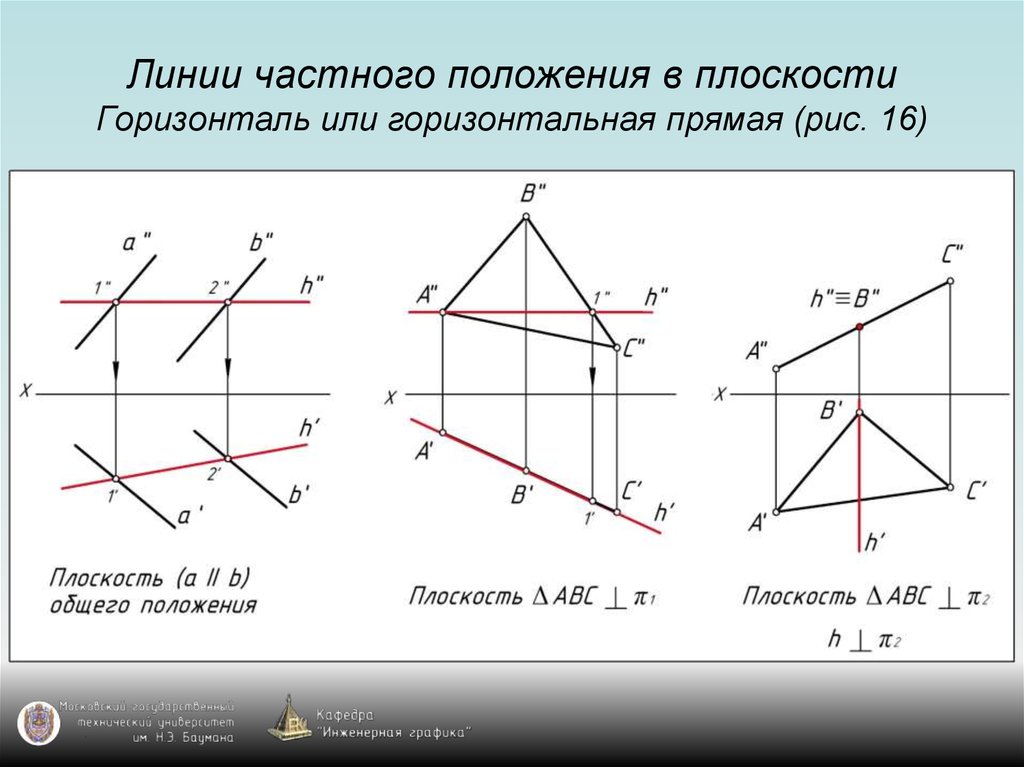
39. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

40. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

41. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

42. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

43. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

44. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

45. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

46. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

47. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

48. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

49. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

50. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

51. Линии частного положения в плоскости Горизонталь или горизонтальная прямая (рис. 16)

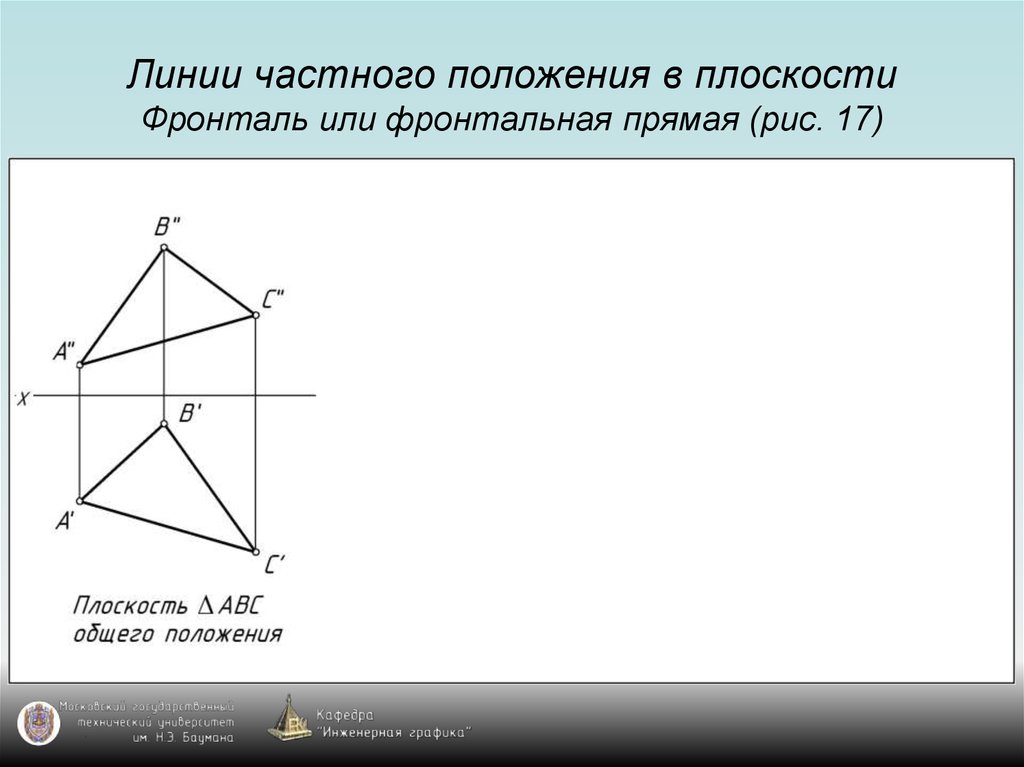
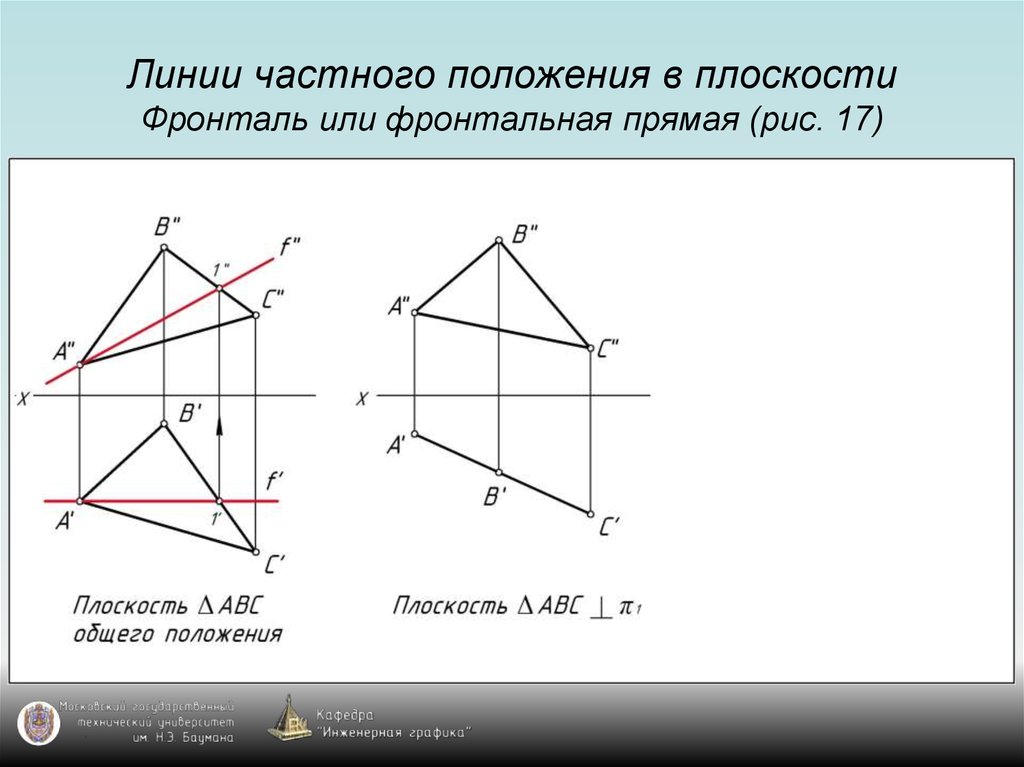
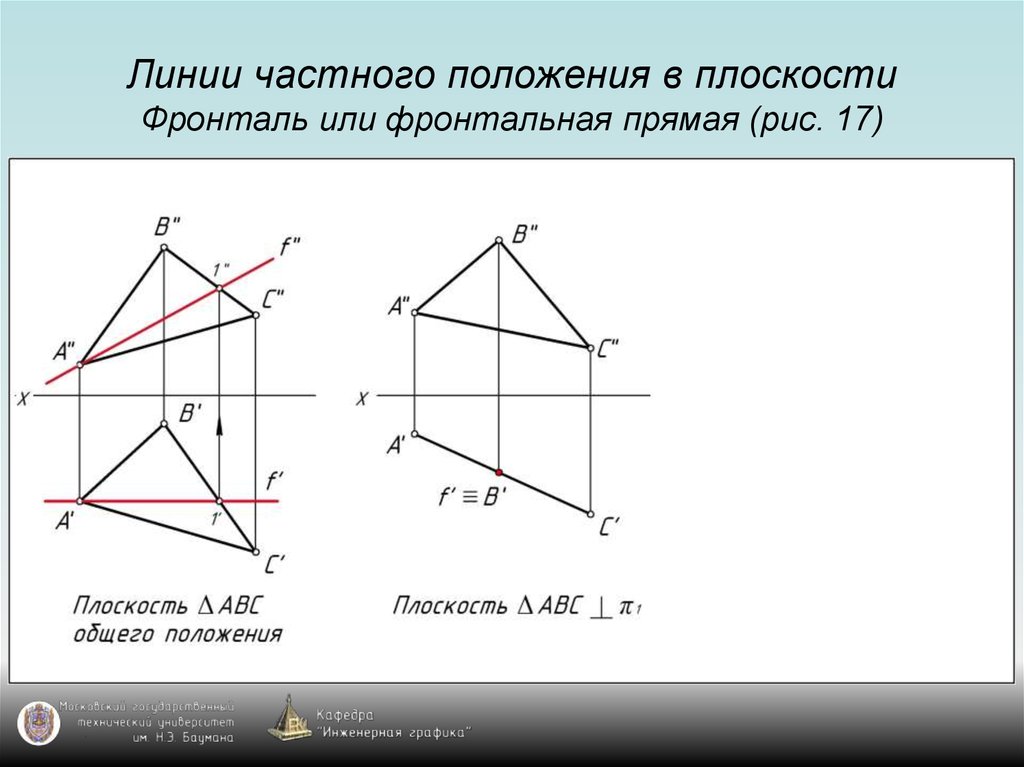
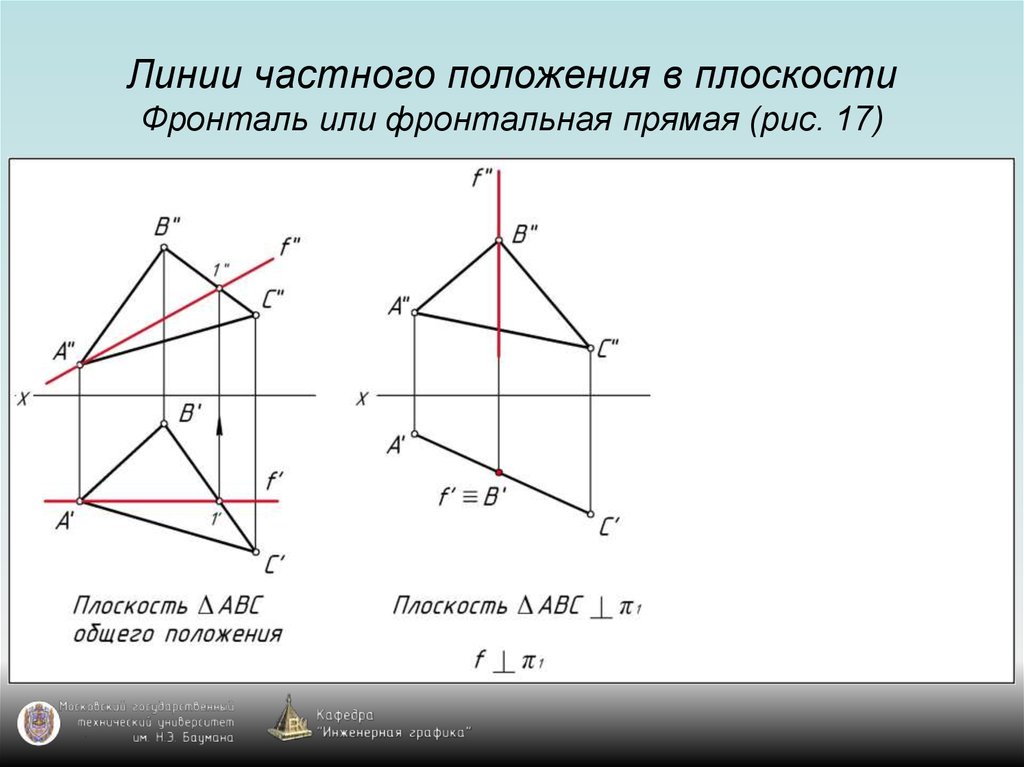
52. Линии частного положения в плоскости Фронталь или фронтальная прямая (рис. 17)

53. Линии частного положения в плоскости Фронталь или фронтальная прямая (рис. 17)

54. Линии частного положения в плоскости Фронталь или фронтальная прямая (рис. 17)

55. Линии частного положения в плоскости Фронталь или фронтальная прямая (рис. 17)

56. Линии частного положения в плоскости Фронталь или фронтальная прямая (рис. 17)

57. Линии частного положения в плоскости Фронталь или фронтальная прямая (рис. 17)

58. Линии частного положения в плоскости Фронталь или фронтальная прямая (рис. 17)

59. Линии частного положения в плоскости Фронталь или фронтальная прямая (рис. 17)

60. Линии частного положения в плоскости Фронталь или фронтальная прямая (рис. 17)

61. Линии частного положения в плоскости Фронталь или фронтальная прямая (рис. 17)

62. Линии частного положения в плоскости Фронталь или фронтальная прямая (рис. 17)

63. 4. Взаимное положение прямой и плоскости, двух плоскостей

64. Параллельность прямой и плоскости

Построение на чертеже параллельных прямой и
плоскости основано на:
1) использовании признака параллельности прямой и
плоскости – прямая параллельна плоскости, если она
параллельна прямой, принадлежащей этой плоскости;
2) использовании свойства прямоугольного
проецирования о проекции параллельных прямых –
если прямые параллельны, то и проекции прямых
параллельны

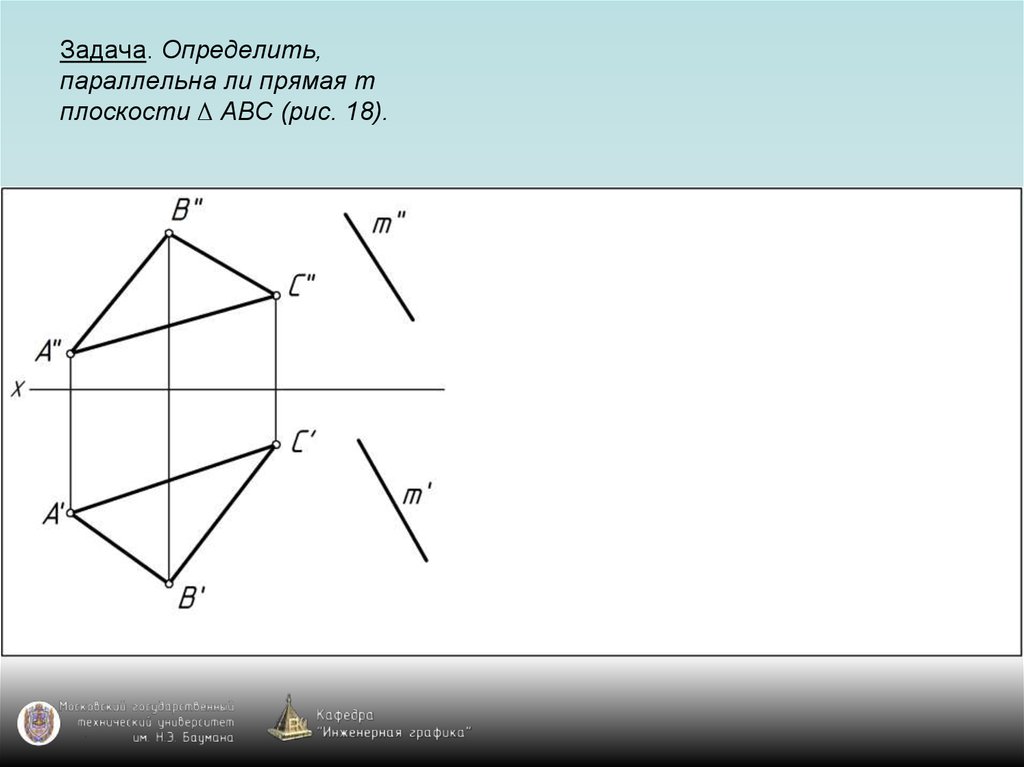
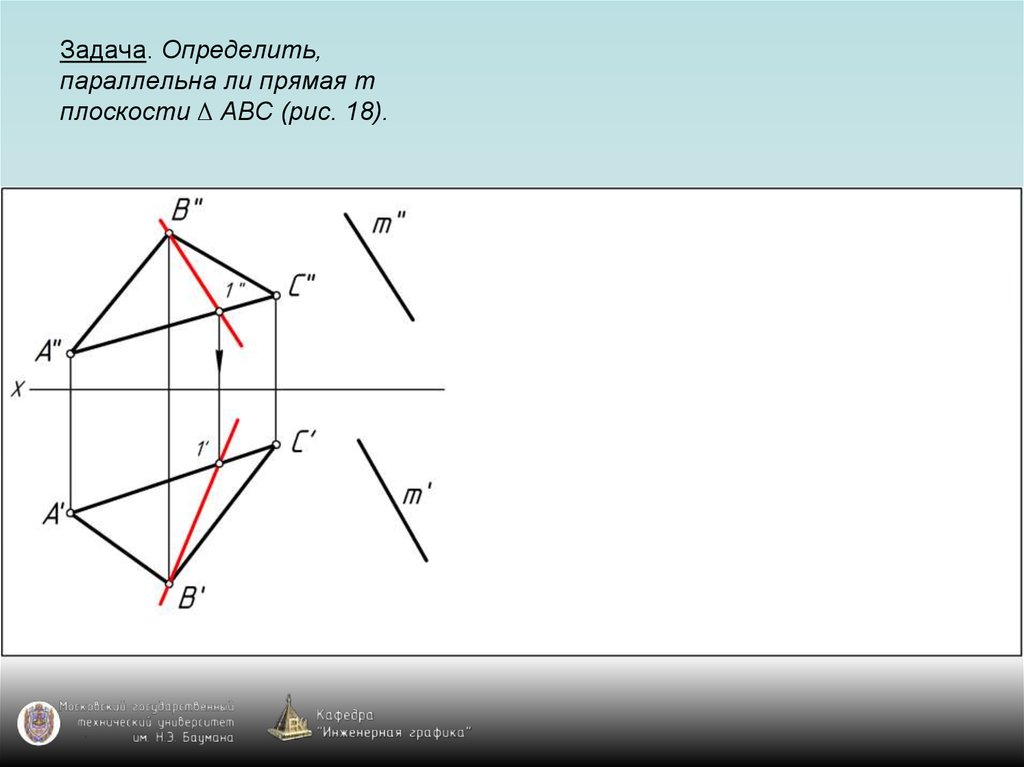
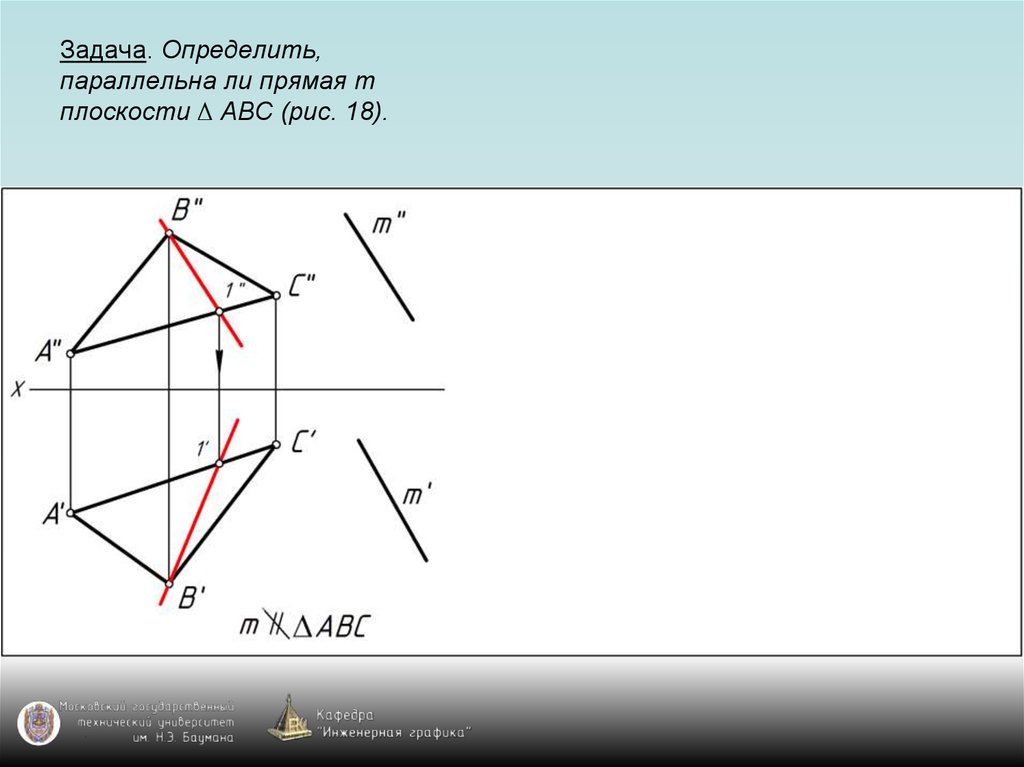
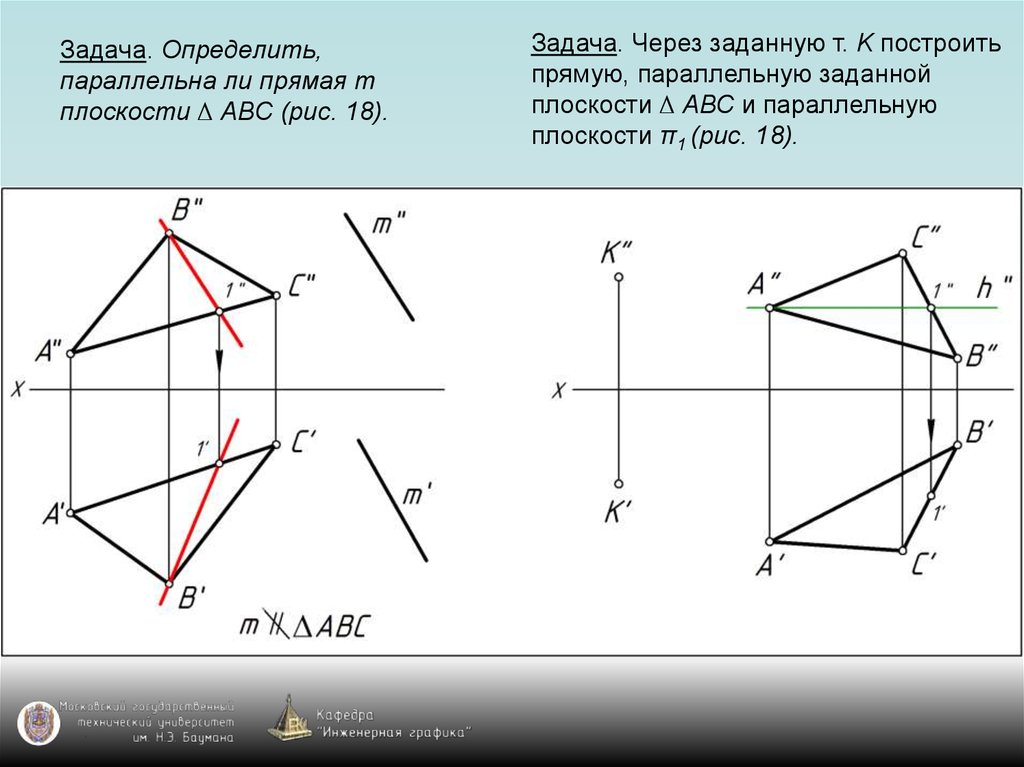
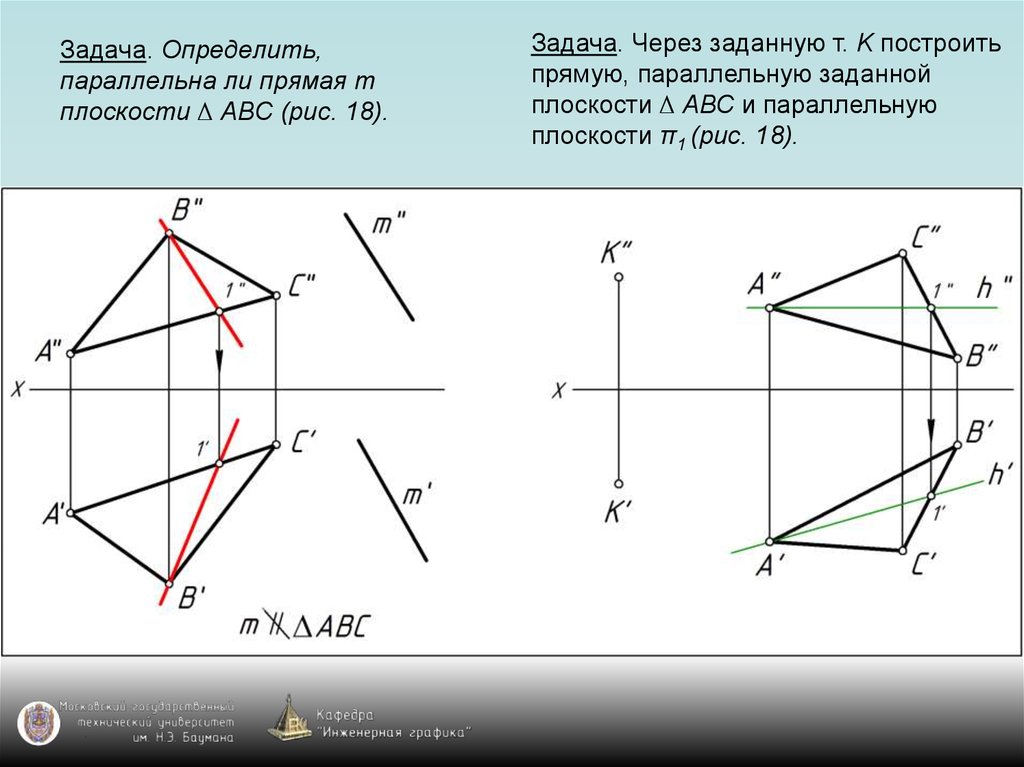
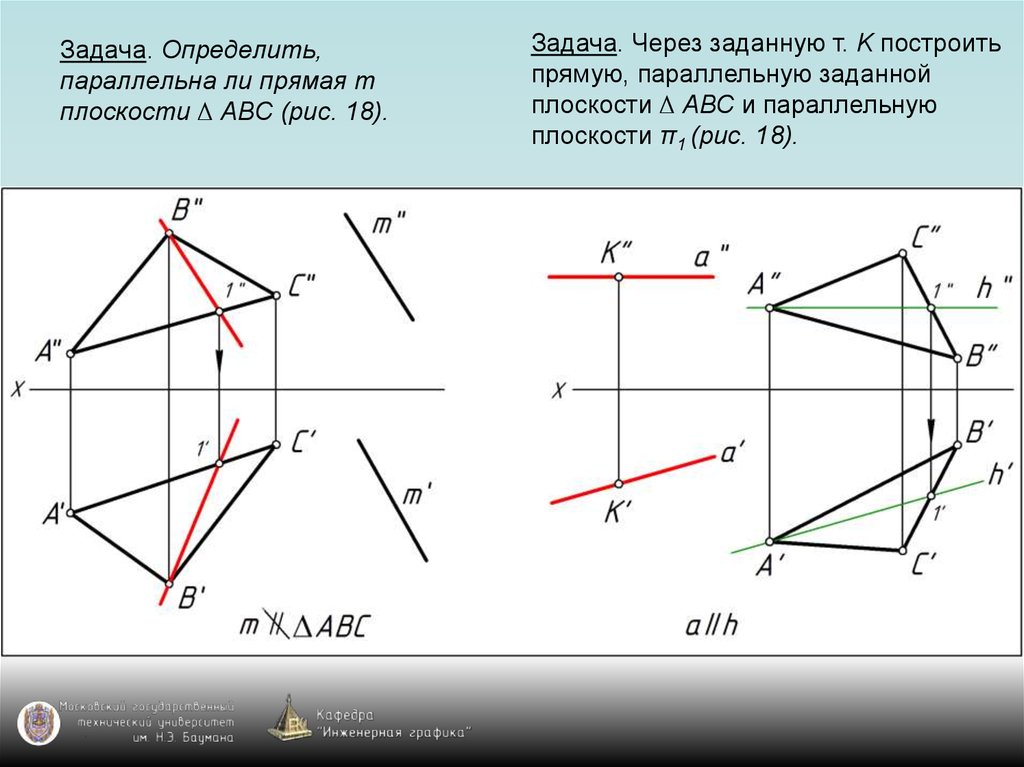
65. Задача. Определить, параллельна ли прямая m плоскости ∆ АВС (рис. 18).

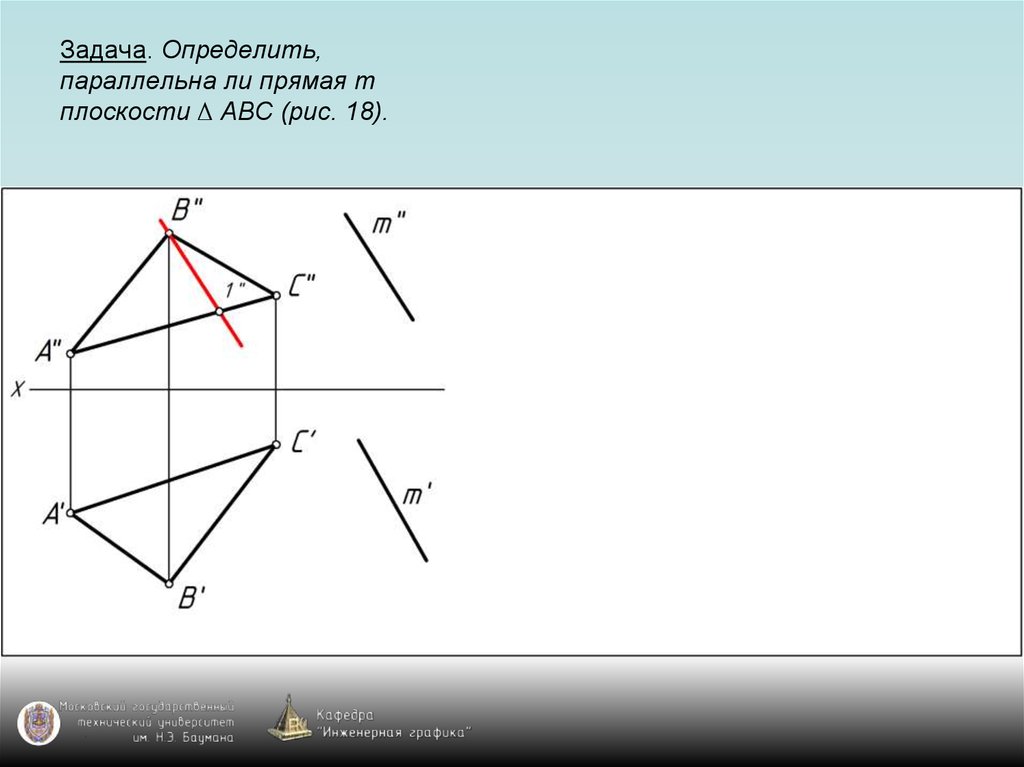
66. Задача. Определить, параллельна ли прямая m плоскости ∆ АВС (рис. 18).

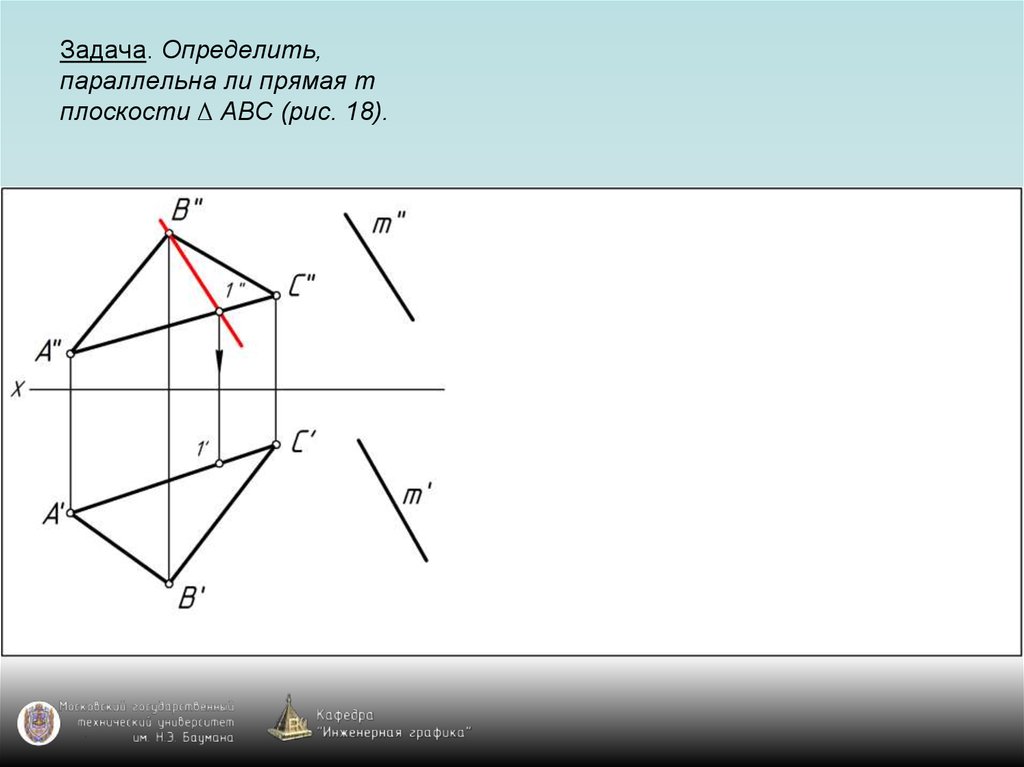
67. Задача. Определить, параллельна ли прямая m плоскости ∆ АВС (рис. 18).

68. Задача. Определить, параллельна ли прямая m плоскости ∆ АВС (рис. 18).

69. Задача. Определить, параллельна ли прямая m плоскости ∆ АВС (рис. 18).

70. Задача. Определить, параллельна ли прямая m плоскости ∆ АВС (рис. 18).

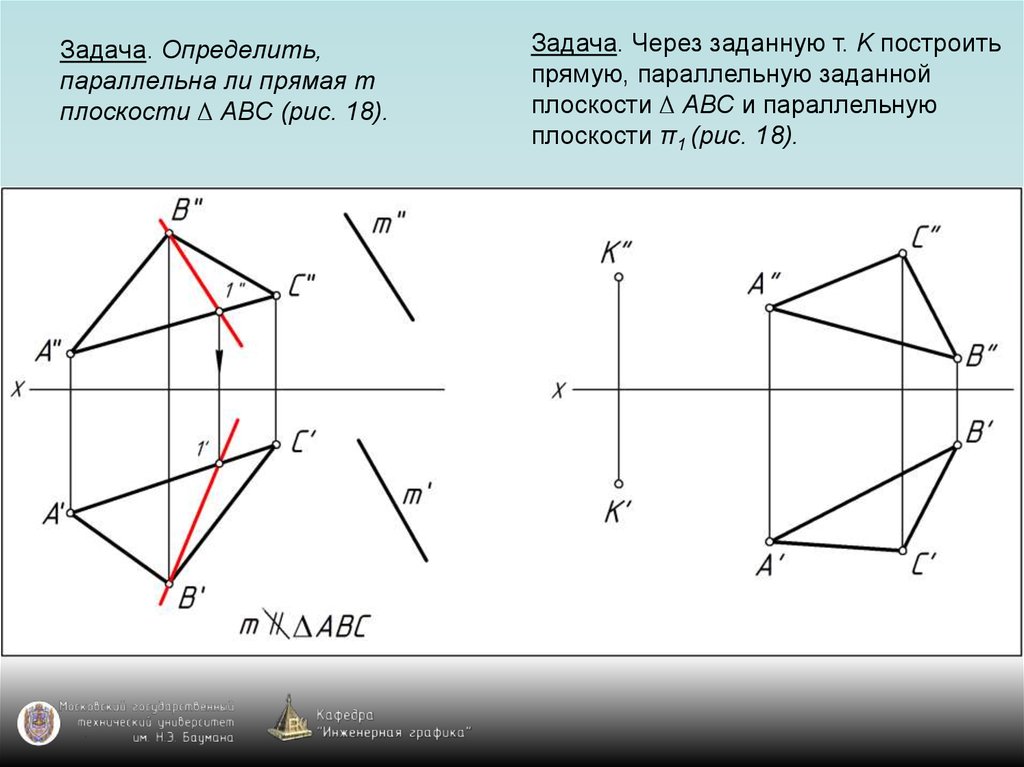
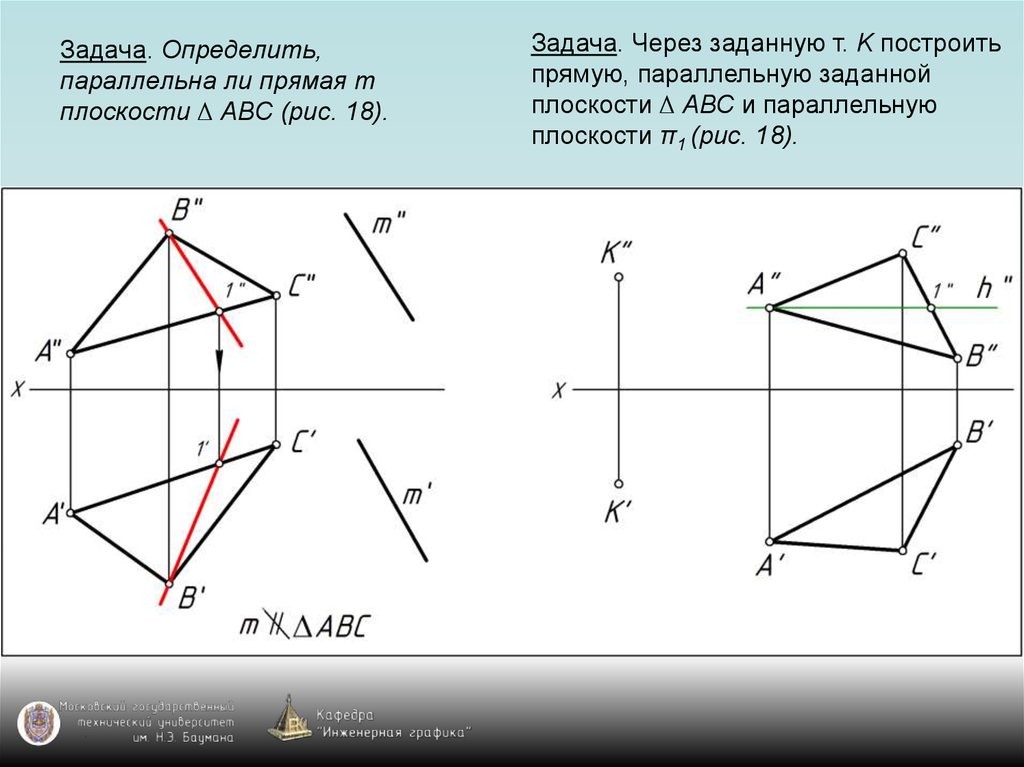
Задача. Через заданную т. K построить
прямую, параллельную заданной
плоскости ∆ АВС и параллельную
плоскости π1 (рис. 18).

71. Задача. Определить, параллельна ли прямая m плоскости ∆ АВС (рис. 18).

Задача. Через заданную т. K построить
прямую, параллельную заданной
плоскости ∆ АВС и параллельную
плоскости π1 (рис. 18).

72. Задача. Определить, параллельна ли прямая m плоскости ∆ АВС (рис. 18).

Задача. Через заданную т. K построить
прямую, параллельную заданной
плоскости ∆ АВС и параллельную
плоскости π1 (рис. 18).

73. Задача. Определить, параллельна ли прямая m плоскости ∆ АВС (рис. 18).

Задача. Через заданную т. K построить
прямую, параллельную заданной
плоскости ∆ АВС и параллельную
плоскости π1 (рис. 18).

74. Задача. Определить, параллельна ли прямая m плоскости ∆ АВС (рис. 18).

Задача. Через заданную т. K построить
прямую, параллельную заданной
плоскости ∆ АВС и параллельную
плоскости π1 (рис. 18).

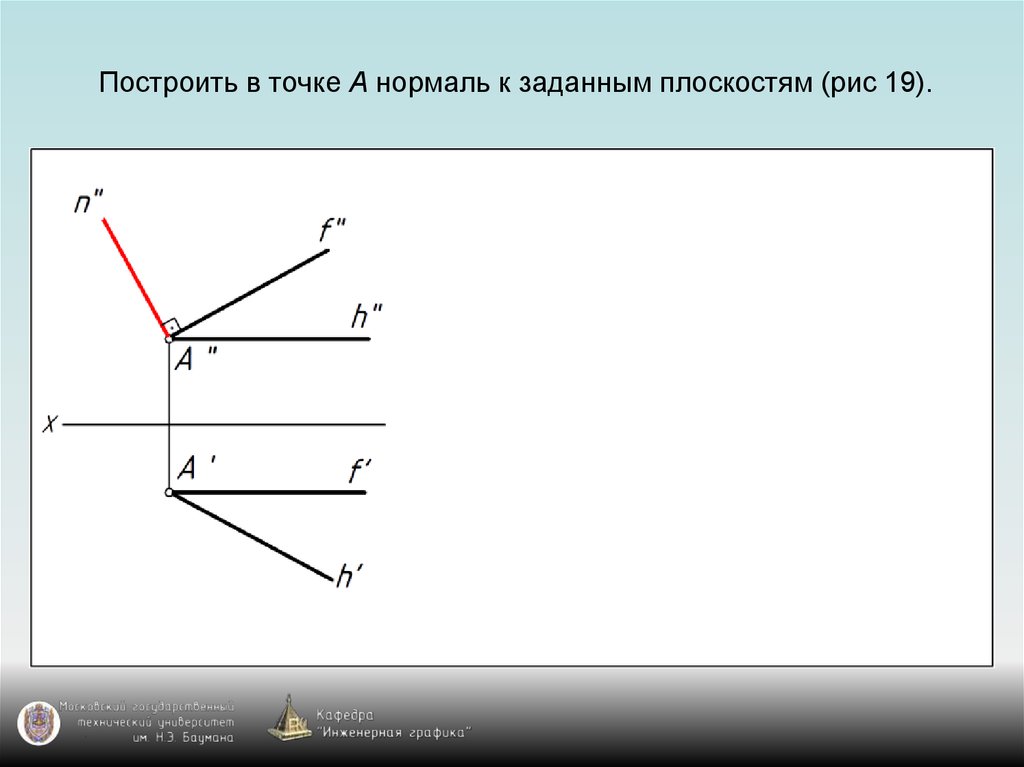
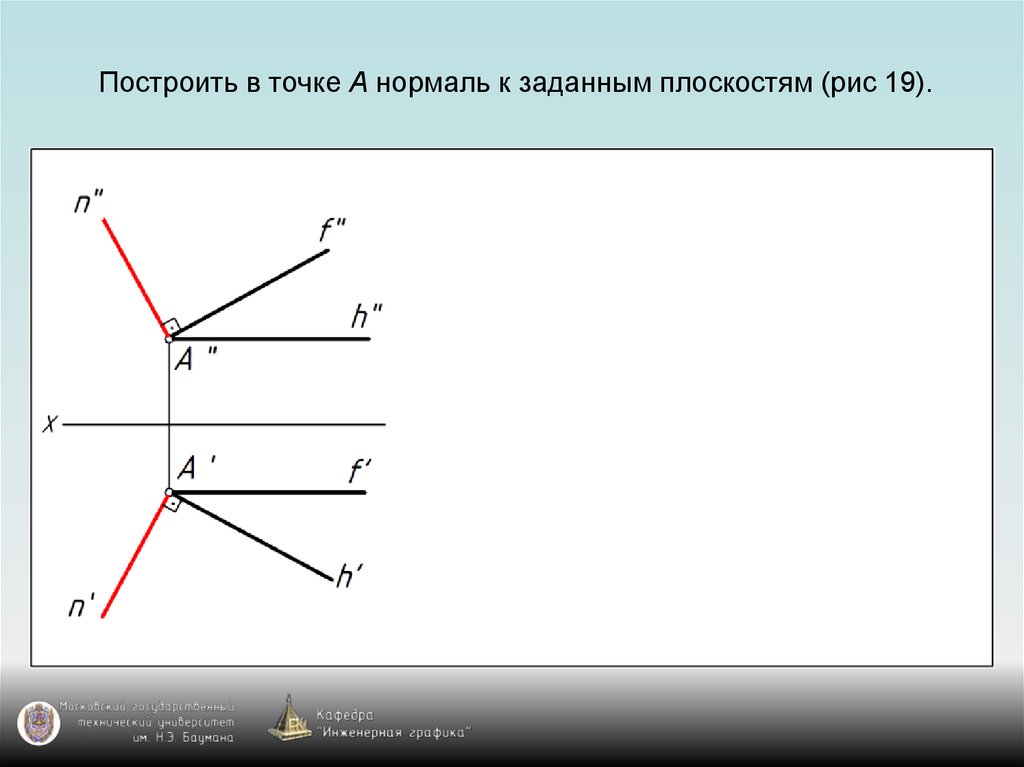
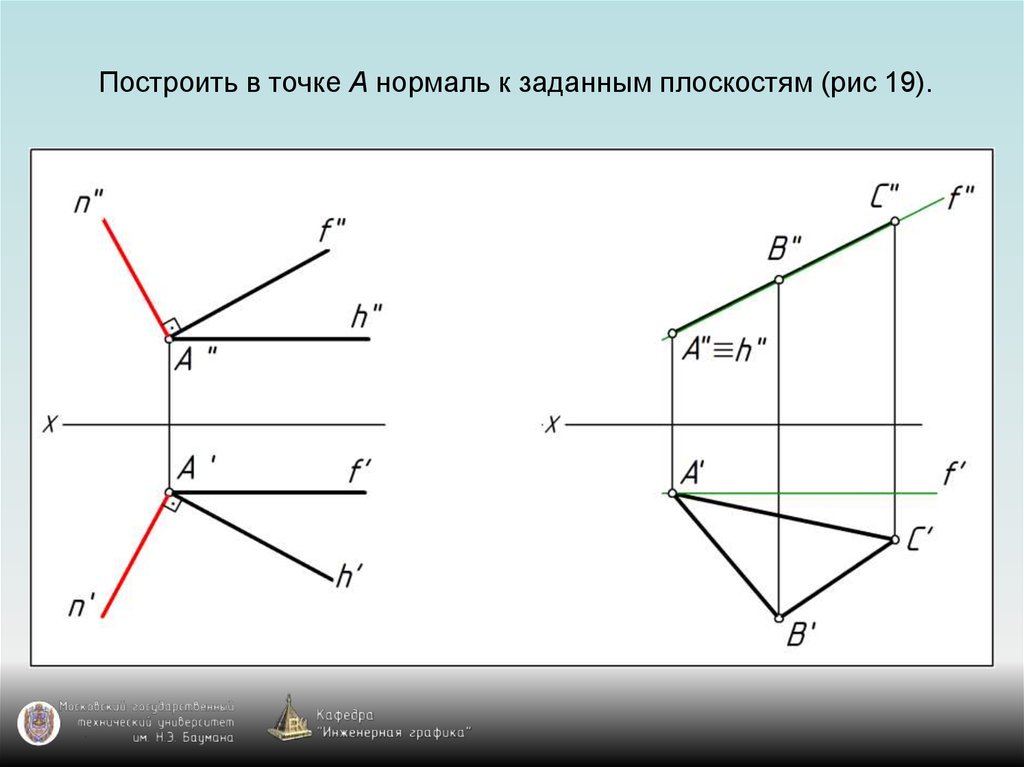
75. Перпендикулярность прямой и плоскости

Построение на чертеже перпендикулярных
прямой и плоскости основано на использовании:
1) признака перпендикулярности прямой и
плоскости – прямая перпендикулярна плоскости,
если она перпендикулярна двум пересекающимся
прямым, принадлежащим этой плоскости;
2) теоремы о проециях прямого угла.

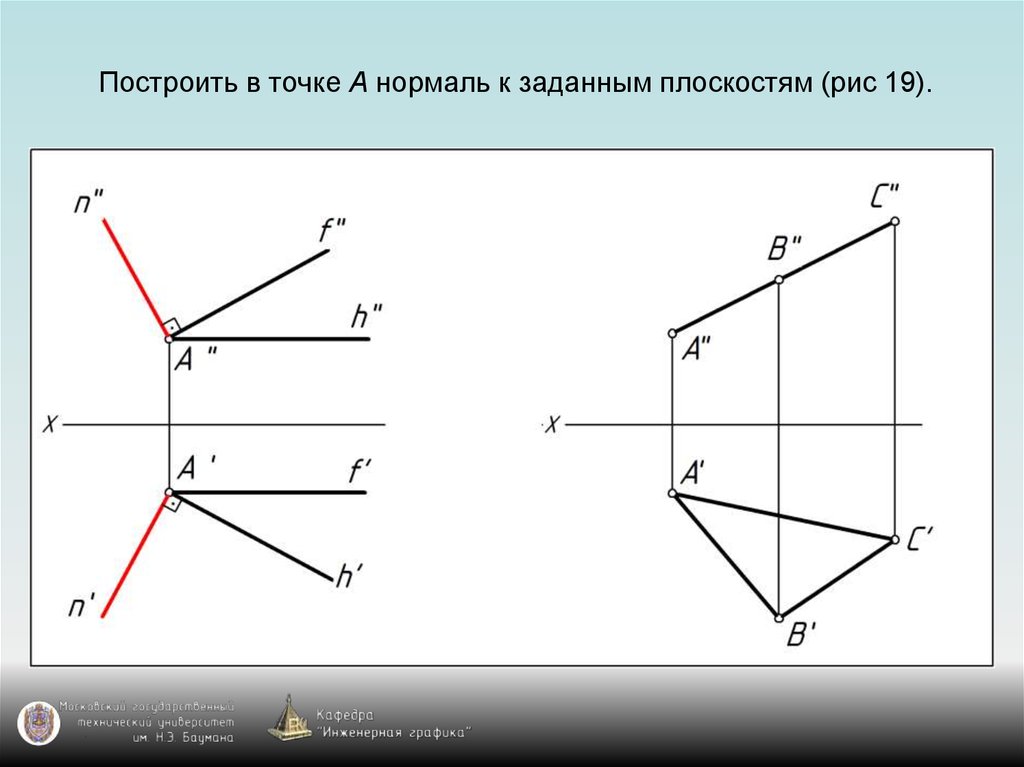
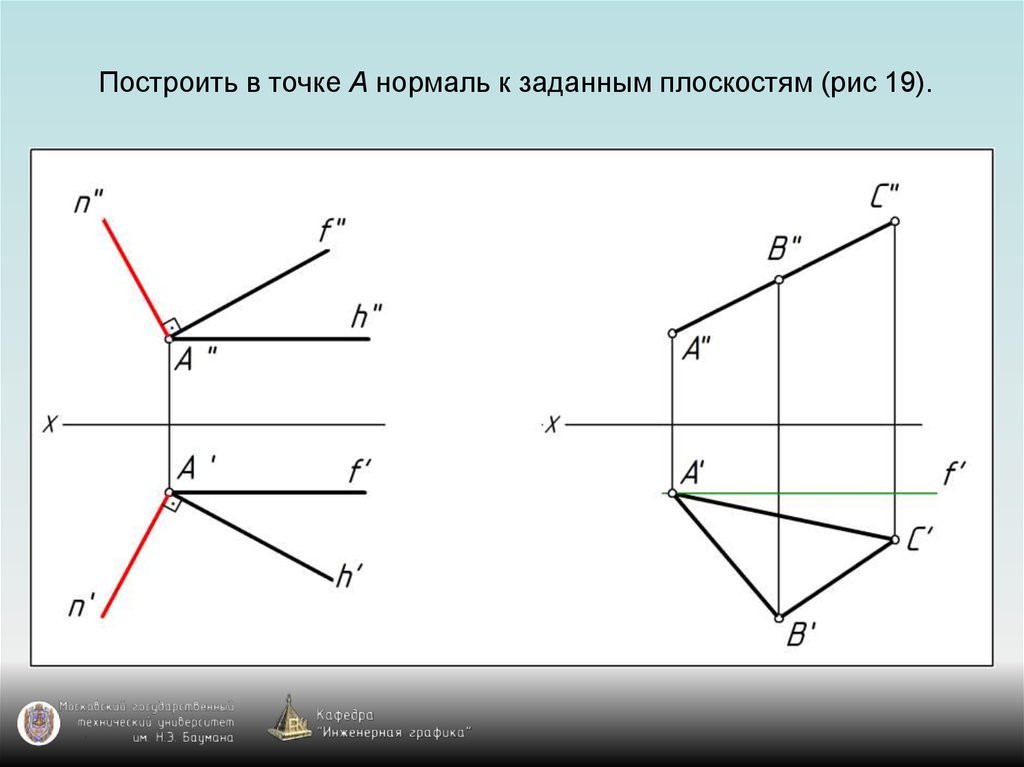
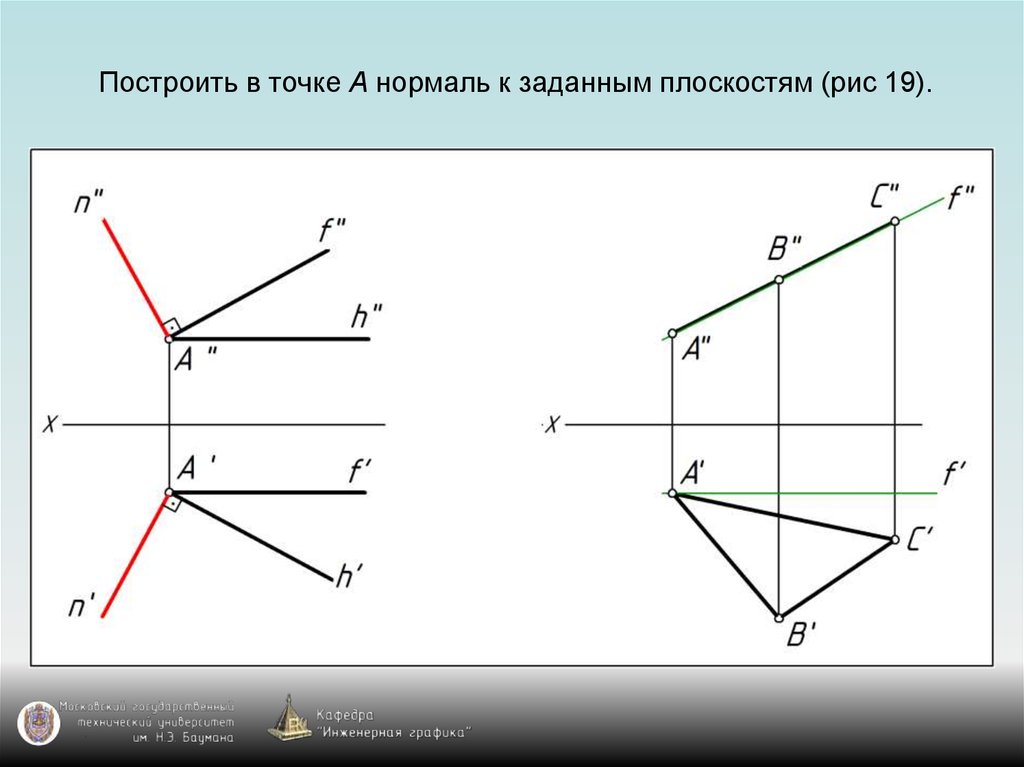
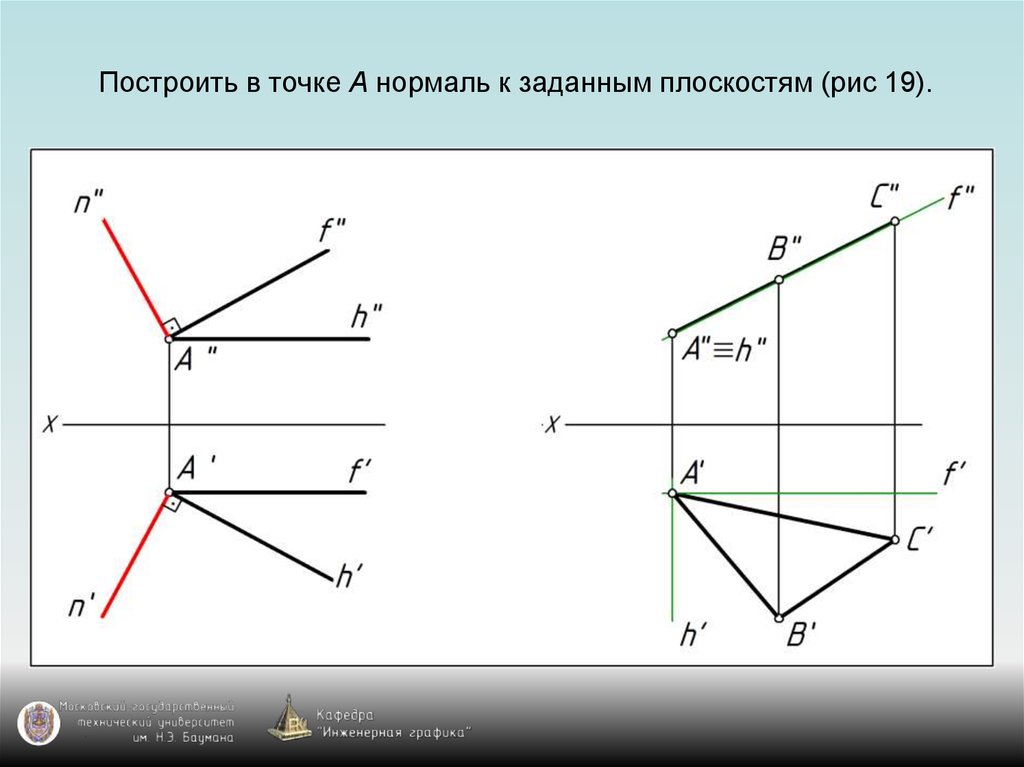
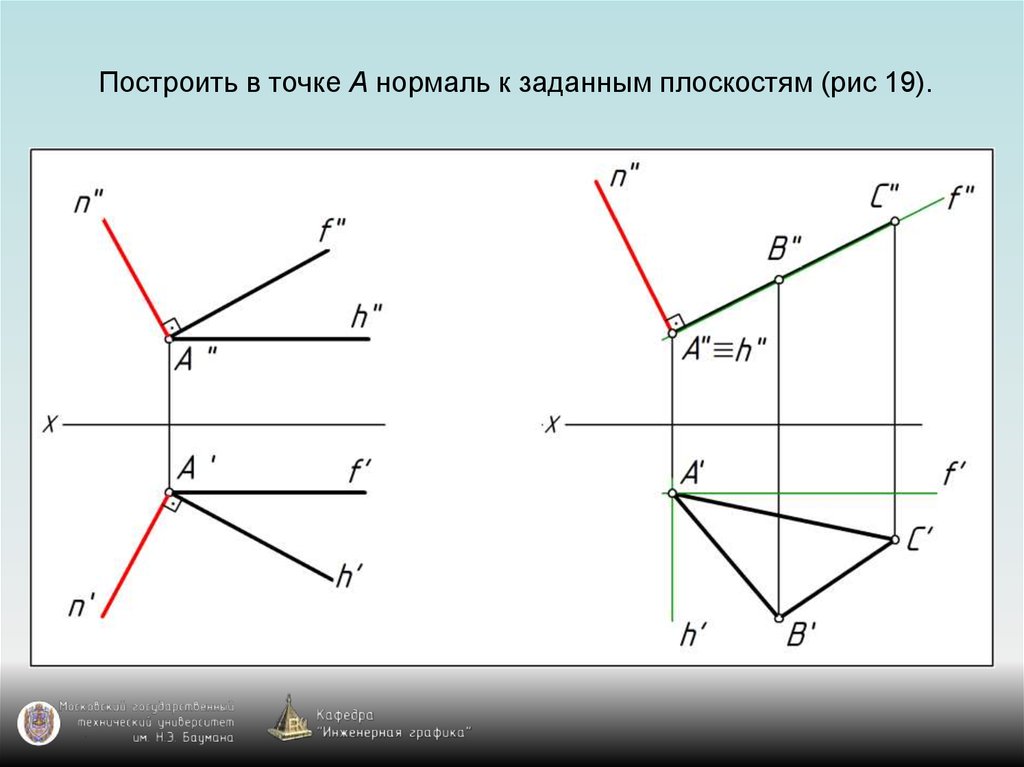
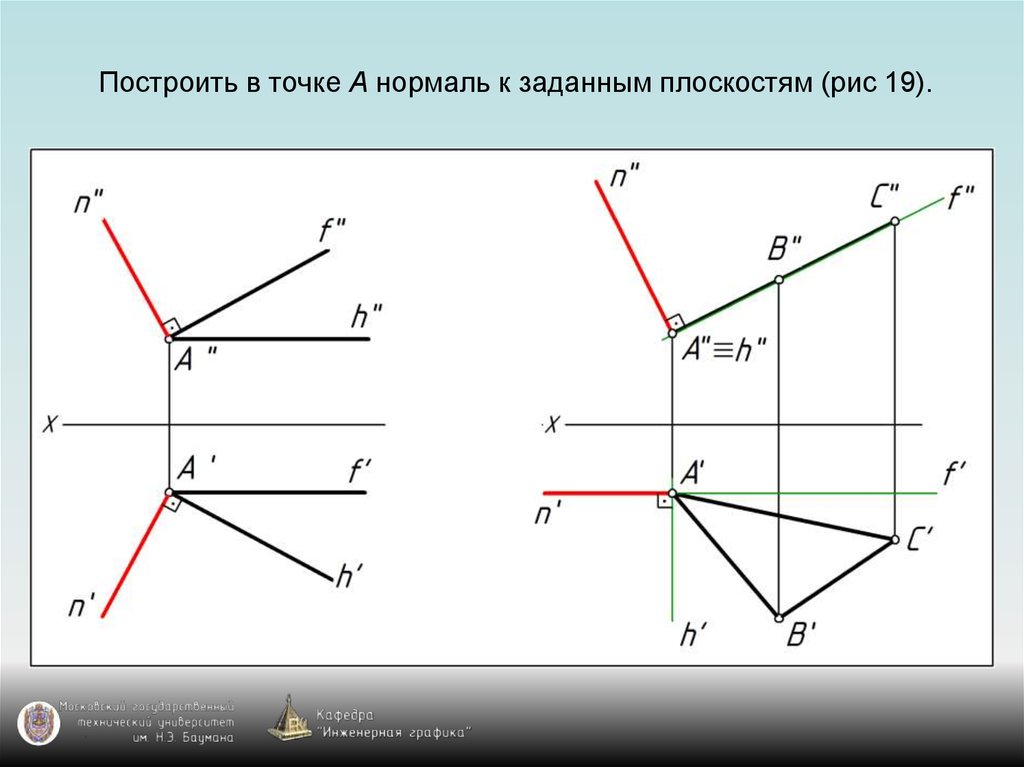
76. Построить в точке А нормаль к заданным плоскостям (рис 19).

77. Построить в точке А нормаль к заданным плоскостям (рис 19).

78. Построить в точке А нормаль к заданным плоскостям (рис 19).

79. Построить в точке А нормаль к заданным плоскостям (рис 19).

80. Построить в точке А нормаль к заданным плоскостям (рис 19).

81. Построить в точке А нормаль к заданным плоскостям (рис 19).

82. Построить в точке А нормаль к заданным плоскостям (рис 19).

83. Построить в точке А нормаль к заданным плоскостям (рис 19).

84. Построить в точке А нормаль к заданным плоскостям (рис 19).

85. Построить в точке А нормаль к заданным плоскостям (рис 19).

86. Параллельность двух плоскостей

Построение на чертеже параллельных
плоскостей основано на:
1) использовании признака параллельности двух
плоскостей – две плоскости параллельны,
если две пересекающиеся прямые одной
плоскости параллельны двум
пересекающимся прямым другой плоскости;
2) использовании свойства проецирования
параллельных прямых.

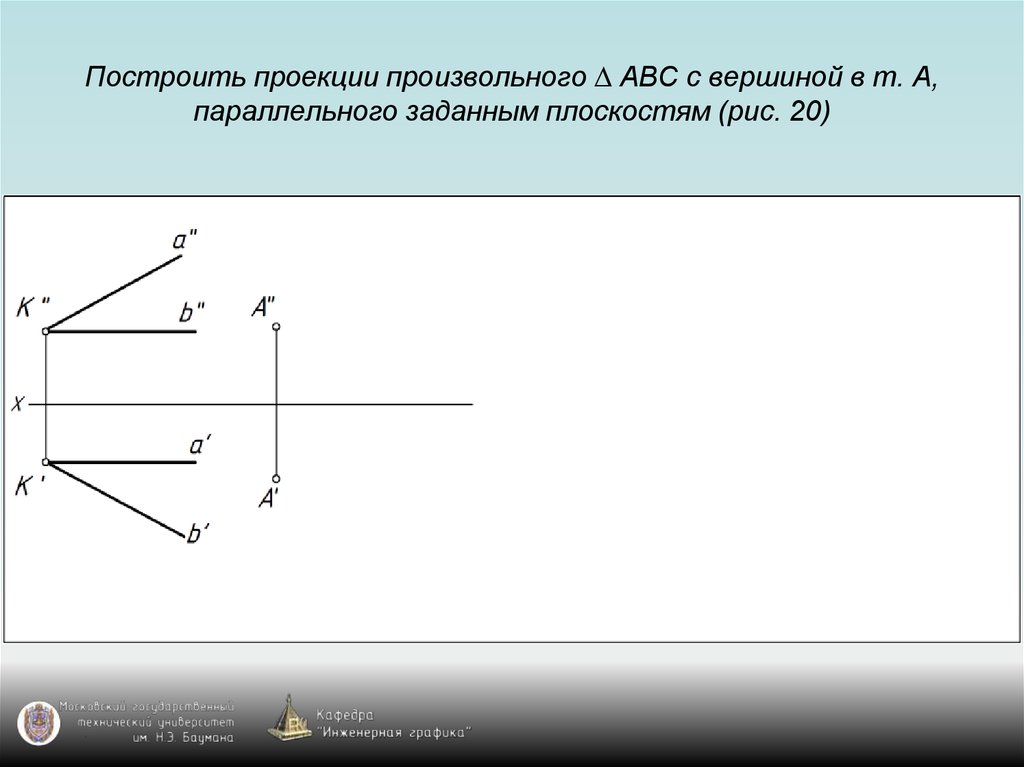
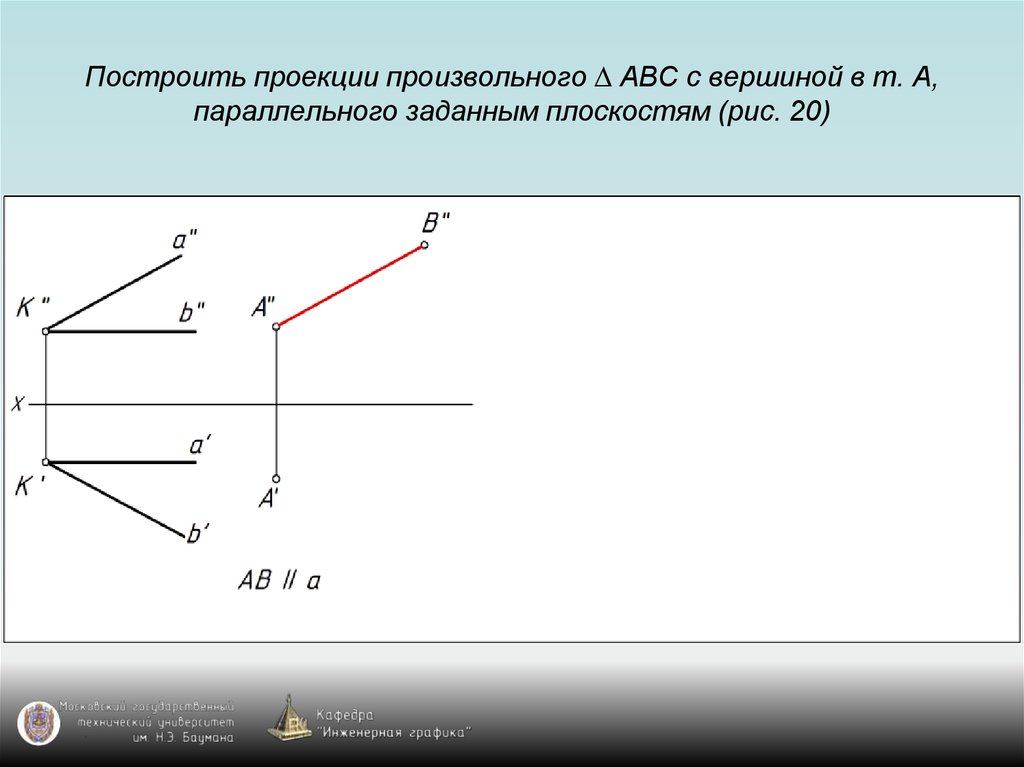
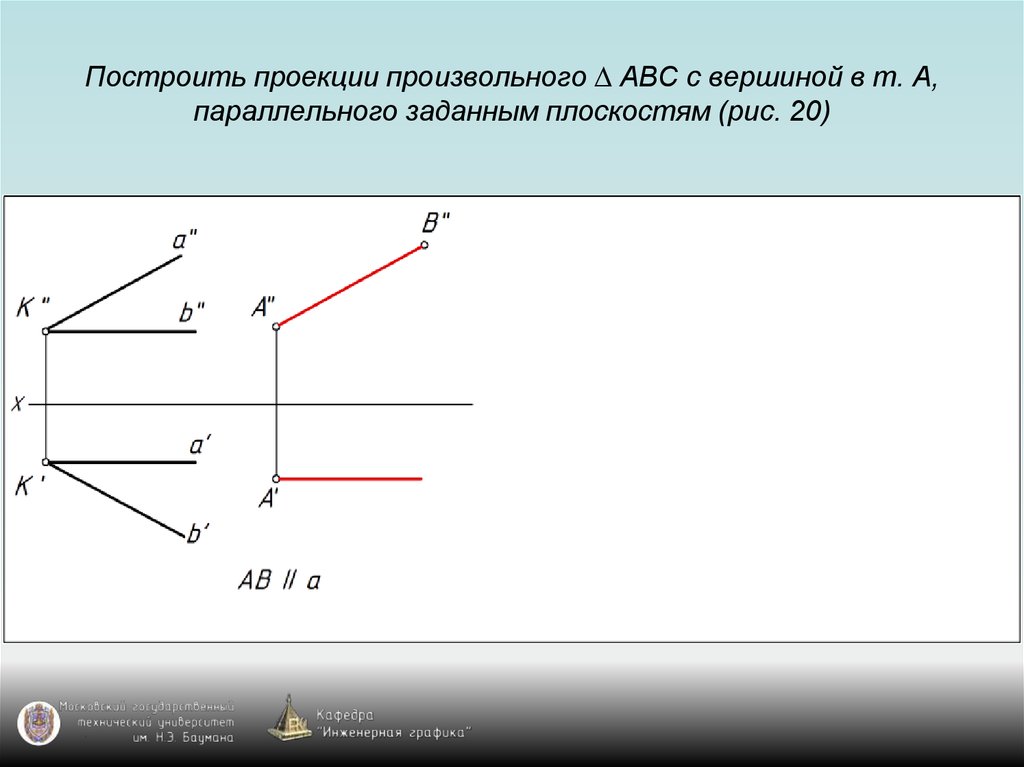
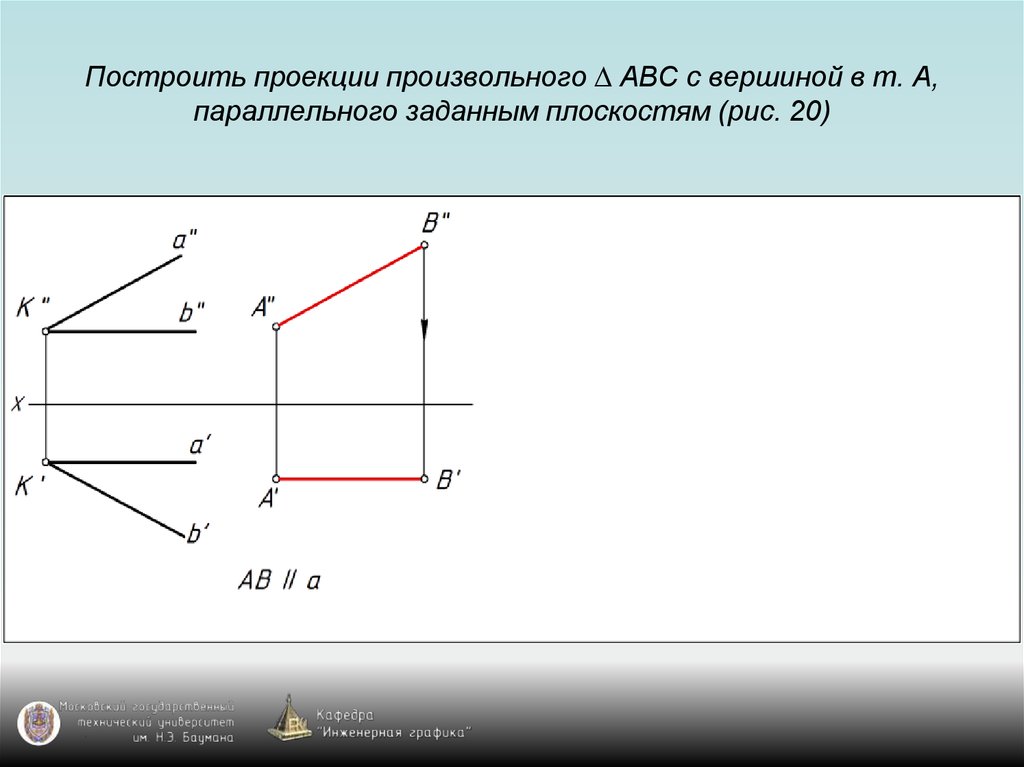
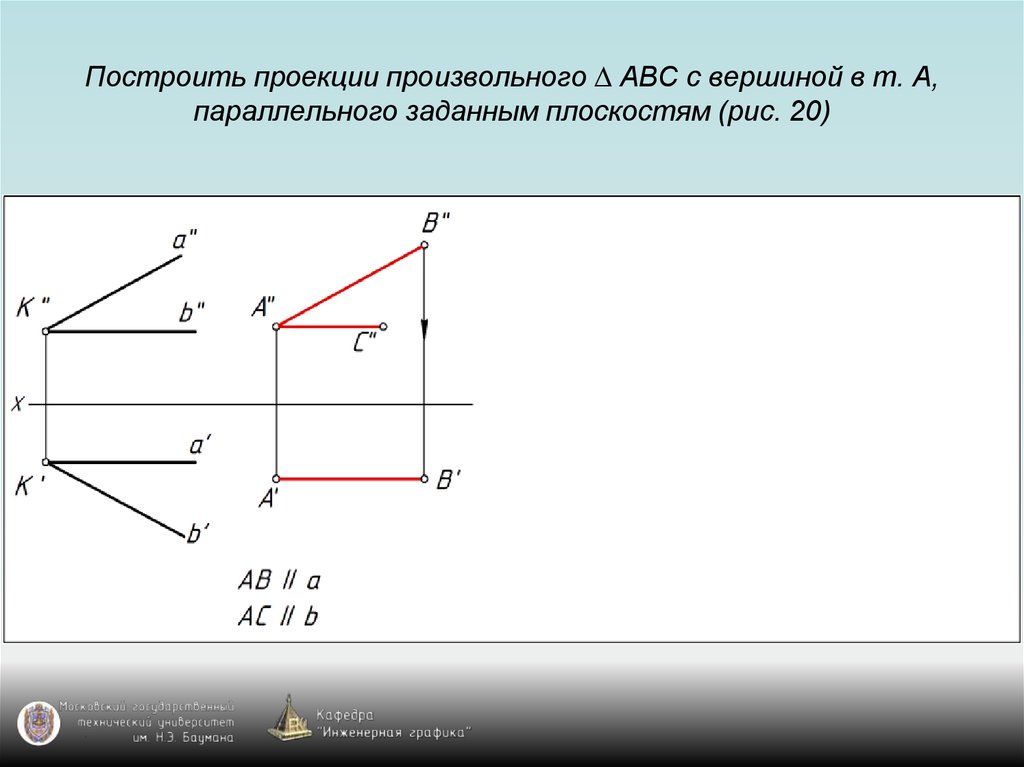
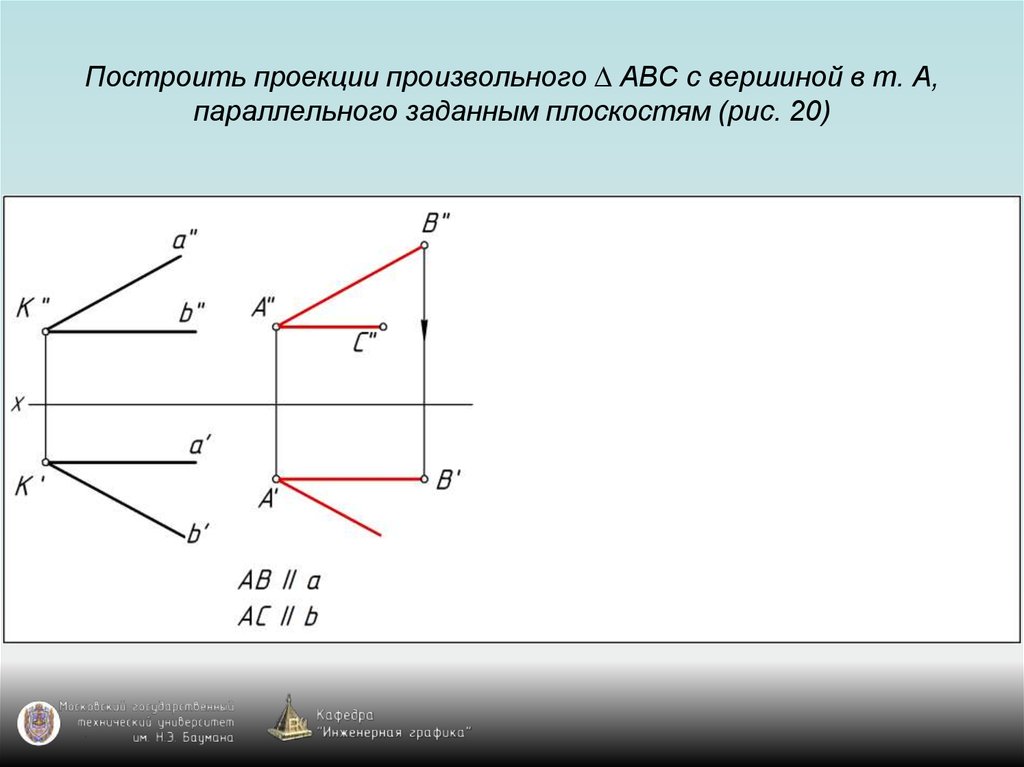
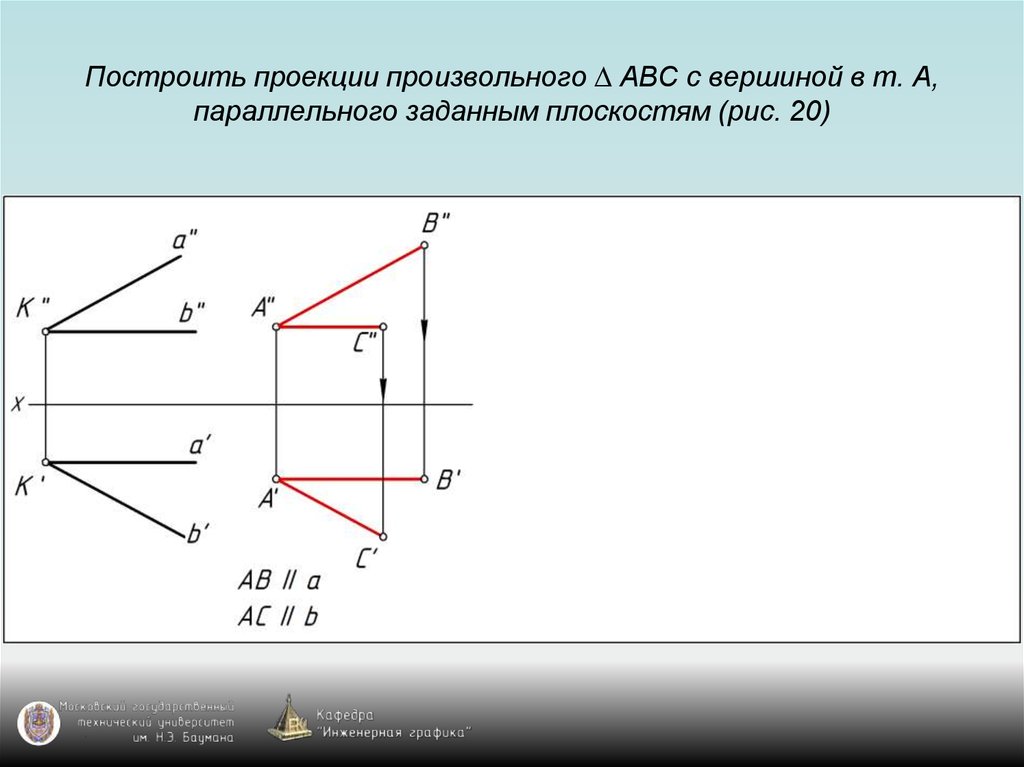
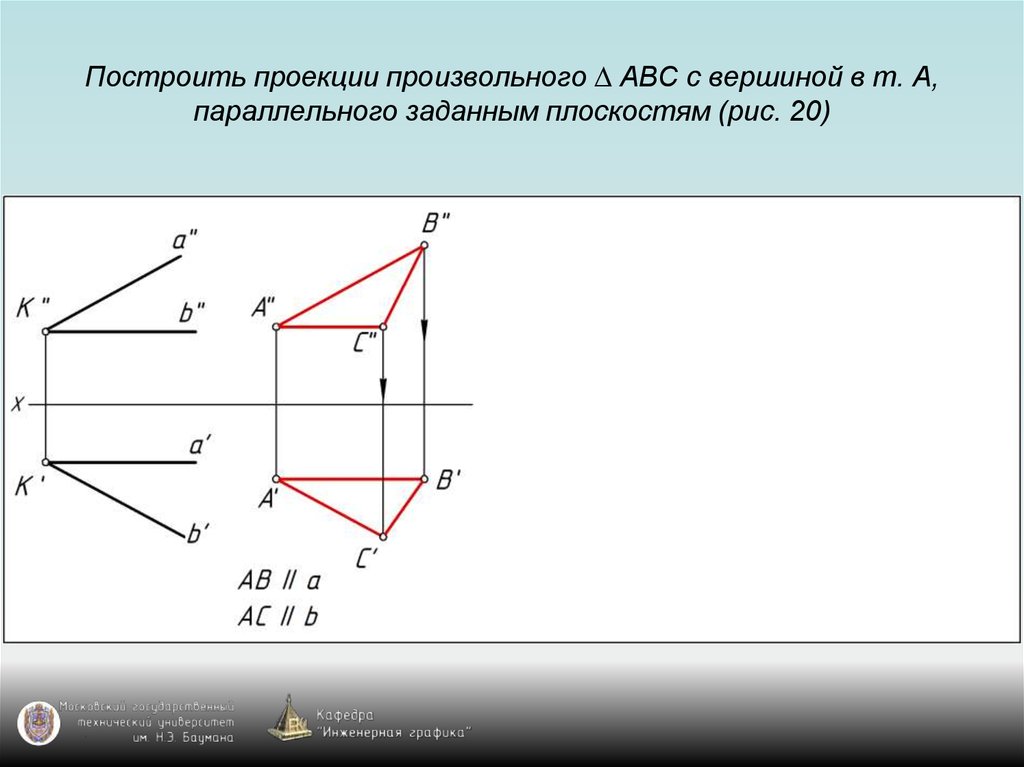
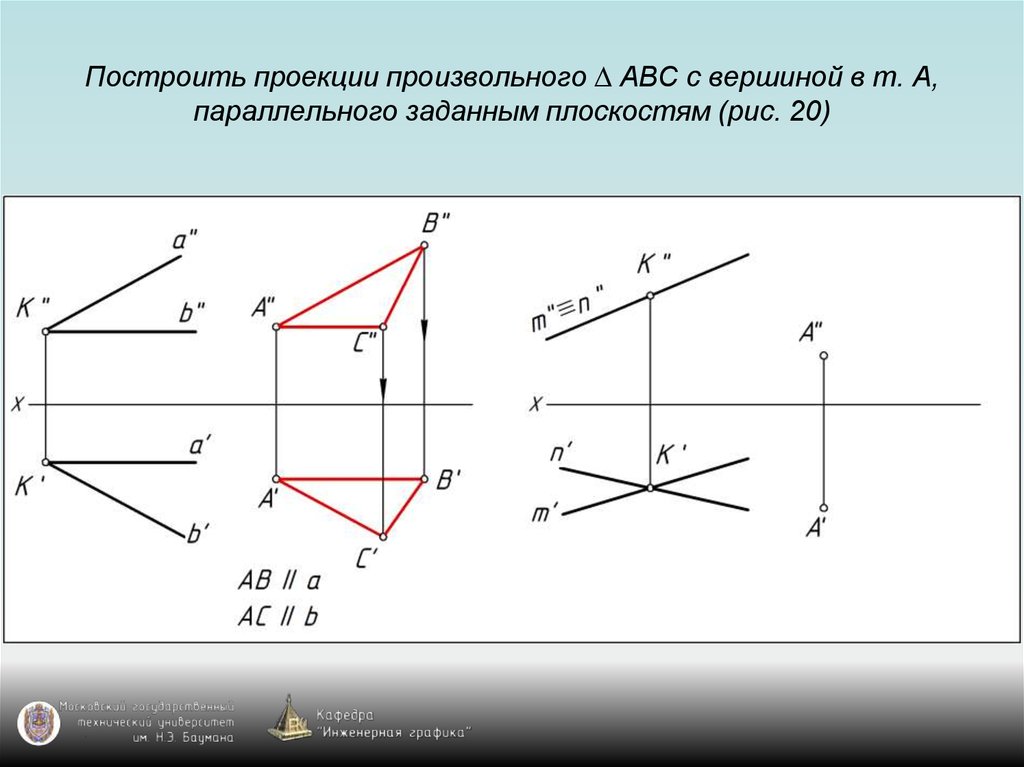
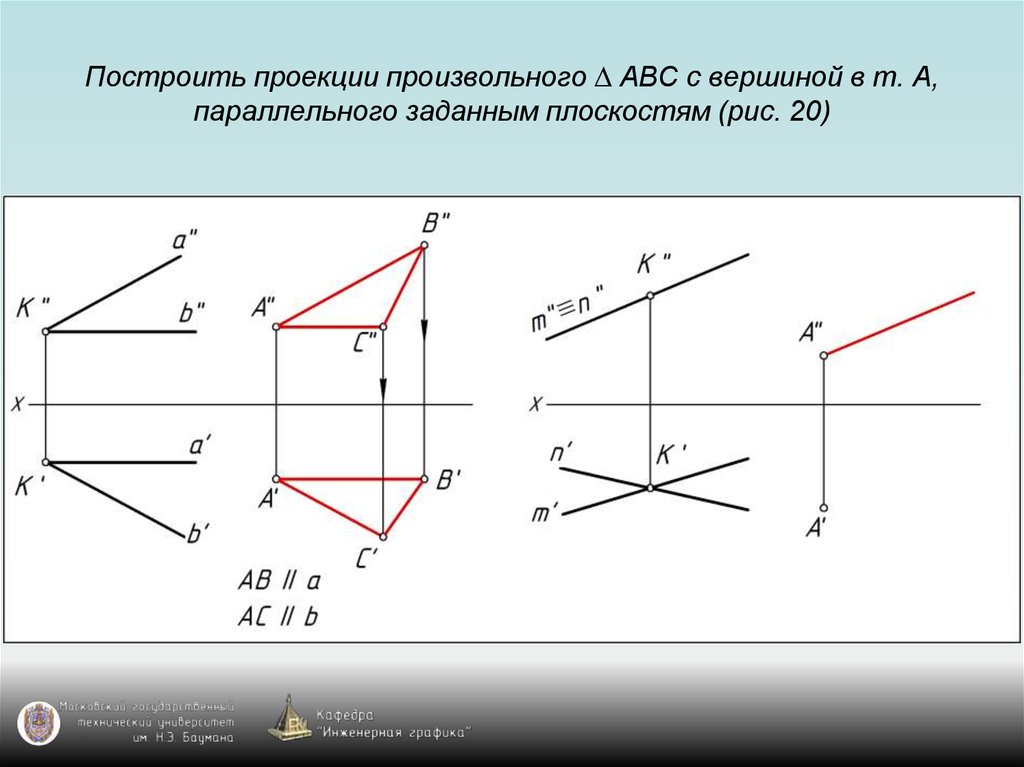
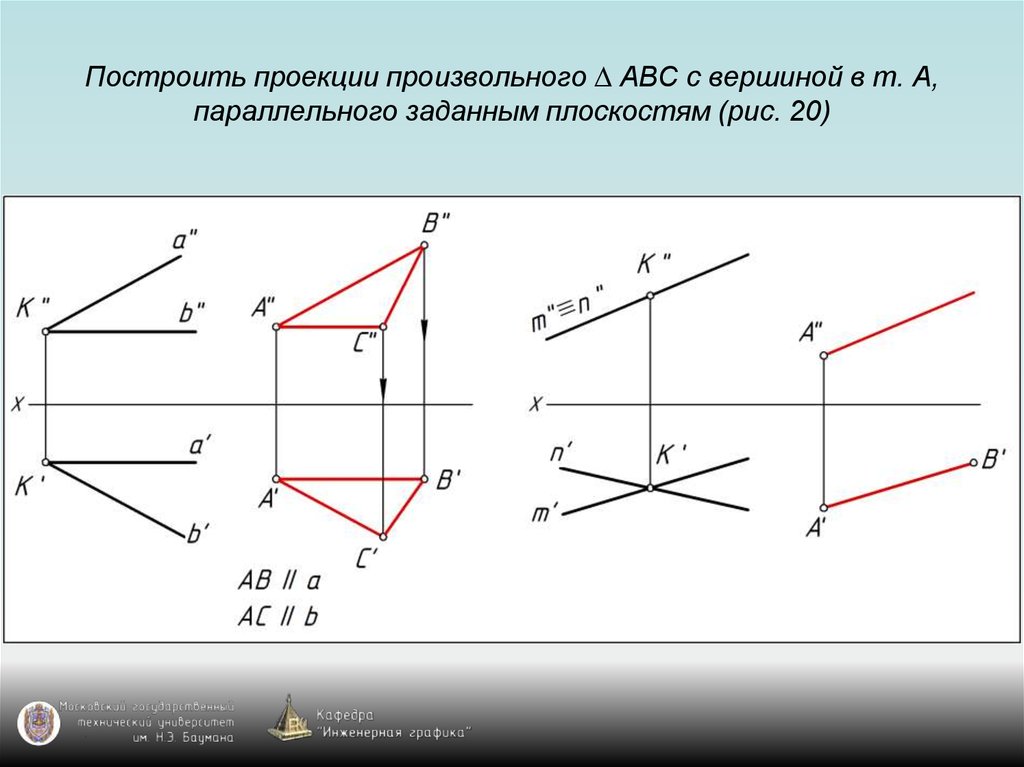
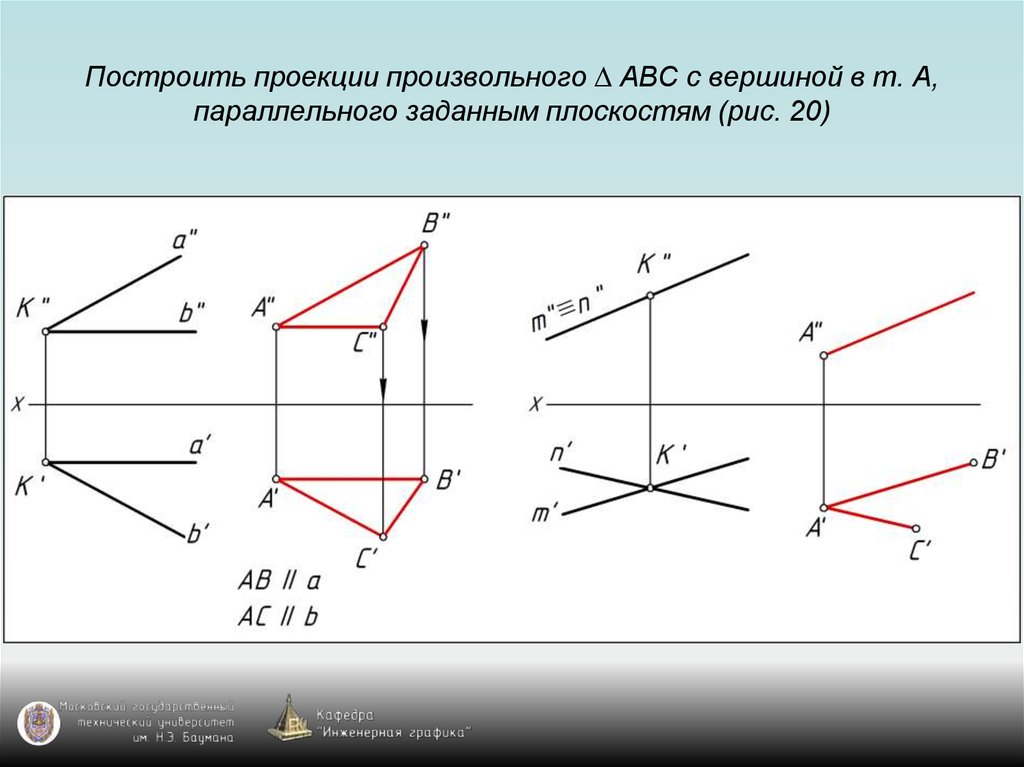
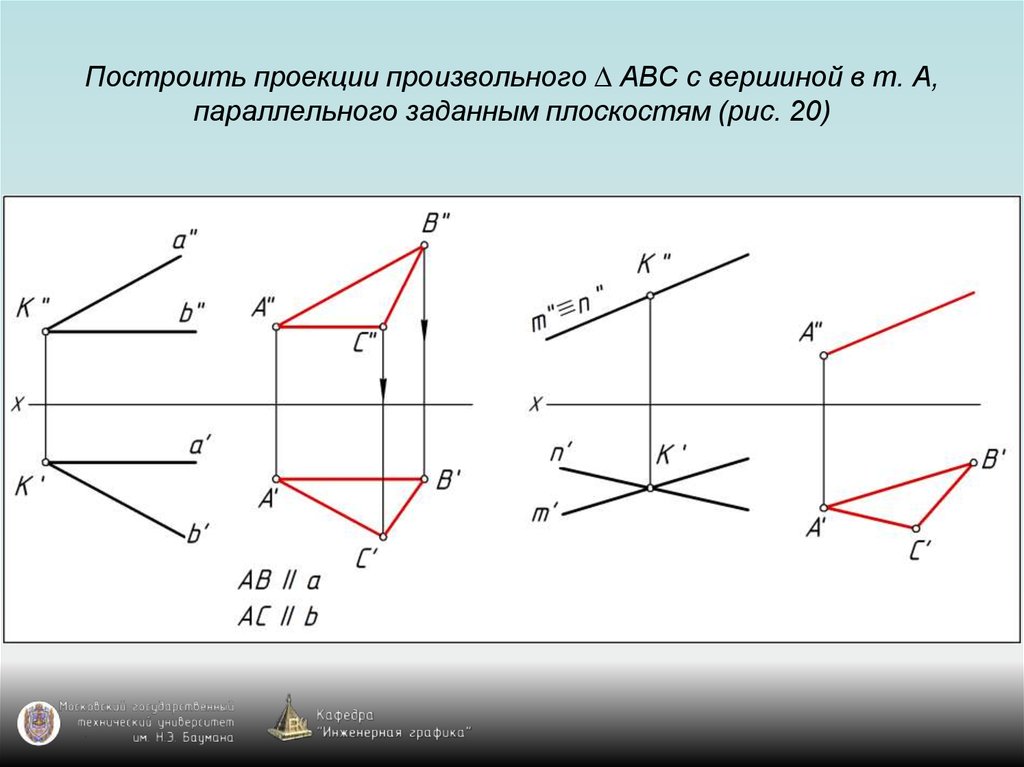
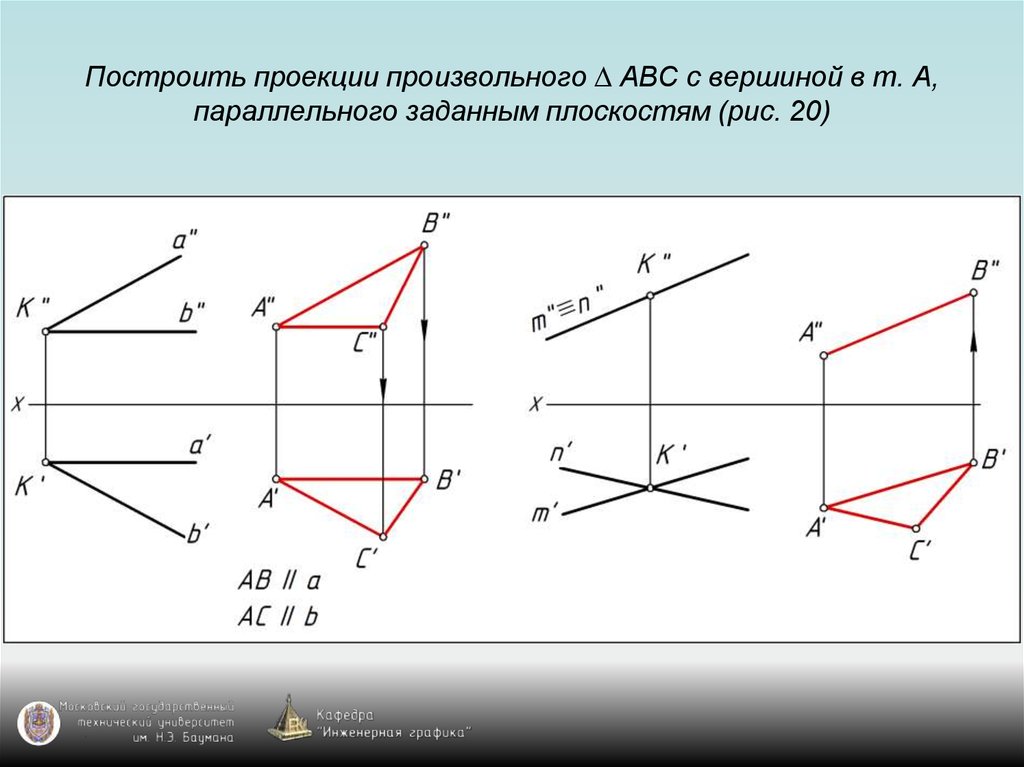
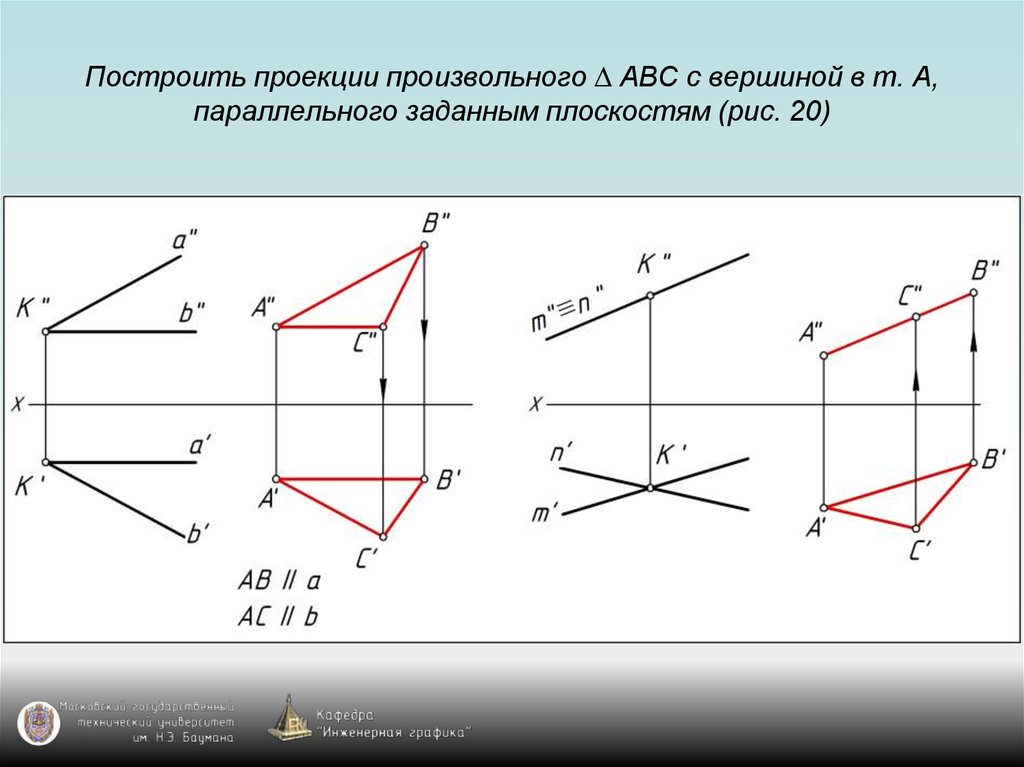
87. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

88. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

89. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

90. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

91. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

92. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

93. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

94. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

95. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

96. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

97. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

98. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

99. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

100. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

101. Построить проекции произвольного ∆ АВС с вершиной в т. А, параллельного заданным плоскостям (рис. 20)

102. Перпендикулярность двух плоскостей

Построение на чертеже перпендикулярных
плоскостей основано на:
1) использовании признака перпендикулярности
двух плоскостей – две плоскости взаимно
перпендикулярны, если одна из этих
плоскостей содержит прямую,
перпендикулярную к другой плоскости;
2) использовании теоремы о проекциях прямого
угла.

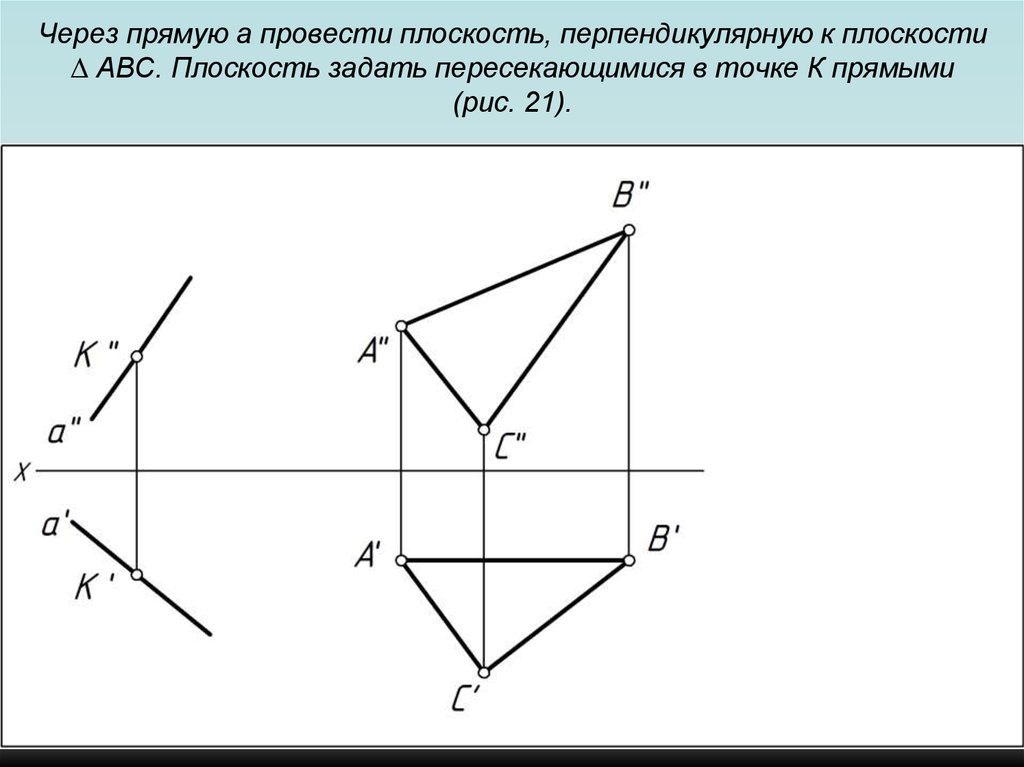
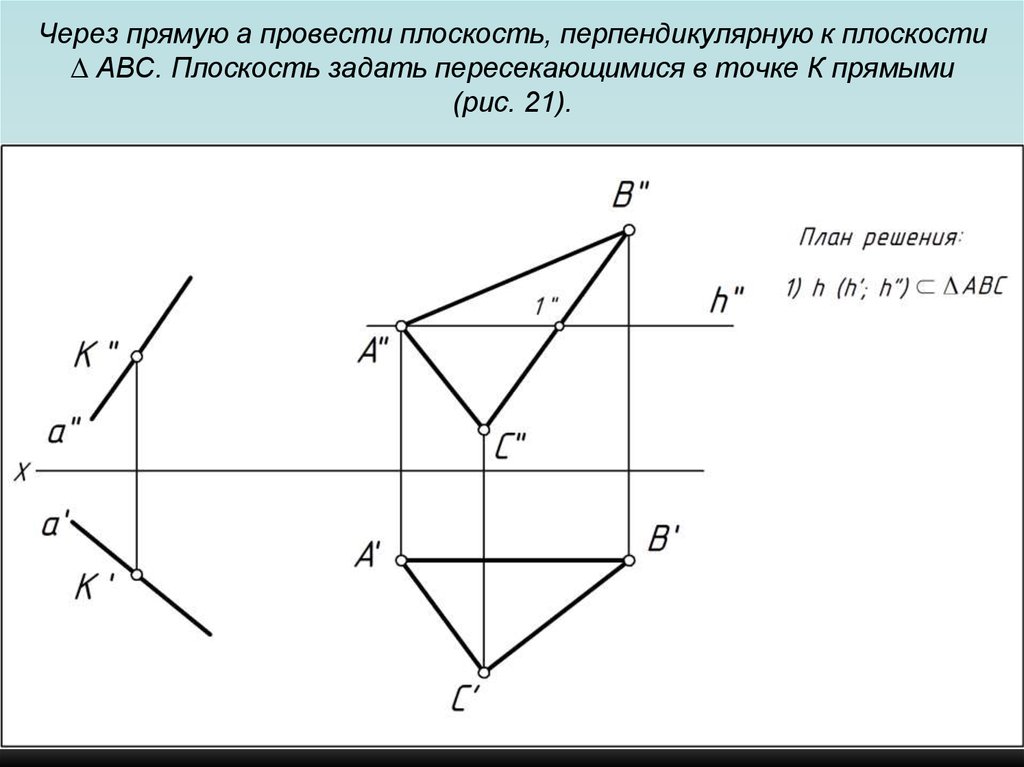
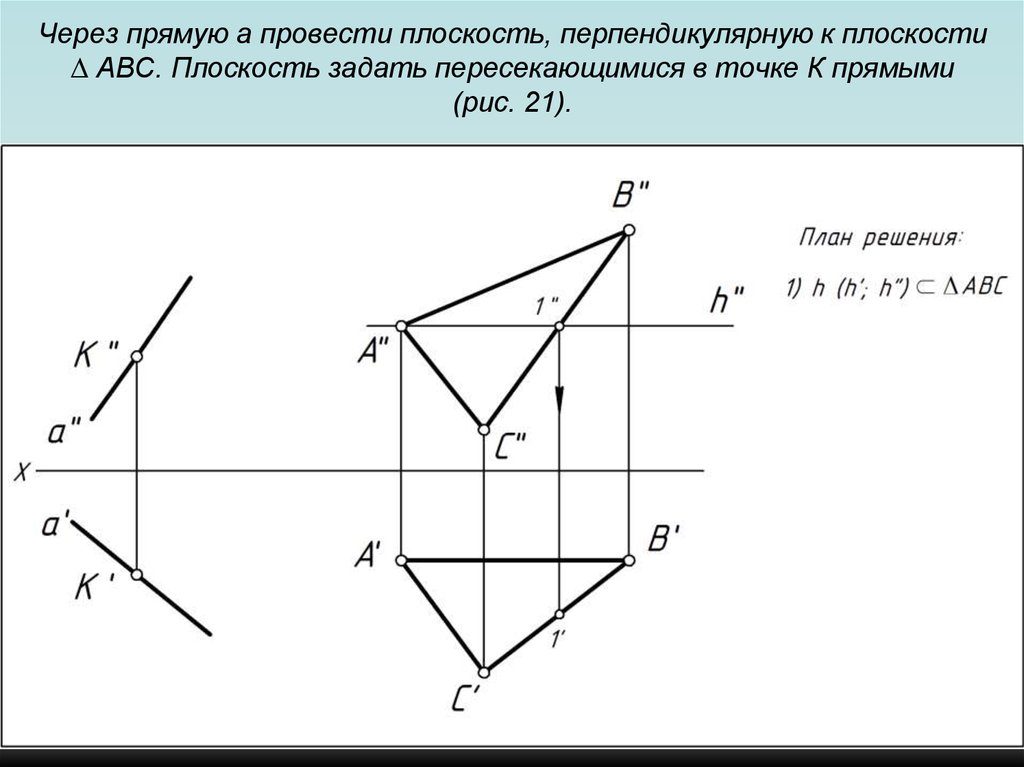
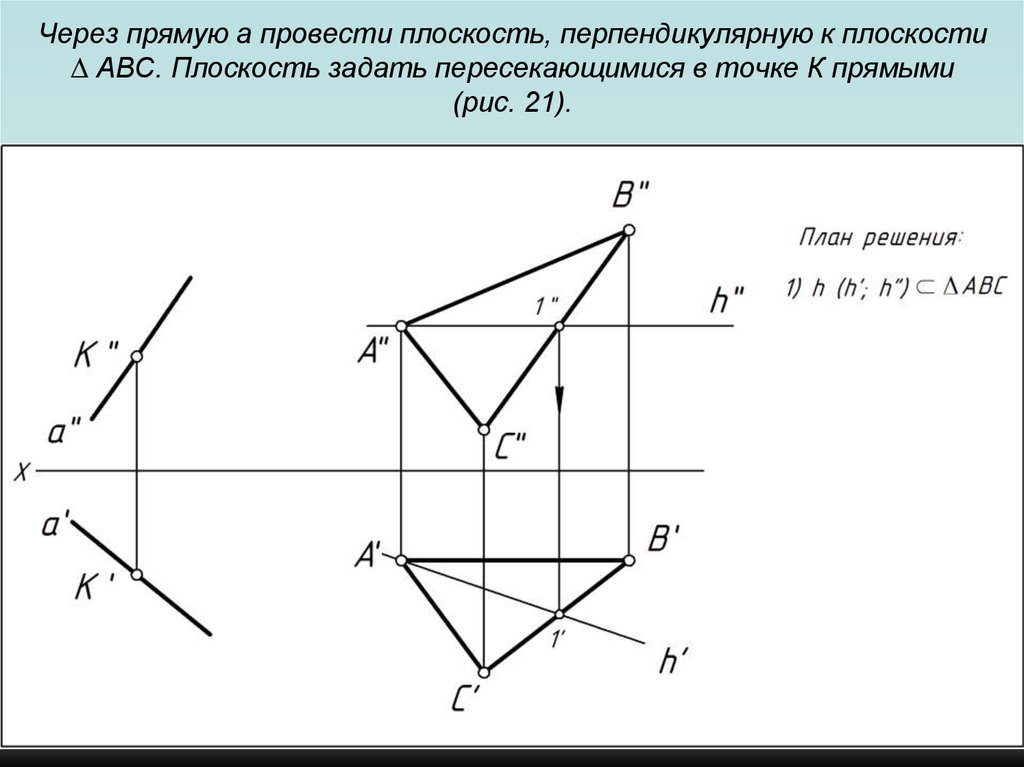
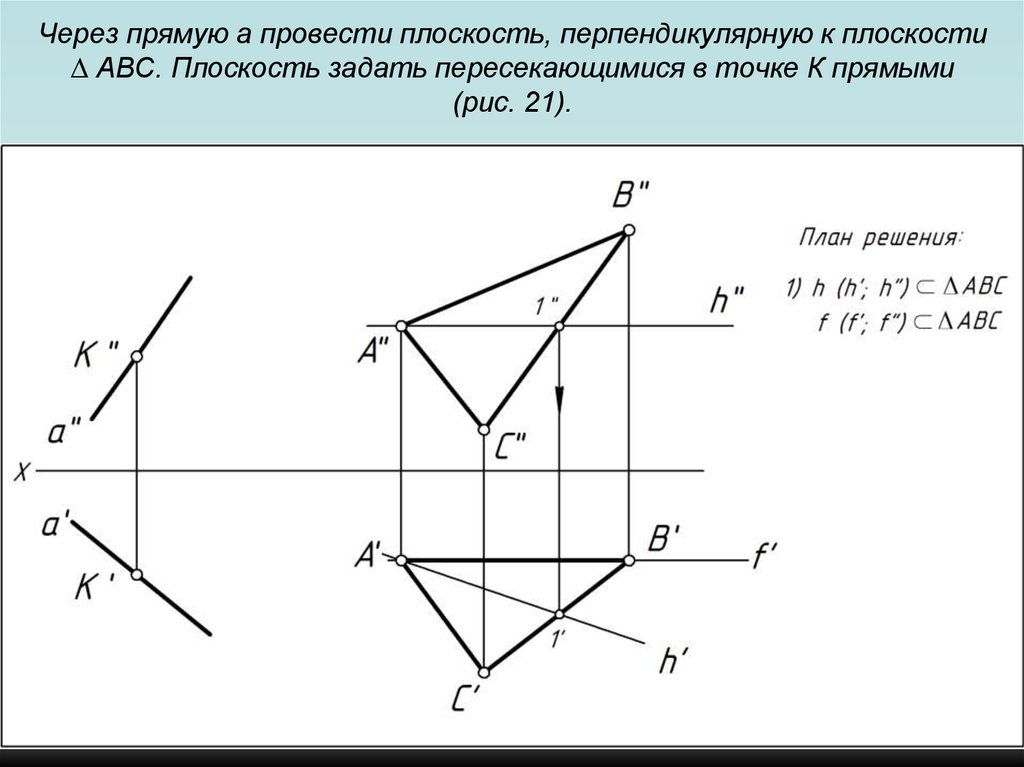
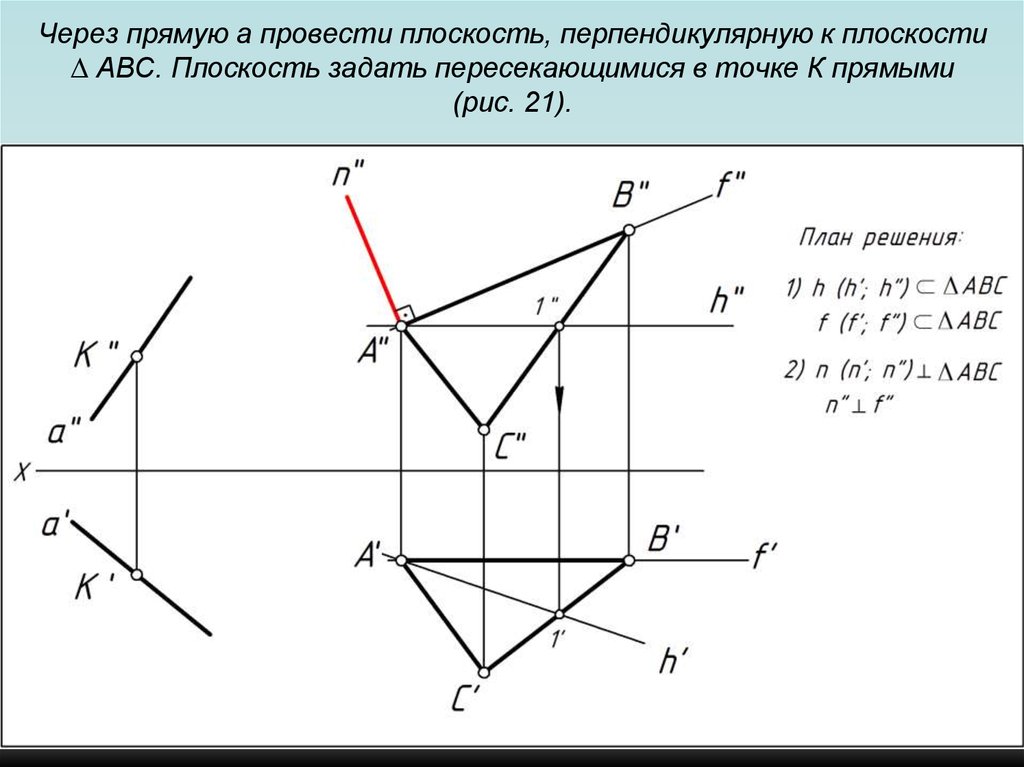
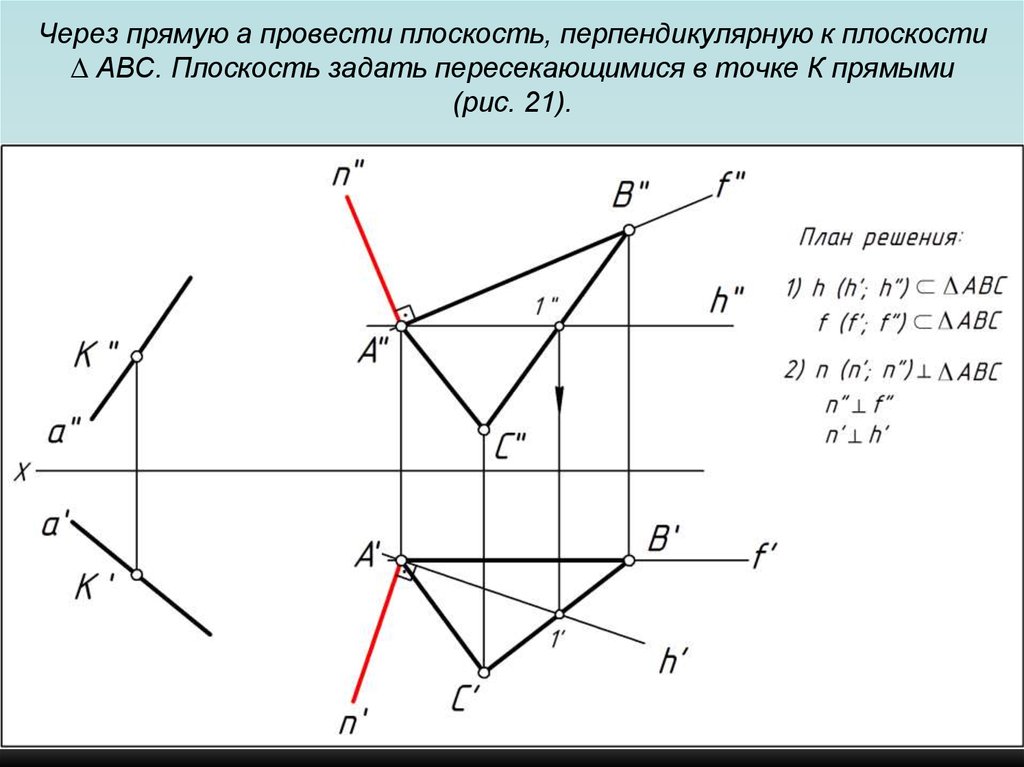
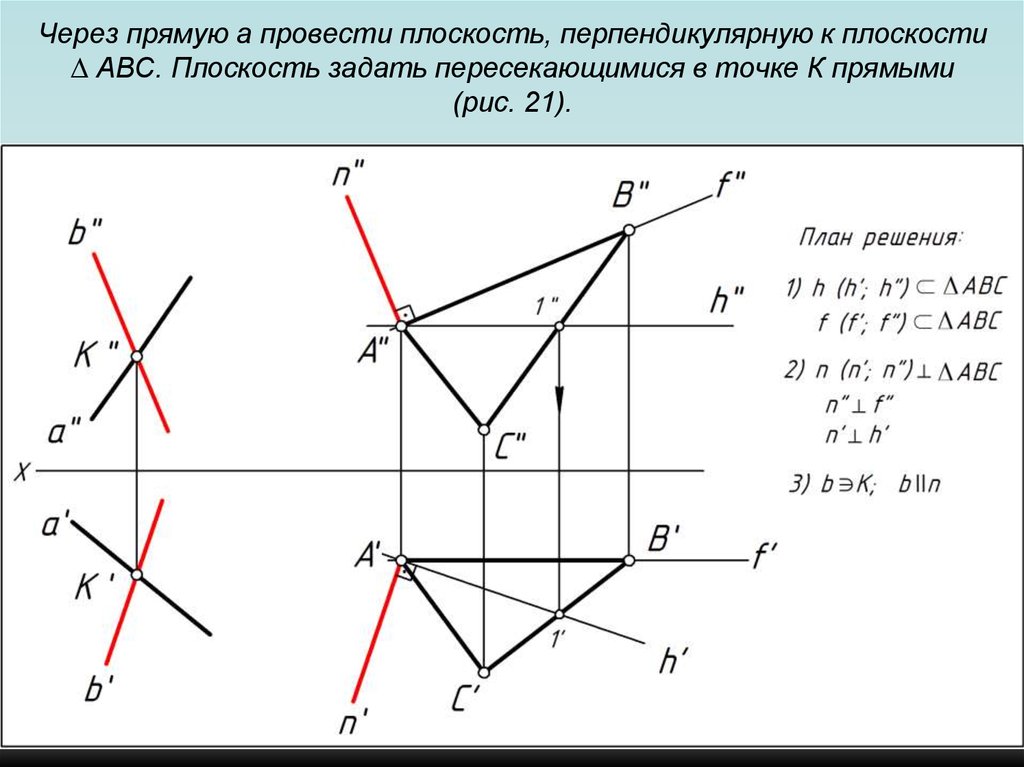
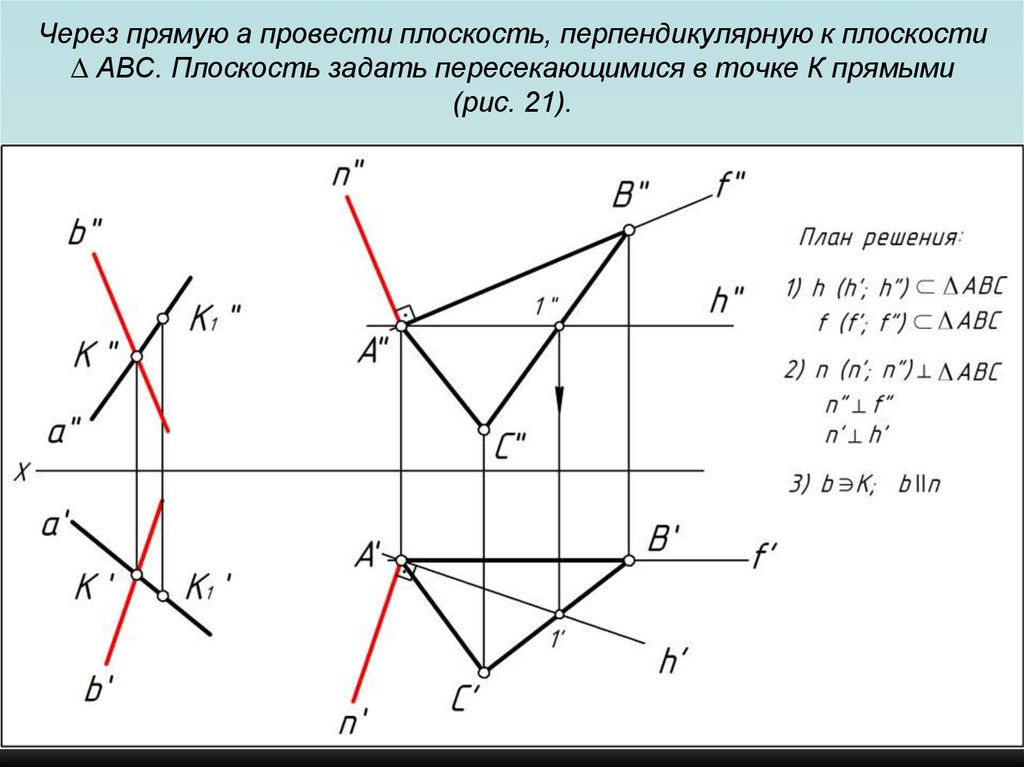
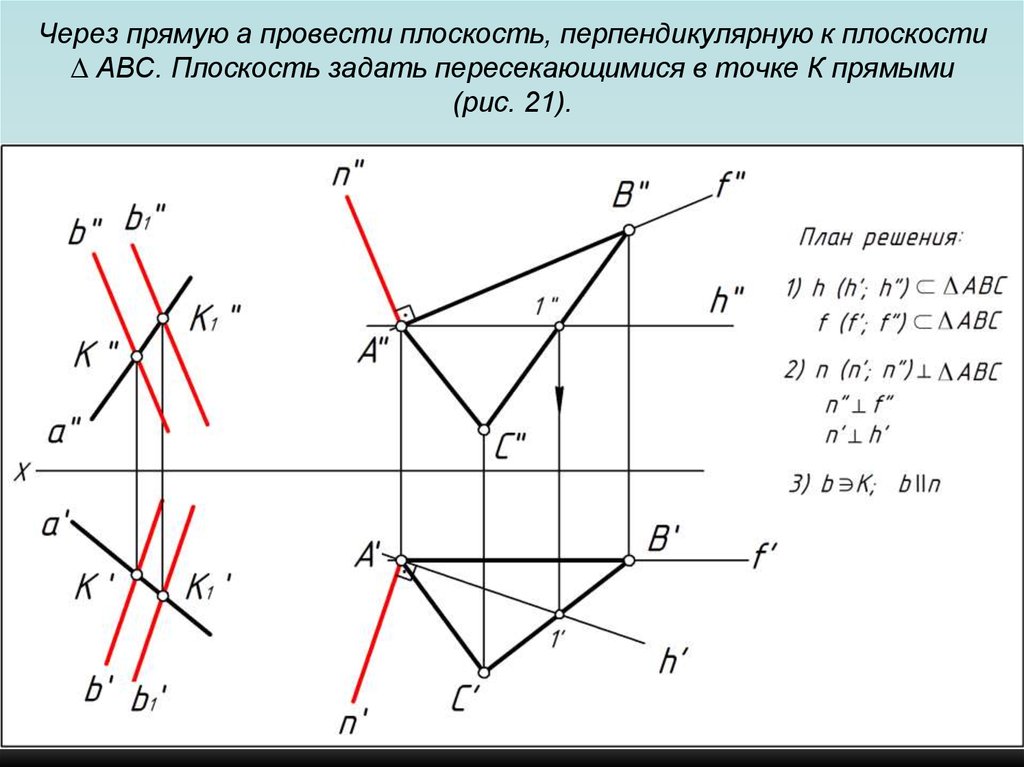
103. Через прямую a провести плоскость, перпендикулярную к плоскости ∆ АВС. Плоскость задать пересекающимися в точке К прямыми (рис.

21).

104. Через прямую a провести плоскость, перпендикулярную к плоскости ∆ АВС. Плоскость задать пересекающимися в точке К прямыми (рис.

21).

105. Через прямую a провести плоскость, перпендикулярную к плоскости ∆ АВС. Плоскость задать пересекающимися в точке К прямыми (рис.

21).

106. Через прямую a провести плоскость, перпендикулярную к плоскости ∆ АВС. Плоскость задать пересекающимися в точке К прямыми (рис.

21).

107. Через прямую a провести плоскость, перпендикулярную к плоскости ∆ АВС. Плоскость задать пересекающимися в точке К прямыми (рис.

21).

108. Через прямую a провести плоскость, перпендикулярную к плоскости ∆ АВС. Плоскость задать пересекающимися в точке К прямыми (рис.

21).

109. Через прямую a провести плоскость, перпендикулярную к плоскости ∆ АВС. Плоскость задать пересекающимися в точке К прямыми (рис.

21).

110. Через прямую a провести плоскость, перпендикулярную к плоскости ∆ АВС. Плоскость задать пересекающимися в точке К прямыми (рис.

21).

111. Через прямую a провести плоскость, перпендикулярную к плоскости ∆ АВС. Плоскость задать пересекающимися в точке К прямыми (рис.

21).

112. Через прямую a провести плоскость, перпендикулярную к плоскости ∆ АВС. Плоскость задать пересекающимися в точке К прямыми (рис.

21).

113. Через прямую a провести плоскость, перпендикулярную к плоскости ∆ АВС. Плоскость задать пересекающимися в точке К прямыми (рис.

21).

114. 5. Проекции многогранников

• Многогранник – часть пространства (тело),
ограниченная отсеками пересекающихся
плоскостей.
• Отсеки плоскостей (многоугольники) – грани,
линии их пересечения – ребра.
• Ребра пересекаются в точках – вершинах
многогранника.
• Построение проекции многогранника сводится к
построению проекций его ребер и вершин.

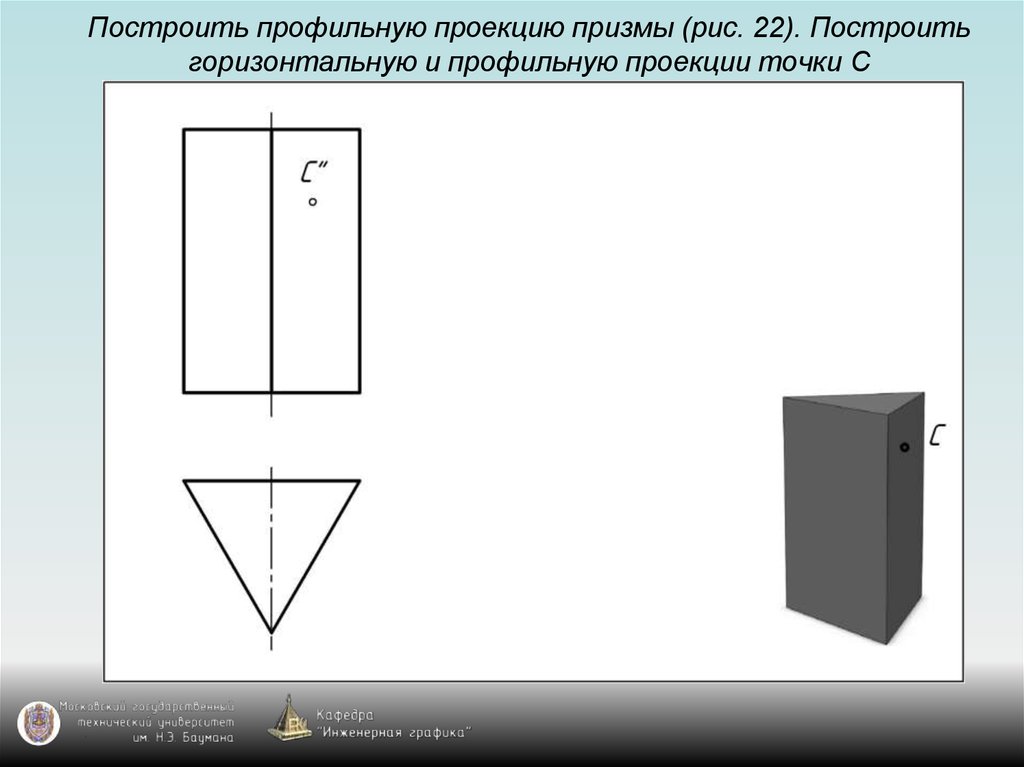
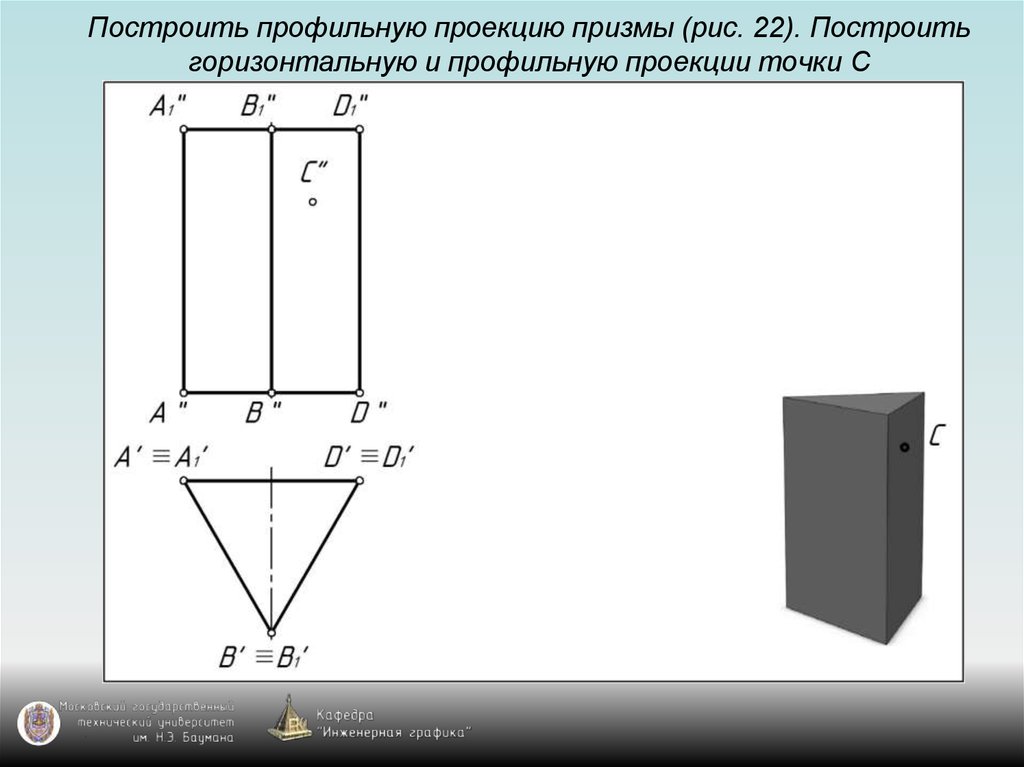
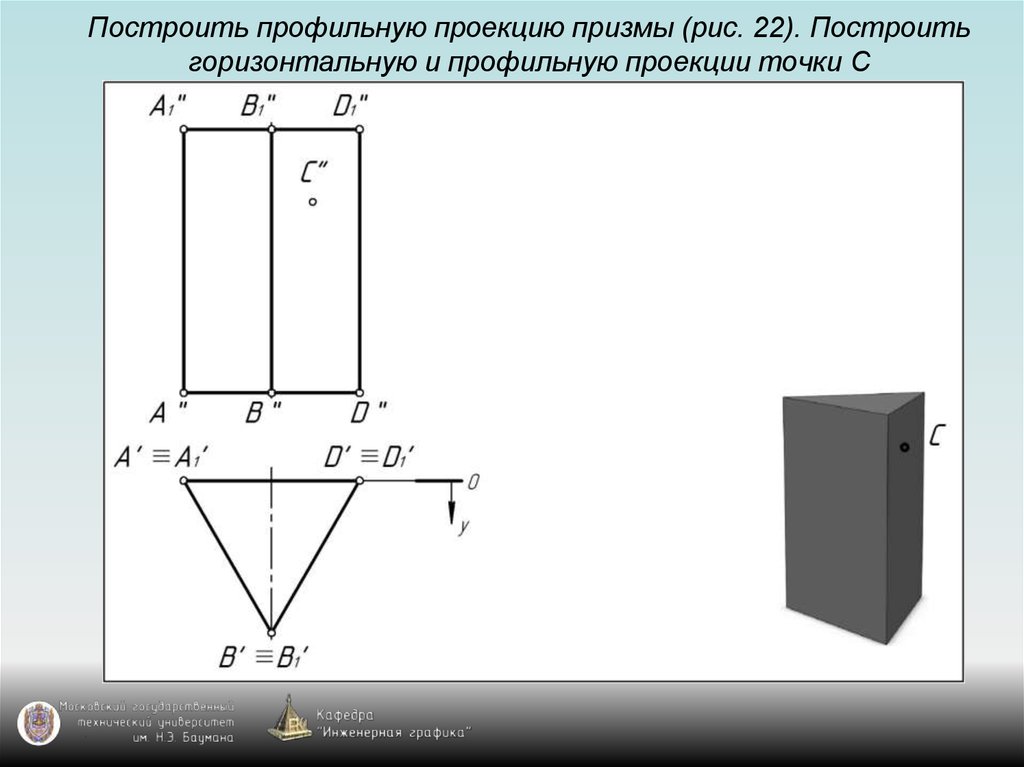
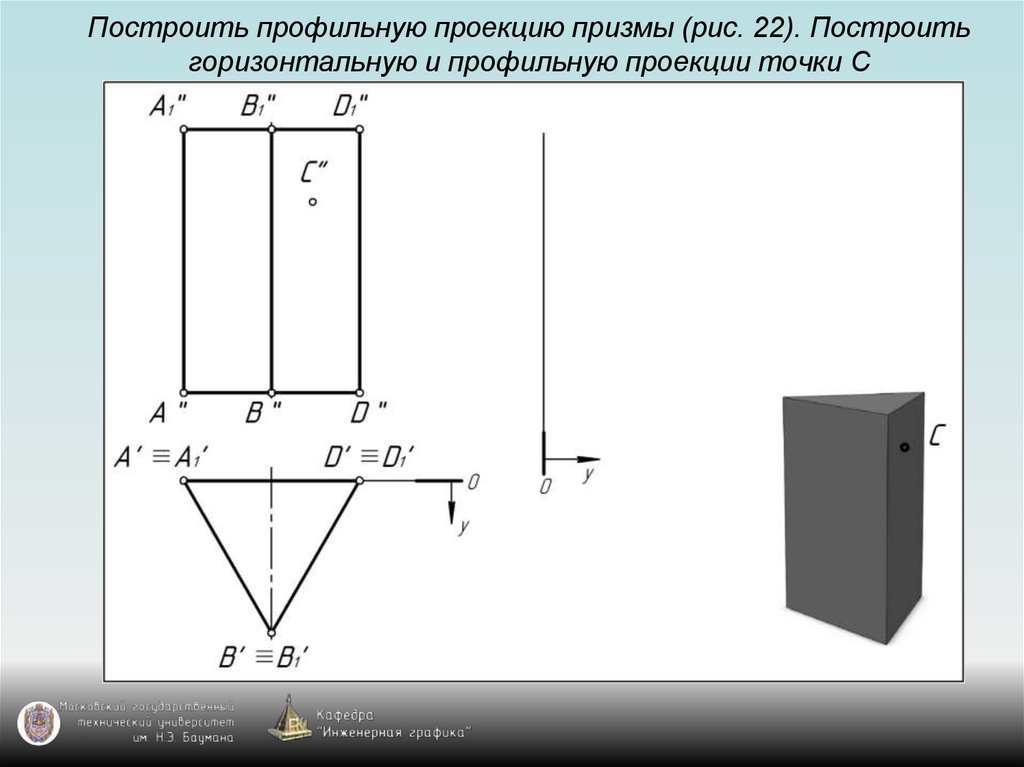
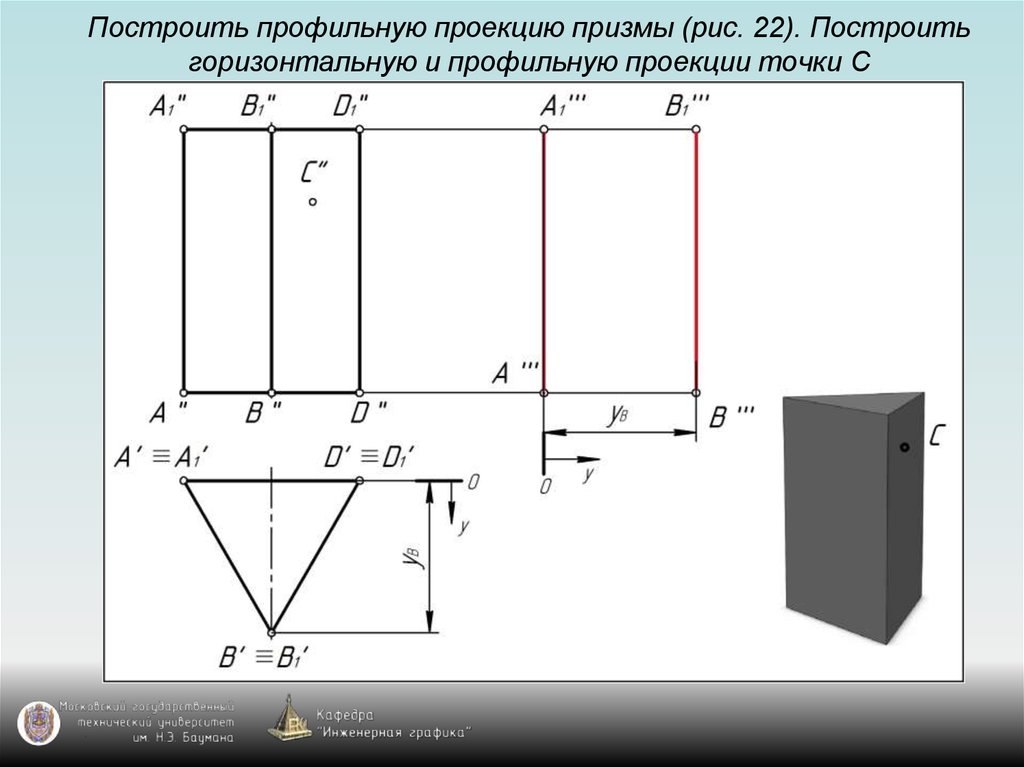
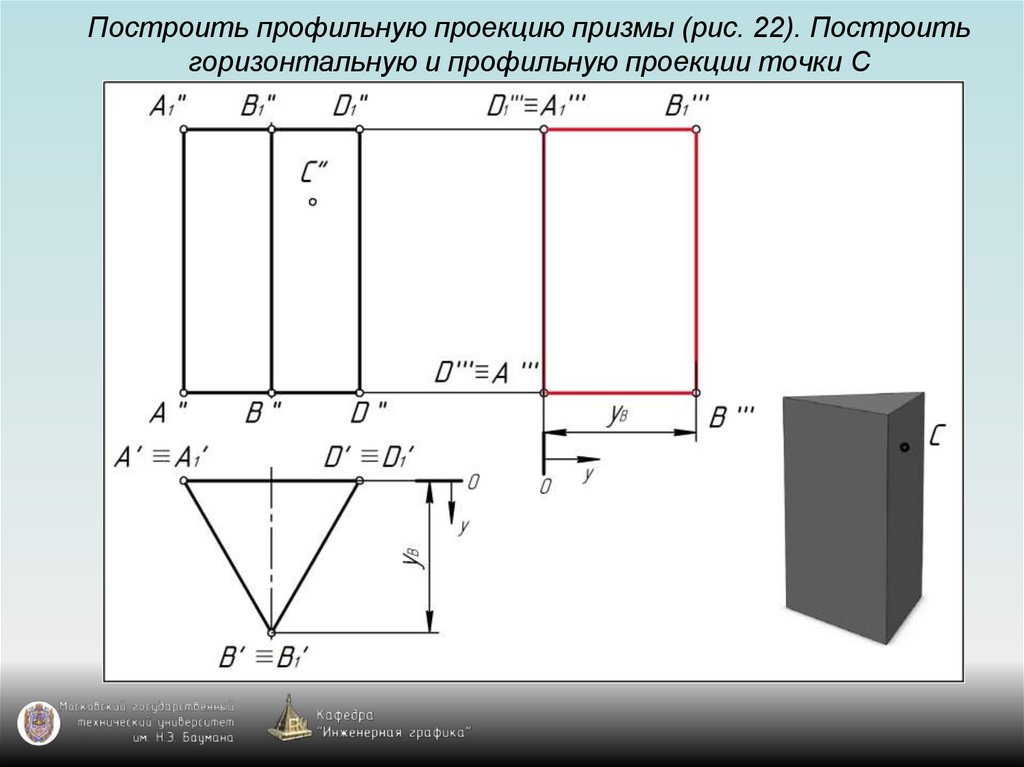
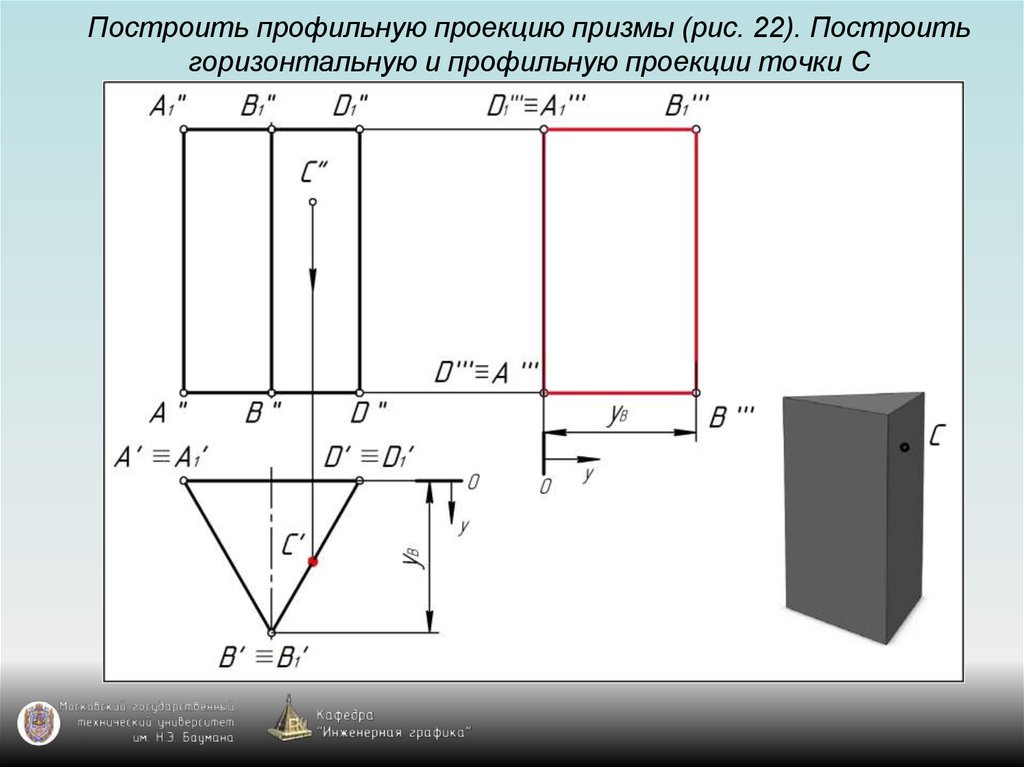
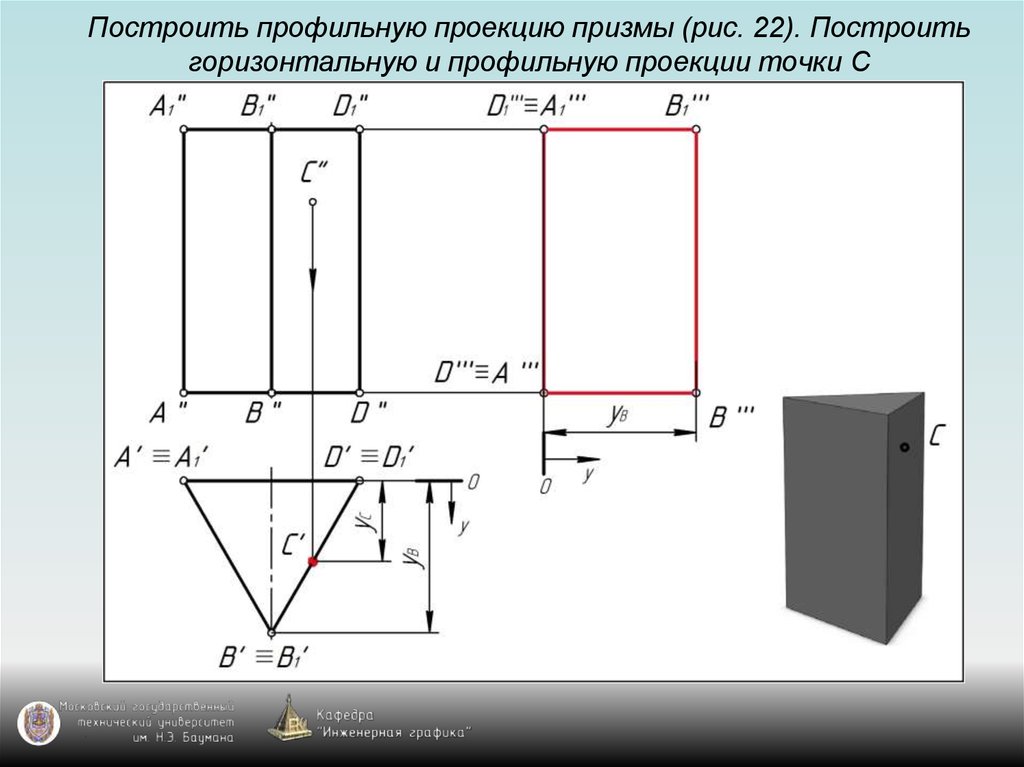
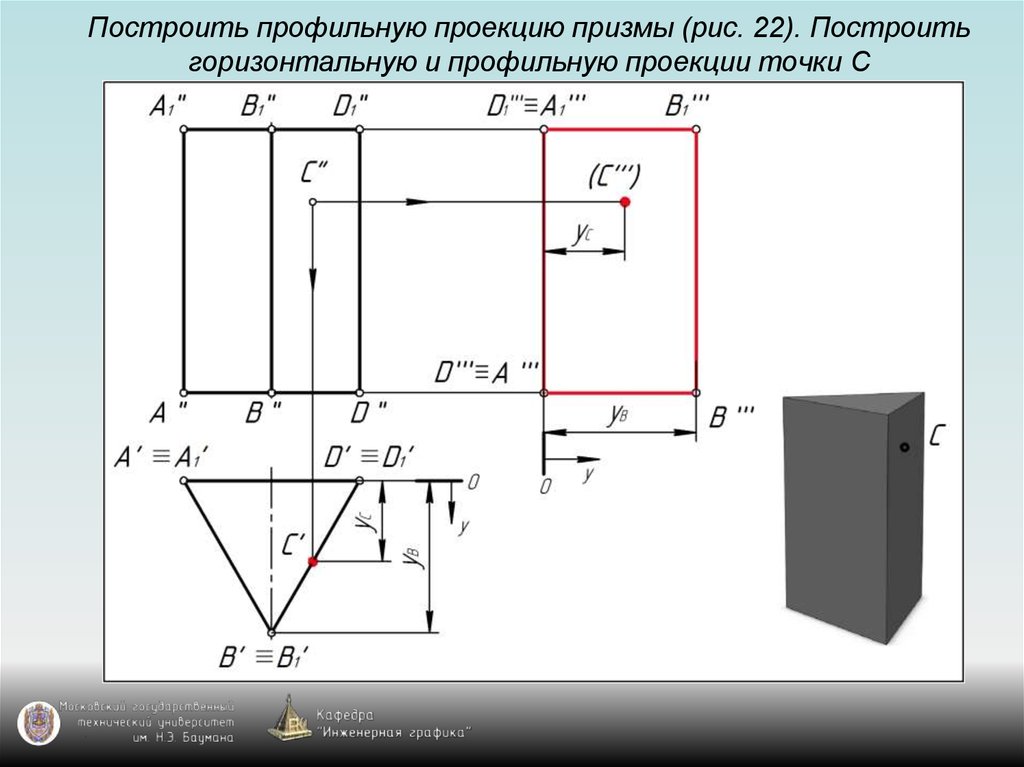
115. Построить профильную проекцию призмы (рис. 22). Построить горизонтальную и профильную проекции точки С

116. Построить профильную проекцию призмы (рис. 22). Построить горизонтальную и профильную проекции точки С

117. Построить профильную проекцию призмы (рис. 22). Построить горизонтальную и профильную проекции точки С

118. Построить профильную проекцию призмы (рис. 22). Построить горизонтальную и профильную проекции точки С

119. Построить профильную проекцию призмы (рис. 22). Построить горизонтальную и профильную проекции точки С

120. Построить профильную проекцию призмы (рис. 22). Построить горизонтальную и профильную проекции точки С

121. Построить профильную проекцию призмы (рис. 22). Построить горизонтальную и профильную проекции точки С

122. Построить профильную проекцию призмы (рис. 22). Построить горизонтальную и профильную проекции точки С

123. Построить профильную проекцию призмы (рис. 22). Построить горизонтальную и профильную проекции точки С

124. Построить профильную проекцию призмы (рис. 22). Построить горизонтальную и профильную проекции точки С

125. Задание призмы на чертеже

Призма на чертеже задаётся с помощью:
1) проекции основания призмы – многоугольника;
2) проекций рёбер призмы – прямолинейных
отрезков, которые являются линиями
пересечения боковых граней призмы
(параллелограммов или прямоугольников).

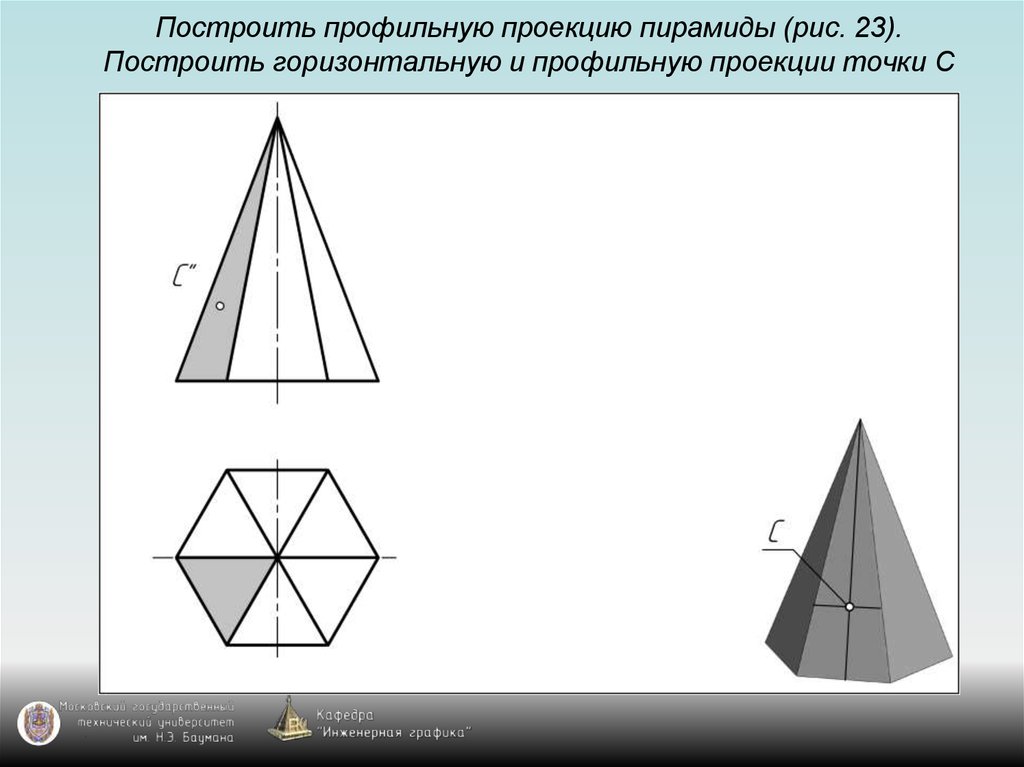
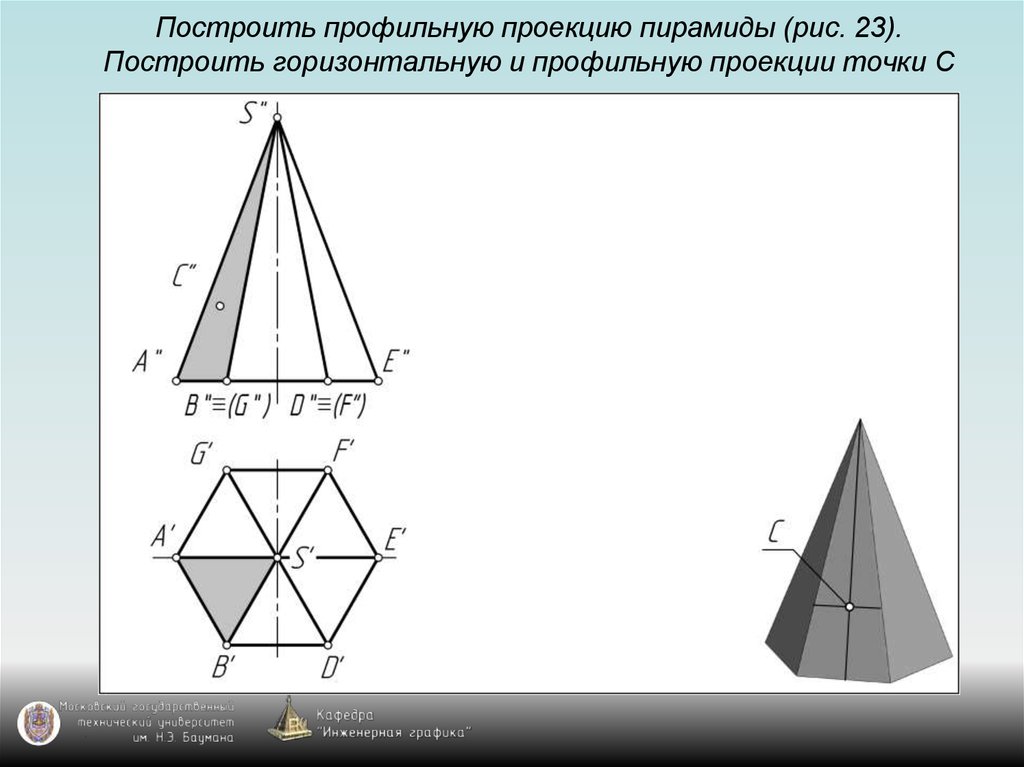
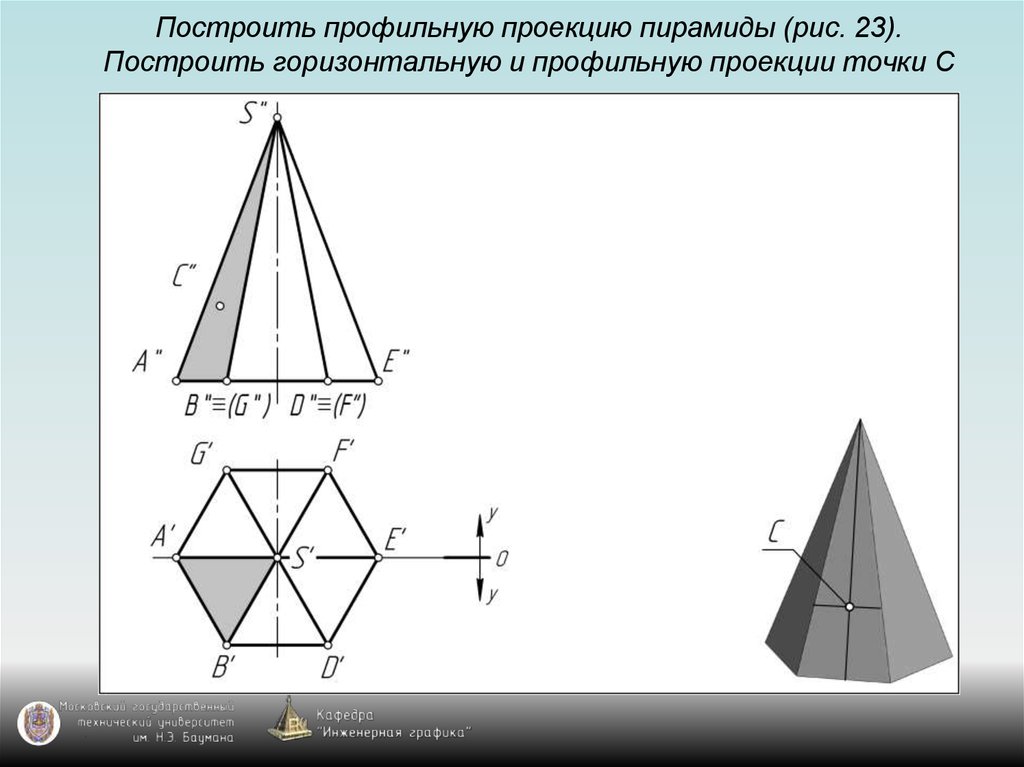
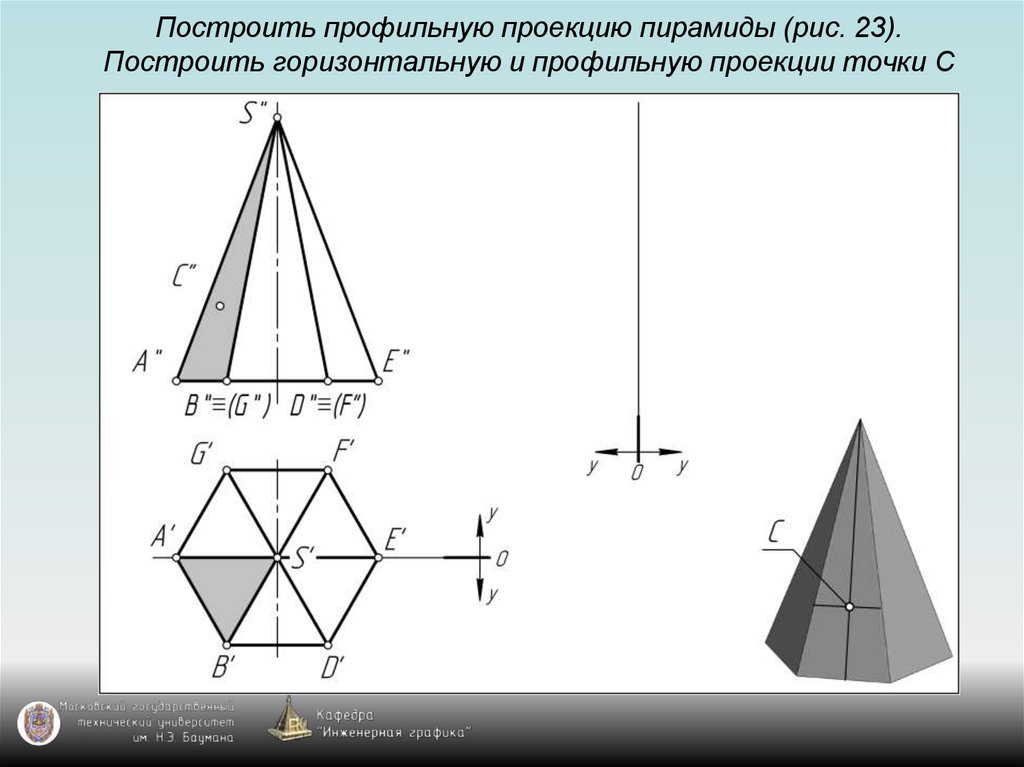
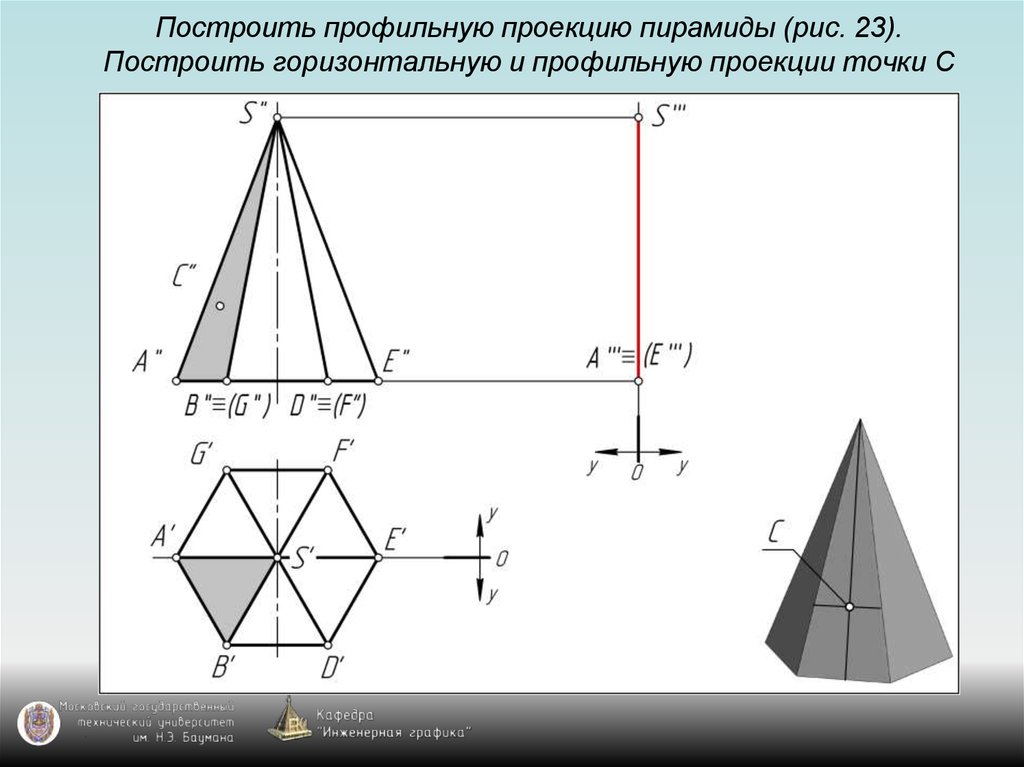
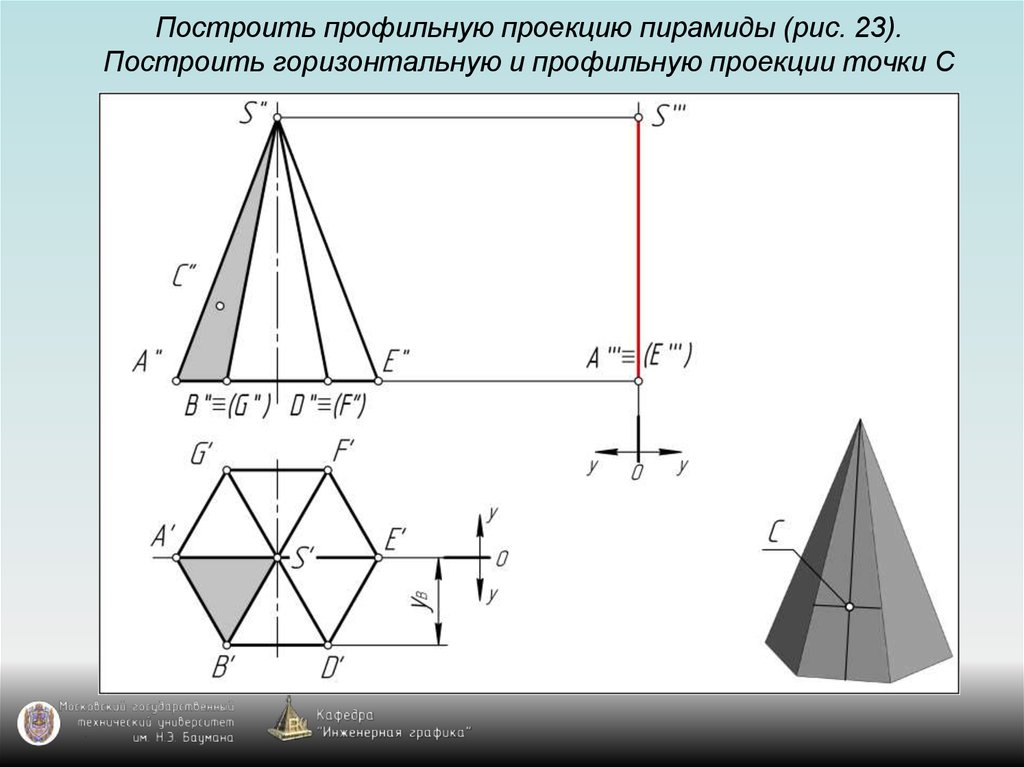
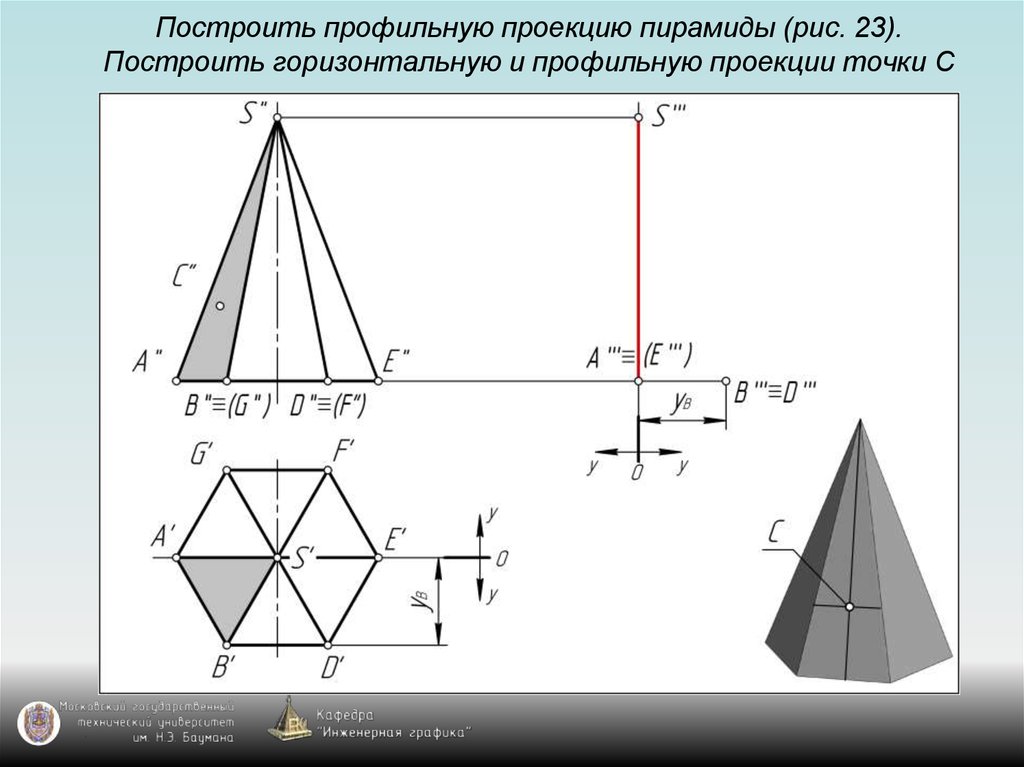
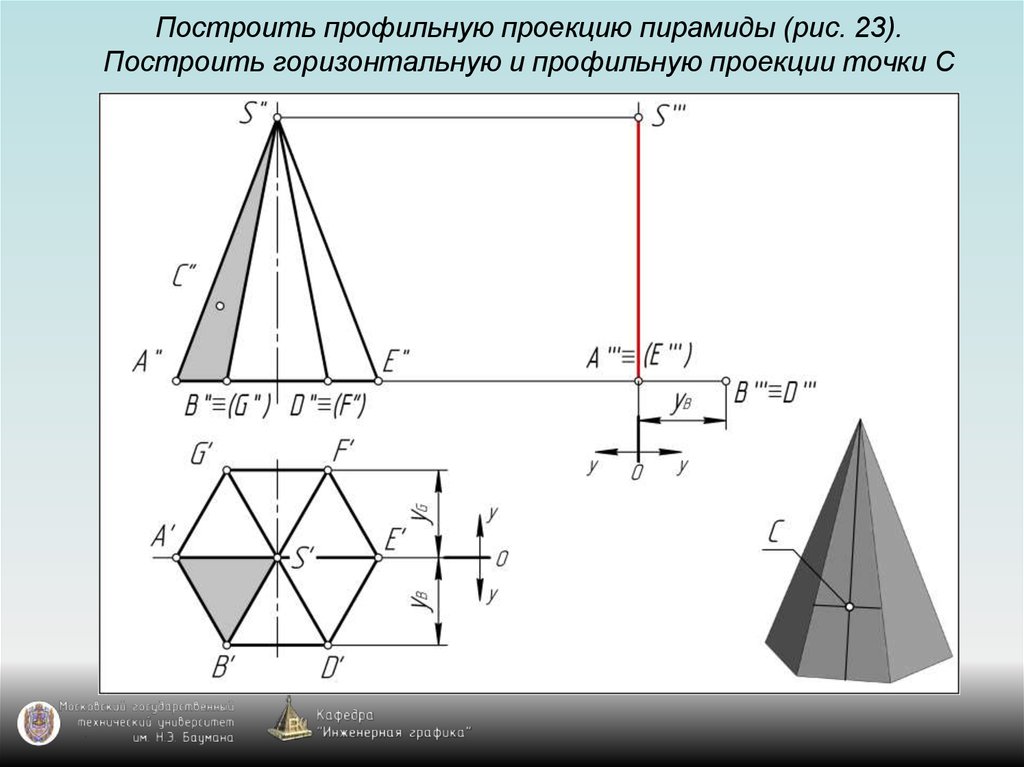
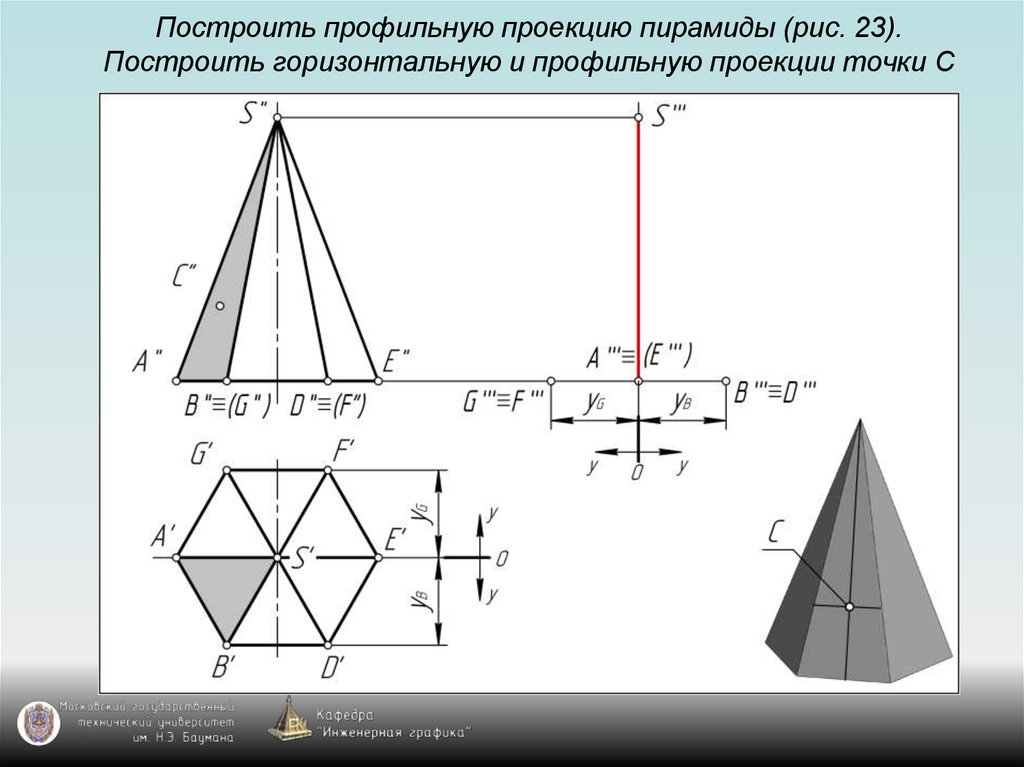
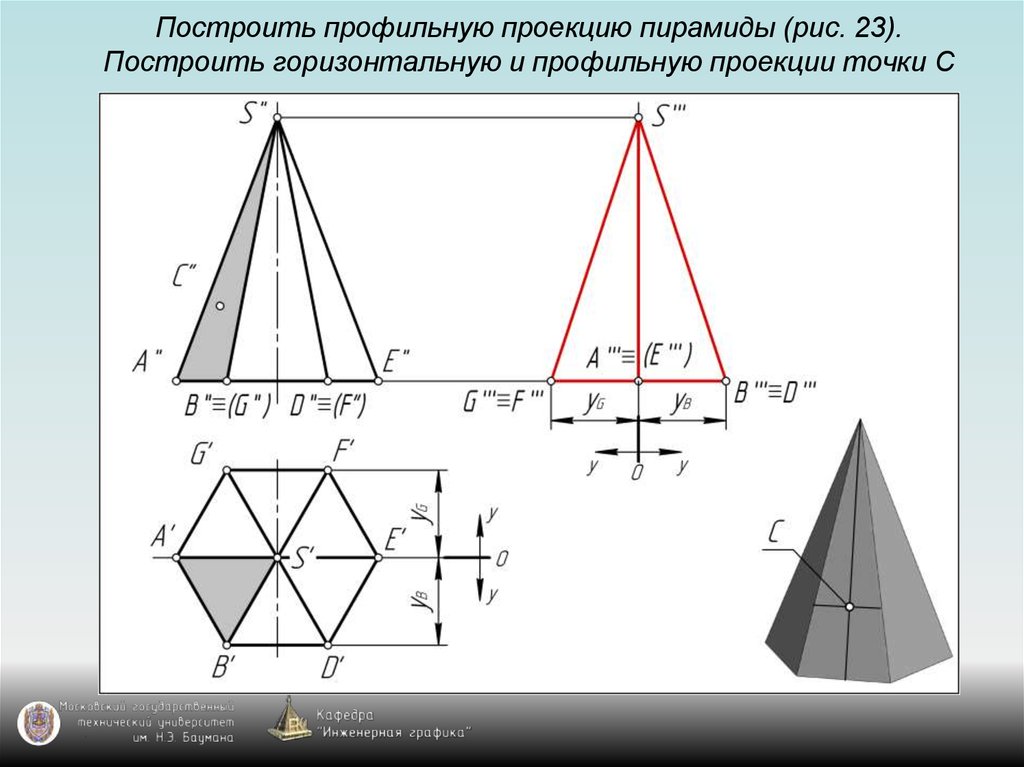
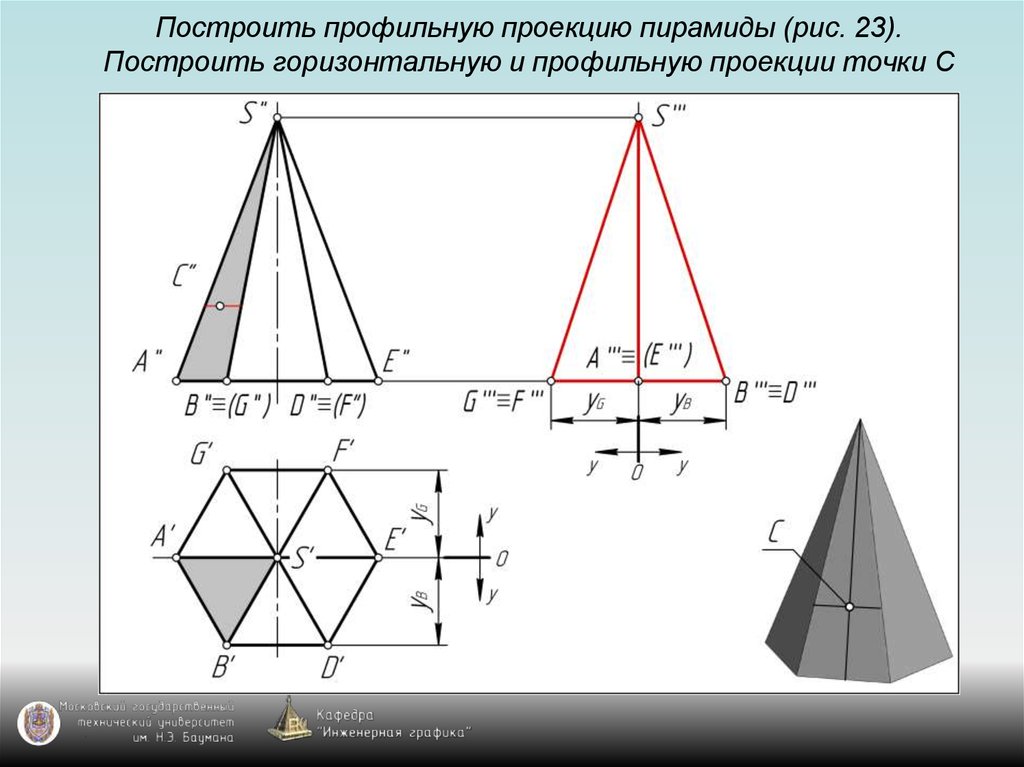
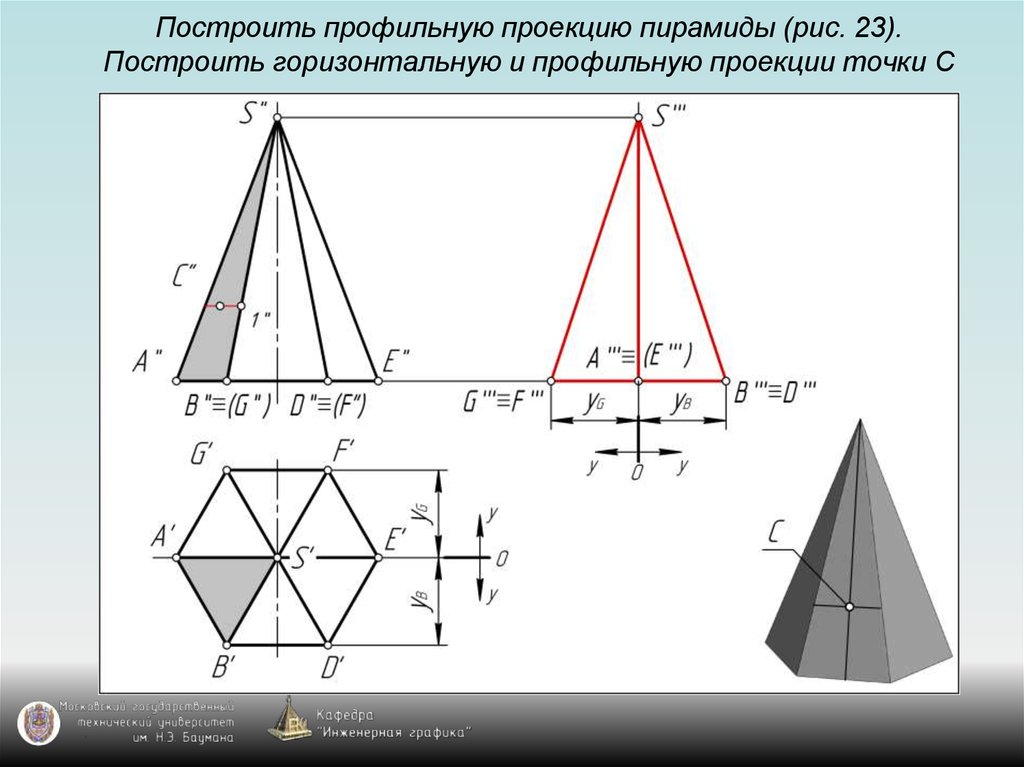
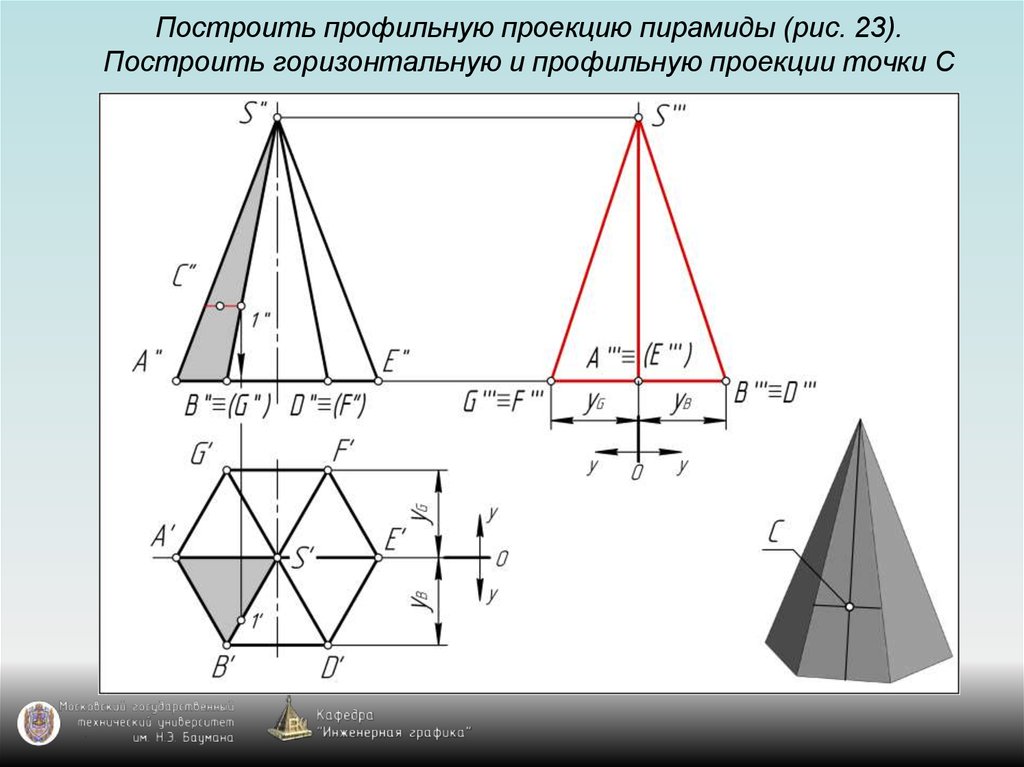
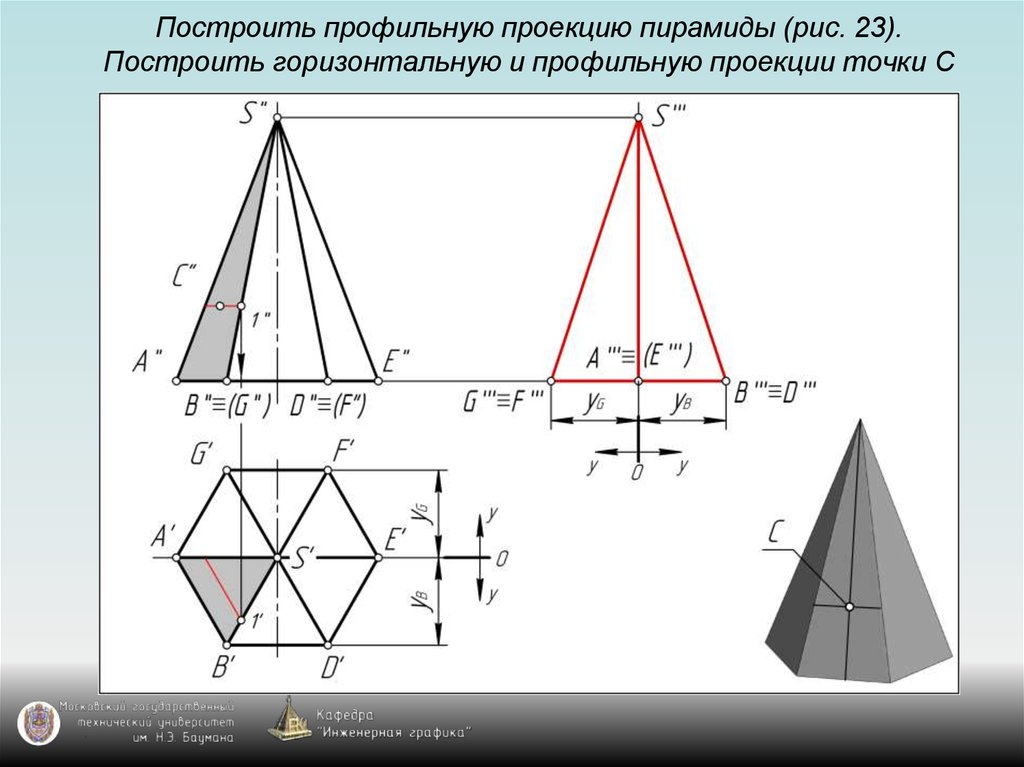
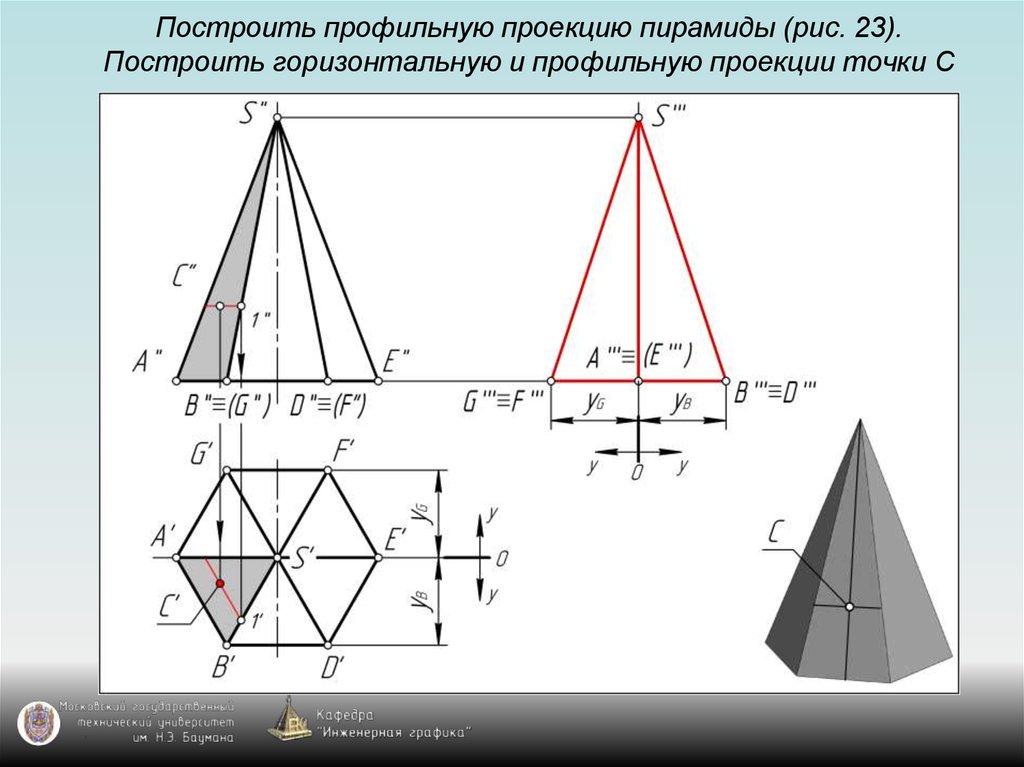
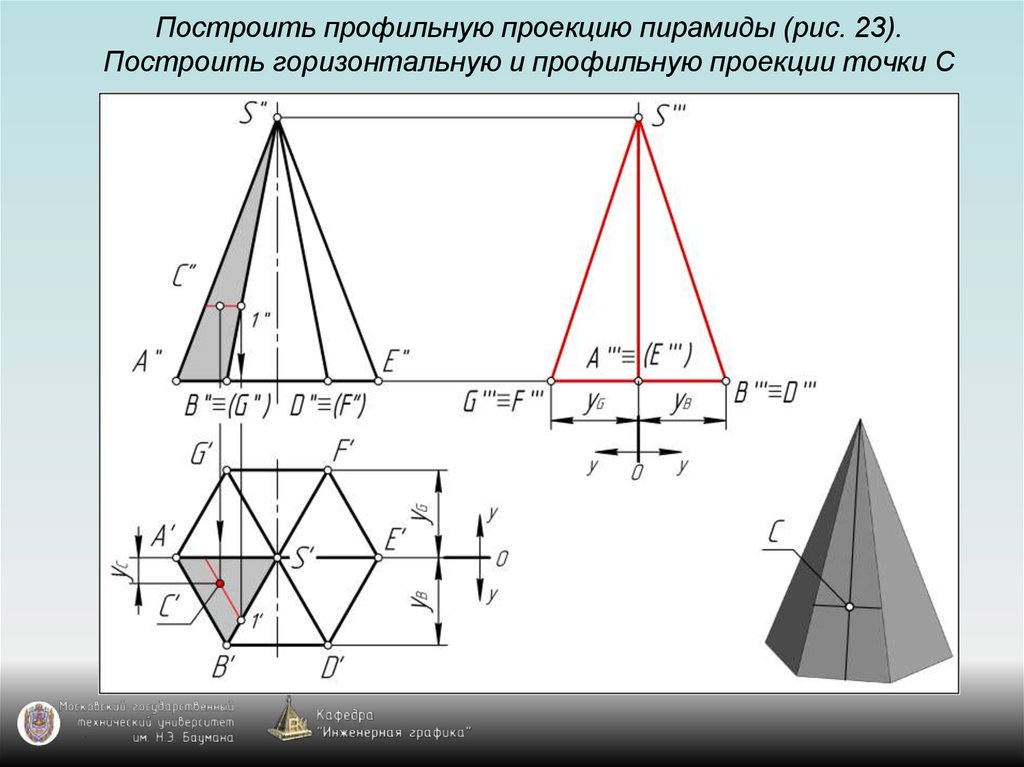
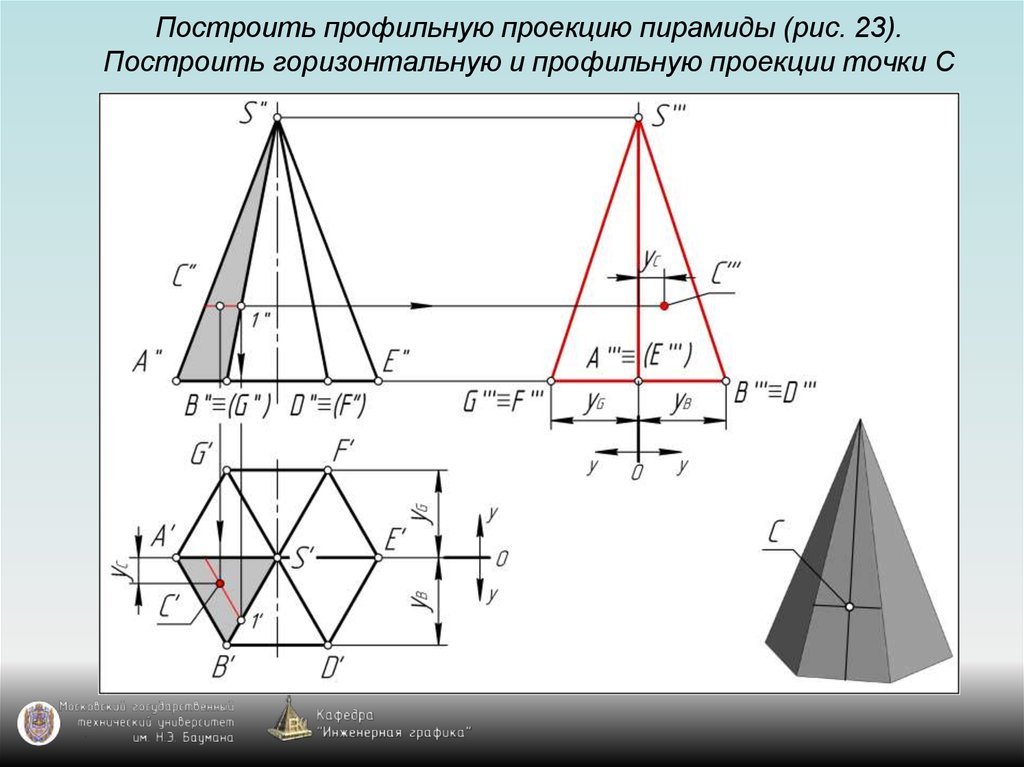
126. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

127. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

128. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

129. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

130. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

131. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

132. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

133. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

134. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

135. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

136. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

137. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

138. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

139. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

140. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

141. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

142. Построить профильную проекцию пирамиды (рис. 23). Построить горизонтальную и профильную проекции точки С

143. Задание пирамиды на чертеже

Пирамида на чертеже задаётся с помощью:
1) проекции основания пирамиды –
многоугольника;
2) проекции вершины пирамиды – точки
пересечения всех рёбер боковых граней
пирамиды.