Кручение стержней некруглого сечения

1.

ФГАОУ ВПО «Северо-Восточный федеральный университет им. М.К. Аммосова»
Инженерно-технический институт
Кафедра прикладной механики
Решение задач
по дисциплине «Техническая механика»
270800 - Строительство

2. Кручение стержней некруглого сечения

3.

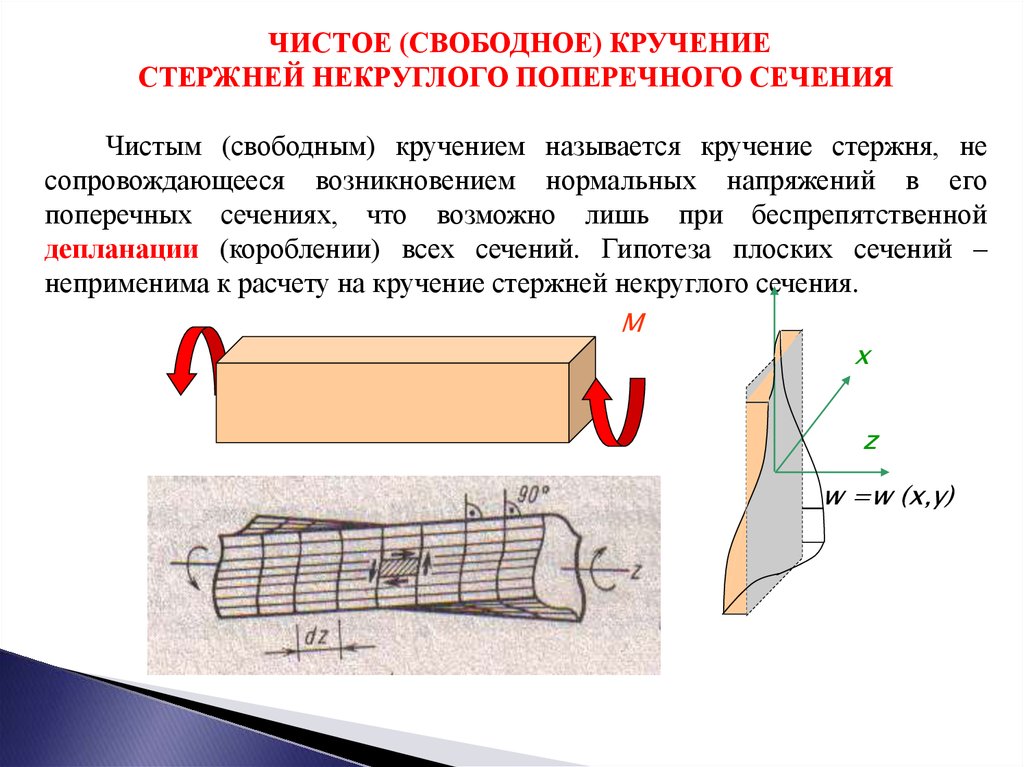
ЧИСТОЕ (СВОБОДНОЕ) КРУЧЕНИЕ
СТЕРЖНЕЙ НЕКРУГЛОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ
Чистым (свободным) кручением называется кручение стержня, не
сопровождающееся возникновением нормальных напряжений в его
поперечных сечениях, что возможно лишь при беспрепятственной
депланации (короблении) всех сечений. Гипотеза плоских сечений –
неприменима к расчету на кручение стержней некруглого сечения.
M
x
z
w =w (x,y)

4.

Для всех видов сечений угол закручивания и наибольшее касательное
напряжение выражаются формулами, подобными формулам для круглого
сечения (только вместо полярного момента инерции сечения I будет
входить Ik – момент инерции сечения при кручении, а вместо W - Wk –
момент сопротивления сечения при кручении.)
Mk z
k
;
GI k
max
Mk
.
Wk
эпюра касательных напряжений - τ
для бруса прямоугольного сечения

5.

а)
б)
h 1 =70
24
10
h 2 =76
16
b3 =17
140
40
36
70
b1 =38
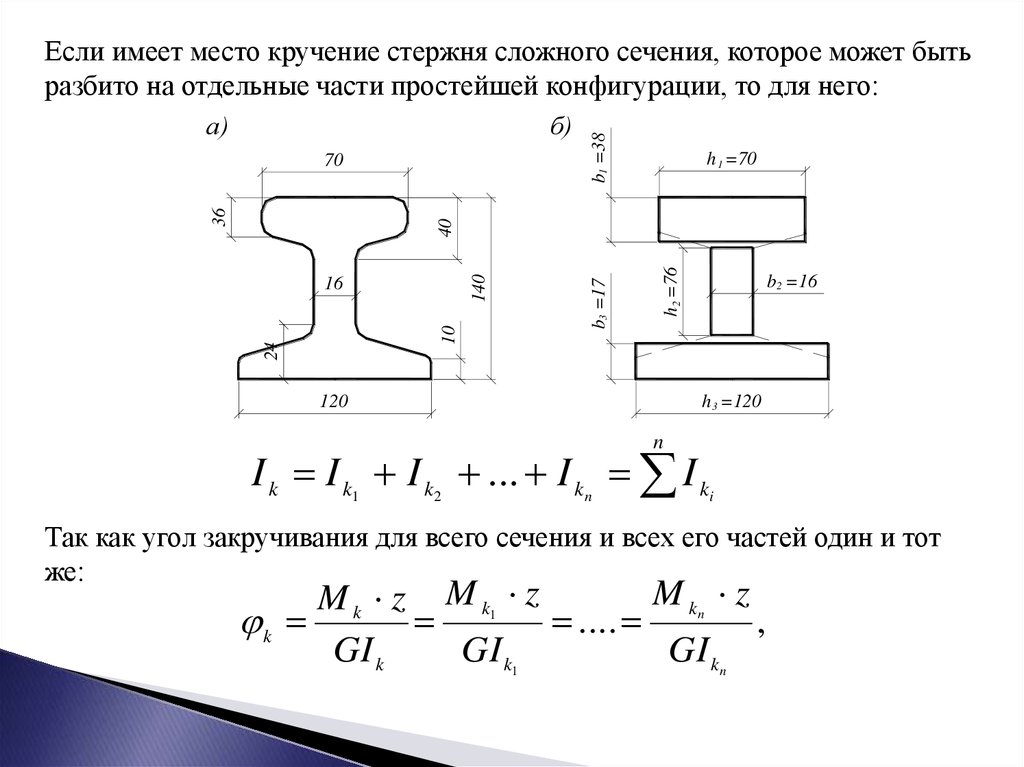
Если имеет место кручение стержня сложного сечения, которое может быть
разбито на отдельные части простейшей конфигурации, то для него:
120
b 2 =16
h 3 =120
n
I k I k I k ... I k I k
1
2
n
i
Так как угол закручивания для всего сечения и всех его частей один и тот
же:
Mk z
Mk z Mk z
k
....
,
GI k
GI k
GI k
n
1
1
n

6.

следовательно, крутящий момент распределяется между отдельными
частями сечения пропорционально их жесткостям:
Mk Mk
1
Ik
1
Ik
, Mk Mk
Ik
2
Ik
2
, ....M k M k
n
Ik
n
Ik
.
Наибольшие касательные напряжения в каждой части сечения будут равны:
Mk
Mk
k
Wk
Wk
i
i
i
Ik
Ik
i
Mk
Ik
Ik
W
k
i
i
.
Для сечений, составленных из узких и длинных прямоугольников
(уголковых, тавровых, двутавровых и т.п.) можно принять:
1 n
3
I k hi i
3

7.

где
I – короткие, а hi – длинные стороны прямоугольников, на которые
можно разбить сечение.
η – коэффициент, зависящий от формы сечения и равный для:
уголкового сечения η=1,00,
таврового сечения η=1,15,
двутаврового сечения η=1,20.
Угол закручивания выразится формулой :
Mk z
k
.
GI k
Наибольшее касательное напряжение можно ожидать в наиболее
широком из прямоугольников, на которые мы разбиваем профиль, и можно
вычислить по формуле:
max
M k max
Ik
где max – наибольшая ширина элемента из всех имеющихся фигур.

8.

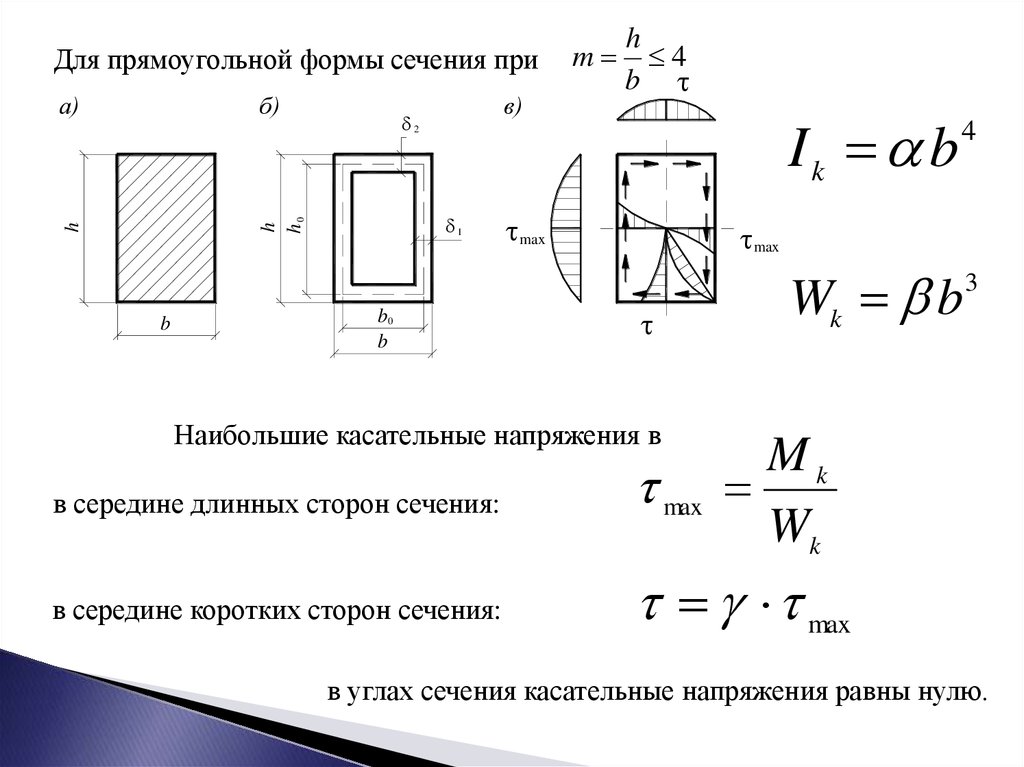
Для прямоугольной формы сечения при
б)
h
b
в)
2
1
h
h0
а)
b0
b
m
h
4
b
Ik b
max
4
max
Наибольшие касательные напряжения в
Wk b
3
Mk
Wk
в середине длинных сторон сечения:
max
в середине коротких сторон сечения:
max
в углах сечения касательные напряжения равны нулю.

9.

Значения коэффициентов , , в зависимости от соотношения сторон
Таблица 1
h
m
b
1,0
1,5
2,0
3,0
4,0
6,0
8,0
10,0
При
h
m 4
b
0,140
0,294
0,457
0,790
1,123
1,789
2,456
3,123
0,208
0,346
0,493
0,801
1,150
1,789
2,456
3,123
1,0
0,859
0,795
0,753
0,745
0,743
0,742
0,741
геометрические характеристики определяются:
Ik
m 0,63 b
3
4
,
Wk
m 0,63 b
3
3
,

10.

Пример1:
Стальной вал переменного сечения закручивается моментами,
действующими в двух крайних и двух пролетных сечениях. Расчетная схема
вала, геометрические размеры, величины и точки приложения внешних
крутящих моментов указаны на рис.
Требуется:
1. Построить эпюру
крутящих моментов;
2. Найти допускаемую
величину момента М;
3. Построить эпюры
касательных напряжений по
сечениям вала, отметив на
сечениях опасные точки;
4. Построить эпюру углов
закручивания;
Модуль упругости при
сдвиге материала вала
G = 8 107 кН/м2. Расчетное
сопротивление материала
вала срезу RC = 105 кН/м2.

11.

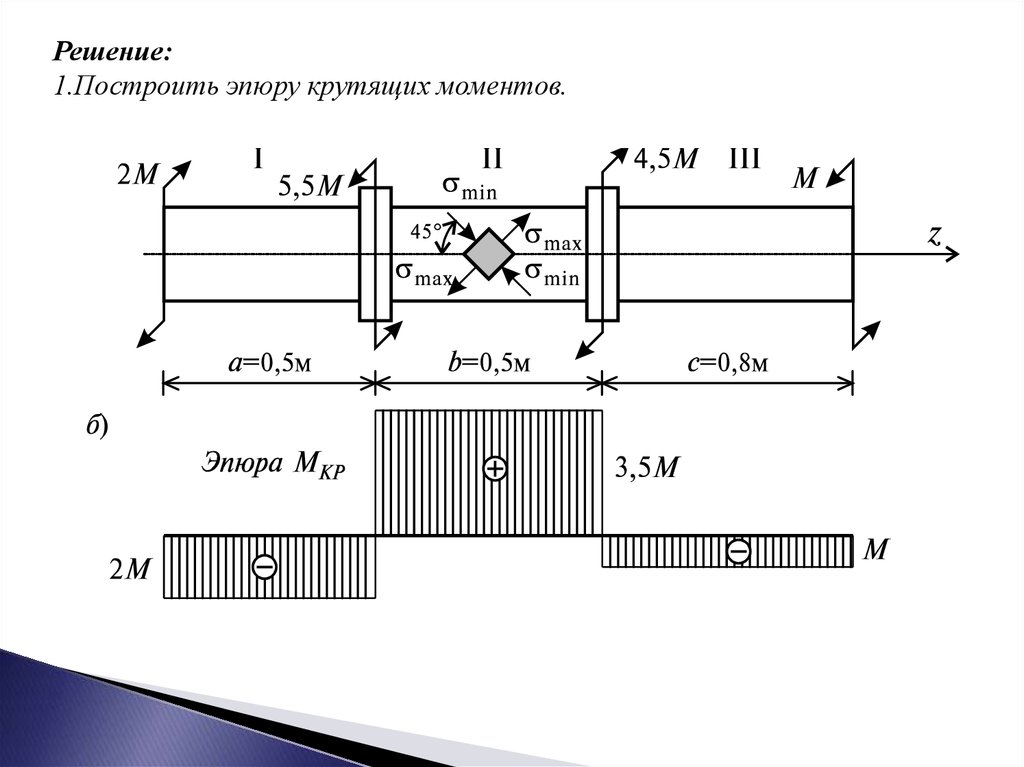
Решение:
1.Построить эпюру крутящих моментов.

12.

2. Найти допускаемую величину момента М.
Допускаемая
величина
момента
МP определяется из условия прочности:
M
k R
c
W
k
Определим моменты сопротивления сечения вала для каждого участка.
I участок (трубчатое сечение):
D 3
d
I
W
(1 4 );
0,8
D
16
3,14 (10 10 2 )3
(1 0,84 ) 116 10 6 м3
16
2 3
3
,
14
(
10
10
)
II участок (круглое сечение):
W II
196 10 6 м3
16
W III b3
III участок (прямоугольное сечение):
W I
где коэффициент, зависящий от отношения сторон прямоугольного
сечения h/b (h > b). В данном случае h / b 8 6 1,333
0,300
W III 0,300 (6 10 2 )3 64,8 10 6 м3

13.

Напряжения по участкам в зависимости от момента М:
М z1 2 M
6
1
116
W
10 0,0172 106 M ,
3,5 M
6
6
10
0
,
0178
10
M,
2
196
W
М z2
3
М z3
W
KP
M
64,8
106 0,0154 106 M
Из сравнения результатов видно, что наиболее напряженным является
участок II, поэтому допускаемая величина момента M определяется из
зависимости:
2 0,0178 106 [M ] Rc
105
[M ]
5,62кН м
17800

14.

3.Построить эпюры касательных напряжений по сечениям вала, отметив
на сечениях опасные точки. Касательные напряжения в точках поперечного
сечения вала определяются по формулам:
D
0
для круглого сечения:
при
Mk
2
для трубчатого сечения :
при
для прямоугольного сечения:
max
d
D
2
2
Mk
Wk
I
- в середине большей стороны
и 1 = max - в середине меньшей стороны.
Моменты инерции сечений :
D 4
4
3
,
14
10
I I
(1 4 )
(1 0,84 ) 580 10 8 м 4
32
32
4
4
D
3
,
14
10
I II
10 8 980 10 8 м 4
32
32
I III b 4 0,243 (6 10 2 ) 4 315 10 8 м 4
где = 0,243 при h/b = 1,33.

15.

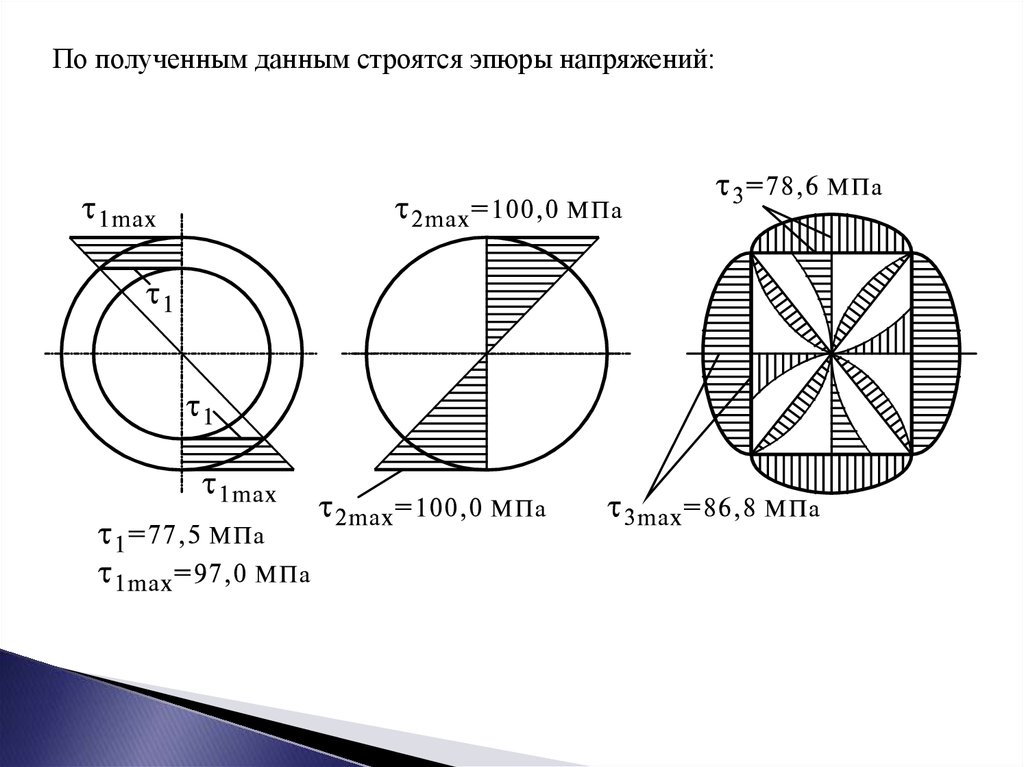
Значения напряжений в характерных точках сечений.
Участок I (0 z 0,5 м):
d
2 5,62 0,04
2
0,04м
77517
Кн
/
м
77,5МПа
1
8
2
580 10
D
0,05м
2
1 max
2 5,62 0,05
2
96896
кН
/
м
97МПа
8
580 10
Участок II ( 0,5 м z 1,5 м):
0,
2 0.
D
,
2
2 max
3,5 2 5,62 0,05
2
100357
кН
/
м
100МПа
8
980 10
Участок III (1,0 м z 1,8 м):
в середине большей стороны
в середине меньшей стороны
где = 0,906 при h/b = 1,33.
3 max
5,62
2
86728
кн
/
м
86,8МПа
6
64,8 10
3 = max = 0,906 86,7 = 78,6 МПа.

16.

По полученным данным строятся эпюры напряжений:

17.

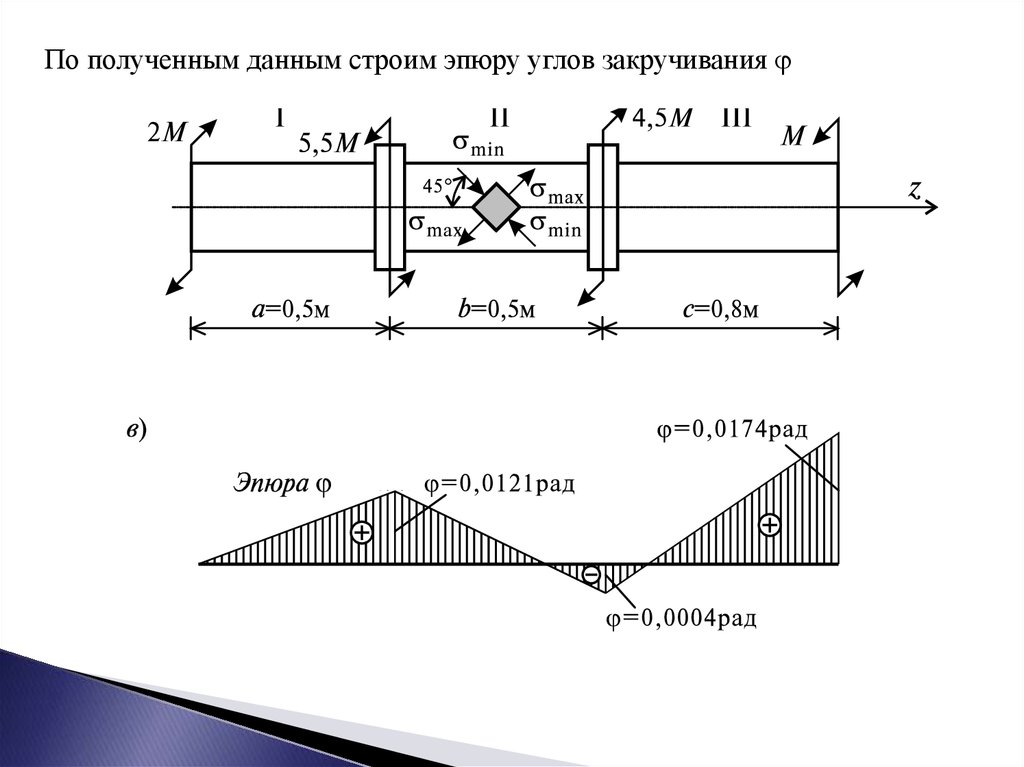
4.Построить эпюру углов закручивания. Угол закручивания на i ом участке
вала определяется:
M L
i i 1
zi
i
GI i
Так как, в пределах каждого из трех участков крутящие моменты и
жесткости на кручение GI постоянны, то эпюры углов закручивания на
каждом из участков будут линейны. В связи с этим, достаточно подсчитать
их значения лишь на границах участков. Приняв, что левый конец вала
защемлен от поворота, т.е. (0) = 0, получим:
I
1
M kI l1
G I I
2 5,62 0,5
0,0121рад
7
8
8 10 580 10
II
M
l
3,5 5,62 0,5
2II 1I k II2 0,0121
0,0004рад
7
8
GI
8 10 980 10
III
3
M kIII l3
1 5,62 0,8
0,0004
0,0174рад
III
7
8
GI
8 10 315 10
II
2

18.

По полученным данным строим эпюру углов закручивания