Similar presentations:
Чистый сдвиг и свободное кручение
1. Чистый сдвиг и свободное кручение
Доцент кафедрысамолетостроения
к.т.н. Мухин Д.В.
2. 1.Анализ напряженного состояния при чистом сдвиге
Чистым сдвигом называется напряженное состояние, в которомотличными от нуля будут только одни касательные компоненты
напряженного состояния
Рассмотрим
элемент находящийся
состоянии чистого
сдвига
Выделим трапецию
ограниченнуюв наклонной
плоскостью
Площадь наклонной
связана
с площадями
и
Составим
уравнение площадки
равновесия
относительно
осей i горизонтальной
иt
вертикальной площадок соотношениями
y
y
τyx
y
i
t
τxy A
τi
ϭi
A
σ2
σ1
А
90-α
τ
xy
A cos
O
z
x
Asin
i A
i
xy
α
O
B
A cos sin yx A sin cos 0;
i xy sin 2 .
t A
i
τyx
2
2
A
cos
A
sin
0;
xy
xy
i xy cos 2 .
B
x
0
σ1
σ2
σ1 > σ2 > σ3
σ1 =τxy, σ2=0, σ3=-τxy
x
3. Закон Гука при чистом сдвиге
Так как нормальные компоненты тензора напряжений равны нулю, то:xy G xy
yz G yz
G
zx
zx
G
E
2 1
Потенциальная энергия при чистом сдвиге
Рассмотри элемент размером axax1. Горизонтальная сила
Q=τ·a·1 совершает работу на перемещении Δ=γ·a. Работа
равна:
1
1
A T a 2
2
2
Отнесем численно равную работе энергию деформации к
единице объема:
A 1
1 2 1
u
G
a 1 2
2G 2
2
2
Δ
a τ
τ
τ
γ
τ
a
u – плотность энергии деформации или удельная потенциальная энергия
деформации при чистом сдвиге.
Полная энергия деформации:
U udV
V
Q
4.
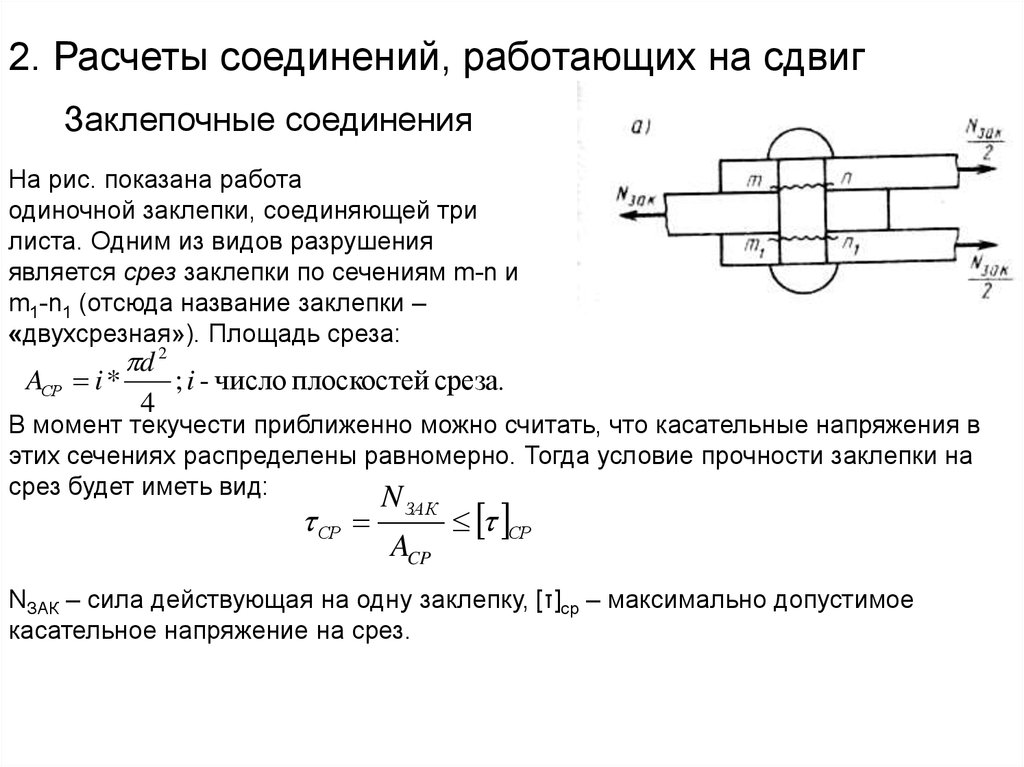
2. Расчеты соединений, работающих на сдвигЗаклепочные соединения
На рис. показана работа
одиночной заклепки, соединяющей три
листа. Одним из видов разрушения
является cрез заклепки по сечениям m-n и
m1-n1 (отсюда название заклепки –
«двухсрезная»). Площадь среза:
AСР i *
d 2
4
; i - число плоскостей среза.
В момент текучести приближенно можно считать, что касательные напряжения в
этих сечениях распределены равномерно. Тогда условие прочности заклепки на
срез будет иметь вид:
N
СР
ЗАК
ACP
СР
NЗАК – сила действующая на одну заклепку, [τ]ср – максимально допустимое
касательное напряжение на срез.
5.
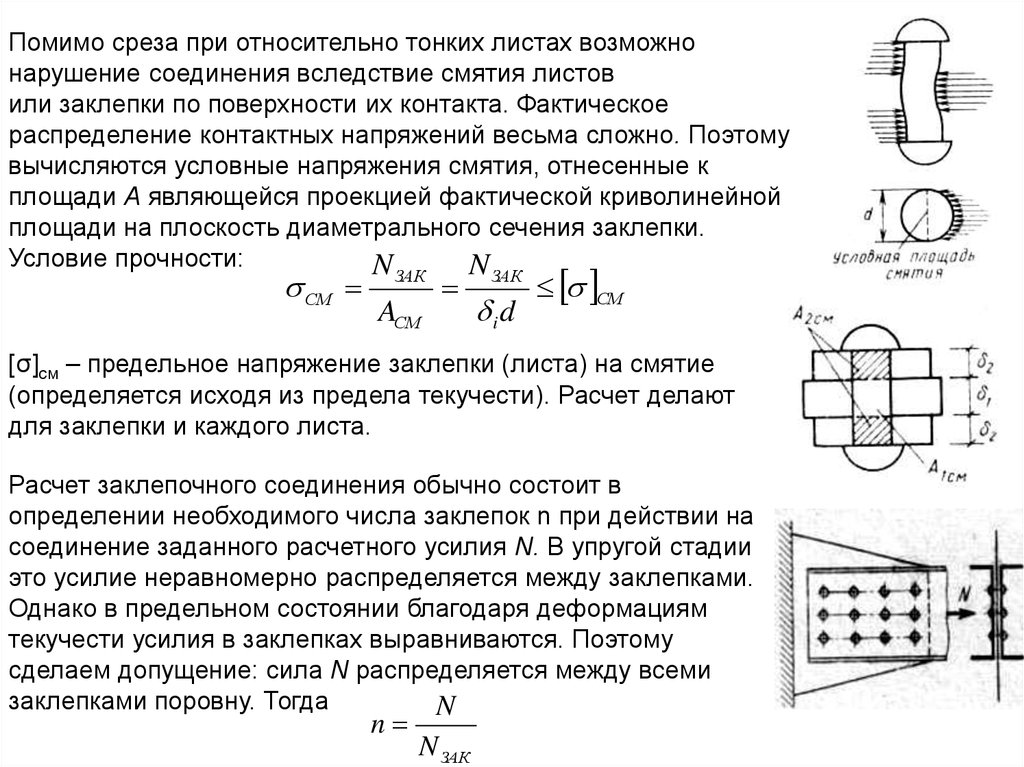
Помимо среза при относительно тонких листах возможнонарушение соединения вследствие смятия листов
или заклепки по поверхности их контакта. Фактическое
распределение контактных напряжений весьма сложно. Поэтому
вычисляются условные напряжения смятия, отнесенные к
площади А являющейся проекцией фактической криволинейной
площади на плоскость диаметрального сечения заклепки.
Условие прочности:
N
N
СМ
ЗАК
AСМ
ЗАК
id
СМ
[σ]см – предельное напряжение заклепки (листа) на смятие
(определяется исходя из предела текучести). Расчет делают
для заклепки и каждого листа.
Расчет заклепочного соединения обычно состоит в
определении необходимого числа заклепок n при действии на
соединение заданного расчетного усилия N. В упругой стадии
это усилие неравномерно распределяется между заклепками.
Однако в предельном состоянии благодаря деформациям
текучести усилия в заклепках выравниваются. Поэтому
сделаем допущение: сила N распределяется между всеми
заклепками поровну. Тогда
N
n
N ЗАК
6.
Сопротивление материаловРаздел: Сдвиг и кручение
Расчет простейших соединений
В основе расчета лежат условия прочности
на растяжение
на срез
на смятие
раст
среза
F
Aраст
F
Aсреза
смят
раст
т
n
среза (0,5 0,6) раст
F
Aсмят
смят 2 раст
Форма условия прочности во всех случаях расчета одинакова. Оно приобретает вид равенства, так
как Mathcad не выполняет численных расчетов с неравенствами.
Для решения равенства используется функция root, которая требует подстановки выражения,
равного нулю, поэтому вместо условия прочности
max
используется выражение
max 0
В получившееся универсальное выражение (функцию прочности) для каждого вида расчета надо
ввести свой неизвестный размер, который нужно найти и вид допускаемого напряжения.
Перед каждым расчетом надо ввести свое выражение для площади поперечного сечения
(растяжения, среза или смятия) как функцию от искомого размера.
7.
3Н N кН 10 Н
м m мм 0.001 м
см 0.01 м
6 Н
МПа 10
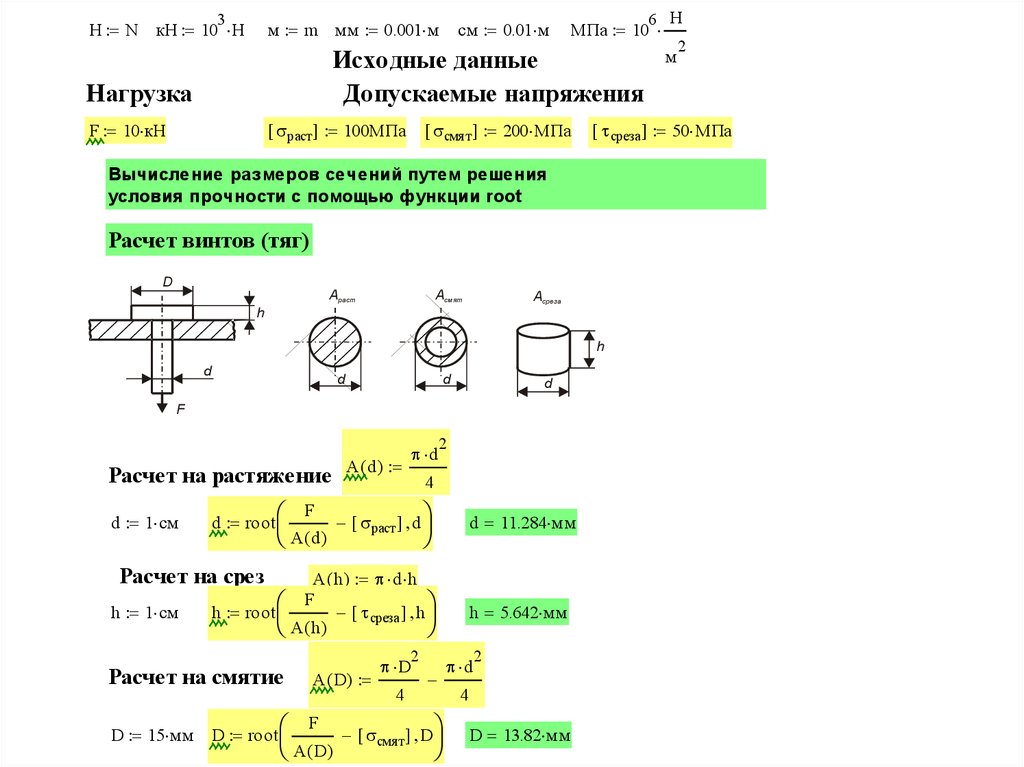
Исходные данные
Допускаемые напряжения
Нагрузка
F 10 кН
раст 100МПа
смят 200 МПа
Расчет винтов (тяг)
D
Aсмят
Aсреза
h
h
d
d
d
d
F
d
2
Расчет на растяжение A ( d ) 4
F
d 1 см
d root
раст d
A( d)
d 11.284 мм
Расчет на срез
h 1 см
A ( h ) d h
F
h root
среза h
A( h)
2
Расчет на смятие
A ( D)
D 15 мм D root
F
A ( D)
D
4
смят D
h 5.642 мм
d
2
4
D 13.82 мм
2
среза 50 МПа
Вычисление размеров сечений путем решения
условия прочности с помощью функции root
Aраст
м
8.
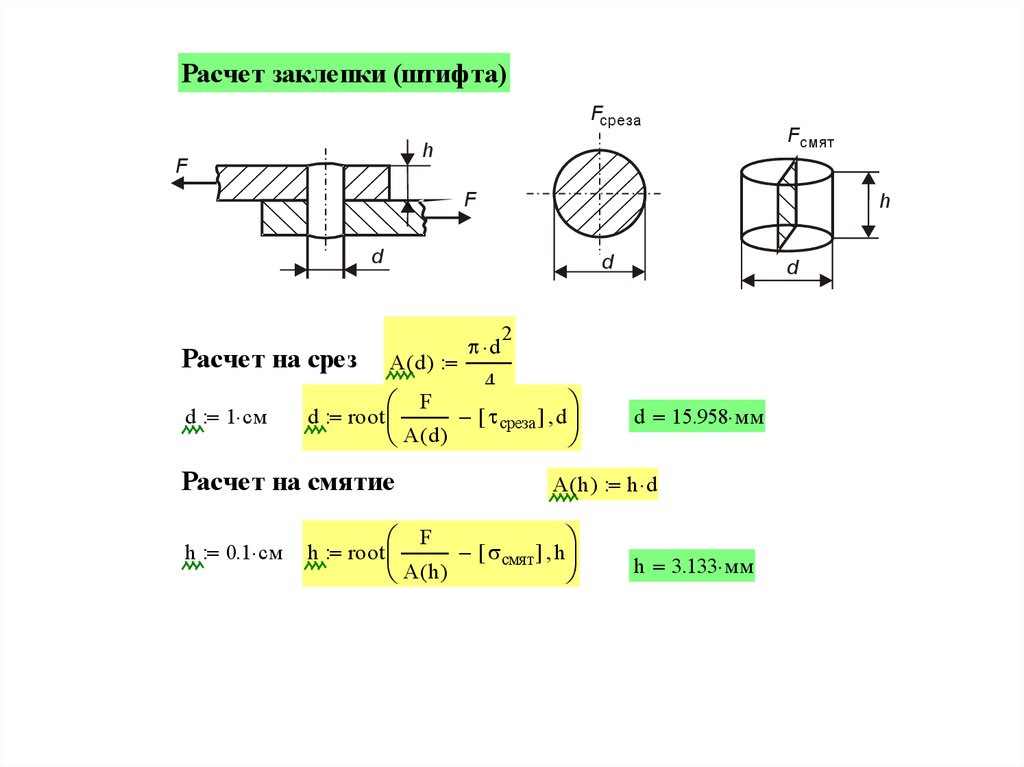
Расчет заклепки (штифта)Fсреза
h
F
Fсмят
F
h
d
Расчет на срез
d 1 см
d
A ( d )
d root
F
A(d)
Расчет на смятие
h 0.1 см
h root
d
d
2
4
среза d
d 15.958 мм
A ( h ) h d
F
A(h)
смят h
h 3.133 мм
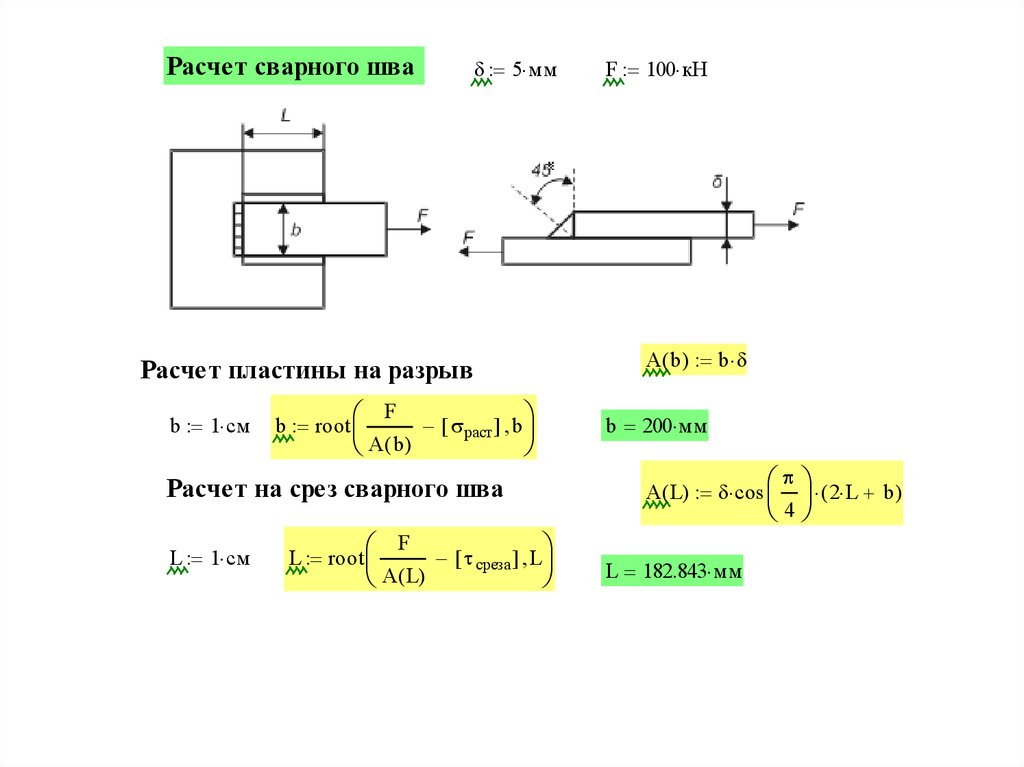
9.
Расчет сварного шва5 мм
A ( b ) b
Расчет пластины на разрыв
b 1 см
b root
F
A( b)
раст b
b 200 мм
A ( L) cos
( 2 L b )
4
Расчет на срез сварного шва
L 1 см
L root
F
A ( L)
F 100 кН
среза L
L 182.843 мм
10. 3. Кручение стержней
Кручением называется деформация стержня, нагруженного парами сил,плоскости действия которых перпендикулярны его продольной оси.
M2
M1
a MIIIK
a
x3
l1
l2
l3
x3
x3
0
0
l4
III
III
m
M
mdx
M
0
,
mdx
M
x 1
K
x3
K M 1 x3
M K M i i M m т
лев
лев
прав
прав
11.
Принимаем предположения, которые подтверждаются решением задами окручении методами теории упругости:
1. При кручении стержней кольцевого сечения поперечные сечения стержня
поворачиваются друг относительно друга около прямой, называемой осью
кручения (в дальнейшем ось x), как недеформирующиеся в своей плоскости
(жесткие) диски. Это предположение называют гипотезой жесткости сечения в
своей плоскости. Точка пересечения оси кручения с поперечным сечением
называется центром кручения. Угол поворота произвольного поперечного
сечения стержня, как жесткого целого, относительно сечения, принятого за
неподвижное, будем обозначать φ = φ(x) и называть углом закручивания, а
через φj-i будем обозначать угол закручивания сечения j относительно сечения
i.
2. Точки поперечного сечения любой формы, за исключением кольцевой,
неодинаково перемещаются в направлении оси кручения, за счет чего оно
превращается в некоторую поверхность (депланирует).
3. Если точки поперечного сечения могут свободно
перемещаться в направлении оси кручения, то
кручение называется свободным, в противном
случае оно называется стесненным. При
свободном кручении в поперечных сечениях
стержня возникают только касательные силы
упругости, а следовательно, только касательные
напряжения.
12.
Максимальное касательное напряжение в сечении любой формы приM
кручении всегда определяется по формуле
max K
Wk
где WK - момент сопротивления сечения кручению, величина которого
зависит от его формы и размеров.
Погонным углом закручивания называется производная от φ по х
Как увидим в дальнейшем, всегда
MK
следовательно:
GI K
d
dx
xi
MK
dx i 0
GI К
0
где φi-0— угол закручивания сечения, находящегося в начале участка
относительно сечения, принимаемого за неподвижное; GIк — жесткость
сечения стержня при кручении; Iк— геометрическая характеристика жескости,
зависящая от размеров и формы сечения.
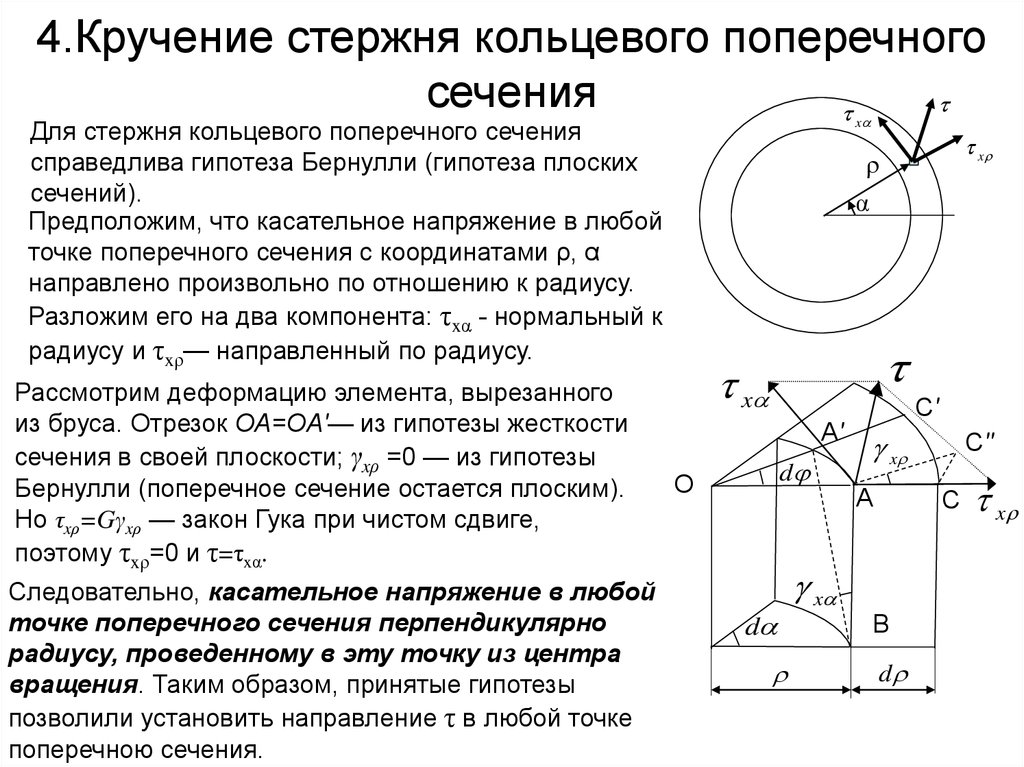
13. 4.Кручение стержня кольцевого поперечного сечения
xДля стержня кольцевого поперечного сечения
справедлива гипотеза Бернулли (гипотеза плоских
сечений).
Предположим, что касательное напряжение в любой
точке поперечного сечения с координатами ρ, α
направлено произвольно по отношению к радиусу.
Разложим его на два компонента: τxα - нормальный к
радиусу и τxρ— направленный по радиусу.
Рассмотрим деформацию элемента, вырезанного
из бруса. Отрезок ОА=ОА'— из гипотезы жесткости
сечения в своей плоскости; γxρ =0 — из гипотезы
Бернулли (поперечное сечение остается плоским).
Но τxρ=Gγxρ — закон Гука при чистом сдвиге,
поэтому τxρ=0 и τ=τxα.
Следовательно, касательное напряжение в любой
точке поперечного сечения перпендикулярно
радиусу, проведенному в эту точку из центра
вращения. Таким образом, принятые гипотезы
позволили установить направление τ в любой точке
поперечною сечения.
x
ρ
α
x
C′
A′
d
O
x
A
d
C′′
C
x
B
d
x
14.
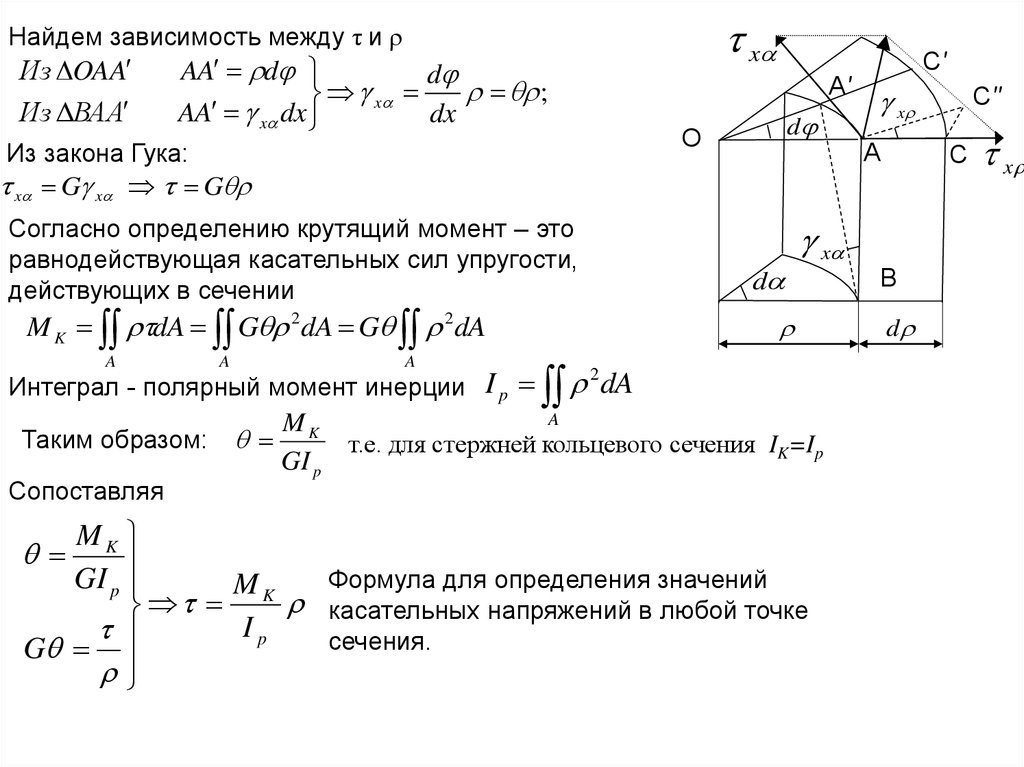
xНайдем зависимость между τ и ρ
Из OAA
Из ΔВAА
AA d
d
;
x
AA x dx
dx
A′
Согласно определению крутящий момент – это
равнодействующая касательных сил упругости,
действующих в сечении
A
Интеграл - полярный момент инерции I p dA
A
MK
Таким образом:
т.е. для стержней кольцевого сечения IK=Ip
GI p
Сопоставляя
2
MK
Формула для определения значений
GI p
MK
касательных напряжений в любой точке
Ip
сечения.
G
C′′
C
x
x
A
d
M K dA G 2 dA G 2 dA
A
d
O
Из закона Гука:
x G x G
A
C′
B
d
x
15.
Касательные напряжения в поперечном сеченииизменяются вдоль радиуса по линейному закону,
достигая максимума в точках наружного контура
сечения.
max
max
2I p
Mkd
d
max
, Wk
2
2I p
d
d1
Для определения IK и WK вычислим Ip для кольца:
2
I p dA d
2
A
0
d 2
d
2
d1 2
где c d1 d
WK
d 3
16
1 c 0,2d 1 c
4
3
Для круга с=0
Ip
WK
d 4
32
d 3
16
0,1d
4
0,2d 3
4
d 4
32
d14
32
d 4
d
1 c 0,1d 1 c
32
4
4
4
При кручении по свойству парности
касательных напряжений будут существовать
касательные напряжения в продольных
сечениях бруса, распределенные по тому же
закону.
Это приводит в частности к растрескиванию
древесины вдоль волокон при кручении
16.
Если двумя парами осевых и поперечных сеченийвыделить из закрученного стержня элемент ABCD,
то на его гранях будут обнаружены только
касательные напряжения. Следовательно, во всех
точках стержня при кручении возникает состояние
чистого сдвига. Здесь, однако, чистый сдвиг не
будет однородным, поскольку значение τ
изменяется по радиусу поперечного сечения. Если
изменить ориентацию сечений, повернув их в
плоскости сдвига на 45°, то в новых площадках
обнаруживаются только нормальные напряжения,
имеющие одинаковое с τ значение. При этом одно
из них является растягивающим, а второе сжимающим.
Наличие растягивающих и сжимающих напряжений в наклонных площадках при
кручении можно наглядно проиллюстрировать следующим способом. На
поверхности цилиндра, изготовленного из пластичного материала, краской
нанести множество мелких кружочков. При закручивании бруса кружки
превратятся в эллипсы с главными осями, направленными под углом 45° к
образующим. По направлению больших осей эллипса произойдет удлинение, а
вдоль малых осей - сжатие.
17.
Потенциальная энергия деформации при крученииВнешние силы, создающие упругую деформацию
стержня, совершают некоторую работу, которая
накапливается в объеме материала стержня в виде
потенциальной энергии деформации. Представим себе
отрезок вала длиной dx, получивший угол закручивания
dφ от момента Μк. Момент упруго возрастает
пропорционально углу dφ. Поэтому работа этого
момента, равная площади графика,
1
dA M K d
2
Энергия, накопленная в элементе стержня,dU=dA, или
1
1 M K2
dU M K d
dx
2
2 GI K
d
Заменим
MK
Получаем
1
d
dU GI K
dx
2
dx
dx
GI K
2
(с учетом)
dx
Mк
Mк
dA
d M K
dx GI K
dφ
18.
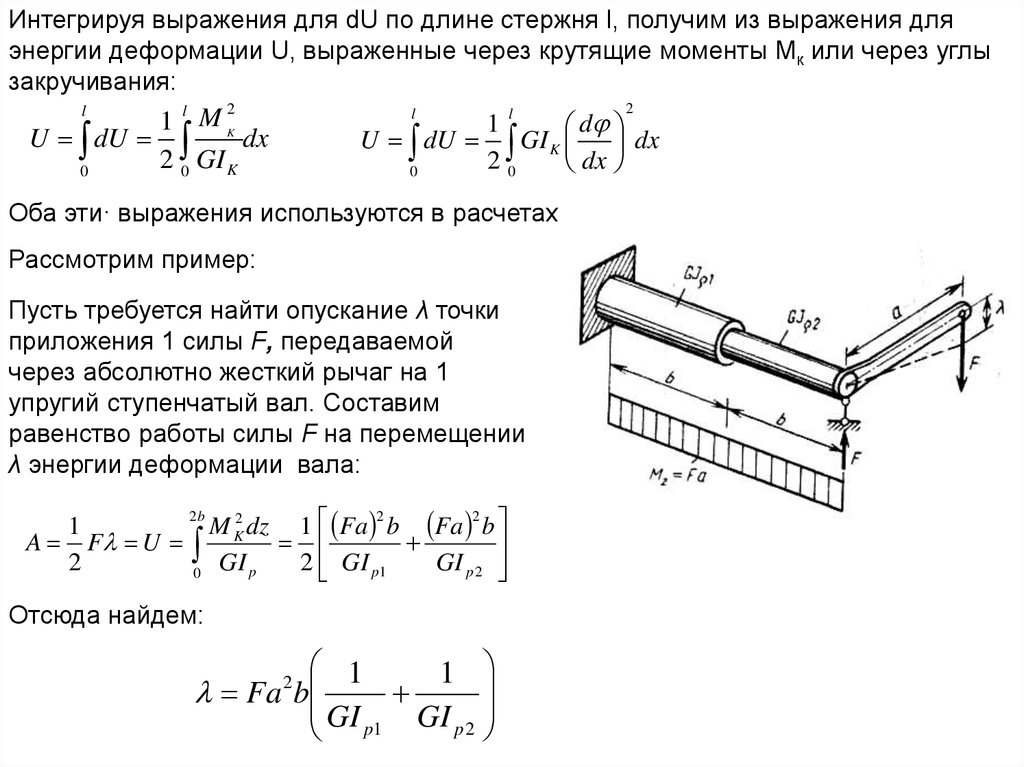
Интегрируя выражения для dU по длине стержня l, получим из выражения дляэнергии деформации U, выраженные через крутящие моменты Mк или через углы
закручивания:
2
l
1 MK
U dU
dx
2
GI
K
0
0
l
l
Оба эти· выражения используются в расчетах
Рассмотрим пример:
Пусть требуется найти опускание λ точки
приложения 1 силы F, передаваемой
через абсолютно жесткий рычаг на 1
упругий ступенчатый вал. Составим
равенство работы силы F на перемещении
λ энергии деформации вала:
1
A F U
2
2
1
d
U dU GI K
dx
2
dx
0
0
l
2
2
M K2 dz 1 Fa b Fa b
0 GI p 2 GI p1 GI p 2
2b
Отсюда найдем:
1
1
Fa b
GI p1 GI p 2
2
19. 5. Результаты механических испытаний при кручении, расчеты на прочность и жесткость
Механические испытания на кручение проводят натонкостенных трубчатых образцах, которые при кручении
будут испытывать чистый однородный сдвиг, так как
распределение напряжений по толщине их сечений в
силу тонкостенности можно считать равномерным. По
результатам испытаний такого образца строится
диаграмма кручения — график зависимости MK=MK(φ).
По диаграмме кручения, в свою очередь, строится
диаграмма сдвига (характеристика материала при чистом
сдвиге, диаграмма сдвига) — график зависимости τ=τ(γ) ,
в котором
MK
d
;
2 r 2 s
2l
Все, что говорилось о диаграмме растяжения, а также о
диаграмме напряжений и расчете на прочность при
растяжении, можно перенести на чистый сдвиг, если
заменить символы P Δ/, А, σ, ε, Е, EF соответственно на
Mк, φ, WK,τ, γ, G, GJK. за исключением явлений
уменьшения площади сечения и образования шейки,
которая при кручении отсутствует.
τВ τ
τ
τУТ
τп
ц
γ
20.
Расчеты на прочность и жесткость при крученииРасчет на прочность
Условие прочности
проектировочного расчета
max
max
MK
WK
max
пр
n
Условие прочности проверочного
расчета расчета
n
пр
max
1
max
Первый max относится к сечению,
второй - к длине стержня.
За τпр для пластичною материала принимается τТ - предел текучести при сдвиге, а для
хрупкого τВ-предел прочности при сдвиге.
Если для материала известны значения предельных характеристик при растяжении и
сжатии, то экспериментальное определение τТ и τВ не является необходимым, так как τТ и τВ
для него могут быть найдены по теориям прочности. Например, для пластичного
материала, одинаково работающего на растяжение
Т 0,6 Т
21.
Расчет на жесткостьУсловие жесткости
max
M
K
GI p
max
θ – в радианах/метр
max
1800 M K
GI p
max
θ – в градусах/метр
Допускаемый погонный угол закручивания [θ] в изделиях общего машиностроения
обычно принимают: [θ]=2°/м = при статической нагрузке, [θ]=0,250/м —переменной
нагрузке, [θ] = 0,5°/м - при ударной нагрузке.
В особых случаях требования могут возрастать (допустимый угол уменьшаться).
Так же как и в случае задач на растяжение-сжатие, задачи на кручение могут быть
статически определимыми и статически неопределимыми. Последние решаются при
помощи составления уравнения совместности деформаций.
22.
6. Расчет винтовых цилиндрических пружинЧтобы установить к каким внутренним силовым
факторам приводятся силы упругости в
поперечном сечении витка пружины, разрезаем
его плоскостью, проходящей через ось пружины,
и рассматриваем равновесие верхней
отсеченной части (рис. б). В силу малости α
сечение витка плоскостью можно считать
поперечным (кругом диаметра d).
Для равновесия отсеченной части силы
упругости в поперечном сечении витка должны
привестись к
Q F и M z FR
На рис. обозначены:
D=2R — средний диаметр
витков пружины;
d=2r — диаметр проволоки;
i — число рабочих витков;
α — угол подъема витка.
23.
Распределение касательныхнапряжений по поперечному
сечению oт Qy и Мк показаны на
рис.
Опасной будет точка К, так как в ней
касательные напряжения от Qy и Мк
достигают наибольших значений и
оба направлены вниз.
Следовательно
max K K KM
Qy
k
Для кручения:
KM
K
Mz
FR
2 FR
3 3
Wp r 2 r
Для сдвига
Qy
K
Q
F
2
A r
Суммируем
max
Здесь
Qy
K
Mk
K
r 2R
F 2 FR 2 FR
2 3 3 1
r
r
r
Второе слагаемое в скобках малои им по сравнению с
единицей можно пренебречь. Это означает, что мы
пренебрегаем напряжением от Qy, как малым но
сравнению с напржением от Мк, считая, что пружина
испытывает только кручение. Тогда
max
2 FR
3
r
24.
Важной характеристикой упругих свойств пружины является жесткость пружиныс — так называется сила F, которая вызывает удлинение пружины λ=1. Для
получения соотношения F и λ применим энергетический метод. Приравняем работу
силы F энергии деформации кручения прутка пружины (энергией деформации
среза пренебрегаем):
1
1 M z ds
FR l
F U KP
2
2 0 GI p
2G r 4 2
2
l
где l — длина прутка пружины, равная длине одного
витка 2πR, умноженной на число витков i в пружине, т. е.
l=2πRi. Подставляя l в формулу, после сокращений
окончательно получим:
4 FR3i
Gr 4
Полагая λ=1, найдем жесткость пружины c=F :
Gr 4
c
4 R 3i
25.
7. Кручение стержней снекруглым поперечным
сечением. Мембранная
Определение напряжений в стержне с некруглым поперечным
сечением
представляет собой задачу, которая не может быть
аналогия.
решена методами сопротивления материалов, так как для
некруглого сечения упрощающая гипотеза неизменности
плоских сечений, оказывается неприемлемой. Сечения
заметно искривляются, в результате чего существенно
меняется картина распределения по ним напряжений. На рис.
в качестве примера показана форма закрученного стержня
прямоугольного поперечного сечения, на поверхность
которого предварительно была нанесена мелкая
прямоугольная сетка.
Сетка деформировалась вместе с
поверхностными частицами металла.
Поперечные линии сетки заметно искривлены,
следовательно, будут искривлены и
поперечные сечения.
Таким образом, при определении углов сдвига
необходимо учитывать не только взаимный
поворот сечений, но также и местный перекос,
26.
Рассмотрим общие положения относительнозаконов распределения напряжений в
поперечных сечениях некруглой формы, а
затем приведем готовые формулы, полученные
методами теории упругости для некоторых,
Касательные
напряжения
в
наиболее часто
встречающихся
форм
поперечных
сечениях для
поперечных сечений.
точек, расположенных вблизи
контура,
направлены
по
Положим, что
в точке А.
касательной
к дуге контура.
касательное напряжение
τ
вблизи контура направлено
под некоторым углом к контуру.
Разложим это напряжение на
две составляющие - по
касательной к контуру τt и по
нормали
τn. По
условию парности
Но внешняя
поверхность
свободна от
на
свободной
поверхности
нагрузки и к ней никаких внешних сил не
стержня
должно
возникнуть
приложено.
Таким
образом, τ' n= 0.
касательное
напряжение
τ`n =τn.
Следовательно
и τ = 0, и касательное
n
напряжение τ вблизи контура направлено по
касательной к контуру.
27.
Если поперечное сечениеимеет внешние углы, то в них
касательные напряжения
обращаются в нуль.
Раскладывая напряжение τ
вблизи угла на две
составляющие по нормалям к
сторонам угла, получаем
напряжения τ1 и τ2. Так как парные
им напряжения τ́1 и τ́2 равны нулю,
На
показана
полученная
то рис.
в нуль
обращаются
и
методами
теории
упругости
напряжения
τ1 и τ2. Значит,
вблизи
эпюра
касательных
напряжений
внешнего
угла касательные
для
бруса прямоугольного
напряжения
в поперечном
сечения.
В углах, как видим,
сечении отсутствуют
M K нулю, а
напряжения равны
A напряжения
max
наибольшие
ab 2
возникают по серединам
в точках В
больших сторон
B max в точках А
где a - большая, а b - малая сторона
прямоугольника.
Коэффициенты α и η зависят от отношения
сторон а/b
28.
Значения коэффициентов α, β и ηα
β
η
α
β
η
1
0,208
0,141
1,00
4
0,282
0,281
0,745
1,5
0,231
0,196
0,859коэффициентов α, β и η 6
Таблица 2.1. Значения
0,299
0,299
0,743
1,75
0,239
0,214
8
0,307
0,307
0,742
2
0,246
0,229
0,795
10
0,313
0,313
0,742
2,5
0,258
0,249
0,766
оо
0,333
0,333
0,742
3
0,267
0,263
0,753
а/b
0,82
а/b
Угловое перемещение для
прямоугольного сечения
Для эллиптического
сечения наибольшие
напряжения
в
2Mвозникают
K
A max
концам
точках
А по
малой
2
ab
оси:
в точках B
2M K
B
ba 2
Ml
G b 3a
29.
Угловое перемещение для стержняэллиптического сечения
имеет следующее
Ml
выражение:
G
a 3b3
a 2 b2
Для сечения, имеющего форму
равностороннего треугольника со
сторонами a, наибольшие напряжения
20 M K
возникают по серединам
сторон и равны
max
a3
Угловое перемещение в этом случае:
Ml
3 4
G
a
80
Обобщая все эти формулы, можно отметить, что
при кручении
max
l
MK
Ml
M K dx
;
; M K GI K ; U
WK
GI K
2GI K
0
30.
Краткие сведения о пленочной(мембранной)
аналогии
В результате
того, что
аналитическое
решение задачи о кручении стержня с
некруглым поперечным сечением является
достаточно сложным, возникла необходимость
создания косвенных методов исследования
этого вопроса. Среди таких методов первое
место занимает метод аналогий.
В задачах механики часто встречаются
случаи, когда решения совершенно различных
по физической сущности задач сводятся к
одним и тем же дифференциальным уравнениям.
Тогда между задачами может быть
установлена аналогия. Можно, не решая
уравнения, сказать, например, что между
переменными x1, и у1 из одной задачи
существует та же зависимость, что и между
переменными x2 и у2 из другой задачи. Тогда
говорят, что переменная x2 является аналогом
переменной x1, а y2 - аналогом переменной у1.
Часто бывает так, что в первой задаче, не
решая уравнений, трудно представить себе
связь между переменными х1 и у1, а физическое
содержание второй задачи допускает
31.
Характер деформациипленки под действием
давления можно всегда
представить себе, если не
точно, то, во всяком
случае, ориентировочно.
Следовательно, всегда
имеется возможность
Положим, например, что нужно установить
представить и закон
закон распределения напряжений в сечении,
распределения
показанном на рисунке. Представим себе, что
напряжений при кручении
на заданный контур натянута пленка, которая
стержня с заданной
нагружена равномерно распределенным
формой сечения.
давлением.
разрезов
При
помощи Изобразим
пленочной несколько
аналогии можно
пленки.
Соответственно
углам наклона
получить
не только качественные,
но и
пленки
покажем ориентировочно
количественные
соотношения. Для этого
распределение
напряжений
по сечению.
используют специальный
прибор.
Он состоит
из подвижного столика, на котором
расположена плоская коробка с натянутой
тонкой резиновой пленкой. Сверху пленка
вплотную накрыта крышкой с отверстием по
форме исследуемого сечения. К нижней части
коробки подведена трубка, сообщающаяся со
стеклянным манометром. Поднимая трубку,
повышают давление под резиновой пленкой, и
32.
Сопротивление материаловРаздел: Сдвиг и кручение
Кручение статически - определимого стержня
ORIGIN 1
Для данного стержня найти максимальные напряжения и углы закручивания
по длине стержня.
Условная расчетная схема нагружения стержня
Ld2
Ld1
mi
Mi
Lmi
LmHi
Lmki
x
L
град deg м m см 0.01 m мм 0.001 m
кН 1000 N
6 N
кНм 1000 N m Нм N m МПа 10
4
2
m
33.
m4
Исходные данные G 8 10 МПа модуль сдвига
Размеры сечения
для круга
D1 50 мм
0.3 L
для кольца
d 40 мм D 50 мм
L 1 м Ld
0.7 L
для прямоугольного сечения
b 50 мм
h 50 мм
hb
h
b
Внешние моменты и координата их приложения
500
10
L
M 700 Нм
LM 30 см
x 0 м
L
100
800
60
3000 Нм
2000 м
m
10
см
70
Lmн
40
см
100
Lmк
Определение крутящих моментов
mm( x)
m
if Lmн x Lmк
m
if Lmн x Lmк
1
1
2
2
Нм
0
otherwise
м
1
Все правильно и просто, но вычисление интеграла от
интеграла (угол закручивания) просходит ну очень долго
2
rows ( M )
M k( x)
i 1
Mi x LMi
x
mm( x) d x
0
Без интеграла расчет идет раз в 100 быстрее
rows ( M )
M k( x)
i 1
rows ( m)
rows( m)
Mi x LMi
mi x Lmнi x Lmнi
mi x Lmкi x Lmкi
i 1
i 1
34.
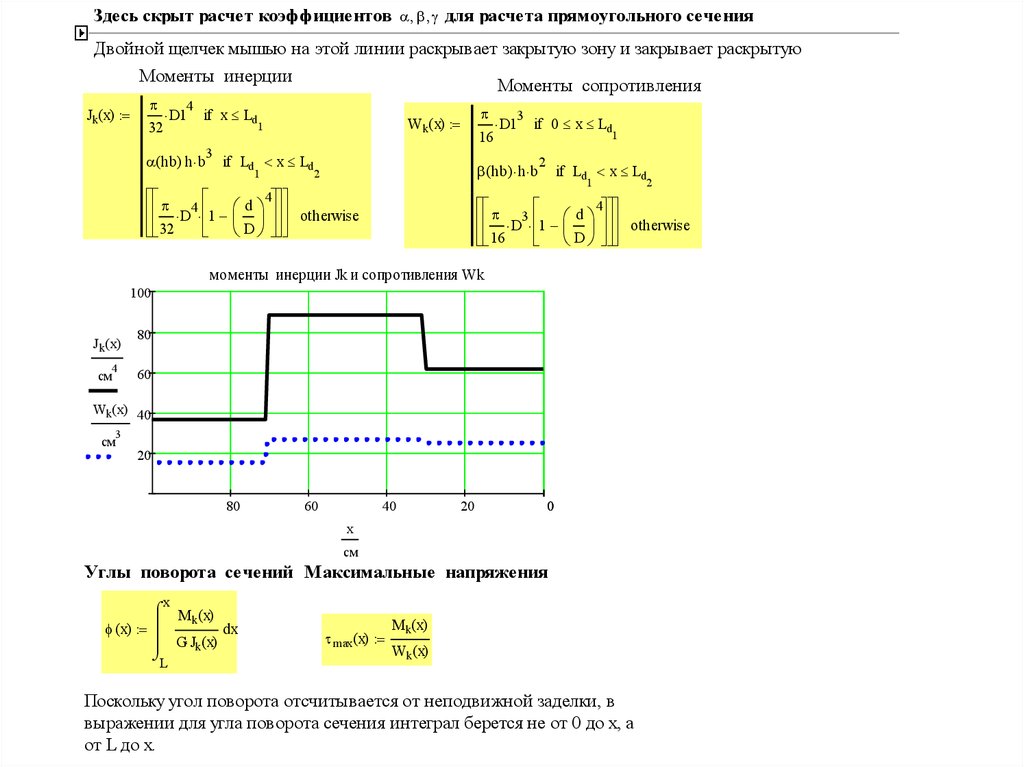
Здесь скрыт расчет коэффициентов для расчета прямоугольного сеченияДвойной щелчек мышью на этой линии раскрывает закрытую зону и закрывает раскрытую
Моменты инерции
Jk( x)
4
32
D1
Моменты сопротивления
if x Ld
( hb ) h b
W k( x)
1
3
if Ld x Ld
1
16
3
D1
if 0 x Ld
( hb ) h b
2
4
4
d
D 1 otherwise
32
D
2
1
if Ld x Ld
1
4
3
d
D 1 otherwise
16
D
моменты инерции Jk и сопротивления Wk
100
Jk( x)
4
см
80
60
Wk( x) 40
3
см
20
80
60
40
20
0
x
см
Углы поворота сечений Максимальные напряжения
x
M ( x)
k
( x)
dx
G Jk( x)
L
2
max( x)
M k( x)
W k( x)
Поскольку угол поворота отсчитывается от неподвижной заделки, в
выражении для угла поворота сечения интеграл берется не от 0 до х, а
от L до х.
35.
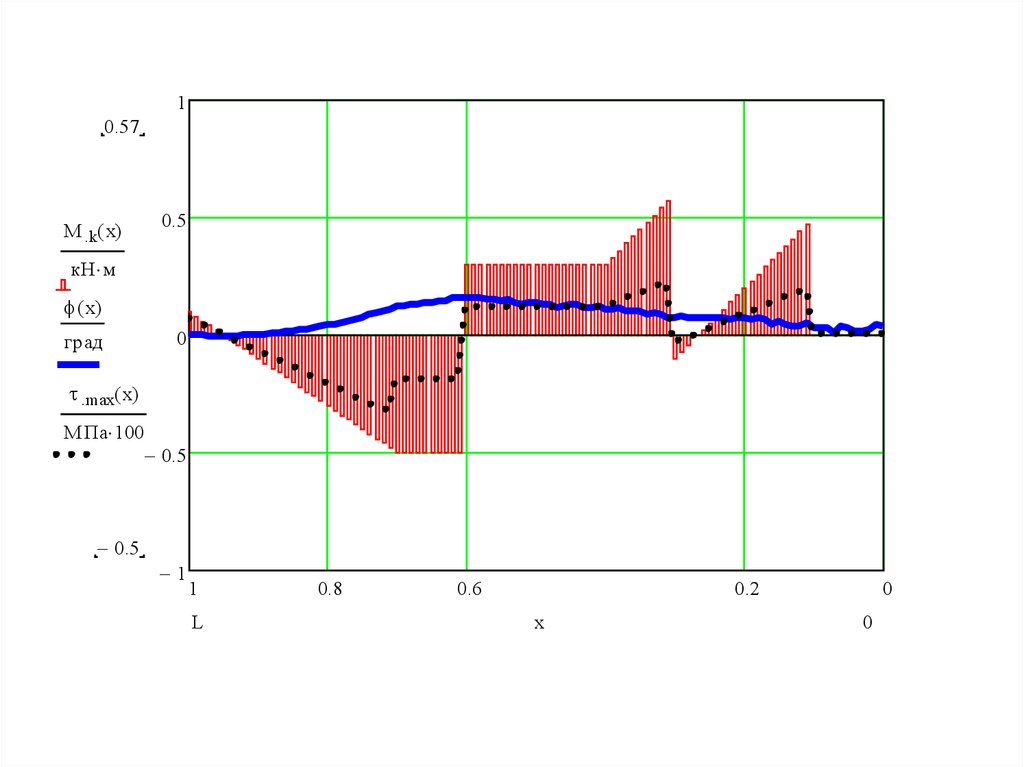
10.57
M .k( x)
0.5
кН м
( x)
град
0
.max( x)
М Па 100
0.5
0.5
1
1
L
0.8
0
0.2
0.6
x
0
36.
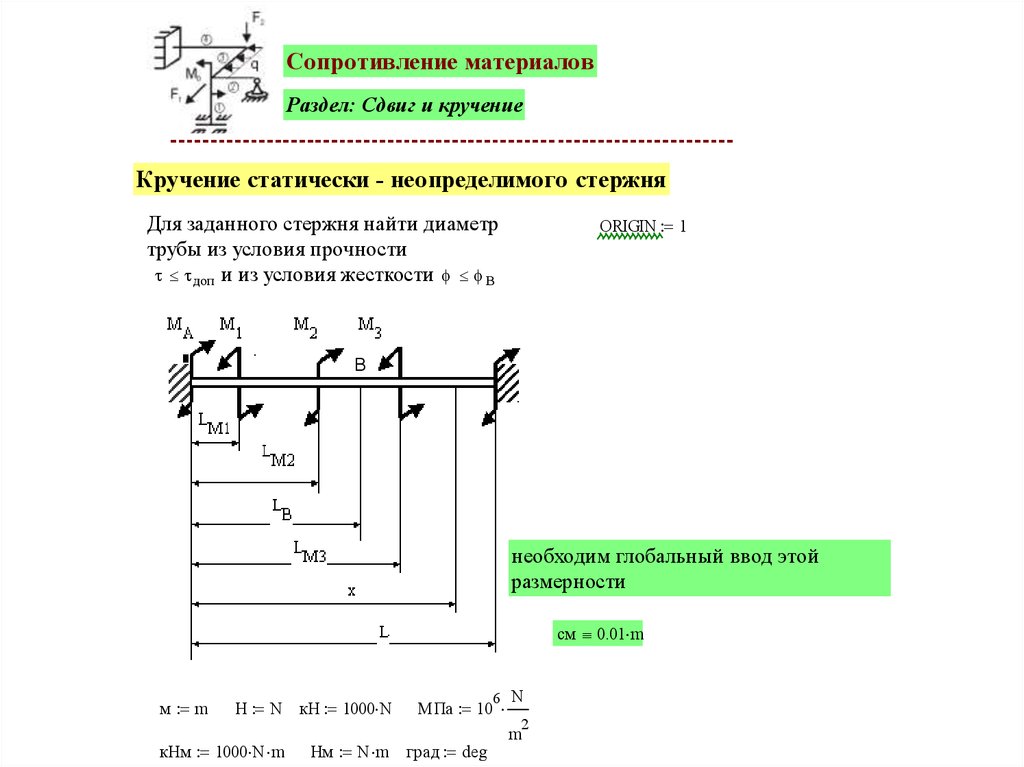
Сопротивление материаловРаздел: Сдвиг и кручение
Кручение статически - неопределимого стержня
Для заданного стержня найти диаметр
трубы из условия прочности
доп и из условия жесткости B
ORIGIN 1
В
необходим глобальный ввод этой
размерности
см 0.01 m
м m
Н N кН 1000 N
кНм 1000 N m
6 N
МПа 10
Нм N m град deg
2
m
37.
Исходные данные4
L 1 м
G 8 10 МПа доп 50 МПа
Диаметр трубы (в первом приближении) задан глобально ниже графика
(Труба = d/D) d D
0.9
Пары сил и координаты их приложения
500
10
M 700 Нм
LM 30 см
800
60
Задаемся положением точки, где наложено ограничение LA
и углом поворота ?A в месте ее наложения
LA 0. м
A 0. град
в левой
заделке
Проверить условие жесткости
в точке В
LB 50 см
поменяйте
LA
и A
LB и B
B 0.3 град
Геометрические характеристики
Jk( D)
32
W k( D)
A ( D)
4
4
4
D 1
16
3
4
D 1
2
момент инерции
2
D 1
момент сопротивления
площадь сечения
Крутящий момент Mk MA x
rows ( M )
i 1
x
Угол поворота
M M x
k
A
D M A x
dx
G Jk( D)
L
Mi x LMi MA x LA
38.
kL
решение уравнения неразрывности деформаций
начальное приближение
M A 1 кНм
M R root D M A LA A M A
M R 280 Нм
Определение максимального
крутящего момента Mmax
L
x 0 м
L
100
M k( x) M k M R x
Здесь скрыта программа Fmax
Fmax F Lн Lк N
L Lн
"F-функция одного аргумента"
A1 F( L)
while L Lк
Lк Lн
L L
N
A2 F( L)
if A2 A1
A1 A2
L2 L
T
( A1 L2 кН )
Поменяйте параметры поиска максимума
Lн 0 м
LA A
Lк L
N 1000 M max Fmax M k Lн Lк N
Возвращение
к исходной размерности
xMmax
Максимальный момент
При D 5 см max( D)
кН
M max 480 Нм
в сечении
xMmax 30.1 см
M max
W k( D)
1
Fmax M k Lн Lк N
max( D) 57 МПа
2
0
39.
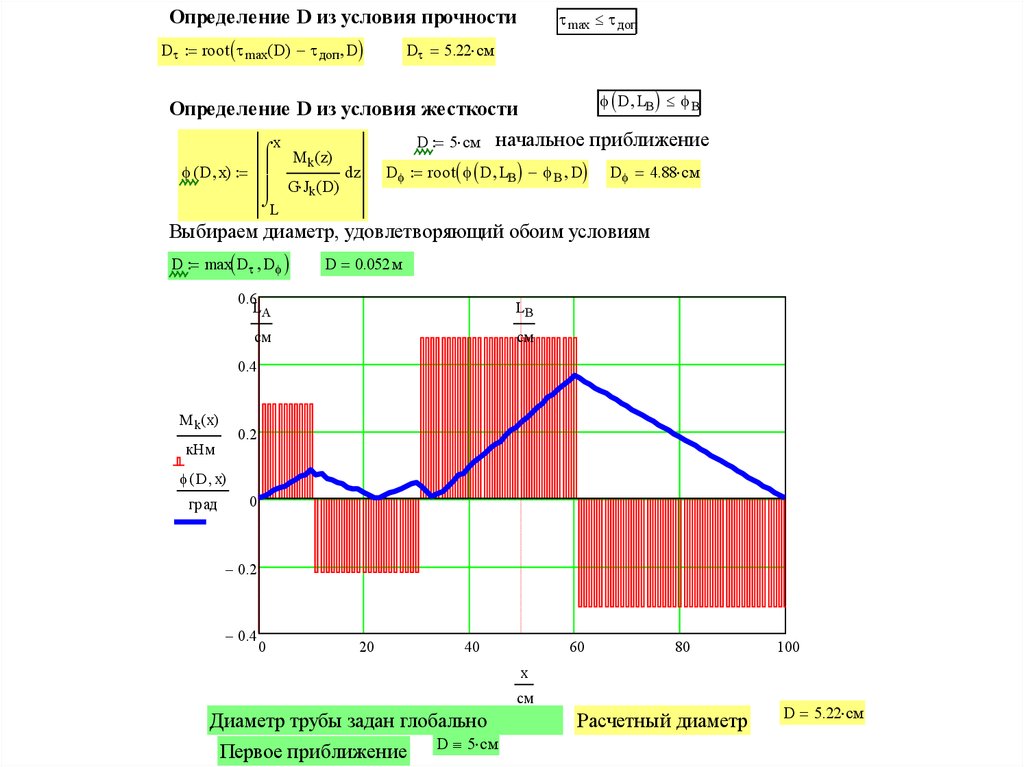
Определение D из условия прочностиD root max( D) доп D
max доп
D 5.22 см
D LB B
Определение D из условия жесткости
D 5 см
x
M ( z)
k
( D x)
dz
G Jk( D)
начальное приближение
D root D LB B D
D 4.88 см
L
Выбираем диаметр, удовлетворяющий обоим условиям
D max D D
D 0.052 м
0.6
LA
LB
см
см
0.4
M k( x)
0.2
кНм
( D x)
град
0
0.2
0.4
0
20
40
60
80
100
x
см
Диаметр трубы задан глобально
Первое приближение
D 5 см
Расчетный диаметр
D 5.22 см
40.
8. Кручениетонкостенного стержня
В практике
машиностроения, и
особенно
самолетостроения,
часто возникает
необходимость
расчета на кручение
так называемых
тонкостенных
стержней. Типичные
формы прокатанных,
гнутых, тянутых и
прессованных
профилей
показаны
Тонкие
профили
разделяются на замкнутые и
на рисунке.
открытые.
Так, первые четыре профиля,
Характерной
показанные
на рисунке, являются открытыми
геометрической
(незамкнутыми),
а последние три - замкнутыми.
особенностью
тонкостенных
стержней является
то, что их толщина
существенно меньше
41.
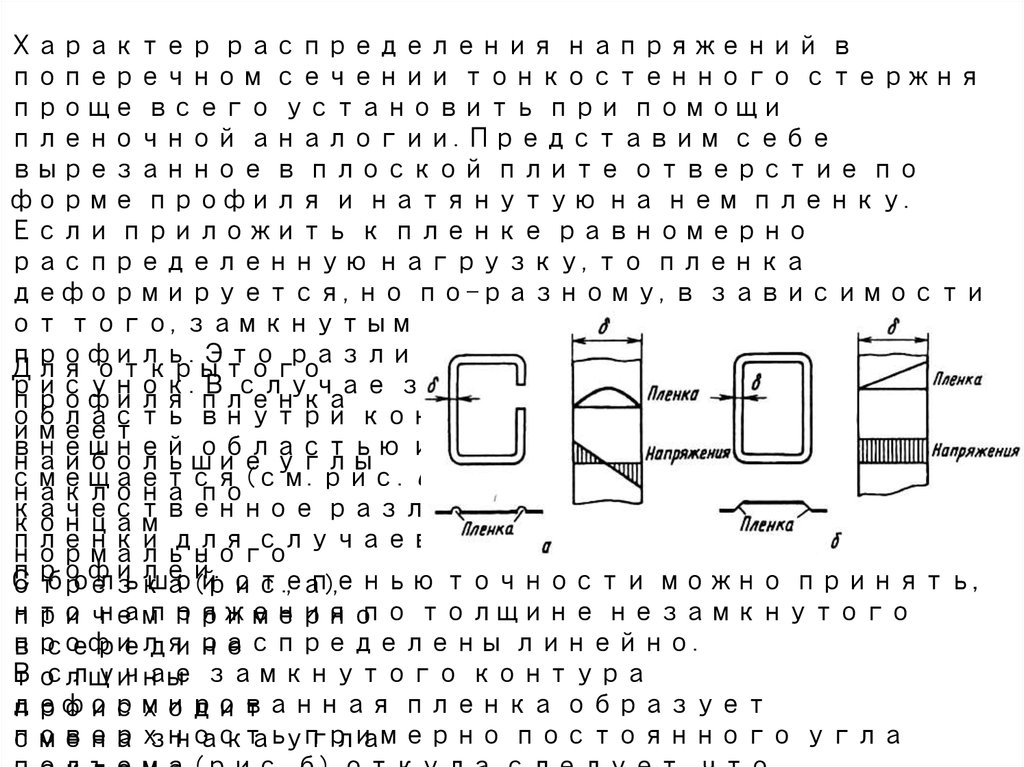
Характер распределения напряжений впоперечном сечении тонкостенного стержня
проще всего установить при помощи
пленочной аналогии. Представим себе
вырезанное в плоской плите отверстие по
форме профиля и натянутую на нем пленку.
Если приложить к пленке равномерно
распределенную нагрузку, то пленка
деформируется, но по-разному, в зависимости
от того, замкнутым или открытым является
профиль. Это различие иллюстрирует
Для открытого
рисунок. В случае замкнутого профиля
профиля пленка
область внутри контура не связана с
имеет
внешней областью и под действием давления
наибольшие углы
смещается (см. рис. б). Это и предопределяет
наклона по
качественное различие между формами
концам
пленки для случаев замкнутого и открытого
нормального
профилей.
С
большой
степенью
точности можно принять,
отрезка
(рис.,
а),
что
напряжения
по толщине незамкнутого
причем
примерно
профиля
распределены линейно.
в середине
В
случае замкнутого контура
толщины
деформированная
пленка образует
происходит
поверхность
примерно постоянного угла
смена знака угла
42.
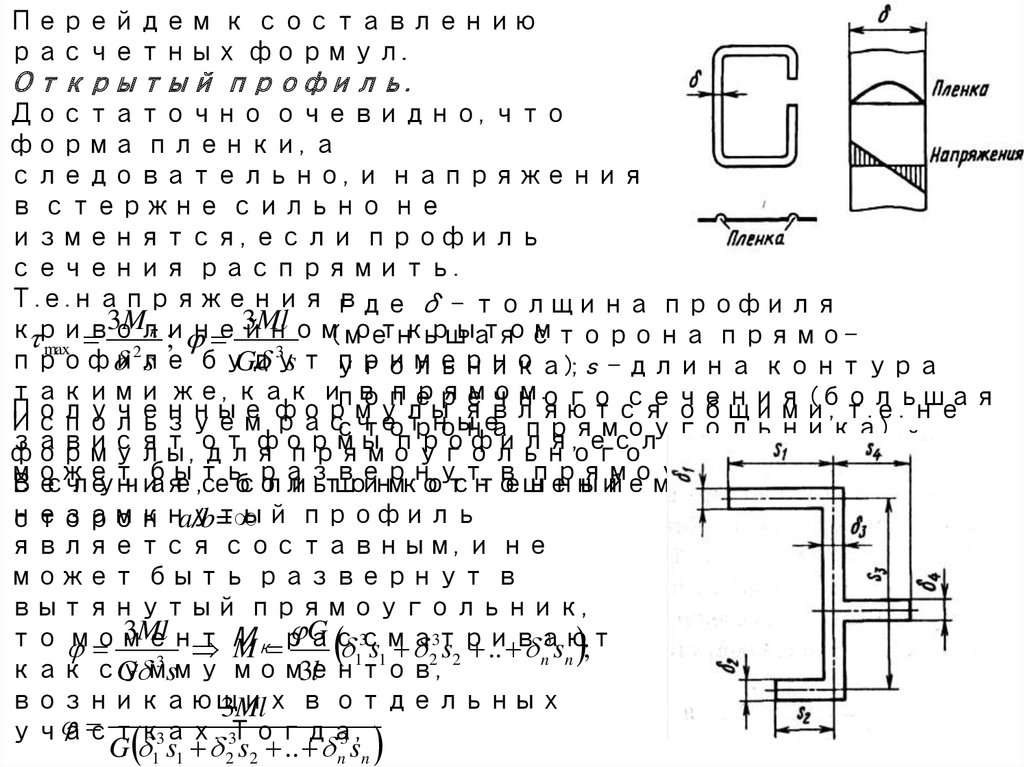
Перейдем к составлениюрасчетных формул.
Открытый профиль.
Достаточно очевидно, что
форма пленки, а
следовательно, и напряжения
в стержне сильно не
изменятся, если профиль
сечения распрямить.
Т.е.напряжения где
в
δ - толщина профиля
3
M
3
Ml
криволинейном
открытом
(меньшая
сторона прямо max 2 к ;
3
профиле
s будут
G s примерно
угольника); s - длина контура
такими же, как и
в прямом.
поперечного
сечения (большая
Полученные
формулы
являются
общими, т.е. не
Используем расчетные
сторона прямоугольника).
зависят
формы
профиля, если последний
формулы, от
для
прямоугольного
может
быть
развернут
в прямоугольник.
сечения
В
случае,
сесли
большим
тонкостенный
отношением
незамкнутый
профиль
сторон a/b=∞
является составным, и не
может быть развернут в
вытянутый прямоугольник,
3Ml
G 3
3
3
то
момент
М
к рассматривают
M
s
s
..
sn ;
1
1
2
2
n
3
как сумму
моментов,
G s
3l
возникающих
3Ml в отдельных
участках.
Тогда,
3
3
3
G 1 s1 2 s2 .. n sn
43.
При помощи пленочной аналогии легкоустановить, что наибольшие напряжения
возникают на участке с наибольшей толщиной
δmах · Для этого отдельно
взятого
участка,
МКk - доля
крутящего
3
M
3
M
l
Kk
которому
припишем
номер
k, справедливы
момента,
k max 2 Kk
;
формулы:
s
G 3 s
соответствующего k-му
k
k
k k
участку; φ- угловое
Исключая из этих
перемещение, единое для
выражений МКk, находим
всех
3M участков.
k max G
max
l
K
max
s 23 s2 .. n3 sn
3
1 1
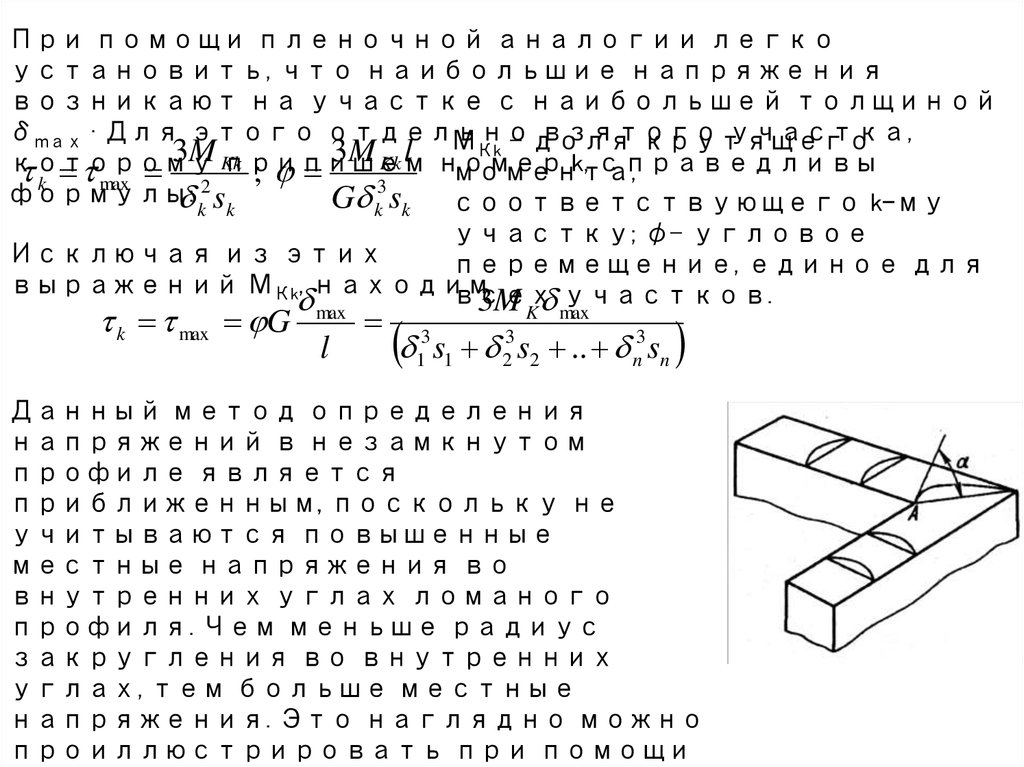
Данный метод определения
напряжений в незамкнутом
профиле является
приближенным, поскольку не
учитываются повышенные
местные напряжения во
внутренних углах ломаного
профиля. Чем меньше радиус
закругления во внутренних
углах, тем больше местные
напряжения. Это наглядно можно
проиллюстрировать при помощи
44.
Замкнутый профильz
Здесь, в отличие от открытого
профиля, напряжения
распределены по толщине
равномерно. Выделим из
dx
стержня элементарную призму
x
длиной dx. Размер призмы в
направлении дуги контура, т.е.
расстояние между точками 1 и 2,
является произвольным. Пусть
толщина контура в точке 1
будет δ1, а в точке 2-δ2.
Соответственно через τ1, и τ2
1 1dxнапряжения
2 2dx
x
обозначим
в
dx
поперечном сечении. В
Так
как точки
1 и 2 взяты произвольно, то τδ= const.
продольных
сечениях
Таким
образом,
произведение
возникают
парные
напряженияτδ по длине
τ́замкнутого
для
контура
не изменяется. На
1=τ1 и τ́ 2=τ2 . Составим
выделенного
элемента
участках,
имеющих
меньшую толщину,
уравнение
равновесия,
напряжения
будут соответственно
большими.
Выразим крутящий
момент через
спроектировав
все
силы
на
напряжения τ. Для
этого
возьмем
на
направление
оси бруса.участок
контуре элементарный
Очевидно:
длиной ds. Момент силы τδds
M K произвольно
OA ds
относительно
взятой
45.
Произведение τδ по длине дуги контура неизменяется
M K OA ds
s
Произведение \OA\ds представляет
собой удвоенную площадь
треугольника ОВС, а интеграл от
этого произведения по длине
замкнутого контура дает
удвоенную площадь,
*
M
2
A
K
ограниченную
средней
линией
контура.
Обозначим эту
M Kплощадь
Наибольшее
maxот
A. Таким
через
A* в отличие
*
напряжение
2
A
min
образом
Угловое перемещение φ для тонкостенного
стержня замкнутого профиля поперечного
сечения определим путем сопоставления
потенциальной энергии, выраженной через
напряжение τ, с потенциальной энергией,
2
выраженной через внешний момент M.
U0
Обратимся к выражению
2G удельной
потенциальной энергии при сдвиге
46.
Энергия, накопленная в элементарном объемес размерами ds, dx, δ, равна
2
dU
2G
dsdx
Это выражение должно быть
проинтегрировано по длине стержня l и по
дуге замкнутого контура.
2 2 Если стержень
l
l
ds
является однородным
U
2 ds по длине, то
2G s
2G
s
Последний интеграл зависит от закона
изменения толщины по дуге контура и
является геометрической
характеристикой
MK
сечения. Учитывая,
что
*
полу
чим
2
2A
M l ds
U
8GA*2 s
Однако энергию U можно выразить как работу
внешнего момента M на угловом перемещении φ:
1
U M
2
47.
Приравнивая оба выражения для U, находимMl
ds
4GA*2 s
Если толщина δ по дуге
контура не меняется, то
Mls
4GA*2
где s - длина замкнутого
контура.
































 mechanics
mechanics








