Сводка, группировка, ряд распределения

1. «Сводка, группировка, ряд распределения

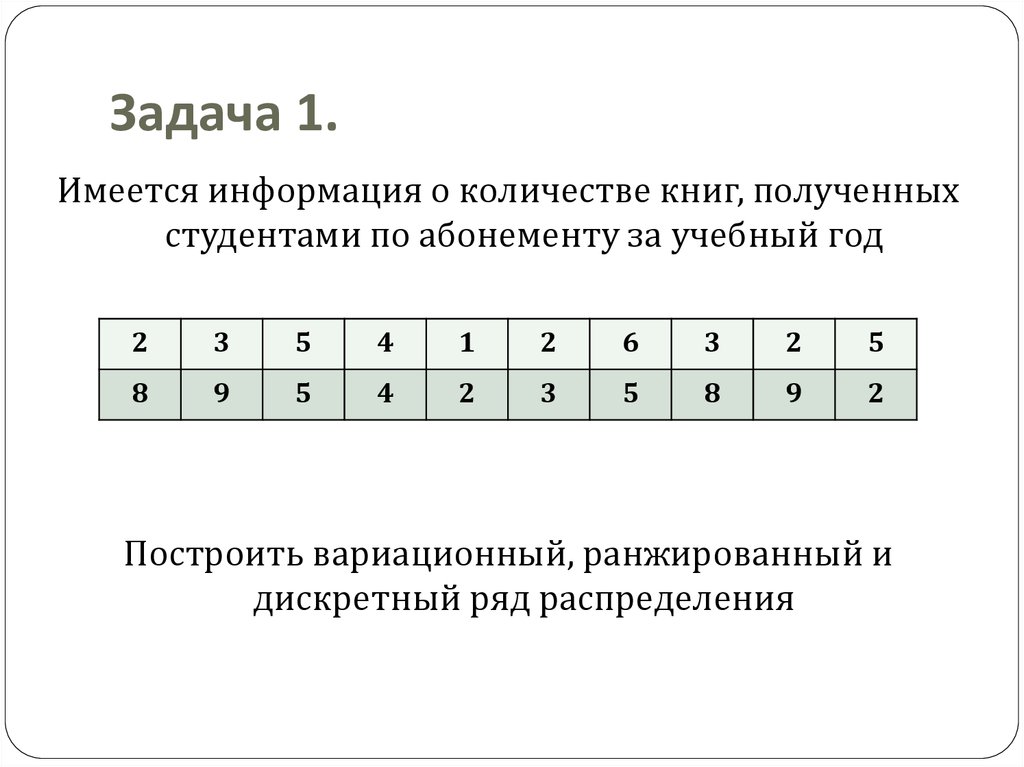
Практическое занятие 2

2. Задача 1.

Имеется информация о количестве книг, полученных
студентами по абонементу за учебный год
2
3
5
4
1
2
6
3
2
5
8
9
5
4
2
3
5
8
9
2
Построить вариационный, ранжированный и
дискретный ряд распределения

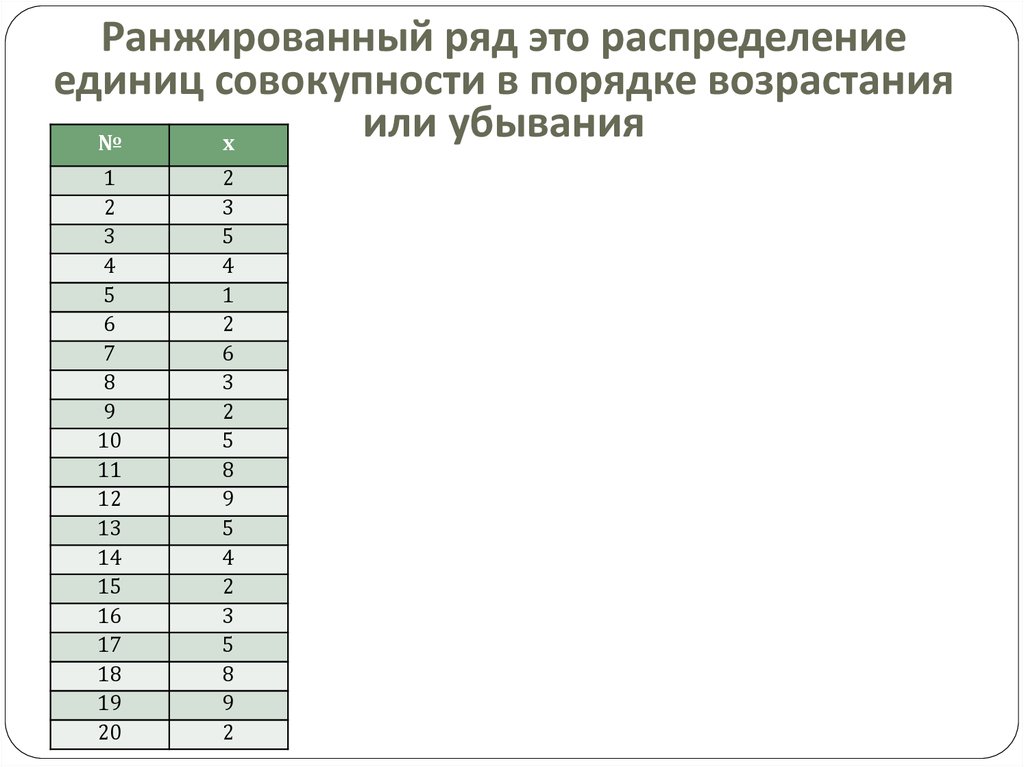
3. Ранжированный ряд это распределение единиц совокупности в порядке возрастания или убывания

4. Ранжированный ряд это распределение единиц совокупности в порядке возрастания или убывания

№
х
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
5
4
1
2
6
3
2
5
8
9
5
4
2
3
5
8
9
2

5. Ранжированный ряд это распределение единиц совокупности в порядке возрастания или убывания

№
х
№
х
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
2
3
5
4
1
2
6
3
2
5
8
9
5
4
2
3
5
8
9
2
5
1
6
9
15
20
2
8
16
4
14
3
10
13
17
7
11
18
12
19
1
2
2
2
2
2
3
3
3
4
4
5
5
5
5
6
8
8
9
9

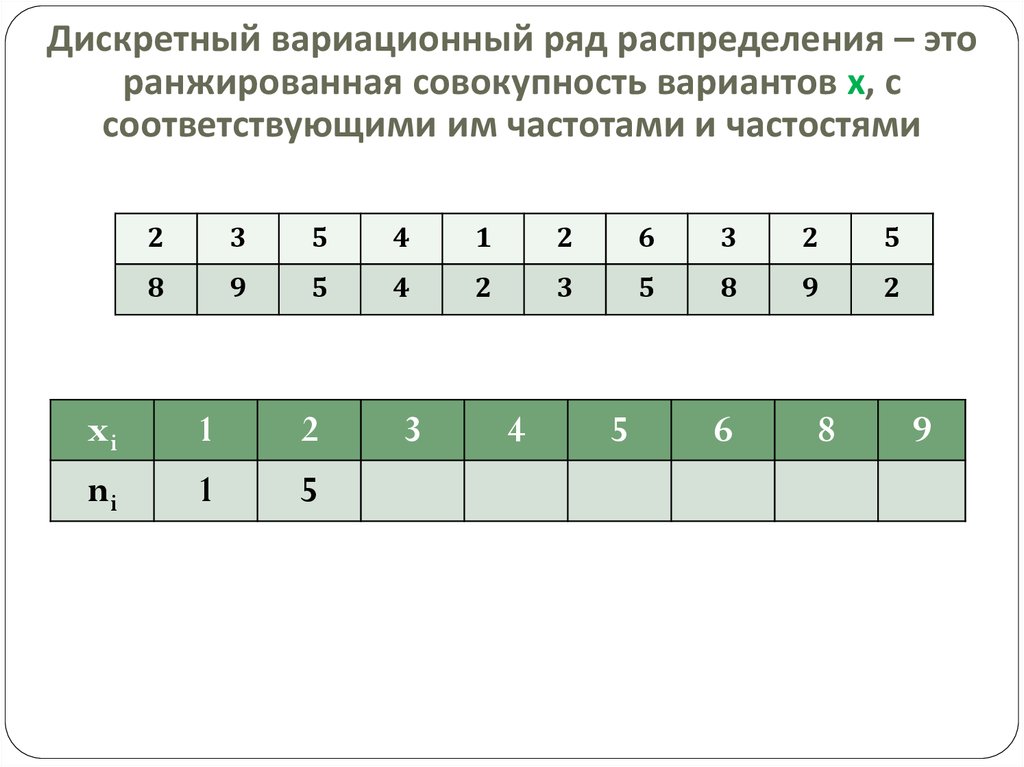
6. Дискретный вариационный ряд распределения – это ранжированная совокупность вариантов х, с соответствующими им частотами и

частостями

7. Дискретный вариационный ряд распределения – это ранжированная совокупность вариантов х, с соответствующими им частотами и

частостями
xi
ni
2
3
5
4
1
2
6
3
2
5
8
9
5
4
2
3
5
8
9
2

8. Дискретный вариационный ряд распределения – это ранжированная совокупность вариантов х, с соответствующими им частотами и

частостями
xi
ni
2
3
5
4
1
2
6
3
2
5
8
9
5
4
2
3
5
8
9
2
1
2
3
4
5
6
8
9

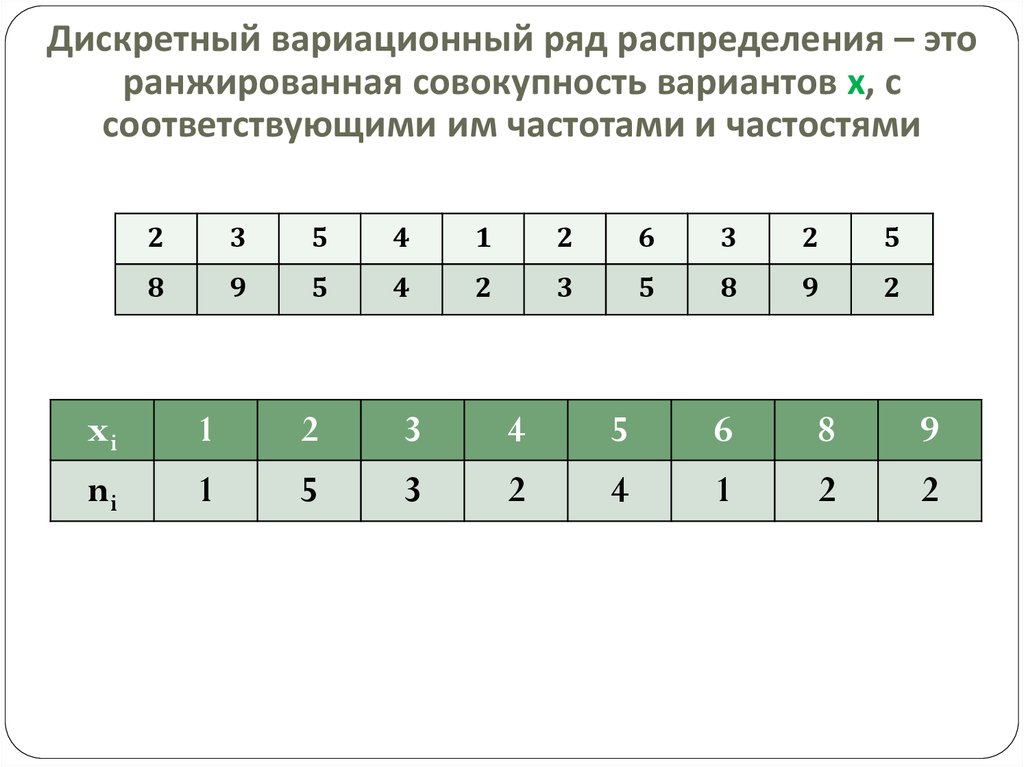
9. Дискретный вариационный ряд распределения – это ранжированная совокупность вариантов х, с соответствующими им частотами и

частостями
2
3
5
4
1
2
6
3
2
5
8
9
5
4
2
3
5
8
9
2
xi
1
2
ni
1
5
3
4
5
6
8
9

10. Дискретный вариационный ряд распределения – это ранжированная совокупность вариантов х, с соответствующими им частотами и

частостями
2
3
5
4
1
2
6
3
2
5
8
9
5
4
2
3
5
8
9
2
xi
1
2
3
4
5
6
8
9
ni
1
5
3
2
4
1
2
2

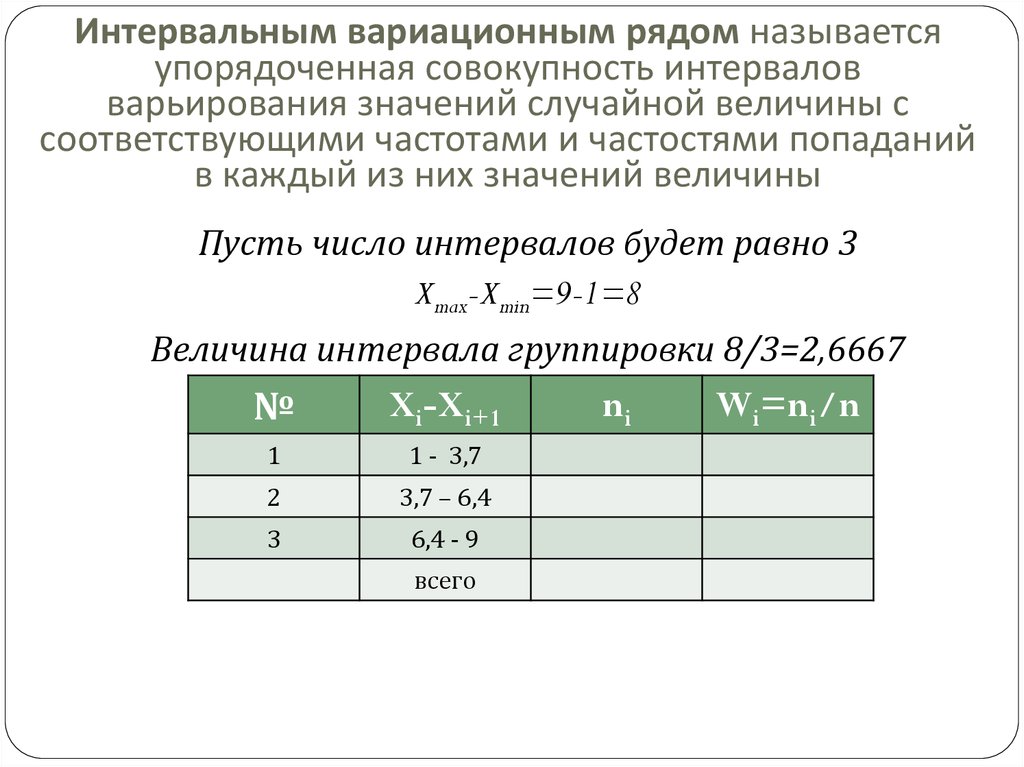
11. Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с

соответствующими частотами и частостями попаданий
в каждый из них значений величины
Пусть число интервалов будет равно 3
Xmax-Xmin=9-1=8
Величина интервала группировки 8/3=2,6667
№
Xi-Xi+1
1
1 - 3,7
2
3,7 – 6,4
3
6,4 - 9
всего
ni
Wi=ni/n

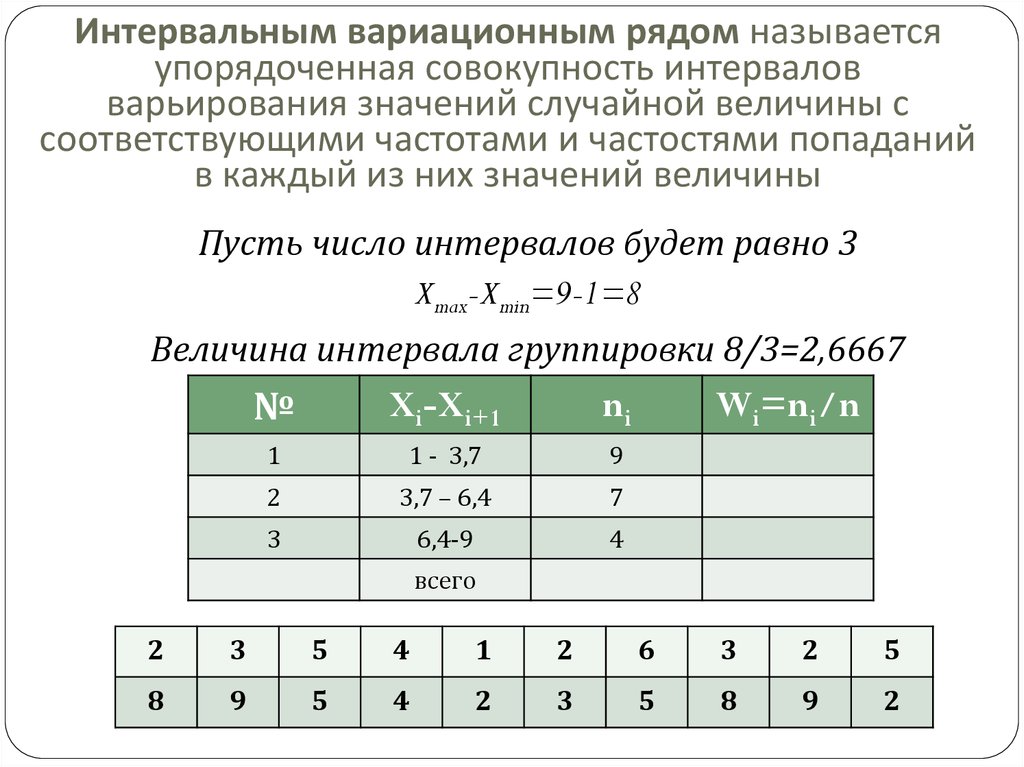
12. Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с

соответствующими частотами и частостями попаданий
в каждый из них значений величины
Пусть число интервалов будет равно 3
Xmax-Xmin=9-1=8
Величина интервала группировки 8/3=2,6667
№
Xi-Xi+1
ni
1
1 - 3,7
9
2
3,7 – 6,4
7
3
6,4-9
4
Wi=ni/n
всего
2
3
5
4
1
2
6
3
2
5
8
9
5
4
2
3
5
8
9
2

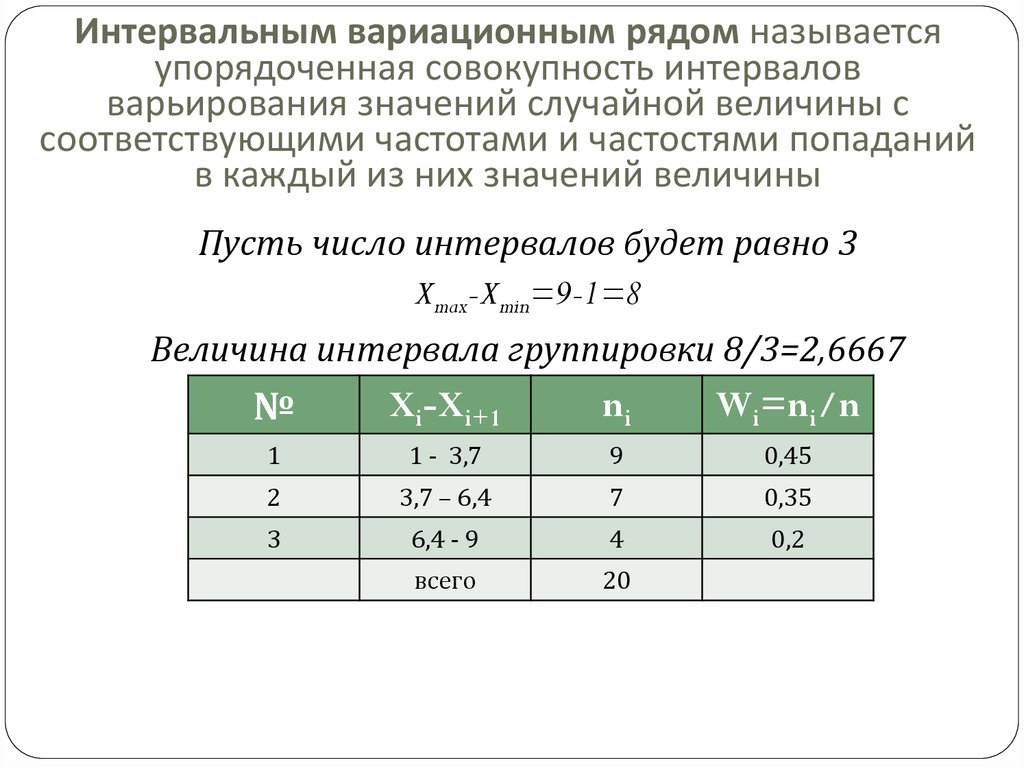
13. Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с

соответствующими частотами и частостями попаданий
в каждый из них значений величины
Пусть число интервалов будет равно 3
Xmax-Xmin=9-1=8
Величина интервала группировки 8/3=2,6667
№
Xi-Xi+1
ni
1
1 - 3,7
9
2
3,7 – 6,4
7
3
6,4 - 9
4
всего
20
Wi=ni/n
2
3
5
4
1
2
6
3
2
5
8
9
5
4
2
3
5
8
9
2

14. Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с

соответствующими частотами и частостями попаданий
в каждый из них значений величины
Пусть число интервалов будет равно 3
Xmax-Xmin=9-1=8
Величина интервала группировки 8/3=2,6667
№
Xi-Xi+1
ni
Wi=ni/n
1
1 - 3,7
9
0,45
2
3,7 – 6,4
7
0,35
3
6,4 - 9
4
0,2
всего
20

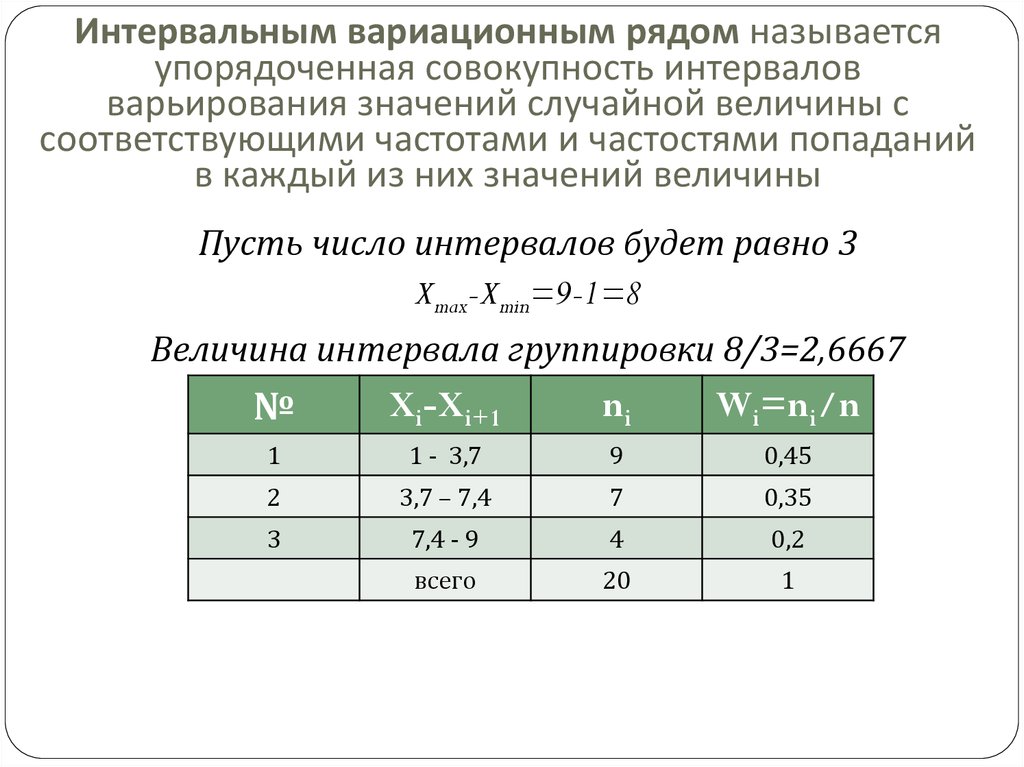
15. Интервальным вариационным рядом называется упорядоченная совокупность интервалов варьирования значений случайной величины с

соответствующими частотами и частостями попаданий
в каждый из них значений величины
Пусть число интервалов будет равно 3
Xmax-Xmin=9-1=8
Величина интервала группировки 8/3=2,6667
№
Xi-Xi+1
ni
Wi=ni/n
1
1 - 3,7
9
0,45
2
3,7 – 7,4
7
0,35
3
7,4 - 9
4
0,2
всего
20
1

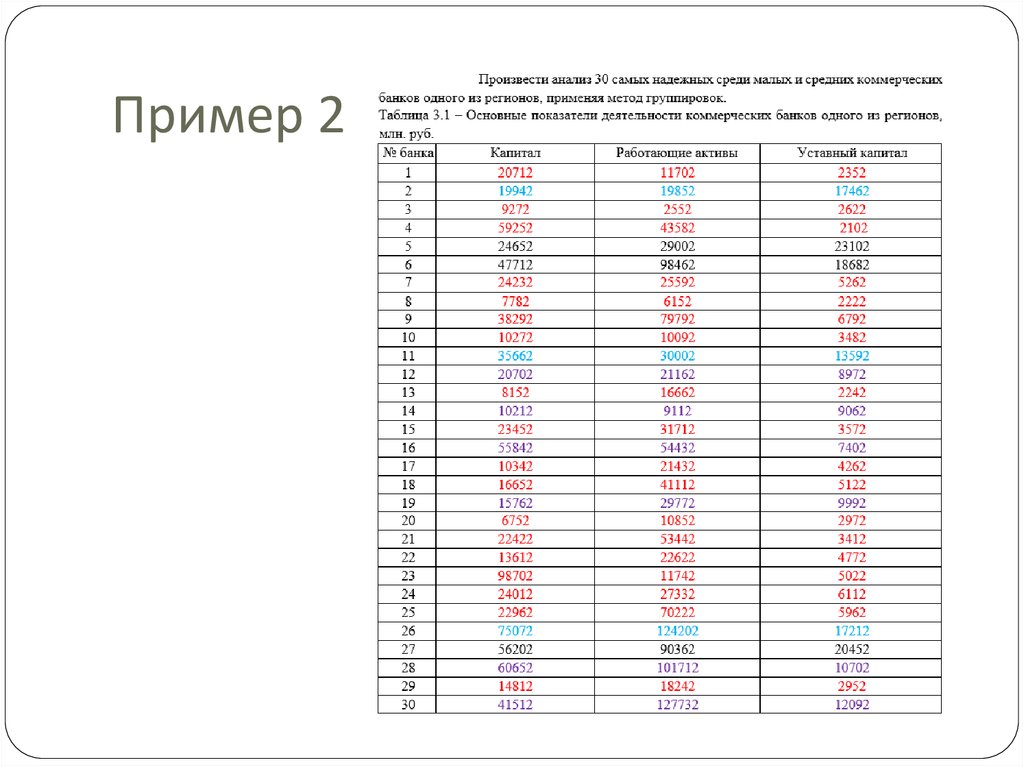
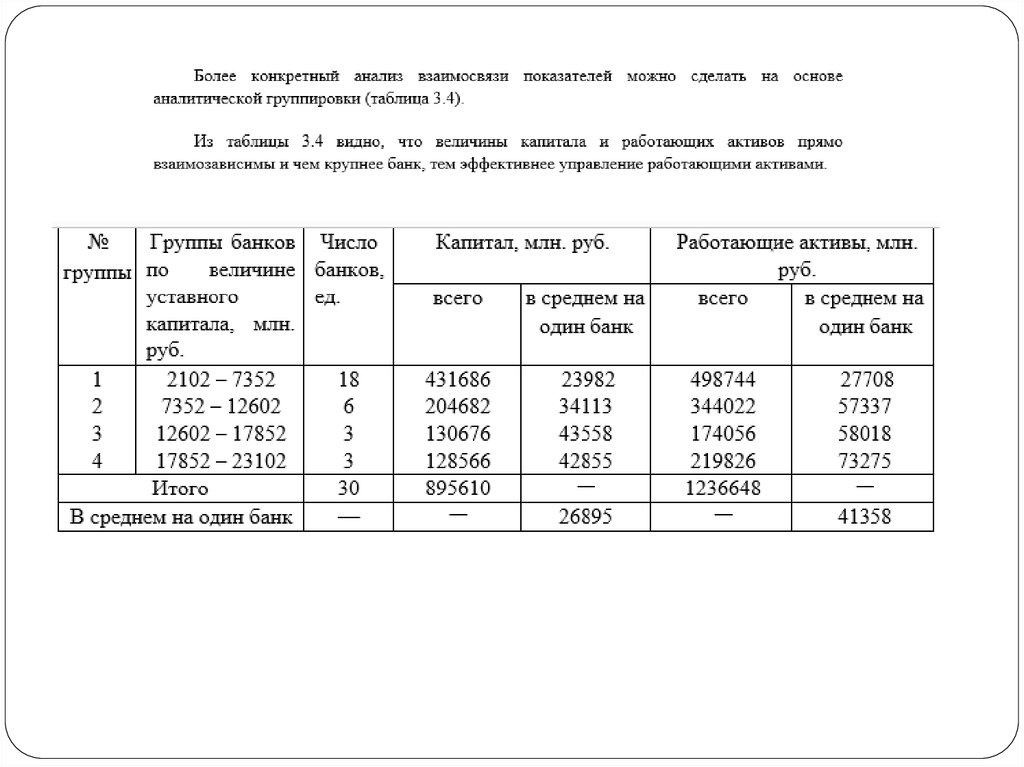
16. Пример 2

17.

18.

19.

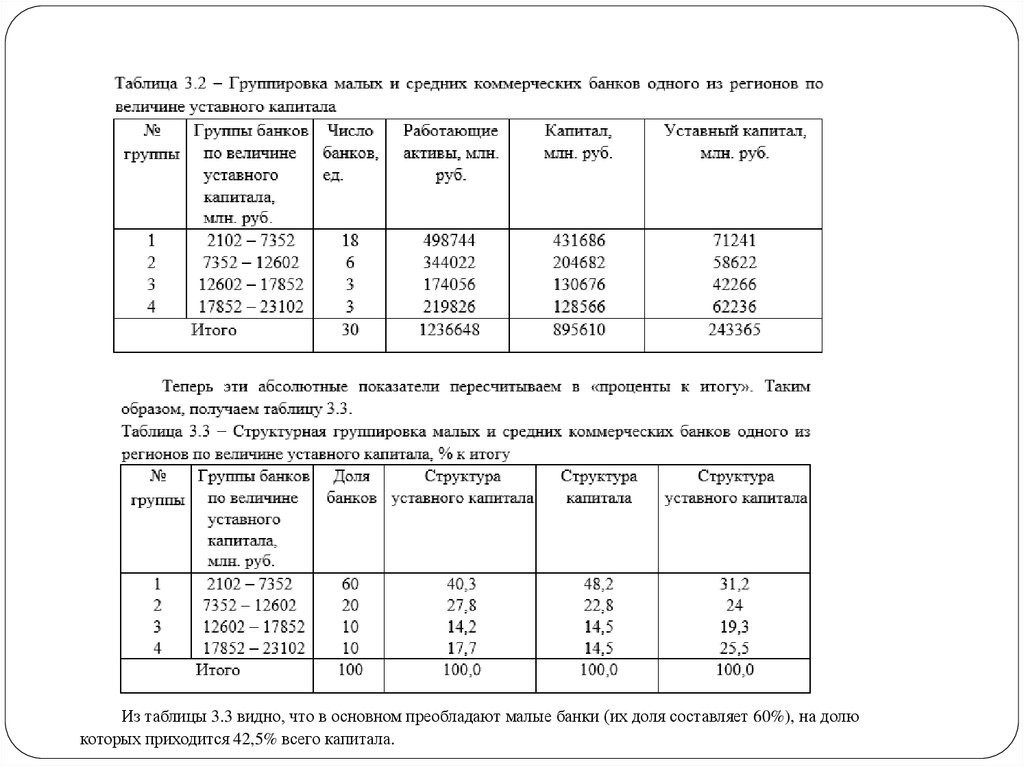
Из таблицы 3.3 видно, что в основном преобладают малые банки (их доля составляет 60%), на долю
которых приходится 42,5% всего капитала.

20.

21. Решить самостоятельно