Similar presentations:
Описательная статистика. Группировка данных. Лекция 2
1. ЛЕКЦИЯ 2
ОПИСАТЕЛЬНАЯСТАТИСТИКА
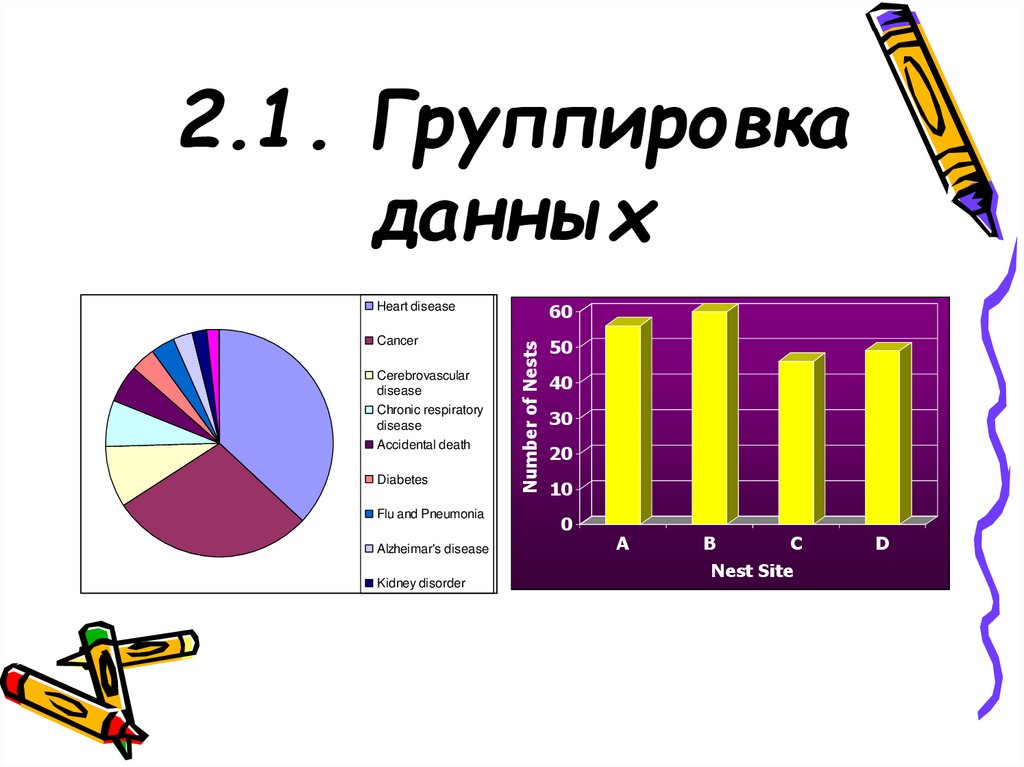
2. 2.1. Группировка данных
60Cancer
50
Cerebrovascular
disease
Chronic respiratory
disease
Accidental death
Diabetes
Flu and Pneumonia
Alzheimar's disease
Kidney disorder
Septicemia
Number of Nests
Heart disease
40
30
20
10
0
A
B
C
Nest Site
D
3. Обработку данных полезно начать с их группировки…
Группировка - это систематизацияпервичных данных, направленная
на извлечение заключенной в них
информации и выявление
закономерностей, которым
подчиняется изучаемое явление
или объект.
4. Пример: медицинские сведения
Пол (м, ж)Возраст (полных лет)
Группа крови (I, II, III, IV)
Систолическое давление (мм рт.ст.)
Курильщик (да, нет)
Рост (см)
Вес (кг)
…
Качественные переменные – определяется
принадлежность объекта к одной из нескольких
категорий
Количественные (непрерывные, дискретные)
– дают числовую величину; к ним применяют
арифметические действия
5. Группировка количественных данных :
по значениямвариант
по классам
Представление частотного распределения графически
6.
При небольшом n и незначительнойвариации признака, количественные
данные группируют по значениям вариант
(полигон распределения)
Частота
встречаемости, fi
Распределение данных о плодовитости
крольчих
6
5
4
3
2
1
0
1
2
3
4
5
Количество крольчат в помете
6
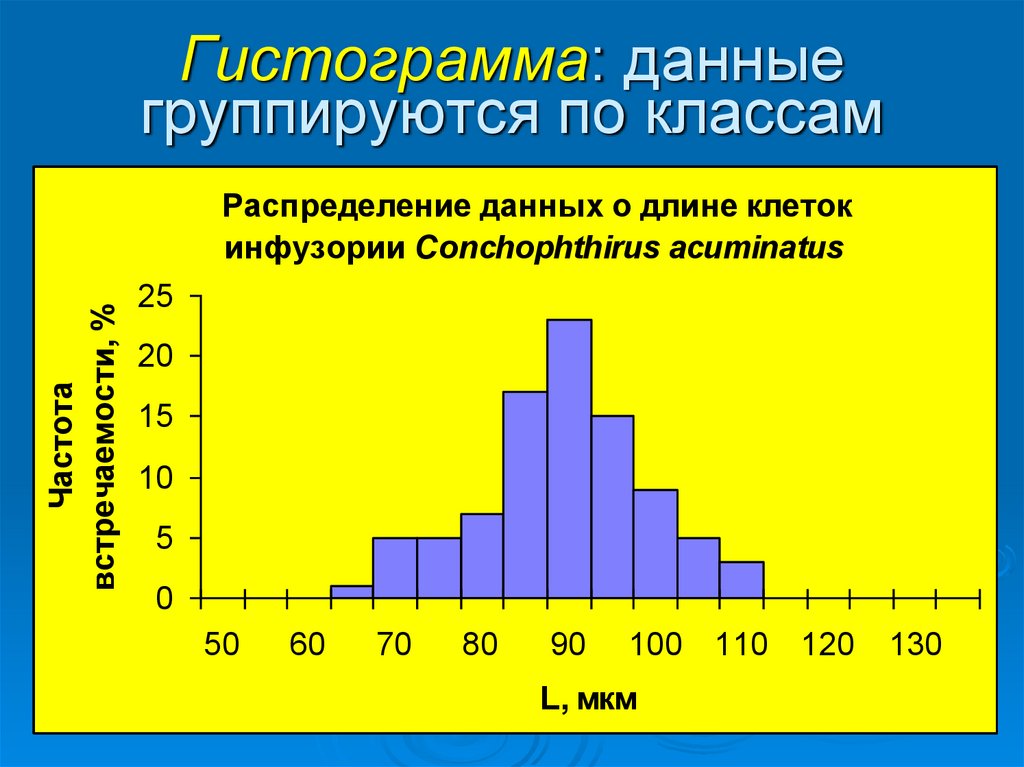
7. Гистограмма: данные группируются по классам
Частотавстречаемости, %
Распределение данных о длине клеток
инфузории Conchophthirus acuminatus
25
20
15
10
5
0
50
60
70
80
90
100
L, мкм
110
120
130
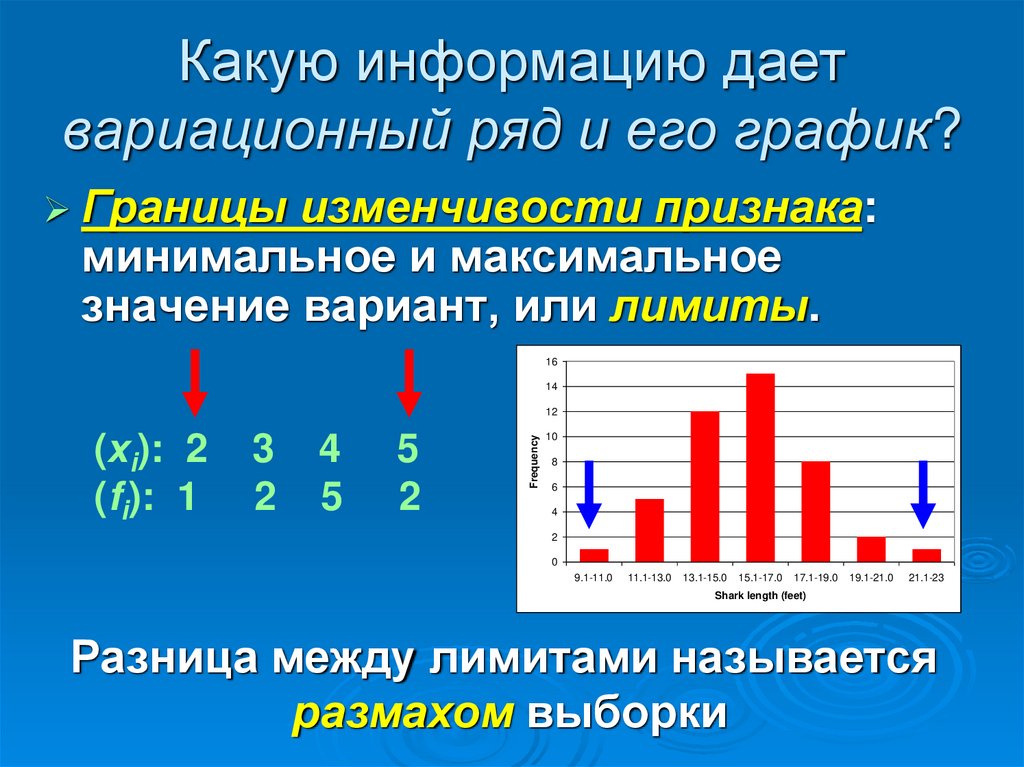
8. Какую информацию дает вариационный ряд и его график?
Границы изменчивости признака:минимальное и максимальное
значение вариант, или лимиты.
16
14
(хi): 2
(fi): 1
3
2
4
5
5
2
Frequency
12
10
8
6
4
2
0
9.1-11.0
11.1-13.0
13.1-15.0
15.1-17.0
17.1-19.0
19.1-21.0
21.1-23
Shark length (feet)
Разница между лимитами называется
размахом выборки
9.
Характер вариации признака:исследователь может установить
симметричность распределения
Percent from total
35
30
вправо
25
20
15
10
5
0
влево
<40 40-50 50-60 60-70 70-80 80-90 90-100 >100
Weight
10.
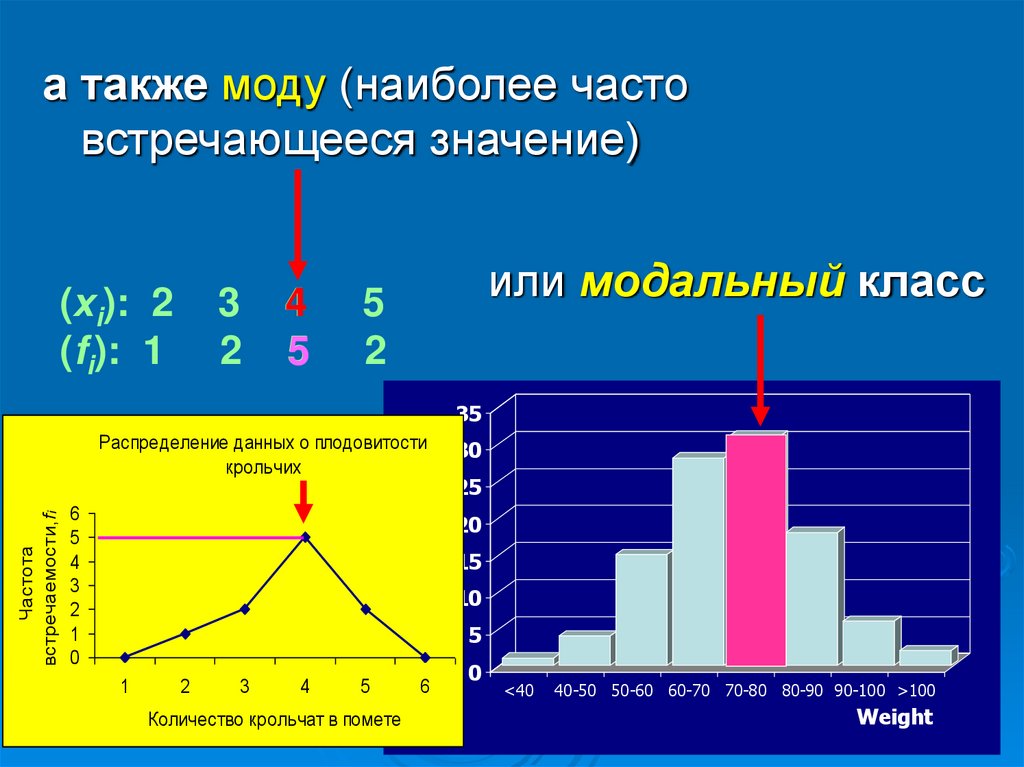
а также моду (наиболее частовстречающееся значение)
(хi): 2
(fi): 1
3
2
4
5
или модальный класс
5
2
35
Percent from total
Частота
встречаемости, fi
Распределение данных о плодовитости
крольчих
6
5
4
3
2
1
0
1
2
3
4
5
Количество крольчат в помете
6
30
25
20
15
10
5
0
<40
40-50 50-60 60-70 70-80 80-90 90-100 >100
Weight
11. Круговые диаграммы (Pie chart) (для качественных признаков)
Включают всекатегории которые
формируют
совокупность
Используют, чтобы
изобразить вклад
каждой категории
Top 10 causes of death
Heart disease
Cancer
Cerebrovascular disease
Chronic respiratory disease
Accidental death
Diabetes
Flu and Pneumonia
Alzheimer's disease
Kidney disorder
Septicemia
Counts of
% of top
deaths
10 case
Heart disease
700,142
37%
Cancer
553,768
29%
163,538
Cerebrovascular 9%
disease
123,013
6%
Chronic respiratory
disease
101,537
5%
Accidental death
71,537
4%
Diabetes
62,034
3%
53,852
Flu and Pneumonia3%
39,480
2%
Alzheimar's disease
32,238
2%
Kidney disorder100%
1,901,139
Septicemia
12. 2.2. Среднее значение и стандартное отклонение
13.
Любое нормальное распределениеможно описать с помощью всего
двух параметров:
среднего значения (µ) и
стандартного отклонения (σ)
14. ВЫБОРОЧНАЯ СРЕДНЯЯ (англ.: sample mean) (= средняя арифметическая)
1x xi
n
Percent from total
35
30
25
20
15
10
5
0
<40
40-50 50-60 60-70 70-80 80-90 90-100 >100
Weight
15. ВЗВЕШЕННАЯ СРЕДНЯЯ (англ.: Weighted mean):
x1n1 x2 n2 ... xk nkx
nk
16. СРЕДНЯЯ ГЕОМЕТРИЧЕСКАЯ (англ.: Geometric mean):
xg n x1 x2 ... xn17.
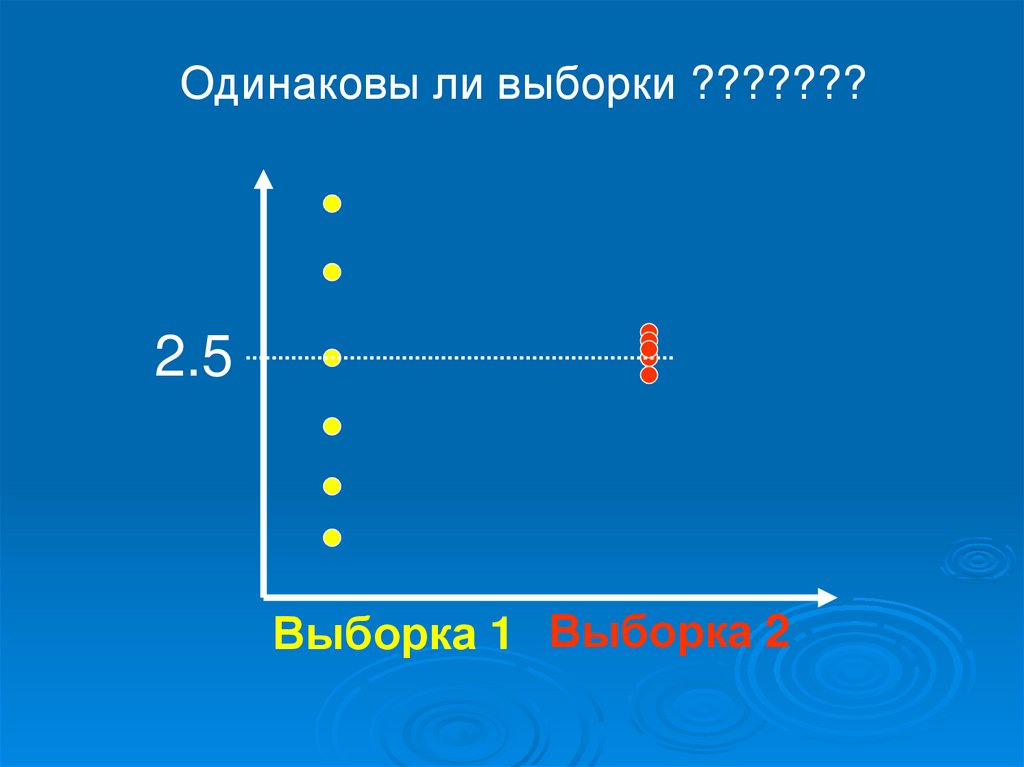
Одинаковы ли выборки ???????2.5
Выборка 1 Выборка 2
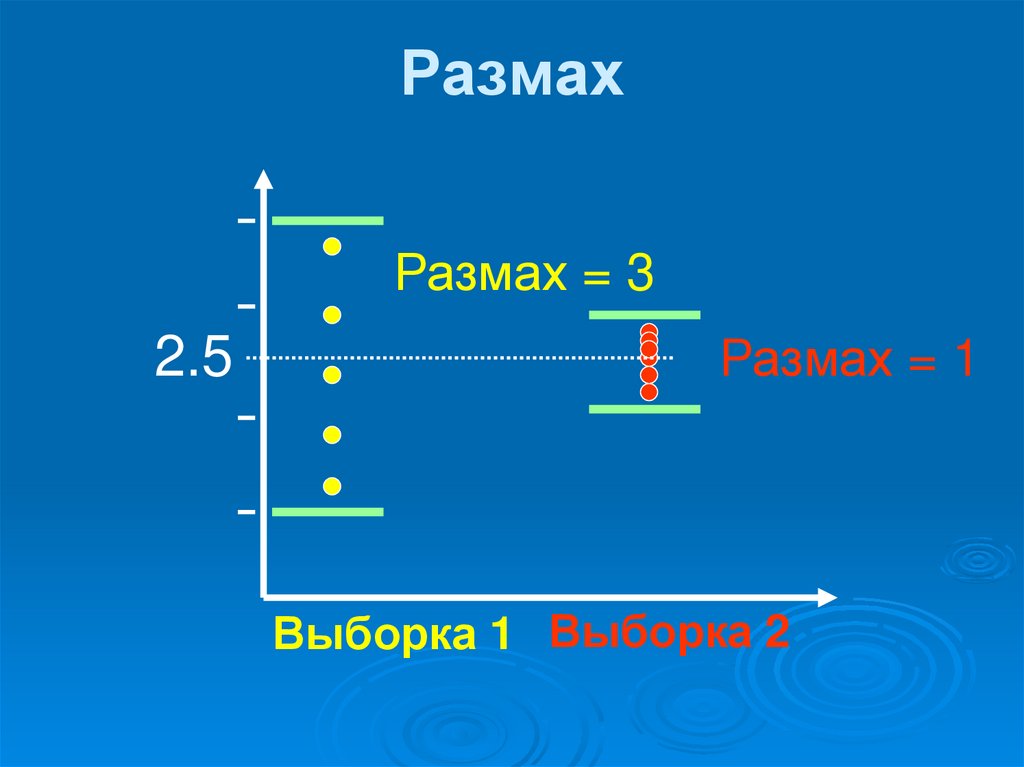
18. Размах
Размах = 32.5
Размах = 1
Выборка 1 Выборка 2
19. Размах одинаковый
10 15 20 25 30 35 40 45 5010 28 28 30 30 30 32 32 50
X = 30; размах = 40
X = 30, размах = 40
Выборки различаются!
20. Находим расстояние, на котором находится каждая единица изучаемой выборки от среднего значения:
( xi x )Избавляемся от
отрицательных значений
( xi x )
2
21. Усредняем вычисленные расстояния и получаем дисперсию (англ.: variance):
SS (sum of squares) –сумма квадратов
(
x
x
)
i
2
s
n
2
22. Извлекая корень из дисперсии, получаем стандартное отклонение (англ.: standard deviation; SD):
(x
x
)
i
s
n
2
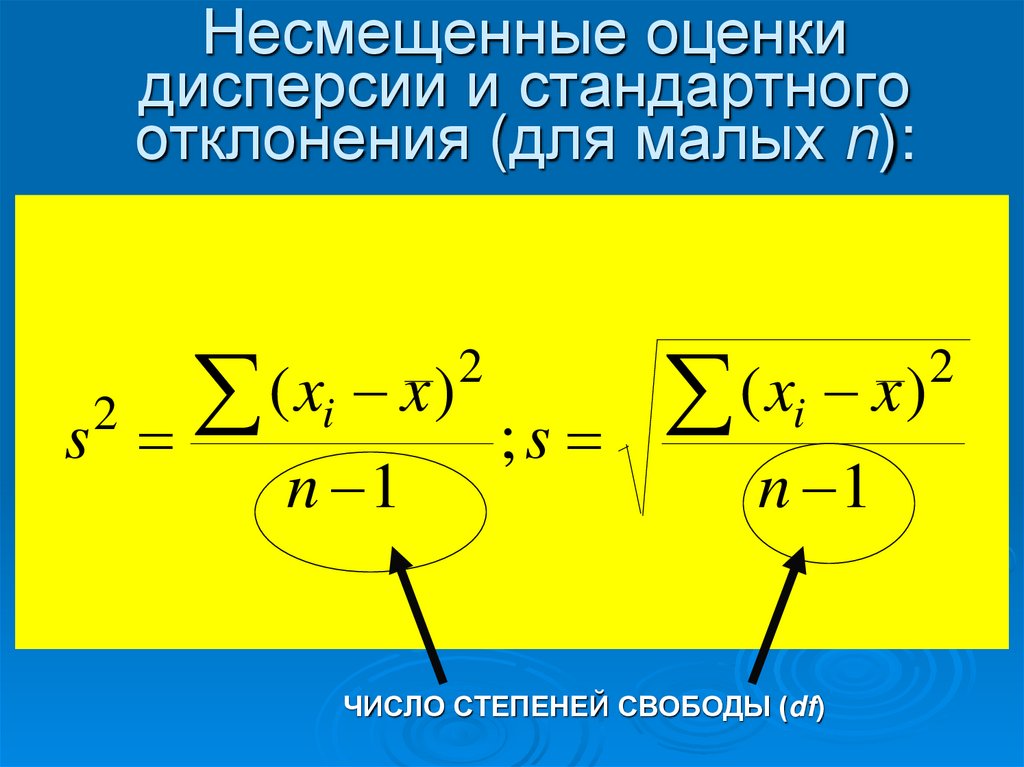
23. Несмещенные оценки дисперсии и стандартного отклонения (для малых n):
( xi x )( xi x )
s
;s
2
2
n 1
n 1
ЧИСЛО СТЕПЕНЕЙ СВОБОДЫ (df)
2
24. 2.3. Медиана и процентили
25.
Медиана (Ме; англ.: Median) значение, которое делитраспределение ровно пополам.
Для нахождения:
выстроить данные min
max
если n нечетное, ищем центральное
значение (n+1)/2
если n четное, находим среднее между
двумя центральными значениями
26. Медиана
Симметричное унимодальноеЗначение, половина
данных в совокупности
больше которого,
а половина – меньше
Средняя, мода, медиана
n – нечетное:
Симметричное бимодальное
34 36 37 39 40 41 42 43 79
n=9
Mе=X(n+1)/2=X(9+1)/2=X5=40
X=43.4
Mode Mean Median Mode
27.
МедианаСкошенное вправо распределение
Скошенное влево
распределение
Мода Медиана Средняя
Mean Median Mode
n – четное:
30 33 34 37 40 41 42 43 44 45
n=10
Mе= X(n+1)/2=X(9+1)/2=X5.5=
(X5+X6)/2 = (40+41)/2 = 40.5
X = 38.9
28. ВЫВОДЫ:
Если известно, что выборка скореевсего принадлежит к совокупности
с нормальным распределением,
для ее описания лучше
использовать выборочное среднее
и выборочное стандартное
отклонение.
29. ВЫВОДЫ:
Если же известно, чтораспределение в совокупности
отличается от нормального,
следует использовать медиану,
25-й и 75-й процентили.





















 informatics
informatics








