Similar presentations:
Первичное описание исходных данных
1. ПЕРВИЧНОЕ ОПИСАНИЕ ИСХОДНЫХ ДАННЫХ
2.
Результатыпсихологических
исследований обычно фиксируются в
протоколах. Собранный материал затем
подвергается статистической обработке.
Цель обработки - извлечение из массы
данных объективных и убедительных
выводов,
подтверждающих
или
отвергающих гипотезу исследователя,
выдвинутую на этапе планирования
исследования.
3.
Метрическиеданные
можно
представить в виде ряда значений,
называемого
статистической
совокупностью (массивом).
Каждый член этой совокупности, в
свою очередь, называется вариантой.
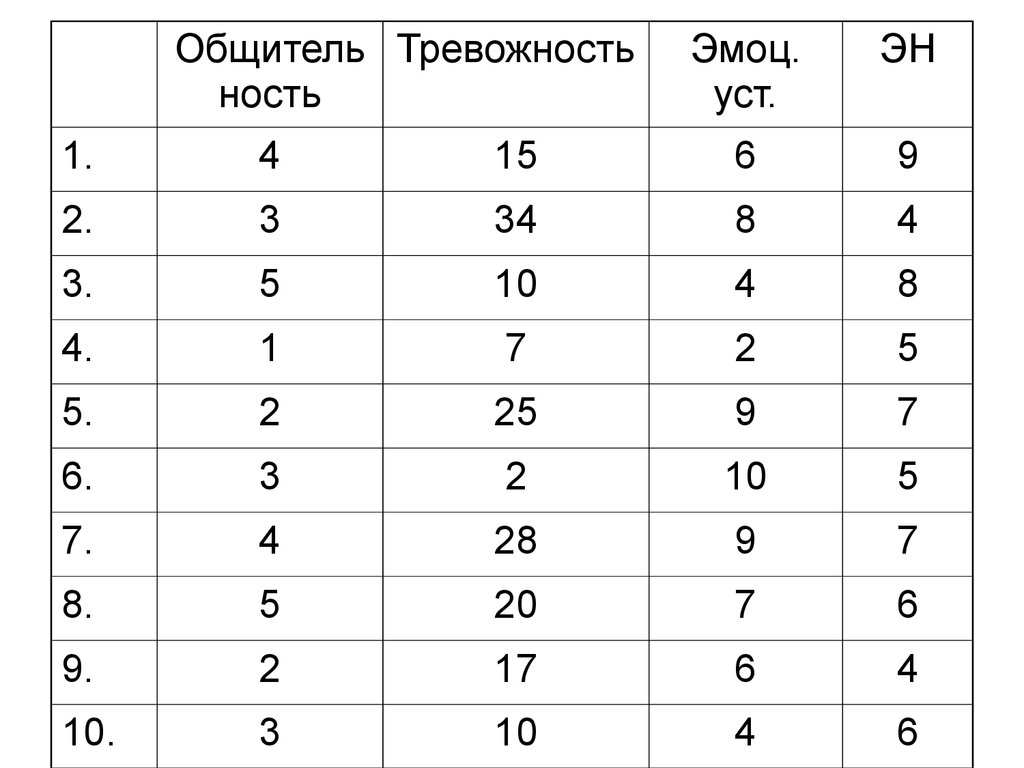
4. Сводный протокол
Первый шаг на пути статистическойобработки данных заключается в
группировке полученных результатов и
их представление в виде сводных
таблиц ( сводных протоколов):
5.
Общитель Тревожностьность
Эмоц.
уст.
ЭН
1.
4
15
6
9
2.
3
34
8
4
3.
5
10
4
8
4.
1
7
2
5
5.
2
25
9
7
6.
3
2
10
5
7.
4
28
9
7
8.
5
20
7
6
9.
2
17
6
4
10.
3
10
4
6
6. Вариационный ряд
В таблице колонка, в которуюзанесены значения первого показателя
для 10 испытуемых, представляет из
себя некоторый числовой ряд: 4 3 5 1 2
3 4 5 2 3. Расположим эту совокупность
в порядке возрастания величины
признака: 1 2 2 3 3 3 4 5 5. Получился
ранжированный ряд. Видно, что наш
признак варьирует в пределах от 1 до 5.
7.
Если же варианты расположить ввиде двойного ряда, учитывая их
повторяемость
в
исходном
ряду,
совокупность данных будет выглядеть
следующим образом:
варианты (х):
12345
повторяемость вариант (p): 1 2 3 2 2
8.
Упорядоченный ряд распределения, вкотором указана повторяемость вариант,
принадлежащих к данной совокупности,
называется
вариационным
рядом.
Числа,
которые
характеризуют
встречаемость отдельных вариант в
исходной
совокупности,
называют
весами или частотами.
9. ПОСТРОЕНИЕ ВАРИАЦИОННЫХ РЯДОВ
Известно два вида вариационных рядов:безинтервальные
и
интервальные.
Безинтервальный вариационный ряд был уже
рассмотрен ранее на примере, взятом из
таблицы.
Когда совокупность достаточно большая,
безинтервальный вариационный ряд плохо
отражает
закономерности
варьирования
признаков. В таких случаях целесообразнее
построить интервальный вариационный ряд.
10. Алгоритм построения интервальных вариационных рядов
1. Определяем число классов поформуле К = 1+3,32 lg n (по
Стерджесу) или К = 5 lg n (по Бруксу и
Краузерсу).
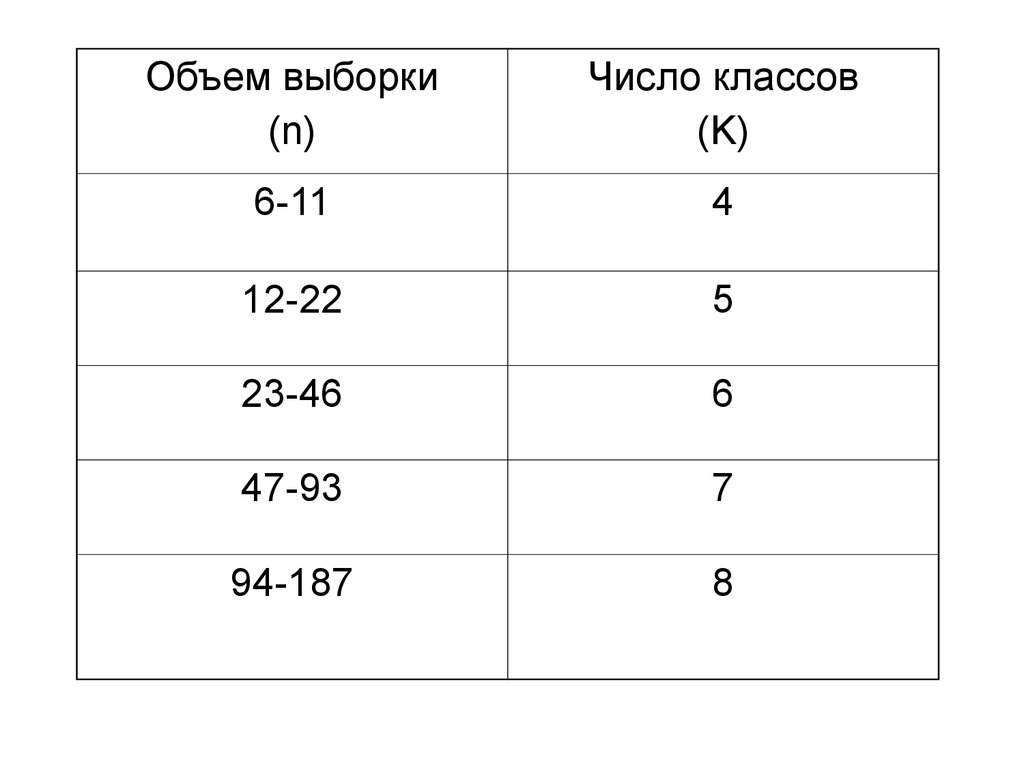
Число классов можно также
определить по таблице (по Н.А.
Плохинскому):
11.
Объем выборки(n)
Число классов
(K)
6-11
4
12-22
5
23-46
6
47-93
7
94-187
8
12.
2. Определяем разность междумаксимальным
и
минимальным
значением
вариант
ряда
R,
называемый
вариационным
размахом.
R = xmax - xmin
13.
3. Определяем ширину классовогоинтервала i по формуле
i = R/(K-1).
14.
4. Находим нижнюю границу первогокласса по формуле
xн = xmin - 0,5 i.
15.
5.Находим верхнюю границу первогокласса по формуле
xв = xmin + 0,5 i
Начальные и конечные значения
всех последующих классов можно
вычислить путем последовательного
прибавления
величины
классового
интервала, начиная от первого.
16.
Номераклассов
Классовые
интервалы
Серединные
значения классов
Частоты
Накопленные
частоты
1
xн1 - xв1
xс1
n1
n1
2
xн2=xв1 –
xв2
xс2
n2
n1+n2
3
xн3 – xв3
xс3
n3
n1+n2+n3
4
xн4 – xв4
xс4
n4
n1+n2+n3+n4
5
xн5 – xв5
xс5
n5
n1+n2+n3+n4
+n5 = n nобщее число
вариант
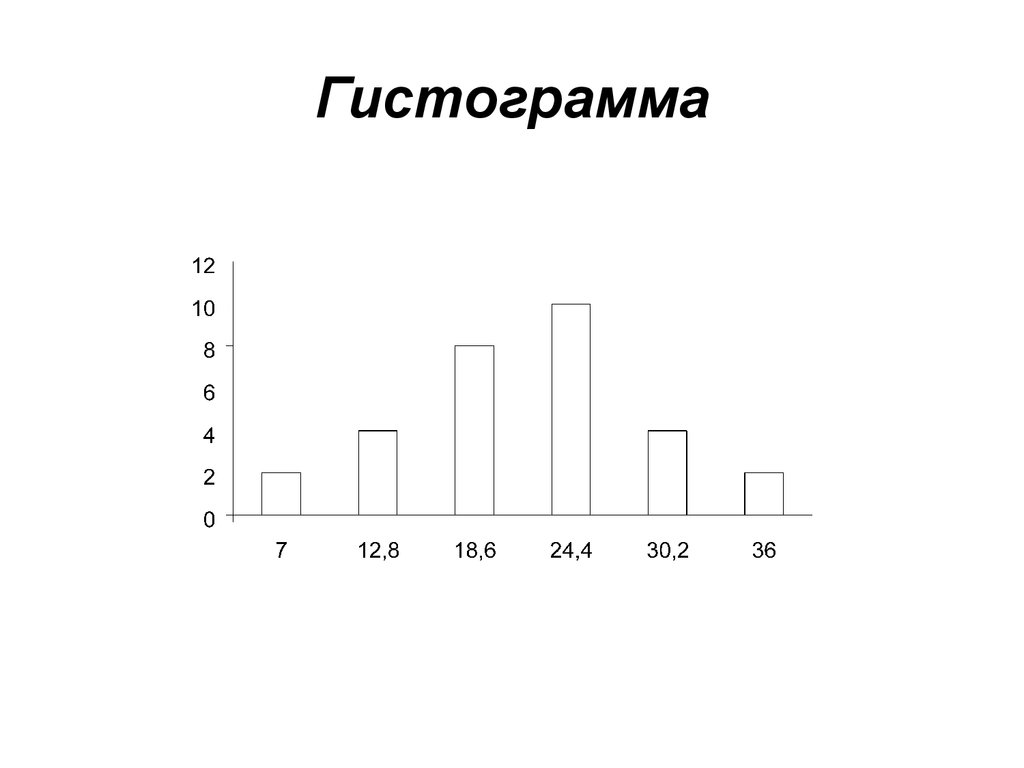
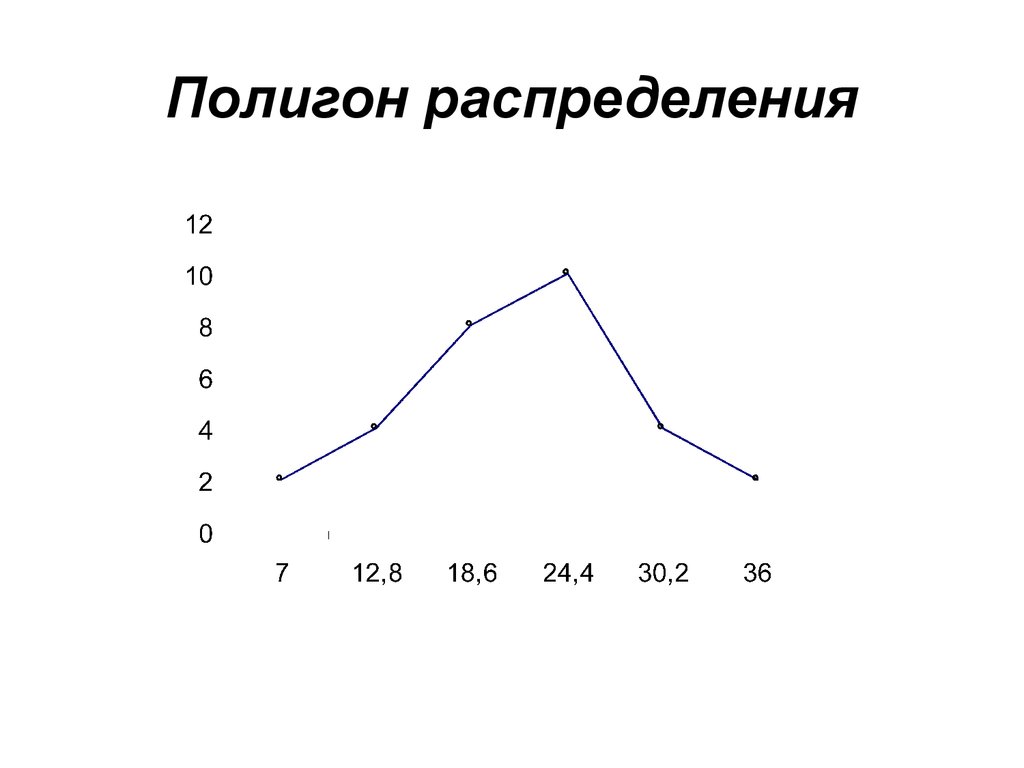
17. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ВАРИАЦИОННЫХ РЯДОВ
Чтобыпридать
большую
наглядность
закономерности
варьирования
признаков,
вариационные
ряды
принято
изображать графически в виде
гистограммы, или полигона.

















 mathematics
mathematics informatics
informatics








