Similar presentations:
Начальная обработка статистических данных
1.
Министерство образования и науки Российской ФедерацииФедеральное государственное бюджетное образовательное
учреждение высшего образования
Российский химико-технологический университет
имени Д.И. Менделеева
______________________________________
ТЕМА 5:
Начальная обработка
статистических данных
2018 г.
2.
Задачи математической статистики• Указать способы сбора и группировки статистических
данных.
• Разработать методы анализа статистических данных в
зависимости от целей исследования:
а) оценить неизвестную вероятность или неизвестную
функцию распределения;
б) оценить величину параметров распределения, вид
которого известен;
в) проверить статистические гипотезы.
• Генеральной совокупностью называют совокупность
всех изучаемых объектов, из которых производится выборка.
• Выборочной совокупностью называют совокупность
объектов, отобранных для изучения.
Объемом совокупности (генеральной или выборочной)
называют число объектов этой совокупности. Обозначение:
N – объем генеральной совокупности;
2
n – объем выборочной совокупности; ( N > n ).
3.
Вариационный рядНаблюдаемые значения признака хi называются вариантами, а
последовательность вариант, записанных в возрастающем порядке, вариационным рядом.
Частотой mi варианты xi называется чиcло объектов выборки, у
которых наблюдалось значение признака xi.
mi
*
Относительной частотой
pi
варианты xi называется отношение
n
Размахом варьирования R называется разность между наибольшей и
наименьшей вариантами
Модой Mо называют варианту, которая имеет наибольшую частоту.
Медианой Mе называют варианту, которая делит вариационный ряд на
две части равные по числу вариант. Если объем выборки – четное число
n=2k, то
xk xk 1
Me
2
Например, для ряда 2, 3, 5, 6, 7 медиана – 5, а для ряда 2, 3, 5, 6, 7, 9
медиана равна (5+6):2=5,5.
3
4.
Статистическим распределением выборки(дискретный статистический ряд) называется
перечень вариант в возрастающем порядке и
соответствующих им частот и/или относительных
частот (Таблица 5.1.).
Таблица 5.1. Статистическое распределение
выборки
xi
x1
x2
x3
…
xk
mi
m1
m2
m3
…
mk
Pi*
P1*
P2*
P3*
…
Pk*
m1 m2 mk n;
1
2
k
p p p 1
4
5.
Полигоном частот называется ломаная линия,соединяющая точки с координатами (xi;mi).
Полигоном относительных частот называется
ломаная линия, соединяющая точки с координатами (xi;pi*).
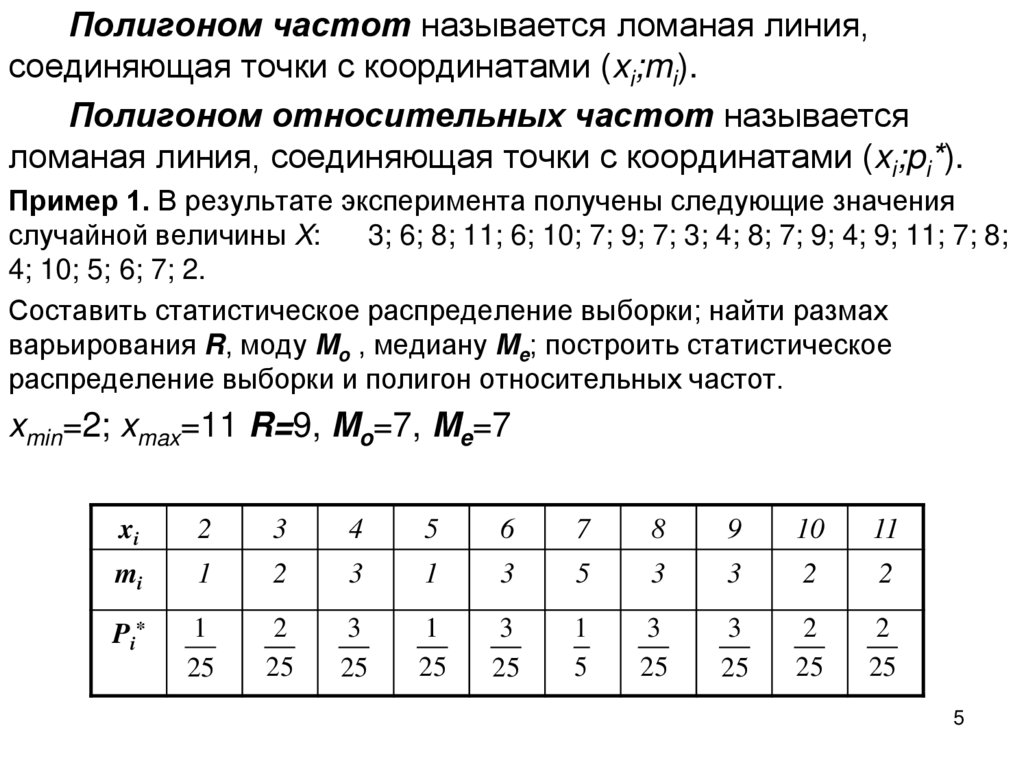
Пример 1. В результате эксперимента получены следующие значения
случайной величины X:
3; 6; 8; 11; 6; 10; 7; 9; 7; 3; 4; 8; 7; 9; 4; 9; 11; 7; 8;
4; 10; 5; 6; 7; 2.
Составить статистическое распределение выборки; найти размах
варьирования R, моду Mo , медиану Me; построить статистическое
распределение выборки и полигон относительных частот.
xmin=2; xmax=11 R=9, Mo=7, Me=7
xi
2
3
4
5
6
7
8
9
10
11
mi
1
2
3
1
3
5
3
3
2
2
Pi*
1
25
2
25
3
25
1
25
3
25
1
5
3
25
3
25
2
25
2
25
5
6.
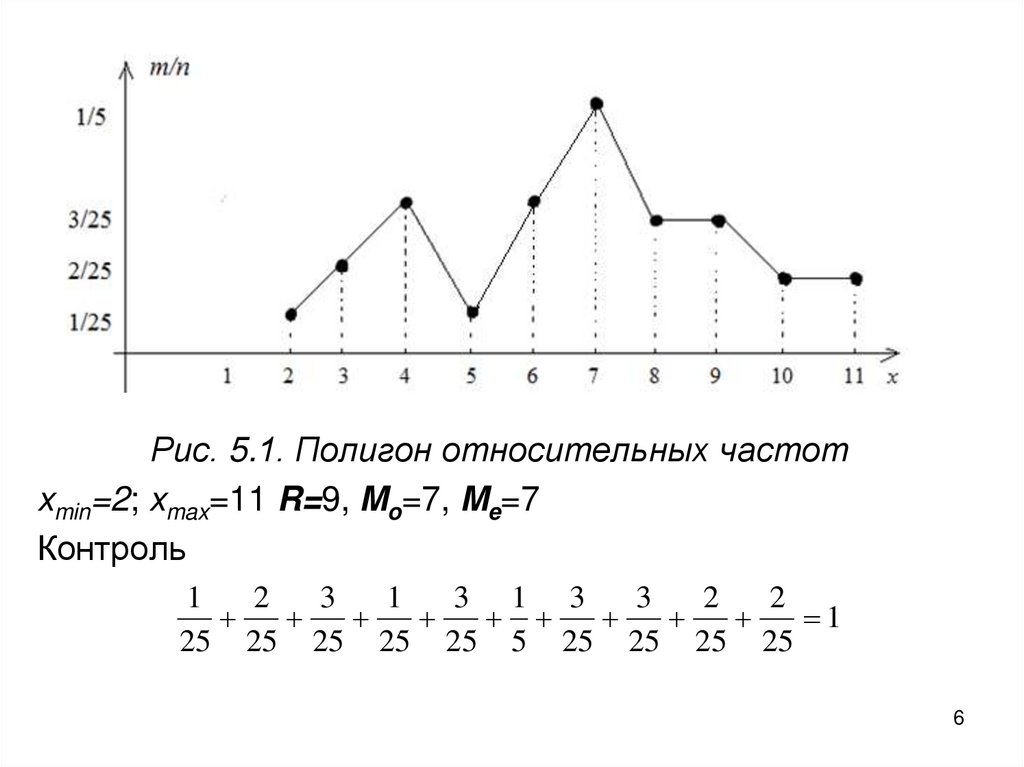
Рис. 5.1. Полигон относительных частотxmin=2; xmax=11 R=9, Mo=7, Me=7
Контроль
1
2
3
1
3 1 3
3
2
2
1
25 25 25 25 25 5 25 25 25 25
6
7.
Интервальный статистический ряд. ГистограммаВ случае непрерывного признака Х и большого объема
выборки, статистическое распределение задают
интервальным статистическим рядом, который
представляет собой упорядоченную последовательность
интервалов
[аi; аi+1), i = 1,2,…k с указанием частоты mi и/или
относительной частоты интервала (Таблица 5.2).
Таблица 5.2. Интервальный статистический ряд
№ интервала
[аi ; аi+1)
mi
Pi*
1
[а1 ; а2)
m1
Pi*
2
[а2 ; а3)
m2
Pi*
…
…
…
…
k
[аk ; аk+1)
mk
Pi*
7
8.
Частотой интервала mi называют число значенийпризнака, попавших в i-ый интервал.
Относительной частотой интервала называют число
mi
p
n
*
i
Число интервалов k не должно быть большим, но и не
малым. Обычно берут 7≤ k ≤ 10. При большом объеме
выборки число интервалов вычисляют по формуле .
k 1 3,322 lg n
Результат округляют до целых значений.
Графическим изображением интервального статистического
ряда является гистограмма частот (гистограмма
относительных частот).
8
9.
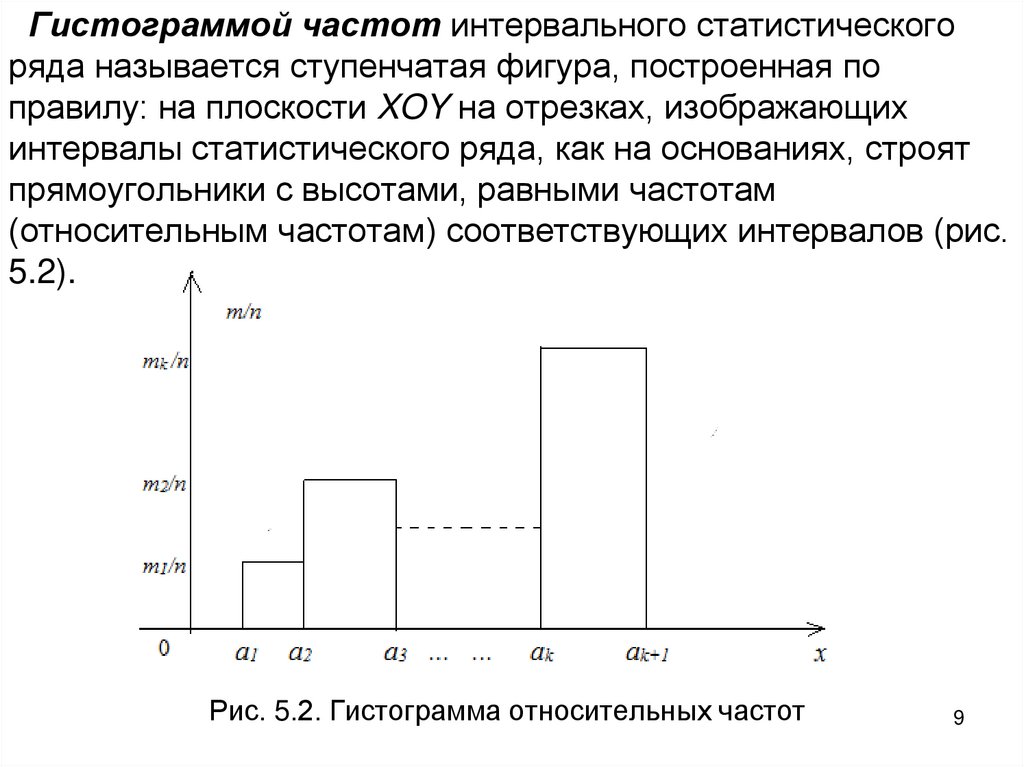
Гистограммой частот интервального статистическогоряда называется ступенчатая фигура, построенная по
правилу: на плоскости XOY на отрезках, изображающих
интервалы статистического ряда, как на основаниях, строят
прямоугольники с высотами, равными частотам
(относительным частотам) соответствующих интервалов (рис.
5.2).
Рис. 5.2. Гистограмма относительных частот
9
10.
Статистическая функция распределенияСтатистической или эмпирической функцией
распределения (или функцией распределения выборки)
называется функция
m
~
F ( x)
x
n
задающая для каждого действительного числа х
относительную частоту события (X < x).
Свойства статистической функции распределения
~
1.
0 F ( x) 1;
~
2.
функция;
F~ ( x ) - неубывающая
~
3.
F ( ) 0; F ( ) 1.
Эмпирическая функция распределения выборки служит для
оценки теоретической функции распределения признака
генеральной совокупности, так как при увеличении объема
выборки она по вероятности стремится к теоретической
10
функции распределения.
11.
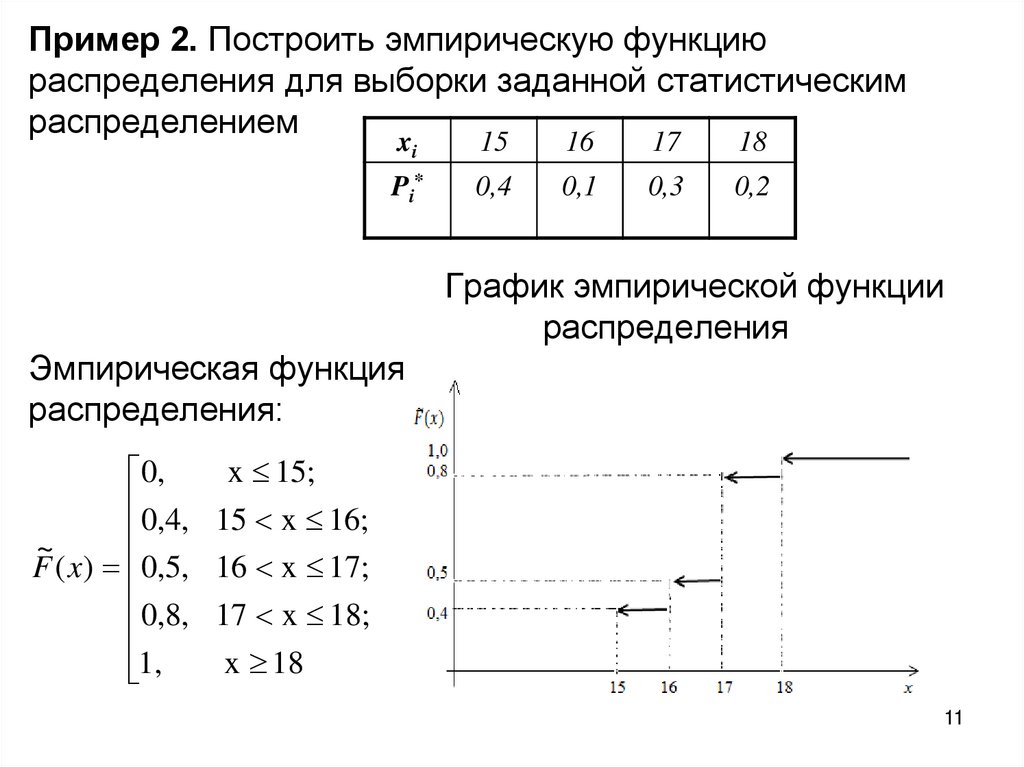
Пример 2. Построить эмпирическую функциюраспределения для выборки заданной статистическим
распределением
xi
15
16
17
18
Pi*
0,4
0,1
0,3
0,2
График эмпирической функции
распределения
Эмпирическая функция
распределения:
x 15;
0,
0,4, 15 x 16;
~
F ( x) 0,5, 16 x 17;
0,8, 17 x 18;
1,
x 18
11







 mathematics
mathematics








