Similar presentations:
Статистические методы обработки данных
1.
Лекционный курс по дисциплине:«Статистические методы обработки
данных»
Что нужно знать, чтобы получить на
экзамене от 4 до 6 баллов.
2.
Шкалы измеренийНоминальная шкала (шкала наименований). Эта шкала
используется только для того, чтобы отнести объект или
индивидуум в определенный класс (Распределения учащихся по классам, по
половому признаку, по месту жительства, по видам спорта)
Порядковая шкала. Эта шкала в дополнение к функции
отнесения объектов в определенный класс также
упорядочивает классы по степени выраженности
заданного свойства (учащихся ранжировать по количеству правильно выполненных тестовых заданий)
Интервальная шкала. Эта шкала позволяет не только
классифицировать и упорядочивать объекты и
индивидуумы, но и количественно оценивать различие
между классами (Шкалы на большинстве физических приборов Шкала коэффициента интеллекта IQ)
Шкала отношений. Эта шкала отличается от
интервальной шкалы лишь тем, что в ней задано
абсолютное начало отсчета (отношений являются меры длины (м, см и т. д.) и массы (кг, г и т.
д.). Предмет длиной 100 см вдвое длиннее предмета длиной 50 см.)
International Sakharov Environmental University
2
3.
Математическое ожиданиеЕсли совокупность случайных величин задана в виде
набора дискретных значений, то математическое
ожидание случайной величины определяется как среднее
значение по выборке:
N
p i xi
i 1
1 N
xi
N i 1
International Sakharov Environmental University
3
4.
ДисперсияЧисловой характеристикой, показывающей степень
разброса значений случайной величины относительно
математического ожидания, называется дисперсия
N
xi pi
2
2
i 1
N
1
2
2
xi
N i 1
International Sakharov Environmental University
4
5.
Среднеквадратическое отклонениеПоскольку дисперсия имеет размерность квадрата
случайной величины, то для характеристики меры
рассеяния значений случайной величины относительно
математического ожидания пользуются
среднеквадратическим отклонением σ, равным значению
квадратного корня из дисперсии:
2
International Sakharov Environmental University
5
6.
Выборочное среднее, дисперсия исреднеквадратическое отклонение
Выборочное среднее, представляющее собой оценку
математического ожидания генеральной совокупности:
1 n
x mx xi
n i 1
Выборочная дисперсия, служащая несмещенной оценкой
дисперсии генеральной совокупности:
1 n
2
s
xi x
n 1 i 1
2
Выборочное среднеквадратическое (стандартное)
отклонение:
s s2
International Sakharov Environmental University
6
7.
Понятие закона распределенияПолное описание случайной величины дается
законом распределения, который устанавливает
зависимость между возможными значениями
случайной величины и их вероятностями
International Sakharov Environmental University
7
8.
Задание закона распределенияЗакон распределения случайной величины можно
задать в виде графика, таблицы или аналитического
выражения:
Xi
X1
X2
X3
X4
X5
Pi
P1
P2
P3
P4
P5
P = f(x)
International Sakharov Environmental University
8
9.
Нормальное распределениеНормальное распределение величины x
описывается следующей функцией:
P (x)
( x m )2
ex p
2
2
2
2
1
Характеристики распределения Гаусса:
оно симметрично относительно m
имеет максимум равный 1
монотонно убывает при возрастании x m
2 2
International Sakharov Environmental University
9
10.
Нормальное распределениеФункция распределения, показывающая вероятность
случайной величине принять значение меньшее x,
определяется выражением
International Sakharov Environmental University
10
11.
Нормальное распределениеInternational Sakharov Environmental University
11
12.
Нормальное распределениеInternational Sakharov Environmental University
12
13.
Нормальное распределениеInternational Sakharov Environmental University
13
14.
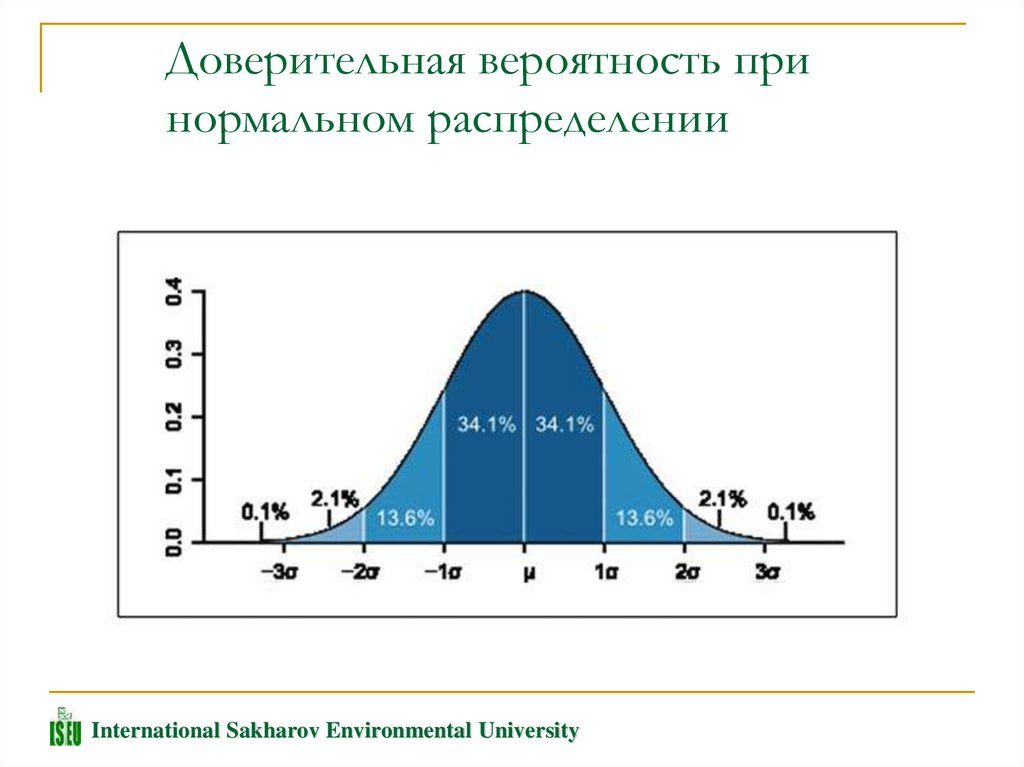
Доверительная вероятность принормальном распределении
Если случайная величина распределена по
нормальному закону с математическим
ожиданием и средним квадратическим
отклонением , то вероятности ее
попадания в интервалы между ( s + s) и
( s - s); между ( s + 2 s) и ( s - 2 s);
между ( s + 3 s) и ( s - 3 s) равны
соответственно: 0,683; 0,955; 0,997
International Sakharov Environmental University
15.
Доверительная вероятность принормальном распределении
International Sakharov Environmental University
16.
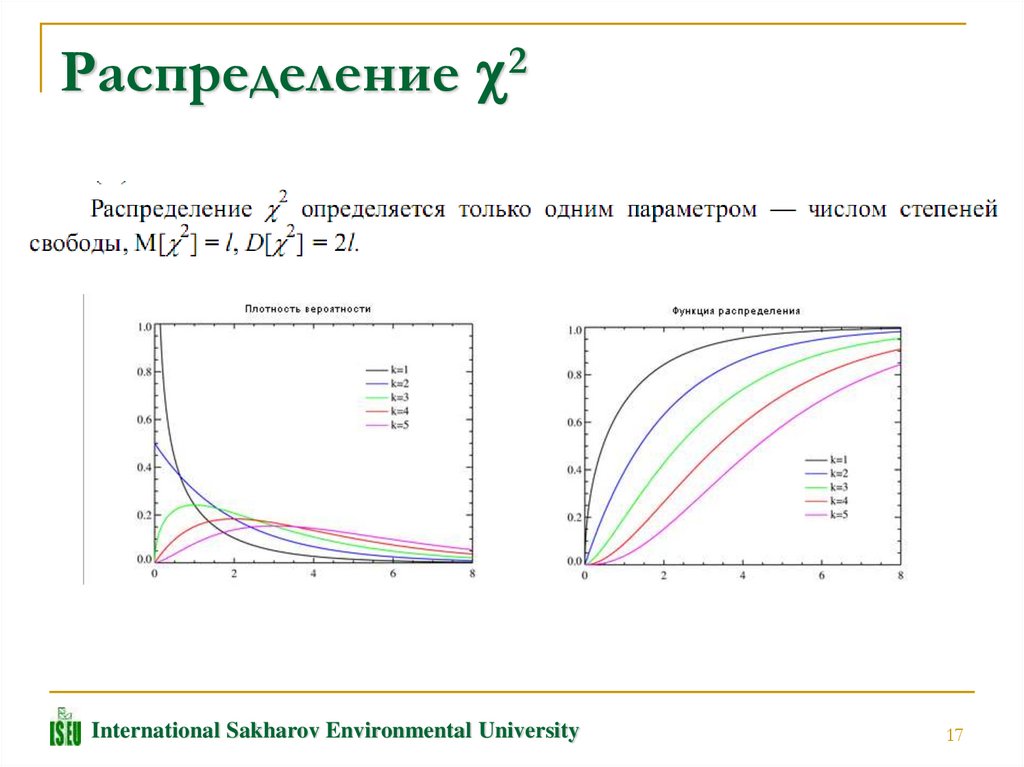
Распределение 2International Sakharov Environmental University
16
17.
Распределение 2International Sakharov Environmental University
17
18.
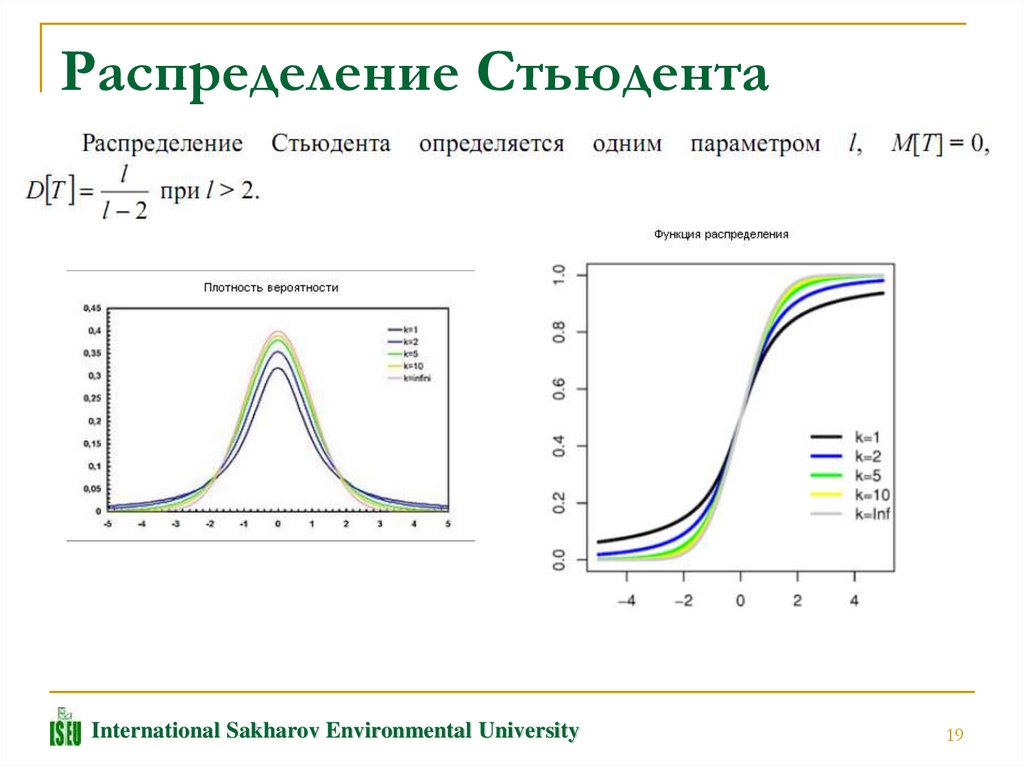
Распределение СтьюдентаInternational Sakharov Environmental University
18
19.
Распределение СтьюдентаInternational Sakharov Environmental University
19
20.
Проверка статистических гипотезДля того чтобы иметь основания принять или
отвергнуть рассматриваемую гипотезу
необходимо выработать некоторый критерий,
который называют критерием согласия
проверяемой гипотезы с результатами
эксперимента
International Sakharov Environmental University
20
21.
Критерий согласия 2 (хи-квадрат)В качестве меры расхождения между
эмпирическим и теоретическим законами
распределения Пирсоном была предложена
статистика
m
n k np k
k 1
np k
2
2
Здесь: m ─ число значений, принятых случайной величиной, n –
общее число наблюдений, pk ─ вероятность появления k-го значения
в теоретическом законе распределения
International Sakharov Environmental University
21
22.
Непараметрический критерийВилкоксона для проверки однородности
двух независимых выборок
Большинство непараметрических критериев
основано на использовании рангов наблюдений.
Рангом наблюдения называют тот номер,
который получит это наблюдение в
упорядоченной совокупности всех данных
после их упорядочения по определенному
правилу, например от меньших значений к
большим или наоборот.
International Sakharov Environmental University
22
23.
Ранги и ранжированиеТрудности в назначении рангов возникают, если
среди элементов выборки встречаются
совпадающие. В этом случае обычно
используют средние ранги.
International Sakharov Environmental University
23
24.
Непараметрический критерийВилкоксона
В критерии Вилкоксона в качестве в качестве статистики
используется случайная величина
W R 1 R 2 ... R n
Здесь Rj – ранги наблюдений второй выборки в общей
объединенной выборке.
International Sakharov Environmental University
24
25.
Непараметрический критерийВилкоксона
Для проверки с уровнем значимости α гипотезы H0 об
однородности выборок при альтернативной гипотезе H1:
Fx(x) > Fy(y) по имеющимся таблицам находят верхнее
критическое значение wв(α, m, n) статистики W, т. е. такое
значение, для которого
P W w в , m , n
Гипотезу об однородности выборок следует отвергнуть с
уровнем значимости α, если рассчитанное значение
статистики W больше критического значения.
International Sakharov Environmental University
25
26.
Критерий Вилкоксона для проверкиоднородности двух зависимых выборок
Порядок применения критерия следующий:
1.
Вычисляются абсолютные разности наблюдений в
паре:
z i x i 2 x i1 ,
2.
i 1,..., n
Осуществляется ранжирование этих разностей в
порядке возрастания и каждому значению ранга
присваивается знак его разности.
International Sakharov Environmental University
26
27.
Критерий Вилкоксона для проверкиоднородности двух зависимых выборок
3.
Вычисляется сумма значений рангов, которая
образует статистику T.
4.
Проверяется, принадлежит ли вычисленное
значение T критической области, границы которой
находятся по таблицам процентных точек
распределения Вилкоксона для парных выборок.
International Sakharov Environmental University
27
28.
Критерий Вилкоксона для проверкиоднородности двух зависимых выборок
Если вычисленное значение статистики T
n n 1
T t , n или T
t ,n
2
2
2
то гипотеза об однородности двух выборок отклоняется при
уровне значимости α в пользу альтернативной гипотезы H1:
выборки неоднородны.
При альтернативной гипотезе H1: распределение разности
смещено вправо относительно нуля, гипотеза об
однородности отклоняется, если вычисленное значение
статистики T превышает критическое значение
T t , n
International Sakharov Environmental University
28
29.
Однофакторный дисперсионный анализ.Проверка гипотезы о влиянии фактора
на исследуемую величину
Рассмотрим простейший случай дисперсионного анализа,
когда изучается влияние на исследуемую величину
какого-либо одного фактора A. Будем считать, что фактор
A изучается на k уровнях A1, A2, ..., Ak. Пусть для
простоты рассмотрения на каждом уровне производится
одинаковое число n наблюдений исследуемой величины.
International Sakharov Environmental University
29
30.
Проверка гипотезы о влиянии фактора наисследуемую величину
Оценка генерального среднего
1 n k
x ..
x ij
n k i 1 j 1
Несмещенная оценка дисперсии генеральной совокупности
1
s
x ij x ..
nk 1 i 1 j 1
n
2
k
2
2
International Sakharov Environmental University
30
31.
Проверка гипотезы о влиянии фактора наисследуемую величину
При справедливости нулевой гипотезы любая из
выборочных дисперсий дает одинаково хорошую оценку.
Поэтому в качестве оценки дисперсии генеральной
совокупности возьмем среднее выборочных дисперсий.
Эта оценка называется внутри групповой дисперсией:
k
n
2
1
1
2
s0
x ij x . j
k j 1 n 1 i 1
International Sakharov Environmental University
31
32.
Проверка гипотезы о влиянии фактора наисследуемую величину
Оценим теперь дисперсию совокупности по
выборочным средним. Поскольку мы предположили,
что все выборки извлечены из одной совокупности, то
стандартное отклонение выборочных средних будет
служить оценкой ошибки среднего:
s
sx
n
Отсюда находим межгрупповую оценку дисперсии
k
s ns n
2
A
2
x
j 1
x . x ..
2
j
k 1
International Sakharov Environmental University
32
33.
Проверка гипотезы о влиянии фактора наисследуемую величину
В результате задача проверки гипотезы H0 сводится к
проверке гипотезы о равенстве дисперсий sA2 и s02. При
справедливости допущения о нормальном распределении
случайных величин εij отношение
s A2
F 2
s0
в случае справедливости нулевой гипотезы подчиняется
F-распределению с l1 = k-1 и l2 = k(n-1) числом степеней
свободы.
International Sakharov Environmental University
33
34.
Проверка гипотезы о влиянии фактора наисследуемую величину
Влияние фактора A на исследуемый признак считается
значимым с уровнем значимости α, если
s A2
f k 1; k n 1 ;
2
s0
т. е. когда расчетное значение статистики F превышает
значение α-процентной точки распределения Фишера.
International Sakharov Environmental University
34
35.
Проверка гипотезы о влиянии фактора наисследуемую величину
Результаты дисперсионного анализа в общем случае обычно
представляют в виде следующей таблицы
Источник
дисперсии
Степени
свободы
Сумма
квадратов
Между
группами
С К А n j x . j x ..
Внутри групп
С К 0 x ij x . j
n
s A2
i 1
k
n
2
j 1 i 1
С К п x ij x ..
k
Полная
k 1
2
Дисперсии
n
j 1 i 1
k
n j k
j 1
2
k
n 1
j 1
s02
F
отношение
СК А
k 1
СК 0
k
n k
j 1
s A2
F 2
s0
j
j
International Sakharov Environmental University
35
36.
Двухфакторный дисперсионныйанализ. Виды взаимосвязи между
двумя факторами
Пусть на исследуемую величину могут оказывать
влияние два фактора A и B, каждый из которых
имеет конечное число уровней. При этом ставится
вопрос, как влияют и влияют ли вообще эти
факторы на исследуемую величину. Здесь уже
необходимо уделить внимание способу
взаимосвязи факторов. Для большинства
практических задач достаточно ограничиться двумя
способами: пересечением и группировкой.
International Sakharov Environmental University
36
37.
Виды взаимосвязи между двумяфакторами
Два фактора A и B
называются
пересекающимися, если в
плане эксперимента
предусмотрены все
возможные сочетания
факторов.
International Sakharov Environmental University
37
38.
Виды взаимосвязи между двумяфакторами
Фактор B группируется фактором A, если каждый
уровень фактора B сочетается не более, чем с
одним уровнем фактора A.
International Sakharov Environmental University
38
39.
Двухфакторный дисперсионныйанализ с пересечением уровней
Рассматривая совокупность данных как одну
выборку из генеральной совокупности, получим
оценку генерального среднего в виде
1 k n m
x ...
x ijt
knm i 1 j 1 t 1
и несмещенную оценку дисперсии генеральной
совокупности
k
n
m
2
1
2
2
s
x ijt x ...
kn m 1 i 1 j 1 t 1
International Sakharov Environmental University
39
40.
Двухфакторный дисперсионныйанализ с пересечением уровней
Входящую в оценку дисперсии генеральной
совокупности сумму квадратов можно представить в
виде суммы четырех отдельных сумм квадратов СКA,
СКB, СКAB, СК0:
характеризует разброс наблюдаемых значений между столбцами
(уровнями фактора A) таблицы данных
k
С К А n m x i .. x ...
2
i 1
характеризует разброс наблюдаемых значений между строками
(уровнями фактора B) таблицы
С К В m k x . j . x ...
n
2
j 1
International Sakharov Environmental University
40
41.
Двухфакторный дисперсионныйанализ с пересечением уровней
характеризует эффект взаимодействия факторов
С К А В m x ij . x i .. x . j . x ...
k
n
2
i 1 j 1
остаточная сумма квадратов
С К 0 x ijt x ij .
k
n
m
2
i 1 j 1 t 1
International Sakharov Environmental University
41
42.
Двухфакторный дисперсионныйанализ с пересечением уровней
С учетом числа степеней свободы каждой суммы
квадратов, получим следующие выражения для
оценок дисперсий:
1
1
2
sA
СК А
k 1
s
1
s
СК B
n 1
1
s
СК0
kn m 1
2
B
2
AB
k 1 n 1
С К АВ
2
0
International Sakharov Environmental University
42
43.
Двухфакторный дисперсионныйанализ с пересечением уровней
Гипотеза H0 : α1 = α2 = ... = αk = 0 проверяется с
помощью отношения
s A2
F 2
s0
Гипотеза H0 : β1 = β2 = ... = βn = 0 проверяется с
помощью отношения
2
B
2
0
s
F
s
International Sakharov Environmental University
43
44.
Двухфакторный дисперсионныйанализ с пересечением уровней
Гипотеза об отсутствии взаимодействия между
факторами (гипотеза об аддитивности) проверяется
с помощью отношения
2
s AB
F 2
s0
International Sakharov Environmental University
44
45.
Двухфакторный дисперсионныйанализ с пересечением уровней
Результаты дисперсионного анализа представляют
следующей таблицей
International Sakharov Environmental University
45
46.
Двухфакторный дисперсионныйанализ с группировкой уровней
Фактор B группируется фактором A, если каждый
уровень фактора B сочетается не более, чем с
одним уровнем фактора A.
International Sakharov Environmental University
46
47.
Двухфакторный дисперсионныйанализ с группировкой уровней
Результаты дисперсионного анализа оформляются в
виде следующей таблицы
International Sakharov Environmental University
47
48.
Двухфакторный дисперсионныйанализ с группировкой уровней
Статистики для проверки гипотез имеют вид:
для гипотезы H0: все αi = 0
s A2
F 2
s0
для гипотезы H0: σb(a) = 0
F
s B2 A
s02
International Sakharov Environmental University
48
49.
Задачи корреляционного анализаВ математическом анализе зависимость между
величинами x и y выражается функцией y = f(x), где
каждому значению x соответствует одно и только одно
значение y. Такая связь называется функциональной.
Для случайных величин X и Y такую зависимость можно
установить не всегда. Связь между случайными
величинами является не функциональной, а случайной
(стохастической), при которой изменение переменной X
влияет на значения переменной Y через изменение закона
распределения случайной величины Y.
International Sakharov Environmental University
49
50.
Задачи корреляционного анализаТаким образом задача корреляционного анализа
исследование наличия взаимосвязей между отдельными
группами переменных и установление тесноты (силы)
связи между ними.
International Sakharov Environmental University
50
51.
Измерители парной статистическойсвязи. Корреляционное отношение
Очевидно, что 0 ≤ ρ2yx ≤ 1. Стремление ρ2yx к нулю
означает, что доля дисперсии, обусловленная
функциональной связью, очень мала. Наоборот,
стремление ρ2yx к единице показывает, что случайными
изменениями Y можно пренебречь и вся дисперсия
обусловлена функциональной зависимостью Y = ϕ(X).
Аналогично определяется квадрат корреляционного
отношения ρ2xy переменной X по Y. Однако между ρ2yx и
ρ2xy нет какой-либо простой зависимости.
International Sakharov Environmental University
51
52.
Измерители парной статистическойсвязи. Корреляционное отношение
Положительный корень из ρ2yx носит название
корреляционного отношения, которое является
показателем статистической связи между двумя
случайными величинами X и Y для самой общей
ситуации, когда закон распределения системы (X,Y)
является произвольным.
International Sakharov Environmental University
52
53.
Измерители парной статистическойсвязи
В общем случае показатели ρ2xy и r2 связаны
неравенствами 0 r 2 xy2 1
При этом возможны следующие варианты:
r2 = ρ2yx=1 только тогда, когда имеется строгая
линейная функциональная зависимость Y от X
r2 < ρ2yx=1 только тогда, когда имеется строгая
нелинейная функциональная зависимость Y от X
r2 = ρ2yx<1 только тогда, когда зависимость Y от X
строго линейна, но нет функциональной зависимости
r2 < ρ2yx<1 указывает на то, что не существует
функциональной зависимости, а некоторая
нелинейная кривая “подходит” лучше, чем
“наилучшая” прямая линия.
International Sakharov Environmental University
53
54.
Измерители парной статистическойсвязи
Таким образом, в качестве показателя статистической
связи между двумя случайными количественными
переменными X и Y следует выбрать корреляционное
отношение ρyx (или ρxy) , если закон распределения
системы (X,Y) вызывает сомнение. Если же можно с
большой степенью уверенности считать закон
распределения системы (X,Y) нормальным, то вместо
корреляционного отношения следует использовать
коэффициент корреляции r.
International Sakharov Environmental University
54
55.
Регрессионный анализInternational Sakharov Environmental University
55
56.
Основные понятия регрессионного анализаДля математического описания статистических связей
между изучаемыми переменными величинами следует
решить следующие задачи:
подобрать класс функций, в котором целесообразно
искать наилучшую (в определенном смысле)
аппроксимацию интересующей зависимости;
найти оценки неизвестных значений параметров,
входящих в уравнения искомой зависимости;
установить адекватность полученного уравнения
искомой зависимости;
выявить наиболее информативные входные
переменные.
International Sakharov Environmental University
56
57.
Простая линейная регрессияПростейшей моделью регрессии является простая
(одномерная, однофакторная, парная) линейная модель,
имеющая следующий вид:
yi a bxi i
i 1, ..., n
где εi – некоррелированные между собой случайные
величины (ошибки), имеющие нулевые математические
ожидания и одинаковые дисперсии σ2, a и b – постоянные
коэффициенты (параметры), которые необходимо
оценить по измеренным значениям отклика yi.
International Sakharov Environmental University
57
58.
Простая линейная регрессияДля нахождения оценок параметров a и b линейной
регрессии, определяющих наиболее удовлетворяющую
экспериментальным данным прямую линию:
fa x a bx
применяется метод наименьших квадратов.
Согласно методу наименьших квадратов оценки
параметров a и b находят из условия минимизации
суммы квадратов отклонений значений yi по вертикали
от “истинной” линии регрессии:
n
n
D yi a b xi i2
2
i 1
International Sakharov Environmental University
i 1
58
59.
Простая линейная регрессияДля минимизации D приравняем к нулю частные
производные по a и b:
n
D
2 yi a b xi 1 0
a
i 1
n
D
2 yi a b xi xi 0
b
i 1
В результате получим следующую систему уравнений
для нахождения оценок a и b:
y a bx 0
n
i 1
n
i
i
y a bx x 0
i 1
i
i
i
International Sakharov Environmental University
59
60.
Простая линейная регрессияРешение этих двух уравнений дает:
b
n
n
n
i 1
i 1
i 1
n xi y i xi y i
n xi x i
i 1
i 1
n
n
2
2
1 n
b n
a yi xi
n i 1
n i 1
International Sakharov Environmental University
60
61.
Простая линейная регрессияВыражения для оценок параметров a и b можно
представить также в виде:
n
n
x y nxy x x y y
b i n1
i
i
x nx
2
i 1
i
i 1
2
i
n
i
n xi x
a y bx
2
i 1
International Sakharov Environmental University
61
62.
Простая линейная регрессияТогда эмпирическое уравнение регрессионной прямой Y
на X можно записать в виде:
y a bx y b x x
International Sakharov Environmental University
62
63.
Простая линейная регрессияНесмещенная оценка дисперсии σ2 отклонений значений
yi oт подобранной прямой линии регрессии дается
выражением (остаточная дисперсия)
2
1 n
s
yi a b xi
n 2 i 1
2
0
International Sakharov Environmental University
63
64.
Проверка значимости линии регрессииНайденная оценка b ≠ 0 может быть реализацией
случайной величины, математическое ожидание которой
равно нулю, т. е. может оказаться, что никакой
регрессионной зависимости на самом деле нет.
Чтобы разобраться с этой ситуацией, следует проверить
гипотезу Н0: b = 0 при конкурирующей гипотезе Н1: b ≠ 0.
Проверку значимости линии регрессии можно провести с
помощью дисперсионного анализа.
International Sakharov Environmental University
64
65.
Проверка значимости линии регрессииВычисления по проверки значимости регрессии
проводят в следующей таблице дисперсионного анализа
International Sakharov Environmental University
65
66.
Проверка адекватности линейной моделирегрессии
Под адекватностью построенной регрессионной модели
понимается то, что никакая другая модель не дает
значимого улучшения в предсказании отклика.
Если все значения откликов получены при разных
значениях x, т. е. нет нескольких значений отклика,
полученных при одинаковых xi, то можно провести лишь
ограниченную проверку адекватности линейной модели.
Основой для такой проверки являются остатки:
d i y i y i - отклонения от установленной
закономерности: y i a b x i
International Sakharov Environmental University
66
67.
Коэффициент детерминацииИногда для характеристики качества линии регрессии
используют выборочный коэффициент детерминации R2,
показывающий, какую часть (долю) сумма квадратов,
обусловленная регрессией СКр, составляет в полной сумме
квадратов СКп:
СК Р
СК0
R
1
СК П
СК П
2
Чем ближе R2 к единице, тем лучше регрессия аппроксимирует
экспериментальные данные, тем теснее наблюдения
примыкают к линии регрессии. Если R2 = 0, то изменения
отклика полностью обусловлены воздействием неучтенных
факторов, и линия регрессии параллельна оси x-ов. В случае
простой линейной регрессии коэффициент детерминации R2
равен квадрату коэффициента корреляции r2 .
International Sakharov Environmental University
67
68.
Коэффициент детерминацииМаксимальное значение R2 = 1 может быть достигнуто
только в случае, когда наблюдения проводились при
различных значениях x-ов. Если же в данных имеются
повторяющиеся опыты, то величина R2 не может достичь
единицы, как бы ни была хороша модель.
Вместо
коэффициента
детерминации
R2 можно
использовать статистику - нормированная (приведенная)
R2– статистика. Она имеет следующий вид:
где p – число параметров линейной модели регрессии.
International Sakharov Environmental University
68
69.
Коэффициент детерминацииПрименительно к простой линейной регрессии
Отметим, что коэффициент R2 имеет смысл рассматривать
только при наличии в уравнении регрессии свободного
члена a, так как лишь в этом случае верно равенство
СКп = СКр + СК0
International Sakharov Environmental University
69
70.
Сравнение двух линий регрессииЧасто требуется сравнить линии регрессии,
рассчитанные по двум выборкам. Это можно сделать
тремя способами:
Сравнить коэффициенты наклона b
Сравнить коэффициенты сдвига a
Сравнить линии в целом
International Sakharov Environmental University
70
71.
Сравнение двух линий регрессииЕсли нужно проверить, значимо ли различие в наклоне
двух прямых регрессии, критерий Стьюдента t
вычисляется по формуле:
b1 b2
t
sb1 b2
где b1–b2 — разность коэффициентов наклона, a sb1–b2 —
ее стандартная ошибка.
Затем вычисленное значение t сравнивают, с
критическим значением, имеющим n1+n2–4 степени
свободы.
International Sakharov Environmental University
71
72.
Сравнение двух линий регрессииЕсли обе регрессии оценены по одинаковому числу
наблюдений, то стандартная ошибка разности
s b1 b 2
s b21 s b22
Если же объемы выборок различны, следует
воспользоваться объединенной оценкой остаточной
дисперсии
2
2
n
2
s
n
2
s
1 01 2 0 2
2
s 0 общ
n1 n 2 4
Тогда стандартная ошибка разности
s b1 b2
s 02общ
n1 2 s
2
x1
International Sakharov Environmental University
s 02общ
n 2 2 s x2
2
72
73.
Сравнение двух линий регрессииАналогично сравниваются и коэффициенты сдвига a1 и
а2. В этом случае
a1 a 2
t
s a1 a2
где a1–a2 — разность коэффициентов сдвига, a sa1–a2 —
стандартная ошибка разности коэффициентов сдвига
Затем вычисленное значение t сравнивают, с
критическим значением, имеющим n1+n2–4 степени
свободы.
International Sakharov Environmental University
73
74.
Сравнение двух линий регрессииТаким образом алгоритм сравнения двух линии
регрессии следующий:
Построить прямую регрессии для каждой из выборок.
2
2
s
s
По остаточным дисперсиям 01 и 02 каждой из
регрессий вычислить объединенную оценку
2
s
остаточной дисперсии 0общ
Объединить обе выборки. Построить прямую
регрессии для получившейся выборки и вычислить
2
остаточную дисперсию s0
International Sakharov Environmental University
74
75.
Множественная линейная регрессияМодель множественной линейной регрессии имеет
следующий вид:
y i b 0 b1 x1i b 2 x 2 i ... b k x k i i
Предположения относительно множественной линейной
регрессии аналогичны тем, которые применялись для
простой линейной регрессии. В частности, что все xi
считаются фиксированными и для любого набора xi
значения yi распределены по нормальному закону с
постоянной дисперсией.
International Sakharov Environmental University
75
76.
Множественная линейная регрессияДля получения оценок параметров b0, b1, ...,bk методом
наименьших квадратов нужно минимизировать по этим
параметрам выражение
n
D y i b 0 b1 x 1 i b 2 x 2 i ... b k x k i
2
i 1
International Sakharov Environmental University
76
77.
Множественная линейная регрессияПриравняв нулю частные производные
D D D
D
,
,
,...,
b 0 b1 b 2
bk
после упрощений получается следующая система
нормальных уравнений для нахождения оценок
параметров:
International Sakharov Environmental University
77
78.
Множественная линейная регрессияПусть b – вектор-столбец размера (k+ 1), состоящий из
коэффициентов b0 , b1, …, bk , y – вектор-столбец из n
наблюдений, ε – вектор-столбец из n ошибок и X – матрица
наблюдений размером n(k+ 1) :
b0
b1
b
...
bk
y1
y2
y
...
yn
ε
1
1
...
n
International Sakharov Environmental University
1 x11
1 x12
X
... ...
1 x1n
... xk 1
... xk 2
... ...
... xkn
78
79.
Множественная линейная регрессияТогда уравнение модели регрессии можно записать в виде:
y X Tb ε
Выражение для D можно представить в матричном виде:
D y Xb y Xb
T
тогда вектор оценок b получается из решения системы
уравнений:
T
T
X
X
b
X
y
решение которой имеет вид:
b X X XTy
T
1
International Sakharov Environmental University
79
80.
Множественная линейная регрессияНесмещенной оценкой дисперсии является:
T
1
s
y Xb
y Xb
n k 1
Дисперсионный анализ множественной линейной регрессии
проводится в следующей таблице:
2
0
International Sakharov Environmental University
80













































































 mathematics
mathematics








