Современные методы статистического анализа кадастровых данных. Этапы построения моделей

1. Землеустроительныйфакультет

Землеустроительн
ыйфакультет
дисциплина:
Современные методы
статистического анализа
кадастровых данных
к.э.н., профессор кафедры землеустройства и земельного
кадастра
Яроцкая Елена Вадимовна
1

2.

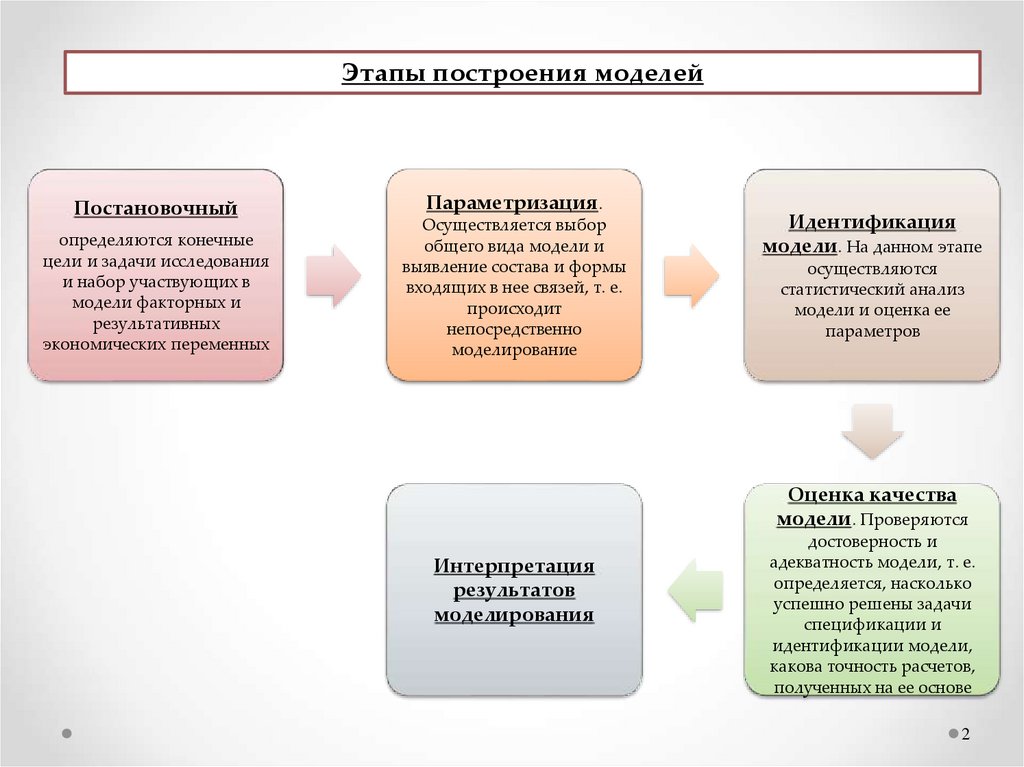
Этапы построения моделей
Постановочный
определяются конечные
цели и задачи исследования
и набор участвующих в
модели факторных и
результативных
экономических переменных
Параметризация.
Осуществляется выбор
общего вида модели и
выявление состава и формы
входящих в нее связей, т. е.
происходит
непосредственно
моделирование
Идентификация
модели. На данном этапе
осуществляются
статистический анализ
модели и оценка ее
параметров
Оценка качества
модели. Проверяются
Интерпретация
результатов
моделирования
достоверность и
адекватность модели, т. е.
определяется, насколько
успешно решены задачи
спецификации и
идентификации модели,
какова точность расчетов,
полученных на ее основе
2

3.

Регрессионный анализ заключается в
определении аналитического
выражения связи (в определении
функции), в котором изменение одной
величины (результативного признака)
обусловлено влиянием независимой
величины (факторного признака).
Количественно оценить данную взаимосвязь можно с помощью построения
уравнения регрессии или регрессионной функции.
3

4.

РЕГРЕССИОННЫЙ
АНАЛИЗ
Парный
(изучение связи между двумя
связанными между собой
признаками)
линейный
нелинейный
Множественный
линейный
(изучение связи между
тремя и более связанными
между собой признаками)
нелинейный
4

5.

Задачи регрессионного анализа
Установление формы зависимости (линейная и нелинейная)
Определение функции регрессии в виде математического уравнения
того или иного типа и установление влияния объясняющих
переменных на зависимую переменную
Оценка неизвестных значений зависимой переменной. С помощью
функции регрессии можно воспроизвести значения зависимой
переменной внутри интервала заданных значений объясняющих
переменных или оценить течение процесса вне заданного интервала
5

6.

Линейная регрессия — используемая в
статистике регрессионная модель
зависимости одной (объясняемой,
зависимой) переменной y от другой
или нескольких других переменных
(факторов, регрессоров, независимых
переменных) x с линейной функцией
зависимости.
6

7.

Линейная парная модель наблюдений
yi xi i , i 1, , n.
если α и β— «истинные» значения параметров линейной модели
связи, то
i yi x i
представляет собой случайный член или ошибку в i-ом
наблюдении
7

8.

Случайная величина ε
характеризует отклонение
реального значения
результативного признака от
теоретического.
Влияет на не учтённые в модели факторы,
случайных ошибок и особенностей измерений.
8

9.

Причины возникновения случайной ошибки:
Невключение объясняющих переменных. Т.е. существуют другие факторы,
влияющие на у, которые не учтены в уравнении. Влияние их приводит к
тому, что точки не лежат на одной прямой.
Агрегирование переменных. Рассматриваемая зависимость является
попыткой объединить некоторое число объектов, которые, возможно,
обладают различными характеристиками.
Неправильное описание структуры модели. Т.е., если зависимость
относится к данным о временном ряде, то значение у может зависеть не от
фактического значения x, а от значения, которое ожидалось в предыдущем
периоде. Если ожидаемое и фактическое значение тесно связаны, то будет
казаться, что между y и x существует зависимость, но это будет лишь
аппроксимация, и расхождение вновь будет связанно с наличием
случайного члена.
Неправильная функциональная спецификация. Т.е. функциональное
соотношение между y и x может быть определено неправильно.
Ошибки измерения. Если в измерении одной или более взаимосвязанных
переменных имеются ошибки, то наблюдаемые значения не соответствуют
такому соотношению, и существующие расхождения будут увеличивать
значения остаточного члена.
9

10.

Параметр β - коэффициент регрессии - на сколько
в среднем изменится результативный признак y при
изменении факторного признака x на единицу своего
измерения.
Знак параметра β в уравнении парной регрессии указывает
на направление связи.
Если, β > 0, то связь между
изучаемыми показателями
прямая, т. е. с увеличением
факторного признака x
увеличивается и результативный
признак, и наоборот.
Если β < 0, то связь между
изучаемыми показателями
обратная, т. е. с увеличением
фактора x результат уменьшается,
и наоборот.
10

11.

Значение параметра α в уравнении парной
регрессии трактуется как среднее значение
результативного признака y при условии, что
факторный признак x равен нулю. Такая
трактовка параметра α возможна только в
том случае, если значение x = 0 имеет смысл.
11

12.

.
y yˆ x
2
min
12

13.

Для линейных и нелинейных уравнений, приводимых к
линейным, решается следующая система относительно
a и b.
na b x y,
2
a
x
b
x
yx .
xy y x
b 2
x x2
a y bx
13

14.

Нелинейная регрессия — это
вид регрессионного анализа, в котором
экспериментальные данные моделируются
функцией, являющейся нелинейной
комбинацией параметров модели и
зависящей от одной и более независимых
переменных
14

15.

Классы нелинейных регрессий
нелинейные относительно
включенных в анализ
объясняющих переменных,
но линейные по
оцениваемым параметрам
нелинейные по
оцениваемым параметрам
полиномы разных степеней
степенная
y a b1 x b2 x 2 b3 x 3
y a xb
равносторонняя гипербола
показательная
y a bx
экспоненциальная
y e a b x
15

16.

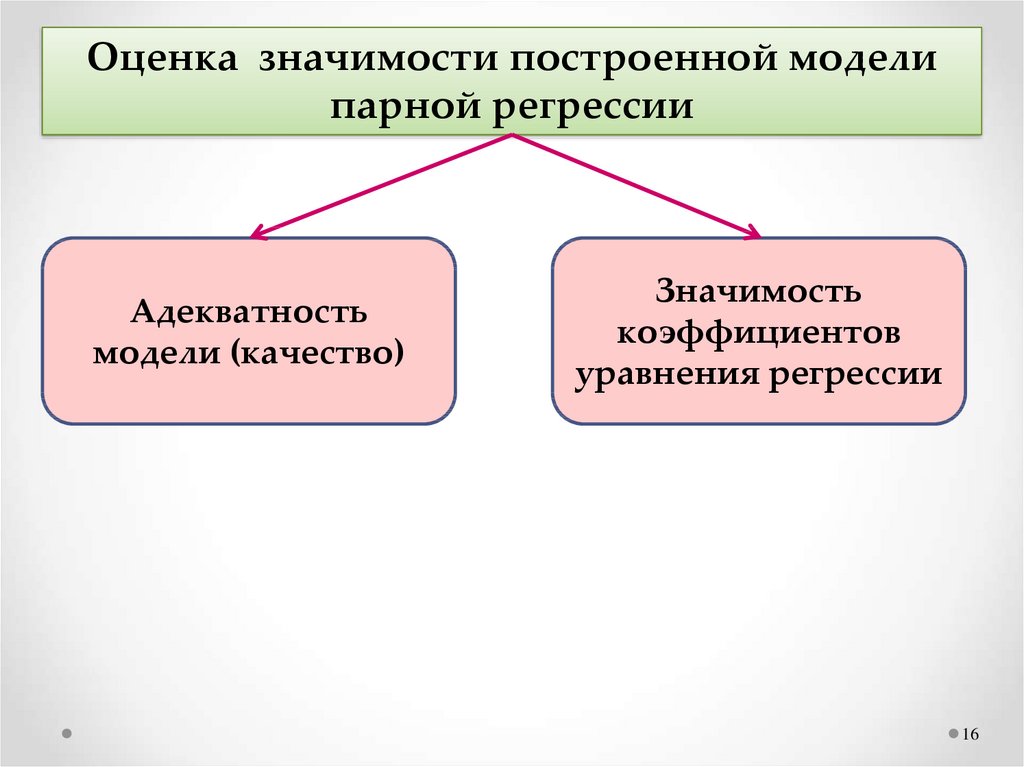
Оценка значимости построенной модели
парной регрессии
Адекватность
модели (качество)
Значимость
коэффициентов
уравнения регрессии
16

17.

Адекватность модели (качество)
1) коэффициент апроксимации – среднее отклонение
расчетных значений от фактических:
y yˆ
1
A
100%
n
yˆ
Допустимый предел значений – не более 8-10%.
17

18.

Адекватность модели (качество)
2) доля дисперсии, объясняемую регрессией, в общей
дисперсии результативного признака y характеризует
индекс детерминации R2:
чем ближе к 1, тем лучше качество модели
18

19.

Адекватность модели (качество)
3) F-тест – оценивание качества уравнения регрессии –
состоит в проверке гипотезы Ho о статистической
незначимости уравнения регрессии и показателя тесноты
связи.
Для этого выполняется сравнение фактического Fфакт и критического
(табличного) Fтабл значений F-критерия Фишера.
Fфакт
2
2
~
r
y
y
/
m
xy
n 2
2
2
~
y y / n m 1 1 rxy
где n – число единиц совокупности,
m – число параметров при переменных x.
19

20.

Fтабл
- это максимально возможное значение критерия под
влиянием случайных факторов при данных степенях свободы и
уровне значимости α
Уровень значимости α - вероятность отвергнуть правильную гипотезу при
условии, что она верна. Обычно α принимается равной 0.05 или 0.01
Fтабл (α; k1; k2) определяется по таблице и зависит от
уровня значимости, числа степеней свободы k1 = m и
числа степеней свободы k2= n – m – 1
Если Fтабл < Fфакт, то гипотеза Ho - гипотеза о случайной
природе оцениваемых характеристик отклоняется и
признается их статистическая значимость и
надежность. В противном случае признается их
статистическая не значимость и не надежность
20

21.

Значимость коэффициентов уравнения регрессии
1) t-критерий
Стьюдента. Выдвигается гипотеза о
случайной природе показателей, т.е. о незначимом их
отличии от нуля.
t-критерия Стьюдента рассчитываются для параметров линейной регрессии и
коэффициента корреляции
tа
а
mа
tb
b
mb
tr
r
mr
Случайные ошибки параметров линейной регрессии и коэффициента корреляции
S
y ~y / n 2
x x
x x
2
mb
ma
2
ост
2
2
y ~y x 2
n 2 n x x 2
2
S
2
ост
x
n 2 x2
2
Sост
x n
Sост
x
mrxy
2
1 rxy2
n 2
xn
21

22.

Оценка значимости коэффициентов регрессии и корреляции с помощью tкритерия Стьюдента проводится путем сопоставления их значений с
величиной случайной ошибки
Сравнивая фактическое и критическое (табличное) значения t-статистики
tтабл и tфакт - принимаем или отвергаем гипотезу Ho
Если tтабл < tфакт, то Ho отклоняется, т.е. a, b, rxy не
случайно отличаются от нуля и сформировались под
влиянием систематически действующего фактора x
Если tтабл > tфакт, то гипотеза Ho не отклоняется и
признается случайная природа формирования a, b, rxy.
22

23.

Значимость коэффициентов уравнения регрессии
2) Доверительный интервал – предельные значения
статистической величины, которая с заданной
доверительной вероятностью будет находится в этом
интервале при выборке большего объема.
определяем предельную ошибку ∆ для каждого показателя
a tтабл ma
b tтабл mb
23

24.

Значимость коэффициентов уравнения регрессии
, ,
расчет
доверительных интервалов
.
a a a
amin a a
amax a a
b b b
bmin b b
bmax b b
24

25.

Значимость коэффициентов уравнения регрессии
Если в границы доверительного интервала попадает ноль,
.
т.е. нижняя граница отрицательная, а верхняя
положительна, то оцениваемый параметр принимается
нулевым, так как он не может одновременно принимать и
положительное, и отрицательное значения.
25

26.

Множественная регрессия - изучение
связи между тремя и более связанными
.
между собой признаками. Требуется
определить аналитическое выражение
связи между признаком y и
объясняющими переменными x1, x2, …, xn
в виде y = f(x1, x2, …, xn).
26

27.

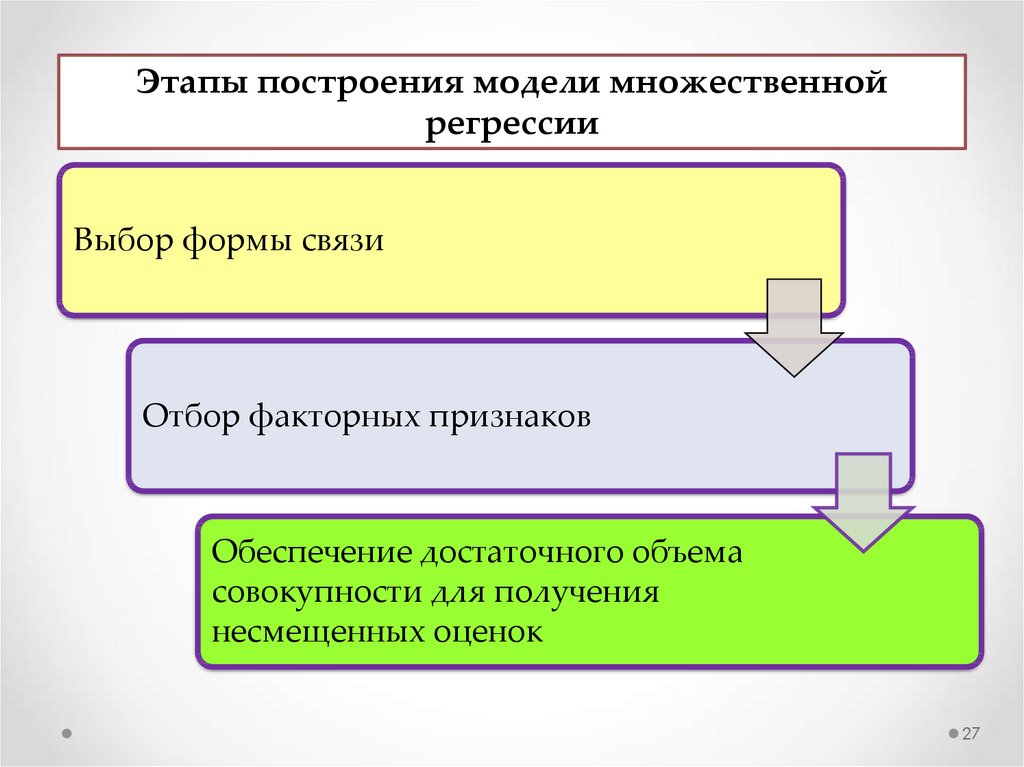
Этапы построения модели множественной
регрессии
Выбор формы связи
.
Отбор факторных признаков
Обеспечение достаточного объема
совокупности для получения
несмещенных оценок
27

28.

Линейная множественная модель
наблюдений
y 0 1 x1 2 x2 ... n xn
α - значения параметров линейной модели связи
28

29.

Оценка значимости построенной модели
1) Коэффициент
множественной детерминации
~2 1 1 R2
R
n 1
,
n m 1
.
Ryx2 1 x2 ... x p
квадрат индекса множественной корреляции
где n – число наблюдений,
m – число факторов
29

30.

4) Мультиколлинеарность –
понятие, которое используется для
описания проблемы, когда
нестрогая линейная зависимость
между факторами приводит к
получению ненадежных оценок
регрессии
.
30

31.

4) F-критерий Фишера
R2 n m 1
F
2
1 R
m
.
Fтабл - это максимально возможное значение критерия под влиянием
случайных факторов при данных степенях свободы и уровне значимости α
Уровень значимости α - вероятность отвергнуть правильную гипотезу при условии, что она верна.
Обычно α принимается равной 0.05 или 0.01
Fтабл (α; k1; k2) определяется по таблице и зависит от уровня
значимости, числа степеней свободы k1 = m и числа степеней
свободы k2= n – m – 1
Если Fтабл < Fфакт, то гипотеза Ho - гипотеза о случайной природе
оцениваемых характеристик отклоняется и признается их статистическая
значимость и надежность. В противном случае признается их
статистическая не значимость и не надежность
31

32.

Значимость коэффициентов уравнения регрессии
1) t-критерий
Стьюдента. Выдвигается гипотеза о
случайной природе показателей, т.е. о незначимом их
отличии от нуля.
bi
tbi
Fxi
mbi
где
mbi - средняя квадратическая ошибка коэффициента регрессии bi,
mbi
y 1 R
xi 1 R
2
yx1 .... x p
2
xi x1 .... x p
1
n m 1
32

33.

Нелинейные множественные регрессионные
модели
Степенная:
y 0 x1 1 x2 2 ...xn n
Показательная
y e 0 1 x1 ... n xn
Параболическая:
y 0 1 x12 ... n xn2
Гиперболическая:
y 0
1
x1
...
n
xn
33

34. Юридический факультет

Землеустроительный
Юридический
факультет
факультет
34