о выборочном методе исследований. Статистические методы обработки экспериментальных данных

1. РАЗДЕЛ II. СТАТИСТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ ЭКСПЕРИМЕНТАЛЬНЫХ ДАННЫХ В АГРОНОМИИ

ЛЕКЦИЯ №6.
СОВОКУПНОСТЬ И
ВЫБОРКА

2. Вопросы лекции:

1. Понятие о совокупности и выборки.
2. Графическое изображение
распределения частот признака.
3. Типы распределений. Статистические
характеристики количественной
изменчивости.
4. Понятие о нулевой гипотезе. Оценка
различий по критериям существенности.
Интервальные и точечные оценки.

3. Совокупность и выборка

Вся исследуемая
совокупность из
однородных
биологических объектов,
подлежащих изучению,
называется генеральной
совокупностью.
Множество объектов
отобранных случайным
образом из генеральной
совокупности называется
выборочной
совокупностью или
выборкой.

4. Графическое изображение распределения частот признака.

Полученную цифровую информацию группируют в k групп с
интервалом каждой группы i. Ориентировочно число групп равно
корню квадратному из объема выборки. k ; n- объем выборки.
Цифровую информацию группируют в такой
последовательности:
1. Определяют размах варьирования результатов
измерения, т.е. разность между наибольшим и
наименьшим значением ряда измерений:
R= Xmax-Xmin
2. Устанавливают число групп k и размер интервала
группы
i=R/k
3. Подготавливают макет таблицы сгруппированного
распределения частот результатов измерений

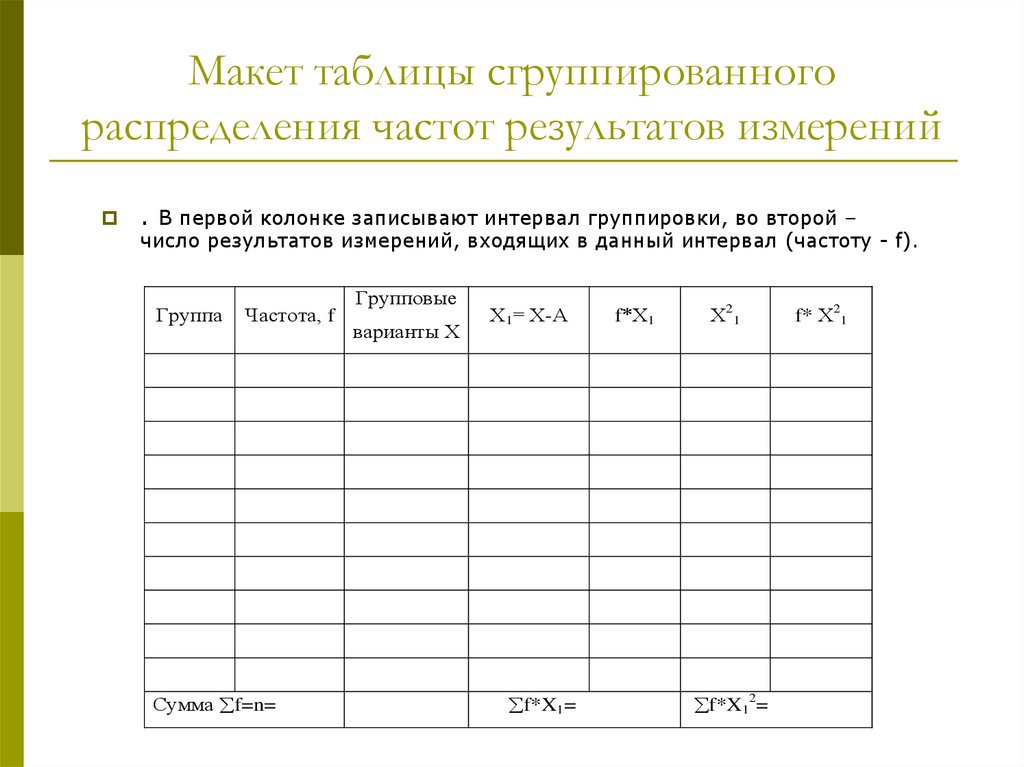
5. Макет таблицы сгруппированного распределения частот результатов измерений

. В первой колонке записывают интервал группировки, во второй –
число результатов измерений, входящих в данный интервал (частоту - f).
Группа
Частота, f
Сумма f=n=
Групповые
варианты Х
Х1= Х-А
f*X1=
f*Х1
Х21
f*X12=
f* Х21

6. Графическое изображение вариационного ряда называется кривой распределения (вариационная кривая).

40
35
30
25
20
15
10
5
0
2
0
2
4
2
8
3
2
3
6
Частота
4
0
4
4
4
8
5
2

7. Типы распределений. Статистические характеристики количественной изменчивости.

Нормальное (Гауссово) – распределение это распределение
вероятностей непрерывной случайной величины X, которое описывается
следующей функцией:
1
1 X
Y
),
e (
2
2
где Y- вероятность; -стандартное отклонение генеральной совокупности (n=
); - генеральная средняя; - 3,14; е- 2,72.

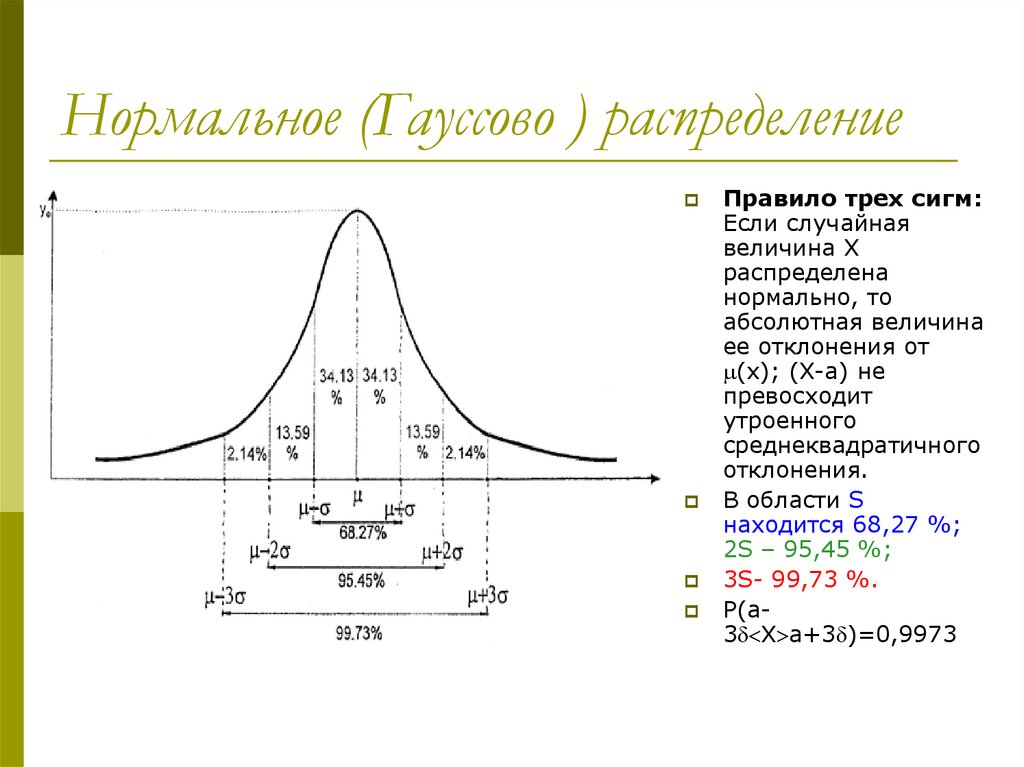
8. Нормальное (Гауссово ) распределение

Правило трех сигм:
Если случайная
величина X
распределена
нормально, то
абсолютная величина
ее отклонения от
(x); (X-а) не
превосходит
утроенного
среднеквадратичного
отклонения.
В области S
находится 68,27 %;
2S – 95,45 %;
3S- 99,73 %.
P(а3 X а+3 )=0,9973

9. Понятие о нулевой гипотезе. Оценка различий по критериям существенности

Статистическая гипотеза – это научное предположение о
тех или иных статистических законах распределения
рассматриваемых случайных величин, которое может
быть проверено на основе выборки. Почти всегда
задача заключается в проверке нулевой гипотезы.
Нулевая гипотеза (Но) - это гипотеза об отсутствии
реального различия между фактическими и ожидаемыми
наблюдениями.
Справедливость Но проверяется вычислением
статистических критериев проверки для определенного
уровня значимости. Отбрасывание гипотезы означает,
что эмпирические данные несовместимы с Но и верна
другая, альтернативная гипотеза.

10.

Для проверки Но используют критерии двух видов:
параметрические и непараметрические.
Параметрические – это критерии, основанные на
предположении, что распределение признака в
совокупности подчиняется известному закону
(например, з-ну нормального распределения). К таким
показателям относятся критерии t и F, использование
которых предполагает вычисление оценок параметров
распределения.
Непараметрические критерии – это такие,
использование которых не требует вычисления оценок
неизвестных параметров распределения и
приближенного значения распределения признака.
Этими критериями пользуются только в
предварительных исследованиях.

11. Распределение Стьюдента (t-распределение)

Распределение Стьюдента (t-распределение) (Госсет) применяют при
работе с малыми выборками выборками, когда n 30-20; для выборочных
средних пользуется равенством:
x
=, где x -отклонение выборочной средней от средней
Sx
генеральной совокупности ; S x -ошибка выборочной средней.
t =
Английский статистик и пионер развития
современных статистических методов. Госсет вывел
статистику t (t-Стьюдента), широко используемую в
критериях различия средних для малых выборок.
Госсет Уильям
Gosset, William S.
(1876-1937).

12. F-распределение Фишера

F-распределение Фишера. Если из одной и той же совокупности, распределяемой по нормальному закону, отобрать случайным способом какое-то
количнество независимых выборок объемом n1,n2, n3, n4, …. nn, то можно
подсчитать дисперсии S1, S2, S3, ….Sn со степенями свободы =n-1 и затем
определить отношение дисперсий: F=S12/S22.Отношение дисперсии берут таким, чтобы в числителе была большая дисперсия, поэтому F всегда больше
или равно единице.
Если Fфакт Fтеор., то Но отвергается, следовательно между средними сравниваемых групп различия достоверные.
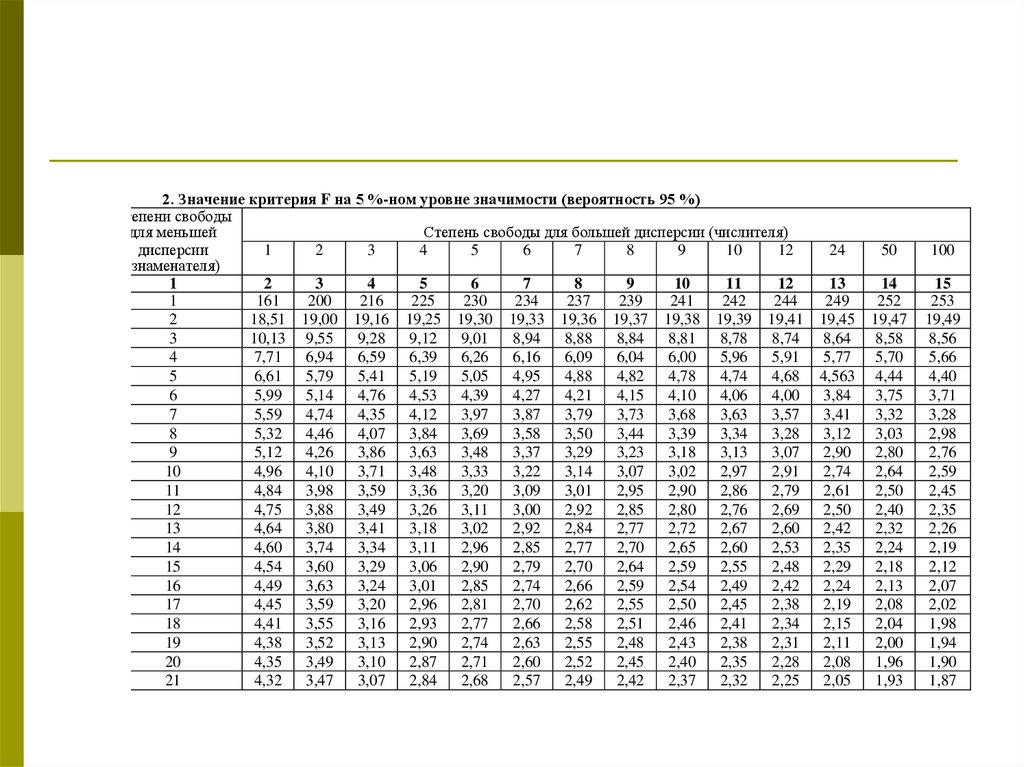
Для определения теоретических значений F пользуются таблицами

13.

2. Значение критерия F на 5 %-ном уровне значимости (вероятность 95 %)
Степени свободы
для меньшей
Степень свободы для большей дисперсии (числителя)
дисперсии
1
2
3
4
5
6
7
8
9
10
12
(знаменателя)
1
2
3
4
5
6
7
8
9
10
11
12
1
161
200
216
225
230
234
237
239
241
242
244
2
18,51 19,00 19,16 19,25 19,30 19,33 19,36 19,37 19,38 19,39 19,41
3
10,13 9,55
9,28
9,12
9,01
8,94
8,88
8,84
8,81
8,78
8,74
4
7,71
6,94
6,59
6,39
6,26
6,16
6,09
6,04
6,00
5,96
5,91
5
6,61
5,79
5,41
5,19
5,05
4,95
4,88
4,82
4,78
4,74
4,68
6
5,99
5,14
4,76
4,53
4,39
4,27
4,21
4,15
4,10
4,06
4,00
7
5,59
4,74
4,35
4,12
3,97
3,87
3,79
3,73
3,68
3,63
3,57
8
5,32
4,46
4,07
3,84
3,69
3,58
3,50
3,44
3,39
3,34
3,28
9
5,12
4,26
3,86
3,63
3,48
3,37
3,29
3,23
3,18
3,13
3,07
10
4,96
4,10
3,71
3,48
3,33
3,22
3,14
3,07
3,02
2,97
2,91
11
4,84
3,98
3,59
3,36
3,20
3,09
3,01
2,95
2,90
2,86
2,79
12
4,75
3,88
3,49
3,26
3,11
3,00
2,92
2,85
2,80
2,76
2,69
13
4,64
3,80
3,41
3,18
3,02
2,92
2,84
2,77
2,72
2,67
2,60
14
4,60
3,74
3,34
3,11
2,96
2,85
2,77
2,70
2,65
2,60
2,53
15
4,54
3,60
3,29
3,06
2,90
2,79
2,70
2,64
2,59
2,55
2,48
16
4,49
3,63
3,24
3,01
2,85
2,74
2,66
2,59
2,54
2,49
2,42
17
4,45
3,59
3,20
2,96
2,81
2,70
2,62
2,55
2,50
2,45
2,38
18
4,41
3,55
3,16
2,93
2,77
2,66
2,58
2,51
2,46
2,41
2,34
19
4,38
3,52
3,13
2,90
2,74
2,63
2,55
2,48
2,43
2,38
2,31
20
4,35
3,49
3,10
2,87
2,71
2,60
2,52
2,45
2,40
2,35
2,28
21
4,32
3,47
3,07
2,84
2,68
2,57
2,49
2,42
2,37
2,32
2,25
24
50
100
13
249
19,45
8,64
5,77
4,563
3,84
3,41
3,12
2,90
2,74
2,61
2,50
2,42
2,35
2,29
2,24
2,19
2,15
2,11
2,08
2,05
14
252
19,47
8,58
5,70
4,44
3,75
3,32
3,03
2,80
2,64
2,50
2,40
2,32
2,24
2,18
2,13
2,08
2,04
2,00
1,96
1,93
15
253
19,49
8,56
5,66
4,40
3,71
3,28
2,98
2,76
2,59
2,45
2,35
2,26
2,19
2,12
2,07
2,02
1,98
1,94
1,90
1,87

14.

2
- распределение Пирсона. Согласно закону, открытому в 1900 г.
Карл Пирсон
(1857-1936)
Пирсоном, теоретические частоты, как правило, не совпадают с
эмпирическими частотами ряда. Поэтому возникает необходимость
сопоставления эмпирических частот с теоретическими. Для этого
применяется критерий 2, который представляет сумму квадратов
отклонений эмпирических частот (f) от теоретических (F), отнесенную к
теоретическим частотам:
( f F )2
=
; где f и F- соответственно фактические и
F
2
теоретические частоты численности объектов выборки.

15.

Задача критерия 2 (критерия согласия, критерия подобия, критерия
соответствия) состоит в том, чтобы определить, являются ли расхождения
данных эмпирического и теоретического распределения случайными или
закономерными. Из формулы видно, что чем больше разность между
эмпирическими и теоретическими частотами (f-F), тем больше величина
критерия 2. Нулевая гипотеза отвергается, если 2факт 2теор., и не
отвергается, если 2факт 2теор.

16.

Средние показатели:
Средняя арифметическая- это обобщенная абстрактная
характеристика совокупности в целом.
Х=
X 1 X ...... Xn Xn
=
n
n
;
где Х – выборочная средняя,
Х - сумма всех членов данной выборки,
n - объем выборки.
Взвешенная средняя арифметическая вычисляется по формуле:
lg Х =
X 1 * f 1 X 2 * f 2 ...... Xn * fn fnXn
=
f 1 f 2 ... fn
fn
где x- значение признака, варианта; f- частота встречаемости признака.
Средняя геометрическая ( Х g) используется для изучения процесса во
времени (например – изменение численности популяции вредителя,
фитопатогена, роста растений и т.д.) Вычисляется по формуле :
Хg =
lg X 1 lg X ...... lg Xn
n
Средняя квадратическая (Q) служит для определения средних
диаметров, радиусов, площадей (например диаметр и площадь корзинок
подсолнечника; площадь листового аппарата т др.). Вычисляют по формуле:
Xq
X
n
2
=
или Xq
fX
n
2
= , где знак - знак
суммирования, n- объем выборки; f- частота.
Средняя гармоническая ( Х h) используется в случаях, когда
изучаемый признак находится в обратной пропорциональной зависимости к
другому, связанному с ним функционально. Вычисляют по формуле:
Xh
n
1
Xn
=, где
1
- обращенные значения вариант; n- объем выборки.
Xn

17. Показатели изменчивости.

Дисперсия и стандартное отклонение. Эти статистические
характеристики являются основными мерами вариации (рассеивания)
изучаемого признака. Дисперсия – это частное от деления суммы квадратов
отклонений на число степеней свободы.
2
Х Х
S
= ; Стандартное отклонение n 1
2
S S2 =
Стандартное отклонение служит показателем наиболее вероятной средней
ошибки отдельного единичного наблюдения, взятого из данной
совокупности. Его называют основным отклонением вариационного ряда.

18.

Часто возникает необходимость в сравнении различных биологических
показателей, которые измеряются в разных единицах. Для этой цели введен
коэффициент вариации. Под которым понимают стандартное отклонение,
выраженное в процентах к средней арифметической данной совокупности:
V
S
* 100 % =
X
Он является относительным показателем изменчивости. Изменчивость
считают незначительной, если коэффициент вариации не превышает 10%,
средней – если он выше 10% , но меньше 20 %; и значительный – если он
более 20%.

19. Ошибка выборочной средней – является мерой отклонения выборочной средней от средней всей генеральной совокупности.

2
S 2 ( x x)
Sx=
,
n(n 1)
n n
S
Ошибки выборки выражаются в тех же единицах измерения, что и
варьирующий признак, и приписывают к соответствующим средним со
знаком , например X S x

20.

Статистические показатели выборочной совокупности- приближенные
оценки параметров генеральной совокупности . Оценка их может быть
точечная (представленная одним числом) или интервальная. Например, x
является точечной оценкой средней , выборочная дисперсия S2 – точечной
оценкой 2. Точечную оценку генеральной средней можно записать так: x S
x , то есть x - оценка генеральной средней с ошибкой S x .
Интервальная оценка характеризуется двумя числами – концами
интервала, покрывающего оцениваемый параметр.
Доверительный интервал – это такой интервал, который с заданной
Центр интервала вероятностью покрывает оцениваемый параметр.
выборочная оценка точки. Пределы, или доверительные границы,
определяются средней ошибкой оценки и уровнем вероятности.
Математически доверительный интервал для генеральной средней
записывается так: x - t05* S x x + t05* S x или X t05*S x .
Крайние точки интервала – начало x - t05* S x и конец x + t05* S x доверительные границы. Интервальную оценку используют для
статистической проверки гипотез при сравнении выборочных средних.