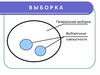
Экспериментальные данные. Характеристики выборки и генеральной совокупности. (Лекция 1)

1. Лекция 1: Экспериментальные данные. Характеристики выборки и генеральной совокупности

1. Классификация видов экспериментальных
исследований.
2. Типы погрешностей измерений и их оценки.
3. Гистограмма и полигон частот.
4. Параметры распределения и их влияние на вид
кривой распределения.
Учебно-исследовательская
работа студента. Лекция 1
1

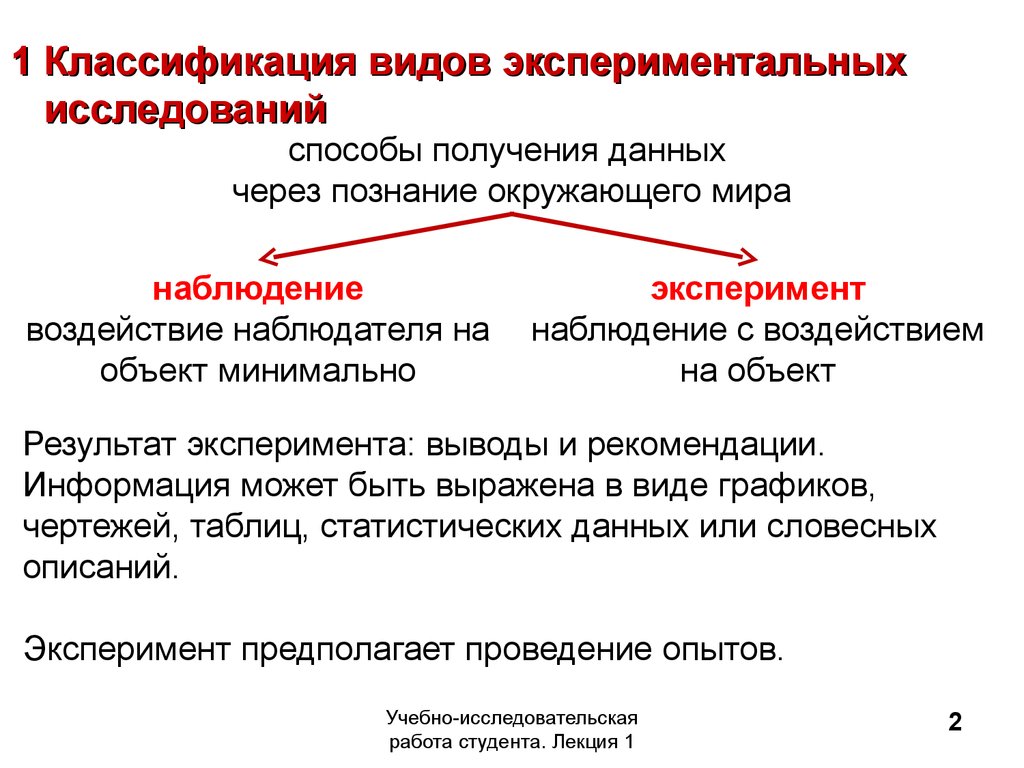
2. 1 Классификация видов экспериментальных исследований

способы получения данных
через познание окружающего мира
наблюдение
воздействие наблюдателя на
объект минимально
эксперимент
наблюдение с воздействием
на объект
Результат эксперимента: выводы и рекомендации.
Информация может быть выражена в виде графиков,
чертежей, таблиц, статистических данных или словесных
описаний.
Эксперимент предполагает проведение опытов.
Учебно-исследовательская
работа студента. Лекция 1
2

3.

Опыт – воспроизведение исследуемого явления в
определенных условиях проведения эксперимента при
возможности регистрации его результатов.
По цели проведения и форме представления полученных
результатов
эксперимент
качественный
устанавливает факт
существования явления,
не дает количественных
характеристик объекта
(словесное описание
результатов
эксперимента)
количественный
фиксирует существование
явления, устанавливает
соотношение между
количественными
характеристиками явления и
внешнего воздействия на объект
(количественное описание
факторов)
Учебно-исследовательская
работа студента. Лекция 1
3

4.

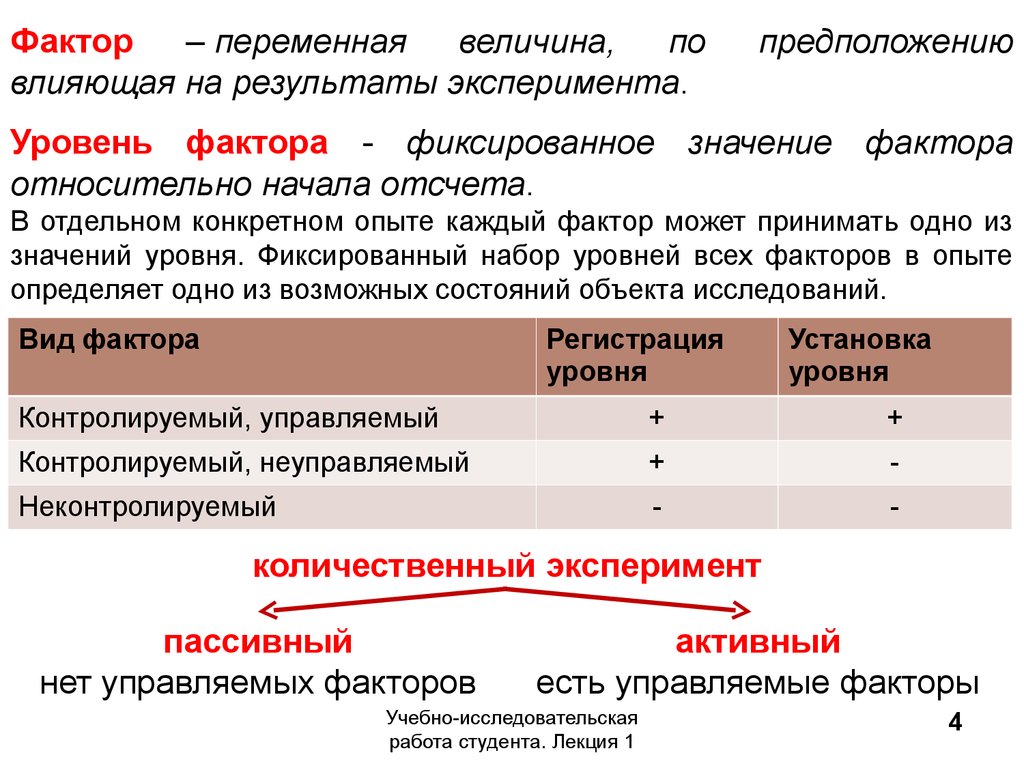
Фактор
– переменная
величина,
по
влияющая на результаты эксперимента.
предположению
Уровень фактора - фиксированное значение фактора
относительно начала отсчета.
В отдельном конкретном опыте каждый фактор может принимать одно из
значений уровня. Фиксированный набор уровней всех факторов в опыте
определяет одно из возможных состояний объекта исследований.
Вид фактора
Регистрация
уровня
Установка
уровня
Контролируемый, управляемый
+
+
Контролируемый, неуправляемый
+
-
Неконтролируемый
-
-
количественный эксперимент
пассивный
нет управляемых факторов
активный
есть управляемые факторы
Учебно-исследовательская
работа студента. Лекция 1
4

5.

Отклик – наблюдаемая случайная величина, по
предположению зависящая от факторов, т.е. некое
исследуемое свойство объекта.
В количественном эксперименте необходимо:
-регистрировать уровни всех контролируемых факторов;
-количественно описать отклик – установить функцию
отклика (зависимость между факторами и откликом).
Вид функции отклика в общем случае:
f ( xi , h j )
xi – контролируемые и управляемые факторы;
hj – контролируемые и неуправляемые факторы;
- ошибка эксперимента (влияние неконтролируемых
факторов)
Учебно-исследовательская
работа студента. Лекция 1
5

6.

2 Типы погрешностей измерений и их оценки
Предмет количественного эксперимента - количественные
величины. Для определения абсолютного значения величины
ее сравнивают с единицей величины - эталоном.
измерения
прямые
непосредственно с
помощью измерительного
прибора
косвенные
расчет по формуле через
величины, измеряемые
напрямую
однократные
непосредственно с
помощью измерительного
прибора
многократные
расчет по формуле через
величины, измеряемые
напрямую
Учебно-исследовательская
работа студента. Лекция 1
6

7.

Погрешность – количественная характеристика
неоднозначности результата измерений.
Нельзя получить экспериментальные данные с абсолютной
точностью => необходимо
• оценить значение измеряемой величины
• указать, насколько оценка близка к истинному
значению
• оценить качество измерений
Пусть результат многократных измерений – случайный
вектор X {x1 , x2 , , x N }, тогда оценка значения 1
X
N
N
xi
i 1
Учебно-исследовательская
работа студента. Лекция 1
7

8.

Абсолютная погрешность ΔХ - разность между истинным
значением измеряемой величины X и его оценкой.
Абсолютная погрешность
• выражается в единицах измеряемой величины X;
• не отражает качества измерений.
Относительная погрешность – критерий качества
измерений. Безразмерная величина.
X
X
или
X
100%
X
Высокой точности измерения соответствует малое значение
относительной погрешности.
Учебно-исследовательская
работа студента. Лекция 1
8

9.

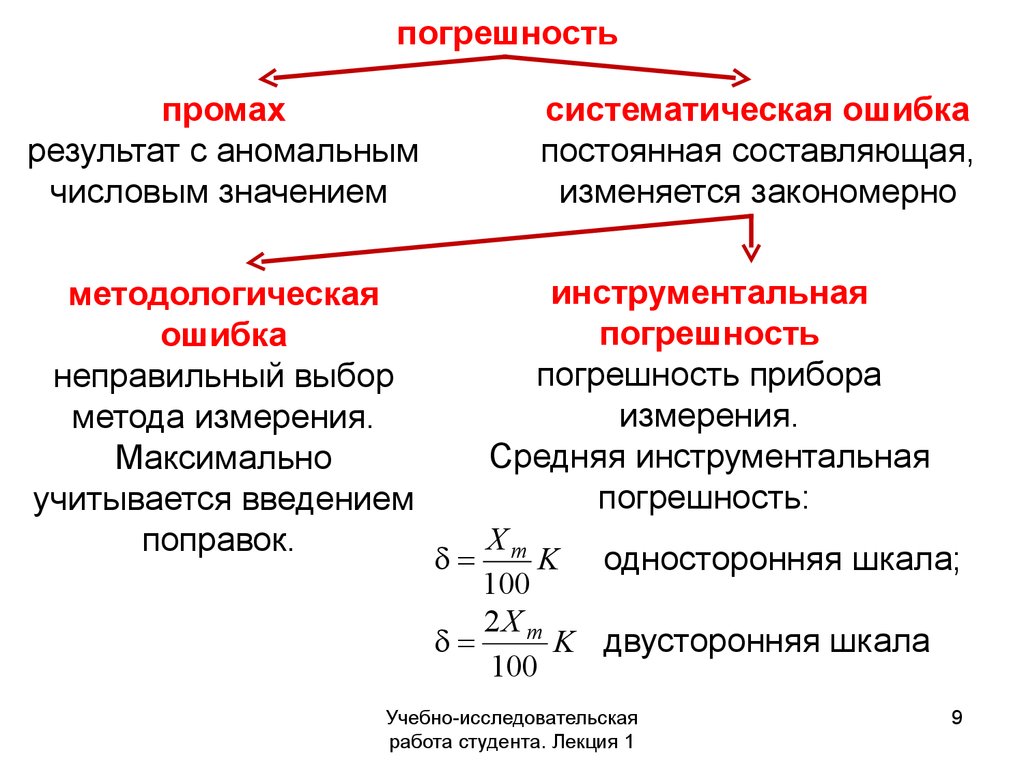
погрешность
промах
результат с аномальным
числовым значением
методологическая
ошибка
неправильный выбор
метода измерения.
Максимально
учитывается введением
поправок.
систематическая ошибка
постоянная составляющая,
изменяется закономерно
инструментальная
погрешность
погрешность прибора
измерения.
Средняя инструментальная
погрешность:
Xm
K односторонняя шкала;
100
2X m
K двусторонняя шкала
100
Учебно-исследовательская
работа студента. Лекция 1
9

10.

Алгоритм обработки данных прямых многократных
измерений:
1
X
1 оценить истинное значение величины
N
N
xi
i 1
2 оценить СКО и среднеквадратическую ошибку среднего
N
2
x
X
i
i 1
N 1
и
x
N
3 вычислить среднюю инструментальную погрешность
Xm
K
100
или
2X m
K
100
4 при априорно известной доверительной вероятности P
найти коэффициенты Стьюдента t ( P, N 1) и t ( P, )
Учебно-исследовательская
работа студента. Лекция 1
10

11.

Алгоритм обработки данных прямых многократных
измерений:
5 вычислить абсолютное значение случайной погрешности
и абсолютное значение инструментальной погрешности
X сл t P, N 1 x
X пр t P,
3
6 рассчитать абсолютную погрешность измерений
2
2
X X сл
X пр
t P, N 1 x 2
t P,
3
2
7 вычислить относительную погрешность
X
X
или
X
100%
X
8 записать результат в виде: X X X при доверительной
вероятности P и погрешности измерений .
Учебно-исследовательская
работа студента. Лекция 1
11

12.

Алгоритм обработки данных косвенных многократных
измерений:
Пусть Z f ( A, B, C ,...) - измеряемая величина; величины A, B,
C,… - измерены прямыми многократными измерениями.
1 результаты измерения величин A, B, C,… обработать по
алгоритму обработки прямых многократных измерений
2 оценить истинное значение измеряемой величины Z
Z f A , B , C ,...
3 найти абсолютную погрешность измеряемой величины Z
2
2
2
f
2 f
2 f
A
B
C 2 ...
Z
A A A , B B ...
B A A ,...
C A A ,...
4 найти относительную погрешность
Учебно-исследовательская
работа студента. Лекция 1
Z
Z
100%
или
Z
Z
12

13.

Соотношения для расчета погрешностей косвенных
измерений для простейших функций
Учебно-исследовательская
работа студента. Лекция 1
13

14.

Соотношения для расчета погрешностей косвенных
измерений для простейших функций
Результат косвенных измерений записывается в виде:
Z Z Z при доверительной вероятности P и погрешности
измерений
Учебно-исследовательская
работа студента. Лекция 1
14

15. 3 Гистограмма и полигон частот.

Предварительная обработка данных начинается с
определения того, какими типами переменных представлены
данные.
Типы переменных (признаков) представления данных:
– непрерывные – представлены действительными
числами (например, длина или вес);
– дискретные – представлены целыми, как правило,
положительными числами;
– категориальные (например, марка кабеля, тип
материала, географический регион). Значения
категориальных данных не могут быть положены на
числовую прямую.
Учебно-исследовательская работа
студента. Лекция 1
15

16.

Построение гистограммы или полигона частот - самый
простой способ наглядного представления о распределении
вероятности выпадения того или иного значения случайной
величины по выборке.
Пусть выборка из экспериментальных данных: x={x1,… xN}.
Алгоритм построения гистограммы и полигона
частот
1. Построение вариационного ряда x1 x2 ... xN
2. Группировка данных: разбиение отрезка [x1, xN] на
«карманы». Как и на сколько «краманов» разбивать?
Рассмотрим рзбиение на «карманы» равной длины.
Определение числа «карманов»
• по правилу Стерджесса: n 1 3,322 lg N ,
• по формуле Брукса и Каррузера: n 5 lg N
• по формуле: n N
Учебно-исследовательская работа
студента. Лекция 1
16

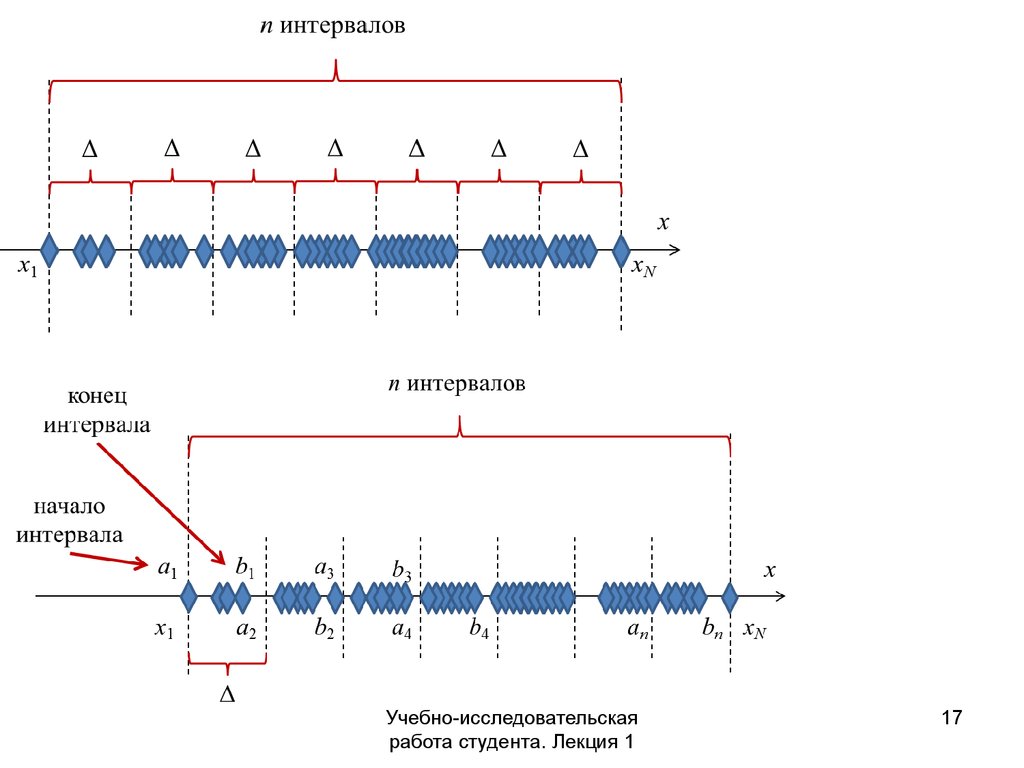
17.

Учебно-исследовательская
работа студента. Лекция 1
17

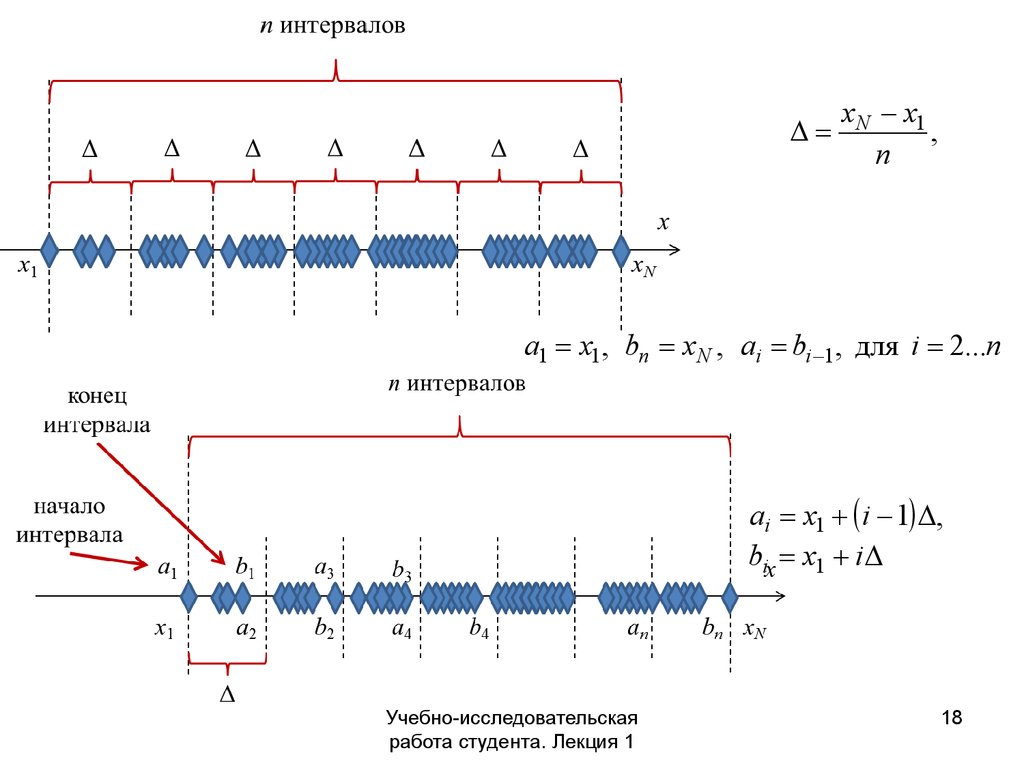
18.

xN x1
,
n
a1 x1, bn xN , ai bi 1, для i 2...n
ai x1 i 1 ,
bi x1 i
Учебно-исследовательская
работа студента. Лекция 1
18

19.

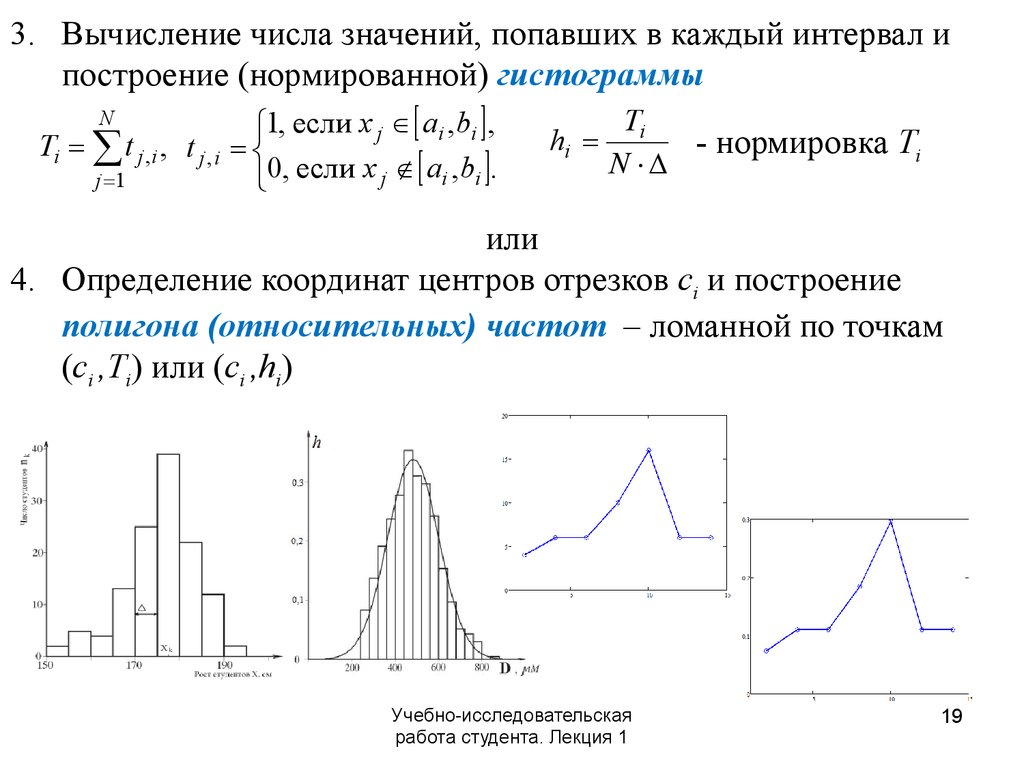
3. Вычисление числа значений, попавших в каждый интервал и
построение (нормированной) гистограммы
N
Ti t j ,i , t j , i
j 1
1, если x j ai , bi ,
0, если x j ai , bi .
Ti
hi
- нормировка Ti
N
или
4. Определение координат центров отрезков ci и построение
полигона (относительных) частот – ломанной по точкам
(сi ,Ti) или (сi ,hi)
Учебно-исследовательская
работа студента. Лекция 1
19

20.

hi ∙Δ - вероятность попадания результата отдельно измерения в
данный интервал. Полная вероятность равна 1, значит
N
hi 1
i 1
При увеличении числа измерений в пределе получаем вместо
гистограммы кривую распределения – график функции
плотности вероятности f(x).
Следовательно,
f ( x)dx 1
Вероятность попадания измеряемой величины в интервал (-∞, x]
называют функцией распределения или интегральной функцией
x
распределения:
F ( x) f ( z )dz
Исходя из определения,
F 0
F 1
( x1 x x2 )
x2
f ( x)dx F ( x2 ) F ( x1 )
Учебно-исследовательская x1
работа студента. Лекция 1
20

21. 4 Параметры распределения и их влияние на вид кривой распределения

Характер кривой распределения описывается специальными
мерами.
Центр распределения характеризуется средним значением μ,
медианой Me и модой Mo.
Среднее значение (первый начальный момент) равно
математическому ожиданию случайной величины:
1 N
R1 xi x f ( x)dx
N i 1
R1 - центр тяжести в геометрии распределения.
Медиана делит площадь, ограниченную функцией плотности
вероятности, на две равные части P X Me F Me 0,5
Мода является наиболее вероятным значением случайной
величины, то есть соответствует значению x, для которого f(x)=max
Учебно-исследовательская работа
студента. Лекция 1
21

22.

Рассеяние случайных величин вокруг центра группирования
оценивается дисперсией, стандартным отклонением,
коэффициентом вариации и размахом.
Дисперсия (второй момент) – это математическое ожидание
квадрата отклонения случайной величины от их среднего
арифметического значения.
1 N
Dx R2 xi 2 ( x ) 2 f ( x)dx
N i 1
Среднее квадратическое отклонение,
отклонение СКО: Dx
Стандартное отклонение:
отклонение
cт
1/ N ,
для выборки
1 / N 1, для генеральной совокупнос ти
Коэффициент вариации – отношение стандартного отклонения к
математическому ожиданию случайной величины.
Размах является разностью между большим и меньшим элементом
выборки, то есть он равен w=xmax-xmin
Учебно-исследовательская
работа студента. Лекция 1
22

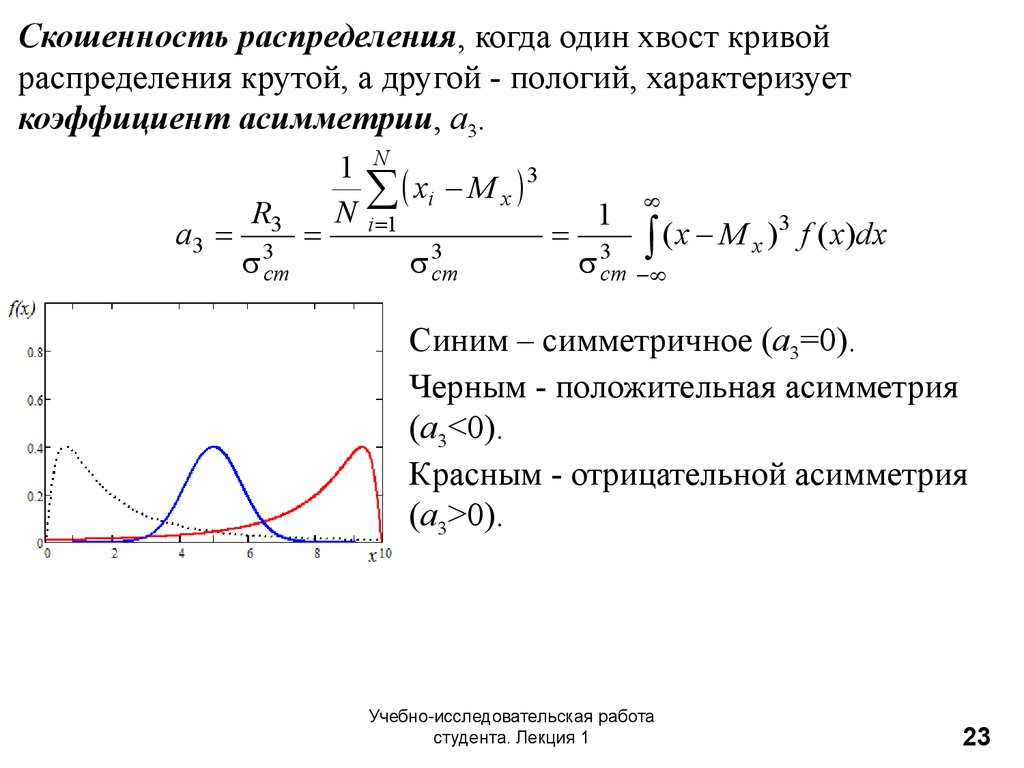
23.

Скошенность распределения, когда один хвост кривой
распределения крутой, а другой - пологий, характеризует
коэффициент асимметрии, a3.
a3
R3
3ст
1 N
xi M x 3
N i 1
3ст
1
3ст
3
(
x
M
)
f ( x)dx
x
Синим – симметричное (a3=0).
Черным - положительная асимметрия
(a3<0).
Красным - отрицательной асимметрия
(a3>0).
Учебно-исследовательская работа
студента. Лекция 1
23

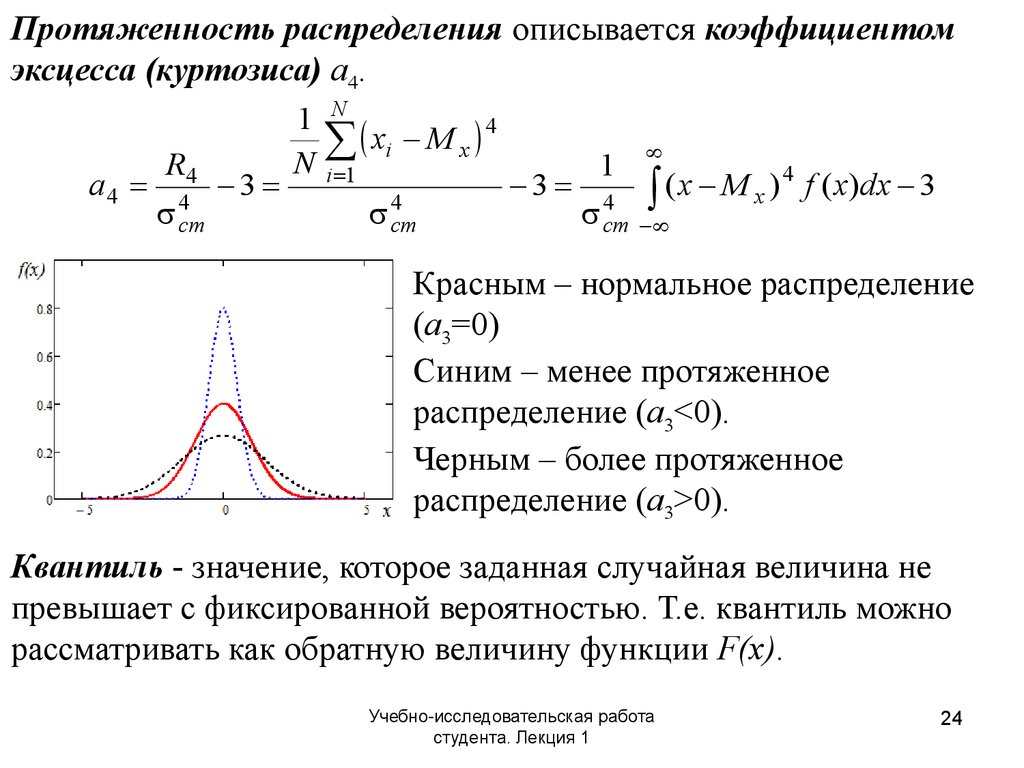
24.

Протяженность распределения описывается коэффициентом
эксцесса (куртозиса) a4.
a4
R4
4
ст
3
1 N
4
x
M
i x
N i 1
4
ст
3
1
4
ст
4
(
x
M
)
f ( x)dx 3
x
Красным – нормальное распределение
(a3=0)
Синим – менее протяженное
распределение (a3<0).
Черным – более протяженное
распределение (a3>0).
Квантиль ‑ значение, которое заданная случайная величина не
превышает с фиксированной вероятностью. Т.е. квантиль можно
рассматривать как обратную величину функции F(x).
Учебно-исследовательская работа
студента. Лекция 1
24