Similar presentations:
От теории вероятностей к статистике. Генеральная совокупность и выборка
1.
Привет!Привет!
2.
7. От Теории вероятностейк Статистике
Генеральная совокупность и выборка
И еще
Наши достижения
Например:
Даже те элементы ТВ, с которыми познакомились,
позволяют решать многие практические задачи
умеем оценить надежность и риск отказа системы, если
известна надежность ее элементов
определить вероятность нарушить норматив по какому-то
критерию, если знаем его ЗР риск отказа
3.
Главное познакомились с основой, теоретическойбазой, которая позволит (при желании и / или необходимости)
овладеть многообразием статистических методов
решения практических задач
Методы один из 3-х главных
«смыслов» термина статистика
(см. «Статистика» Т.В. Ляшенко, стр. 5)
О связи
Статистики с ТВ
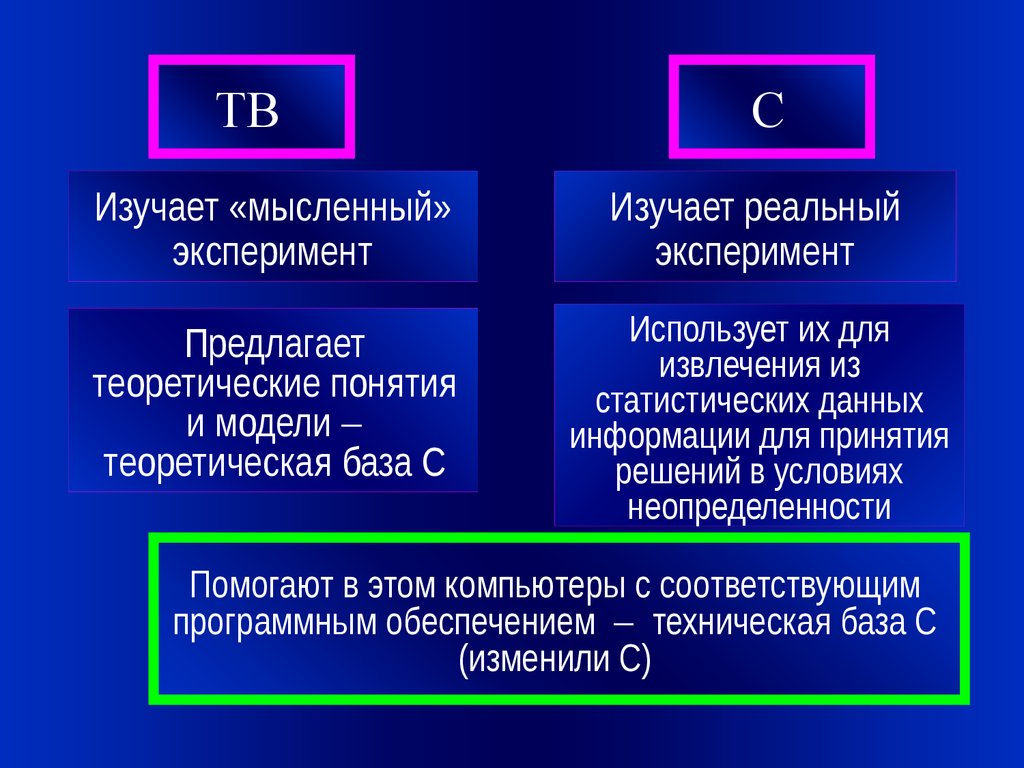
4.
ТВС
Изучает «мысленный»
эксперимент
Изучает реальный
эксперимент
Предлагает
теоретические понятия
и модели
теоретическая база С
Использует их для
извлечения из
статистических данных
информации для принятия
решений в условиях
неопределенности
Помогают в этом компьютеры с соответствующим
программным обеспечением техническая база С
(изменили С)
5.
ТВИзучает
СВ ЗР
Вероятность P
Аналогии
С
Статистическая
совокупность предмет
статистики
Данные сырьевая база
^
статистики
Оценка P =
частота f ( или w)
Проверяемая по статистическим
2 данным теоретическая модель ^
Параметр
Его стат. оценка
распределения
распределения
ФР и ПР,
F(x) и f(x)
Распределения частот,
Fn(x) и fn(x) 1
6.
Структура «Статистики»(науки и учебного курса) МС
3 направления
Эффективный сбор данных подготовка сырья
(должно
быть качественным)
извлечь полезную
информацию
из доступных данных !
Описательная статистика свертка данных,
их обобщение и представление
Статистический анализ исследование данных
«Коснемся»
этих
и выводы
на его основе
Цель статистических
3-х разделов
средств и процедур
Статистики
7.
СЫРЬЕ(см. версии
этих понятий
В статистических исследованиях используются
на стр. 8)
2 связанных друг с другом понятия:
генеральная совокупность (совокупность)
в ТВ
выборка
(массовые
однородные )
(выборочная совокупность
испытания)
Г.С. совокупность всех мыслимых
наблюдений за случайной величиной
(снятых с однородных объектов)
значения x интересующего признака X,
который варьирует от одного объекта к другому
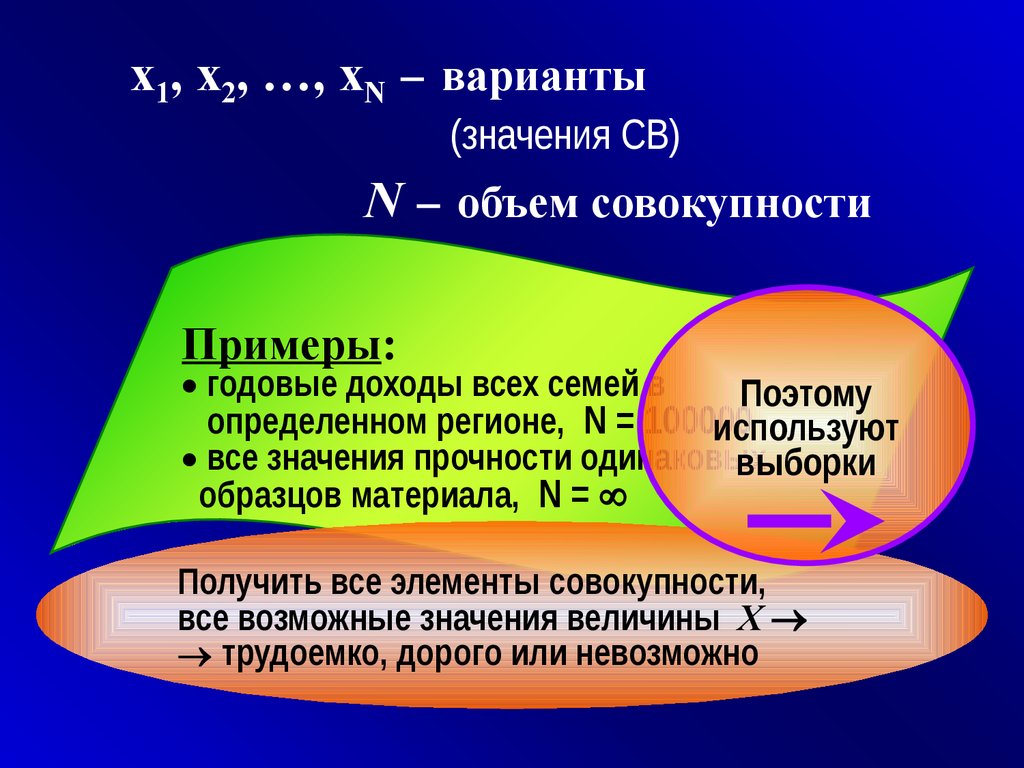
8.
x1, x2, …, xN варианты(значения СВ)
N объем совокупности
Примеры:
годовые доходы всех семей в
Поэтому
определенном регионе, N = 100000
используют
все значения прочности одинаковых
выборки
образцов материала, N =
Получить все элементы совокупности,
все возможные значения величины X
трудоемко, дорого или невозможно
9.
Выборка объема n из совокупностирезультаты ограниченного ряда наблюдений
x1, x2, …, xn
за случайной величиной X
Примеры:
годовые доходы 100 семей из 100000
Результаты испытаний 6 образцов
материала
10.
Возможность по выборочным данным сделатьзаключение о свойствах совокупности суть
статистического метода
Его назначение по выборке получить
количественные основания для решений
относительно всей совокупности
Выборочный эмпирический
статистический метод
11.
Судить по частио целом
Важно и нужно
судить ВЕРНО
Пример
?
Выборка должна быть
репрезентативной
равный шанс для
каждого элемента
попасть в выборку
достаточный
объем
выборки
12.
8. Описательная статистикаЧеткое, яркое
представление
конфигурации
данных
(не «куча»)
См. «практику» и
пособие
Выборочные
числовые
характеристики
распределений
статистики
(в частности, оценки
параметров)
13.
Числовые характеристикиэмпирических распределений
ЧХ распределения признака X получаемые по
статистическим данным числа, характеризующие
наиболее существенные черты распределения
По всей совокупности генеральные
( в частности, параметры : , , …)
По выборочным данным выборочные
( в частности, оценки ^
параметров :
^
= X , ^
= s, …)
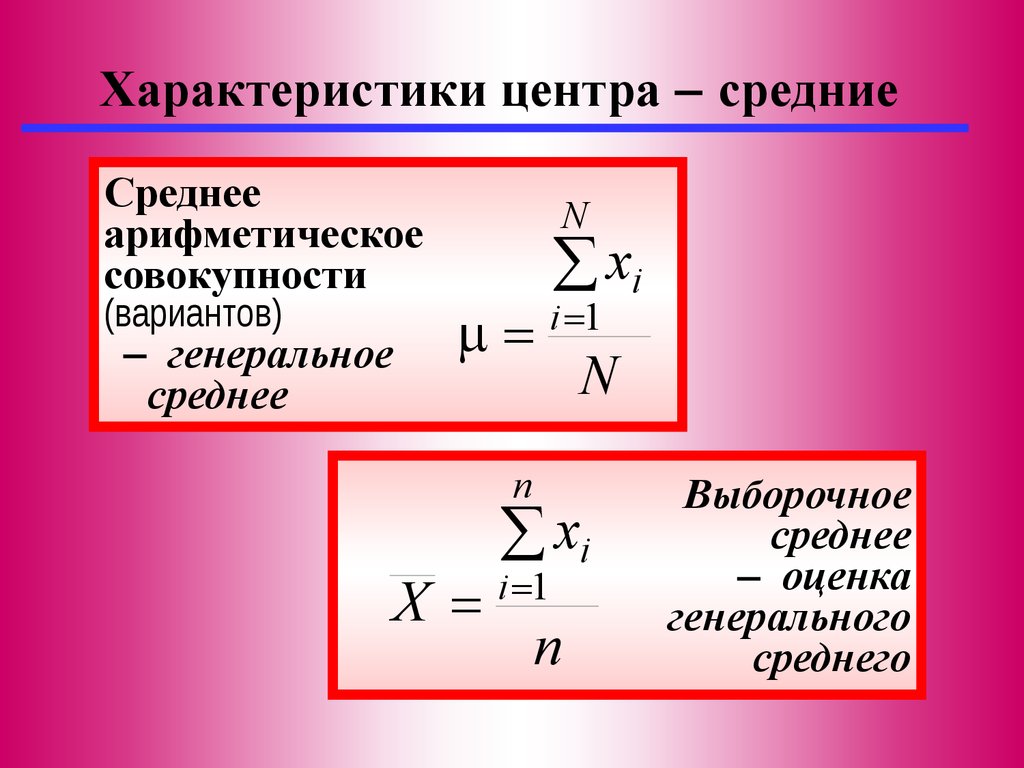
14.
Характеристики центра средниеСреднее
арифметическое
совокупности
(вариантов)
генеральное
среднее
N
xi
i 1
N
n
X
xi
i 1
n
Выборочное
среднее
оценка
генерального
среднего
15.
Свойства среднегоПлохой пример
Медиана (Ме) срединный элемент
вариационного ряда
Номер медианного элемента (n + 1) / 2
В плохом примере
Процентили на 100, децили на 10,
Выборочные
характеристик,
определяемые
квантили
на равные
порядком элементов в вариационном ряду
порядковые статистики
Ме делит на 2 секции.
Квартиль Q на 4: Q1, Q2 = Ме, Q3
16.
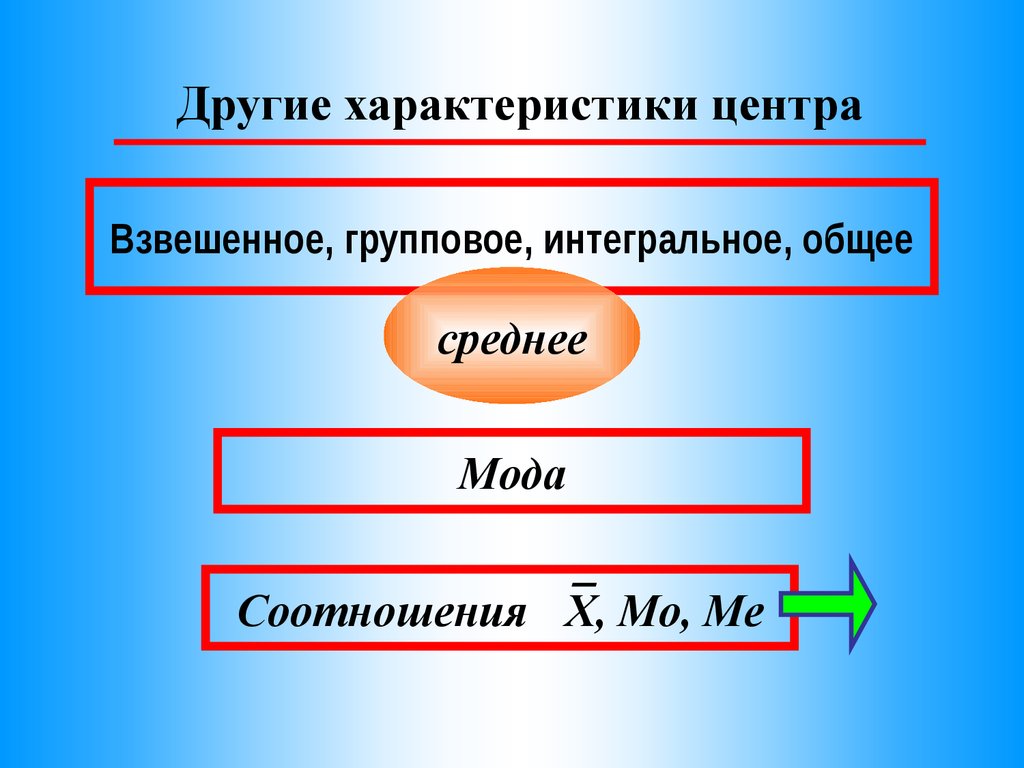
Другие характеристики центраВзвешенное, групповое, интегральное, общее
среднее
Мода
Соотношения X, Мо, Ме
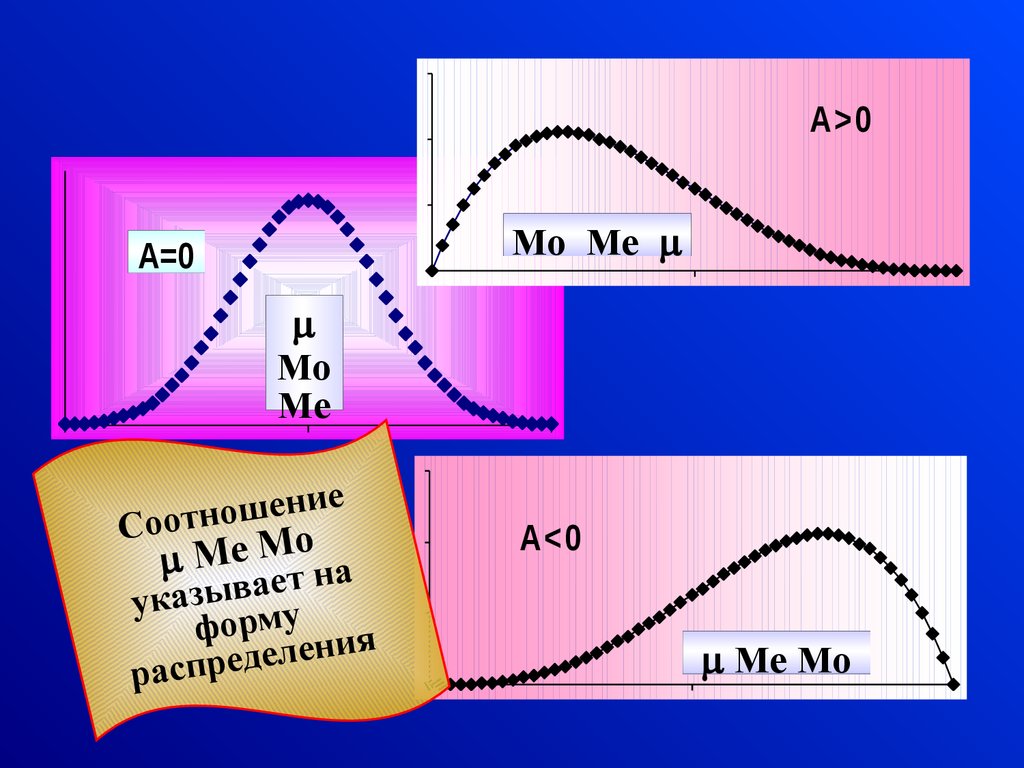
17.
A>0Mo Me
A=0
Mo
Me
ие
н
е
ш
о
н
Соот
o
Me M
а
н
т
е
а
в
указы му
фор
я
и
н
е
л
е
д
распре
A<0
Me Mo
18.
Характеристики рассеянияГенеральные
Генеральная дисперсия
Генеральное
стандартное отклонение
(x
)
z
( xi )
N
2
2
( xi )
N
2
Нормализованное отклонение
19.
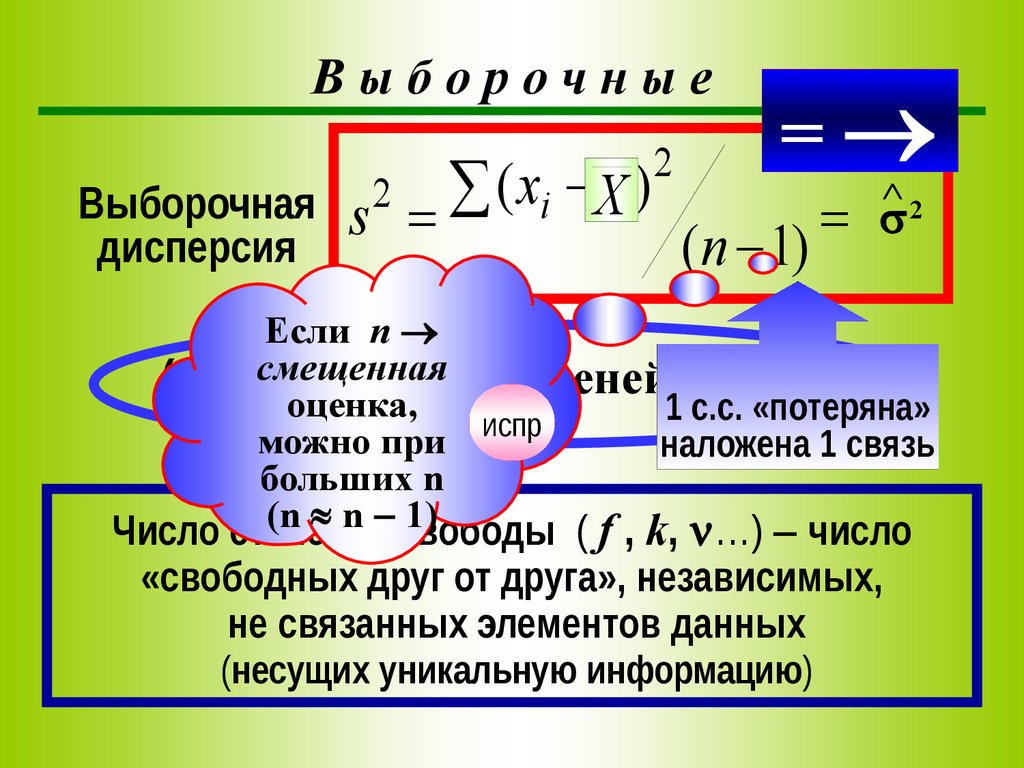
ВыборочныеВыборочная
дисперсия
2
=
( xi X )
s
(n 1)
2
^
2
Если n
смещенная
( n 1)
число
степеней
свободы
оценка,
1 с.с. «потеряна»
испр
можно при
наложена 1 связь
больших n
(n n свободы
1)
Число степеней
( f , k, …) число
«свободных друг от друга», независимых,
не связанных элементов данных
(несущих уникальную информацию)
20.
Выборочноестандартное
отклонение
2
s
n
z =(x
2
( xi X )
^
s
(n 1)
2
xi
( xi )
n(n 1)
2
X)/s
Выборочное
нормализованное
отклонение
s s
2
21.
Генеральныйкоэффициент
вариации
v = /
Выборочный
коэффициент
вариации
^
v = s /
И другие статистики
The End
X















 mathematics
mathematics software
software