Предмет и задачи математической статистики. Генеральная совокупность и выборка. Вариационный ряд

1.

2.

Математическая статистика – раздел
математики, изучающий методы сбора,
систематизации и обработки результатов
наблюдений массовых случайных явлений.
Задачи математической статистики:
• Сбор, хранение и обработка информации.
•Установление и исследования различного рода
зависимостей на основании экспериментальных
данных.
• Изучение вероятностных характеристик
моделей реальных явлений.
• Разработка прогнозов, оценка их
достоверности.

3. Немного истории

Математическая статистика возникла в
XVIII веке и развивалась параллельно с
теорией вероятностей.
Дальнейшее развитие (вторая половина XIX
века – начало XX века) обязано, в первую
очередь, П. Л. Чебышеву, А. А. Маркову, А. М.
Ляпунову, а так же К. Гауссу, А. Кетле, Ф.
Гальтону, К. Пирсону и другие. XX век –
советские учёные : В. И. Романовский, Е. Е.
Слуцкий, А. Н. Колмогоров. Английские:
Стьюдент, Фишер, Смирнов. Американские:
С. Нейман, Вальд.

4.

Статистические данные – сведения о числе объектов,
какой- либо обширной совокупности, обладающих теми
или иными признаками (число студентов, родившихся в
1980 г; балловые результаты ЕГЭ в городе).
Основной метод обработки статистических данных
– выборочный метод.
Алгоритм обработки статистических
данных:
Упорядочение и группировка данных;
Составление таблиц распределения данных;
Построение графиков распределения данных;
Расчет основных числовых характеристик
статистических данных.

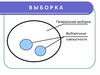
5. Генеральная и выборочная совокупность

Пусть требуется изучить совокупность однородных
объектов относительно некоторого качественного
или количественного признака, характеризующего
эти объекты.
Генеральная совокупность – это совокупность всех
объектов, которые имеют типичную характеристику
или признак. Это все возможные значения случайной
величины.

6. Генеральная и выборочная совокупность

Выборочная совокупность (выборка) – это
отобранная тем или иным способом часть генеральной
совокупности.
Из одной генеральной совокупности можно отбирать
сколь угодно много выборок, главное, чтобы выборка
была репрезентативной (представительной), а для
этого элементы выборки должны отбираться
случайным образом.
Варианта – это числовое значение изучаемого
признака( отдельные значения случайной величины).

7. Основные понятия математической статистики:

8.

Основные понятия математической
статистики:
Объем выборки – число объектов выборки или
генеральной совокупности.
Размах выборки – разность между наибольшим
и наименьшим значением числовой выборки.
Выборку, представляющую собой неубывающую
последовательность чисел, называют
вариационным рядом.

9.

Основные понятия математической статистики:
Вариантой называют каждое полученное значение данных
конкретного измерения: x1 ; x2 ;... xk
Кратностью или частотой варианты называют число,
показывающее, сколько раз варианта встретилась в данном
измерении: n1 ; n2 ;...nk
nk
n1 n2
; ;...;
n n
n
Перечень вариантов и соответствующих им частот называется
статистическим распределением выборки или статистическим
рядом.
x1 , n1 ; x2 , n2 ;... xk , nk

10.

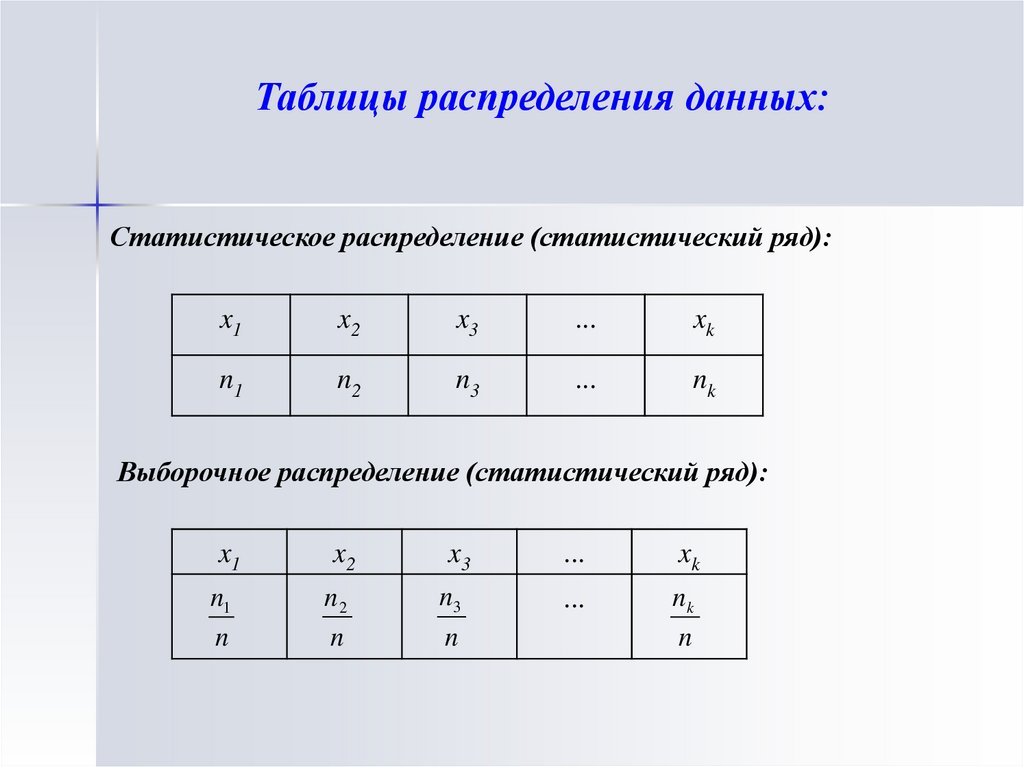
Таблицы распределения данных:
Статистическое распределение (статистический ряд):
x1
x2
x3
...
xk
n1
n2
n3
...
nk
Выборочное распределение (статистический ряд):
x1
n1
n
x2
n2
n
x3
n3
n
...
xk
...
nk
n

11.

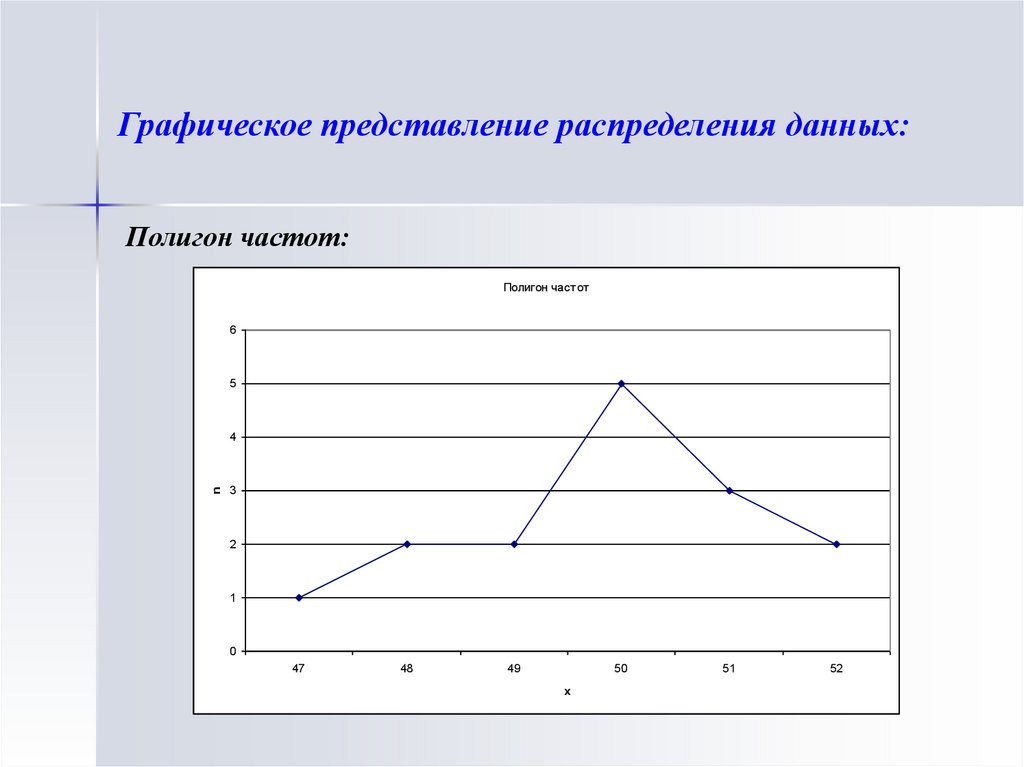
Графическое представление распределения данных:
Полигон частот:
Полигон частот
6
5
n
4
3
2
1
0
47
48
49
50
x
51
52

12.

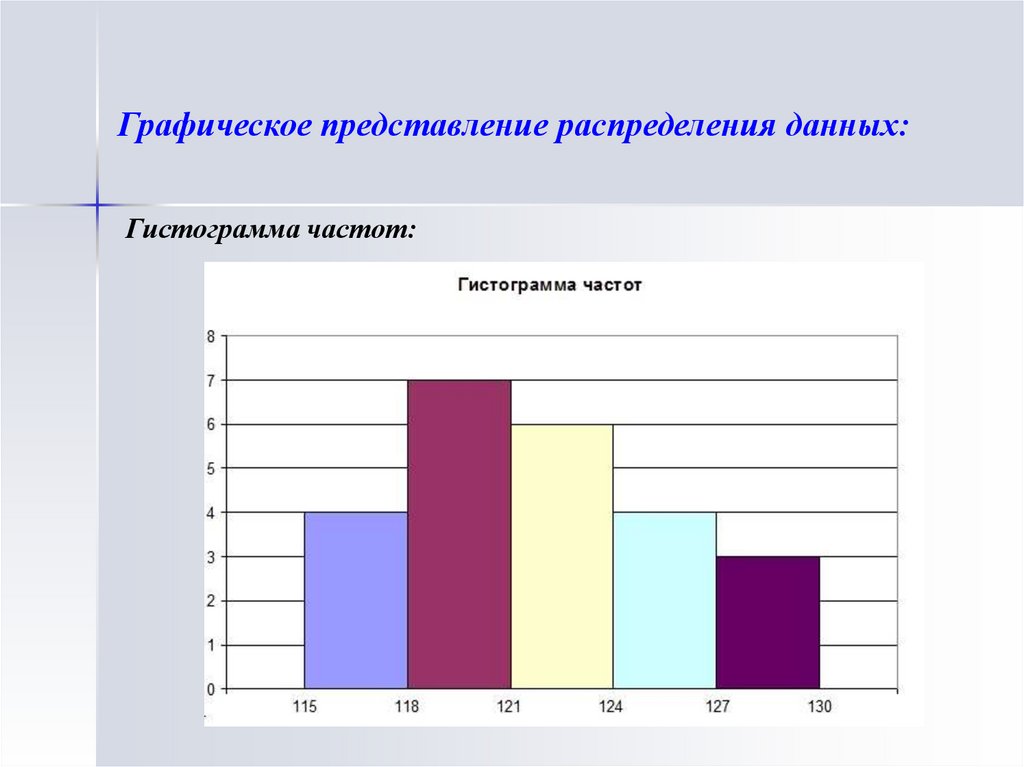
Графическое представление распределения данных:
Гистограмма частот:

13. Схема предварительной обработки экспериментальных данных.

1). Сбор экспериментальных данных.
Чтобы определить закон распределения случайной
величины, нужно провести серию измерений или
подсчётов для интересующей нас случайной величины
(признака).
В результате получаем вариационный ряд – это
совокупность числовых данных или выборка объёмом n:
Затем производят упорядочивание членов выборки –
эта операция называется ранжирование.
Ранжирование -- это расположение всех
имеющихся вариант по возрастанию. Получаем
ранжированный вариационный ряд.

14. Пример:

При измерении частоты пульса у 10
пациентов получены следующие результаты:
90, 110, 65, 80, 90, 60, 70, 80, 70, 80
Ранжированный ряд имеет вид: 60, 65, 70,
70, 80, 80, 80, 90, 90, 110.
Колебания изучаемого признака называются
варьирование. В нашем примере варьирование это изменение частоты пульса.

15. Схема предварительной обработки экспериментальных данных.

2).Составление статистического ряда.
Статистический ряд (статистическое
распределение) -- это двойной ряд чисел в котором
каждому значению случайной величины
соответствует её частота ni (то есть сколько раз
случайная величина принимала данное значение).
Если случайная величина (признак) изменяется
дискретно, то составляем дискретный
статистический ряд.

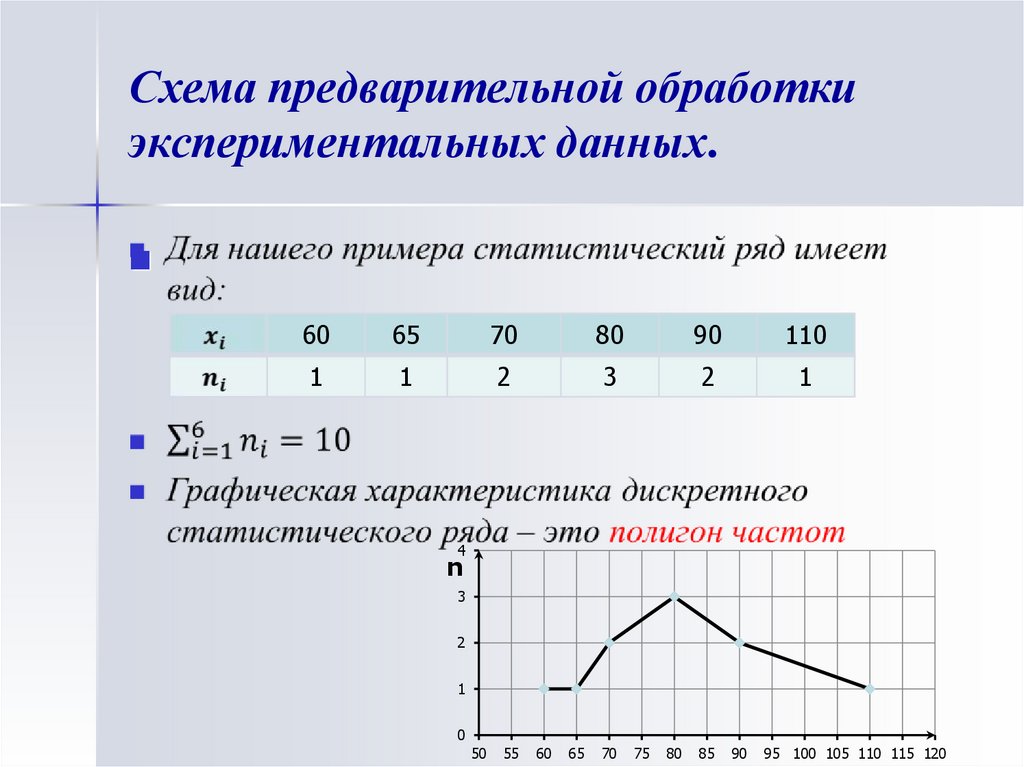
16. Схема предварительной обработки экспериментальных данных.

60
65
70
80
90
110
1
1
2
3
2
1
4
n
3
2
1
0
50
55
60
65
70
75
80
85
90
95 100 105 110 115 120

17. Схема предварительной обработки экспериментальных данных.

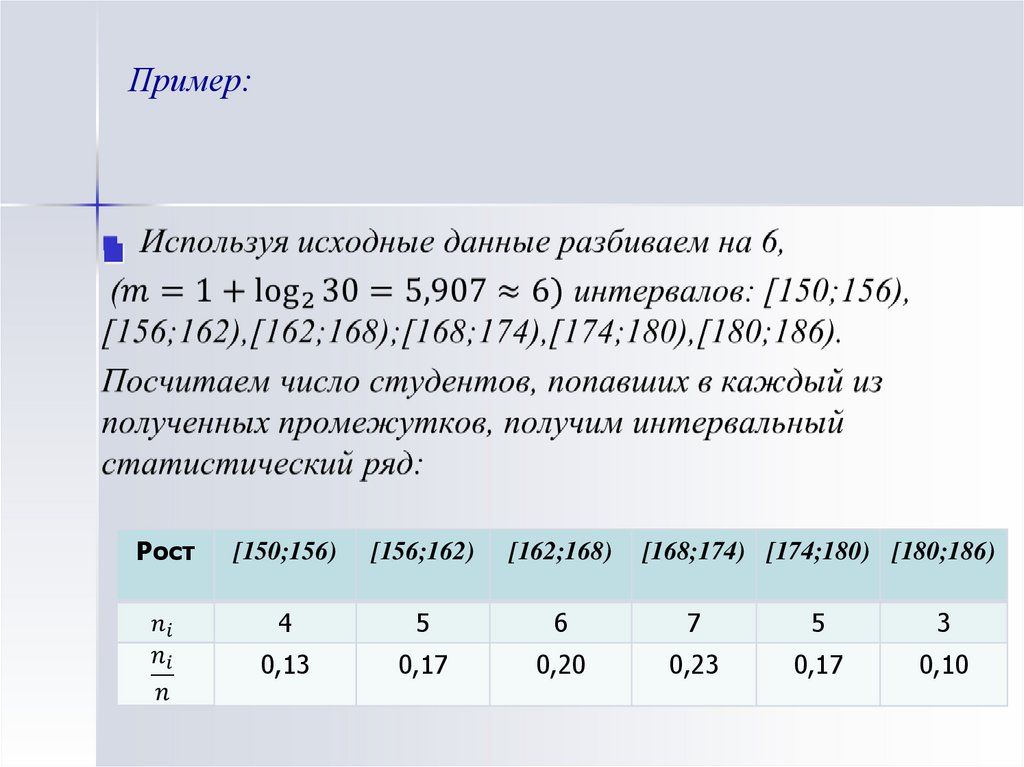
18. Пример:

19. Пример:

Рост
[168;174) [174;180) [180;186)
[150;156)
[156;162)
[162;168)
4
5
6
7
5
3
0,13
0,17
0,20
0,23
0,17
0,10

20.

Выборочные характеристики:
n1 x1 n2 x2 n3 x3 ... nk xk
x
n
или

21. Выборочные характеристики:

22.

Задача:
В результате измерения роста 7 - летних детей (см) получена выборка: 118,
121, 115, 125,125,117,124,120,120,119,121,119, 122, 127, 118, 120,123,130,123,116,
124, 127, 120, 122.
Представьте эти данные в виде дискретного статистического ряда
распределения и постройте полигон частот. Постойте гистограмму, если
число частичных промежутков равно 5. Определите среднее значение роста
детей и отклонение от него.
Решение:
Составим вариационный ряд выборки: 115, 116, 117, 118, 118, 119, 119, 120,
120, 120, 120, 121, 121, 122, 122, 123, 123, 124,124, 125, 125, 127, 127, 130.
Запишем статистическое распределение (статистический ряд):
115
116
117
118
119
120
121
122
123
124
125
127
130
1
1
1
2
2
4
2
2
2
2
2
2
1

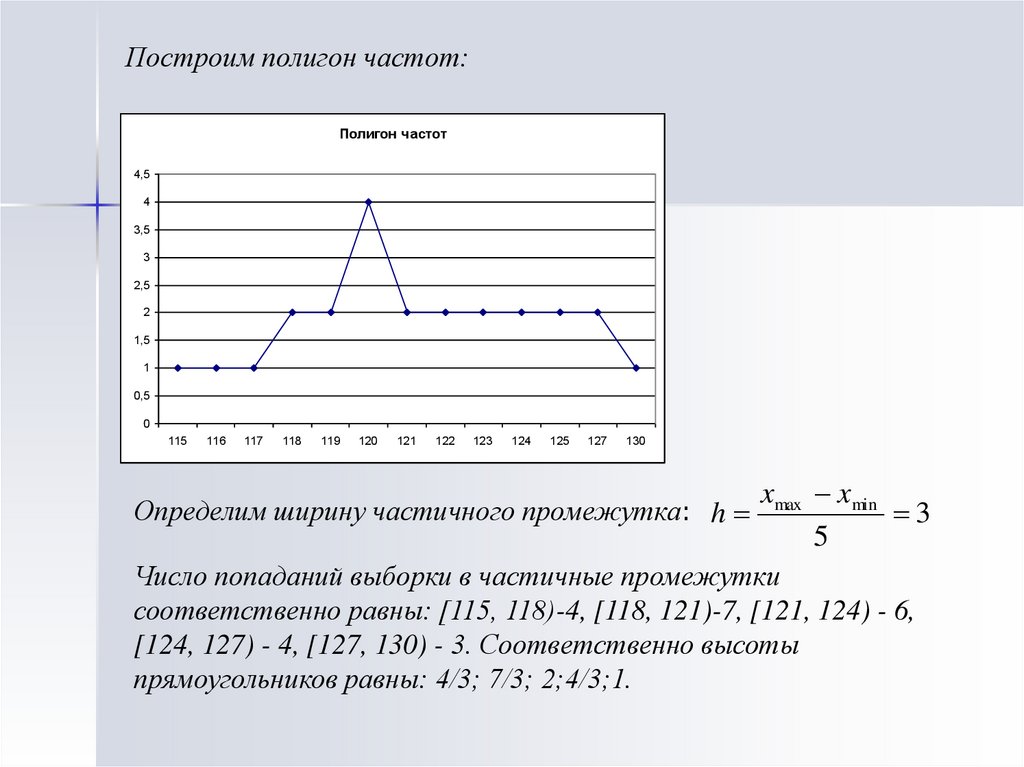
23.

Построим полигон частот:
Полигон частот
4,5
4
3,5
3
2,5
2
1,5
1
0,5
0
115
116
117
118
119
120
121
122
123
124
125
127
130
xmax xmin
3
5
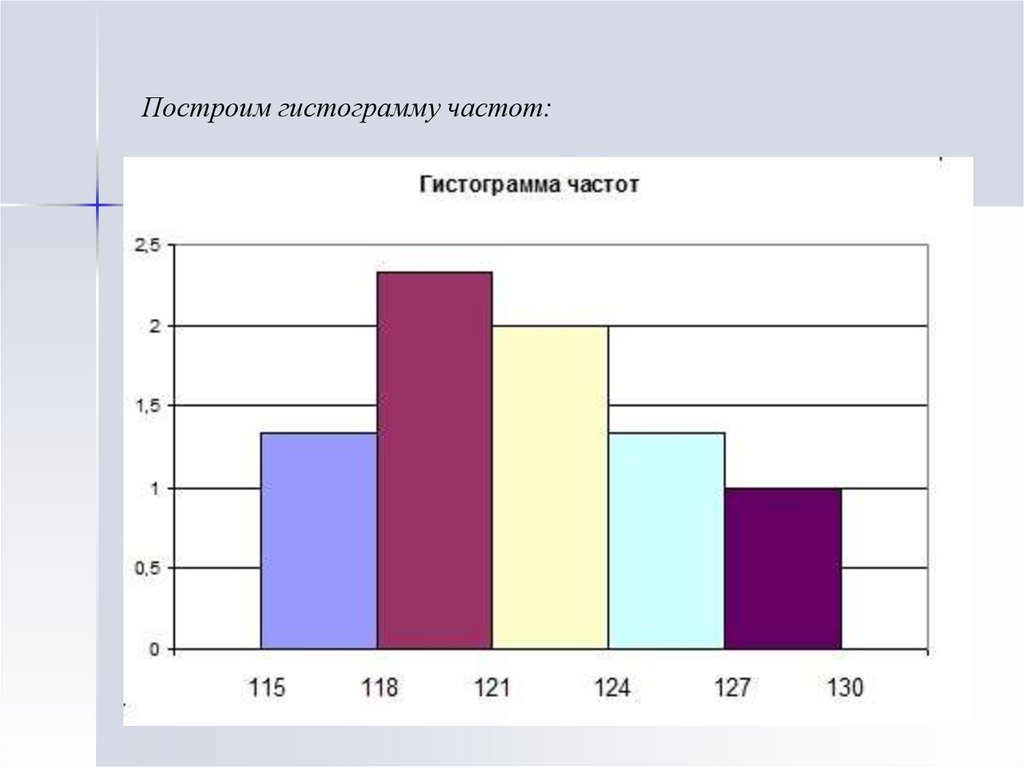
Число попаданий выборки в частичные промежутки
соответственно равны: [115, 118)-4, [118, 121)-7, [121, 124) - 6,
[124, 127) - 4, [127, 130) - 3. Соответственно высоты
прямоугольников равны: 4/3; 7/3; 2;4/3;1.
Определим ширину частичного промежутка: h

24.

Построим гистограмму частот:

25.

Вычислим среднее значение выборки (средний рост детей):
x
1 115 1 116 1 117 2 118 ... 2 124 2 125 2 127 1 130
121,5 см
24
Вычислим дисперсию:
1 115 121,5 1 116 121,5 ... 2 127 121,5 1 130 121,5
S0
13,06
24
2
2
Вычислим среднее квадратичное отклонение:
S 0 13,06 3,6
см
2
2

26.

Тест «Методы обработки и представления статистических данных»
Выберите правильный вариант ответа.
1. Исходным материалом для статистического исследования
являются:
а) статистические данные;
б) генеральные совокупности;
в) выборки.
2.
а)
б)
в)
Совокупность всех исследуемых объектов называют:
общей совокупностью;
выборкой;
генеральной совокупностью.
3. Совокупность случайно отобранных объектов из генеральной
совокупности называют:
а) выборкой;
б) гистограммой;
в) полигоном.

27.

Тест «Методы обработки и представления статистических данных»
Выберите правильный вариант ответа.
4.
а)
б)
в)
Основной метод обработки статистических данных:
разборный метод;
выборочный метод;
отборочный метод.
5. Размах выборки - это:
xmin xmax
xmax xmin
б)
в) x max x min
а)
6. Относительными частотами выборки называют:
а)
б)
n
n1 n2
; ;...; k
n n
n
n1 ; n2 ;...nk
n1 n2 ... nk
в)
n

28.

Тест «Методы обработки и представления статистических данных»
Выберите правильный вариант ответа.
7. Статистический ряд - это последовательность пар:
а)
x1 , x2 ; x2 , x3 ;... xk 1 , xk
в)
n1 , x1 ; n2 , x2 ;... nk , xk
x1 , n1 ; x2 , n2 ;... xk , nk
8.
а)
б)
в)
Полигон выборки представляет собой:
кривую;
ломаную линию;
прямую.
9.
а)
б)
а)
Дана выборка: 1,-2,10,-2,8,-5,4,7. Объем и размах выборки равен:
объем - 8; размах - 15;
объем - 10; размах - 13;
объем - 3; размах – 5.
б)

29.

Тест «Методы обработки и представления статистических данных»
Выберите правильный вариант ответа.
10. Дана выборки 1,-2,10,-2,8,-5,4,7.
Вариационный ряд этой выборки имеет вид:
а) 10, 8, 7, 4, 1, -2, -2, -5;
б) -5, -2, -2, 1, 4, 7, 8, 10;
в) -2 ,-2 ,-5, 10, 4, 1, 7, 8.

30.

Эталоны ответов к тесту:
Критерии оценивания: за каждый
правильный ответ - 1 балл
1
2
3
4
5
6
7
8
9
10
а
в
а
б
б
а
в
б
а
б

31.

Домашнее задание:
1. Изучить материал лекции.
2. Десять абитуриентов проходят тестирование. Каждый из них
может набрать от 0 до 5 баллов включительно. Группа
абитуриентов набрала следующие баллы: 5,3,0,1,4,2,5,4.1,5.
Записать полученную выборку в виде: а)вариационного ряда, б)
статистического ряда.
Спасибо за работу !