Similar presentations:
Обобщающие характеристики статистической совокупности
1. Обобщающие Характеристики Статистической Совокупности.
2. СРЕДНИЕ ВЕЛИЧИНЫ.
Средняя–
это
обобщающая
характеристика
выборочной
совокупности, исчисляемая для
однородных
статистических
совокупностей,
которая
имеет
двойственный характер.
3.
Для данной совокупности средняявеличина
является
конкретной
величиной,
но
в
отношении
индивидуальных значений признаков
средняя
является
величиной
абстрактной.
Средние бывают двух видов:
1. Средние объема
2. Структурные средние.
4. Формула степенной средней,
Служит базой для исчисления всехсредних объемов.
x
x f
f
z
1
z
i
i
Формула конкретной средней
зависит от показателя степени Z.
5. Формулы исчисления некоторых средних объема:
Вид среднейZ
гармоническая
-1
геометрическая
0
арифметическая 1
Формулы средней
простых
взвешенных
_
x
_
x
n
_
x
n
1
x
x1 x2 xn
x
n
M
x
M
x
_
_
x
_
x
f
(M x f )
f 1 f 2 fn
xn
x1 x2
x f
f
6. Средняя гармоническая
применяется в тех случаях, когдав
ряду
распределения
представлены
не
отдельно
варианты, а их произведения.
7. Средняя геометрическая
применяется в рядах динамикидля
расчетов
среднего
коэффициента
роста
и
прироста.
8. Средняя арифметическая простая
применяется в двух случаях:- если известен ряд не сгруппированных
данных, в которых число наблюдений
равно числу элементов.
- если имеется вариационный ряд, в
котором частоты равны между собой.
9. Средняя арифметическая взвешенная
применяетсяесли
в
представленном вариационном
ряду частоты не равны между
собой.
10. ПРИМЕР 1
Определите средний стаж работников предприятия,еслиизвестно
Стаж (х)
Число работников (f)
2
3
4
5
6
3
2
4
1
3
13
11.
_ xf 2 3 3 2 4 4 6 3 5 13,9л
x
13
f
12. ПРИМЕР 2
Определите среднюю процентную ставку по каждому видукредита по следующим данным:
№
бан
ка
1
2
Краткосрочный кредит
Долгосрочный кредит
Средняя
процентная
ставка(х)
Сумма
кредита (f)
Средняя
процентная
ставка(x)
Доход банка
(M)
40
50
400
600
18
15
27
45
Доход=процент*сумму кредита. Процент=доход/сумму кредита.
Если неизвестен числитель в формуле соотношений исходной
средней, то расчет средней производится по арифметической
взвешенной. Если неизвестен знаменатель,то средняя
рассчитывается по средней гармонической взвешенной.
13.
_xf
x кр.кредит f
_
x дол.кредит
40 400 50 600
46%
400 600
27 45
M
16%
M
27 45
X
18 15
14. ПРИМЕР 3
Определите среднюю внешнеторговую цену товара А, поданным
Страна Внешнеторговая
Стоимость
импортер цена,тыс.долл. экспорта,тыс.долл. (М)
(х)
Китай
10,2
7000
США
15,4
1900
Турция
7,8
970
15.
7000 1900 970M
x M 7000 1900 970 10,56
x
10,2 15,4 7,8
16. Расчет средних величин в интервальных рядах распределения.
Рассчитать по имеющимся данным средний объем полученногокредита
предприятиями
отрасли,моду
медиану,
дециль,коэффициент дифференциации, все показатели вариаций.
Стоимость
импортных
автомобилей,
тыс.$.
Число
автомобилей
f
X’
интервалы
X’
1-3
2
2
3-5
3
5-7
_
x x
_
x x f
2
_
x x
2
_
x x f
4
5,16
10,32
26,62
53,24
4
12
3,16
9,48
9,98
29,94
21
6
126
1,16
24,36
1,34
28,14
7-9
12
8
96
0,84
10,08
0,70
8,4
9 и свыше
12
10
120
2,84
34,08
,8,06
96,72
x
50
358
88,32
216,44
17.
Стоимостьимпортных
автомобилей,
тыс.$.
Число
автомобилей
f
x
1-3
2
3-5
3
5-7
21
7-9
12
9 и свыше
12
50
18. Продолжение таблицы
Стоимостьимпортных
автомобилей,
тыс.$.
x
Число
автомобилей
f
X’
интервалы
1-3
2
3-5
x A x A 2 x A 2
f
f
i
i
i
x A
x A
i
2
-4
-2
-4
4
8
3
4
-2
-1
-3
1
3
5-7
21
6
0
0
0
0
0
7-9
12
8
2
1
12
1
12
9 и свыше
12
10
4
2
24
4
48
50
29
71
19. Расчет средних величин в интервальных рядах распределения.
Дляпознания
статистической
совокупности
применяются
следующие структурные средние:
- мода;
- медиана;
- квартель;
- квантель;
- дециль;
- продциль.
20. Мода
это значение признака, котороечаще всего встречается в
ряду распределения.
Используется в торговле. В
интервальном
ряду
распределения
мода
рассчитывается
по
следующей формуле:
21.
MO
xMo i Mo
f
2
f
Mo
Mo
f
f
Mo 1
Mo 1
f
,
Mo 1
где X mo – нижняя граница модального
интервала;
i Mo – величина модального интервала;
f Mo - модальная максимальная частота;
f Mo-1 – частота, предшествующая
модальной;
f Mo+1 – частота, следующая за модальной.
Мо=5+(7-5)*(21-3)/(2*21+3-12)=6,36 тыс.$
Вывод:чаще всего встречаются автомобили со
стоимостью 6,36 тыс.$
22. Медиана
средняяобобщающая
характеристика, которая делит
всю совокупность на две равные
части, причем первая часть
должна иметь значения больше,
чем средний вариант, а другая
меньше.
В
интервальном
ряду
распределения
медиана
рассчитывается по специальной
формуле:
23.
Mе
x
Me
i
Me
f
2
f
S
Me 1
,
Me
где X Me – нижняя граница медиального
интервала;
i Me – величина медиального интервала;
f Me – медиальная частота, которая находится
там, где есть половина всех частот;
S Me-1 = сумма накопленных частот до
медиальной частоты.
Ме=5+2(50/2-92+3))/21=6,9 тыс.$
Вывод:половина автомобилей имеет стоимость 6,9
тыс.$
,а другая половина больше.
24. Дециль
средняя обобщающая характеристика,которая делит всю совокупность на
10 разных частей.
Нижний дециль показывает средний
признак для 10 % минимальных
значений. Частота нижнего дециля
будет находиться там, где будет
находиться 10% частот. Частота
верхнего дециля будет находиться
там, где будет находиться 9/10 всей
суммы частот.
25. Производится расчет нижнего и верхнего дециля.
Нижний дециль = d1 и рассчитывается поформуле:
f
d
1
x
10
i
d1
d1
f
S d1
.
d2
Верхний дециль = d9 и рассчитывается по
формуле:
9 f
d9
xd 9 i d 9
10
f
S d9
d9
.
26.
Децильный коэффициентдифференциации
K
K
d
d
d0
d1
10,16
2,03 раза
5
27. Показатели вариации
Для изучения строения статистическойсовокупности, для оценки ее однородности
и расчетов насколько точной является
представленная
средняя
величина,
рассчитывают показатели вариации.
Показатели
вариации
характеризуются
абсолютными, относительными и средними
величинами.
28. Расчет показателей вариации
Наименованиепоказателя
Для
несгруппированных
данных
R=max-min
Размах вариаций
Среднее линейное
отклонение
Дисперсия
Среднее
квадратическое
отклонение
Коэффициент
вариации
Для
сгруппированных
данных
x x
d
d
n
x x
2
2
2
2
x
x
x x f
f
2
x
x
f
2
n
n
x x f
f
x
100%
f
29. Размах вариаций
Это разница между максимальным иминимальным показателями.
R=max-min
R=10-2=8 тыс. долларов
30. Среднее линейное отклонение
Применяется в экономических расчетах дляхарактеристики территориальных и региональных
различий и показывает насколько каждый признак
отклоняется от средней величины.
x x f
d
d 88,32/50 1,76
f
– на эту сумму в среднем отличается каждый
признак.
31. Дисперсия
Более объективно отражает меру вариацийв статистике на практике.
x x
f
2
2
f
216,44/50 4,33 ттыс$
2
32. Среднее квадратическое отклонение
Является мерилом надежности средней.Чем меньше среднее квадратическое
отклонение, тем точнее среднее
представляет собой всю статистическую
совокупность.
2
2,08 ттыс$
33. Коэффициент вариации
Относительный показатель, которыйхарактеризует вариацию.
Если 10% , то колеблемость показателя
слабая, от 10% до 30% - умеренная, >30% высокая.
x
100%
2,08/7,16 *100% 29,1%
34.
При расчете дисперсии по интервальному рядураспределения с равными интервалами вычисления
можно производить по способу расчета от условного
0 или способу моментов по следующим формулам:
X A 2
(
) f
i
2
i 2 ( X A),
f
i – величина интервала
А – любое число в ряду распределения, которое как
правило находится или в середине ряда или имеет
наибольшую частоту.
35.
Расчет дисперсии по способу моментовпроводится по следующей формуле:
i (m2 m1 ),
2
2
2
X A
( i ) f
m1
f
где
X A 2
( i ) f
m2
f
m1 29/50 0,58
m2 71/50 1,42
2
2
1
,
42
2
(7,16 6) 4,33
2 (1,42 0,58 ) 4,33
2
2
2
36. Общая дисперсия
Показывает изменчивость признака,вызванную за счет группировочного
признака и дисперсии, возникающие в
каждой отдельной группе
37. Межгрупповая дисперсия
Обуславливает вариацию результативногопризнака за счет группировочного и
рассчитывают по следующей формуле:
2
2
2
x
x
i 0
n
2
x
x
i 0 f
f
где
,
- среднее, исчисленное в каждой группе
X 0 - среднее, исчисленной для всей
статистической совокупности
Xi
38. Среднее из групповых дисперсий
Характеризует случайную вариацию вкаждой отдельной группе и
рассчитывается по следующей формуле:
2
2
i fi
где
i - частная или групповая дисперсия,
которая рассчитывается:
i
2
fi
,
2
(
X
X
)
i i
n
39. Правило сложения дисперсий
По правилу сложения дисперсий общаядисперсия представляет собой сумму из
межгрупповой и средней из групповых
дисперсий:
0
2
2
2
40. Эмпирическое корреляционное отношение
Для характеристики тесноты связи междугруппировочными и результативными признаками
применяется эмпирическое корреляционное
отношение, которое рассчитывается:
2
2
0
Если показатель тесноты связи находится в пределах
от 0,1 до 0,3, то связь слабая; 0,3-0,5 – умеренная;
от 0,5 до 0,7 – заметная; 0,7–0,9 – тесная; 0,9–0,99 –
весьма тесная.
41. Коэффициент детерминации
Коэффициент детерминации – показываетдолю межгрупповой дисперсии в общей
дисперсии результативного признака и
характеризует силу влияния
группировочного признака на образование
общей вариации. Это эмпирическое
корреляционное отношение в квадрате:
2
0
2
2
42. Пример 4: Определите тесноту связи между формой собственности банка и размером его капитала, рассчитав эмпирическое
корреляционноеотношение и коэффициент детерминации по следующим данным:
Акционерные банки
банк
Собственный
капитал
1
2
3
4
5
100
150
80
190
230
x x( x x )
50
0
70
40
80
2500
0
4900
1600
6400
Частные банки
2 банк Собственный
капитал
1
2
3
4
5
80
95
150
60
40
x x ( x x )2
5
10
65
25
45
25
100
4225
625
2025
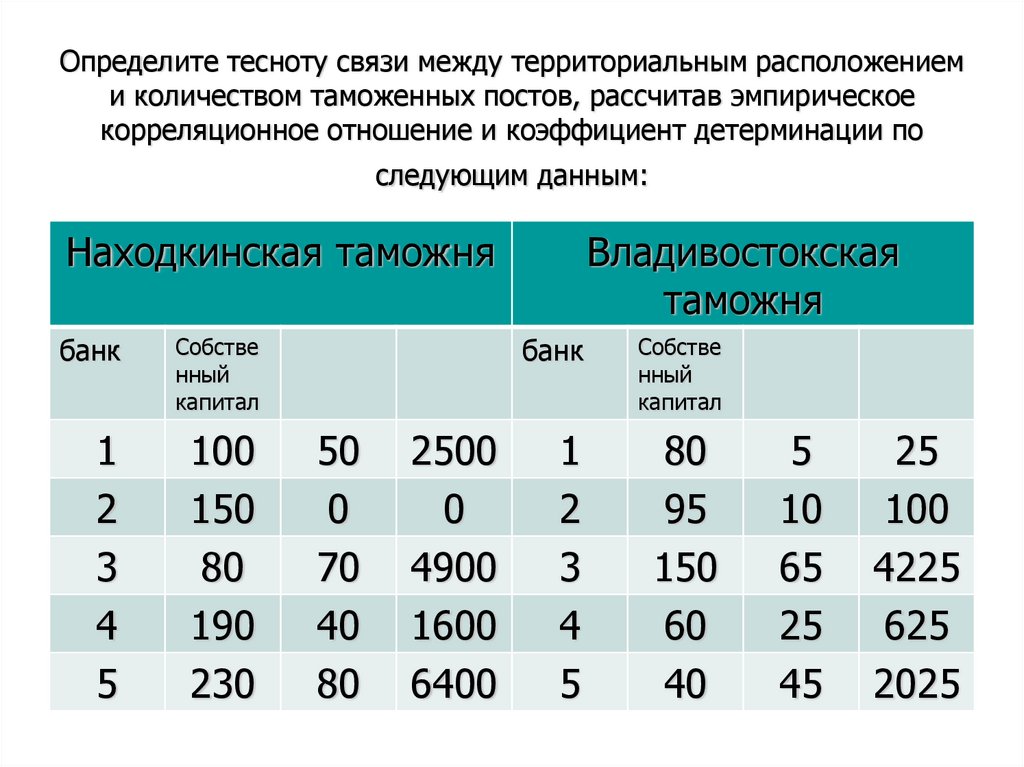
43. Определите тесноту связи между территориальным расположением и количеством таможенных постов, рассчитав эмпирическое
корреляционное отношение и коэффициент детерминации последующим данным:
Находкинская таможня
банк
Собстве
нный
капитал
1
2
3
4
5
100
150
80
190
230
50
0
70
40
80
2500
0
4900
1600
6400
Владивостокская
таможня
банк
Собстве
нный
капитал
1
2
3
4
5
80
95
150
60
40
5
10
65
25
45
25
100
4225
625
2025
44. Расчеты:
22
0
2
2
x
x
i 0 f
f
425
100 150 80 190 230
xаб
150 xчб
5
5
2
2
(150 117,5) 5 (85 117,5) 5
2
1056,25
10
2
fi
( X i X i )2
i
2
2
i
85 x0
150 85
117,5
2
f
а
2
i
n
3080 1400
7000
2
2
15400
2240
1400
3080 ч
2
5
5
0 2 2 2 1056,25 2240 3296,25
1056,25
0,32
3296,25
Коэффициент детерминации – это эмпирическое корреляционное отношение в квадрате:
Показывает, что на 12% вариация капитала обусловлена различиями в форме собственности и
на 88% зависит от влияния прочих факторов.
2 0,322 0,12
45.
При расчете дисперсии качественных признаков если имеются 2взаимоисключающих варианта, применяется дисперсия
альтернативного признака.
Если присутствующий альтернативный признак обозначить 1, а
его отсутствие 0 и принять, что p – это доля единиц, у которых
данный признак присутствует в статистической совокупности, а
q – это доля единиц, у которых данный признак отсутствует, то
тогда расчет средней и дисперсий альтернативных признаков
будет производится следующим образом:
x
1
0
f
P
q
x
x f 1 p 0 q p
p q
f
( x x ) f (1 p)
f
2
2
2
p (0 p ) 2 q
pq
p q










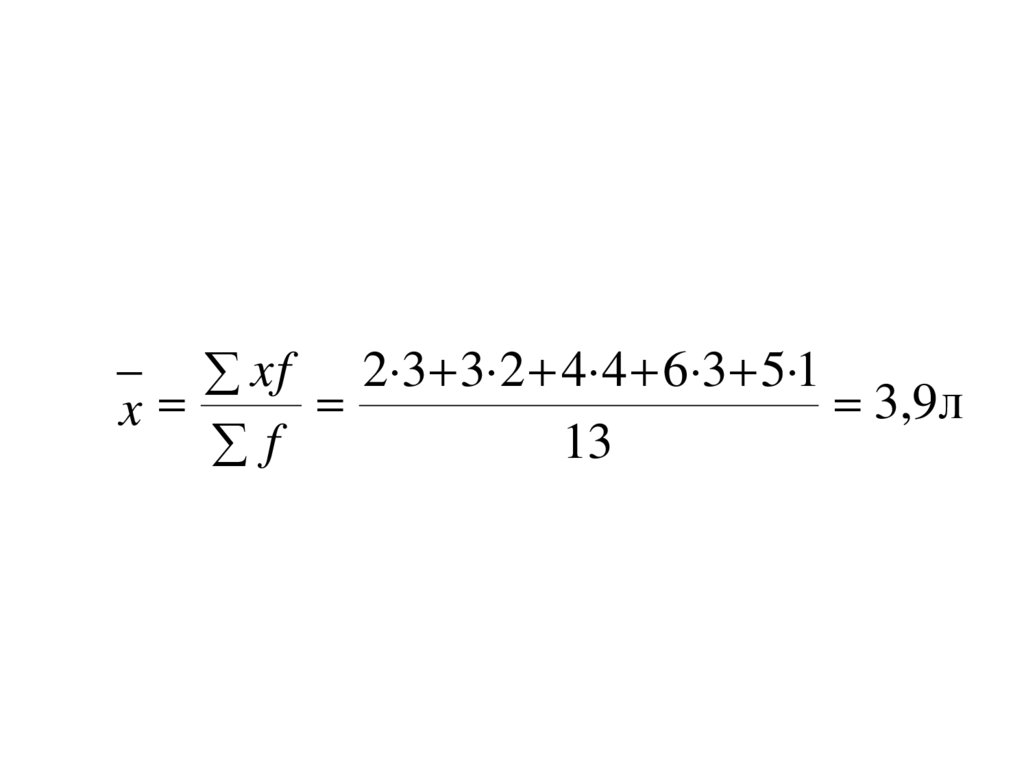

































 mathematics
mathematics