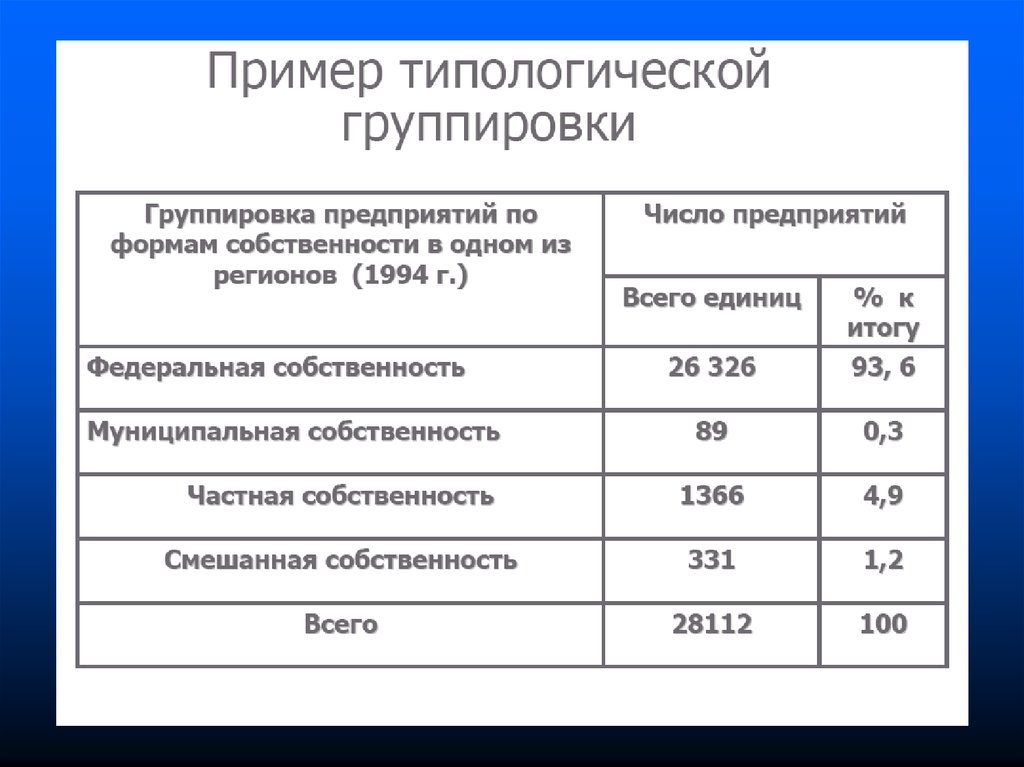
Группировка. Группировочные признаки

1.

2.

3.

4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

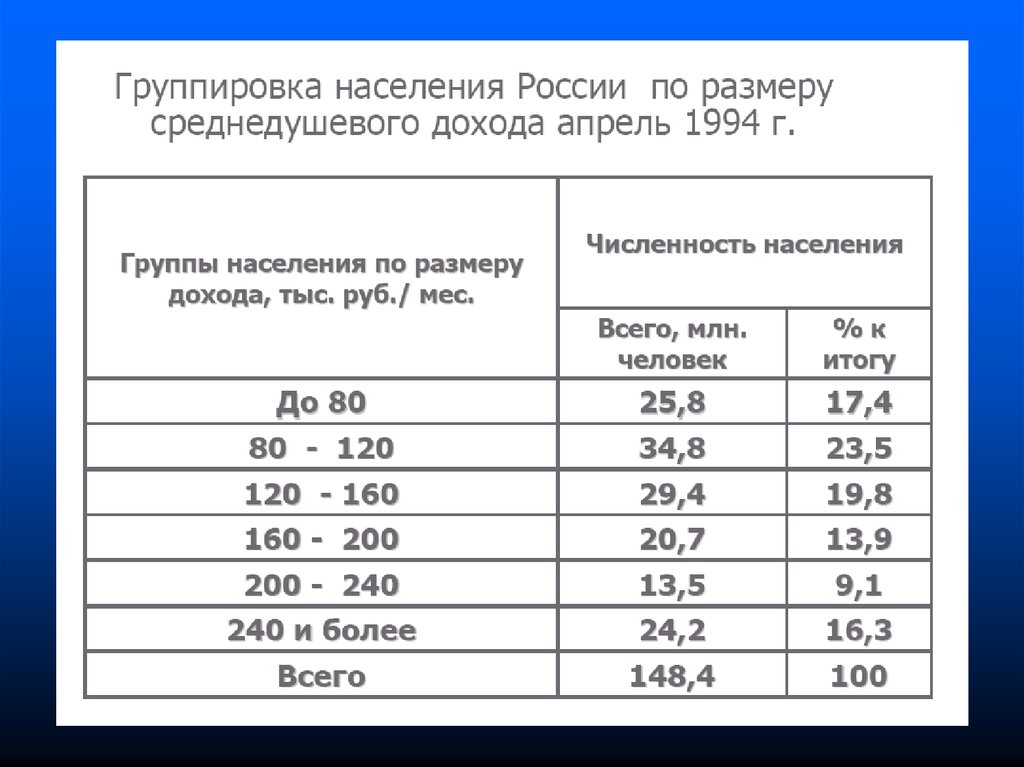
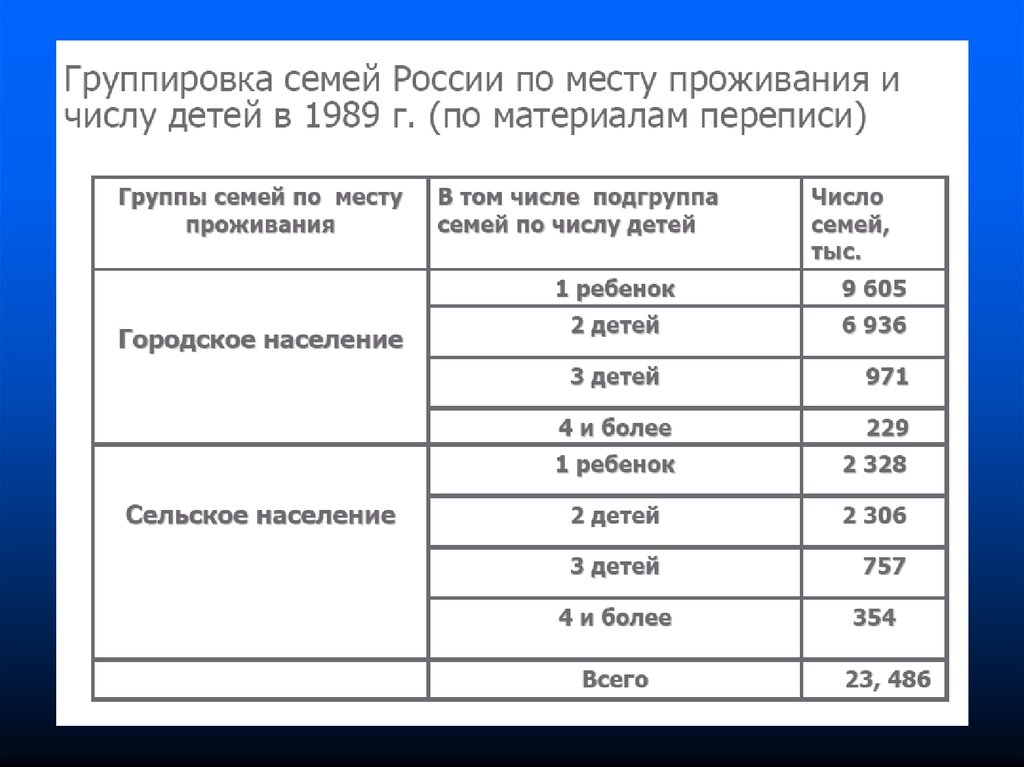
16. 1 Относительные и абсолютные показатели

17.

18.

19.

20.

21.

22.

23.

24.

25.

26.

27.

28.

29.

30.

31.

32.

33.

34.

35. 2 Статистические показатели, используемые для характеристики рядов распределений. Виды средних.

36. Статистические показатели вариационного ряда

1. Среднее значение, мода, медиана
- характеризуют наиболее
типичные значения признака
2. Среднеквадратичное отклонение,
среднее линейное отклонение,
размах вариации
- характеризуют разброс значений
признака в статистической
совокупности

37.

38.

39.

40.

41.

42.

43.

xi

44.

45.

46.

47.

48.

49.

50.

51. 3 Медиана и мода

52. Медиана распределения - значение признака, которое приходится на середину ранжированной статистической совокупности Признаку,

определяющий медиану
дискретного ряда (медианному интервалу
непрерывного ряда)
соответствует первое значение накопленной
доли, превышающее 0.5
Для интервальных рядов медиана
вычисляется по специальной формуле

53.

Функция распределения интервального ряда
1,2
1
0,8
F(x) 0,6
0,4
Me
0,2
0
1
3
5
7
9
x
11
13
15

54.

55.

xi
Дискретный ряд
fi
Середина совокупности приходится на 48 по
счету квартиру (95/2=47.5). В этой квартире
3 комнаты. Медиана равна 3

56.

Интервальный ряд

57.

Середина совокупности приходится на
57500-ю семью (115/2=57.5).
Медианный интервал (на котором
накопленная частота впервые
превышает 115/2 ) - интервал (7-9).
Me=7+(57.5-30)/40.2

58.

59.

Диаграмма интервального ряда
50
40
fi
30
20
10
0
3
5
7
Mo
x
9
11
13

60.

Модальным является интервал
(7-9)
Mo= 7+(40-20)/(40-20+40-30) .2

61. 5.4. Показатели вариации

62. Размах вариации

Размах вариации R = xmax - xmin
показывает, насколько велико различие
между максимальным и минимальным
значением признака.
Поскольку размах вариации исчисляется
только с использованием крайних значений
совокупности, то он может содержать
большие ошибки (из-за влияния случайных
факторов крайние точки могут вообще
оказаться выбросами)

63. Среднее линейное отклонение

Важной структурной характеристикой
вариационного ряда является среднее
линейное отклонение, которое вычисляется
по формулам
xi x
d
n
;
xi x
d
fi
fi
в зависимости от формы представления
вариационного ряда. В первой из этих формул
суммирование производится по всем членам
вариационного ряда, а во второй - по всем
группам.

64. Дисперсия

Дисперсия характеризует степень рассеяния
индивидуальных значений признака в совокупности
от среднего значения и вычисляется по формулам
xi x
.
2
2
n
Записанное выражение называется формулой
простой дисперсии. Ряд предполагается не
сгруппированным и суммирование идет по всем
членам ряда совокупности.

65. Взвешенная дисперсия

В этом случае (взвешенная дисперсия)
вариационный ряд предполагается
сгруппированным и суммирование ведется по всем
группам. fi - частота повторения признака в i - й
группе.
xi x f i
fi
2
2

66. Среднее квадратическое отклонение

Среднее квадратическое отклонение
2
представляет собой характеристику
вариационного ряда, которая отражает
рассеянность членов совокупности относительно
среднего значения. Чем меньше среднее
квадратическое отклонение, тем лучше среднее
значение характеризует всю совокупность.

67. Другие показатели вариации

Коэффициент осцилляции VR
R
VR 100 %;
x
Линейный коэффициент вариации Vd
d
Vd 100 %;
x
Коэффициент вариации
V
V 100 % .
x

68. Пример вычисления показателей вариации

Рассмотрим вычисление среднего линейного
отклонения, дисперсии и среднеквадратичного
отклонения для интервального ряда
распределения промышленных предприятий
одного из районов города по вооруженности
работников промышленно – производственными
основными фондами (ППОФ) представленного в
табл. 24 (см. следующий слайд)

69. Табл.

Группы фирм по ППОФ
на одного работника,
тыс. руб. Xi
До 1
1,0 – 2,0
2,0 – 3,0
3,0 – 5,0
5,0 – 10,0
10,0 – 20,0
20 и более
Всего
Число фирм
в % к итогу
fi
7,8
12,2
14,9
23,3
24,3
10,6
6,9
100
Середина
интервал
а Xi’
0,5
1,5
2,5
4
7,5
15,0
25
-

70. Вычисление дисперсии в случае интервального ряда

В случае интервального ряда в качестве
значения вариационного признака xi берутся
середины интервалов

71. Схема вычисления среднего линейного отклонения

f
7,80
12,20
14,90
23,30
24,30
10,60
6,90
Средн. Знач.
x
xf
0,50
3,90
1,50 18,30
2,50 37,25
4,00 93,20
7,50 182,25
15,00 159,00
25,00 172,50
6,66
|(x - средн.Зн)|*f
48,08
63,00
62,04
62,07
20,31
88,36
126,52
470,39
ср. лин откл.
4,7039

72. Схема вычисления дисперсии

f
7,80
12,20
14,90
23,30
24,30
10,60
6,90
ср. знач.=
x
0,50
1,50
2,50
4,00
7,50
15,00
25,00
6,664
(x - ср. знач.)^2*f
296,36
325,34
258,35
165,36
16,98
736,58
2319,84
4118,81
4118,81
41,1881
100
2

73. 6. Эмпирическое определение тесноты корреляционной связи. Правило сложения дисперсий.

74.

Рассмотрим
аналитическую
группировку
данных по двум признакам. По первому
признаку (группировочный или факторный
признак)
мы
разобьем
статистическую
совокупность на несколько групп, а затем
исследуем в каждой группе характеристики
второго признака (результативный признак). А
именно, найдем для каждой группы среднее
значение
и
дисперсию
результативного
признака. Для этих величин вводятся новые
названия - групповое среднее и групповая
(внутригрупповая) дисперсия.

75.

№ группы
Объем
группы
ni
1
n1
2
n2
3
n3
...
...
Среднее для
группы
Внутригрупповая
дисперсия
...
...
Внутригрупповой дисперсией j -ой группы называется
обычная дисперсия, вычисленная для группы с номером j .

76.

Внутригрупповая дисперсия вычисляется по
формуле
где xij - значения вариант,
fij - частот,
- среднее значение , а
- объем для j -ой группы.

77.

По имеющимся данным можно вычислить общее
среднее:

78. Межгрупповая дисперсия

Межгрупповой дисперсией называется
дисперсия групповых средних, рассчитанная с
учетом объема каждой группы nj

79. Средняя из групповых дисперсий. Формула сложения дисперсий

В математической статистике показано, что между
общей дисперсией, межгрупповой дисперсией и
средней из групповых дисперсией, определяемой
формулой
2
2
j n j
j
/ n, n n j .
j
существует простая связь, выражающая правило
сложения дисперсий
.
2
2
2

80. Эмпирическое корреляционное отношение - количественная характеристика тесноты связи факторного и результативного признаков -

Эмпирическое
корреляционное
отношение
количественная
характеристика
тесноты
связи
факторного
и
результативного признаков
- равно
корню квадратному из отношения
межгрупповой дисперсии к общей
дисперсии

81. По величине эмпирического корреляционного отношения можно определить, насколько сильно связаны факторный и результативный

признаки.
0-0.3 связь отсутствует
0.3-0.5 слабая
0.5-0.7 умеренная
0.7-1 сильная связь.

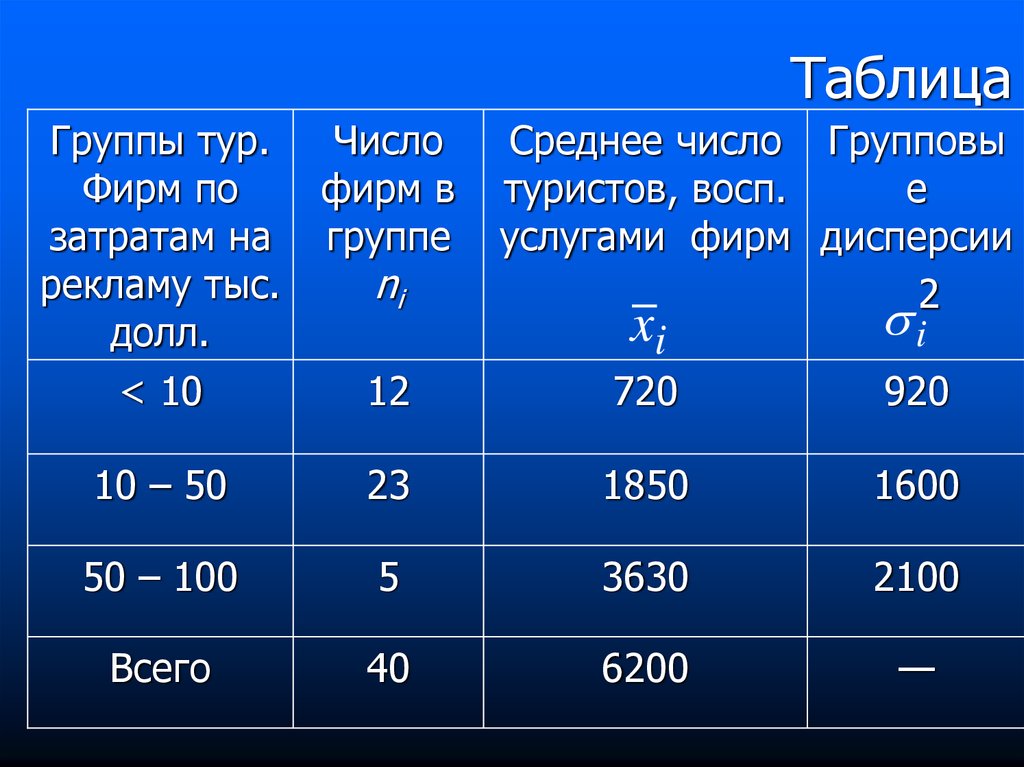
82. Пример решения задачи

Задача. По данным таблицы (см. след слайд)
вычислить общую дисперсию, а также
характеризовать степень влияния объема затрат
туристических фирм на рекламу, на вариацию
количества туристов, воспользовавшихся услугами
этих фирм.

83. Таблица

Группы тур.
Фирм по
затратам на
рекламу тыс.
долл.
< 10
Число
фирм в
группе
10 – 50
23
1850
1600
50 – 100
5
3630
2100
Всего
40
6200
—
ni
12
Среднее число Групповы
туристов, восп.
е
услугами фирм дисперсии
2
i
xi
720
920

84. Решение задачи

1. Вычисляем среднее значение
xi ni
x
ni
720 12 1850 23 3630 5
12 23 5
1733,5 чел.
2. Найдем среднюю групповую дисперсию
920 12 1600 23 2100 5
1458,5.
12 23 5
2

85.

3. Вычислим межгрупповую дисперсию
1
1
2
2
( xi x ) ni [ 12 ( 1733,5 720 )
n
40
2
2
23 ( 1850 1733,5 ) 5 ( 3630 1733,5 ) ]
766548.
2
4. Общая дисперсия равна
766548 1458 ,5 768006 ,5.
2
2
2

86. Сделаем выводы

• Средняя из групповых дисперсий значительно
меньше межгрупповой дисперсии. Это значит,
что группы существенно отличаются одна от
другой. Это в свою очередь означает, что
затраты на рекламу существенно сказываются на
число туристов, воспользовавшихся услугами
данной фирмы . Формальным признаком этого
является большое значение эмпирического
корреляционного отношения
766548
0
,
999
.
2
768006 ,5
2

87. 7. Альтернативный признак. Среднее значение и дисперсия. Эмпирическая оценка тесноты связи в случае альтернативного признака.

88. Рассмотрим вариационный ряд с двумя возможными значениями признака (альтернативный признак)

Пусть p - доля единиц совокупности,
обладающих некоторым признаком, а q - доля
единиц совокупности, не обладающих этим
признаком. Тогда можно построить
вариационный ряд для альтернативного
признака x, принимающего всего два значения:
xi
wi
0
q
1
p

89. Вычисление среднего значения и дисперсии

Среднее значение и дисперсия такого ряда
вычисляется по формулам:
0 q 1 p
x
p;
q p
2
2
2 ( 0 p ) q (1 p ) p
p
p q.
p q

90. Внутригрупповая и межгрупповая дисперсии для альтернативного признака

Пусть
имеется аналитическая группировка,
включающая несколько групп, характеризуемых
альтернативным признаком (с двумя возможными
значениями варианты). Так же, как и в случае
вариационного признака с большим количеством
градаций, для этих групп можно ввести понятия
внутригрупповой,
межгрупповой,
полной
и
средней из групповых дисперсий.

91.

Внутригрупповая дисперсия и
среднегрупповая дисперсии определяются
по формулам:
2
pi
pi qi ;
k
2
p
pi qi ni
i 1
k
ni
i 1
, i номер группы.

92.

Формула межгрупповой дисперсии имеет вид
(p - доля признака во всей совокупности, она
же - общее среднее)

93.

Общая дисперсия вычисляется по формуле
Как и в случае рядов, построенных по
количественному признаку, справедлива
формула сложения дисперсий
2
p
2
p
2
p.

94. Пример вычисления дисперсий доли

Данные об удельном весе рабочих основных
специальностей в трех цехах предприятия
представлены в таблице
1
Удельный вес рабочих
основных спец. , % Pi
80
Численность
всех рабочих ni
100
2
75
200
3
90
150
Всего
—
450
Цех

95.

Найдем среднюю долю основных рабочих
0,8 100 0,75 200 0,9 150
p
0,81 .
100 200 150
Вычислим общую дисперсию
2
p p( 1 p ) 0,81( 1 0,81 ) 0,154.

96.

Вычислим внутригрупповые дисперсии
2
p1 0,8(1 0,8) 0,154 ;
2
p 2 0,75(1 0,75) 0,19;
2
p 3 0,9(1 0,9) 0,09 .
Средняя из групповых дисперсий
2
p
0,16 100 0,19 200 0.09 150
0,15
100 200 150

97.

Найдем межгрупповую дисперсию
1
2
2
[( 0,8 0,81 ) 100 ( 0,75 0,81 ) 200
450
2
( 0,9 0,8 ) 150 ] 0,004.
2
Проверяем вычисления, используя формулу
сложения дисперсии
2
p
2
2
p;
0,154 0,15 0,004.

98. Выводы

1. Межгрупповая дисперсия является малой. Она
существенно меньше средней из
внутригрупповых дисперсий. Это означает,
что цеха различаются по числу основных
рабочих незначимо.
2. Тот же самый вывод можно получить,
вычислив эмпирический коэффициент
корреляции
2
0,004
0
,
16
.
2
0,154