Similar presentations:
Средние величины
1. Тема: Средние величины
2.
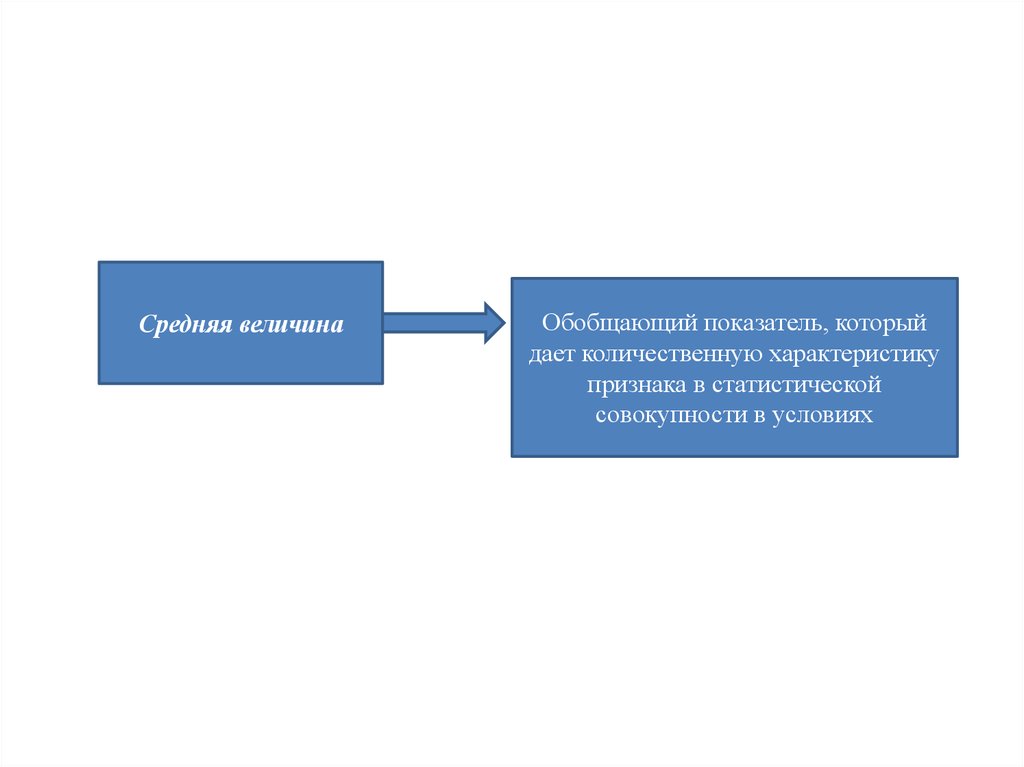
Средняя величинаОбобщающий показатель, который
дает количественную характеристику
признака в статистической
совокупности в условиях
3.
Условия правильного применения средней величины:Средняя величина должна исчисляться лишь для совокупностей, состоящих из
однородных единиц
Совокупность, неоднородную в качественном отношении, необходимо разделять
на однородные группы и вычислять для них групповые типичные средние,
характеризующие каждую из этих групп. В этом проявляется связь между
методами группировок и средних величин
Средняя величина сглаживает индивидуальные значения и тем самым может
элиминировать различные тенденции в развитии, скрыть передовое и отстающее,
поэтому кроме средней величины следует исчислять другие показатели
Среднюю величину целесообразно исчислять не для отдельных единичных фактов,
взятых изолированно друг от друга, а для совокупности фактов
4.
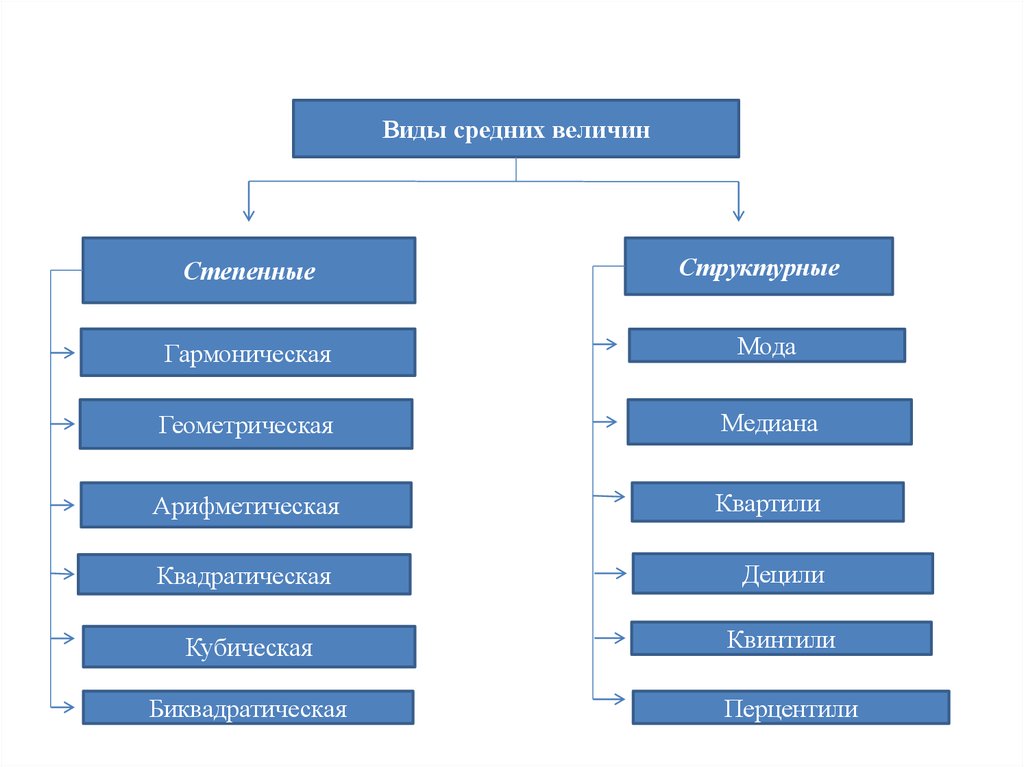
Виды средних величинСтепенные
Структурные
Гармоническая
Мода
Геометрическая
Медиана
Арифметическая
Квартили
Квадратическая
Децили
Кубическая
Квинтили
Биквадратическая
Перцентили
5.
XСредняя степенная
простая
K
X
K
n
где К – показатель степени.
где К – показатель
степени.
Применяется
в случае,
если каждая
Применяется
в
случае,
каждая
варианта Х встречается в если
совокупности
варианта
один
или Х встречается в совокупности
один или
6.
X ff
K
X
Средняя степенная
взвешенная
i
i
где fi - показатель повторяемости вариант
(веса, частоты).
Применяется в случае, если каждая варианта
Х встречается в совокупности не одинаковое
число раз, т.е. по сгруппированным данным
7.
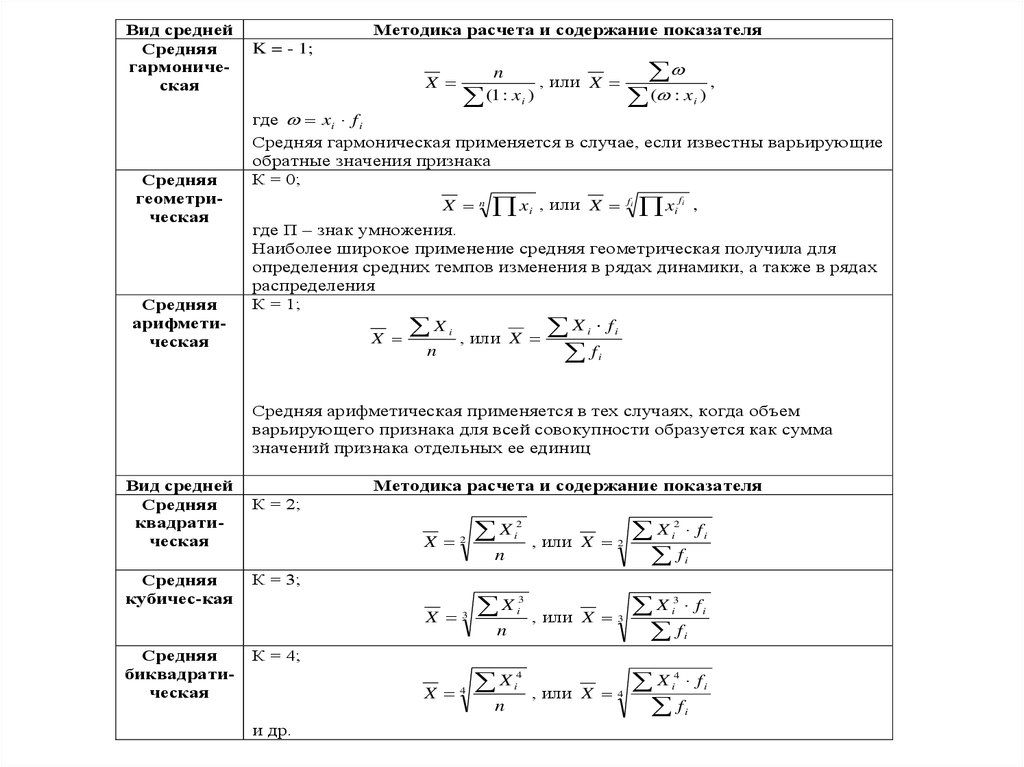
Вид среднейСредняя
гармоническая
Средняя
геометрическая
Средняя
арифметическая
Методика расчета и содержание показателя
K = - 1;
X
n
, или X
(1 : xi )
,
( : x )
i
где xi f i
Средняя гармоническая применяется в случае, если известны варьирующие
обратные значения признака
К = 0;
X
n
x
i
, или X
fi
x
fi
,
i
где П – знак умножения.
Наиболее широкое применение средняя геометрическая получила для
определения средних темпов изменения в рядах динамики, а также в рядах
распределения
К = 1;
X i , или X X i f i
X
n
fi
Средняя арифметическая применяется в тех случаях, когда объем
варьирующего признака для всей совокупности образуется как сумма
значений признака отдельных ее единиц
Вид средней
Средняя
квадратическая
Средняя
кубичес-кая
Средняя
биквадратическая
Методика расчета и содержание показателя
К = 2;
X
2
X
2
i
n
, или X
2
X f
f
2
i
i
i
К = 3;
X
3
X
3
i
n
, или X 3
X f
f
3
i
i
i
К = 4;
X
и др.
4
X
n
4
i
, или X
4
X f
f
4
i
i
i
8.
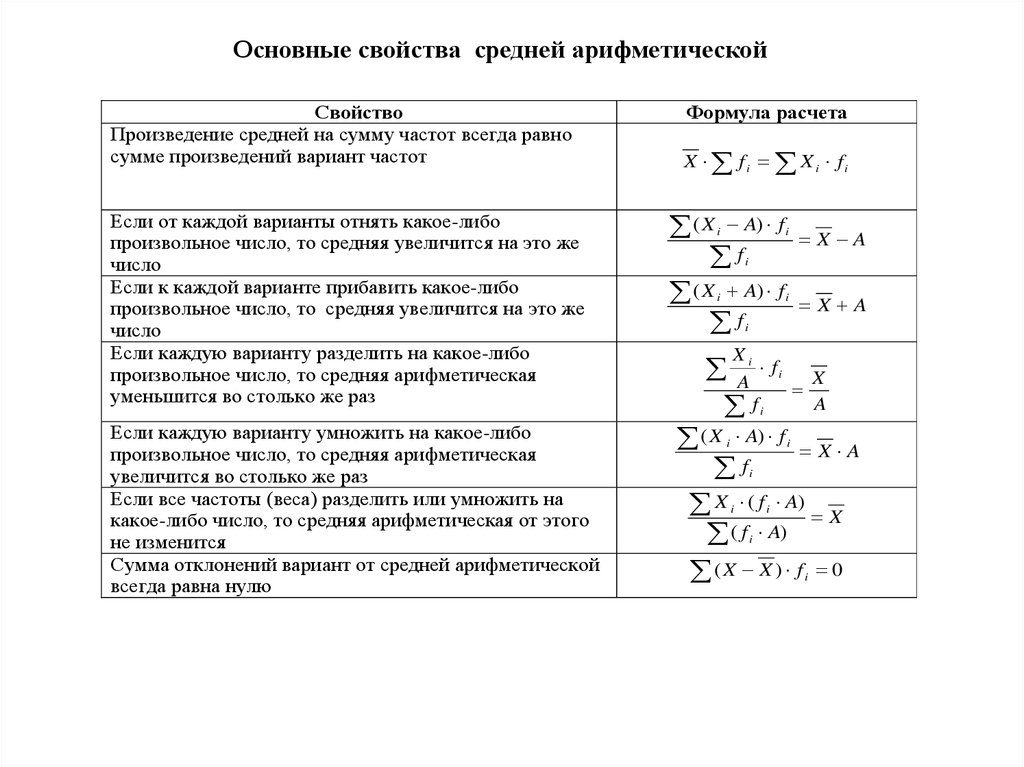
Основные свойства средней арифметическойСвойство
Произведение средней на сумму частот всегда равно
сумме произведений вариант частот
Если от каждой варианты отнять какое-либо
произвольное число, то средняя увеличится на это же
число
Если к каждой варианте прибавить какое-либо
произвольное число, то средняя увеличится на это же
число
Если каждую варианту разделить на какое-либо
произвольное число, то средняя арифметическая
уменьшится во столько же раз
Формула расчета
X fi X i fi
( X A) f
f
( X A) f
f
i
i
X A
i
X A
i
i
i
Xi
A f
f
i
X
A
i
Если каждую варианту умножить на какое-либо
произвольное число, то средняя арифметическая
увеличится во столько же раз
Если все частоты (веса) разделить или умножить на
какое-либо число, то средняя арифметическая от этого
не изменится
Сумма отклонений вариант от средней арифметической
всегда равна нулю
( X A) f X A
f
X ( f A) X
( f A)
(X X ) f 0
i
i
i
i
i
i
i
9.
МодаВеличина признака (варианта),
которая чаще всего встречается
в данной совокупности. В
вариационном дискретном ряду
модой выступает варианта,
имеющая наибольшую частоту
10.
Медианаварианта, которая находится в
середине вариационного ряда.
Медиана делит ряд пополам, по обе
стороны от нее (вверх и вниз)
находится одинаковое количество
единиц совокупности
11.
Виды структурных (непараметрических) среднихВид
Средней
Мода
Методика расчета показателя
В интервальных рядах с равными интервалами мода вычисляется по
формуле
( f m f m 1 )
,
Mo X 0 i
( f m f m 1 ) ( f m f m 1 )
Где X0 – минимальная граница модального интервала;
i – величина модального интервала;
fm – частота модального интервала;
fm-1 – частота интервала, предшествующего модальному интервалу;
fm+1 – частота интервала, следующего за модальным.
Модальный интервал в интервальном ряду определяется по наибольшей
частоте
12.
МедианаВ дискретном вариационном ряду определение медианного значения
признака сводится к определению номера медианной единицы ряда по
формуле
n 1
,
N ME
2
где n – объем совокупности.
Полученное значение показывает, где точно находится номер медианной
единицы (номер середины ряда). Медианное значение характеризуется тем,
что его кумулятивная частота (сумма накопленных частот по группам) равна
половине суммы всех частот или превышает ее.
В интервальном ряду с равными интервалами медиана рассчитывается по
формуле
1
f S m 1
2
,
Me X 0 i
fm
где X0 – начальное значение медианного интервала;
i - величина медианного интервала;
∑f – сумма частот ряда;
Sm-1 - сумма накопленных частот в интервалах, предшествующих
медианному;
fm – частота медианного интервала.
Для определения медианного интервала необходимо рассчитать суммы
накопленных частот. Медианный интервал характерен тем, что его
кумулятивная частота равна полусумме всех частот ряда или превышает ее
13.
КвартилиЗначения признака, делящие ранжированную совокупность на четыре
равные части. Различают нижний квартиль (Q1), отделяющий ¼ часть
совокупности с наименьшими значениями признака, и верхний квартиль
(Q3), отсекающий ¼ часть с наибольшими значениями признака. Средний
квартиль (Q2) совпадает с медианой (Me). Для расчета квартилей по
интервальному вариационному ряду используют формулы
1
f S Q1 1
4
Q1 X Q1 i
;
f Q1
Q3 X Q3
3
f S Q3 1
4
i
,
f Q3
где XQ (XQ ) – нижняя граница интервала, содержащего нижний квартиль
(верхний) квартиль;
i - величина интервала;
SQ -1 (SQ -1) – накопленная частота интервала, предшествующего
интервалу, содержащему нижний квартиль (верхний) квартиль;
fQ (fQ ) – частота интервала, содержащего нижний квартиль (верхний)
квартиль
1
3
1
1
3
3
14.
ДецилиВарианты, делящие ранжированный ряд на десять равных частей; они
вычисляются по той же схеме, что и квартили:
1
f S d1 1
;
d1 X d1 i 10
f d1
2
f S d2 1
10
d 2 X d2 i
f d2
и т.д.
Квинтили Значения признака, делящие ряд на пять равных частей. Они вычисляются
по той же схеме, что квартили и децили
Перцентили Значения признака, делящие ряд на 100 равных частей
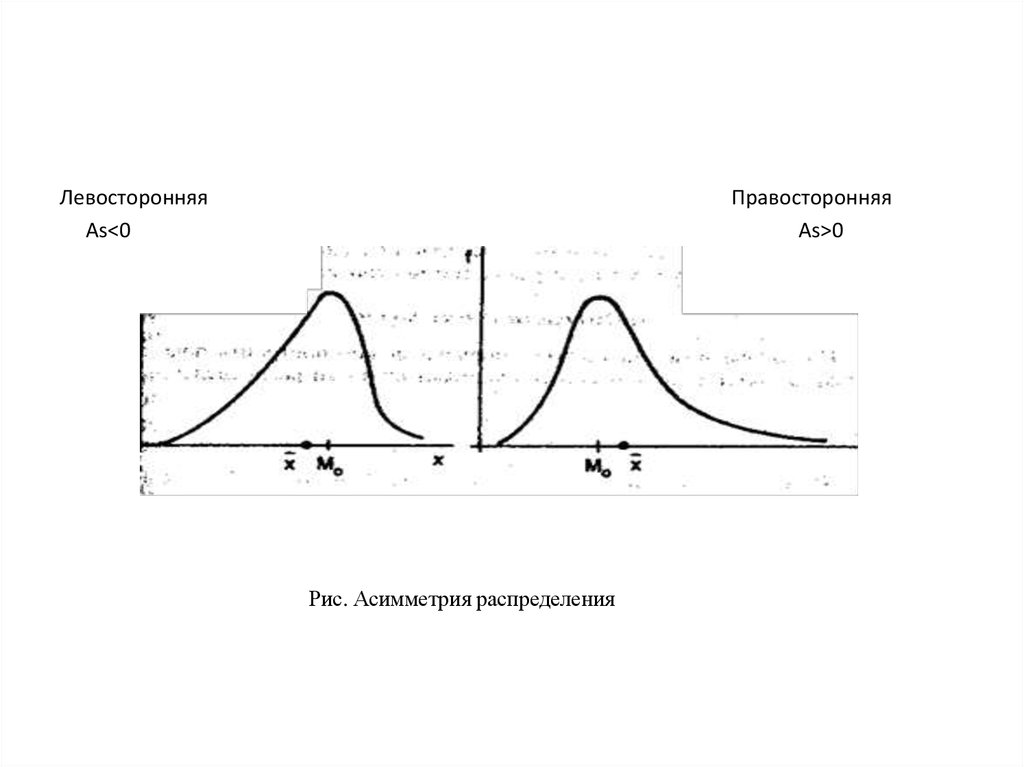
15. ТЕМА «ПОКАЗАТЕЛИ ВАРИАЦИИ И АНАЛИЗ ЧАСТОТНЫХ РАСПРЕДЕЛЕНИЙ»
1. АБСОЛЮТНЫЕ И ОТНОСИТЕЛЬНЫЕ ПОКАЗАТЕЛИВАРИАЦИИ.
2. ВИДЫ ДИСПЕРСИЙ. ПРАВИЛО СЛОЖЕНИЯ
ДИСПЕРСИЙ.
3. МОМЕНТЫ
РАСПРЕДЕЛЕНИЯ.
ПОКАЗАТЕЛИ
ФОРМЫ РАСПРЕДЕЛЕНИЯ.
16.
ПоказательМетодика расчета и содержание
Характеристика границ вариации изучаемого признака. Определяется по
Размах
вариации формуле
R X max X min ,
где Xmax - максимальное значение варьирующего признака;
Xmin - минимальное значение варьирующего признака.
Показывает, сколь велико различие между единицами совокупности,
имеющими самое маленькое и самое большое значение признака, основан
на крайних значениях варьирующего признака и не отражает отклонений
всех вариант в ряду
17.
ДисперсияСредний квадрат отклонений индивидуальных значений признака от их
средней величины. Вычисляется по следующим формулам.
1-й способ определения дисперсии
( X i X )2 fi
( X i X )2
2
2
,
, или
fi
n
где Xi - индивидуальные значения варьирующего признака (варианты);
X - среднее значение варьирующего признака;
n – количество разновидностей вариант;
fi – показатель повторяемости вариант (частоты, веса)
2-й способ определения дисперсии
2
2 X ( X )2 ,
2
где X - средняя из квадратов индивидуальных значений;
( X ) 2 - квадрат средней величины признака
3-й способ определения дисперсии – метод моментов
2 i (m2 m12 ) ,
где i – величина интервала в интервальном ряду;
m1 - момент первого порядка;
m2 - момент второго порядка, который определяется по формуле
2
Xi A
i f i
m2
fi
18.
Обобщающая характеристика размеров вариации признака в совокупностиСреднее
определяется по формуле
квадратическое
2
2
(
X
X
)
fi
(
X
X
)
i
i
2
отклонение
, или
.
n
fi

















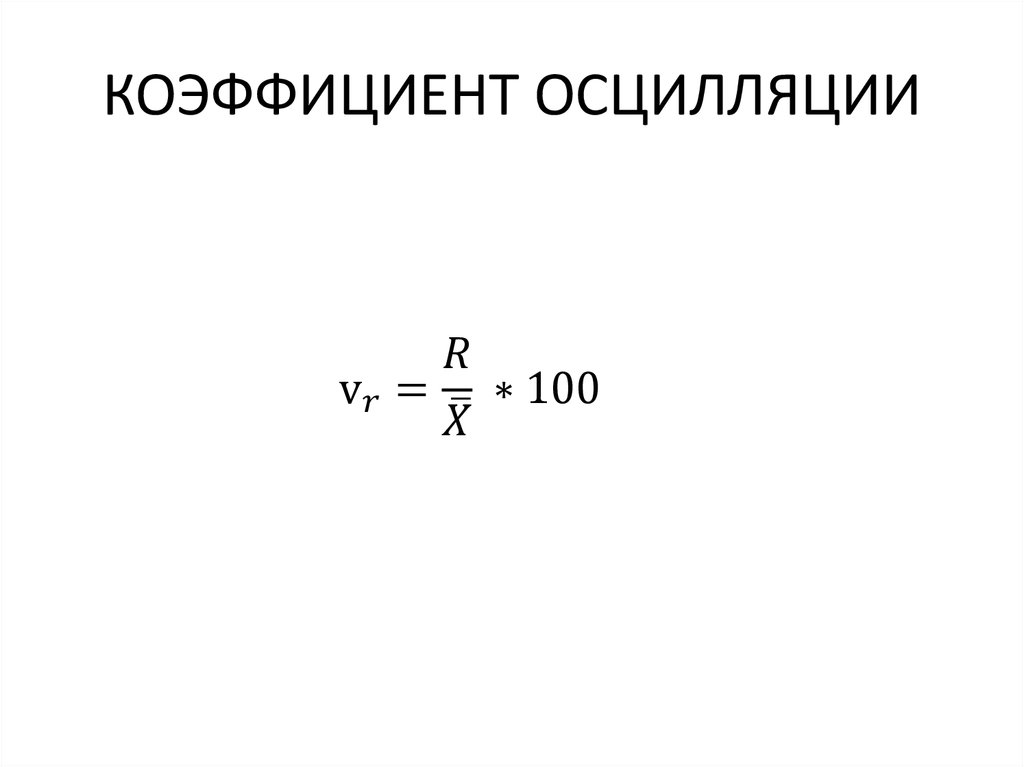


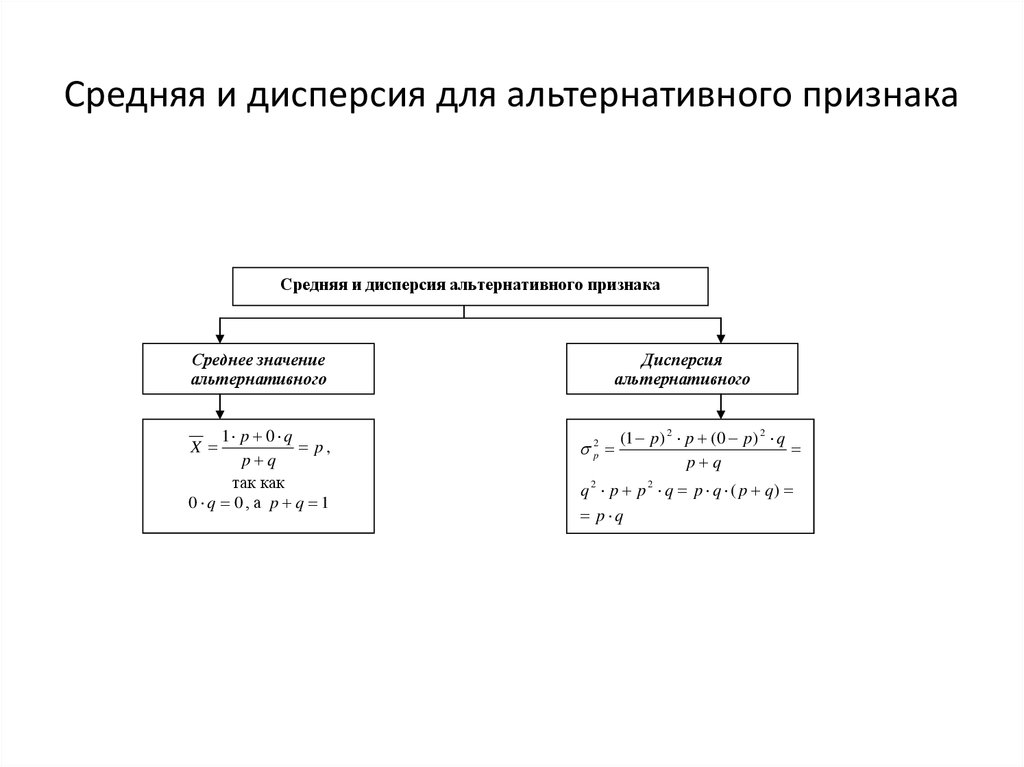

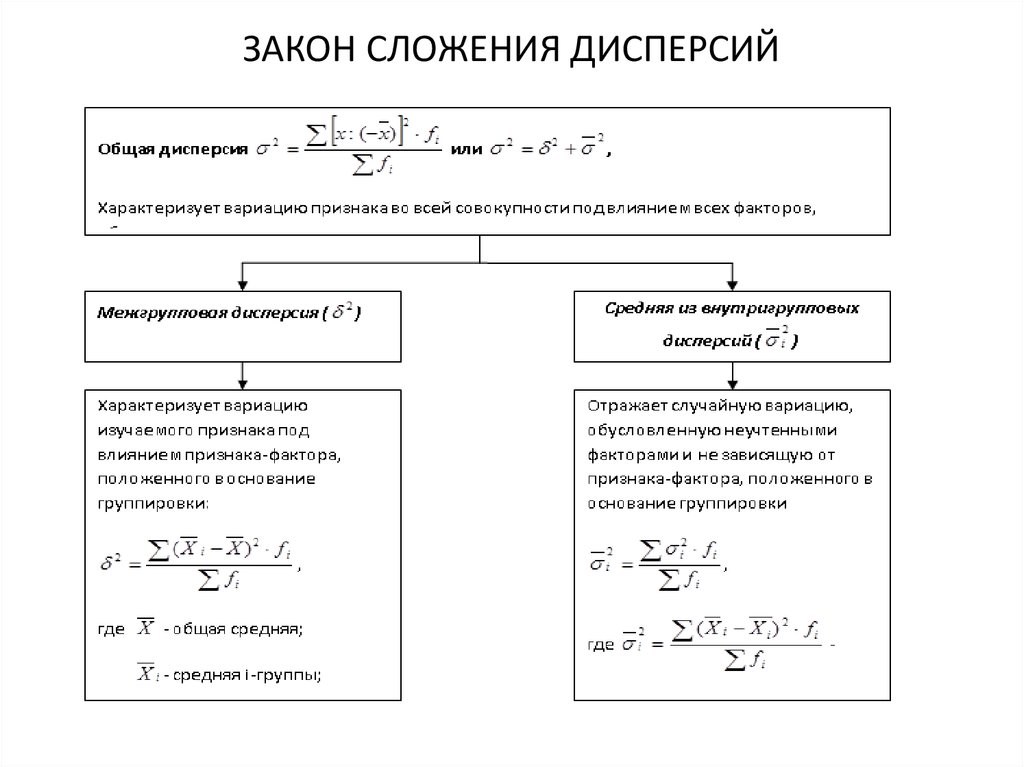


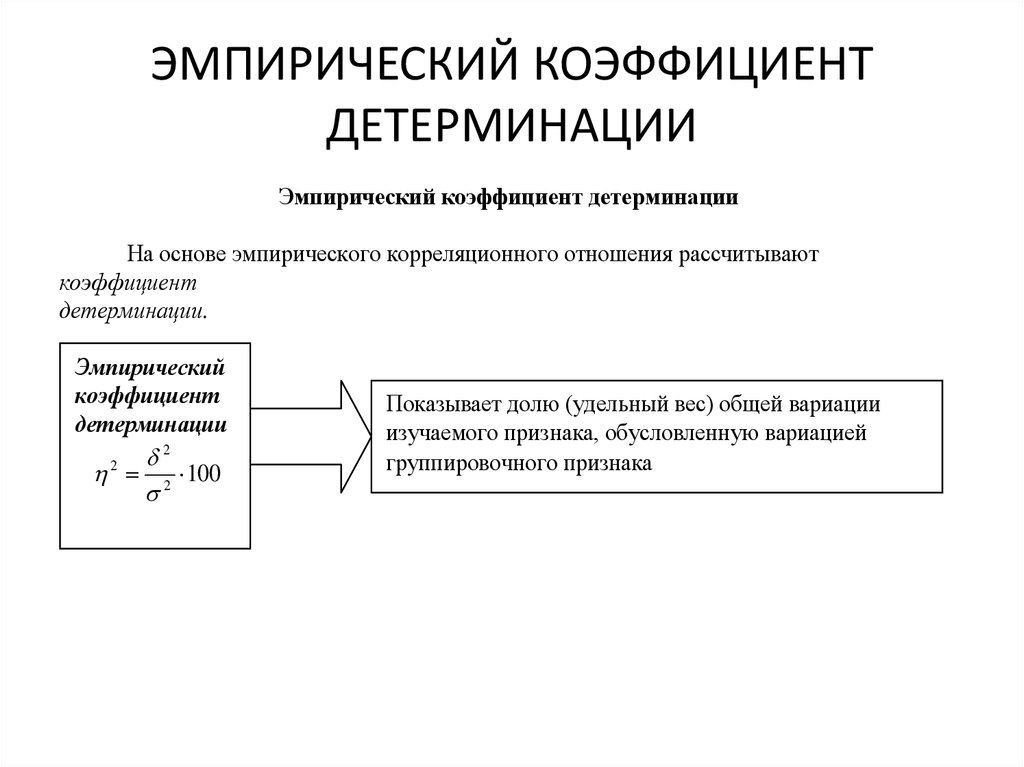






 mathematics
mathematics








