Similar presentations:
Средние величины. Понятие средней величины
1. Тема: Средние величины
Выполнила: Худойназарова Н.Группа: 19р-17
Проверила: Кадырова Л. Г.
2. Понятие средней величины
Средняявеличин
а
Обобщающий показатель, который дает
количественную характеристику
признака в статистической совокупности
в условиях конкретного время и места
3.
Условия правильного применения среднейвеличины
Средняя величина должна исчисляться лишь для
совокупностей, состоящих из однородных единиц
Совокупность, неоднородную в качественном отношении,
необходимо разделять на однородные группы и вычислять для
них групповые типичные средние, характеризующие каждую из
этих групп. В этом проявляется связь между методами
группировок и средних величин
Средняя величина сглаживает индивидуальные значения и тем
самым может элиминировать различные тенденции в развитии,
скрыть передовое и отстающее, поэтому кроме средней
величины следует исчислять другие показатели
Среднюю величину целесообразно исчислять не для отдельных
единичных фактов, взятых изолированно друг от друга, а для
совокупности фактов
4.
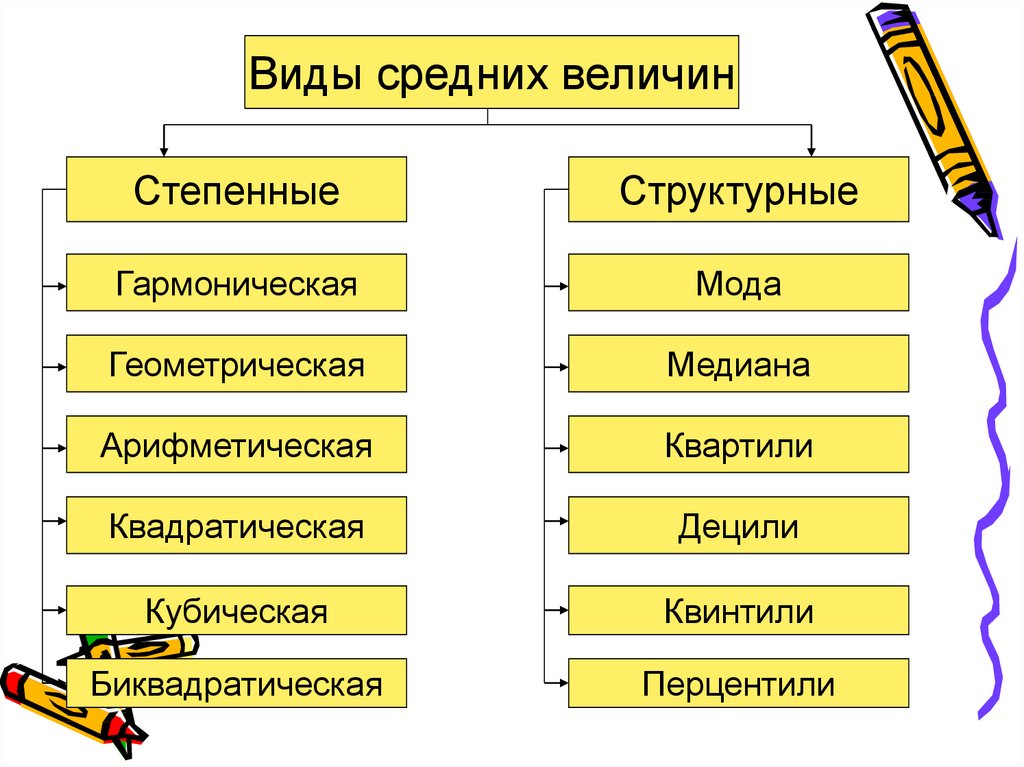
Виды средних величинСтепенные
Структурные
Гармоническая
Мода
Геометрическая
Медиана
Арифметическая
Квартили
Квадратическая
Децили
Кубическая
Квинтили
Биквадратическая
Перцентили
5.
Элементыстепенной средней
Варианта (Х)
Число единиц (n)
Веса, частоты (f)
Признак, для которого
исчисляется средняя
величина является
варьирующим,
осредняемым.
Единицы
варьирующего
признака,
принимающие
определенное
числовое выражение,
есть варианта
Количество
вариант в
исследуемой
совокупности
Показатели
повторяемости
вариант в
исследуемой
совокупности
6.
Средняястепенная
простая
X K
X
K
n
где К – показатель степени
Применяется в случае,
если каждая варианта Х
встречается
в
совокупности один или
одинаковое число раз
7.
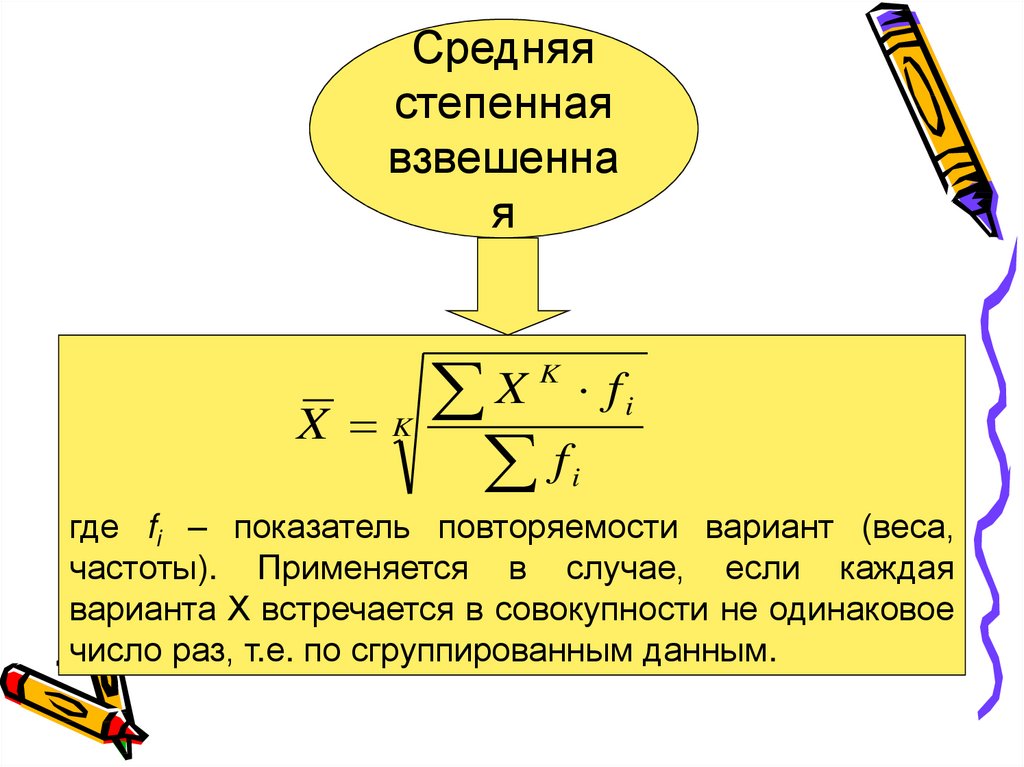
Средняястепенная
взвешенна
я
X
K
K
X
fi
f
i
где fi – показатель повторяемости вариант (веса,
частоты). Применяется в случае, если каждая
варианта Х встречается в совокупности не одинаковое
число раз, т.е. по сгруппированным данным.
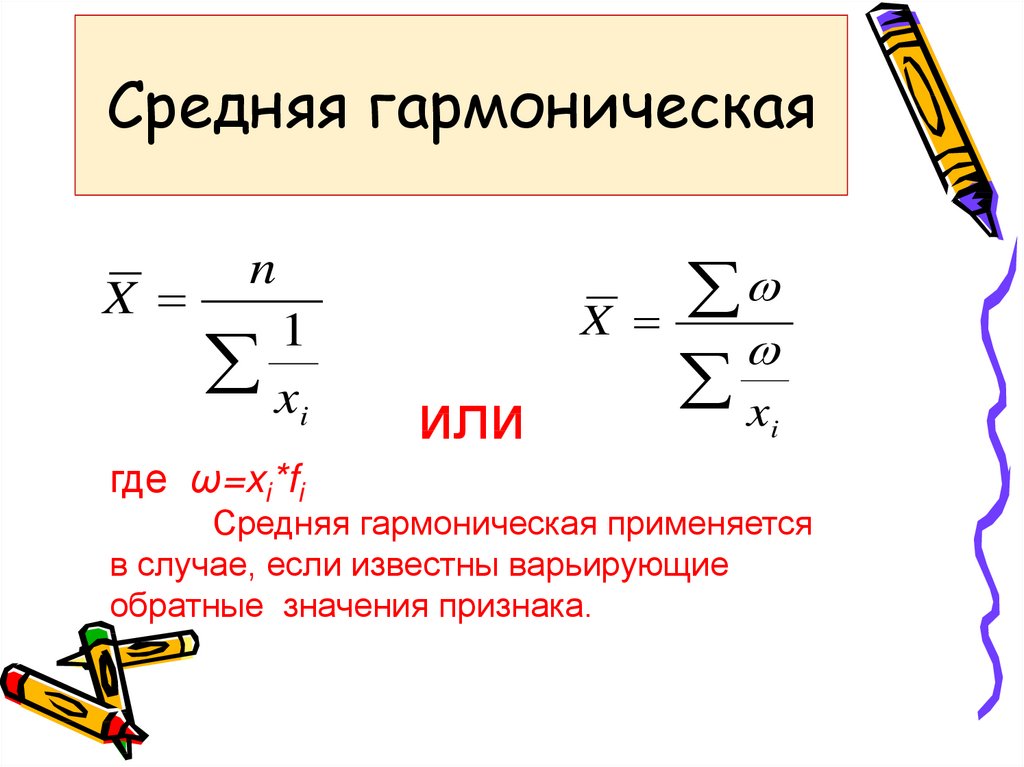
8. Средняя гармоническая
Xn
1
x
i
где ω=xi*fi
X
или
x
i
Средняя гармоническая применяется
в случае, если известны варьирующие
обратные значения признака.
9. Средняя геометрическая
Xn
x
i
или
fi
X
x
fi
i
Наиболее широкое применение средняя
геометрическая получила для определения
средних темпов изменения в рядах динамики, а
также в рядах распределения
10. Средняя арифметическая
XXi
n
X i fi
или
X
f
i
Средняя арифметическая применяется в
тех случаях, когда объем варьирующего
признака для всей совокупности образуется как
сумма значений признака отдельных ее единиц.
11. Средняя квадратическая
X2
X
n
2
i
2
X
i fi
2
X или
f
i
12. Средняя кубическая
X3
X
n
3
i
3
X
i fi
или
X 3
fi
13. Средняя биквадратическая
X4
X
n
4
i
X f
X
f
или
4
4
i
i
i
14. Правило мажорантности средних
Для одной и той же совокупности существуютстрого определенные соотношения между
разными видами средних. Эти соотношения
называют правилом мажорантности средних.
X ГАРМОНИЧЕСКАЯ X ГЕОМЕТРИЧЕСКАЯ
X АРИФМЕТИЧЕСКАЯ X КВАДРАТИЧЕСКАЯ
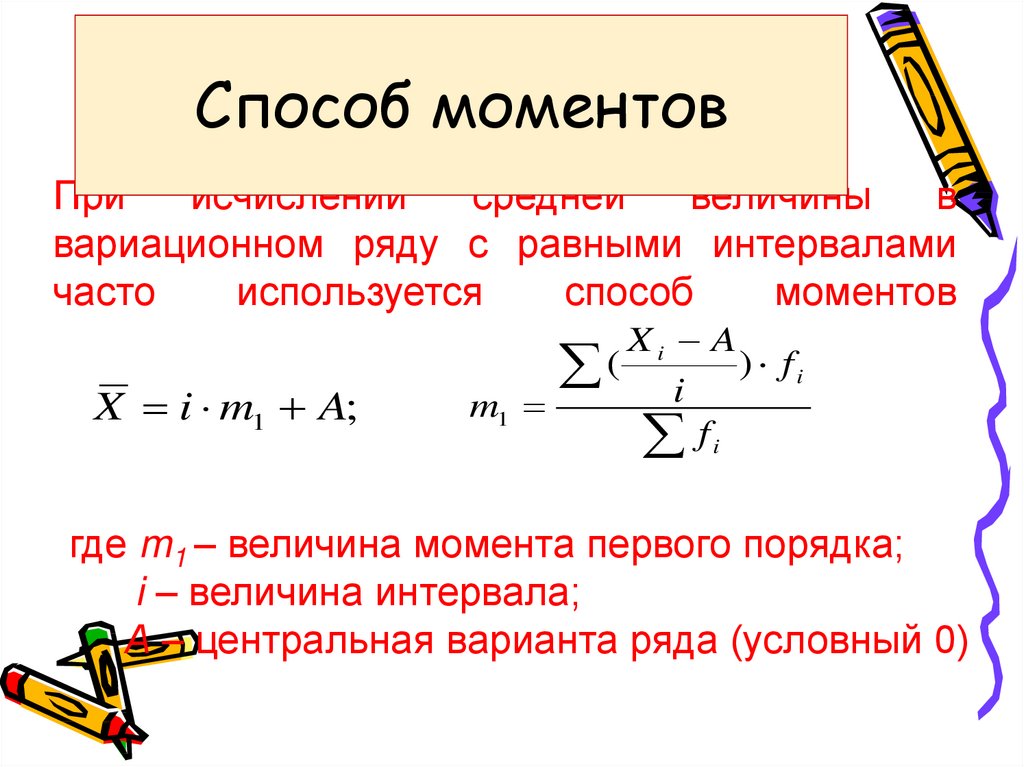
15. Способ моментов
Приисчислении
средней
величины
в
вариационном ряду с равными интервалами
часто
используется
способ
моментов
X i m1 A;
Xi A
( i ) fi
m1
fi
где m1 – величина момента первого порядка;
i – величина интервала;
А – центральная варианта ряда (условный 0)
16. Понятие моды
МодаВеличина признака (варианта), которая чаще
всего встречается в данной совокупности.
В вариационном дискретном ряду модой
выступает варианта, имеющая наибольшую
частоту
17. Понятие медианы
Медиана - этоварианта,
которая
находится в середине
вариационного
ряда.
Медина делит ряд
пополам, по обе стороны
от нее (вверх и вниз)
находится
одинаковое
количество
единиц
совокупности.
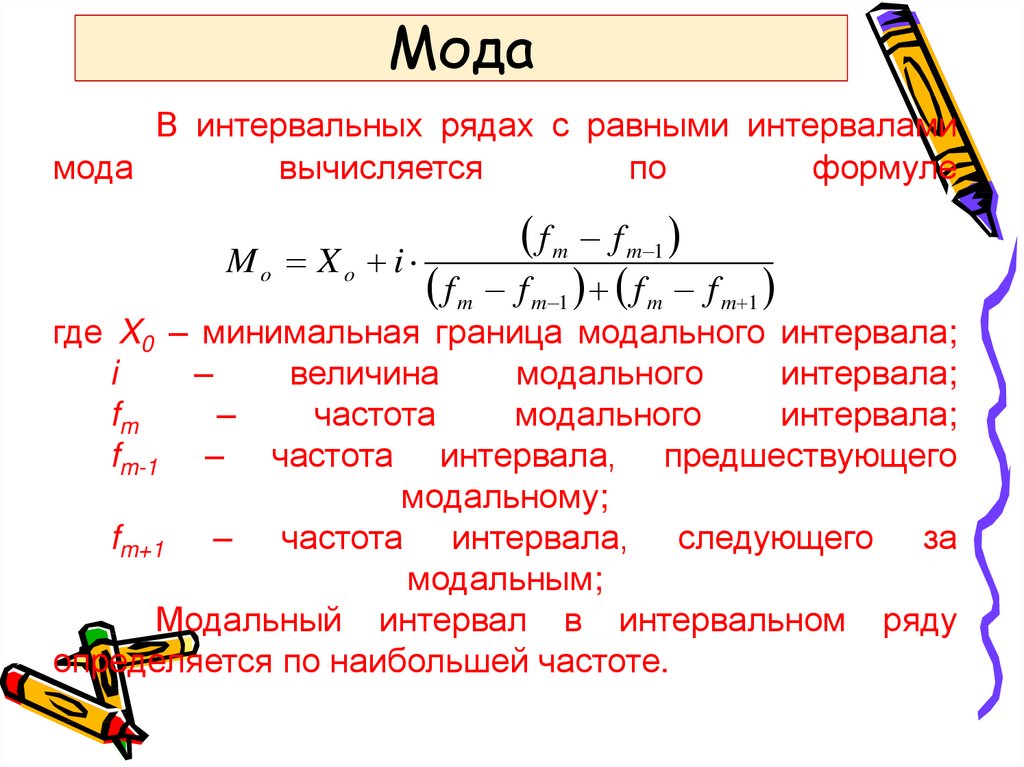
18. Мода
В интервальных рядах с равными интерваламимода
вычисляется
по
формуле
f m f m 1
Mo Xo i
f m f m 1 f m f m 1
где X0 – минимальная граница модального интервала;
i
–
величина
модального
интервала;
fm
–
частота
модального
интервала;
fm-1 – частота интервала, предшествующего
модальному;
fm+1 – частота интервала, следующего за
модальным;
Модальный интервал в интервальном ряду
определяется по наибольшей частоте.
19. Медиана
Вдискретном
вариационном
ряду
определение медианного значения признака
сводится к определению номера медианной
единицы
ряда
n 1
N ME
2
где
n
–
объем
совокупности.
Полученное значение показывает, где
точно находится номер медианной единицы
(номер середины ряда). Медианное значение
характеризуется тем, что его кумулятивная
частота равна половине суммы всех частот или
превышает ее.
20. Медиана
В интервальных рядах с равными интерваламимедиана
исчисляется
по
формуле
1
f S m 1
Me X 0 i 2
fm
где X0 – начальное значение медианного интервала;
i
–
величина
медианного
интервала;
Σf
–
сумма
частот
ряда;
Sm-1 – сумма накопленных частот в интервалах,
предшествующего
медианному;
fm
–
частота
медианного
интервала.
Для определения медианного интервала необходимо
рассчитать сумму накопленных частот. Медианный интервал
характерен тем, что его кумулятивная частота равна
полусумме всех частот ряда или превышает ее.
21. Список литературы
1.Годин А.М. Статистика: Учебник.-М.:Издательскоторговая корпорация «Дашков и Ко», 2007.-464с.2.Назаров М.Г., Варагин В.С., Великанова Т.Б.
Статистика: учебно-практическое пособие.: 2-е
изд., М.: КНОРУС, 2006-480с.
3. http://studepedia.org/index.php?vol=1&post=68933
4. http://be5.biz/ekonomika/s011/5.html













 mathematics
mathematics








