Статистические показатели в форме средних величин

1. Статистические показатели в форме средних величин

Т.Н. Тарасова – к.п.н., доцент кафедры
административного и финансового
права

2. План лекции

1 Степенные средние
1.1 Средняя арифметическая и её свойства
1.2 Средняя геометрическая
1.3 Средние более высоких порядков
2 Структурные средние
2.1 Определение моды вариационного ряда
2.2 Определение медианы вариационного ряда
3 Показатели вариации

3. 1 Степенные средние

4.

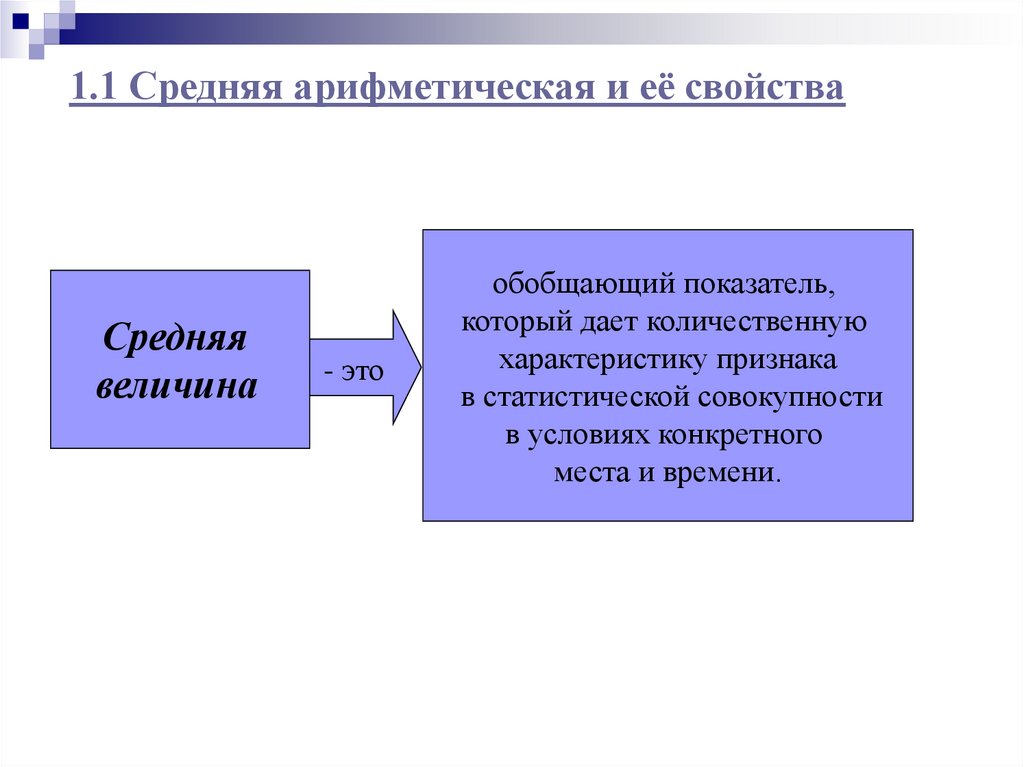
1.1 Средняя арифметическая и её свойства
Средняя
величина
- это
обобщающий показатель,
который дает количественную
характеристику признака
в статистической совокупности
в условиях конкретного
места и времени.

5.

Показатель в форме средней величины обладает
следующими свойствами:
представляет собой универсальную обобщающую характеристику
статистической совокупности;
отражает типичный уровень изучаемого признака;
является центром распределения.

6.

Условия правильного применения средней величины:
исчисляется
единиц;
только для совокупностей, состоящих из однородных
для
совокупности, неоднородной в качественном отношении,
необходимо разделение на однородные группы и вычисление для них
групповых средних, характеризующих каждую из этих групп;
кроме
средней величины следует исчислять другие показатели,
поскольку средняя величина сглаживает индивидуальные значения
среднюю
величину исчисляют не для отдельных единичных фактов, а
для их совокупности.

7.

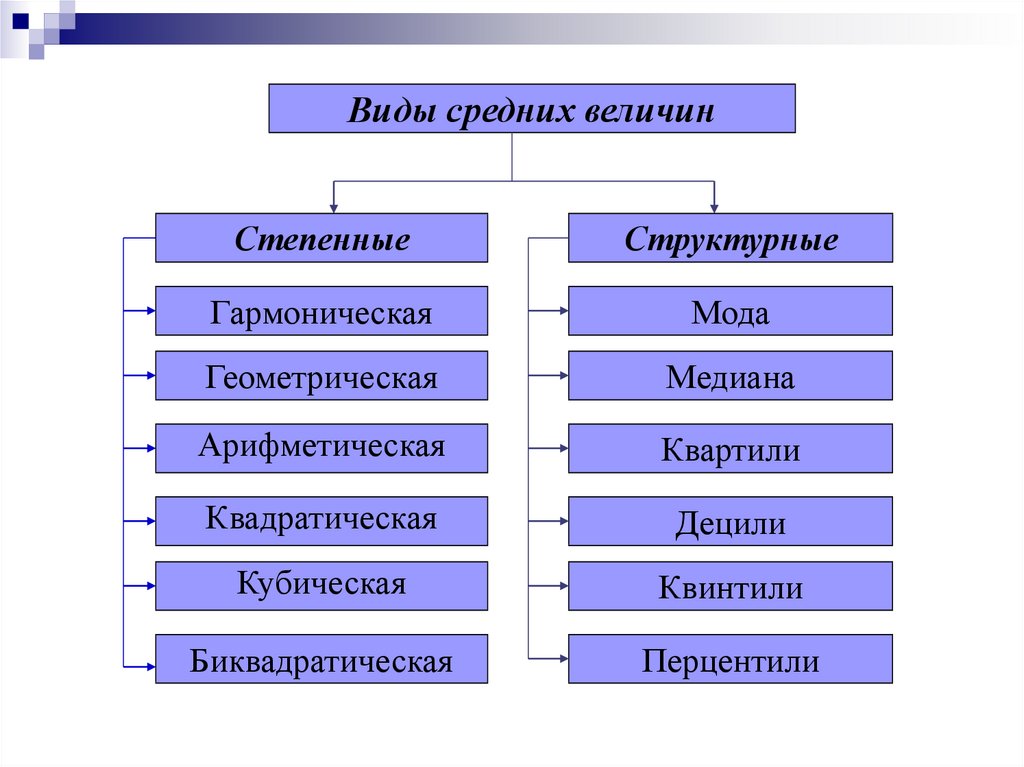
Виды средних величин
Степенные
Структурные
Гармоническая
Мода
Геометрическая
Медиана
Арифметическая
Квартили
Квадратическая
Децили
Кубическая
Квинтили
Биквадратическая
Перцентили

8.

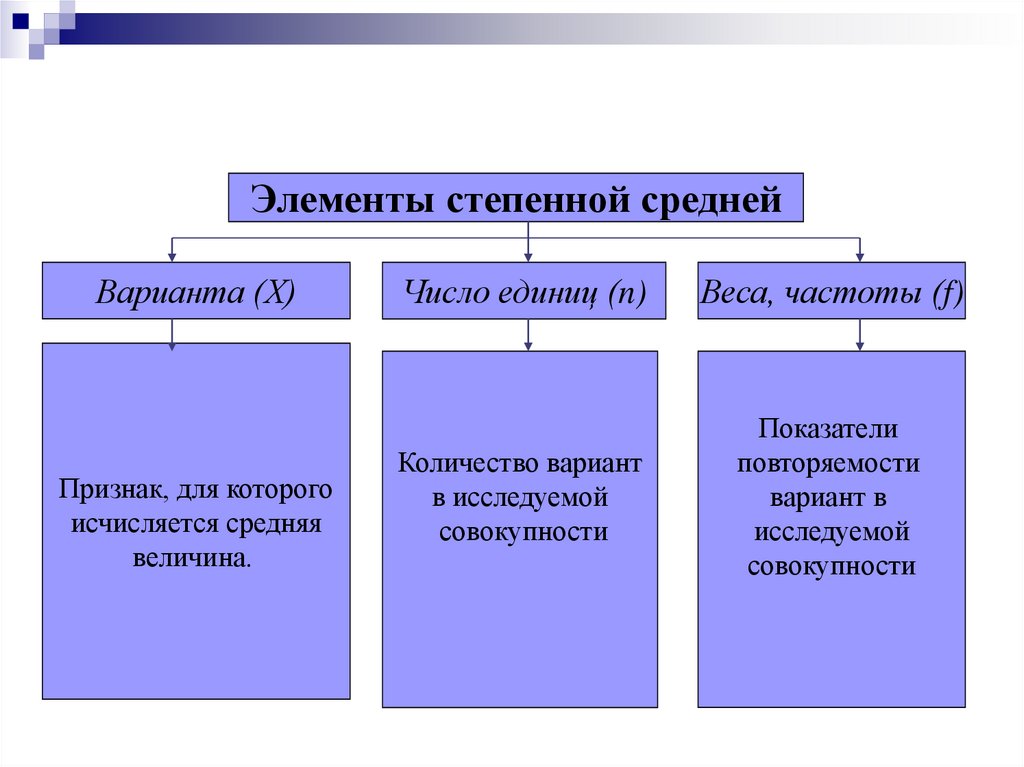
Элементы степенной средней
Варианта (Х)
Признак, для которого
исчисляется средняя
величина.
Число единиц (n)
Веса, частоты (f)
Количество вариант
в исследуемой
совокупности
Показатели
повторяемости
вариант в
исследуемой
совокупности

9.

Средняя арифметическая простая:
х
х
n
где
i
,
x - значение признака i-й единицы совокупности;
n – объём совокупности.
Пример: Доходы пяти банков по операциям с ценными
бумагами за отчетный период составили: 0,6; 0,7; 0,9; 1,1;
1,3 млн. руб. Определить средний доход банка по данной
операции.
0,6 0,7 0,9 1,1 1,3 4,6
0,92ìëí . ðóá.
5
5

10. Средняя арифметическая взвешенная

x f
х
f
i i
,
i
f – частота.
Пример.
Сделки по акциям элемента «Х» за торговую сессию
Сделка
Количество
проданных акций, шт.
Курс продажи,
руб.
Общая сумма сделок,
xf
1
2
3
700
200
950
420
440
410
294000
88000
389500
Итого
1850
Х
771500
771500
417,03 руб.
1850

11. Свойства средней арифметической:

1.Произведение средней на сумму частот равно сумме
произведений отдельных вариантов на соответствующие им
частоты:
х f xf
2. Сумма отклонений индивидуальных значений признака от
средней арифметической равно нулю:
(x x) f
0

12.

3. Если все значения признака уменьшить или увеличить на
постоянное число А, то средняя арифметическая соответственно
уменьшится или увеличится на ту же величину
( x A) f
f
x A

13.

4. Если все варианты значений признака уменьшить или
увеличить в А раз, то средняя также соответственно увеличится
или уменьшится в А раз
x
1
A f A xf 1
x
A
f
f
.

14.

5.Если все веса уменьшить или увеличить в А раз, то средняя
арифметическая от этого не изменится
f
1
x A A xf
x
f
1
A A f

15.

1.2 Средняя геометрическая
Средняя геометрическая невзвешенная (простая)
х n x1 x2 x3 xn n
где
n
Пx
i
i 1
õi çíà÷åíèå ïðèçíàêà i é åäèíèöû ñîâîêóïíîñ òè ;
n îáúåì ñîâîêóïíîñ òè
Средняя геометрическая взвешенная
х x1f 1 x2f 2 x3f 3 xkfk f
f
где
хi i й вариант признака ;
fi вес i го варианта;
k число вариантов осредняемо го признака.
f
fi
x
П i,
i 1

16.

1.3 Средние более высоких порядков
Средняя квадратическая
х
х
x
2
i
n
невзвешенная;
x f
f
2
i i
взвешенная;
i
Применяется при изучении вариации признака.

17.

Средняя кубическая
х
3
х 3
x
3
i
n
невзвешенная;
3
x
i fi
f
взвешенная;
i
Основная область применения степенных средних второго и более высоких
порядков – расчет показателей вариации, взаимосвязи, структурных
изменений, асимметрии и эксцесса.

18.

Правило
мажорантности
средних
X ãåîìåòð X àðèôìåò X êâàäðàò

19. 2 Структурные средние

20.

2.1 Определение моды вариационного ряда
Мода (Мо) – вариант изучаемого признака, имеющий
наибольшую частоту. Мода отражает то значение
признака, которое является наиболее типичным,
преобладающим, доминирующим.
При большом числе наблюдений совокупность
может характеризоваться двумя и более модальными
вариантами.

21.

При определении моды по дискретному ряду распределения подсчитываются частоты,
соответствующие каждому варианту изучаемого признака:
Вариант признака
xi
Частота
fi
x1
x2
x3
.
.
xMo(Mo)
.
.
xk
f1
f2
f3
Итого
..
.
fmax
.
.
fk
fi
Модальным вариантом, или модой, является вариант, которому соответствует
максимальная частота

22. Пример При обследовании 500 семей рабочих одной из отраслей промышленности установлены следующие показатели количества членов

семей:
Количество членов семьи, человек
Число семей
2
3
4
5
6
7
8
9
50
80
260
40
30
20
10
10
Определить моду данного вариационного ряда распределения

23.

При определении моды по интервальному ряду распределения
необходимо первоначально определить модальный
интервал - интервал, имеющий наибольшую частоту.
Значение моды внутри данного интервала определяется по
формуле:
Mo x0 i
f Mo f Mo 1
,
( f Mo f Mo 1 ) ( f Mo f Mo 1)
где x0 – нижняя граница модального интервала;
i
– величина интервала;
fMo – частота модального интервала;
fMo-1 – частота интервала, предшествующего модальному;
fMo+1 – частота интервала, следующего за модальным.

24. Пример Определить моду продолжительности стажа работы работников предприятия

Распределение работников предприятия по
продолжительности стажа работы
Группы работников по
продолжительности стажа работы, лет
Число работников, человек
До 2
2-4
4-6
6-8
8-10
Свыше 10
4
23
20
35
11
7
Мода продолжительности стажа работы работников торгового предприятия
составит:
35 20
М0 6 2
6,77 года
(35 20) (35 11)

25.

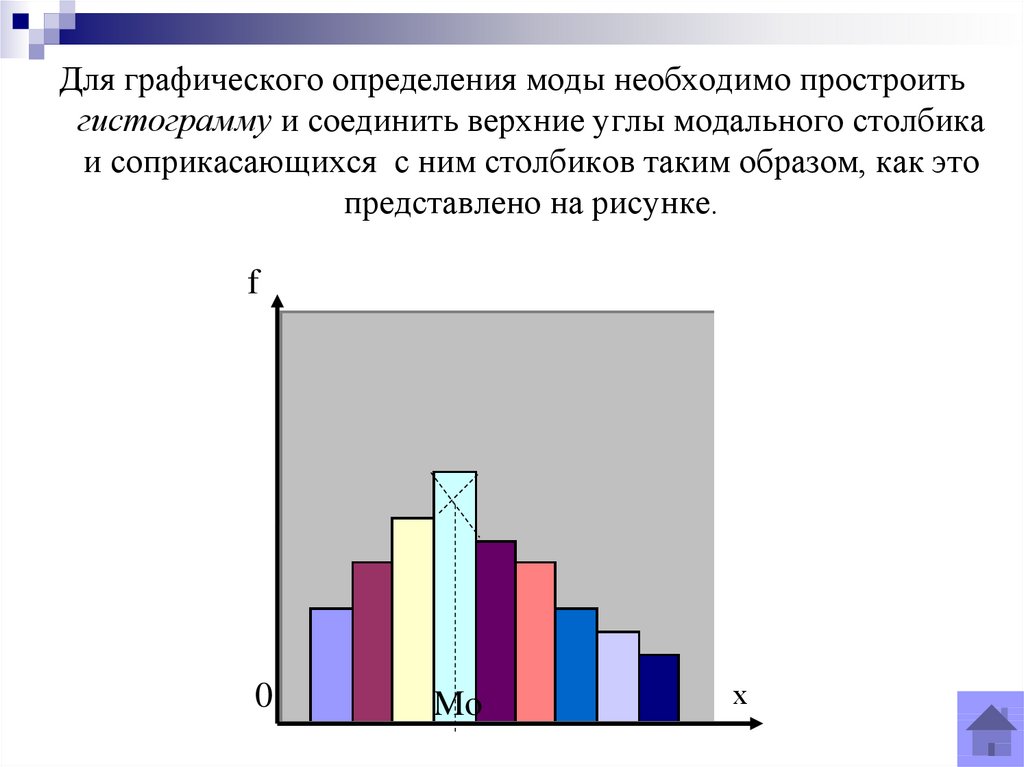
Для графического определения моды необходимо простроить
гистограмму и соединить верхние углы модального столбика
и соприкасающихся с ним столбиков таким образом, как это
представлено на рисунке.
f
0
Mo
х

26.

2.2 Определение медианы по ряду распределения
Медиана (Ме) – вариант изучаемого признака,
находящийся в середине ранжированного
(упорядоченного) ряда всех его значений.
Основное свойство медианы:
Сумма модулей отклонений всех значений
признака от медианы всегда меньше, чем сумма
таких отклонений от любой другой произвольной
постоянной:
x Ìå
i
min

27.

При определении медианы по дискретному ряду распределения рассчитываются накопленные
частоты.
Накопленная частота,
Вариант признака, xi
Частота, fi
x1
f1
f i H f1
x2
f2
x3
f3
f 2H f1H f 2
f 3H f 2H f 3
xMe-1
fMe-1
xMe(Me)
fMe
xk
fk
f kH
Итого
fi
X
fi H
H
f Me
1
1
2
H
f Me
1
1
2
fi
fi
Медианным вариантом, или медианой, будет первый вариант, накопленная частота которого
превышает половину суммы всех частот.

28.

Для дискретного ранжированного ряда с
нечетным числом членов медианой является
варианта, расположенная в центре ряда.
Пример
Процент выполнения плана товарооборота за месяц 13
торговых предприятий составил (%): 95; 98; 101; 104; 109;
115; 119; 126; 135; 144; 176; 202; 223. Определить медиану.
Решение
Медианой будет седьмая варианта, которая делит
упорядоченный ряд пополам и соответствует 119%
выполнения плана товарооборота.

29.

Для дискретного ранжированного ряда с чётным
числом членов, медианой будет варианта,
рассчитанная как средняя арифметическая двух
смежных центральных вариант
Пример
Сведения о стаже работы шести работников предприятия:
1, 3, 4, 5, 7, 9 лет.
Определить медиану стажа работы работников.
Решение
М е (4 5) 2 4,5года

30.

При определении медианы по интервальному ряду
распределения необходимо рассчитывать медианный интервал,
т.е. первый интервал, накопленная частота которого превышает
половину общей суммы частот.
Значение медианы внутри данного интервала определяется по
формуле:
1
H
f
f
Me 1
i
2
Mе x0 i
,
f Me
где х0 – нижняя граница медианного интервала;
i – величина интервала;
fMe – частота медианного интервала;
H
– накопленная частота интервала, предшествующего медианному.
f Me
1

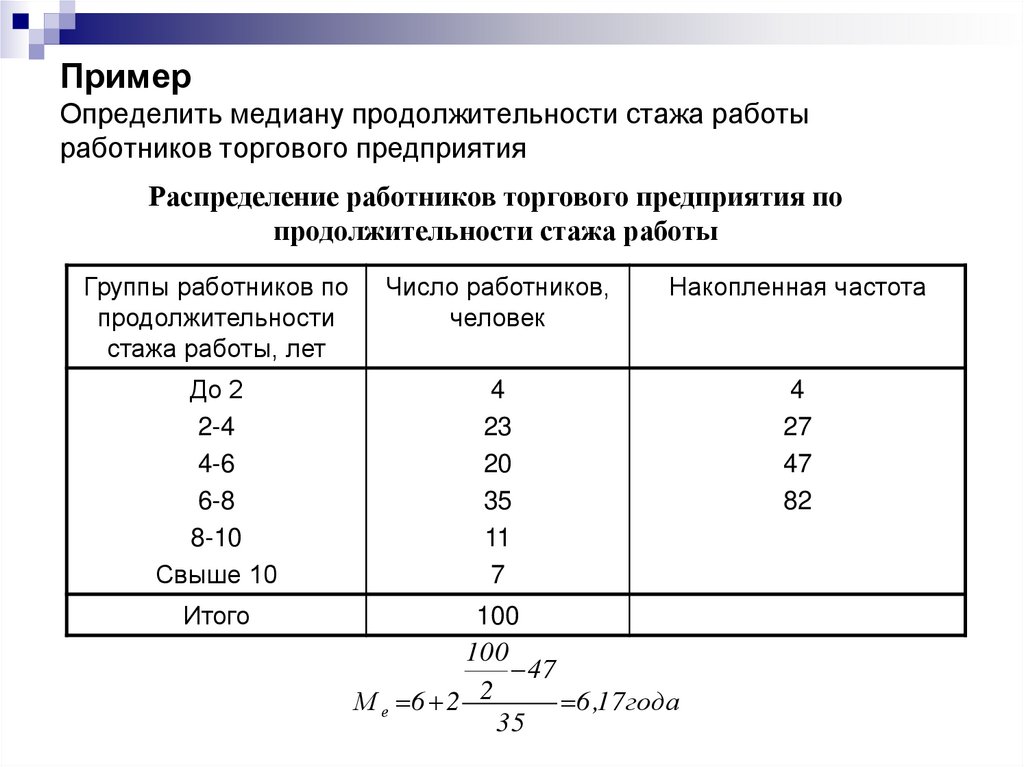
31. Пример Определить медиану продолжительности стажа работы работников торгового предприятия

Распределение работников торгового предприятия по
продолжительности стажа работы
Группы работников по
продолжительности
стажа работы, лет
Число работников,
человек
Накопленная частота
До 2
2-4
4-6
6-8
8-10
Свыше 10
4
23
20
35
11
7
4
27
47
82
Итого
100
100
47
2
М е 6 2
6 ,17 года
35

32. 3 Показатели вариации

Если отдельные значения изучаемого
признака существенно отличаются от средней
величины, то наряду с самой средней
величиной выявляют и величину отклонения
(вариации) отдельных признаков.
Поэтому средние характеристики дополняют
показателями вариации признака.

33. 1) размах вариации (R)

равен разности между наибольшим и
наименьшим значениям признака:
R = X max – X min

34. 2) среднее линейное отклонение (d):

n
x x
i
d
i 1
n
2) среднее линейное отклонение (d):
для сгруппированных данных:
x x f
n
i
d
i
i 1
n
fi
i 1
для несгруппированных данных:
n
x x
i
d
i 1
n

35. 3) дисперсия (D):

для сгруппированных данных:
(x x) f
k
2
D
i
i 1
i
k
f
для несгруппированных данных:
i
i 1
x
n
i
D
2
x
i 1
n

36. 4) среднее квадратическое отклонение ():

4) среднее квадратическое
отклонение ( ):
для сгруппированных и
несгруппированных данных:
D

37. Свойства дисперсии и среднего квадратического отклонения:

1) дисперсия и среднее квадратическое
отклонение постоянной величины равны нулю;
2) дисперсия и среднее квадратическое
отклонение не меняются, если все варианты
увеличить или уменьшить на какое-то
постоянное число;
3) если все варианты умножить на какое-то
постоянное число А 0, то дисперсия увеличится
в А квадрат раз, а среднее квадратическое
отклонение – в А раз.

38. 5) коэффициент вариации:

V
x
100%
Если V достаточно большой (более 40 %) – это
означает, что типичность средней невысока и,
наоборот, если его значение мало, то средняя
величина признается типической и надежной
характеристикой изучаемой совокупности.