Статистическая сводка и группировка

1. ТЕМА 3. СТАТИСТИЧЕСКАЯ СВОДКА И ГРУППИРОВКА

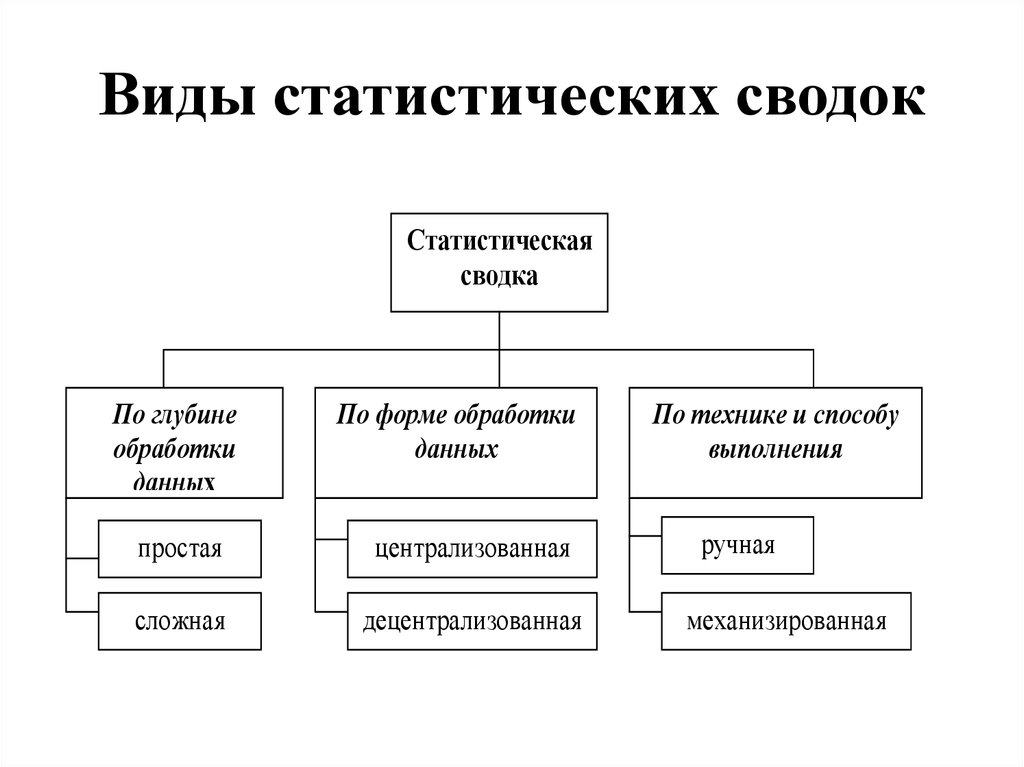
2. Виды статистических сводок

Статистическая
сводка
По глубине
обработки
данных
По форме обработки
данных
простая
централизованная
сложная
децентрализованная
По технике и способу
выполнения
ручная
механизированная

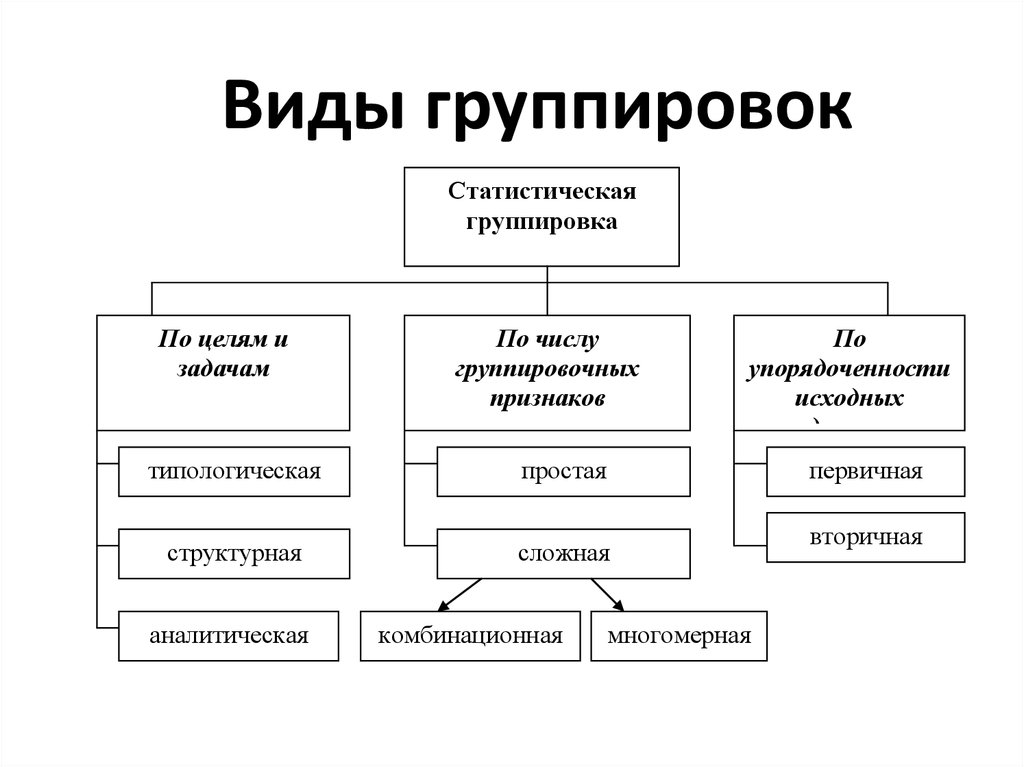
3. Виды группировок

Статистическая
группировка
По целям и
задачам
По числу
группировочных
признаков
типологическая
простая
структурная
сложная
аналитическая
комбинационная
По
упорядоченности
исходных
данных
первичная
многомерная
вторичная

4.

• Если группировка проводится по
количественном признаку, оптимальное
количество групп определяется по формуле
американского ученого Стерджесса:
n=1+3,322 lgN, где
N – число единиц совокупности;
n – число групп.

5.

Интервалы
Открытые
(со словами свыше, до и т.д.)
-указана только одна граница
интервала
Закрытые
-обозначены две границы
Интервалы
Равные
Неравные

6.

Величина равного интервала определяется по формуле:
X max X min
,
i
n
где X max – наибольшее значение признака;
X min – наименьшее значение признака;
n – количество групп.

7.

• Пример для равных интервалов. Требуется
провести группировку с равными интервалами
по данным об уровне месячной заработной
платы работников, которая колеблется в
пределах от 600 до 750 руб. Требуется
выделить 5 групп.
i=
x
max
xmin
n
600-630
630-660
660-690
690-720
720-750
=
750 600
=30
5

8.

Неравные интервалы могут быть:
1) прогрессивно возрастающие;
2) прогрессивно убывающие;
3) произвольные.
Прогрессивно возрастать или прогрессивно
убывать значения интервалов могут:
- в арифметической прогрессии:
hi+1=hi+a
- в геометрической прогрессии:
hi+1=hi*q
Если прогрессия возрастающая, а>0, q>1.
Если прогрессия убывающая, а<0, q<1.

9.

Ряды распределения
Атрибутивные
Вариационные
- ряды, построенные по атрибутивным признакам.
это
ряды,
построенные
количественному признаку.
Варианты
xi
x1
x2
x3
·
·
·
xn
Итого
Частоты
fi
f1
f2
f3
·
·
·
fn
f
i
по

10.

Частоты могут быть выражены в виде:
- числа, абсолютного значения;
- доли (сумма=1);
- процентов (сумма=100%).
Если
частоты
величинами
(доли,
название – частости.
выражены
проценты),
относительными
то
они
носят

11.

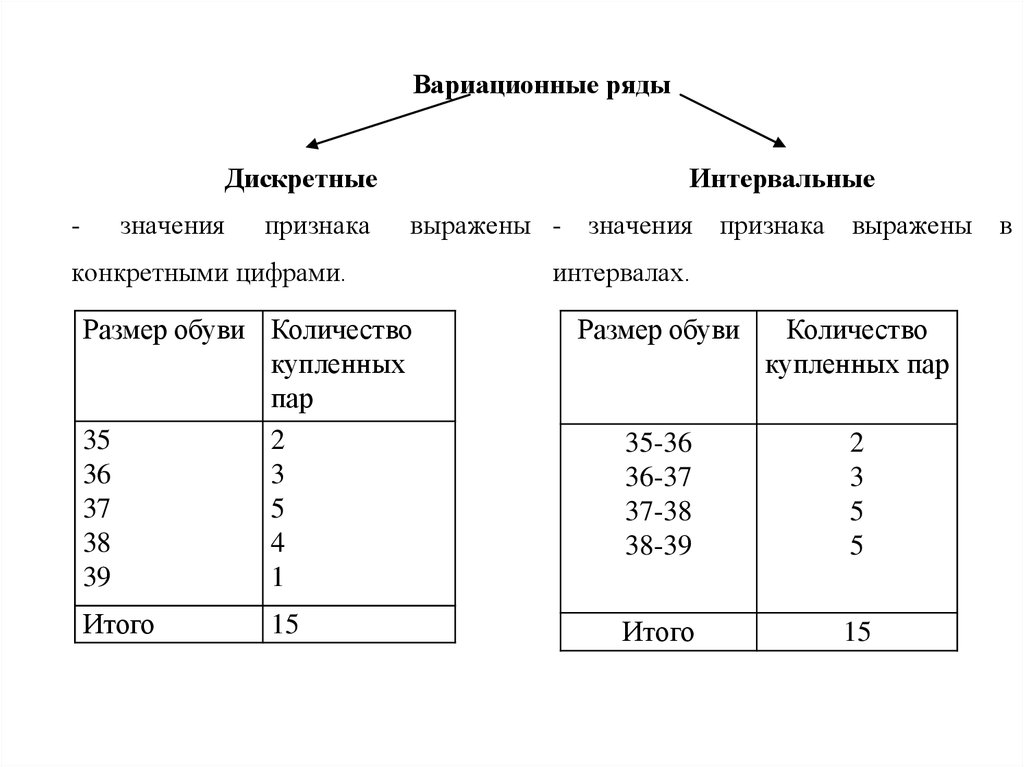
Вариационные ряды
Дискретные
-
значения
признака
Интервальные
выражены - значения признака выражены в
конкретными цифрами.
Размер обуви Количество
купленных
пар
35
2
36
3
37
5
38
4
39
1
Итого
15
интервалах.
Размер обуви
Количество
купленных пар
35-36
36-37
37-38
38-39
2
3
5
5
Итого
15

12. Ряд накопленных частот

Размер обуви
35
36
37
38
39
Итого
Количество
купленных
пар
2
3
5
4
1
15
Накопленные
частоты
Si, fн
2
2+3
2+3+5
2+3+5+4
2+3+5+4+1
-

13.

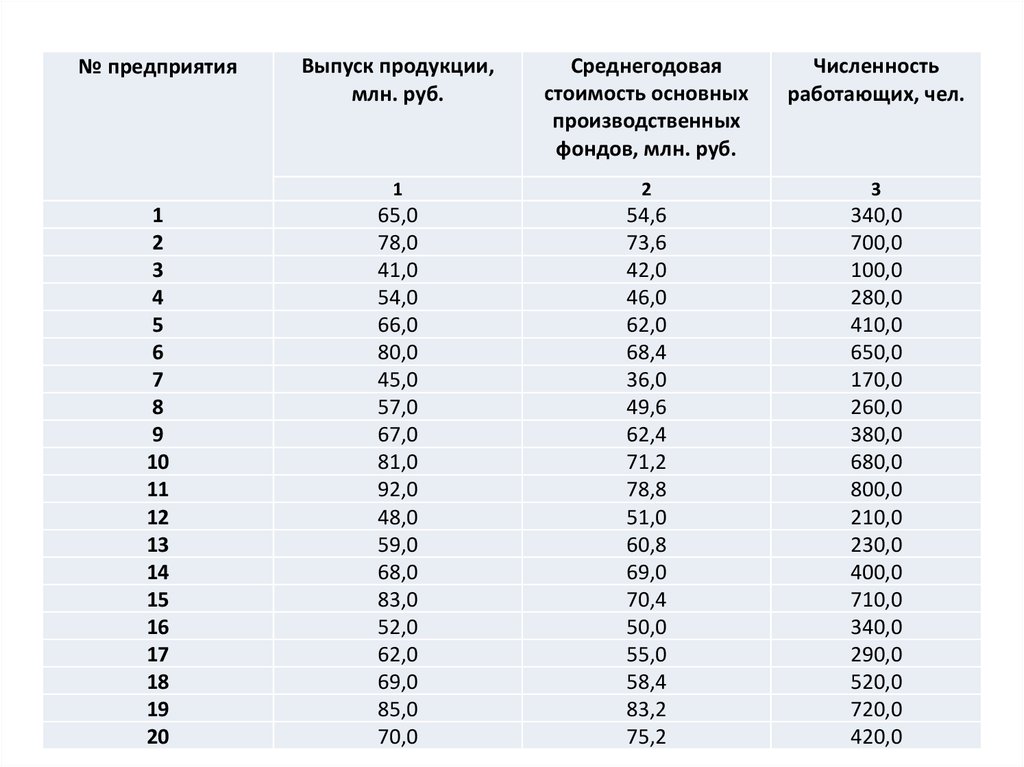
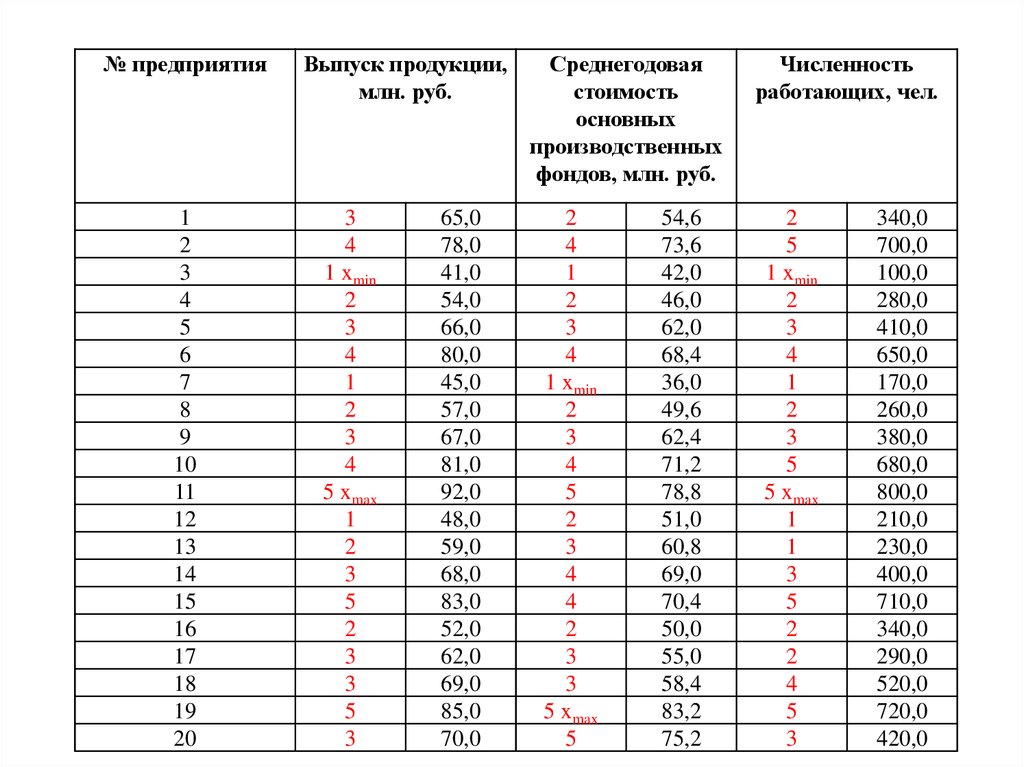
№ предприятия
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Выпуск продукции,
млн. руб.
Среднегодовая
стоимость основных
производственных
фондов, млн. руб.
Численность
работающих, чел.
1
2
3
65,0
78,0
41,0
54,0
66,0
80,0
45,0
57,0
67,0
81,0
92,0
48,0
59,0
68,0
83,0
52,0
62,0
69,0
85,0
70,0
54,6
73,6
42,0
46,0
62,0
68,4
36,0
49,6
62,4
71,2
78,8
51,0
60,8
69,0
70,4
50,0
55,0
58,4
83,2
75,2
340,0
700,0
100,0
280,0
410,0
650,0
170,0
260,0
380,0
680,0
800,0
210,0
230,0
400,0
710,0
340,0
290,0
520,0
720,0
420,0

14. Структурная группировка по 1 признаку. n=1 +3,322lgN= i=

Таблица 1
Структурная группировка по выпуску продукции
Выпуск
продукции,
млн. руб.
Количество
единиц
в группе
В % к итогу
Итого
20
100
1
2
3
4
5

15.

№ предприятия
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
Выпуск продукции,
млн. руб.
3
4
1 xmin
2
3
4
1
2
3
4
5 xmax
1
2
3
5
2
3
3
5
3
65,0
78,0
41,0
54,0
66,0
80,0
45,0
57,0
67,0
81,0
92,0
48,0
59,0
68,0
83,0
52,0
62,0
69,0
85,0
70,0
Среднегодовая
стоимость
основных
производственных
фондов, млн. руб.
2
4
1
2
3
4
1 xmin
2
3
4
5
2
3
4
4
2
3
3
5 xmax
5
54,6
73,6
42,0
46,0
62,0
68,4
36,0
49,6
62,4
71,2
78,8
51,0
60,8
69,0
70,4
50,0
55,0
58,4
83,2
75,2
Численность
работающих, чел.
2
5
1 xmin
2
3
4
1
2
3
5
5 xmax
1
1
3
5
2
2
4
5
3
340,0
700,0
100,0
280,0
410,0
650,0
170,0
260,0
380,0
680,0
800,0
210,0
230,0
400,0
710,0
340,0
290,0
520,0
720,0
420,0

16.

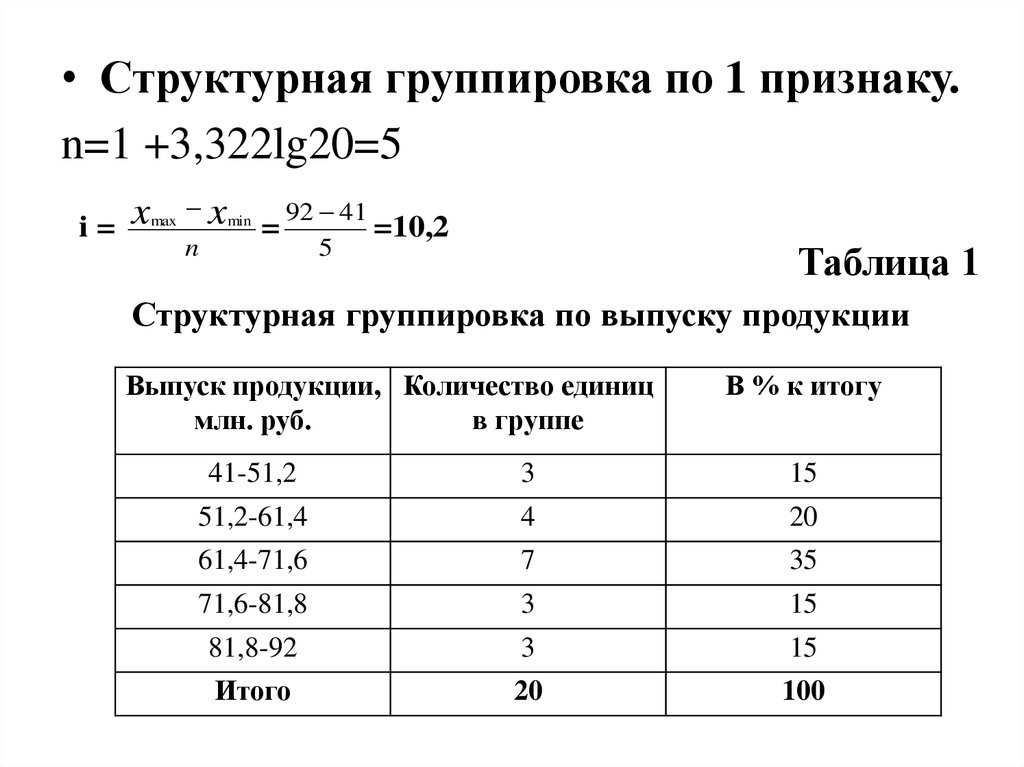
• Структурная группировка по 1 признаку.
n=1 +3,322lg20=5
i=
x
max
x min
n
=
92 41
=10,2
5
Таблица 1
Структурная группировка по выпуску продукции
Выпуск продукции, Количество единиц
млн. руб.
в группе
В % к итогу
41-51,2
3
15
51,2-61,4
4
20
61,4-71,6
7
35
71,6-81,8
3
15
81,8-92
3
15
Итого
20
100

17.

• Структурная группировка по 2 признаку.
i=
x
max
xmin
n
=
83,2 36,0
=9,44
5
Таблица 2
Структурная группировка по среднегодовой стоимости
основных производственных фондов
Среднегодовая
стоимость основных
производственных
фондов, млн. руб.
Количество единиц
в группе
В % к итогу
36-45,44
45,44-54,88
54,88-64,32
64,32-73,76
73,76-83,2
Итого
2
5
5
5
3
20
10
25
25
25
15
100

18.

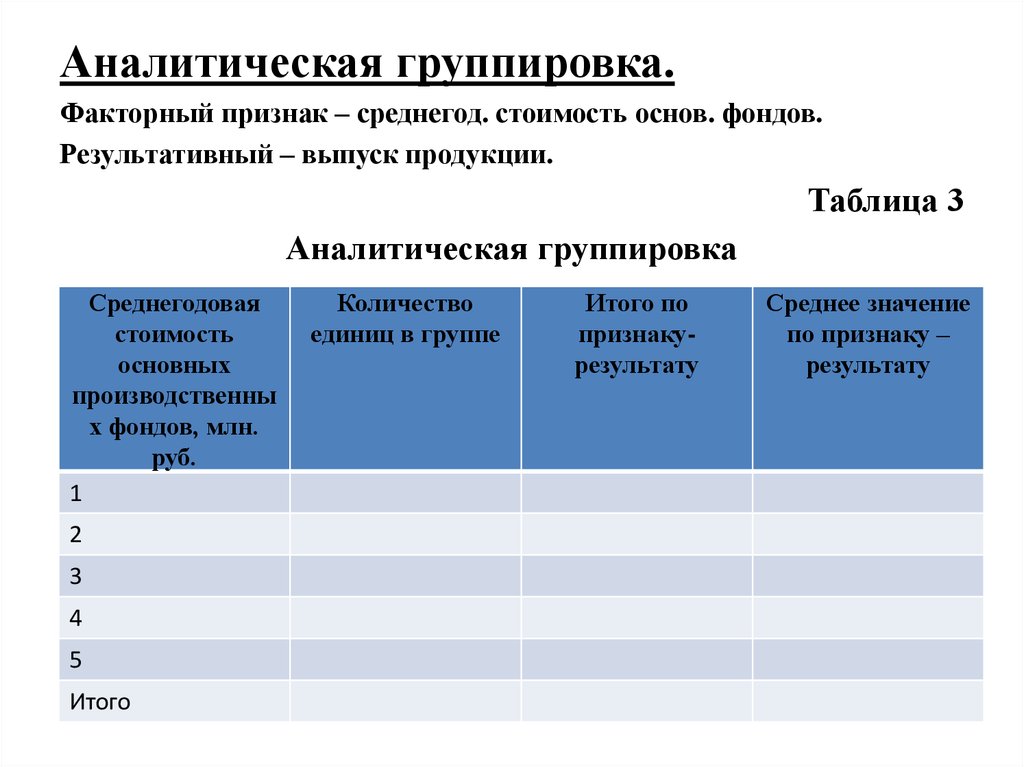
Аналитическая группировка.
Факторный признак – среднегод. стоимость основ. фондов.
Результативный – выпуск продукции.
Таблица 3
Аналитическая группировка
Среднегодовая
стоимость
основных
производственны
х фондов, млн.
руб.
1
2
3
4
5
Итого
Количество
единиц в группе
Итого по
признакурезультату
Среднее значение
по признаку –
результату

19.

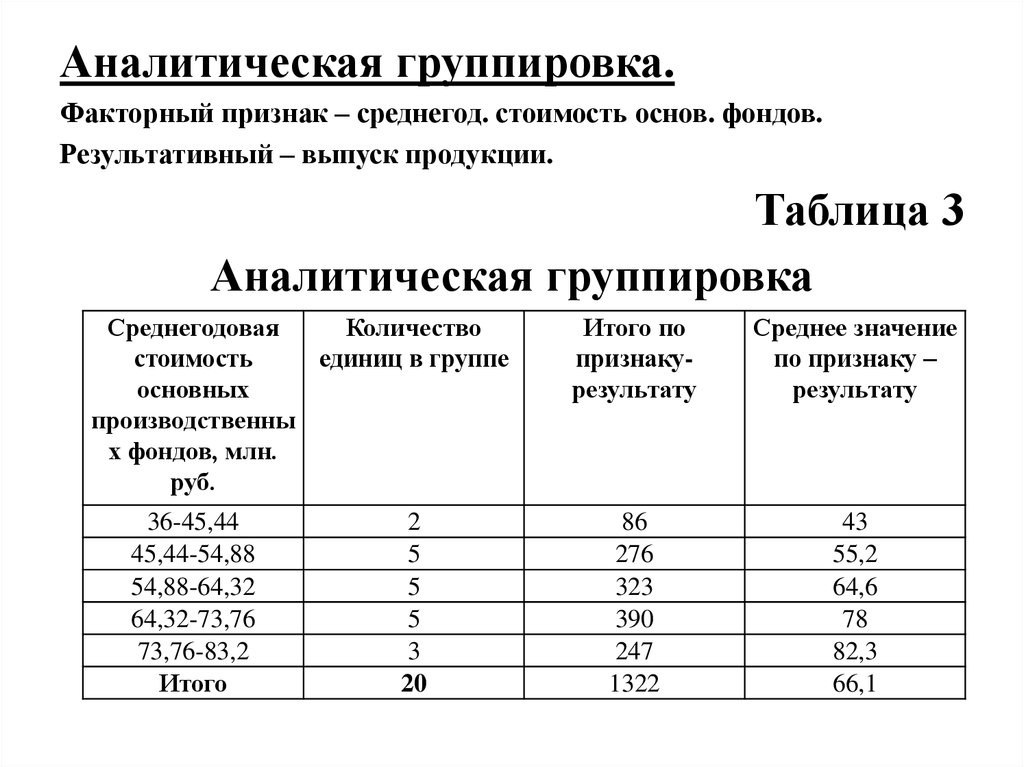
Аналитическая группировка.
Факторный признак – среднегод. стоимость основ. фондов.
Результативный – выпуск продукции.
Таблица 3
Аналитическая группировка
Среднегодовая
Количество
стоимость
единиц в группе
основных
производственны
х фондов, млн.
руб.
36-45,44
45,44-54,88
54,88-64,32
64,32-73,76
73,76-83,2
Итого
2
5
5
5
3
20
Итого по
признакурезультату
Среднее значение
по признаку –
результату
86
276
323
390
247
1322
43
55,2
64,6
78
82,3
66,1

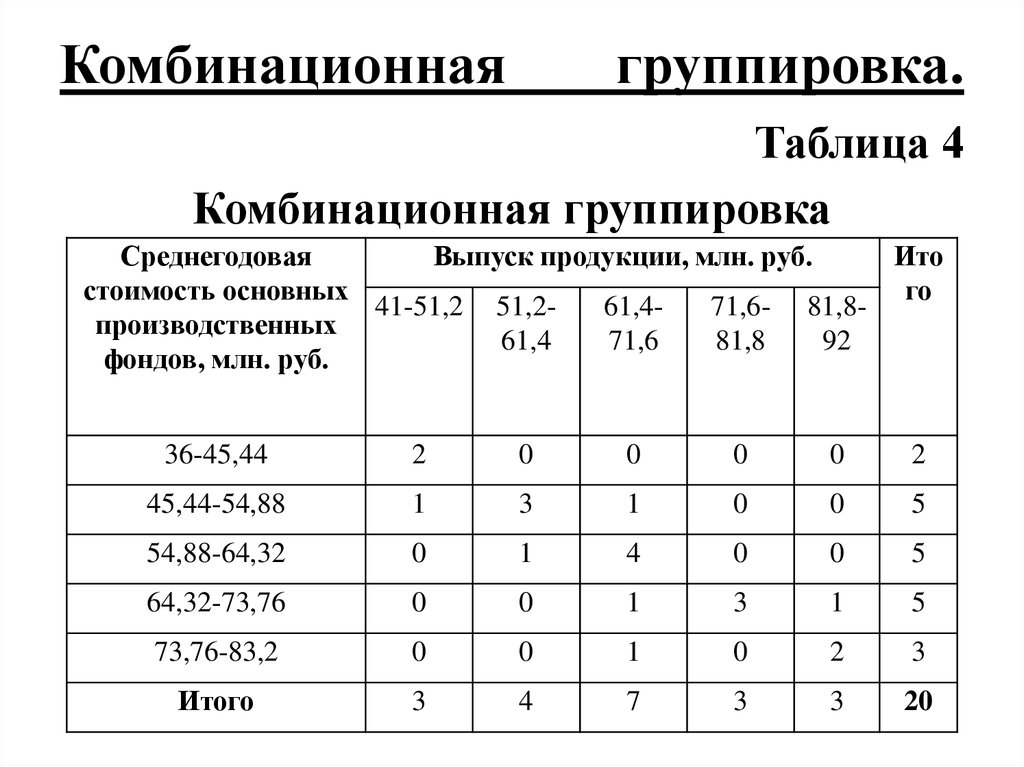
20. Комбинационная группировка.

Таблица 4
Комбинационная группировка
Среднегодовая
Выпуск продукции, млн. руб.
Ито
стоимость основных
го
41-51,2 51,261,471,6- 81,8производственных
61,4
71,6
81,8
92
фондов, млн. руб.
36-45,44
2
0
0
0
0
2
45,44-54,88
1
3
1
0
0
5
54,88-64,32
0
1
4
0
0
5
64,32-73,76
0
0
1
3
1
5
73,76-83,2
0
0
1
0
2
3
Итого
3
4
7
3
3
20