Similar presentations:
Основы математической обработки информации
1. Основы математической обработки информации
2. Информация
Информация – сведения об объектах иявлениях окружающей среды, их
параметрах свойствах и состояниях,
которые
воспринимают
информационные системы (это живые
организмы, машины и др.) в процессе
жизнедеятельности и работы.
Мы будем понимать под информацией
отражения предметного мира с
помощью знаков и сигналов.
3. Термин информация
Термин информация происходит отлатинского слова informatio, это
означает «сведения, разъяснения,
ознакомление». Понятие информации
является
базовым
общенаучным
понятием, поэтому невозможно дать
его определение через другие, более
простые понятия.
4. Виды информации.
Информация может существовать в виде:- текстов, рисунков, чертежей,
фотографий;
- световых или звуковых сигналов;
- радиоволн;
- электрических и нервных импульсов;
- магнитных записей;
- жестов и мимики;
- запахов и вкусовых ощущений;
- хромосом, посредством которых
передаются по наследству признаки и
5. Информационные объекты
Предметы,процессы,
явления
материального и нематериального
свойства, рассматриваемые с точки
зрения их информационных свойств,
называются
информационными
объектами.
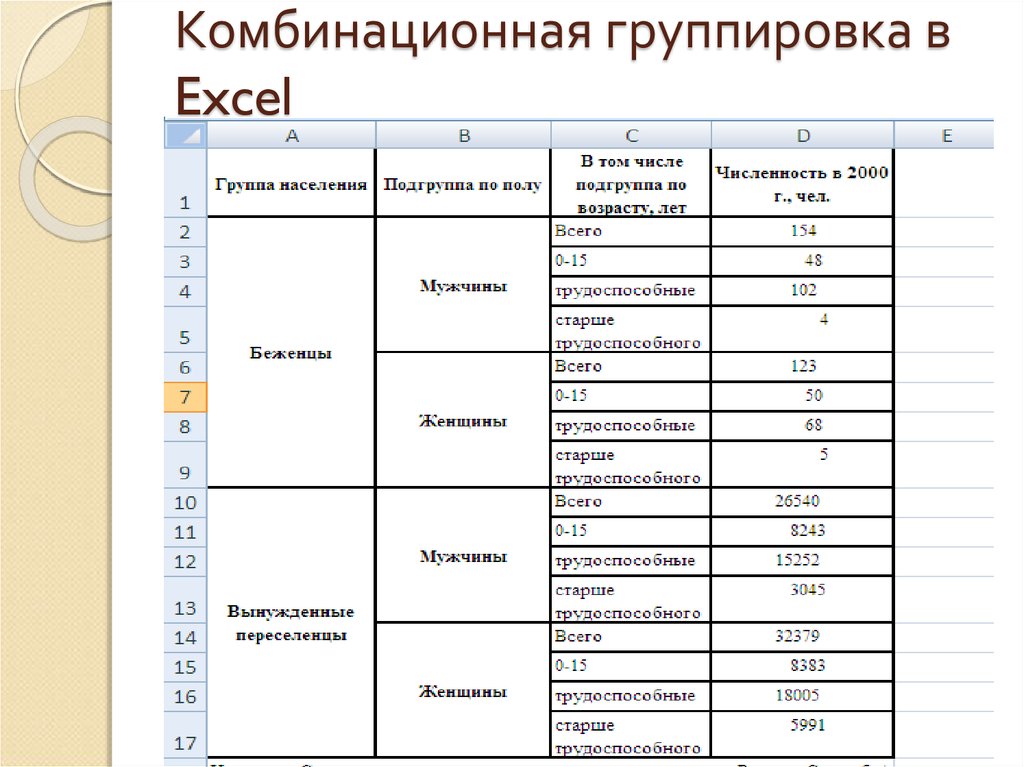
6. Свойства информации
1. Достоверность. Информация достоверна,если она отображает истинное положение дел.
Недостоверная информация может привести к
неправильному пониманию или принятию
неправильных
решений.
Достоверная
информация со временем может становиться
недостоверной, т.к. она обладает свойством
устаревать, т.е. перестает отражать истинное
положение дел.
7. Свойства информации
2. Полнота. Информация полна, если еедостаточно для понимания и принятия
решений. Как неполная, так и
избыточная информация сдерживает
принятие решений или может повлечь
ошибки.
8. Свойства информации
3. Точность информации определяетсястепенью ее близости к реальному
состоянию объекта, процесса, явления
и т.п.
4. Ценность информации зависит от
того насколько она важна для решения
задачи, а также от того, насколько в
дальнейшем она найдет применение в
каких-либо
видах
деятельности
человека.
9. Свойства информации
5. Актуальность. Только своевременнополученная информация может принести
ожидаемую
пользу.
Одинаково
нежелательны как преждевременная
подача информации (когда она еще не
может быть усвоена), так и ее задержка.
6. Понятность. Информация становится
понятной, если она выражена языком, на
котором
говорят
те,
кому
она
предназначена.
10. Свойства информации
7. Доступность. Информация должнапреподносится в доступной (по уровню
восприятия) форме. Поэтому одни и те же
вопросы по-разному излагаются в
школьных учебниках и научных изданиях.
8. Краткость. Информацию по одному и
тому же вопросу можно изложить кратко
(сжато без несущественных деталей) или
пространно (подробно, многословно).
Краткость информации необходима в
справочниках,
энциклопедиях,
всевозможных инструкциях.
11. Информационные процессы
Информационные процессы – действия,выполняемые с информацией Это
процесс, в ходе которого изменяется
либо содержание информации, либо
форма ее представления.
12. Информационные процессы
- создавать;- принимать;
-комбинировать;
- передавать; - копировать; - обрабатывать;
- использовать; - распространять;
- упрощать;
- запоминать; - преобразовывать; - собирать;
- хранить;
- искать;
- измерять;
- разрушать и т.д.
13. Математические средства представление информации
Числа;Формулы;
Таблицы;
Графики.
14. Представление числовой информации с помощью систем счисления.
Числа записываются с использованиемособых знаковых систем, которые
называются системами счисления.
Алфавит систем счисления состоит из
символов, которые называются
цифрами. Например, в десятичной
системе числа записываются с помощью
десяти цифр: 0, 1, 2 и т.д.
15. Системы счисления
Система счисления – это знаковаясистема, в которой числа записываются
по определенным правилам с помощью
символов
некоторого
алфавита,
называемых цифрами.
Все системы счисления делятся на две
большие
группы:
позиционные
и
непозиционные. В позиционных системах
счисления значение цифры зависит от ее
положения в числе, а в непозиционных –
не зависит.
16. Римская непозиционная система счисления.
В качестве цифр в ней используются: I (1), V (5), X (10),L(50), C(100), D(500), M(1000).
Значение цифры не зависит от ее положения в числе.
Например, в числе XXX (30) цифра X встречается
трижды и, в каждом случае, обозначает одну и ту же
величину – число 10, три раза по 10 в сумме дают 30.
Величина числа в римской системе счисления
определяется как сумма или разность цифр в числе.
Если меньшая цифра стоит слева от большей, то она
вычитается, если справа – прибавляется. Например,
запись десятичного числа 1998 в римской системе
счисления будет выглядеть следующим образом:
MCMXCVIII = 1000 + (1000 – 100) + (100 – 10) + 5 + 1 + 1 +1.
17. Позиционные системы счисления
Первая позиционная система счисления была придуманаеще в древнем Вавилоне, причем вавилонская
нумерация была шестидесятиричной, т.е. в ней
использовались 60 цифр. Интересно, что до сих пор при
измерении времени мы используем основание, равное
60 (в 1 мин. содержится 60 секунд, а в 1 часе – 60 мин.)
В девятнадцатом веке довольно широкое
распространение получила двенадцатеричная система
счисления. До сих пор мы часто употребляем дюжину
(число 12): в сутках две дюжины часов, круг содержит
тридцать дюжин градусов и т.д.
В позиционных системах счисления количественное
значение цифры зависит от ее позиции в числе.
18. Позиционные системы счисления
Наиболее распространенными в настоящеевремя позиционными системами счисления
являются десятичная, двоичная, восьмеричная
и шестнадцатеричная. Каждая позиционная
система имеет определенный алфавит цифр и
основание.
В позиционных системах счисления основание
системы равно количеству цифр (знаков в ее
алфавите) и определяет, во сколько раз
различаются
значения
цифр
соседних
разрядов числа.
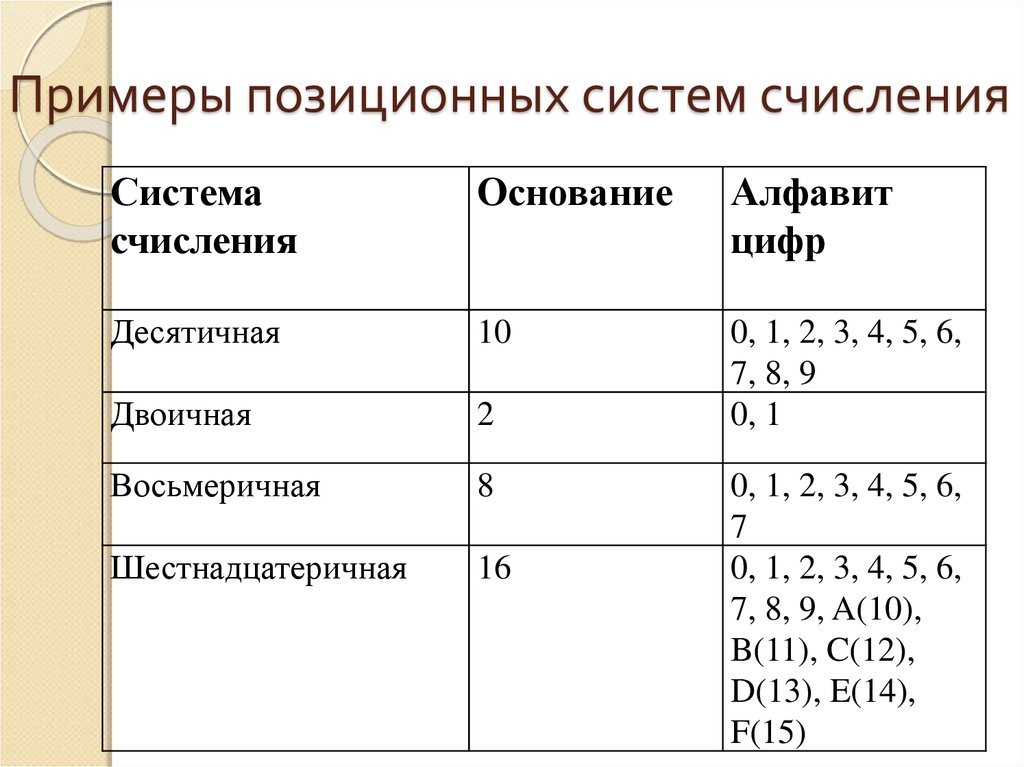
19. Примеры позиционных систем счисления
Системасчисления
Основание
Алфавит
цифр
Десятичная
10
Двоичная
2
0, 1, 2, 3, 4, 5, 6,
7, 8, 9
0, 1
Восьмеричная
8
Шестнадцатеричная
16
0, 1, 2, 3, 4, 5, 6,
7
0, 1, 2, 3, 4, 5, 6,
7, 8, 9, A(10),
B(11), C(12),
D(13), E(14),
F(15)
20. Запись числа в позиционной системе счисления
Позиция цифры в числе называется разрядом. Разрядчисла возрастает справа налево, от младших разрядов к
старшим. Например, в десятичной системе крайняя справа
позиция соответствует первому разряду, в котором цифра
обозначает единицы.
Число 555 в десятичной системе счисления записано в
привычной для нас свернутой форме. В развернутой
форме запись числа 555 будет выглядеть следующим
образом.:
55510 = 5*102 + 5*101 + 5*100.
Для записи
дробей используются разряды с
отрицательными значениями степеней основания.
Например, число 555,55 в развернутой форме будет
записываться следующим образом:
555,5510 = 5*102 + 5*101 + 5*100 + 5*10-1 + 5*10-2.
21. Запись числа в позиционной системе счисления
Как видно из примера, число в позиционных системахсчисления записывается в виде суммы числового ряда
степеней основания (в данном случае 10), в качестве
коэффициентов которых выступают цифры данного
числа.
В общем случае в десятичной системе счисления
запись числа А10, которое содержит n целых разрядов
числа и m дробных разрядов, производится
следующим образом:
А10 = аn-1*10n-1 + … +a0*100 +a-1*10-1 + …a-m*10-m.
Коэффициенты аi в этой записи являются цифрами
десятичного числа, которое в свернутой форме
записывается следующим образом:
A10 = an-1an-2…a0a-1…a-m.
22. Позиционные системы с произвольным основанием.
В системах счисления с основанием q (qичная система счисления) числа вразвернутой форме записываются в виде
Aq = an-1qn-1 + an-2qn-2 + … + a0q0 + a-1q-1 +
…+a-mq-m.
Коэффициенты ai в этой записи являются
цифрами числа, записанного
23. Введение в основы математической обработки информации
Изучением сбора, обработки, анализаи публикации данных,
характеризующих изучаемый предмет,
занимается статистика.
Статистика широко использует
математику как наиболее точный
инструмент исследования.
Статистика позволяет количественно
определить меру взаимосвязи между
явлениями и процессами.
24. Статистика
25. Объект статистики
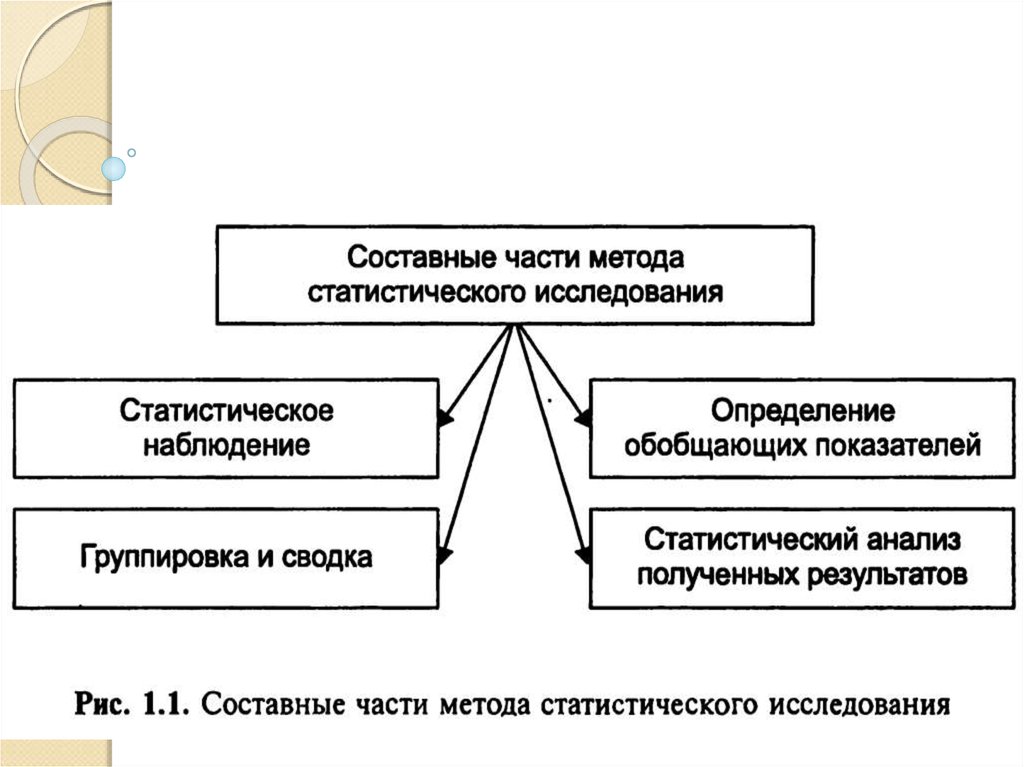
26. Статистическая совокупность
27. Метод статистического исследования
28.
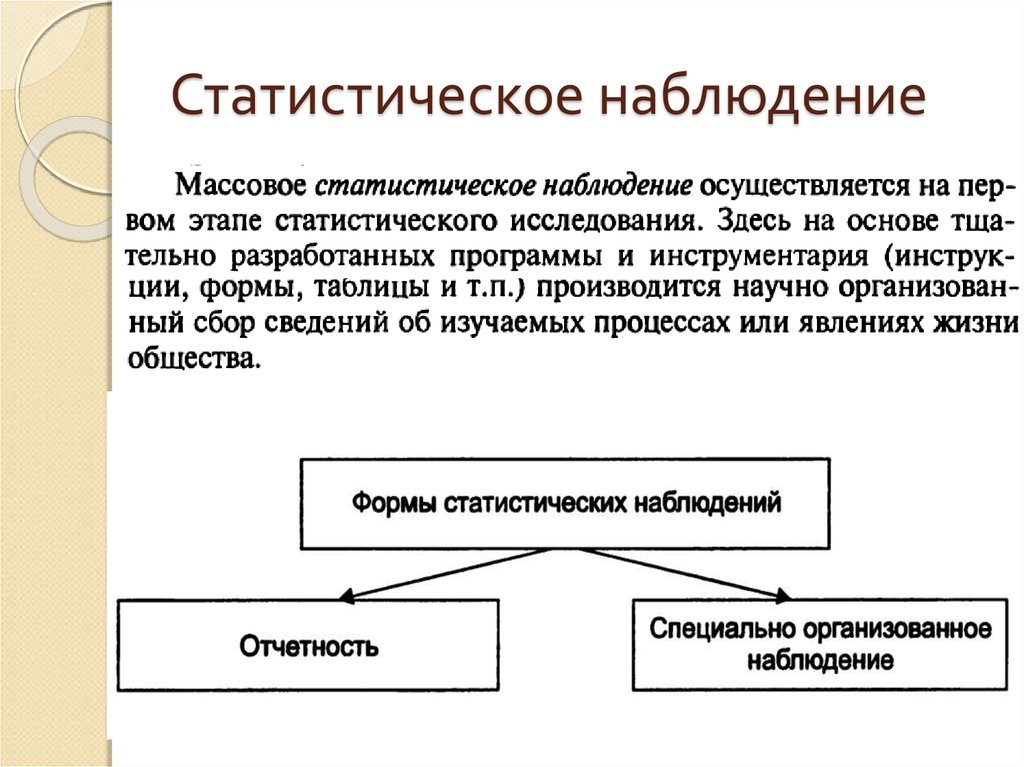
29. Статистическое исследование
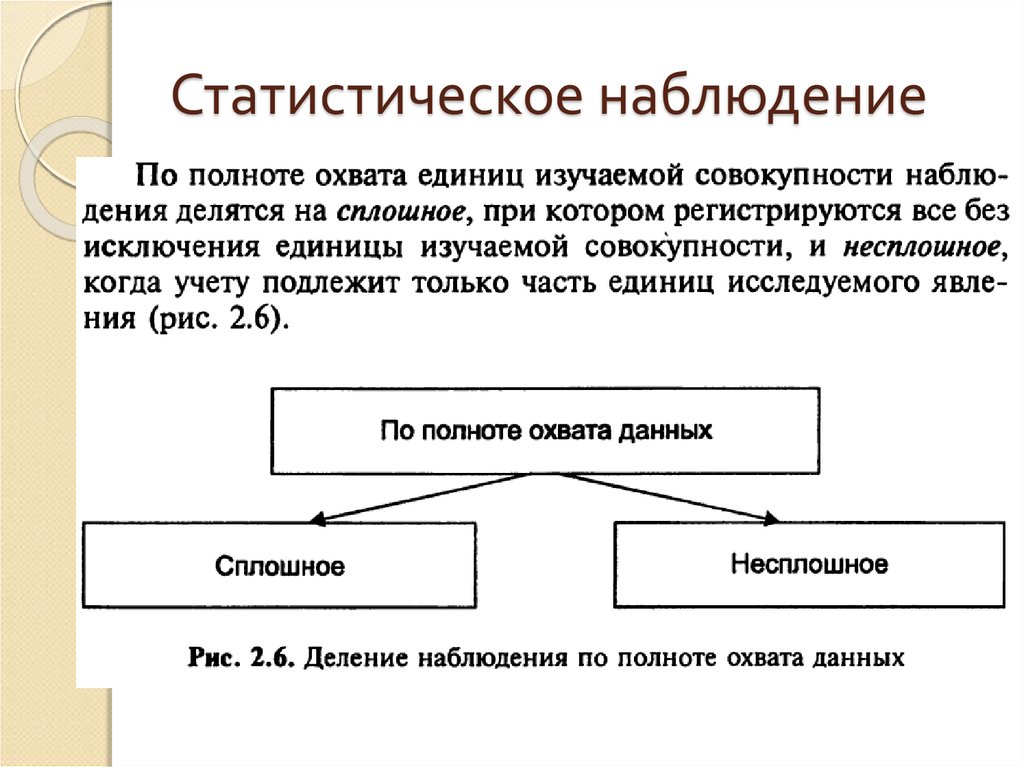
30. Статистическое наблюдение
31. Статистическое наблюдение
32. Выборочное наблюдение
33. Преимущества выборочного исследования
34. Сводка и группировка
35. Статистический анализ
36. Пакеты прикладных программ
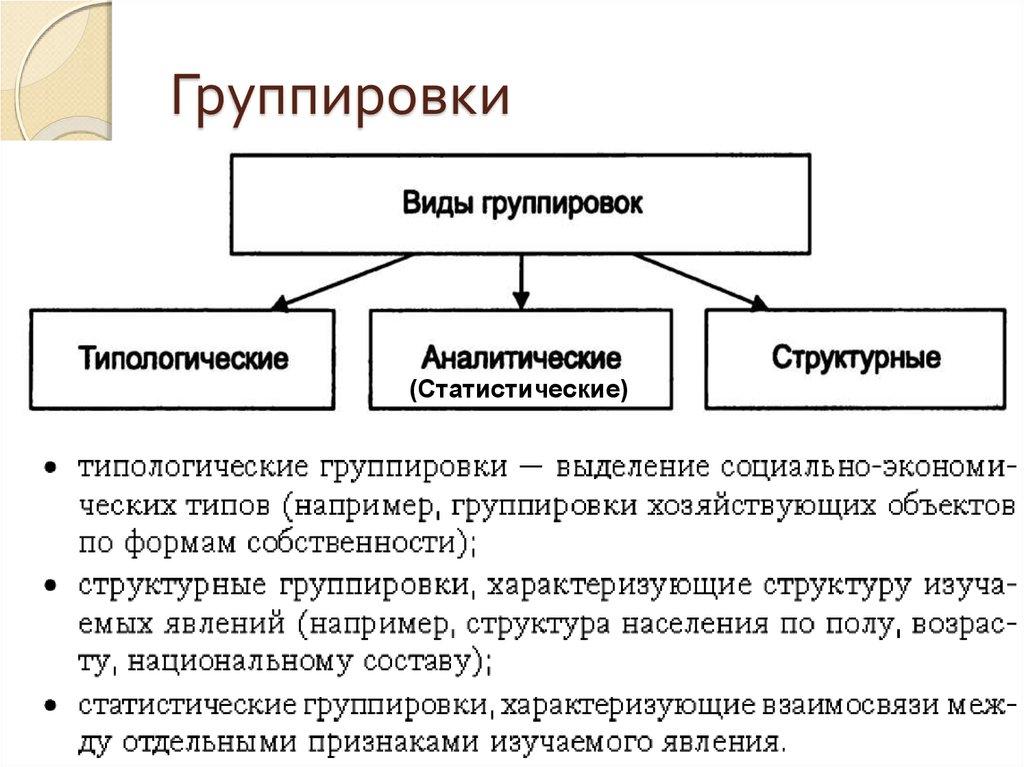
37. Группировки
(Статистические)38. Типологическая группировка
Это типологическая группировка высших учебных заведений .Группировочный признак – форма собственности. Вывод: наблюдался более
значительный ежегодный рост негосударственных высших учебных
заведений, чем государственных .
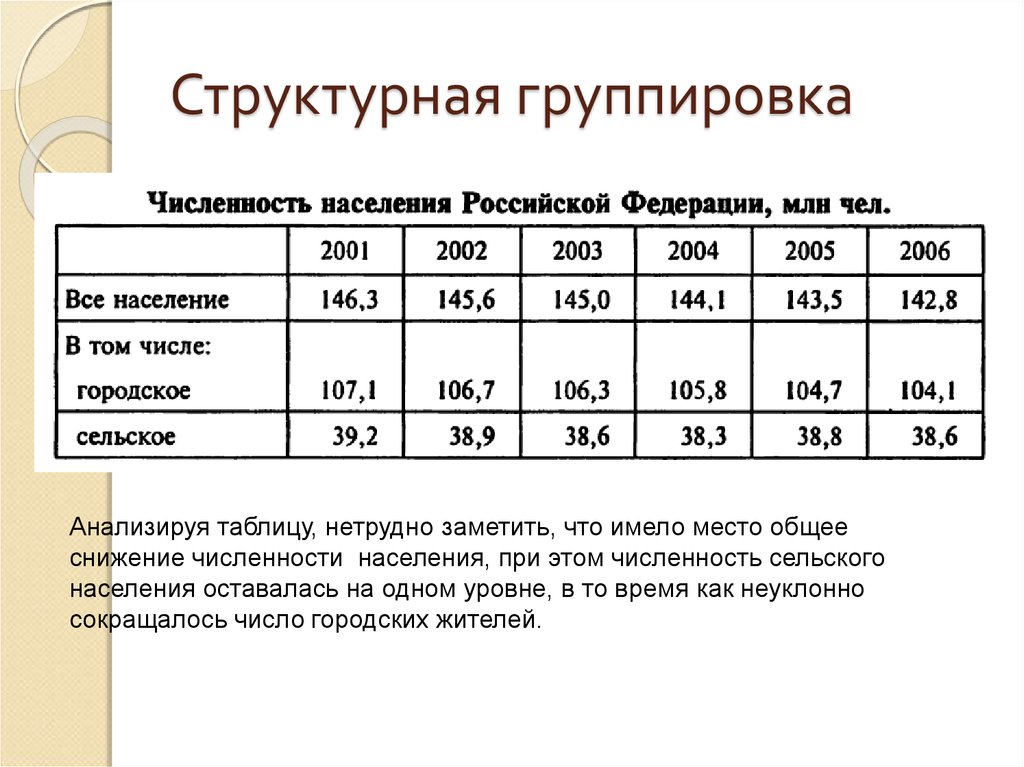
39. Структурная группировка
Анализируя таблицу, нетрудно заметить, что имело место общееснижение численности населения, при этом численность сельского
населения оставалась на одном уровне, в то время как неуклонно
сокращалось число городских жителей.
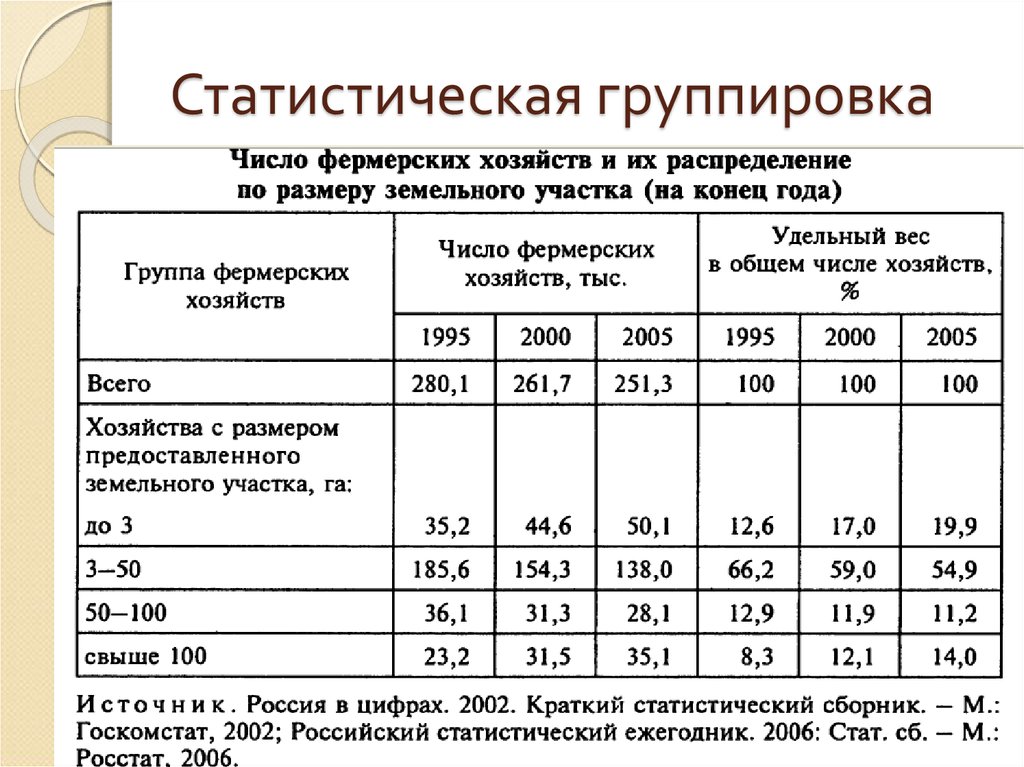
40. Статистическая группировка
41. Статистическая группировка
42. Группировки
43. Простая группировка
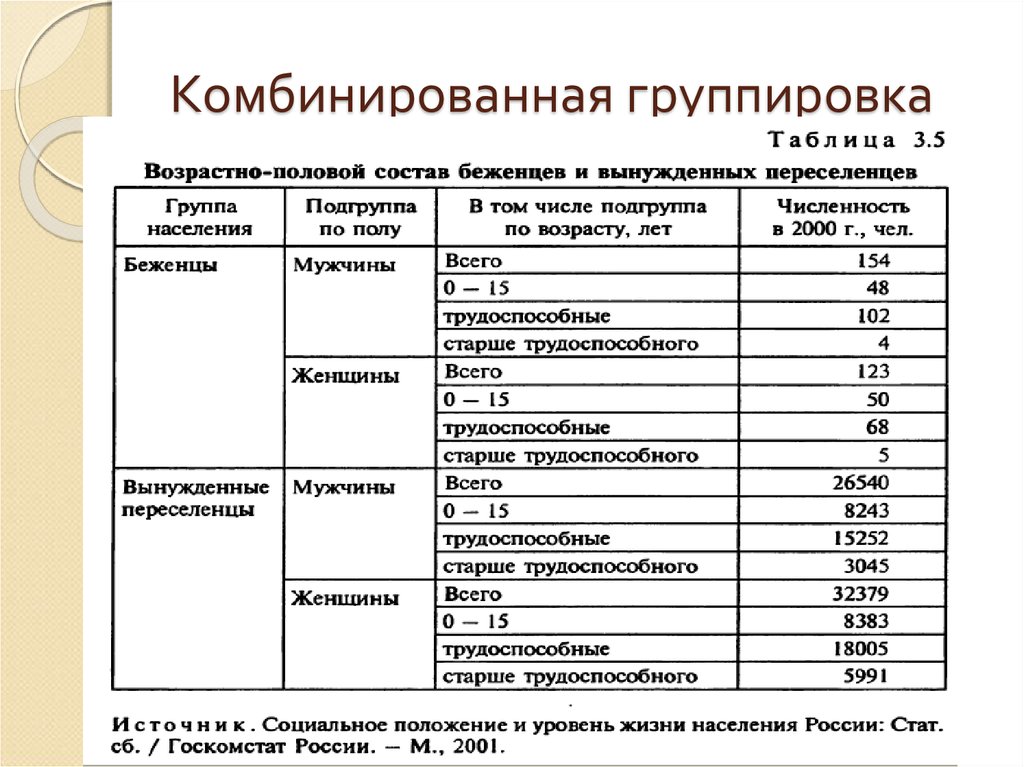
44. Комбинированная группировка
45. Комбинированная группировка
46. Комбинационная группировка в Excel
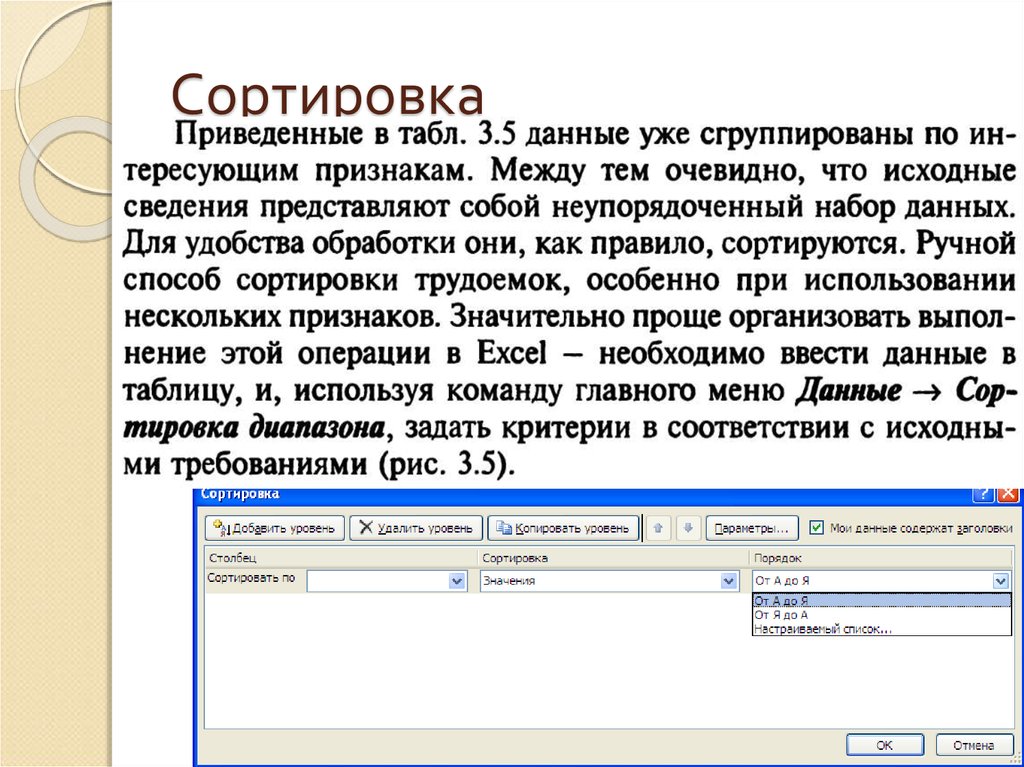
47. Сортировка
48. Сортировка в MS Excel 2003
49. Сортировка
50. Фильтрация
51. Группировки c равными интервалами
52. Группировки с неравными интервалами
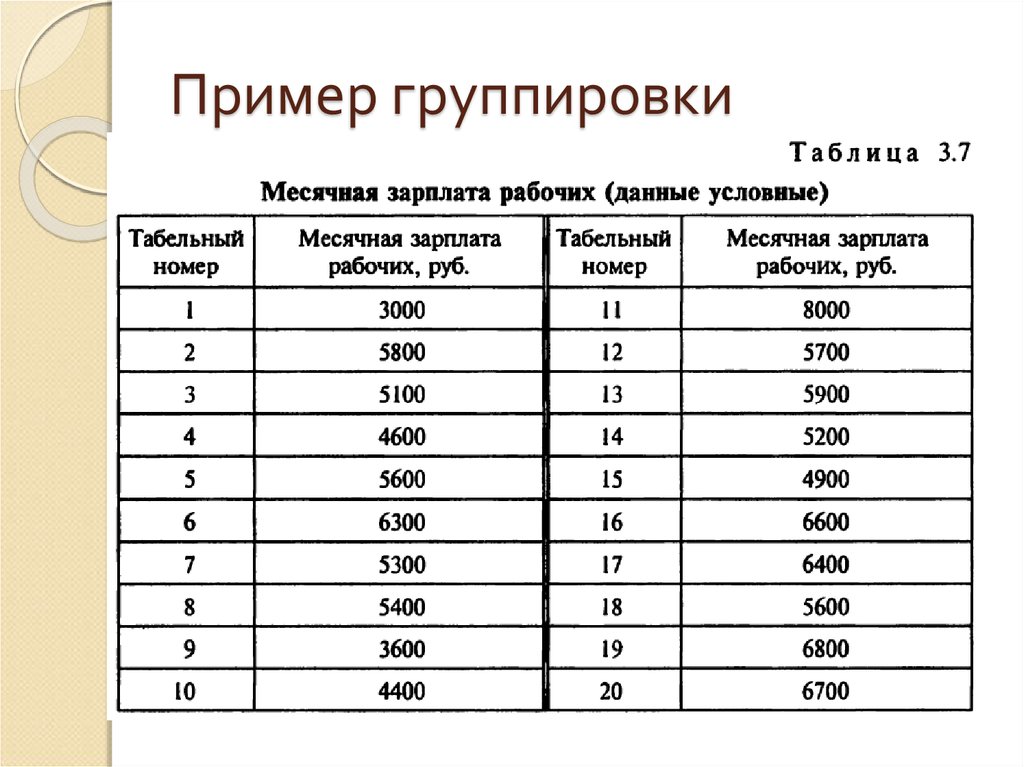
53. Пример группировки
54. Пример группировки
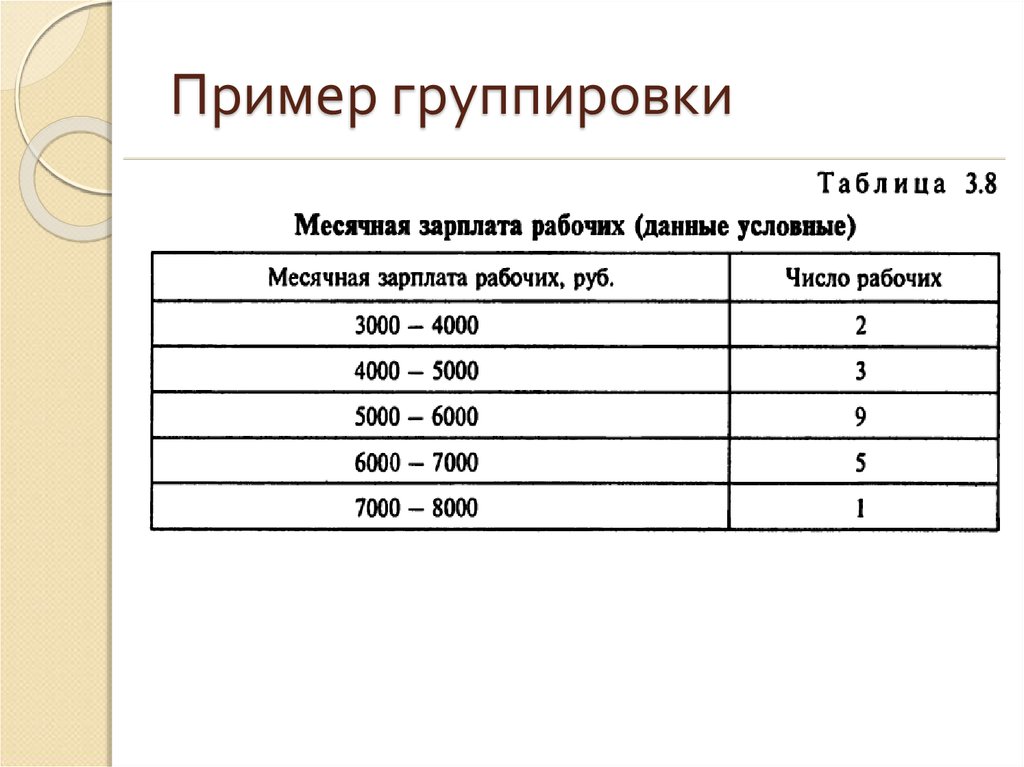
55. Пример группировки
56. Пример группировки
57. Группировки с закрытыми и открытыми интервалами
58. Группировки
59. Сводки
Простая сводка подразумевает подсчет (суммирование) данных очисле единиц совокупности и значении их признаков.
60. Сводки
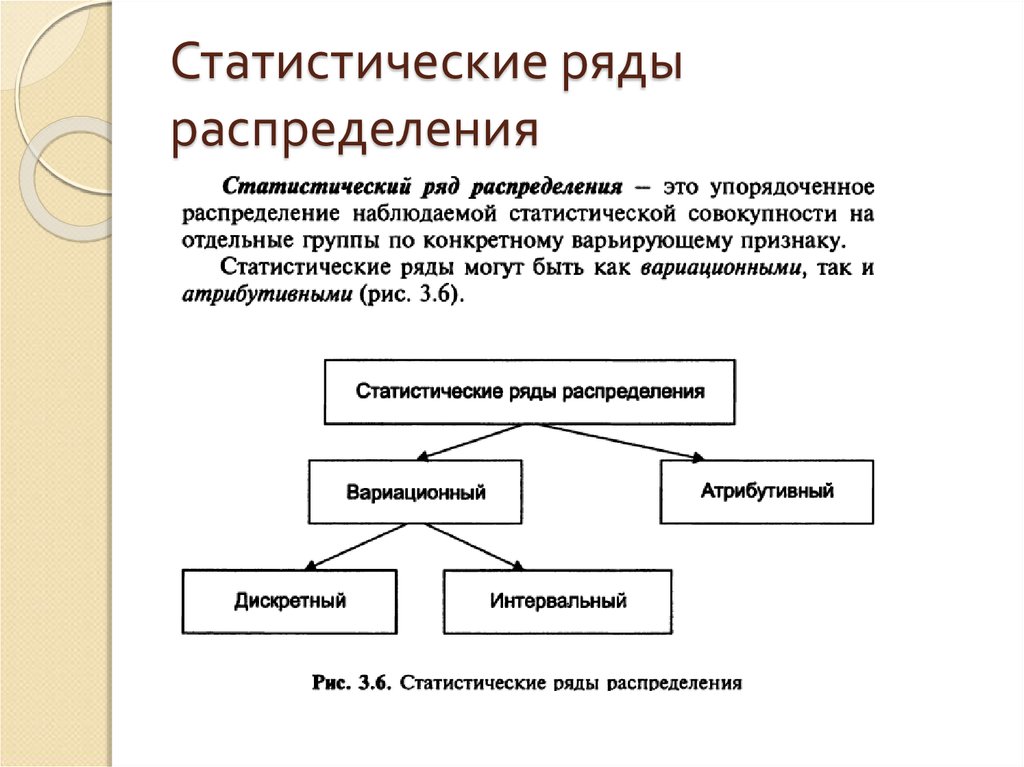
61. Статистические ряды распределения
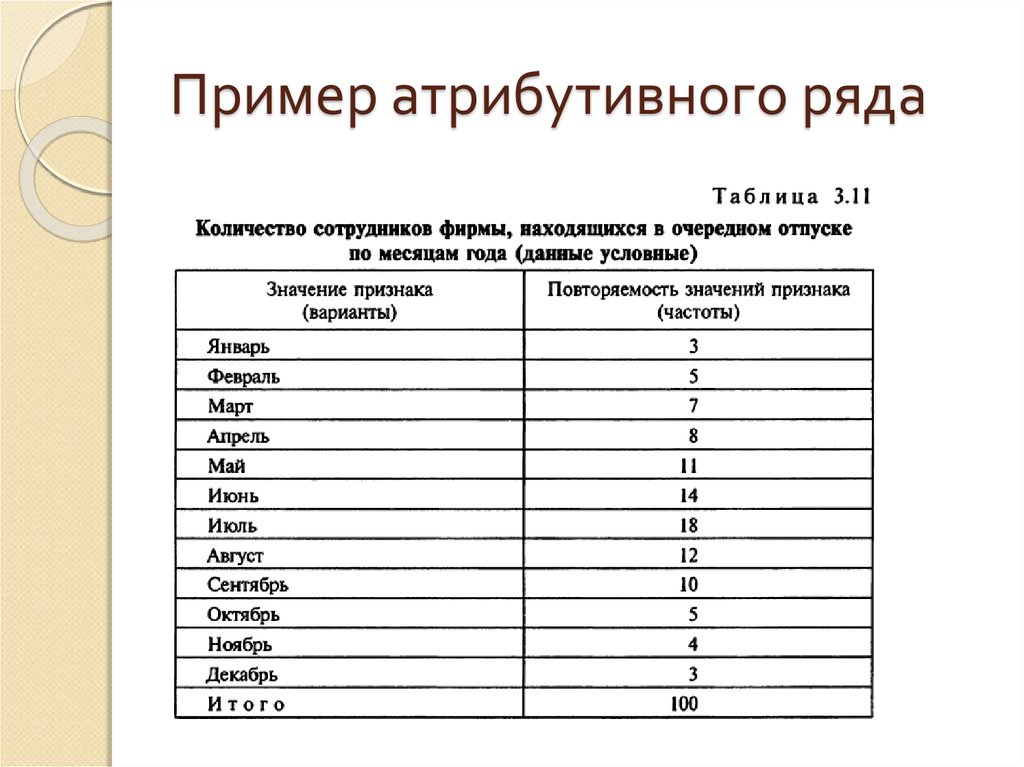
62. Атрибутивный ряд
Для атрибутивного ряда каждаяварианта регистрируется в виде
текстовой записи с указанием
соответствующей частоты повторения.
63. Пример атрибутивного ряда
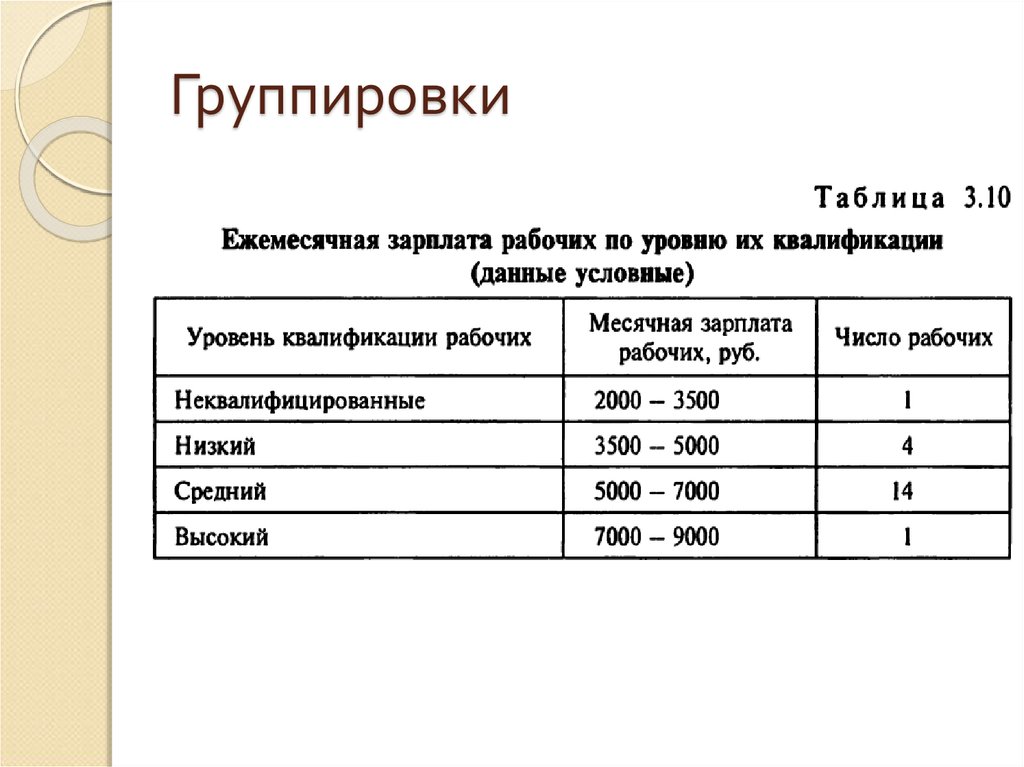
64. Вариационный ряд
Примером вариационного ряда может служить табл. 3.8 Месячнаязарплата рабочих
65. Вариационный ряд
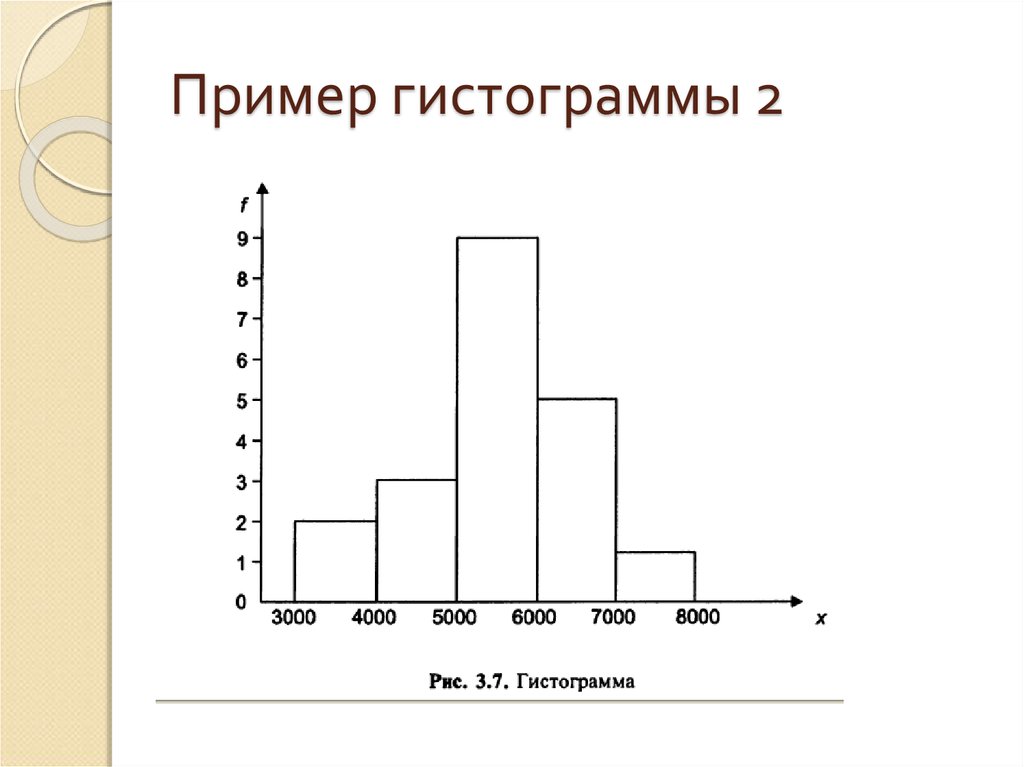
66. Гистограмма
67. Пример гистограммы 2
68. Гистограмма
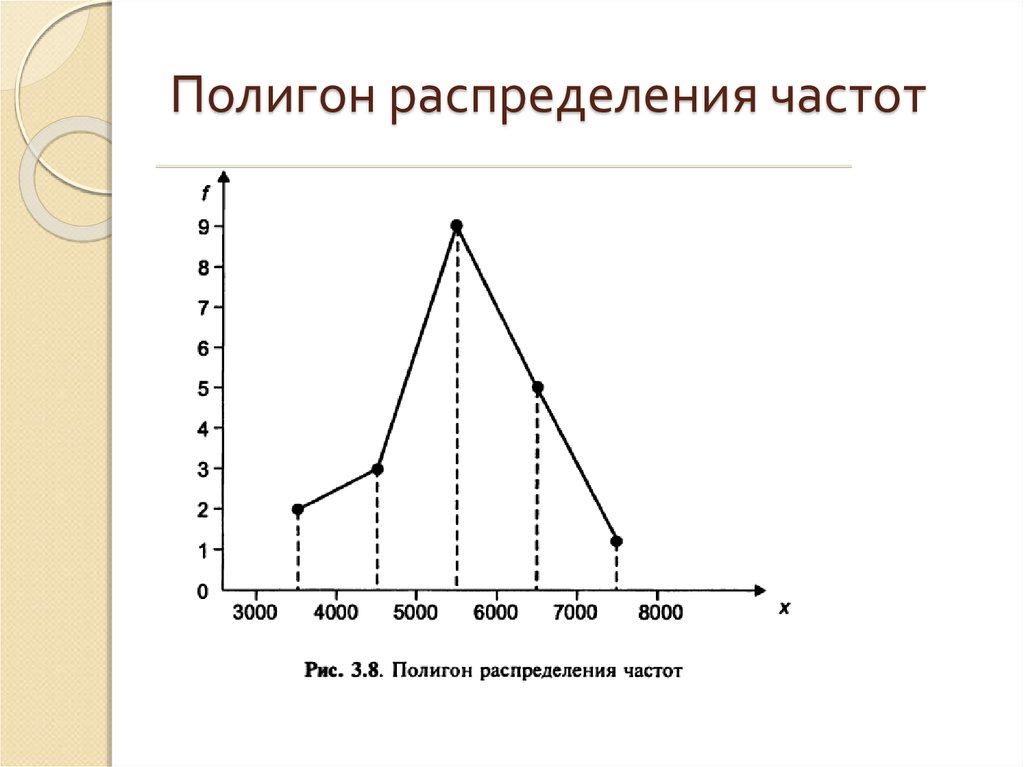
69. Полигон частот
70. Полигон распределения частот
71.
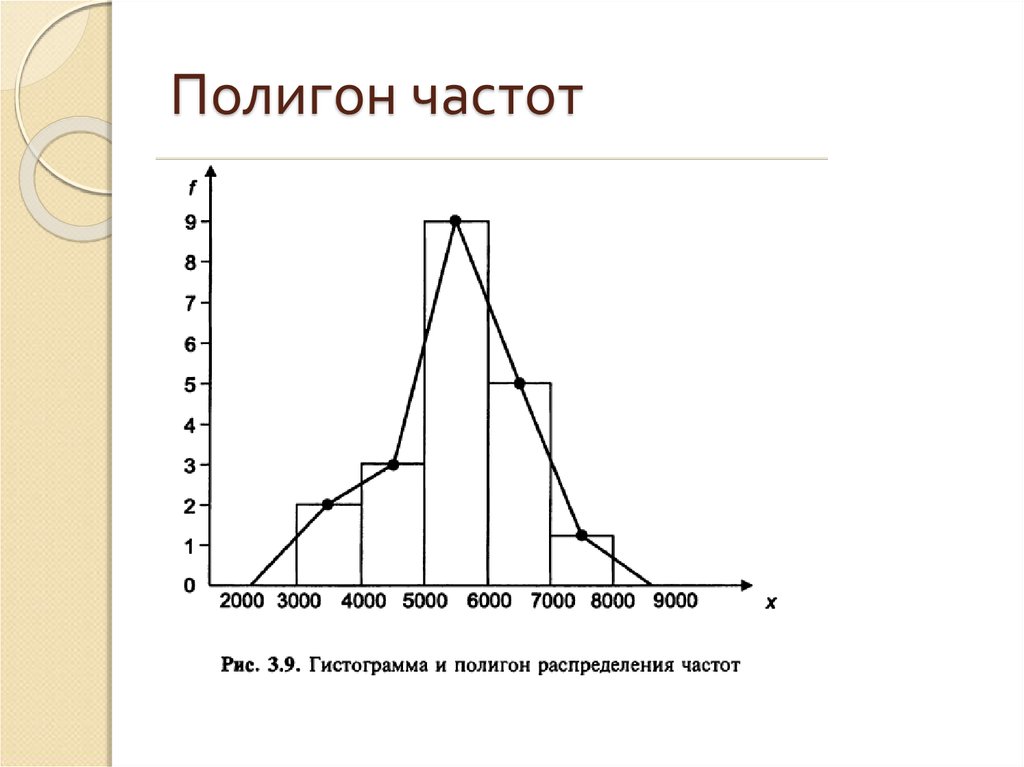
72. Полигон частот
73. Ряд накопленных частот
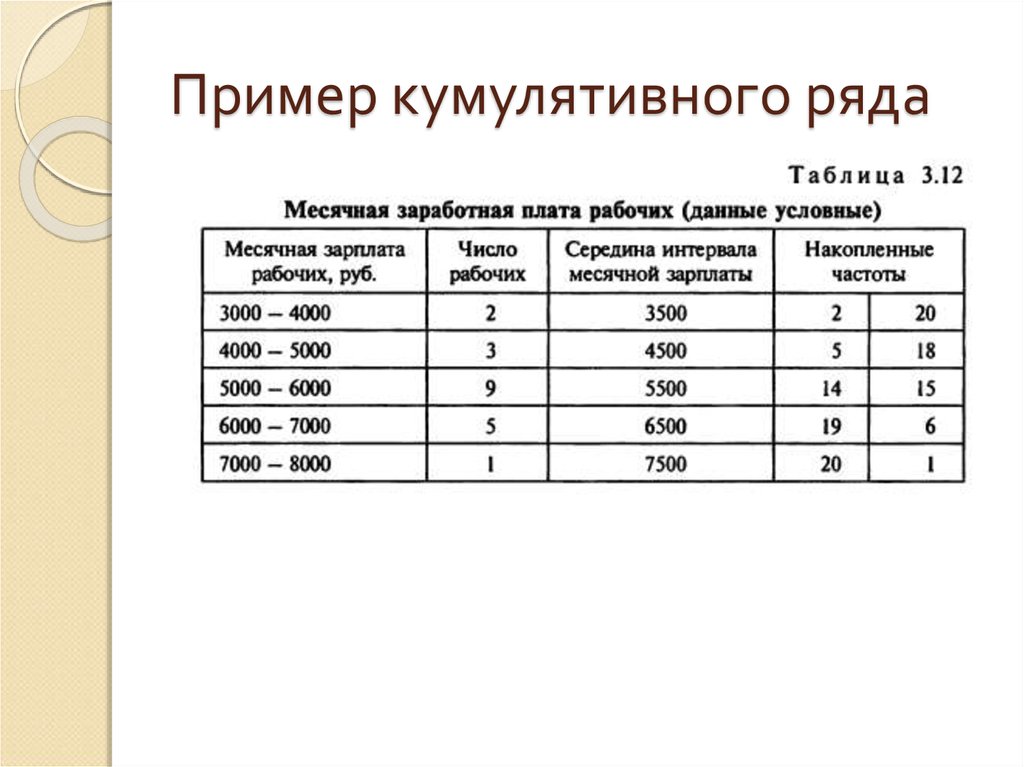
74. Пример кумулятивного ряда
75. Огива
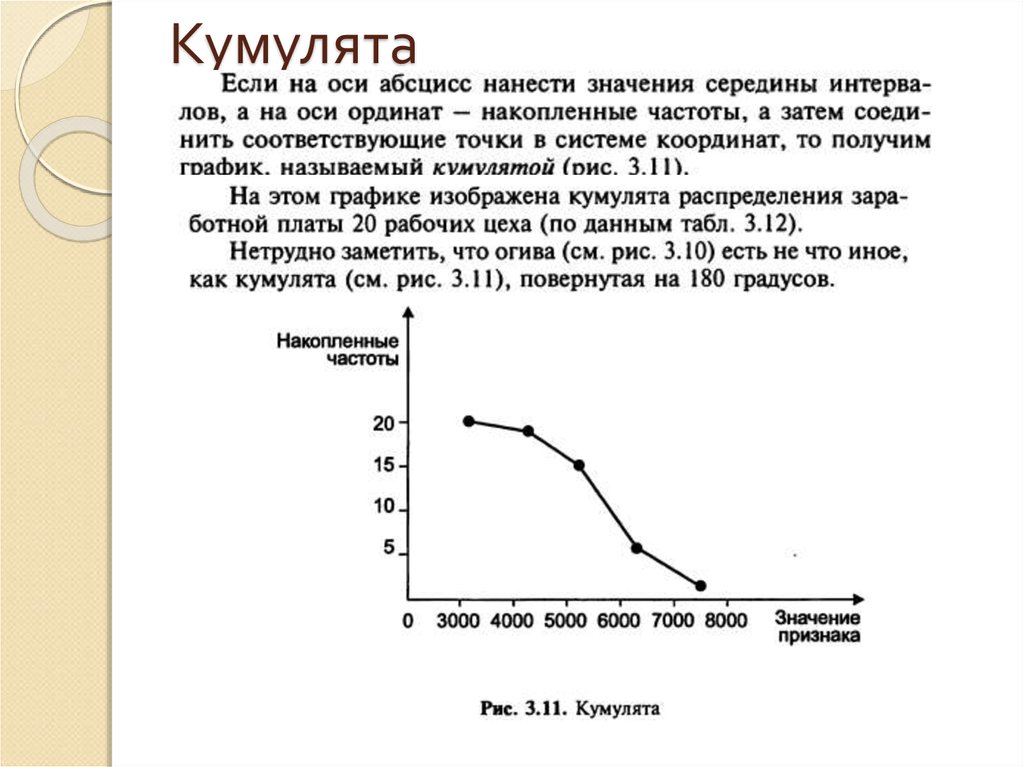
При построении огивы по оси абсцисс76. Кумулята
77. Расчеты и диаграммы в Excel
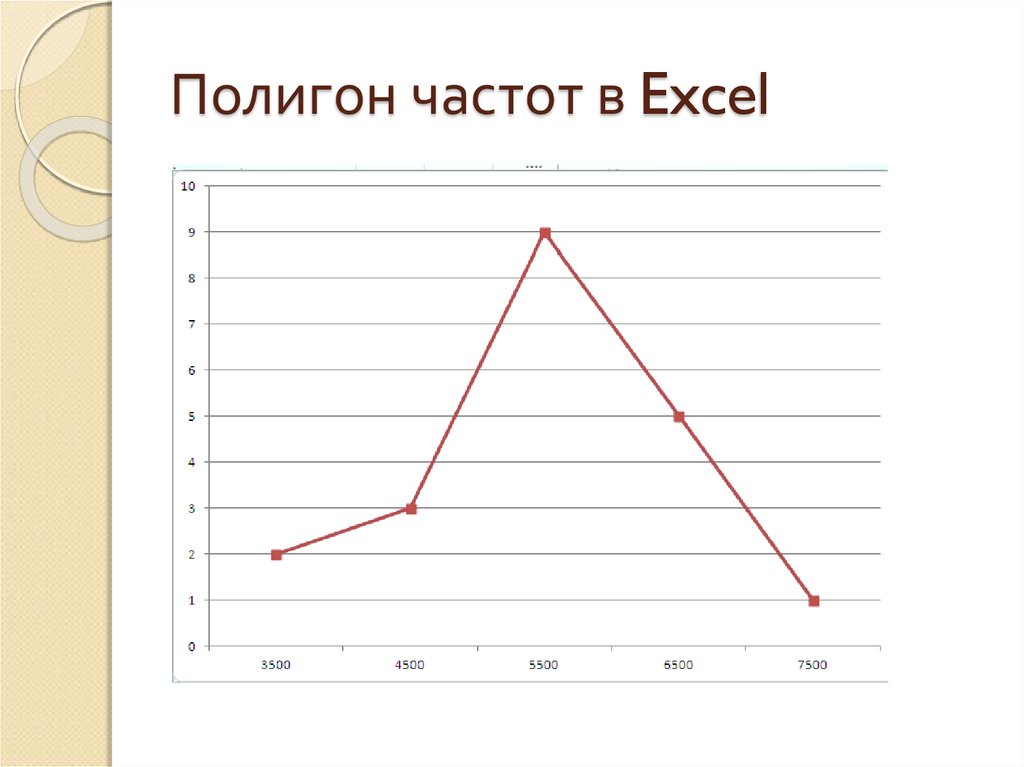
78. Полигон частот в Excel
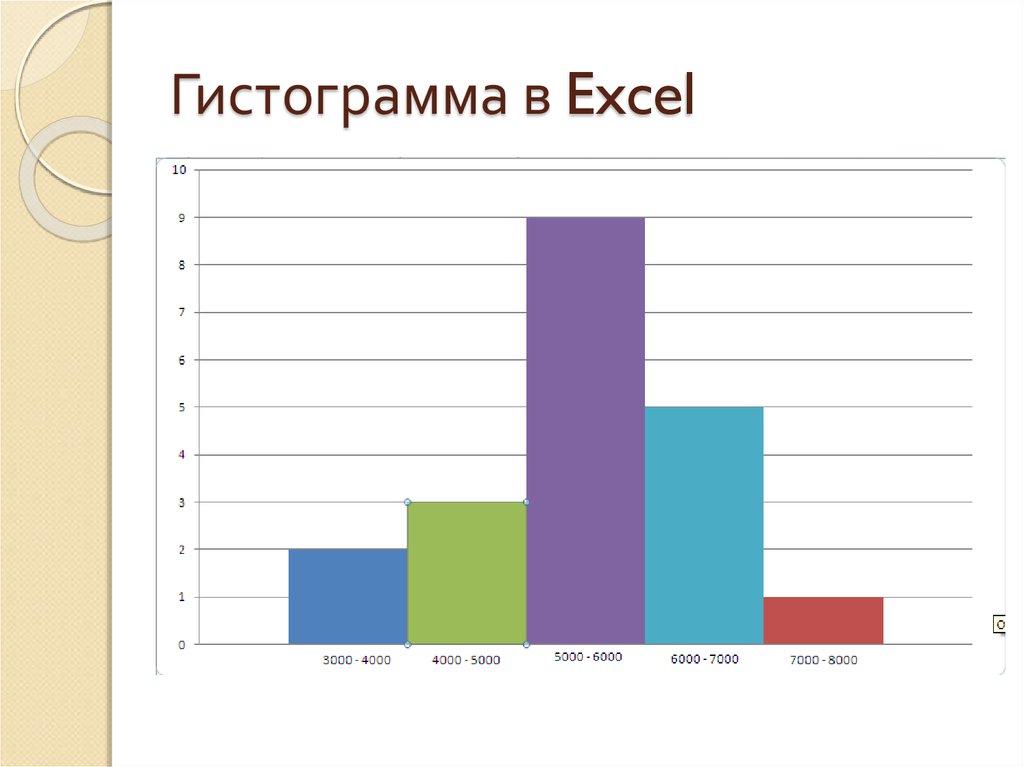
79. Гистограмма в Excel
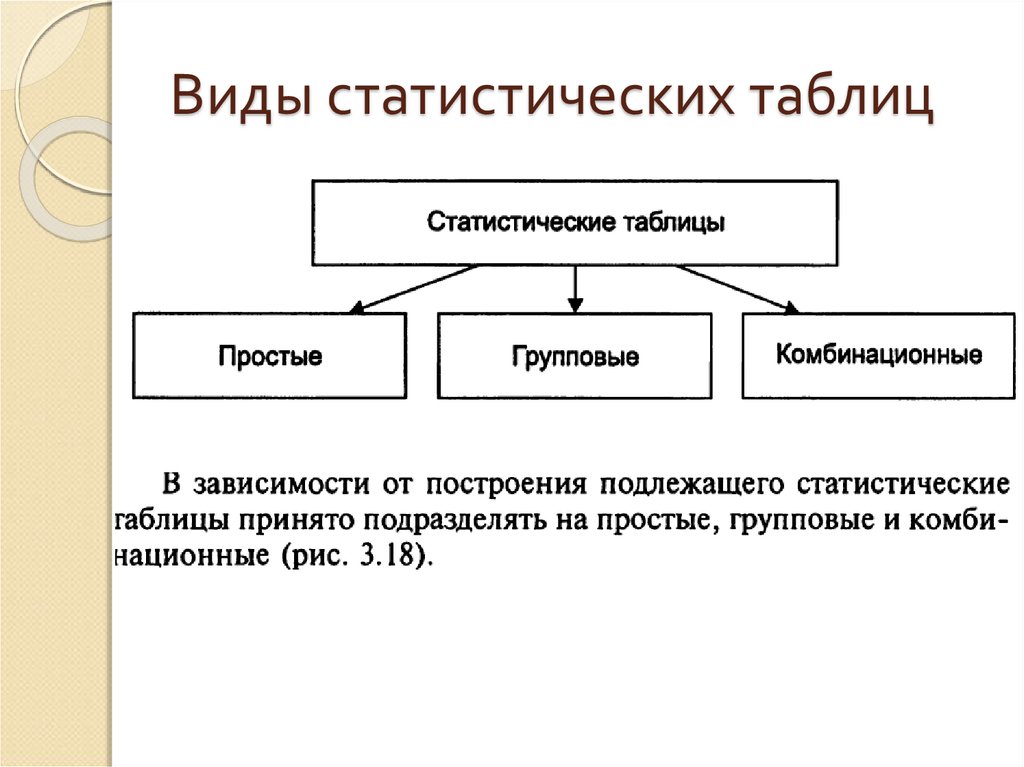
80. Статистические таблицы
81. Подлежащее и сказуемое статистических таблиц
82. Виды статистических таблиц
83. Простые таблицы
84. Пример простой таблицы
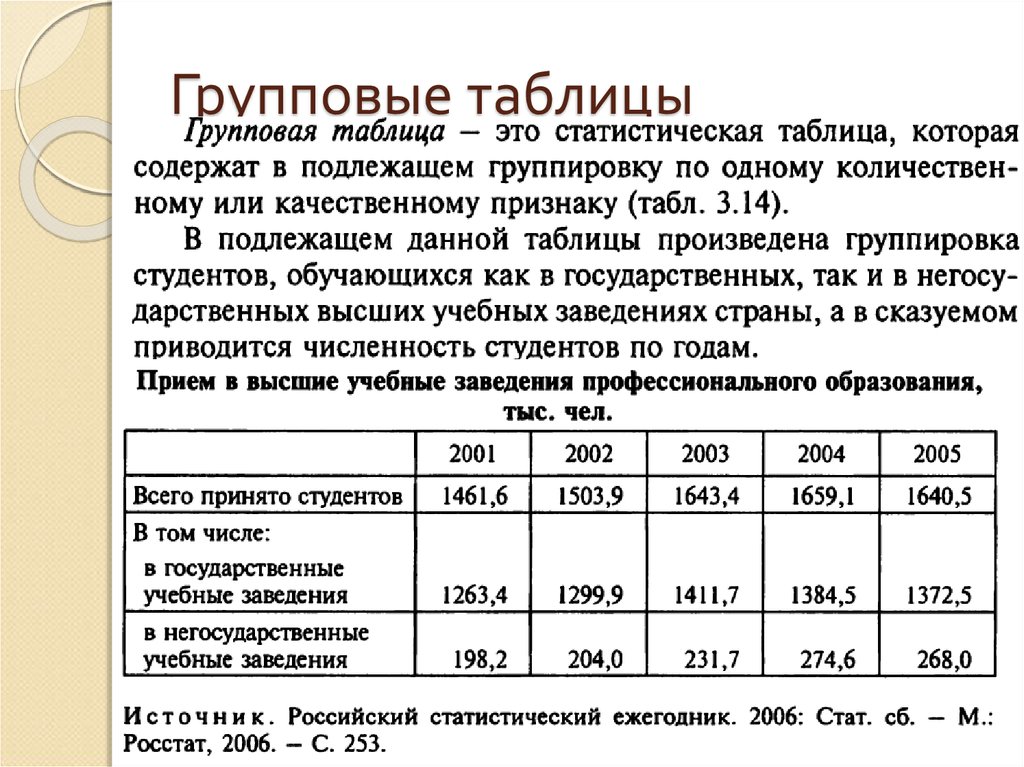
85. Групповые таблицы
86. Комбинационные таблицы
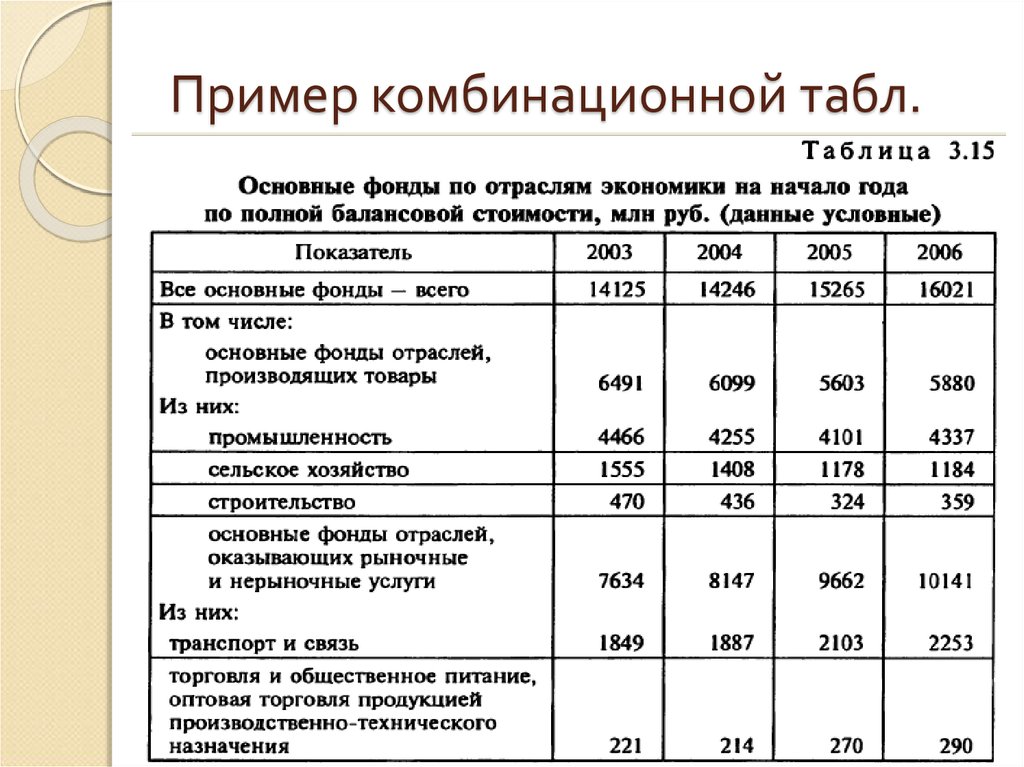
87. Пример комбинационной табл.
88. Правила построения таблиц
89. Графики в статистике
90. Основные элементы графика
91. Диаграммы
92. Диаграммы в Excel
93. Линейные диаграммы
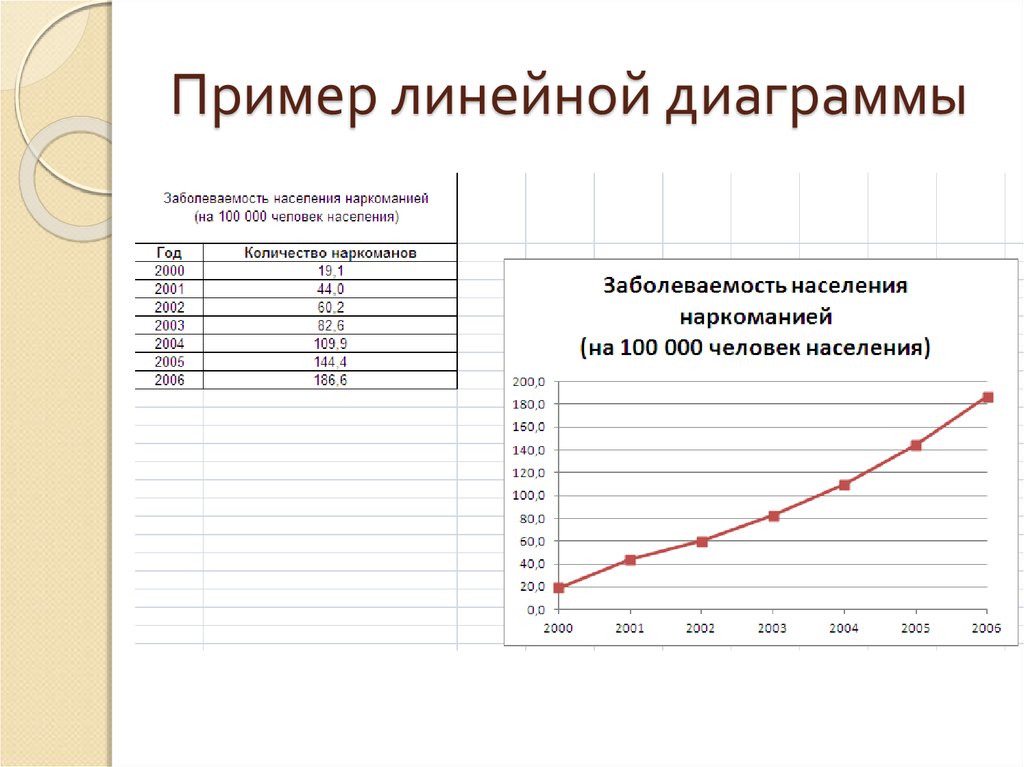
94. Пример линейной диаграммы
95. Диаграммы с двумя кривыми
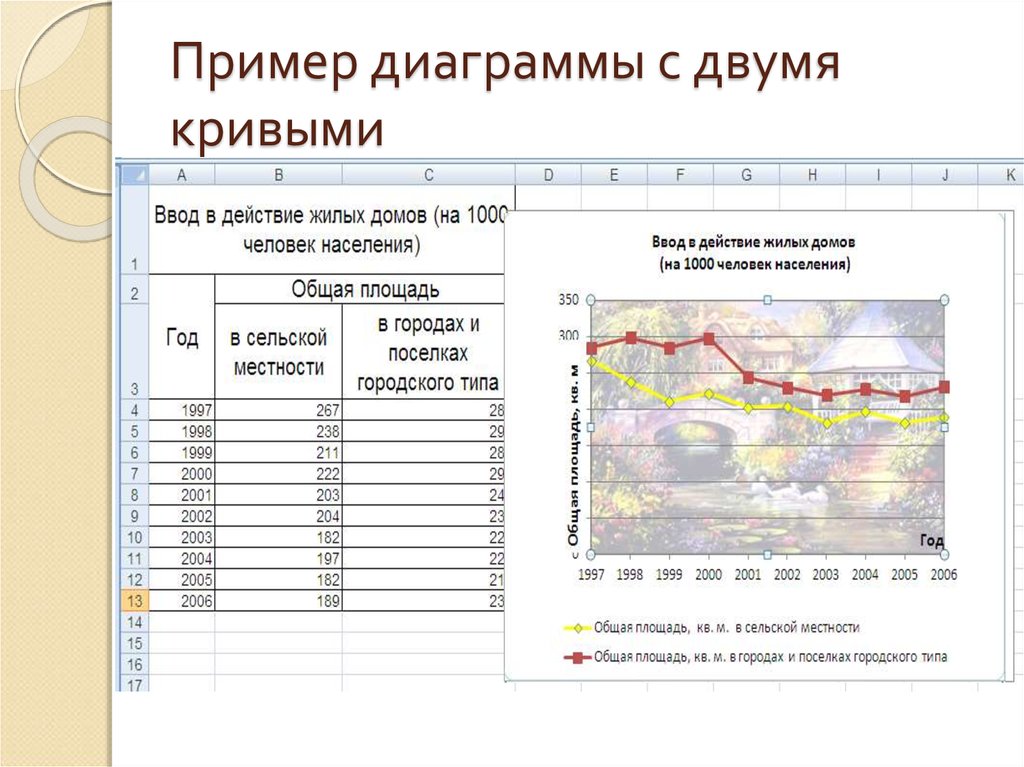
96. Пример диаграммы с двумя кривыми
97. Столбиковые диаграммы
98. Пример столбиковой диаграммы
Дляпостроения
диаграммы
использован
тип объемной
гистограммы с
накоплением
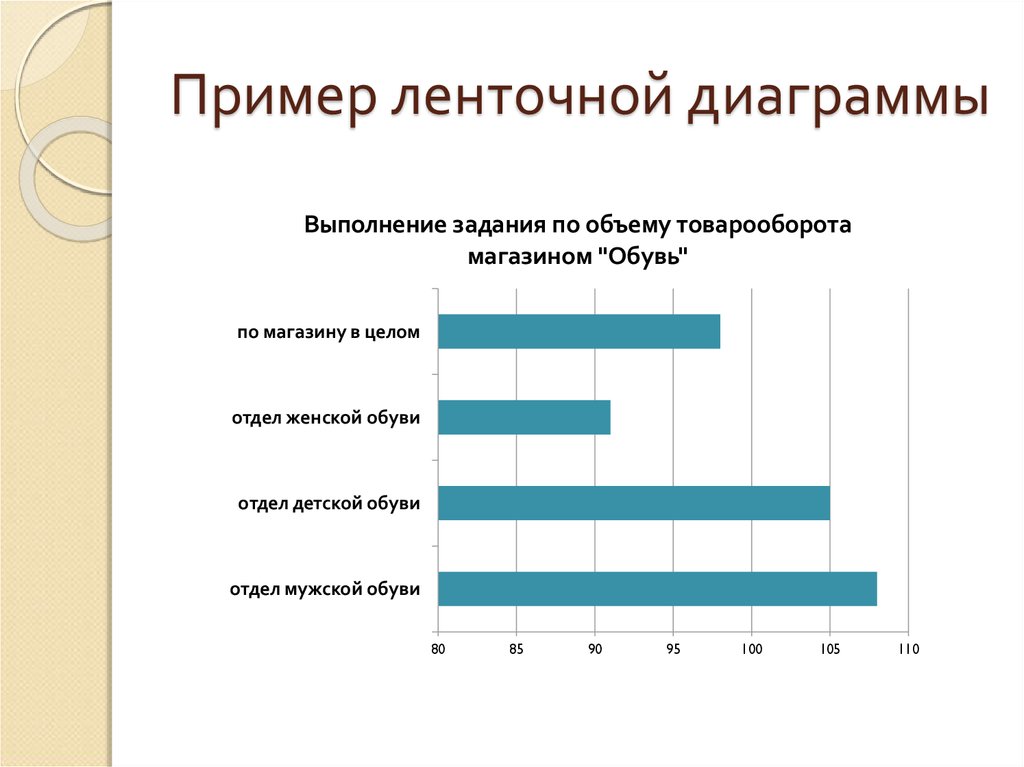
99. Ленточные диаграммы
100. Пример ленточной диаграммы
Выполнение задания по объему товарооборотамагазином "Обувь"
по магазину в целом
отдел женской обуви
отдел детской обуви
отдел мужской обуви
80
85
90
95
100
105
110
101. Секторные диаграммы
102. Пример секторной диаграммы
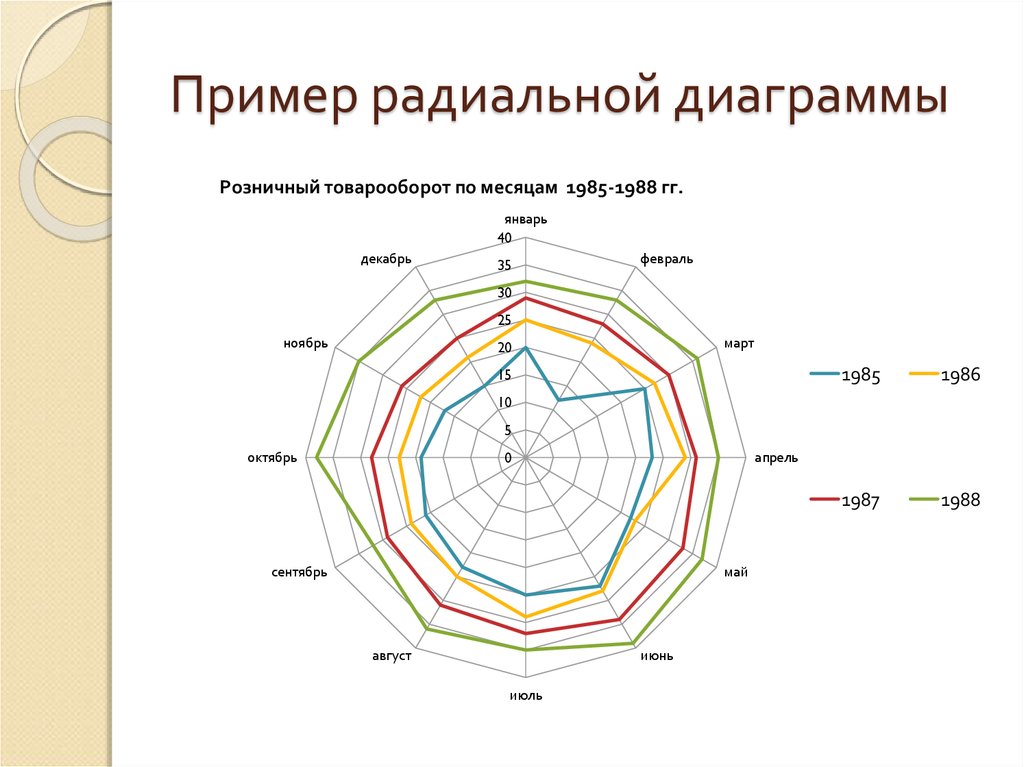
103. Радиальные диаграммы
104. Пример радиальной диаграммы
Розничный товарооборот по месяцам 1985-1988 гг.январь
40
декабрь
35
февраль
30
25
ноябрь
март
20
15
1985
1986
1987
1988
10
5
0
октябрь
апрель
сентябрь
май
август
июнь
июль

















































































 mathematics
mathematics informatics
informatics








