Информация и системы счисления. Основы теории информации

1. Информация и системы счисления

2. Основы теории информации

Термин информация происходит от латинского «informatio», что
означает разъяснение, осведомление, изложение.
Информация – это сведения, изменяющие наши знания об
окружающем мире и понимание его. Важнейший ресурс
управления.
Материальные свойства: информацию можно получить,
записать, удалить, передать; информация не может возникнуть
из ничего.
Абстрактное свойство: при передаче информации количество
информации передающей системы не уменьшается, а в
принимающей - увеличивается.

3. Формы адекватности информации

Синтаксическая – информация рассматривается с точки
зрения формально-структурных характеристик: тип носителя,
способ представления, скорость передачи и обработки, формат
кодов представления, надежности и точность преобразования
и
т.д.
Информацию,
рассматриваемую
только
с
синтаксических позиций, обычно называют данными.
Семантическая – учитывается смысловое содержание
информации, учитываются сведения, которые отражает
информация.
Прагматическая – анализируются потребительские свойства
информации.
Прагматический
аспект
рассмотрения
информации связан с ценностью, полезностью информации
для выработки управленческого решения
3

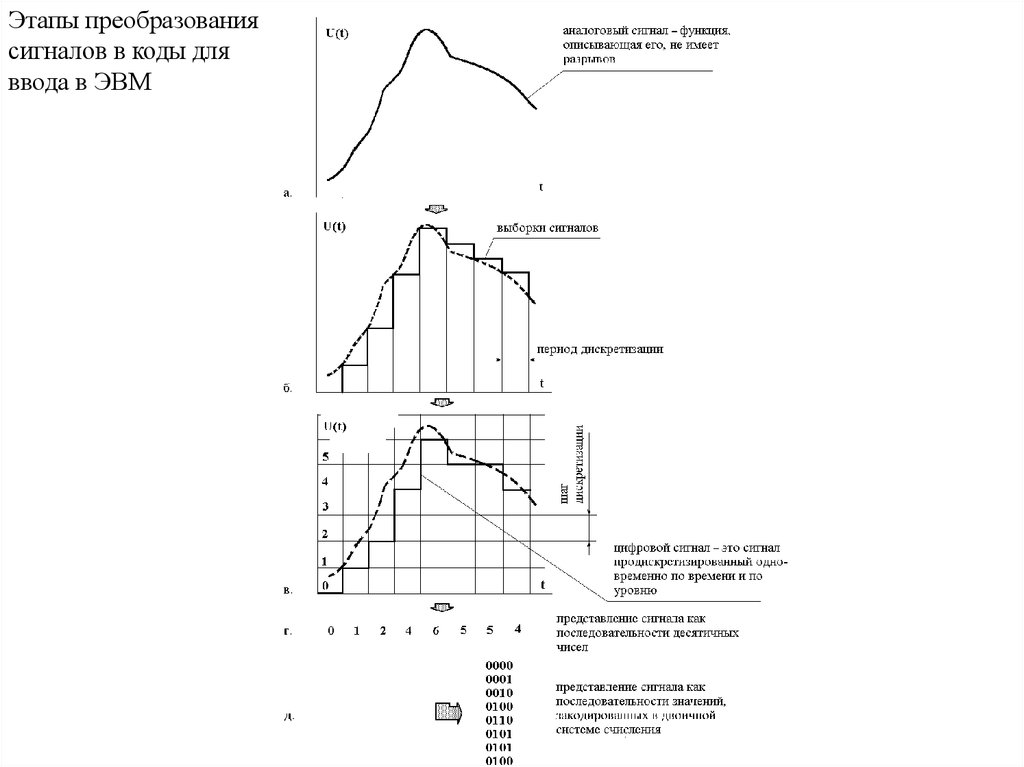
4.

Этапы преобразования
сигналов в коды для
ввода в ЭВМ

5.

СИСТЕМЫ СЧИСЛЕНИЯ
Система счисления – принятый способ записи чисел.
Различают
позиционные
и
непозиционные системы
счисления.
Непозиционная система счисления – система счисления, в
которой количественный эквивалент каждой цифры не
зависит от ее положения (места, позиции) в записи числа.
I – 1 V – 5 X – 10 L – 50 C – 100 D – 500 M – 1000
Система счисления называется позиционной, если
значение цифры зависит от ее места (позиции) в записи
числа.

6.

Основанием системы счисления называется количество
знаков или символов, используемых для изображения числа в
данной системе счисления.
Положение,
занимаемой
цифрой
при
письменном
обозначении числа называется разрядом.
1978,1 = 1*103+9*10 2+ 7*10 1+ 8*10 0 + 1*10 -1
весовые коэффициенты разрядов («веса»)
Любое число можно представить в развернутом виде:
Am-1*Pm-1+ Am-2*Pm-2 + …+A1*P1 + A0*P0 + A-1*P-1 +…+A-s*P-s
P – основание системы счисления
1978,1(10)
Базис системы счисления – это последовательность
ключевых чисел, каждое из которых задает значение цифры в
ее позиции или «вес» каждого разряда (Pm-1, Pm-2 ,…, P-s ).

7.

Основание Система счисления
2
Двоичная
Знаки
0,1
3
Троичная
0,1,2
4
Четвертичная
0,1,2,3
5
Пятиричная
0,1,2,3,4
8
Восьмиричная
0,1,2,3,4,5,6,7
10
Десятичная
0,1,2,3,4,5,6,7,8,9
12
Двенадцатиричная
0,1,2,3,4,5,б,7,8,9,А,В
16
Шестнадцатиричная
0,1,2,3,4,5,6,7,8,9,A.B,С,D,E,F

8.

Представление чисел
В общем случае запись любого смешанного числа в системе счисления
с основанием Р будет представлять собой ряд вида:
am-1Pm-1+am-2Pm-2+...+a1P1+a0PO+a-1P-1+a-2P-2+...+a-sP-s
P – основание системы счисления. Значения цифр лежат в пределах от
0 до Р-1.
положительные значения индексов - для целой части числа (m
разрядов);
отрицательные значения - для дробной (s разрядов).
Единице каждого разряда приписан определенный вес рk

9.

Алгоритм перевода целого десятичного числа в систему счисления с
основанием P:
•последовательно выполнять деление целого десятичного числа и получаемых
целых частных на P до тех пор, пока не получится частное, меньшее P (в
процессе деления выписываются остатки от 0 до P-1);
•записать полученные остатки в обратной последовательности.
Алгоритм перевода правильной десятичной дроби в систему
счисления с основанием P:
•последовательно выполнять умножение десятичной дроби и получаемых
дробных частей произведения на P до тех пор, пока не получится нулевая
дробная часть или не будет достигнута требуемая точность (в процессе
умножения в остатки выписываются полученные целый части от 0 до P-1);
•записать полученные целые части произведения в прямой последовательности.
Алгоритм перевода смешанного десятичного числа систему
счисления с основанием P:
•перевести целую часть;
•перевести дробную часть;
•сложить полученные результаты.

10.

Примеры перевода чисел из одной системы счисления в другую
Пример 1. Перевести число 11 из
десятичной системы счисления в
двоичную систему.
Ответ: 1110 = 10112
Пример 3. Перевести число 0,75 из
десятичной системы счисления в
двоичную систему.
Ответ: 0,7510 = 0,112
Пример 2. Если десятичное число
достаточно большое, то можно применить
следующий вид записи:
Ответ: 36310 = 1011010112
Пример 5. Перевести число 15, 2510
из десятичной системы счисления в
двоичную систему.
Ответ: 15,2510 = 1111,012

11.

12.

Представление чисел в разных системах исчисления
Десятичная система исчисления
7 2 9,
3
2
4 = 7*102 + 2*101 + 9*100 + 3*10–1 + 2*10–2 + 4*10–3
102 101 100 10 –1 10 –2 10–3
весовые коэффициенты
разрядов
27,625D =
=
=
1 1 0 1 0
Двоичная система исчисления
1* 2 + 1* 23 + 0* 22 + 1* 21 + 1* 20 + 1* 2–1 + 0* 2–2 + 1* 2–3 =
1*16 + 1* 8 + 0* 4 + 1* 2 + 1* 1 + 1* 0,5 + 0* 0,25 + 1* 0,125 =
(1
1
0
1
1,
1
0
1)В.
1, 1 = 1* 25+ 1* 24+ 0* 23+1* 22+ 0* 21+ 1* 20+ 1* 2–1 = 53,5D
4
25 24 23 22 21 20 2–1
весовые коэффициенты
разрядов Шестнадцатеричная
система исчисления
= 10*162 + 11*161 + 9*160 + 12*16 –1 + 2*16 –2 + 15*16–3 =
162 161 160 16–1 16–2 16–3
весовые коэффициенты
A
B
9
C
2
F
A B 9, C 2 F
разрядов
= 2745,7614745D.
Т а б л и ц а 4.1
Представление чисел в различных системах счисления
Десятична Двоичная Шестнадцат Десятичная Двоичная Шестнадцат
я
форма
еричная
форма
форма
еричная
форма
форма
форма
0
0000
0
8
1000
8
1
0001
1
9
1001
9
2
0010
2
10
1010
А
3
0011
3
11
1011
В
4
0100
4
12
1100
С
5
0101
5
13
1101
D
6
0110
6
14
1110
Е
7
0111
7
15
1111
F

13.

Перевод чисел из двоичной системы счисления в шестнадцатеричную
Табли
Представление чисел в разли
Для перевода целого двоичного числа в
шестнадцатеричное надо:
Десятична Двоичная Шестнадцат Д
я
форма
еричная
форма
форма
•Разбить двоичное число по четыре цифры начиная справа;
0
0000
0
1
0001
1
•Если в последней группе будет меньше четырех цифр, то
2
0010
2
дополнить ее слева нолями;
3
0011
3
4
0100
4
•Преобразовать каждую группу в шестнадцатеричное число.
5
0101
5
Пример: 1001101112 = 0001 0011 0111 = 13716 Т а б л и ц а 64.1
0110
6
7
0111
7
Представление чисел в различных системах счисления
Чтобы перевести дробное двоичное число в
шестнадцатеричноеДесятична
необходимо:
Двоичная Шестнадцат Десятичная Двоичная Шестнадцат
я
форма
еричная
форма
•Разделить дробную часть по четыреформа
цифры слева направо,
0 цифр,
0000
0 ее
если в группе окажется меньше четырех
дополнить
1
0001
1
справа нолями;
2
0010
2
3
0011
3
•Преобразовать дробную часть в шестнадцатеричные
числа;
4
0100
4
0101
5
•Объединить целую и дробную части. 5
6
0110
6
7
0111 = 0, 298
7
Пример: 0,001010011 = 0, 0010 1001
1000
2
16
форма
форма
8
9
10
11
12
13
14
15
1000
1001
1010
1011
1100
1101
1110
1111
еричная
форма
8
9
А
В
С
D
Е
F
Удобнее всего преобразовывать группы при помощи таблицы соответствия.