Динамика. Область применимости классической механики

1.

Динамика
Область применимости классической механики
Классическая механика, основанная на законах Ньютона,
применима к макроскопическим объектам, движущихся с
нерелятивистскими скоростями v = c
С одной стороны – движение тел с релятивистскими скоростями
изучает специальная теория относительности.
С другой стороны – законы микромира объясняются в
квантовой механике.
Таким образом, классическая механика является механиком
макроскопических тел, движущихся с нерелятивистскими
скоростями.

2.

Динамика
Первый закон Ньютона. Инерциальные системы отсчета
Свободное тело: тело, не взаимодействующее с другими телами.
Опыт: свободные тела движутся относительно друг друга
прямолинейно и равномерно.
Инерциальная СО: СО, связанная со свободным телом.
1-й закон Ньютона:
Тело (материальная точка) находится в состоянии покоя или равномерного
и прямолинейного движения относительно ИСО, пока воздействие со
стороны других тел не заставит изменить это состояние.

3.

Динамика
Масса. Импульс
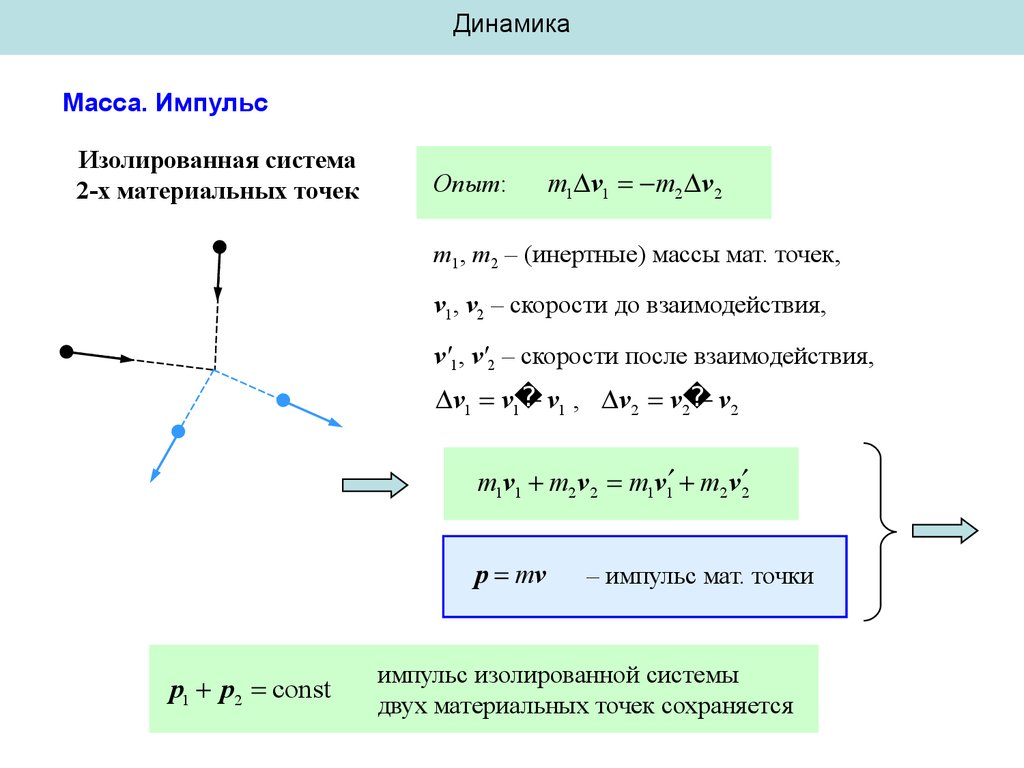
Изолированная система
2-х материальных точек
Опыт:
m1 v1 m2 v2
m1, m2 – (инертные) массы мат. точек,
v1, v2 – скорости до взаимодействия,
v'1, v'2 – скорости после взаимодействия,
v1 v1
v1 , v2 v2 v2
m1v1 m2 v2 m1v1 m2 v2
p mv
p1 p2 const
– импульс мат. точки
импульс изолированной системы
двух материальных точек сохраняется

4.

Динамика
Второй закон Ньютона
1) Импульс свободного тела не меняется p = const
2) Воздействие (со стороны других тел) приводит к изменению
импульса p const
3) Чем интенсивнее воздействие, тем больше
dp
dt
Логично силу, как меру воздействия, просто приравнять
dp
dt
2-й закон Ньютона:
Сила, действующая на материальную точку, равна производной ее
импульса по времени
F
dp
dt
или
F ma (если m = const)

5.

Динамика
Третий закон Ньютона
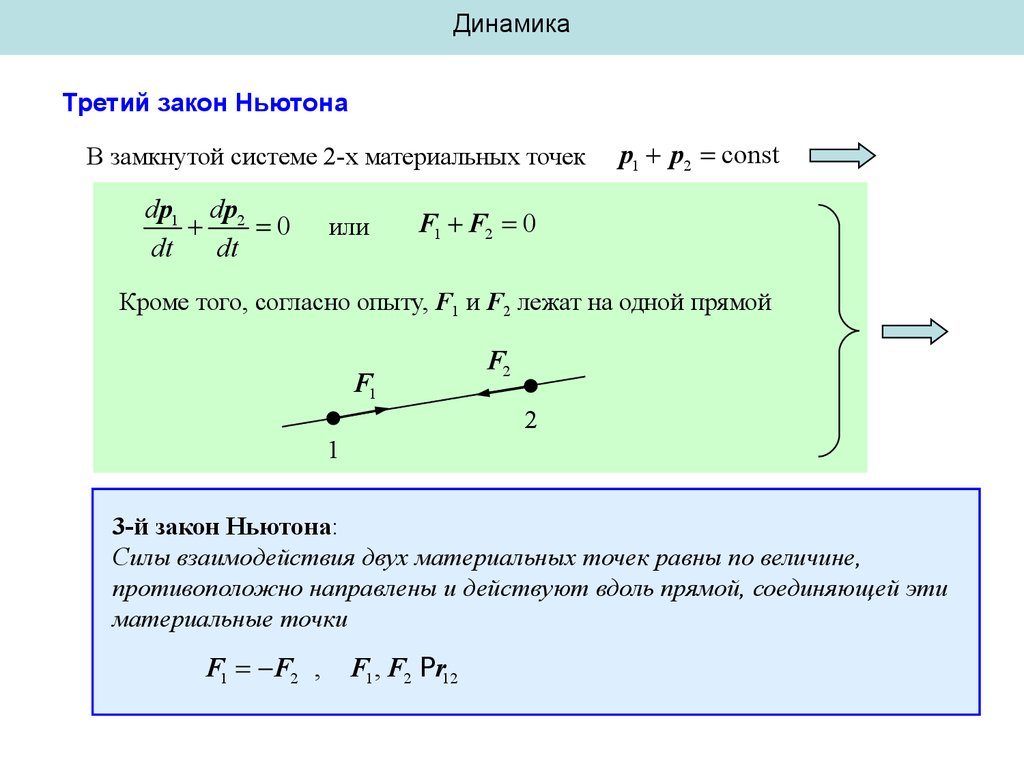
В замкнутой системе 2-х материальных точек
dp1 dp2
0
dt
dt
или
p1 p2 const
F1 F2 0
Кроме того, согласно опыту, F1 и F2 лежат на одной прямой
F1
F2
2
1
3-й закон Ньютона:
Силы взаимодействия двух материальных точек равны по величине,
противоположно направлены и действуют вдоль прямой, соединяющей эти
материальные точки
F1 F2 ,
F1 , F2 Pr12

6.

Динамика
Принцип суперпозиции
Для системы материальных точек
Fi
Fi Fik
k i
i
Фундаментальные взаимодействия:
Гравитационное
Электромагнитное
Сильное (ядерное)
Слабое

7.

Динамика
Сила тяжести. Движение под действием силы тяжести
При свободном падении
a const g 9.8м/с 2
F ma
F mg
m
Земля действует на m как точечная масса, с массой
равной массе Земли и находящейся в ее центре.
По закону всемирного тяготения –
F
Rз
F
Mз
m
mM З
mM З
mg ,
R2
RЗ2
dv
mg
dt
dr
v
dt
g
v v0 gt
gt 2
r r0 v0t
2
MЗ
RЗ2

8.

Динамика
Упругие силы. Движение под действием упругих сил
Fу F k l
l0
Fу
F
– закон Гука
k – коэффициент упругости (жесткости)
l
k
Fу kx
Уравнение движения
m
0
x
&
x& 2 x 0 , где
Решение: гармонические колебания
ma Fу
& kx
mx&
2 k m
x A cos( t )
x0 A cos
A и находятся из начальных условий
v0 A sin
A – амплитуда,
– угловая частота,
– начальная фаза

9.

Динамика
Силы трения. Движение при наличии трения
Трение
внешнее – между различными телами
внутреннее – между частями одного тела
сухое – между поверхностями твердых тел
вязкое (жидкое) – при наличии жидкости (газа)
Сухое трение
трение скольжения
трение качения

10.

Динамика
Силы трения. Движение при наличии трения
Сухое трение
N
Fтр
P – вес бруска
N – сила реакции
N=P
F
P
1) F < F0 , брусок покоится
Fтр = F – трение покоя
2) F > F0 , брусок скользит
Fтр = µN – трение скольжения
Fтр N
µ – коэффициент трения

11.

Динамика
Силы трения. Движение при наличии трения
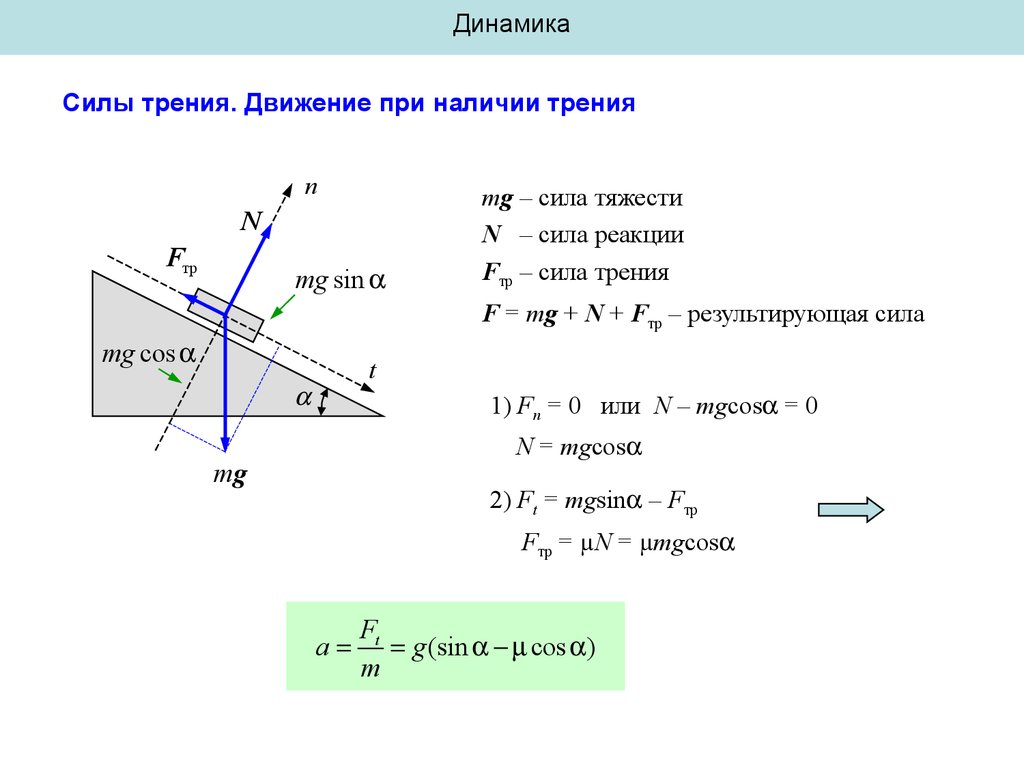
n
N
Fтр
mg sin
mg – сила тяжести
N – сила реакции
Fтр – сила трения
F = mg + N + Fтр – результирующая сила
mg cos
t
1) Fn = 0 или N – mgcos = 0
N = mgcos
mg
2) Ft = mgsin – Fтр
Fтр = µN = µmgcos
a
Ft
g (sin cos )
m

12.

Динамика
Силы трения. Движение при наличии трения
Вязкое трение
При v = 0, Fтр = 0
Fтр
v
При небольших скоростях
Fтр kv
k – коэффициент
Падение тела в вязкой среде
Fтр
Начальные условия: при t = 0, v = 0
m
z
v
dv
mg kv
dt
ma
F
g dt
mg kv

13.

Динамика
Силы трения. Движение при наличии трения
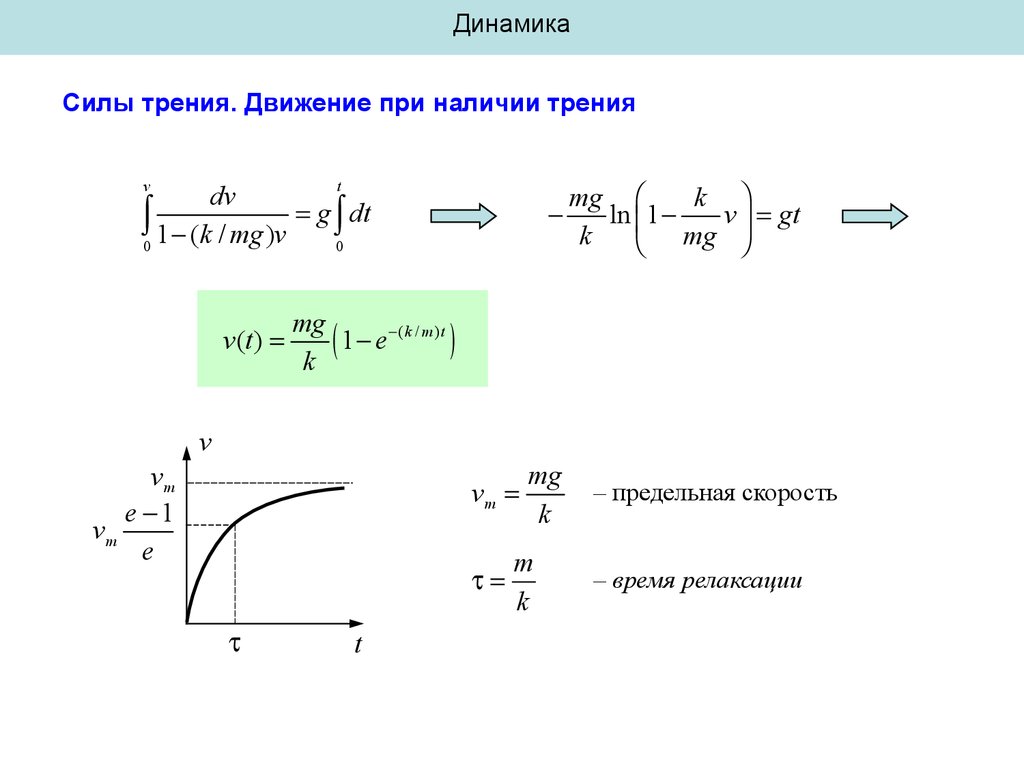
v
t
dv
0 1 (k / mg )v g 0 dt
v(t )
mg
k
ln 1
v gt
k
mg
mg
1 e ( k / m) t
k
v
vm
e 1
vm
e
vm
t
mg
k
m
k
– предельная скорость
– время релаксации