Similar presentations:
Элементы векторной алгебры. Декартовая система координат
1.
ФИЗИКАЛИТЕРАТУРА:
Иродов И.Е. Общая физика
Матвеев А.Н. Курс физики
Джанколи Д. Физика
Савельев И.А. Курс общей физики
Трофимова Т.И. Курс физики
Сивухин Д.В. Общий курс физики
2.
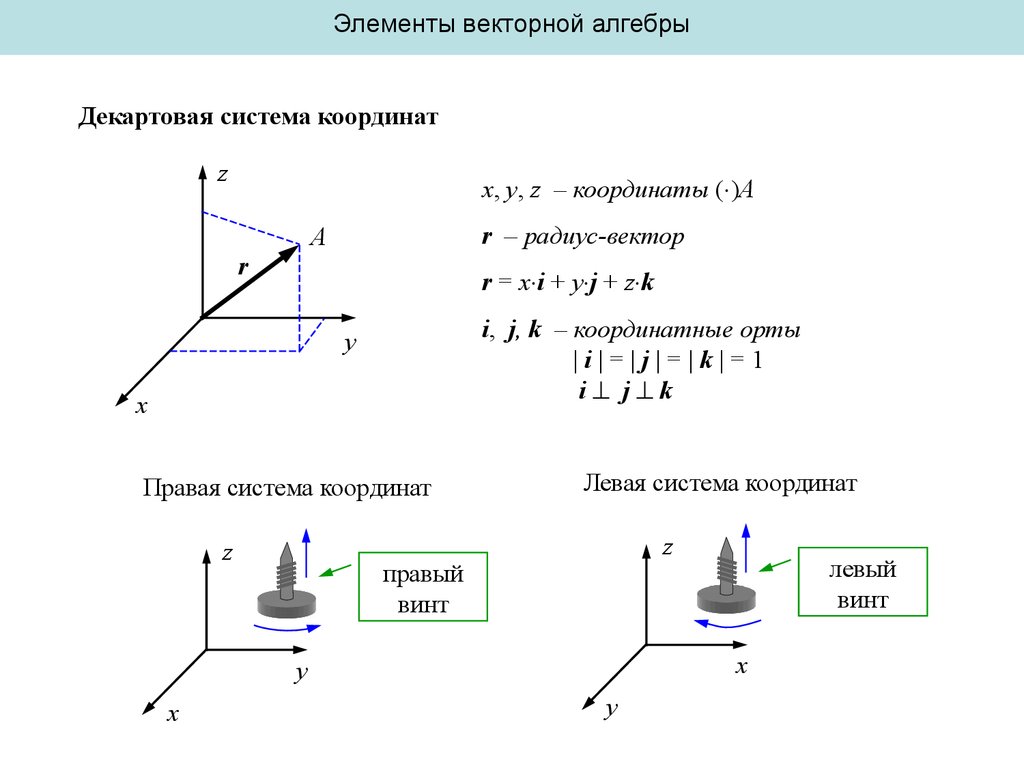
Элементы векторной алгебрыДекартовая система координат
z
x, y, z – координаты ( )A
r – радиус-вектор
A
r
r = x i + y j + z k
i, j, k – координатные орты
|i|=|j|=|k|=1
i j k
y
x
Правая система координат
z
Левая система координат
z
правый
винт
x
y
x
левый
винт
y
3.
Элементы векторной алгебрыОбозначение вектора:
A, B, C
r r r
A, B, C
Определение вектора: вектор – упорядоченный набор чисел.
A (Ax, Ay, Az), Ai (i = x, y, z) – составляющие (компоненты) вектора
Сложение векторов и умножение вектора на число
C A B ,где
Ci Ai B, i i , x , y z
A ( Ax , Ay , Az )
Сложение по правилу
параллелограмма
A+B
A
B
Сложение по правилу
треугольника
B
A
A+B
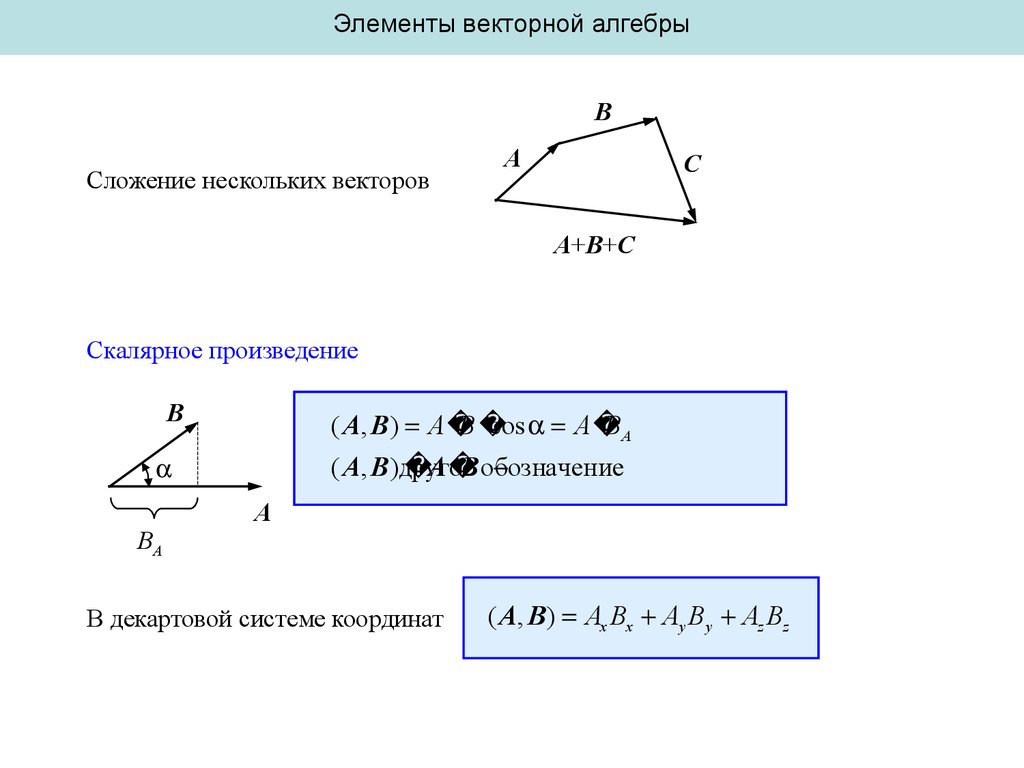
4.
Элементы векторной алгебрыB
Сложение нескольких векторов
A
С
A+B+С
Скалярное произведение
B
( A, B) A
B
cos A
BA
( A, B)другое
A
B обозначение
A
BA
В декартовой системе координат
( A, B ) Ax Bx Ay By Az Bz
5.
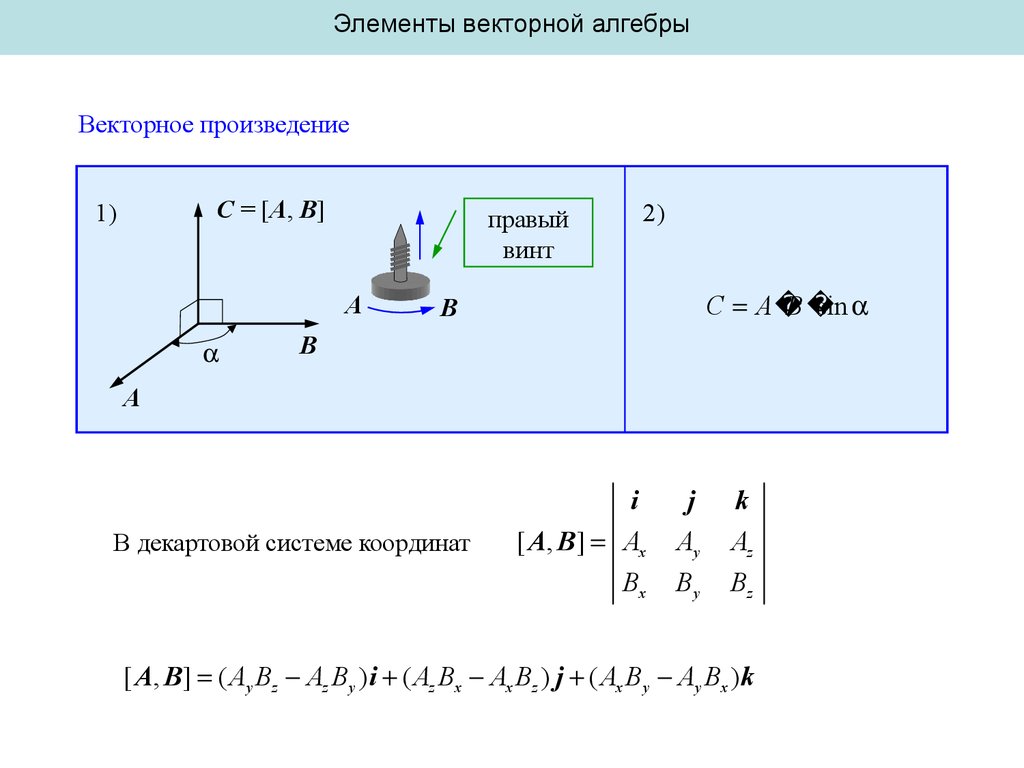
Элементы векторной алгебрыВекторное произведение
С = [A, B]
1)
правый
винт
A
2)
C A
B
sin
B
B
A
В декартовой системе координат
i
[ A, B ] Ax
Bx
j
Ay
By
k
Az
Bz
[ A, B ] ( Ay Bz Az By )i ( Az Bx Ax Bz ) j ( Ax By Ay Bx )k
6.
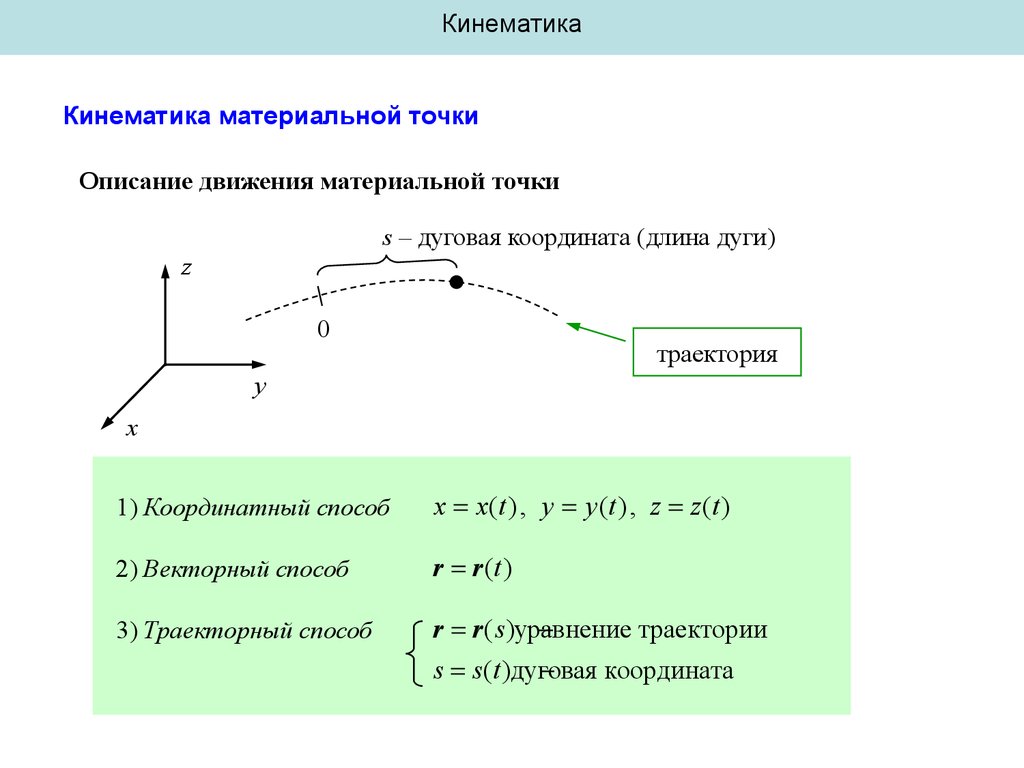
КинематикаКинематика материальной точки
Описание движения материальной точки
s – дуговая координата (длина дуги)
z
0
траектория
y
x
1) Координатный способ
x x (t ), y y (t ), z z (t )
2) Векторный способ
r r (t )
3) Траекторный способ
r r ( s )уравнение
траектории
s s (t )дуговая
координата
7.
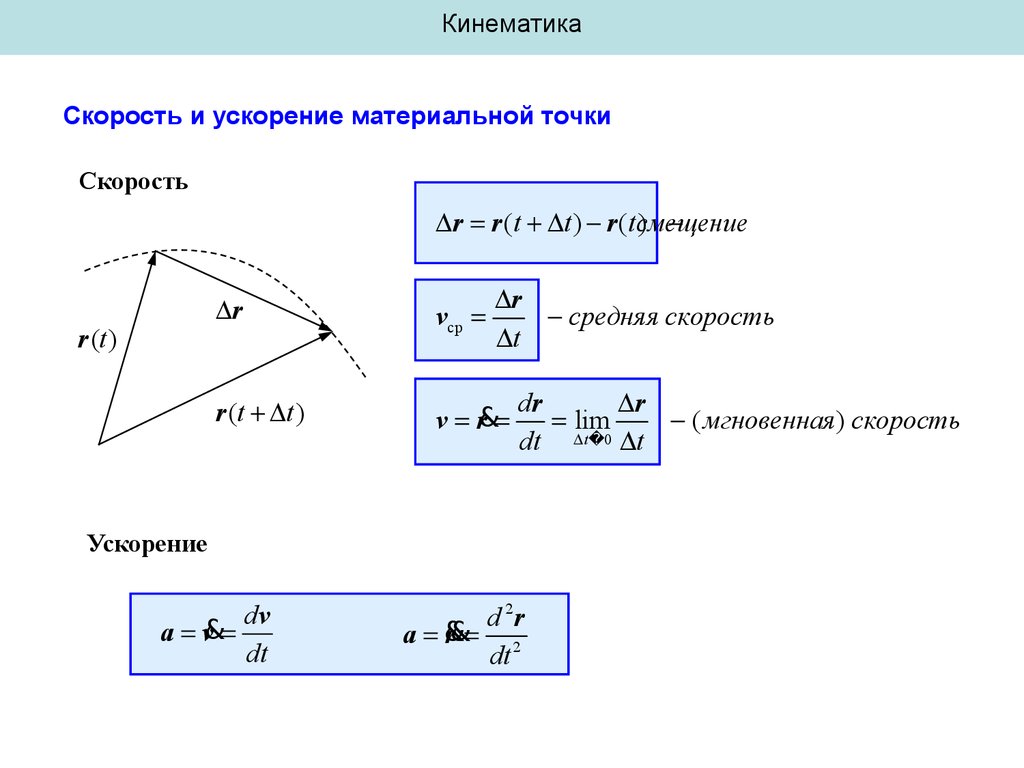
КинематикаСкорость и ускорение материальной точки
Скорость
r r (t t ) r (tсмещение
)
r (t )
r
средняя скорость
t
r
vср
r (t t )
v r&
dr
r
lim
( мгновенная) скорость
t
0
dt
t
Ускорение
dv
a v&
dt
d 2r
a &
r& 2
dt
8.
КинематикаПрямолинейное движение
1) Равномерное движение, v const
0
x(t)
x x (t )
dx
v
dt
dv d 2 x
a
2
dt dt
x
a
dv
dt
dx
v
dt
a 0
x x0 vt
2) Равноускоренное движение,
a const
dv
a
dt
v v0 at
dx
v
dt
at 2
x x0 v0t
2
x0 – начальные координата
v0 – начальная скорость
9.
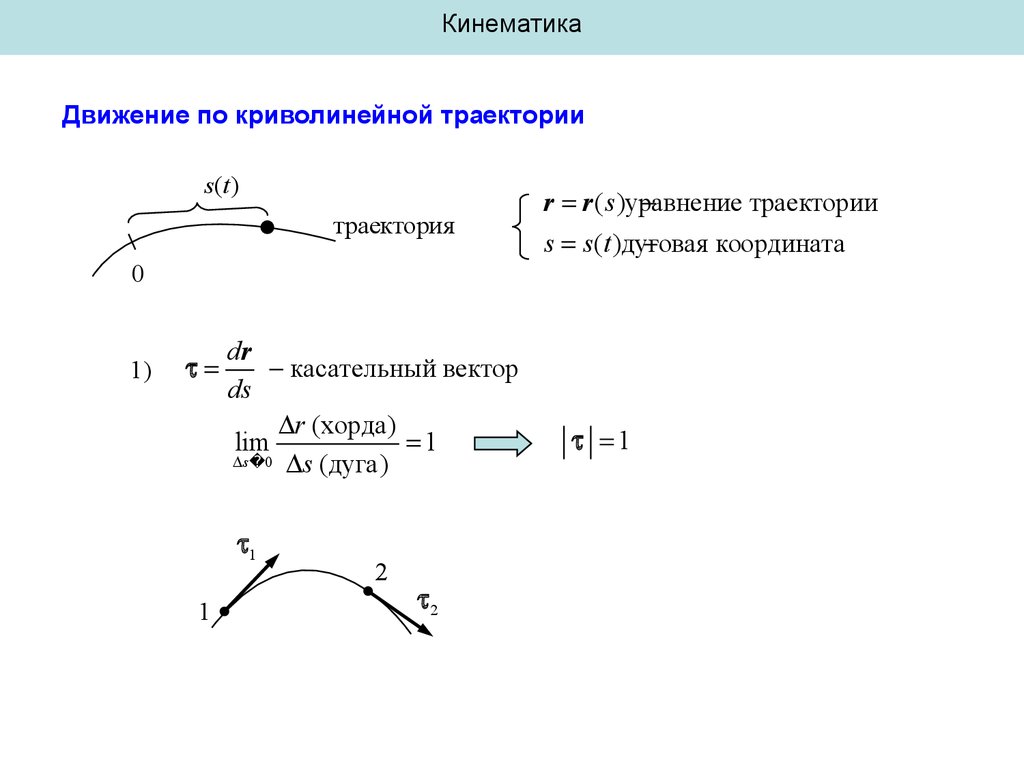
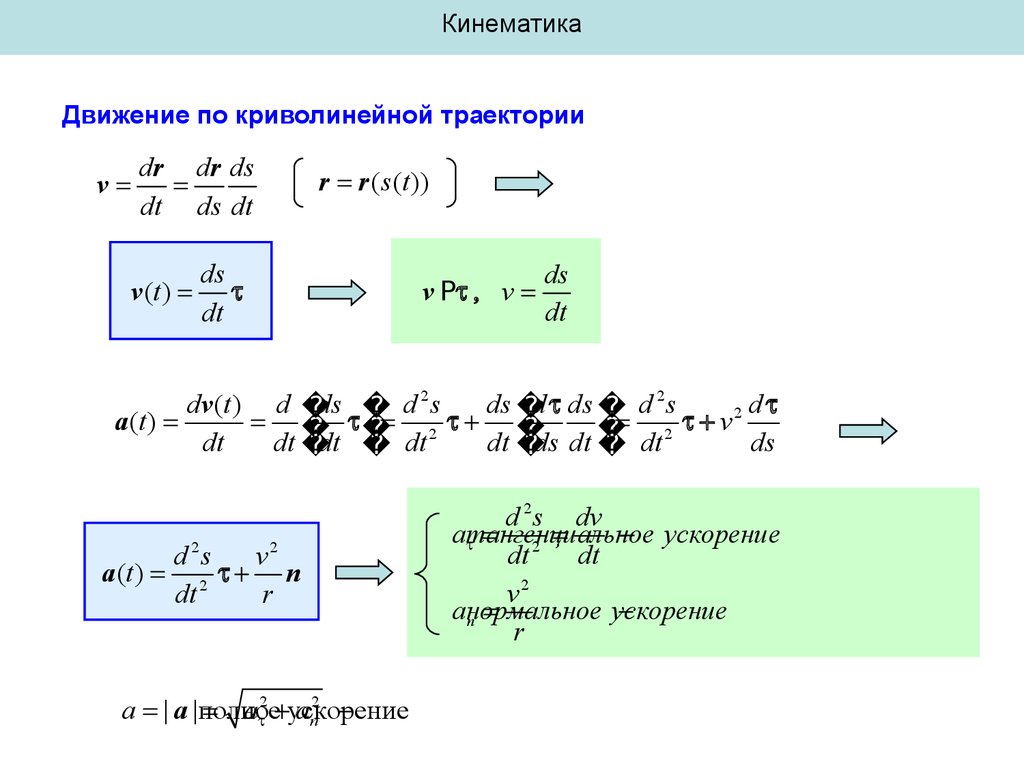
КинематикаДвижение по криволинейной траектории
s(t)
траектория
0
1)
dr
касательный вектор
ds
r (хорда)
lim
1
s 0 s (дуга)
1
1
2
2
r r ( s )уравнение
траектории
s s (t )дуговая
координата
1
10.
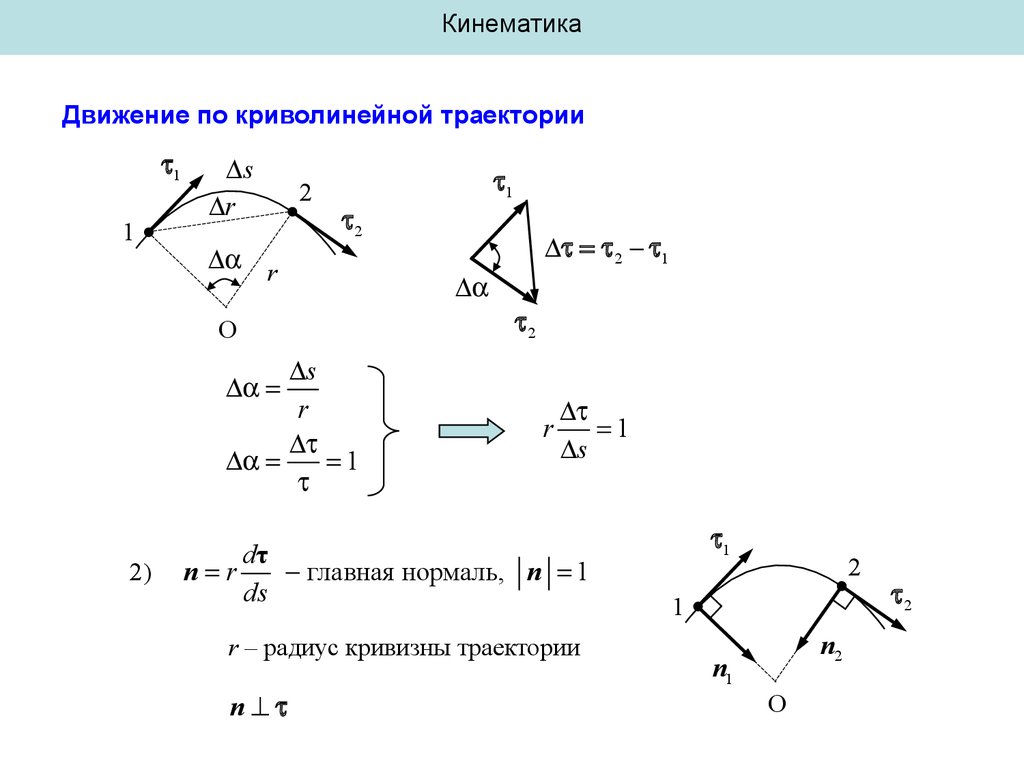
КинематикаДвижение по криволинейной траектории
1
1
s
r
2
1
2
r
O
s
r
1
2 1
2
2)
r
1
s
dτ
n r
главная нормаль, n 1
ds
r – радиус кривизны траектории
n
1
2
1
n2
n1
O
2
11.
КинематикаДвижение по криволинейной траектории
dr dr ds
v
dt ds dt
v (t )
r r ( s(t ))
ds
dt
v P v
ds
dt
dv (t ) d ds d 2 s
ds d ds d 2 s
2 d
a( t )
2
v
dt
dt dt dt
dt ds dt dt 2
ds
d 2s
v2
a (t ) 2 n
dt
r
a | a |полное
a 2 ускорение
an2
d 2 s dv
aтангенциальное
ускорение
2
dt
dt
v2
aнормальное
ускорение
n
r
12.
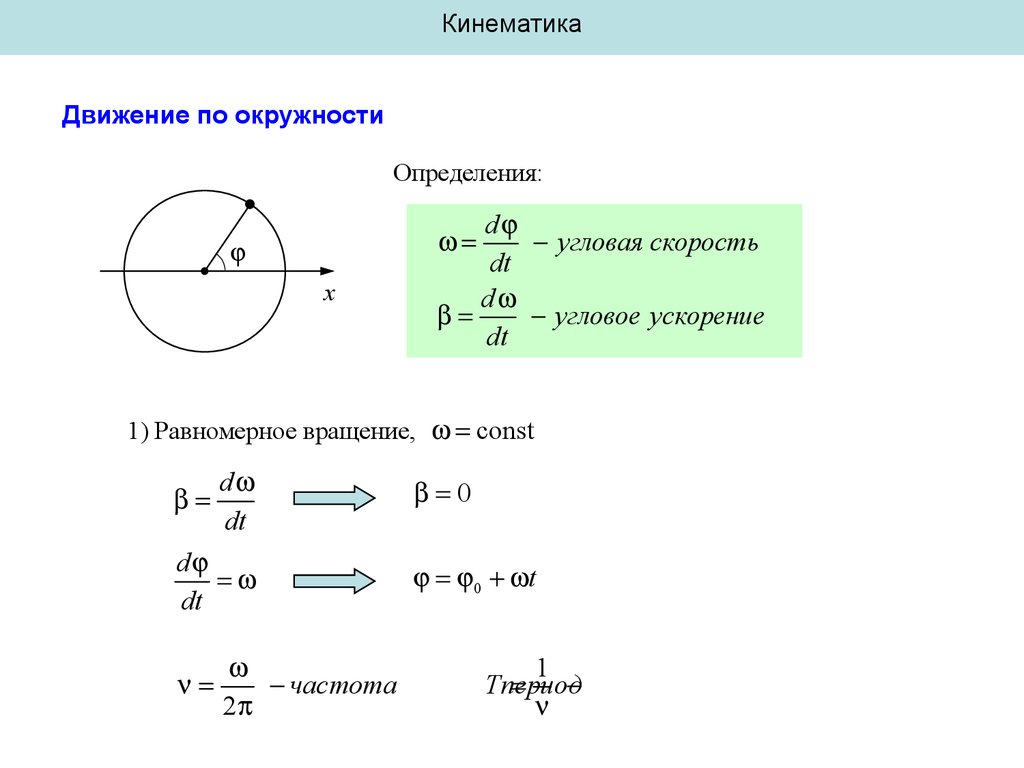
КинематикаДвижение по окружности
Определения:
d
угловая скорость
dt
d
угловое ускорение
dt
x
1) Равномерное вращение, const
d
dt
d
dt
частота
2
0
0 t
1
Tпериод
13.
КинематикаДвижение по окружности
2) Равноускоренное вращение,
const
d
dt
0 t
d
dt
t 2
0 0t
2
Связь линейный и угловых величин
r
s r
x
ds
d
r
r
dt
dt
d 2s
d 2
a 2 r 2 r
dt
dt
v2
an 2 r
r
v
14.
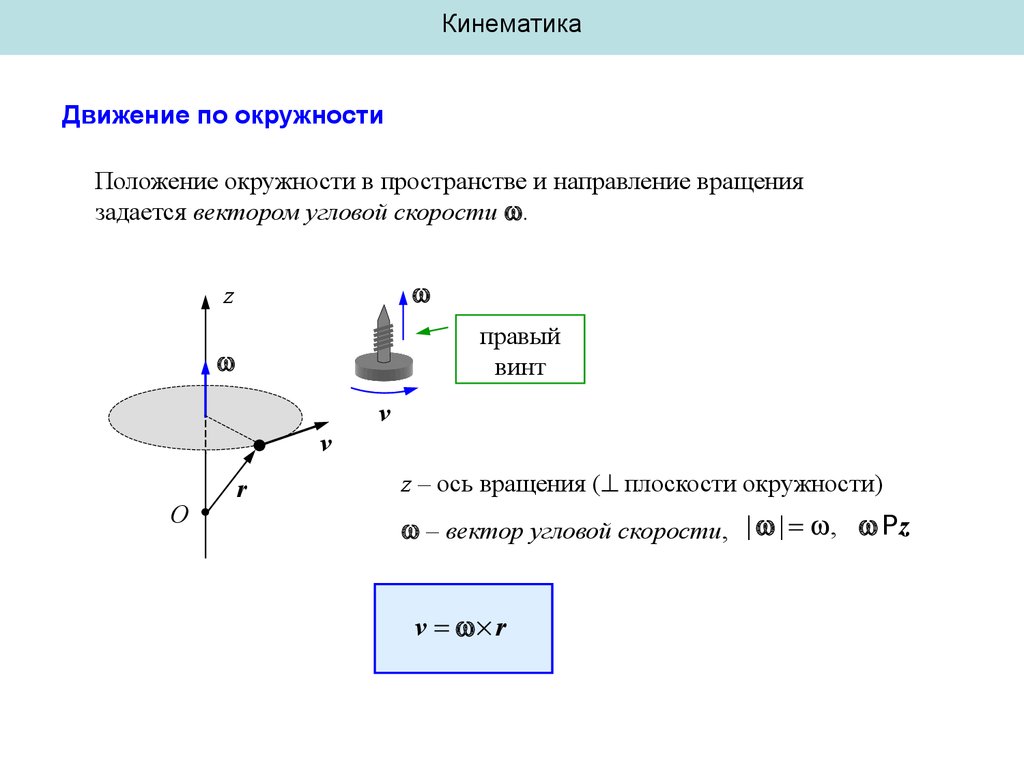
КинематикаДвижение по окружности
Положение окружности в пространстве и направление вращения
задается вектором угловой скорости .
z
правый
винт
v
v
O
r
z – ось вращения ( плоскости окружности)
– вектор угловой скорости, | | , Pz
v r




 physics
physics