Similar presentations:
Кинематика материальной точки (лекция 2)
1. ЛЕКЦИЯ 2
Кинематика материальной точки2.
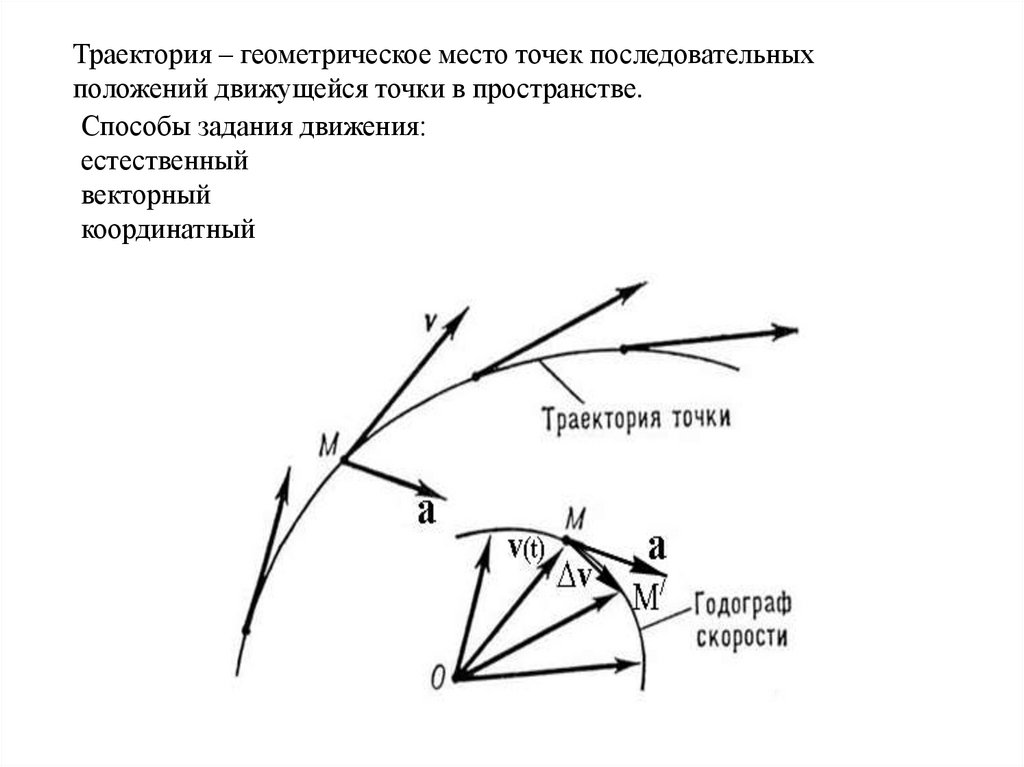
Траектория – геометрическое место точек последовательныхположений движущейся точки в пространстве.
Способы задания движения:
естественный
векторный
координатный
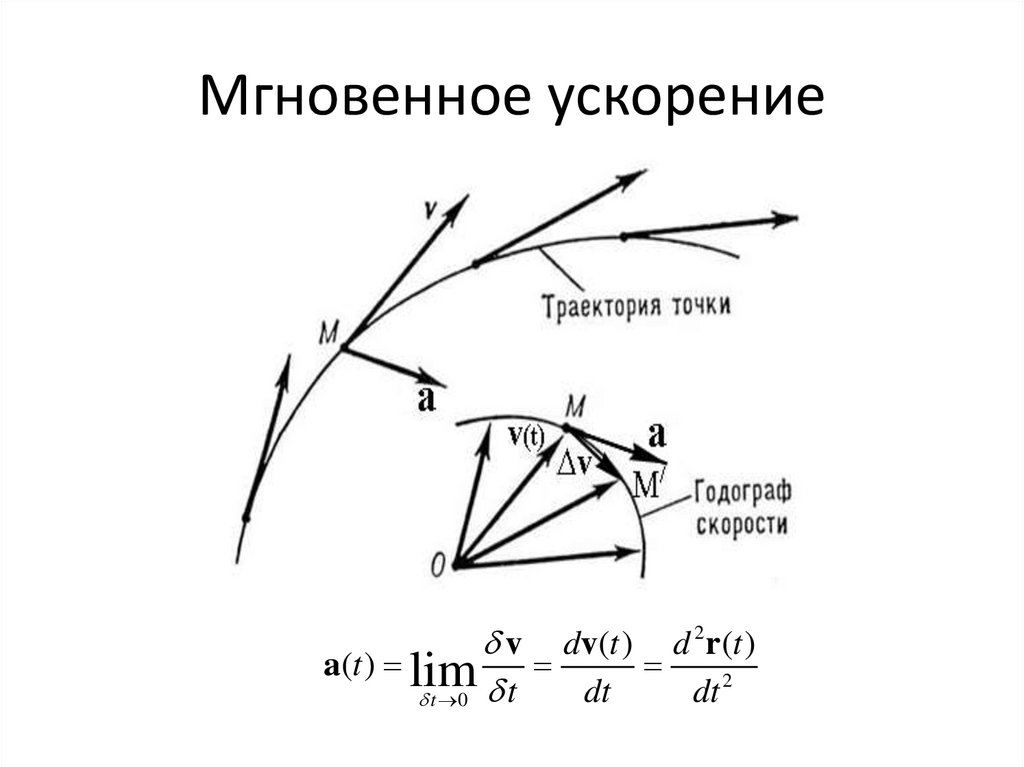
3. Мгновенное ускорение
v dv (t ) d 2r (t )a(t ) lim
dt
dt 2
t 0 t
4. Координатное представление физических величин.
Описание прямолинейного движения вкоординатном представлении
rˆ r / r e x
5.
r (t ) rx (t )e x xe x ;r (t ) rx (t )e x x(t )e x ;
r (t ) x(t )
v
e x v x e x ;
t
t
dr (t ) dx(t )
v (t ) lim v
e x v xe x ;
t 0
dt
dt
2
d v x (t )
dv (t ) dv x (t )
a(t )
ex
e
.
x
2
dt
dt
dt
6. Полезные замечания
r dr v dv;
t dt
t dt
d r r
2
2
dt
t
2
2
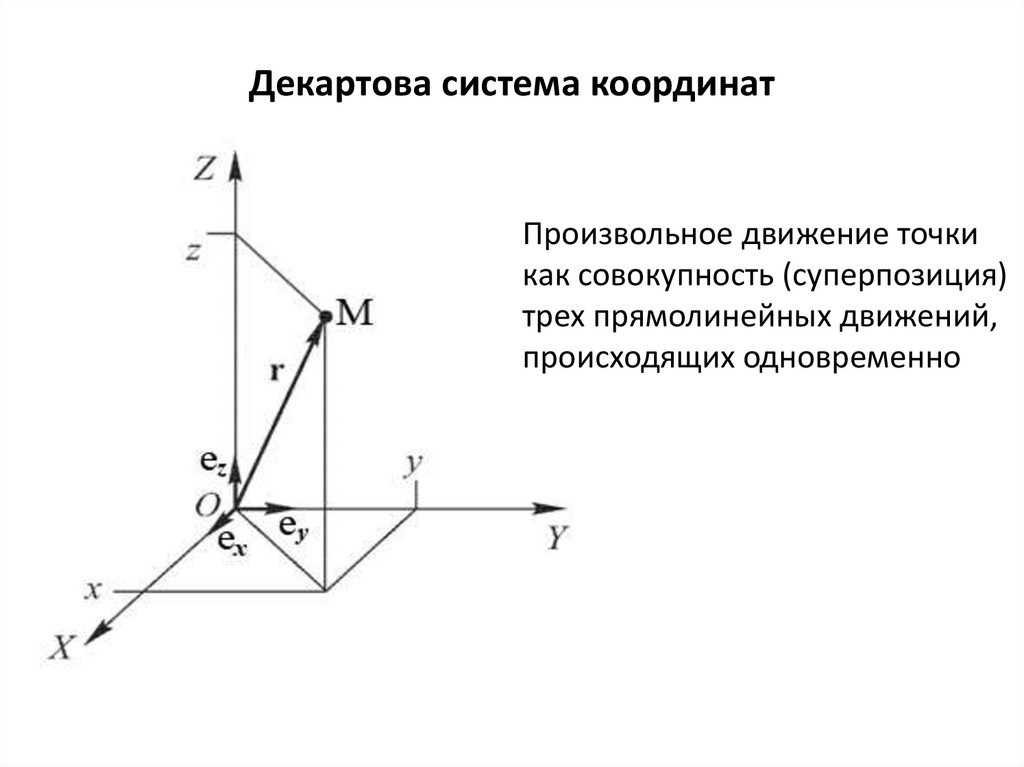
7. Декартова система координат
Произвольное движение точкикак совокупность (суперпозиция)
трех прямолинейных движений,
происходящих одновременно
8.
9.
Кинематический закон движенияr (t ) rx (t ), ry (t ), rz (t ) ( x(t ), y (t ), z (t ))
r (t ) rx (t )e x ry (t )e y rz (t )e z x(t )e x y(t )e y z (t )e z
r (t ) rx (t )e x ry (t )e y rz (t )e z x(t )e x y (t )e y z (t )e z ;
r (t ) x(t )
y (t )
z (t )
v
ex
ey
e z v x e x v y e y v z e z ;
t
t
t
t
dr (t ) dx(t )
dy (t )
dz (t )
v(t ) lim v
ex
ey
e z v xe x v y e y v z e z ;
t 0
dt
dt
dt
dt
2
dv y (t )
d v y (t )
d 2 v x (t )
dv z (t )
d 2 v z (t )
dv(t ) dv x (t )
a(t )
ex
ey
ez
ex
ey
ez .
2
2
2
dt
dt
dt
dt
dt
dt
dt
v(t) v2x v 2y v 2z ; a ax2 a y2 az2 .
10.
Составляющих вектора на декартовы оси в видескалярного произведения
x rx r cos (r, e x );
y ry r cos (r, e y ); z rz r cos (r, e z )
v x v cos ( v, e x ); v y v cos ( v, e y ); v z v cos ( v, e z )
v x v cos ( v, e x ); v y v cos ( v, e y ); v z v cos ( v, e z )
11. ПАРАМЕТРИЧЕКСКОЕ ЗАДАНИЕ ПРОЙДЕННОГО ПУТИ КАК ФУНКЦИИ СКОРОСТИ
S S (V )dS (t ) dS (V ) dV
dV
V
S (V )
dt
dV dt
dt
V (t )
S (V )
dt
dV
V
V0
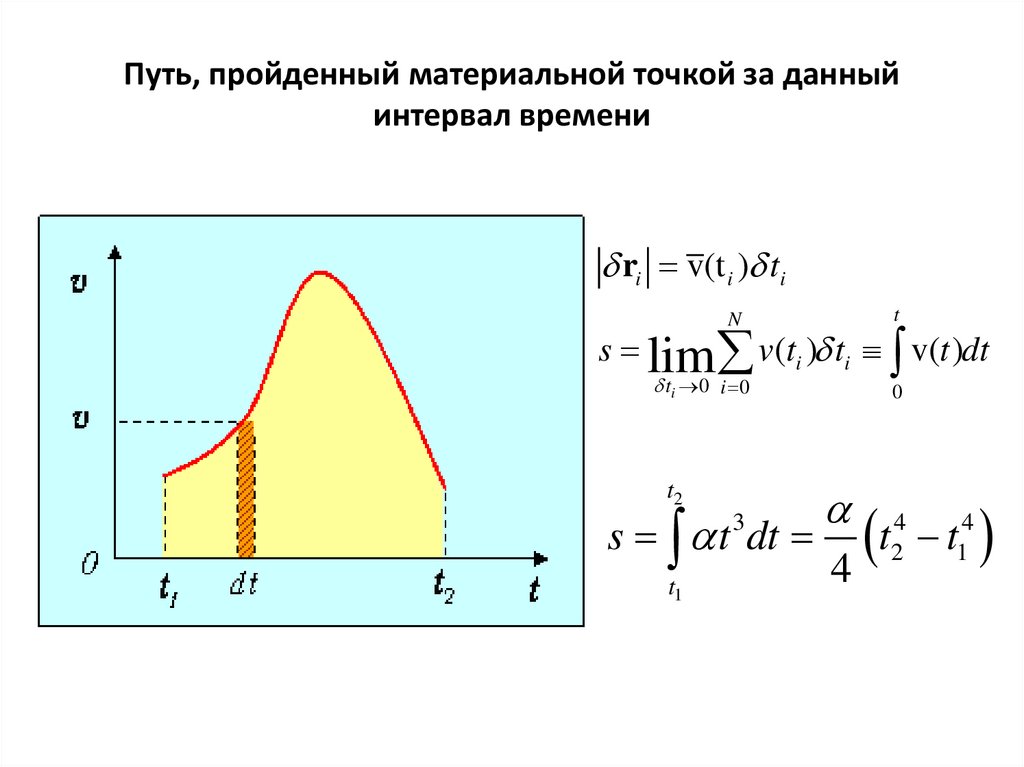
12. Путь, пройденный материальной точкой за данный интервал времени
ri v(t i ) tiN
t
ti 0 i 0
0
s lim v(ti ) ti v(t )dt
t2
s t dt
3
t1
4
4
4
t
t
2 1
13. Движение тела, брошенного под углом к горизонту
Движение тела, брошенного под углом к горизонтуНачальные условия и конкретный вид ускорения
v0 cos
r (0) 0 , v(0) v0 sin ,
0
0
a g
0
Уравнение траектории тела, брошенного под углом к горизонту.
rx
t
v0 cos
2
g
ry (rx ) (tg ) rx 2
rx
2
2v0 cos
14.
Зависимость от времени компонент скорости тела,брошенного под углом к горизонту.
v0 cos
v(t ) v0 sin gt
0
Зависимость координат тела от времени
v0t cos
2
r (t ) v0t sin gt 2
0
15.
Время подъема и максимальная высота подъема тела,брошенного под углом к горизонту
v 0 sin
v y (T ) 0 T
g
v 02 sin 2
H ry (T )
2g
Время и дальность полета тела, брошенного под углом к горизонту.
v 0 sin
ry (T ) 0 T 2
2T
g
v 02
L rx (T ) sin 2
g
16.
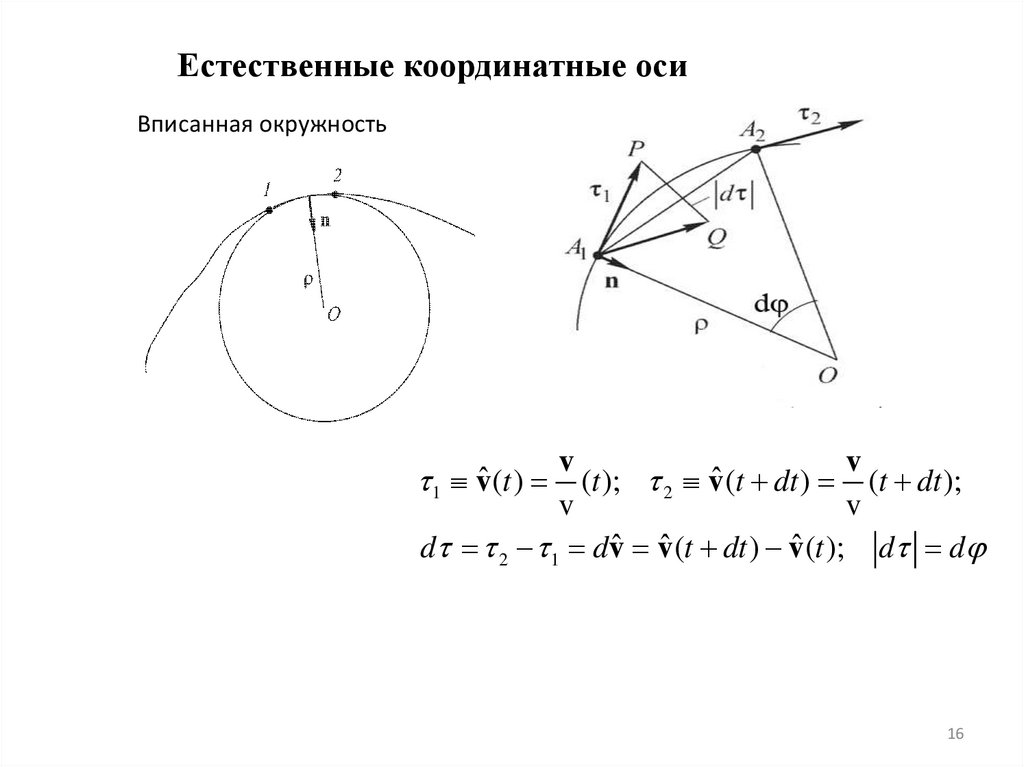
Естественные координатные осиВписанная окружность
v
v
ˆ
(t ); 2 v(t dt ) (t dt );
v
v
d 2 1 dvˆ vˆ (t dt ) vˆ (t ); d d
1 vˆ (t )
16
17.
ˆ Vd ndV dVV
dV dV ˆ
d
a
V V
n a a n
dt
dt
dt
17
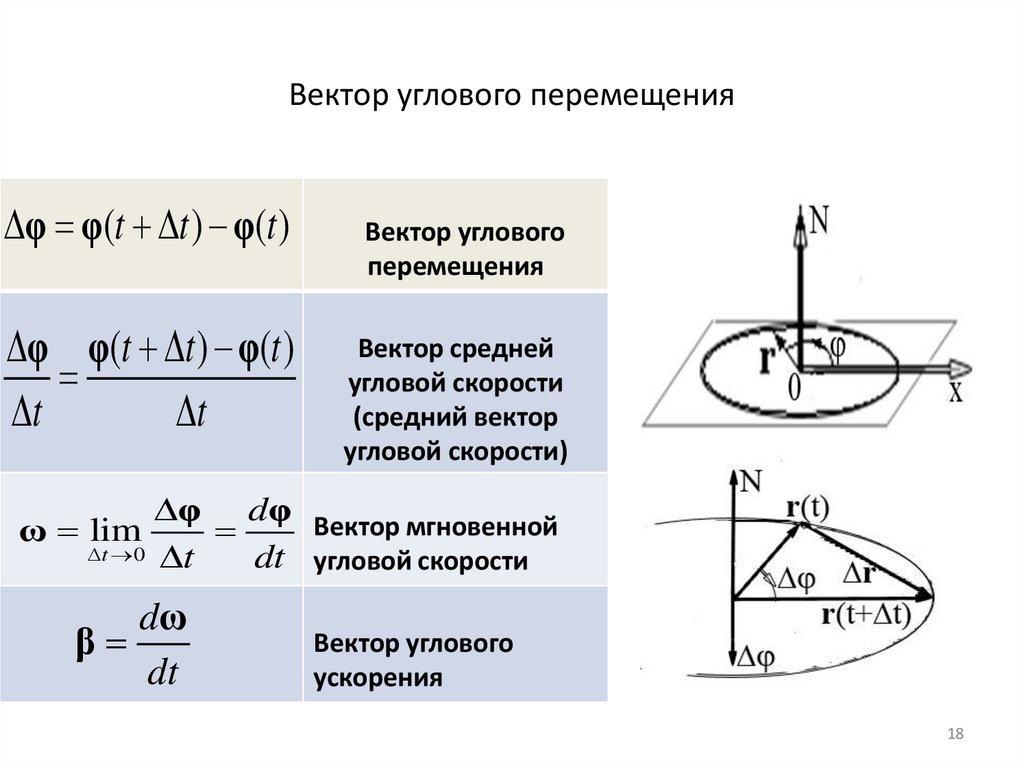
18. Вектор углового перемещения
φ φ(t t ) φ(t )φ φ(t t ) φ(t )
t
t
Вектор углового
перемещения
Вектор средней
угловой скорости
(средний вектор
угловой скорости)
φ dφ Вектор мгновенной
ω lim
t 0 t
dt угловой скорости
dω
β
dt
Вектор углового
ускорения
18
19.
Связь линейных и угловых характеристикdv
d N
R
R N .
dt
dt
ds Rd
v
R ;
dt
dt
dv dv
v2
dv
a vˆ n vˆ 2r a a n ;
dt dt
R
dt
2
dv
v
2
a vˆ , a n n r,
dt
R
2
dv
2 4
2
4
a a a R R
dt
2
2
n
19
20.
Векторное произведение.ex
S x a y bz az by
S a, b S y az bx axbz ; S ax
S a b a b
bx
y x
z x y
ey
ay
by
ez
az ;
bz
S S ab sin(ab)
20
21. Свойства векторного произведения
Антикоммутативностьa, b b, a
Дистрибутивность
a c, b d a, b c, b a, d c, d
a, b a, b a, b ;
a, b a, b a, b
( ) a, b a, b a, b
Векторное произведение двух полярных или двух аксиальных векторов
является аксиальным вектором.
Векторное произведение полярного и аксиального вектора является полярным
вектором.
21
22.
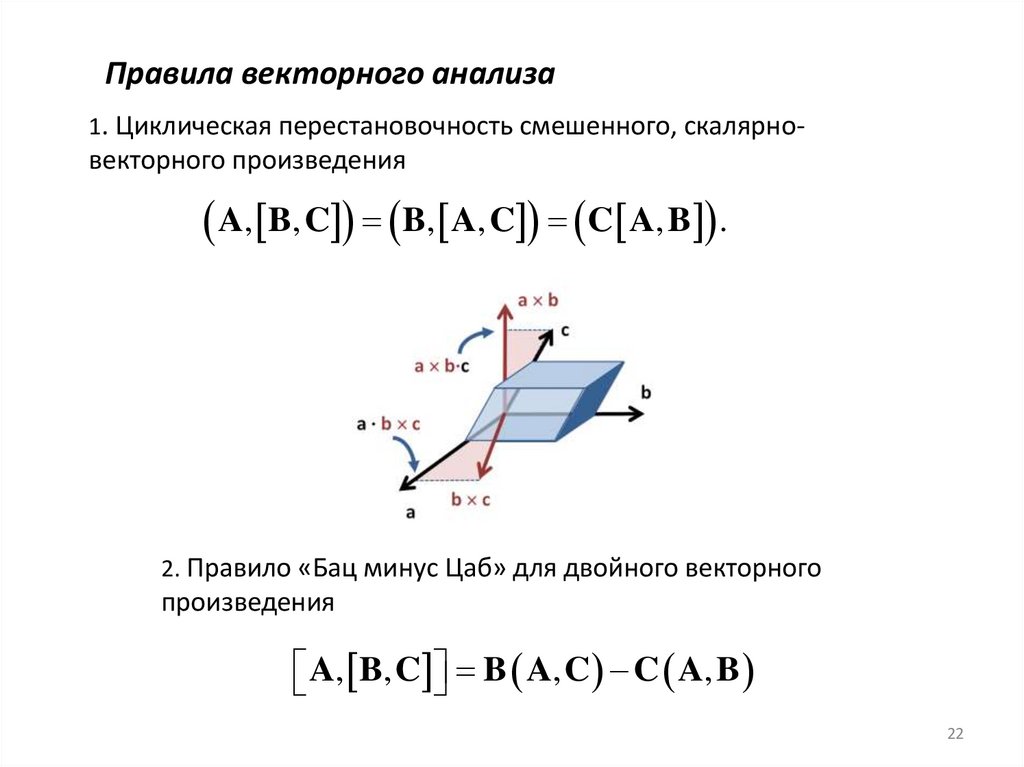
Правила векторного анализа1. Циклическая перестановочность смешенного, скалярно-
векторного произведения
A, B, C B, A, C C A, B .
2. Правило «Бац минус Цаб» для двойного векторного
произведения
A, B, C B A, C C A, B
22
23.
Векторная связь угловых и линейных характеристикдвижения
v ω,r ; an ω, v ; a β,r
Равномерное вращение
const , 0; v R const , a 0, a an R 2 ;
(t ) 0 t
Равноускоренное вращение
const , 0 t , 0 0t
t2
;
2
v ω, R , v R R( 0 t ), a a a n β, R R 2 ,
a a 2 an2 R 2 4 R 2 ( 0 t )4
23
24.
Правая тройка ортов декартовой системыe , e , e
x
y
z
e x e y , e z e y e z , e x e z e x , e y
Правая тройка сопутствующей системы координат
vˆ , n, N
N vˆ , n
Векторы линейных и угловых кинематических характеристик движения
в разложении на оси сопутствующей системы координат:
v
dv/dt a
v 0 , a v 2 / R an ;
0
0 0
0
0
0
φ 0 , ω 0 β 0
N
24
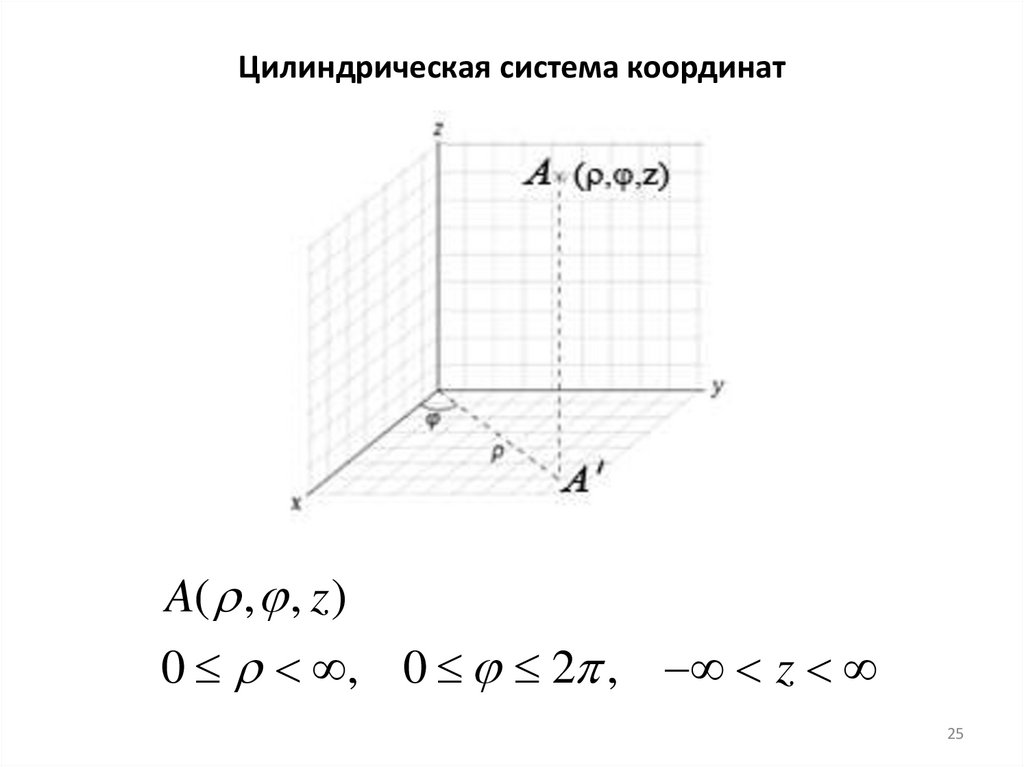
25. Цилиндрическая система координат
A( , , z )0 , 0 2 , z
25
26.
Связь с декартовыми координатами соответствующейдекартовой системы отсчета
1) Начала отсчета обеих систем совмещены;
2) Ось абсцисс декартовой системы совпадает с полярной осью цилиндрической
системы;
3) Ось аппликат декартовой системы совпадает с осью OZ цилиндрической
системы
y
x y ; Arctg ; z z.
x
2
2
x cos ; y sin ; z z.
26
27.
Тройка ортогональных ортов цилиндрической системы(e , e , e z )
e e , e z e e z , e e z e , e
27
28.
Связь между ортами цилиндрической и соответствующейдекартовой системы координат
e e x cos( ) e y sin( ),
e e x sin( ) e y cos( ),
ez ez
de
dt
e
de
dt
e
28
29.
Радиус-вектор и скорость частицы в цилиндрическойсистеме координат
r (t ) (t )e (t ) z (t )e z (t ) 0
z
v
de dz
d
v
e
e
v
z
dt dt
dt
z v
z
v v v v v r z
2
2
2
z
2
2
2
2
29
30.
Вектор ускорения в цилиндрических координатах2
a (v v )
a a (v v ) 2
a
v
z
z
z
a a a a a
2
2
2
z
2 z
2 2
2
30
2
31.
Сферическая система координат(r , , )
0 r ; 0 2 ; 0
31
32.
Связь между координатами в сферической идекартовой системе
2
2
2
r
x
y
z
x rsin( )cos( )
y rsin( )sin( ) Arctg y / x
z r cos( )
2
2
2
arccos z / x y z
32
33.
Правая тройка ортогональных базисных векторовсферической системы
(er , e , e )
e r sin (e x cos e y sin ) e z cos
e e x sin e y cos
e cos (e x cos e y sin ) e z sin
33



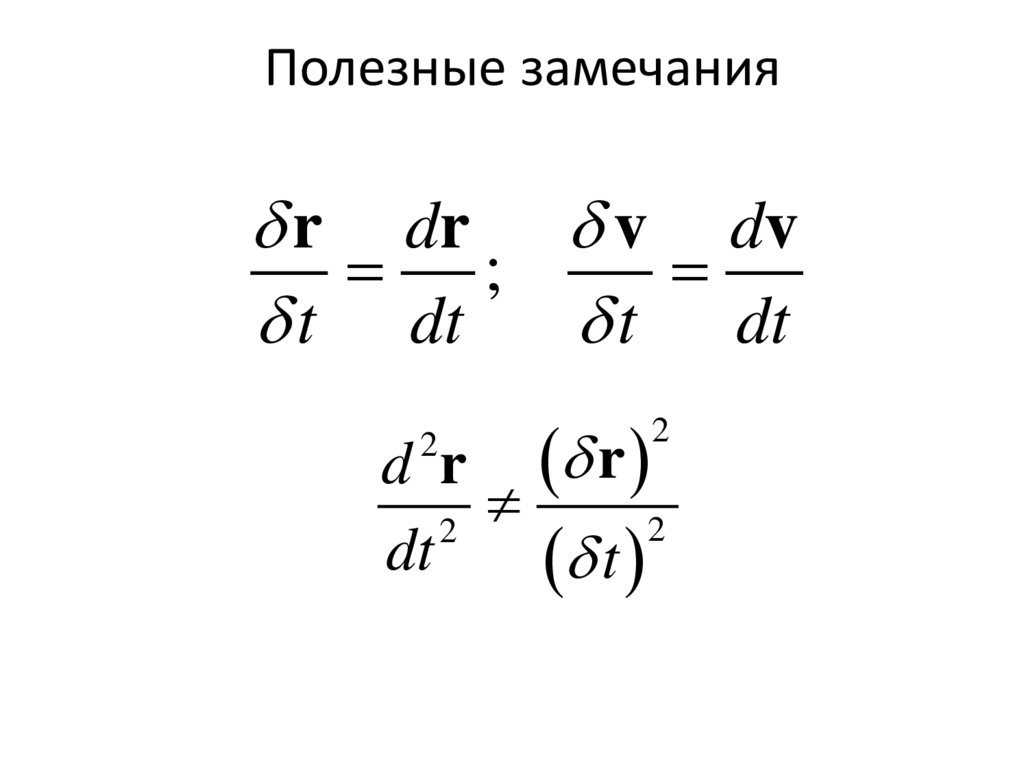





















 physics
physics








