Similar presentations:
Кинематика. Общая физика
1.
Общая Физика НИЯУ МИФИМеханика
Лекция 02
Кинематика
Лектор: Доцент НИЯУ МИФИ.
Андрей Станиславович ОЛЬЧАК
2.
КинематикаКинематика: Описание движения (но НЕ объяснение!)
Материальная точка
Координаты (x, y, z)
С.О.= С.К. + часы
r = (x, y, z)
ПеремещениеΔr
Пройденное расстояние S
Скорость v
Ускорение a или w
3.
Some mathematics!Операции с векторами (1)
a
Параллельные вектора = равные!.
a
a
b
b = ka
=> k = |b| / |a|
a
b
b = ka
=> k = - |b| / |a|
a
4.
Some mathematics!Операции с векторами (2)
c=a+b
b
а
с
с
b = c - a = c + (- a)
-а
b
5.
Some mathematics!Операции с векторами (3)
a = {ax, ay, az}; b = {bx, by, bz};
а
α
b
Скалярное произведение:
(a, b) = ax bx + ay by + az bz = |a||b|cos(α)
Абсолютное значение (модуль):
|a|2 = (a, а) = ax 2 + ay 2 + az 2 =>
a ax2 a y2 az2
6.
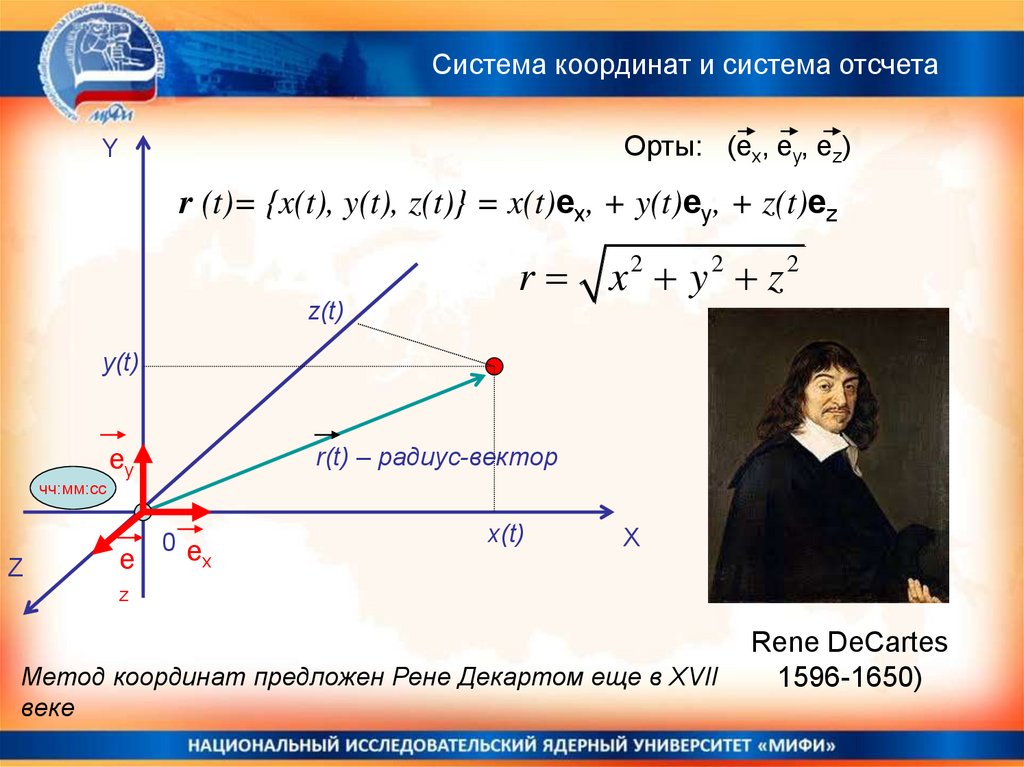
Система координат и система отсчетаОрты: (ex, ey, ez)
Y
r (t)= {x(t), y(t), z(t)} = x(t)ex, + y(t)ey, + z(t)ez
r x y z
2
2
2
z(t)
y(t)
чч:мм:сс
Z
r(t) – радиус-вектор
ey
e
0e
x(t)
X
x
z
Метод координат предложен Рене Декартом еще в XVII
веке
Rene DeCartes
1596-1650)
7.
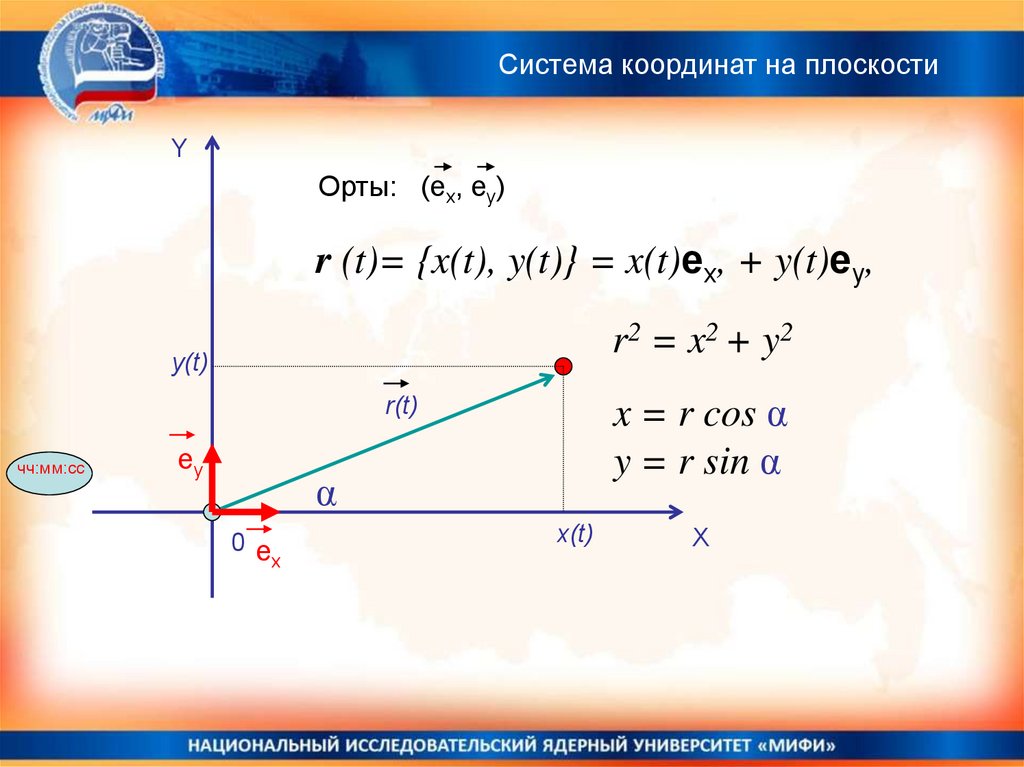
Система координат на плоскостиY
Орты: (ex, ey)
r (t)= {x(t), y(t)} = x(t)ex, + y(t)ey,
r2 = x2 + y2
y(t)
x = r cos α
y = r sin α
r(t)
чч:мм:сс
ey
α
0e
x(t)
x
X
8.
Перемещание (Δr) и пройденный путьY
Δr = r(t+Δt) - r(t)
r(t+Δt)
Δr
S
Путь S > | Δ r|
чч:мм:сс
r(t)
Z
0
x(t)
X
9.
Средняя и мгновенная скоростьΔr / Δt = V
Средняя скорость движения
Но если Δ->0 – это мгновенная скорость
Y
r (t t ) r (t )
r dr
lim
t 0
t 0 t
t
dt
v (t ) lim
r(t+Δt)
Δr
S
r(t)
чч:мм:сс
Z
X
0
vx = dX(t)/dt
vy = dY(t)/dt
vz = dZ(t)/dt
Δx = x(t0)-x(t)
x(t) = ʃvx(t)dt
То же и для y(t), z(t)
10.
Скорость и перемещениеΔx = x(t0)-x(t)
x(t) = ʃvx(t)dt
То же и для y(t), z(t)
Sx(t) = ʃ|vx(t)|dt
Vх
t
0
t0
t
Δx = x(t0)-x(t) численно равна площади под графиком функции Vх(t) между t0 и t
.
Площадь ниже оси OX кчитывается со знаком «минус».
А если надо найти пройденный путь – то со знаком «плюс»
11.
УскорениеМгновенное ускорение:
V(t)
V(t)
v dv
w lim
t 0 t
dt
V(t+Δt)
w(t) = dw(t)/dt = d2r(t)/dt2
V(t+Δt)
V(t+Δt) - V(t) = ΔV
w = wx2 + wy2 + wz2
wx = dvx(t)/dt = d2x(t)/dt2
wy = dvy(t)/dt = d2y(t)/dt2
wz = dvz(t)/dt = d2z(t)/dt2
12.
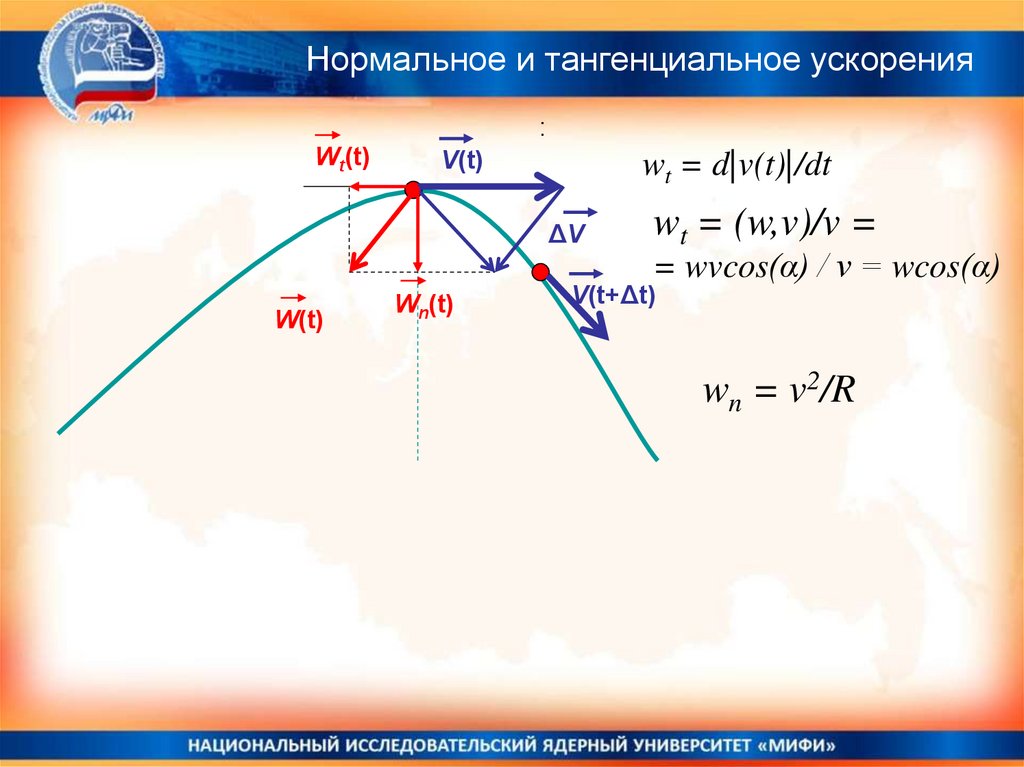
Нормальное и тангенциальное ускорения:
Wt(t)
V(t)
wt = d|v(t)|/dt
ΔV
W(t)
Wn(t)
wt = (w,v)/v =
= wvcos(α) / v = wcos(α)
V(t+Δt)
wn = v2/R
13.
Нормальное и тангенциальное ускоренияWt(t)
V(t)
wn = v2/R
Wn(t)
W(t)
wt = d|v(t)| / dt
R
w = (dv/dt)2 +(v2/R)2
14.
Нормальное ускорениtПокажем, что при
движении по окружности
wn = v2/R
•Рассмотрим положение тела в два близких момента времени t и
t+dt. Угол поворота радиуса окружности, упирающегося в
точку, где находится тело, за это же малое время, очевидно,
составит dφ = |V|dt/R. Модуль ускорения тела равен:
•|(V(t+dt) - V(t))/dt| = |V|dφ/dt = V2/R
15.
Вращение и полярные координатыУгловая скорость:
ω = dφ/dt [rad / s] = [s-1 ]
v = dr/dt = Rdφ/dt = Rω = ωrsin(α)
v = [ω,r] = ωrsin(α) = Rω
Направление угловой скорости определяется
правилом правого винта.
Правого, а не левого – это договорное условие.
Угловая скорость – это псевдо-вектор («не совсем»
вектор)
16.
Some mathematics!Векторное произведение
с = [a, b] = a x b
с
c перпендикулярен и a , и b. с = absin(α),
cx = aybz - azby
cy = azbx - axbz
cz = axby - aybx
c=
a
α
c
Правило левой руки (именно левой –
договорное условие).
Вектор x вектор = псевдовектор
Вектор x псевдовектор = вектор
i j k
ax ay az
bx by bz
b
b
a
= i(aybz - azby) - j(axbz - azbx) +
+ k(axby - aybx)
17.
Вращение и полярные координатыУгловое ускорение:
β = dω/dt [rad/s2] = [s-2 ]
wt = βR
wt = [β, r]
w = wt2 + wn2 = (βrsin(α))2 + (V2/R)2 = R β2 + ω4
18.
Общая Физика НИЯУ МИФИМеханика
Продолжение следует…..















 physics
physics








