Similar presentations:
Общая физика
1. Общая физика 1)Механика 2)МКТ и термодинамика 3)Электромагнетизм 4)Геометрическая и волновая оптика 5)Элементы атомной физики
2. Лекция 1 Система отсчета. Материальная точка. Радиус-вектор и вектор перемещения, их связь с координатами точки. Траектория.
Средняя имгновенная скорости. Ускорение. Закон равноускоренного движения.
Тело относительно, которого происходит определение
положения рассматриваемого нами тела, называется телом
отсчета.
Совокупность тела отсчета, связанной с ним координатной
системы и синхронизированных между собой часов образует
систему отсчета.
Тело размерами, которого можно пренебречь в условиях
данной задачи называется материальной точкой.
3. Кинематика. 1.3
Тело размерами, которого можно пренебречь вусловиях данной задачи называется материальной
точкой.
Положение материальной точки в пространстве
можно определитьс помощью радиус вектора.
Радиус вектор r – это вектор проведенный из
начала координат системы отсчета в место где
находится материальная точка в данный момент
времени
При движении радиус вектор материальной точки
изменяется как по модулю, так и по направлению
r(t).
Геометрическое место концов радиуса вектора r
называется траекторией движения материальной
точки
4. Кинематика. 1.4
Пусть при своем движении материальная точка двигалась вдольтраектории из начального положения в конечное, тогда
Длина траектории называется путем s пройденным материальной
точкой.
Разница радиус векторов начального и конечного положений
материальной токи называется перемещением Δr12.
Всякое движение можно разложить на два вида: поступательное и
вращательное.
Поступательное движение – это движение, при котором любая
прямая связанная с движущимся телом остается параллельной
самой себе.
5. Кинематика. 1.5
В случае вращательного движения все точки тела движутся поокружностям центры, которых лежат на одной прямой,
называемой осью вращения.
Ось вращения может находиться и вне тела.
При движении материальной точки за время Δt из
начального положения в конечное ее
перемещение составляет величину Δr.
Тогда отношение Δr/Δt называют средним
вектором скорости <v> за время Δt.
При стремлении Δt к нулю средний вектор скорости <v> стремится к
определенному пределу – этот предел называется скоростью
материальной точки в данный момент времени v.
r dr
t 0 t
dt
v lim
6. Кинематика. 1.6
Модуль вектора скорости v определяется следующим способомdr
r
v = v lim
lim
t 0 t
t 0 dt
7. Кинематика. 1.7
Путь, пройденный материальной точкой за промежуток времени от t1 доt2 равен определенному интегралу:
t2
s= v(t)dt
t1
На графике зависимости модуля вектора скорости от времени
пройденный путь графически изображается, как площадь под
графиком между двумя моментами времени.
8. Кинематика. 1.8
Движение материальной точки характеризуется также ускорением.Вектор ускорения w определяет скорость изменения вектора скорости
материальной точки со временем, т.е равен производной от вектора
скорости по времени:
v dv d 2r
w = lim
2
t 0 t
dt dt
Прямолинейное движение с постоянным ускорением называется
равнопеременным.
В зависимости от поведения скорости со временем различают
равномерно-ускоренное и равномерно-замедленно движения.
9. Кинематика. 1.9
Зная, проекции радиус вектора r(t) на оси X, Y, Z декартовойсистемы координат связанной с телом отсчета: x=x(t), y=y(t),
z=z(t), можно получить координатное представление радиус
вектора:
r (t) = x(t)e x +y(t)e y +z(t)e z
Взяв производную по времени от
выражения для радиус вектора, получим:
v=
dr dx
dy
dz
e x e y ez v x e x v ye y vzez
dt dt
dt
dt
Аналогично получаем координатное выражение
для ускорения w
dv y
dvz d 2 x
dv dvx
d2 y
d2 z
w=
ex
ey
e z 2 e x 2 e y 2 e z w x e x w ye y w z e z
dt dt
dt
dt dt
dt
dt
10. Кинематика. 1.10
Для полного решения задачи о движении материальной точки –определения ее скорости v и положения r в зависимости от времени – не
достаточно знать зависимость w(t), еще необходимо знать и начальные
условия.
Рассмотрим случай движения материальной точки с постоянным
ускорением w=const.
t
Δv w.dt=wt
0
v=v0+Δv
v=v0 +wt
t
2
w
t
Δr = v (t)dt=v 0 t+
0
r=r0+Δr
2
w
t
r =r0 +v 0 t+
2
2
11. Лекция 2 Движения тела по окружности. Угловая скорость, нормальное и тангенициальное ускорение. Движение по криволинейной
тракектории.Введем единичный вектор τ, связанный с движущейся материальной
точкой и направленный по касательной к траектории в сторону скорости.
Вектор скорости v материальной точки направлен по касательной к траектории,
поэтом его можно определить следующим образом:
v=vτ τ
Тогда ускорение материальной точки:
dv dv τ
dτ
w= =
τ +v τ
dt dt
dt
После ряда преобразований получаем выражение для ускорения материальной
точки
dv dv τ
v2
w= =
τ+ n
dt dt
R
12. Кинематика. 2.2
При стремлении начальной и конечной точек траектории друг к другу отрезоктраектории между ними стремится к дуге окружности с центром в некоторой
точке. Эту точку называют центром кривизны траектории в данной точке, а
радиус R соответствующей окружности - радиусом кривизны траектории в
данной точке
Первое слагаемое в этом выражении называется тангенциальным ускорением
wτ, второе нормальным wn:
dv
w τ = τ τ,
dt
v2
wn = n
R
13. Кинематика. 2.3
Таким образом, полное ускорение w материальной точки может бытьпредставлено как сумма двух векторов тангенциального и нормального
ускорений. Один из, которых wn перпендикулярен к вектору скорости v, а
второй wτ направлен по касательной к траектории
Тангенциальное ускорение характеризует изменение скорости по
величине. Если скорость по величине не изменяется, тангенциальное
ускорение равно нулю. Нормальное ускорение характеризует изменение
скорости по направлению. Если направление скорости не изменяется,
движение происходит по прямолинейной траектории.
14. Кинематика. 2.4
Ускорение материальной точки, движущейся по произвольнойкривой, также будет зависеть от кривизны траектории, которая в
разных точках будет различна. Модуль полного ускорения
R
w= w +w = v + v
2
τ
2
n
2
2
2
Предположим, что материальная точка движется вокруг неподвижной в данной
системе отсчета оси по окружности радиуса r.
15. Кинематика. 2.5
Соответствующий угол поворота будем характеризовать вектором dφ,модуль которого равен углу поворота, а направление совпадает с
осью вращения, причем так, что направление поворота отвечает
правилу правого винта по отношению к направлению вектора dφ.
Тогда элементарное перемещение материальной точки при таком
повороте связано с углом поворота соотношением:
dr =r sin d
или в векторном виде:
dr d ,r
.
16. Кинематика. 2.6
dlim
t 0 t
dt
ω называется угловой скоростью
тела. Вектор ω направлен вдоль
оси, вокруг которой движется
материальная точка, в сторону,
определяемую правилом правого
винта, и представляет собой
аксиальный вектор.
17. Кинематика. 2.7
при равномерном вращении ω показывает, на какой уголповорачивается тело за единицу времени. Равномерное
вращение можно характеризовать периодом обращения Т, под
которым понимают время, за которое тело делает один
оборот, т.е. поворачивается на угол 2π. Поскольку промежутку
времени Т соответствует угол поворота 2π,
2
T
откуда период Т равен:
T
2
Число оборотов в единицу времени ν, равно:
1
T 2
18. Кинематика. 2.8
Из предыдущего соотношения следует, что угловая скорость равна 2π,умноженное на число оборотов в единицу времени
2
Вектор угловой скорости может изменяться, как по величине, так и по
направлению. В первом случае изменяется значение вектора
линейной скорости материальной точки, тогда как во втором случае
изменяется ось вращения. Изменение вектора угловой скорости со
временем характеризуют величиной называемой угловым ускорением:
d
t 0 t
dt
lim
Направление вектора β совпадает с направлением dω – приращения
вектора ω.
19. Кинематика. 2.9
Зная радиус окружности, по которой движется материальная точка,угловую скорость, можно определить линейную скорость движения
материальной точки по окружности. Для этого разделим в формуле,
определяющей перемещения материальной точки, левую и правую
части на dt. Так как dr/dt=v и dφ /dt=ω, то
v ,r
Продифференцировав выражения связывающее угловую и линейную
скорости найдем полное ускорение материальной точки
w d / dt,r , dr / dt
w ,r , ,r
20. Кинематика. 2.10
В рассматриваемом случае ось вращения неподвижна, поэтомувектор ,r представляет собой тангенциальное ускорение
Вектор , ,r - это нормальное ускорение wn.
Модули этих ускорений равны:
w r;
wn r
2
Окончательно получаем модуль полного ускорения:
w w 2 w 2n r 2 4
21. Лекция 3 Инерциальные системы отсчета, первый закон Ньютона. Масса и импульс материальной точки. Сила. Второй закон Ньютона.
Третийзакон Ньютона. Преобразования Галилея.
Классическая динамика основана на трех законах сформулированных
Ньютоном. Классическая ньютоновская динамика (механика) описывает
обширный круг явлений. Однако существуют границы ее применимости.
Классическая динамика применима при скоростях на много меньших
скоростей света 3 108 м/с и на расстояниях значительно больших
атомных 10-13см.
Первый закон Ньютона формулируется следующим образом:
всякое тело находится в состоянии покоя или равномерно и
прямолинейно движется, пока воздействие со стороны других тел не
заставит его изменить это состояние.
Оба этих состояния характеризуются тем, что ускорение тела равно
нулю. Формулировке первого закона можно придать следующий вид:
скорость любого тела остается постоянной, пока воздействие на это
тело со стороны других тел не вызовет ее изменение
22. Динамика. 3.2
Система отсчета, в которой выполняется первый законНьютона, называется инерциальной.
Система отсчета в которой первый закон Ньютона не
выполняется называется неинерциальной системой отсчета.
Любая система, движущаяся относительно инерциальной системы
отсчета прямолинейно и равномерно тоже будет
инерциальной.
Для инерциальных систем справедлив
принцип относительности, согласно которому все
инерциальные системы по своим механическим свойствам
эквивалентны друг другу.
Данное утверждение составляет
содержание принципа
относительности Галилея.
23. Динамика. 3.3
Пусть инерциальная система К’ движется со скоростью Vотносительно другой инерциальной системы К. Выберем оси
координат x’, y’, z’ K‘-системы параллельно соответствующим осям
x, y, z К-системы так, чтобы оси x’ и x совпадали между собой и
были направлены вдоль вектора V. Взяв за начало отсчета времени
момент, когда начала координат О’ и О совпадали, запишем
соотношение между радиус-векторами r’ и r одной и той же
материальной точки в K’- и К-системах:
r =r-Vt
и, кроме того,
t =t
24. Динамика. 3.4
Подразумевается, что длина отрезков и ход времени не зависятот состояния движения и, следовательно, одинаковы в обеих
системах отсчета. В координатах преобразования Галилея
имеют вид:
x =x-Vt,
y =y,
z =z,
t =t.
Продифференцировав по времени преобразования Галилея, найдем
классический закон преобразования скорости материальной точки
при переходе от одной инерциальной системы отсчета к другой
v =v-V
Дифференцируя это выражение по времени с учетом того, что
V=const, получаем w’=w, т.е. ускорение точки одинаково во всех
инерциальных системах отсчета.
25. Динамика. 3.5
В динамике рассматривается движение материальной точки всвязи с теми причинами (взаимодействиями), которые
обуславливают тот или иной характер движения.
Влияние другого тела или тел, вызывающее ускорение тела
(изменение скорости), называют силой .
Опыт показывает, что всякое тело оказывает сопротивление при
любых попытках изменить его скорость – как по модулю, так и
по направлению.
Свойство, выражающее степень сопротивления тела
изменению его скорости, называют инертностью.
Мерой инертности служит величина, называемая массой
26. Динамика. 3.6
Понятие массы m, вводится по определению отношений массдвух различных тел по обратному отношению ускорений,
сообщаемых им равными силами:
m1 m2 = w 2 w1
В рамках ньютоновской механики масса обладает следующими двумя
важнейшими свойствами:
1) масса – величина аддитивная, т.е. масса составного тела
равна сумме масс его частей;
2) масса тела как такового – величина постоянная, не
изменяющаяся при его движении.
27. Динамика. 3.7
Второй закон Ньютона формулируется следующим образом:ускорение всякого тела прямо пропорционально действующей
на него силе и обратно пропорционально массе тела.
F
w=
m
Опыт показывает, что если на тело действуют несколько сил, то
результирующая сила F определяется следующим образом:
F =F1 +F2 +...,
28. Динамика. 3.8
Во всех случаях, когда в опытах участвуют два тела А и В и тело Асообщает ускорение телу В, обнаруживается, что и тело В
сообщает ускорение телу А. Отсюда мы заключаем, что действия
тел друг на друга имеют характер взаимодействия. Ньютон
постулировал общее свойство всех сил взаимодействия третьим
законом Ньютона:
силы, с которыми две материальные точки действуют друг на
друга, всегда равны по модулю и направлены в противоположные
стороны вдоль прямой, соединяющей эти точки, т.е.
F12 =-F21
Чтобы свести нахождение закона движения частицы к чисто
математической задаче, необходимо, прежде всего, знать зависимость
силы от определяющих ее величин. Такие зависимости являются
следствием обобщения результатов опыта. Наиболее часто
встречаемые силы это гравитационные, электрические, сила
упругости, сила трения скольжения, однородная сила тяжести.
29. Динамика. 3.9
Сила гравитационного притяжения, действующая между двумятелами в соответствии с законом всемирного тяготения имеет
вид:
m1m2
F 2
r
где γ – гравитационная постоянная.
r – растояние между центрами масс тел.
30. Динамика. 3.10
Кулоновская сила действующая между двумя точечнымизарядами q1 и q2
q1q 2
F k 2
r
где r – расстояние между зарядами
k - коэффициент пропорциональности, зависящий от выбора системы
единиц.
Упругая сила – сила, пропорциональная смещению материальной точки
из положения равновесия
и направленная к положению
равновесия:
Fупр=-χr,
где r – радиус-вектор, характеризующий
смещение материальной точки из
положения равновесия;
χ – положительный коэффициент,
зависящий от упругих свойств среды.
31. Динамика. 3.11
Сила трения скольжения, возникающая при скольжении данного телапо поверхности другого тела:,
F=kN
где k – коэффициент трения скольжения, зависящий от природы и состояния
соприкасающихся поверхностей;
N – сила нормального давления, прижимающая трущиеся поверхности друг к
другу.
Сила F направлена в сторону противоположную направлению движения данного
тела относительно другого
32. Лекция 4 Замкнутая система материальных точек. Закон сохранения импульса. Момент импульса, закон сохранения момента импульса.
Любое тело или совокупность тел представляет собой системуматериальных точек. Для описания системы материальных точек
необходимо знать закон движения каждой материальной точки
системы, т.е. знать зависимость координат и скоростей каждой
материальной точки от времени. Оказывается, есть общие
принципы, которые можно применить к описанию системы в целом.
Это законы сохранения. Существуют такие величины, которые
обладают свойством сохраняться во времени. Среди этих величин
наиболее важную роль играют энергия, импульс и момент импульса.
Эти три величины имеют важное общее свойство аддитивности: их
значения для системы, равно сумме значений для каждой из частей
системы в отдельности.
По определению, импульс материальной точки:
p =mv
где m и v – ее масса и скорость.
33. Законы сохранения. 4.2
Воспользовавшись определением импульса, запишем второй законНьютона в иной форме:
mw =m
dv d(mv) dp
=
=
=F
dt
dt
dt
т.е. производная импульса материальной точки по времени равна
результирующей всех сил действующих на материальную точку.
Например если F=0 то p=const.
Это уравнение позволяет найти приращение импульса материальной
точки за любой промежуток времени, если известна зависимость силы F
t
от времени:
p2 p1 Fdt
0
Таким образом, приращение импульса частицы за любой промежуток
времени зависит не только от значения силы, но и от
продолжительности ее действия
34. Законы сохранения. 4.3
Материальные точек, входящие в систему могут взаимодействовать, какмежду собой, так и с другими телами не входящими в систему. В
соответствие с этим
силы взаимодействия между материальными точками системы
называются внутренними,
а силы обусловленные взаимодействием с телами не входящими в
систему называются внешними.
В случае если на систему не действуют внешние силы, она называется
замкнутой.
Импульс системы определим, как векторную сумму импульсов ее
отдельных частей:
p pi
35. Законы сохранения. 4.4
Рассмотрим импульс системы состоящей из двх материальных точек.Тогда импульс такой системы равен p=p1+p2. Напишем для каждой
материальной точки второй закон Ньютона:
dp1
=F12 +F1 ,
dt
dp2
=F21 +F2
dt
Сложим эти два уравнения вместе.
Сумма внутренних сил будет равна
нулю (по третьему закону Ньютона,
F12=-F21), вследствие чего получим:
d
dp
(p1 +p 2 )=
=F1 +F2
dt
dt
36. Законы сохранения. 4.5
Если на систему не действуют внешние силы то получается, чтоdp
0
dt
следовательно для замкнутой системы р постоянен.
Аналогичные рассуждения можно обобщить и на систему из N
материальных точек. Закон сохранения импульса формулируется
следующим образом:
импульс замкнутой системы материальных точек остается
постоянным.
Импульс остается постоянным и для не замкнутой системы при
условии, что внешние силы, действующие на материальные точки
системы, в сумме дают ноль. Даже если сумма внешних сил не равна
нулю, но проекция этой суммы на некоторую ось равна нулю, то
проекция импульса системы на эту ось будет оставаться постоянной.
37. Законы сохранения. 4.6
Момент импульса относительно точки О равен:L= r,p m r,v
где r – радиус-вектор, проведенный из точки О в
ту точку пространства, в которой находится
материальная точка. Из этого определения
следует, что L является аксиальным вектором. Его
направление выбрано так, что вращение вокруг
точки О направлении вектора р и вектор L
образуют правовинтовую систему. Модуль вектора
L равен:
L=rp sin lp
где α – угол между r и р, l=rsinα – плечо вектора
р относительно точки О
38. Законы сохранения. 4.7
Момент импульса материальной точки может изменяться современем, продифференцировав выражение для момента импульса,
можно определить причину вызывающую изменение момента
импульса
dL
= dr dt ,p + r, dp dt
dt
Первое слагаемое в правой части равенства обращается в ноль так,
как dr/dt=v, а скорость параллельна импульсу р. Далее, согласно
второму закону Ньютона, dp/dt=F, получаем:
dL
= r ,F
dt
Величину, стоящую в правой части этого уравнения, называют
моментом силы F относительно точки О. Обозначим ее буквой М:
39. Законы сохранения. 4.8
M= r,FМодуль этого вектора равен
M=lF.
Таким образом производная от момента импульса относительно
некоторой точки О равна моменту М равнодействующей силы
относительно той же точки О
dL
=M
dt
Это уравнение называют уравнением моментов. Из
уравнения моментов, в частности, следует, что если
М=0, то L=const. Другими словами, если
относительно некоторой точки О выбранной системы
отсчета момент всех сил, действующих на частицу,
равен нулю в течение интересующего нас промежутка
времени, то относительно этой точки момент
импульса частицы остается постоянным в течение
этого времени.
40. Законы сохранения. 4.9
Для определения приращения момента импульса частицы относительноточки О за любой промежуток времени, если известна зависимость
от времени момента силы необходимо проинтегрировать выражение
dL=Mdt. В результате найдем приращение вектора L за конечный
t
промежуток времени t:
L2 -L1 Mdt
0
Момент импульса системы - векторная сумма моментов
импульсов ее отдельных частиц:
L Li
Подобно тому, как это делалось для импульса системы. Рассмотрим
случай системы состоящей из двух материальных точек.
41. Законы сохранения. 4.10
Момент внутренней силы действующей на 1 частицу со стороны второйобозначим M12, результирующий момент внешних сил действующих на
эту частицу M1. Аналогично введем обозначения и для второй
материальной точки M21 и M2. Тогда уравнения моментов для
материальных точек системы будут выглядеть следующим образом:
d
d
L1 =M12 +M1 ,
L 2 =M 21 +M 2
dt
dt
Сложив эти выражения получим:
d
(L1 + L 2 )=M12 + M 21 +M1 +M 2
dt
Рассмотрим сумму двух первых слагаемых в правой части :
M12 +M21 = r1,F12 + r2 ,F21 = r1,F12 - r2 ,F12 = r1 -r2 ,F12 r12 ,F12 0
42. Законы сохранения. 4.11
Радиус-вектор r12 коллинеарен силе F12, поэтому векторное произведениеэтих двух векторов равно нулю. Таким образом, получаем:
dL
M1 M 2 M
dt
Данное соотношение можно обобщить на систему из произвольного
числа материальных точек. Следовательно, получаем, что изменение
момента импульса системы обусловлено действием на нее момента
внешних сил. Если же внешние силы не действуют, то момент импульса
остается постоянным. Таким образом, мы пришли к закону сохранения момента
импульса:
момент импульса замкнутой системы материальных точек остается постоянным.
43. Лекция 5 Работа и мощность силы. Консервативные силы, работа консервативных сил. Потенциальная энергия. Закон сохранения
механической энергииПусть на материальную точку действует сила F, и под действием этой
сила произошло перемещение по некоторой траектории из точки 1 в
точку 2. В общем случае сила F меняется в процессе движения.
Действие силы F на перемещении dr характеризуют величиной,
равной скалярному произведению Fdr, эту величину называю
работой силы F на перемещении dr:
dA = Fdr =F cos ds=Fs ds
где α – угол между вектором силы и
перемещения, ds – элементарный отрезок
пути, Fs – проекция вектора силы на
перемещение.
44. Законы сохранения. 5.2
Работа А – величина алгебраическая: в зависимости от угла междусилой и перемещением работа может быть как положительной,
отрицательной так и равной нулю. Если же необходимо определит
работу, совершенную силой F на всей траектории необходимо
вычислить интеграл:
2
2
A Fdr Fs ds
1
Построив график зависимости проекции
силы Fs от положения материальной
точки (s) на траектории. Можно придти к
выводу, что графически элементарная
работа dA будет выглядеть как площадь
под графиком между двумя точками. При
этом площадь над осью s будет
положительной, а под ней
отрицательной.
1
45. Законы сохранения. 5.3
На практике часто имеет значение не само значение работы, а то время,за которое данная работа была выполнена. Поэтому вводится
величина, характеризующая работу, совершаемую в единицу времени
– мощность.
A
N
t
Если работа, совершаемая за одинаковые промежутки времени не
одинакова то можно определить мгновенную мощность:
A dA
t 0 t
dt
N lim
Пусть за время dt точка получает перемещение dr. Тогда элементарная
работа равна dA=Fdr и мощность можно представить в виде:
N=
dA Fdr
=
=Fv
dt
dt
46. Законы сохранения. 5.4
Если в каждой точке пространства на помещенную туда материальнуюточку действует сила, то говорят, что материальная точка находится в
поле сил.
Поле, остающееся постоянным во времени, называют
стационарным.
Стационарные силовые поля, в которых работа не зависит от пути
между точками 1 и 2, называют консервативными.
Силы, не являющиеся консервативными,
называют
неконсервативными.
Силы, зависящие только от расстояния между
взаимодействующими частицами и направленные по прямой,
проходящей через эти частицы называют центральными
47. Законы сохранения. 5.5
Тот факт, что работа консервативных сил зависит только от начальногои конечного положения материальной точки, дает возможность
сопоставить полю некоторую функцию координат(радиус-вектора)
U(r).
2
A12 Fdr U 1 -U 2
1
Таким образом, работа сил поля на пути 1-2 равна убыли
потенциальной энергии материальной точки в данном поле.
48. Законы сохранения. 5.6
Для этого достаточно вычислить работу, совершаемую силами поля налюбом пути между точками, и представить ее в виде убыли некоторой
функции, которая и есть потенциальная энергия U(r). Именно так и
были получены работы в полях упругой, гравитационной и
кулоновской сил
В поле упругой силы:
kr 2
U(r)
2
В кулоновском поле материальной точки:
U(r)
r
В однородном поле силы тяжести:
U(z)=mgz
49. Законы сохранения. 5.7
При перемещении материальной точки из одной точки поляконсервативных сил в другую работа сил поля равна убыли
потенциальной энергии. В случае элементарного перемещения
получим:
Fdr=-dU
Так как Fdr=Fsds имеем: F ds=-dU Отсюда: Fs
s
U
s
В декартовых координатах это соотношение имеет вид:
U U
U
F
i
j
k
y
z
x
Величину, стоящую в скобках, называют градиентом скалярной
функции U и обозначают grad U или U
F U
50. Законы сохранения. 5.8
Найдем элементарную работу, которую совершает эта сила приэлементарном перемещении dr
mv2
dv
dv
dA=Fdr =m dr =m dtv=mvdv = mvdv=d
dt
dt
2
Отсюда видно, что работа результирующей силы F идет на приращение
некоторой величины, которую называют кинетической энергией:
mv 2
T=
2
Таким образом, при конечном перемещении из точки 1 в точку 2:
T2 -T1 =A12
приращение кинетической энергии частицы на некотором перемещении равно
алгебраической сумме работ всех сил, действующих на материальную точку на
том же перемещении.
51. Законы сохранения. 5.9
Результирующая всех сил может быть представлена какF=Fконс.+Fстор.
Тогда работа этих сил идет на приращение кинетической энергии:
Аконс.+Астор.
Так же работа сил консервативного поля равна убыли потенциальной
энергии
Аконс.=-ΔU.
В итоге получаем:
ΔT=-ΔU+Aстор.
Δ(T+U)=Астор.
Из этого соотношения видно, что работа сторонних сил идет на
приращение величины
T+U.
Эту величину – сумму кинетической и потенциальной энергий –
называют полной механической энергией материальной точки и
обозначают Е.
52. Законы сохранения. 5.10
Полная механическая энергия, как и потенциальная, определяется сточностью до произвольной постоянной.
Изменение полной механической энергии материальной точки
обусловлено совершением над ней работы сторонними силами.
Отсюда непосредственно следует закон сохранения механической
энергии: если сторонние силы отсутствуют или таковы, что не
совершают работы в течении интересующего нас времени, то полная
механическая энергия частицы в стационарном поле консервативных
сил остается постоянной за это время.
E=T+U const
Если же рассматривать не одну материальную точку, а систему, то помимо
потенциальной энергии во внешнем поле сил необходимо также учитывать
энергию взаимодействия между отдельными материальными точками
системы
E -E =Aдис. +А
2
1
внутр.
внеш.
Механическая энергия замкнутой системы, в которой не E=T+U const
соб.
действуют диссипативные силы, сохраняется в процессе
движения т.е
53. Лекция 6 Упругие и квазиупругие силы. Закон Гука. Гармонические колебания: частота, период, амплитуда и фаза колебаний.
Дифференциальноеуравнение гармонических колебаний. Гармонические колебания
пружинного и математического маятников.
Колебаниями называются процессы, отличающиеся той или
иной степенью повторяемости.
В зависимости от характера воздействия на колеблющуюся
систему различают свободные (или собственные) колебания и
вынужденные колебания.
Свободными называют такие колебания, которые происходят в
системе, предоставленной самой себе после того, как ей был
сообщен толчок либо она была выведена из положения
равновесия.
Вынужденными называют такие колебания, в процессе
которых колеблющаяся система подвергается воздействию
внешней периодически изменяющейся силы.
Простейшим примером по характеру описания являются
гармонические колебания. Это такие колебания, при которых
колеблющаяся величина изменяется со временем по закону
синуса или косинуса.
54. Колебания. 6.2
Простейшим примером системы, где возникают свободныегармонические колебания, является движение тела под действием
силы упругости пружины.
Примером такой системы является тело
массы m, прикрепленное к пружине
жесткостью k, движущееся по
горизонтальной поверхности без
трения. В этом случае х – растяжение
пружины (смещение тела из положения
равновесия).
Начало координат выбирается в точке, соответствующей положению
конца нерастянутой пружины, поэтому x=l-l0 – растяжение пружины.
Если силы вида
F =-kx
x
имеют другую природу (т.е. не являются силами упругости) то их
называют квазиупругими. В этом случае k – коэффициент квазиупругой
силы.
55. Колебания. 6.3
Напишем второй закон Ньютона, в проекции на ось х, для этой системыd2x
Fx = mw x =m 2 = - kx
dt
Дифференциальное уравнение, описывающее колебания данной системы:
mx=-kx
Преобразуем это уравнение следующим образом:
k
x+ x=0
m
k
m
получим
окончательный
вид
линейного
дифференциального уравнения второго порядка,
гармонические колебания:
2
Введя обозначение 0
x 02 x 0
однородного
описывающего
56. Колебания. 6.4
Решение данного уравнения имеет вид:x(t ) A cos( 0t 0 )
Величина наибольшего отклонения системы от положения равновесия
называется амплитудой колебаний А.
Величина ( 0t 0 ) стоящая под знаком косинуса, называется
начальной фазой колебания.
Величину ω0 называют циклической или круговой частотой колебаний.
Промежуток времени Т, за который фаза колебаний изменится на 2π,
называется периодом колебания. Он определяется из следующего
условия
( (t+T) ) ( t ) 2
0
0
T
2
0
0
0
Число колебаний в единицу времени называется частотой колебания ν.
1
T
57. Колебания. 6.5
Продифференцировав зависимость смещения от времени x(t)получим выражение для зависимости скорости от времени. Взяв
вторую производную, получим зависимость ускорения от
времени:
x(t ) A cos( 0t 0 )
v x A 0 sin( 0 t 0 ) A 0 cos( 0 t 0 )
2
w x A 02 cos( 0 t 0 ) A 02 cos( 0 t 0 )
Как следует из этих соотношений
ускорение, и смещение находятся в
противофазе. Т.е. в тот момент, когда
смещение достигает наибольшего
положительного значения, ускорение
достигает наибольшего отрицательно
значения, и наоборот.
58. Колебания. 6.6
Другим примером колебательной системы может служитьматематический маятник.
Математическим маятником называют идеализированную систему,
состоящую из легкой и нерастяжимой нити, на которой подвешена
масса, сосредоточенная в одной точке.
Достаточно хорошим приближением к математическому маятнику служит
небольшой шарик, подвешенный на длинной тонкой нити.
В такой системе при малых углах отклонения
нити происходят гармонические колебания. В
этом случае собственная частота
g
0
l
период
T 2
l
g
59. Колебания. 6.7
Физическим маятником называется твердое тело, способноесовершать колебания вокруг неподвижной точки, не
совпадающей с его центром инерции.
В процессе колебаний происходит
превращение кинетической энергии в
потенциальную и обратно, причем в
моменты наибольшего отклонения от
положения равновесия полная энергия
Е состоит только из потенциальной,
которая достигает своего
максимального значения Umax:
E U max
kA 2
2
60. Колебания. 6.8
При прохождении же системы через положение равновесия полнаяэнергия состоит лишь из кинетической энергии, которая в эти моменты
достигает своего наибольшего значения Тmax:
E Tmax
mv2max mA 2 02
2
2
Определим, как изменяется со временем кинетическая и потенциальная
энергии гармонических колебаний. Кинетическая энергия в произвольный
момент времени равна:
mx 2 mA 2 02
T
sin 2 ( 0 t 0 )
2
2
Потенциальная энергия выражается формулой:
kx 2 kA2
U
cos 2 ( 0t 0 )
2
2
61. Колебания. 6.9
Сложив вместе кинетическую и потенциальную энергии, получимформулу для полной энергии:
kA 2 mA 2 02
E U T
const
2
2
62. Колебания. 6.10
Сложение колебанийодного направления
Сложение перпендикулярных
колебаний. Фигуры Лиссажу.
63. Лекция 7 Затухающие колебания. Коэффициент затухания и логарифмический декремент затухания. Энергия гармонических и затухающих
колебаний.При движении тела в среде последняя всегда оказывает сопротивление,
стремящееся замедлить движение. При этом энергия движущегося
тела, в конце концов, переходит в тепло. В таких случаях говорят, что
имеет место диссипация энергии. если движение тела в среде
достаточно медленное по сравнению со скоростью внутренних
диссипативных процессов, то реакция среды на движение тела в
некоторых случаях может быть приближенно описана введением так
называемой силы трения, действующей на тело и зависящей лишь от
скорости последнего. Такая ситуация возникает, например, при
движении тела в вязкой среде, жидкости или газе.
В ряде случаев можно считать, что сила сопротивления пропорциональна
величине скорости
Fсопр. -rx
64. Колебания. 7.2
Уравнение второго закона Ньютона для пружинного маятника вприсутствие сил сопротивления имеет вид:
mx kx rx
Перепишем его следующим образом:
x 2 x 02 x 0
Где применены следующие обозначения:
2
r
,
m
02
k
m
ω0 представляет собой ту частоту, с которой совершались бы свободные
колебания системы при отсутствии сопротивления среды, т.е. при r=0.
Наличие сопротивления среды приводит к тому, что размах колебаний
уменьшается. Поэтому в зависимости смещения от времени амплитуда
колебаний должна изменяться.
65. Колебания. 7.3
При небольшой силе трения полученное выше дифференциальноеуравнение имеет следующее решение:
x(t) A 0 e t cos( t 0 )
66. Колебания. 7.4
В соответствии с видом функции движение системы можно рассматриватькак гармонические колебания частоты ω с амплитудой, изменяющейся во
времени по закону:
A(t) A 0 e
t
r
Скорость затухания колебаний определяется величиной
называют коэффициентом затухания. 2m
которую
Найдем время τ, за которое амплитуда колебаний уменьшается в е раз.
e 1 откуда βτ=1.
По определению e
Следовательно, коэффициент затухания обратен по величине тому промежутку
времени, за который амплитуда уменьшается в е раз. Период затухающих
колебаний равен:
2
2
T
02 2
67. Колебания. 7.5
Видно, что период затухающих колебаний больше, чем периоднезатухающих колебаний с теми же параметрами колебательной
системы. При незначительном сопротивлении среды ( 2 02 ) , период
колебаний практически равен T 2 . С ростом коэффициента
0
0
затухания период колебаний увеличивается. При приближении
коэффициента затухания(сопротивления среды) к величине равной ω0
период колебаний становится равным бесконечности и колебания
становятся апериодическими – выведенная из положения равновесия
система возвращается в положение равновесия, не совершая
колебаний. Запас механической энергии тела к моменту его
возвращения в положение равновесия полностью расходуется на
преодоление трения.
68. Колебания. 7.6
Апериодические колебания69. Колебания. 7.7
Последующие наибольшие отклонения в какую-либо сторону (напримерА’, А”, А”’ и т.д.) образуют геометрическую прогрессию.
Действительно, если
A A 0 e t , то
(t+2T)
A e T
A A 0 e (t+T) A e T , A A 0e
Вообще, отношение значений амплитуд, соответствующих моментам
времени, отличающимся на период, равно
A(t)
e T
A t+T
Это отношение называют декрементом затухания, а его логарифм –
логарифмическим декрементом затухания:
ln
A(t)
T
A(t+T)
70. Колебания. 7.8
Выразив β через λ и Т, закон убывания амплитуды можно записать в виде:A A0e
t
T
За время τ, за которое амплитуда уменьшается
в е раз, система успевает
совершить Ne=τ/T колебаний. Из условия T
1 получается, что
Ne 1
e
e
T
Следовательно, логарифмический декремент затухания обратен по
величине числу колебаний, совершаемых за то время, за которое
амплитуда уменьшается в е раз.
Для характеристики колебательной системы часто употребляется также величина:
Q Ne
называемая добротностью колебательной системы. Как видно из ее
определения, добротность пропорциональна числу колебаний Ne,
совершаемых системой за то время τ, за которое амплитуда колебаний
уменьшается в е раз.
71. Колебания. 7.9
Найдем импульс системы, совершающей затухающие колебания.Продифференцировав зависимость, смещение в затухающих
колебаниях по времени и умножив полученный результат на массу m,
получим:
p mx mA0e t cos( t 0 ) sin( t 0 )
Это выражение может быть преобразовано к виду
p p0 e t cos( t 0 )
t
то, исключив t из этих уравнений, мы
Если бы не множитель e
получили бы в координатах x и p уравнение эллипса, повернутого по
отношению к координатным осям. Наличие экспоненциального
множителя приводит к тому, что эллипс превращается в
скручивающуюся спираль. Эта спираль и представляет собой фазовую
траекторию затухающего колебания. Она будет наклонена по
отношению к координатным осям тем сильнее, чем больше
коэффициент затухания
72. Колебания. 7.10
При затухающих колебаниях энергия системырасходуется на преодоление сопротивления
среды. Если восполнять эту убыль энергии,
колебания станут незатухающими. Пополнение
энергии системы может осуществляться за счет
толчков извне, однако эти толчки должны
сообщаться системе в такт с ее колебаниями,
иначе они могут уменьшить колебания системы
и даже прекратить их совсем.
Можно сделать так, чтобы колеблющаяся система
сама управляла внешним воздействием,
обеспечивая согласованность сообщаемых ей
толчков со своим движением. Такая система
называется автоколебательной, а
совершаемые ею незатухающие колебания –
автоколебаниями.
73. Лекция 8 Вынужденные колебания. Резонанс
Если колебательная система подвергается воздействию внешнейпериодической силы, то возникают так называемые вынужденные
колебания, имеющие незатухающий характер. Вынужденные
колебания следует отличать от автоколебаний. В случае
автоколебаний в системе предполагается специальный механизм,
который в такт с собственными колебаниями "поставляет" в систему
небольшие порции энергии из некоторого резервуара энергии. Тем
самым поддерживаются собственные колебания, которые не затухают.
В случае автоколебаний система как бы сама себя подталкивает. В
случае вынужденных колебаний система подталкивается посторонней
силой. Особый интерес представляет случай, когда внешняя сила,
изменяющаяся по гармоническому закону с частотой ω, воздействует
на колебательную систему, способную совершать собственные
колебания на некоторой частоте ω0. Если свободные колебания
происходят на частоте ω0, которая определяется параметрами
системы, то установившиеся вынужденные колебания всегда
происходят на частоте ω внешней силы.
74. Вынужденные колебания. 8.2
Уравнение второго закона Ньютона для пружинного маятника, накоторый действует периодически изменяющаяся сила, будет иметь
вид:
mx kx rx F cos t
0
Разделив это уравнение на m, и перенеся члены с x и в левую часть,
получим неоднородное линейное дифференциальное уравнение
второго порядка:
x 2 x 02 x f 0 cos t
Решение данного уравнения имеет следующий вид:
x(t) A 0 e
t
cos(( )t )
2
0
2
2
cos t arctg 2
2
2 2
2 2
0 2
( 0 ) 4
f0
Первое слагаемое в правой части этой формулы представляет свободные
колебания их частота ω определяется внутренними свойствами системы, а
амплитуда А0 и фаза φ’ — начальными условиями и внешними воздействиями.
Второе слагаемое, называемое вынужденными колебаниями, обусловлено
наличием внешней (вынуждающей) силы.
75. Вынужденные колебания. 8.3
Первое слагаемое в этом выражении играет заметную роль только вначальной стадии процесса, при так называемом установлении
колебаний. С течением времени из-за экспоненциального множителя
роль первого слагаемого все больше уменьшается, и по прошествии
достаточного времени им можно пренебречь, сохраняя лишь второе
слагаемое.
f0
2
x(t)
cos t arctg 2
2
( 02 2 ) 2 4 2 2
0
76. Вынужденные колебания. 8.4
Зависимость амплитуды вынужденных колебаний от частотывынуждающей силы приводит к тому, что при некоторой определенной
для данной системы частоте амплитуда колебаний достигает
максимального значения. Колебательная система оказывается особенно
отзывчивой на действие вынуждающей силы при этой частоте. Это
явление называется резонансом, соответствующая частота –
резонансной частотой.
Чтобы определить резонансную частоту ωрез, нужно найти максимум
функции определяющей зависимость амплитуды вынужденных
колебаний от частоты вынуждающей силы. Продифференцировав
f0
выражение
A(t)
( 02 2 ) 2 4 2 2
по ω и приравняв нулю, получим условие, определяющее ωрез:
4 02 2 8 2 0
77. Вынужденные колебания. 8.5
22
Данное уравнение имеет три решения: ω=0 и 0 2 .
Решение равное нулю, соответствует максимуму знаменателя. Из
остальных двух решений отрицательное не подходит, как не имеющее
физического смысла. В результате, для резонансной частоты
получается значение:
рез 02 2
Если частота ω внешней силы приближается к собственной частоте ω,
возникает резкое возрастание амплитуды вынужденных колебаний. Это
явление называется резонансом. Зависимость амплитуды А вынужденных
колебаний от частоты ω вынуждающей силы называется резонансной
характеристикой или резонансной кривой.
78. Вынужденные колебания. 8.6
При очень большом затуханиивыражение для резонансной частоты
становится мнимым. Это означает,
что при этих условиях резонанс не
наблюдается – с увеличением
частоты амплитуда вынужденных
колебаний монотонно убывает. При
стремлении ω к нулю все кривые
приходят к одному и тому же,
отличному от нуля, предельному
значению, равному
f 0 / 02
т.е. F0 /k . Это значение
представляет собой смещение из
положения равновесия, которое
получает система под действием
постоянной силы величины F0
79. Вынужденные колебания. 8.7
При резонансе амплитуда Арез колебания может во много разпревосходить амплитуду А колебаний свободного конца пружины,
вызванного внешним воздействием. В отсутствие трения амплитуда
вынужденных колебаний при резонансе должна неограниченно
возрастать. В реальных условиях амплитуда установившихся
вынужденных колебаний определяется условием: работа внешней
силы в течение периода колебаний должна равняться потерям
механической энергии за то же время из-за трения. Чем меньше
трение (т. е. чем выше добротность Q колебательной системы), тем
больше амплитуда вынужденных колебаний при резонансе. У
колебательных систем с не очень высокой добротностью (< 10)
резонансная частота несколько смещается в сторону низких частот
80. Вынужденные колебания. 8.8
Зависимость φ от ω при различных значения коэффициентазатухания β. Частоте ω0 соответствует φ=π/2.
81. Вынужденные колебания. 8.9
Оказывается, существует иной вид воздействияизвне, с помощью которого можно сильно
раскачать систему.
Этот вид воздействия заключается в
совершаемом в такт с колебаниями
периодическом изменении какого-либо
параметра системы, вследствие чего само
явление называется параметрическим
резонансом.
Простейшим примером системы, в которой
возможен параметрический резонанс, является
простейший маятник – шарик на нитке. Если
периодически изменять длину маятника l,
увеличивая ее в моменты, когда маятник
находится в крайних положениях, и уменьшается
в моменты, когда маятник находится в среднем
положении, то маятник сильно раскачается.
82. Вынужденные колебания. 8.10
Увеличение энергии маятника при этом происходит за счет работы,которую совершает сила, действующая на нить. Сила натяжения
нити при колебаниях маятника непостоянна: она меньше в крайних
положениях, когда скорость обращается в нуль, и больше в среднем
положении, когда скорость маятника максимальна. Поэтому
отрицательная работа внешней силы при удлинении маятника
оказывается меньше по величине, чем положительная работа,
совершаемая при укорочении маятника. В итоге работа внешней
силы за период оказывается больше нуля.
83. Лекция 9 Основные положения молекулярно-кинетической теории. Масса и размеры молекул. Термодинамическая система и параметры ее
состоянияВ основе молекулярно-кинетической теории
лежат три основных положения:
1) Все вещества – жидкие, твердые и
газообразные – образованы из
мельчайших частиц – молекул, которые
сами состоят из атомов («элементарных
молекул»). Молекулы химического
вещества могут быть простыми и
сложными и состоять из одного или
нескольких атомов. Молекулы и атомы
представляют собой электрически
нейтральные частицы.
2) Атомы и молекулы находятся в
непрерывном хаотическом движении.
3) Частицы взаимодействуют друг с другом
силами, имеющими электрическую
природу. Гравитационное взаимодействие
между частицами пренебрежимо мало.
84. Основы МКТ. 9.2
Идеальным газом называется газ, молекулы которого являютсяматериальными точками, то есть расстояния между молекулами
намного превосходят их размеры, а единственный вид их
взаимодействий между собой – упругие механические столкновения.
Модель идеального газа достаточно хорошо описывает поведение
реальных газов в широком диапазоне давлений и температур.
Относительной молекулярной (или атомной) массой вещества Мr называют
отношение массы молекулы (или атома) m0 данного вещества к 1/12
массы атома углерода m0c:
В молекулярно-кинетической теории количество вещества принято
считать пропорциональным числу частиц. Единица количества
вещества называется молем (моль).
Моль – это количество вещества, содержащее столько же частиц
(молекул), сколько содержится атомов в 0,012 кг углерода 12C
85. Основы МКТ. 9.3
Таким образом, в одном моле любого вещества содержится одно и то жечисло частиц (молекул). Это число называется постоянной Авогадро
NA=6.02 1023 моль-1.
Количество вещества ν определяется как отношение числа N частиц
(молекул) вещества к постоянной Авогадро NA
N
NA
Молярной массой μ вещества называют массу вещества, взятого в
количестве 1 моля. Молярная масса равна произведению массы m0
одной молекулы данного вещества на постоянную Авогадро:
m0 N A
86. Основы МКТ. 9.4
Всякая система может находиться в различных состояниях,отличающихся температурой, давлением, объемом и т.д. Подобные
величины, характеризующие состояние системы, называются
параметрами состояний. Не всегда какой-либо параметр имеет
определенное значение. Например, если температура в разных точках
тела не одинакова, то телу нельзя приписать определенное значение
параметра Т. В этом случае состояние называется неравновесным. То
же самое может иметь место и для других параметров. Равновесным
состоянием системы называется такое состояние, при котором все
параметры системы имеют определенные значения, остающиеся при
неизменных внешних условиях постоянными сколь угодно долго.
Процесс, состоящий из непрерывной последовательности равновесных
состояний, называется, равновесны процессом.
87. Основы МКТ. 9.5
Состояние некоторой массы газа определятся значениями трехпараметров: давления р, объема V и температуры T. Эти параметры
связаны друг с другом, так что изменение одного из них влечет за собой
изменение других. Данная связь может быть задана аналитически в виде
функции:
F ( p, V , T ) 0
Оказывается, что для идеального газа уравнение состояния принимает
следующий вид:
pV
B
T
88. Основы МКТ. 9.6
где В – постоянная для данной массы газа величина. В соответствии сзаконом установленным Авогадро одинаковые количества различных
идеальных газов при одинаковых условиях (давление, температура)
занимают одинаковый объем. Следовательно, когда количество газа
равно одному молю, величина В будет одинакова для всех газов.
Обозначив соответствующую величину через R можно записать:
pV1м
R
T
Это уравнение называют уравнением Клайперона. Оно связывает
параметры состояния моля идеального газа и, следовательно,
представляет собой уравнение состояния идеального газа. Его обычно
пишут в виде
pV RT
1м
Величина R называется универсальной газовой постоянной. Ее значение
можно вычислить, подставив атмосферное давление, объем 22.4 л и
температуру 273 К:
1.01 105 22.4 10 3
Дж
R
273
8.31
моль К
89. Основы МКТ. 9.7
От уравнения для одного моля легко перейти к уравнению для любоймассы газа m, приняв во внимание, что при одинаковых давлении и
температуре n молей газа будут занимать в n раз больший объем чем
m
один моль: V=nV. Умножив уравнение Клайперона на n
и заменив
nV через V, получаем:
pV
m
RT
Это и есть уравнение состояния идеального
газа, написанное для любой
массы газа m.
Изотермическим процессом называют равновесный процесс,
протекающий при постоянной температуре T. Из уравнения состояния
идеального газа следует, что при постоянной температуре T и
неизменном количестве вещества ν в сосуде произведение давления p
газа на его объем V должно оставаться постоянным:
PV const
90. Основы МКТ. 9.8
На плоскости (p, V) изотермические процессыизображаются при различных значениях
температуры T семейством гипербол p ~ 1 / V,
которые называются изотермами. Так как
коэффициент пропорциональности в этом
соотношении увеличивается с ростом
температуры, изотермы, соответствующие более
высоким значениям температуры, располагаются
на графике выше изотерм, соответствующих
меньшим значениям температуры. Уравнение
изотермического процесса было получено из
эксперимента английским физиком Р. Бойлем
(1662 г.) и независимо французским физиком Э.
Марриотом (1676 г.). Поэтому это уравнение
называют законом Бойля–Мариотта.
91. Основы МКТ. 9.9
Изохорный процесс – это процесс равновесного нагревания илиохлаждения газа при постоянном объеме V и при условии, что
количество вещества ν в сосуде остается неизменным. Как следует из
уравнения состояния идеального газа, при этих условиях давление
газа p изменяется прямо пропорционально его абсолютной
температуре: p ~ T или
p
const
T
На плоскости (Т, р) изохорные процессы для
заданного количества вещества ν при
различных значениях объема V
изображаются семейством прямых линий,
которые называются изохорами.
Большим значениям объема соответствуют изохоры с меньшим наклоном
по отношению к оси температур. Экспериментально зависимость давления
газа от температуры исследовал французский физик Ж. Шарль (1787 г.).
Поэтому уравнение изохорного процесса называется законом Шарля.
92. Основы МКТ. 9.10
Изобарным процессом называют квазистатический процесс,протекающий при неизменным давлении p. Уравнение изобарного
процесса для некоторого неизменного количества вещества ν имеет
вид:
V
const
T
На плоскости (V, T) изобарные
процессы при разных значениях
давления p изображаются семейством
прямых линий, которые называются
изобарами.
Зависимость объема газа от температуры при неизменном давлении
была экспериментально исследована французским физиком Ж. ГейЛюссаком (1862 г.). Поэтому уравнение изобарного процесса
называют законом Гей-Люссака.
93. Лекция 10 Связь кинетической энергии молекул газа с температурой и давлением. Равнораспределение энергии по степеням свободы.
Числостепеней свободы и средняя энергия многоатомной молекулы.
Молекулярно-кинетическая теория (МКТ) устанавливает связи между
макро- и микропараметрами идеального газа. Основное уравнение
МКТ выражает связь давления газа со средней кинетической
энергией поступательного движения молекул. Давление газа на
стенки сосуда является результатом многочисленных ударов
молекул. При каждом ударе стенка получает силовой импульс,
величина которого зависит от скорости молекул и, следовательно, от
энергии их движения. При огромном числе ударов создается
постоянное давление газа на стенку. Число ударов зависит от
концентрации молекул n. Таким образом, можно ожидать, что
давление газа связано с концентрацией молекул и с энергией их
движения.
Для нахождения этой связи введем некоторые
упрощения:
1) все молекулы движутся по взаимно
перпендикулярным направлениям;
2) скорости всех молекул одинаковы.
94. Основы МКТ. 10.2
При ударе о стенку сосуда молекула сообщает ей импульс, численноравный изменению импульса молекулы. Каждый элемент поверхности
dS непрерывно подвергается бомбардировке большим количеством
молекул, в результате чего за время dt получает суммарный импульс
dp направленный по нормали к dS. Отношение dр к dt дает, как
известно из второго закона Ньютона, силу, действующую на dS, а
отношение этой силы к dS дает давление Р.
До удара о стенку импульс молекулы
направлен по внешней нормали к dS и равен
mv. В результате удара импульс меняет знак.
Таким образом, приращение импульса
молекулы оказывается равным:
( mv) (mv) 2mv
95. Основы МКТ. 10.3
По третьему закону Ньютона стенка получает при ударе импульс 2mv,имеющий направление нормали. За время dt до элемента стенки dS
долетят все движущиеся по направлению к нему молекулы,
заключенные в объеме цилиндра с основанием dS и высотой vdt.
Число этих молекул равно:
N
1
nvdSdt
6
где n – число молекул в единице объема.
Таким образом, число ударов о единицу
поверхности за единицу времени будет равно:
N 1
nv
dtdS 6
96. Основы МКТ. 10.4
Умножив число ударов на импульс, сообщаемый стенке при каждомударе, получим суммарный импульс dp, сообщаемый элементу стенки
dS за время dt:
1
1
p 2mv nvdSdt nmv 2dSdt.
6
3
Отнеся импульс dp к промежутку времени dt, получим силу, действующую
на dS. Наконец, отнеся полученную силу к площадке dS, получим
давление газа, оказываемое им на стенки сосуда. Следовательно
P
dp
1
nmv 2 .
dSdt 3
mv 2
представляет собой кинетическую энергию
Учитывая, что Е к =
2
поступательного движения молекулы, выражению для давления можно
придать следующий вид:
2
P= nE к
3
Основное уравнение МКТ
97. Основы МКТ. 10.5
Отказ о предположении, о равенстве всех скоростей приводит к тому,что необходимо учитывать среднюю квадратичную скорость молекул
газа или среднюю кинетическую энергию.
Давление равно двум третям кинетической энергии поступательного
движении молекул, заключенных в единице объема.
Из полученного закона следует, что давление пропорционально средней
кинетической энергии поступательного движение молекул. Вместе с
тем оно пропорционально температуре газа. Следовательно, средняя
кинетическая энергия пропорциональна температуре газа.
2
PV= nE к V,
3
m
PV= RT
Первое соотношение получается из основного уравнение МКТ
умножением на V, второе это уравнение состояния идеального газа.
Приравняв правые части получим:
98. Основы МКТ. 10.6
2m
nE к V RT
3
Принимая во внимание, что
n=
N
m
, N= Na
V
получим:
2m
m
NaE к RT
3
3 R
Eк =
T
2 Na
Введя обозначение
k=
R
Дж
1.38 10 23
Na
К
окончательно получим:
постоянная Больцмана,
3
Е к = kT
2
99. Основы МКТ. 10.7
Получается, что кинетическая энергия зависит только от температуры ине зависит от массы молекулы. Заменив в уравнении состояния
идеального газа R на Nak и учитывая, что n/V равно концентрации n,
получим:
P=nkT
Для смеси газов справедлив закон Дальтона:
давление смеси идеальных газов равно сумме парциальных давлений
входящих в нее газов:
Р Рк
к
где k – номер газовой компоненты в смеси, Pk – ее парциальное
давление, т.е. то давление, которое имел бы k–ый газ, если бы только он
один занимал весь объём, занимаемый смесью.
100. Основы МКТ. 10.8
Очевидно, что число координат в трехмерномпространстве, а следовательно и число
степеней свободы одноатомного газа,
равно трем. Газ может быть двухатомным,
трёхатомным и т. д. Для молекул таких
газов характерно наличие внутренней
структуры и, соответственно,
дополнительных степеней свободы. Если
атомы в молекуле жестко связаны между
собой, в качестве дополнительных
степеней свободы выступают
вращательные степени, характеризующие
угловое положение молекулы в
пространстве.
101. Основы МКТ. 10.9
В одноатомном газе молекула имеет три степени свободы,соответствующие трем пространственным координатам. Вследствие
равноправности этих координат, можно, на основании связи
кинетической энергии с температурой, сделать предположение, что на
каждую степень свободы молекулы одноатомного газа приходится в
среднем кинетическая энергия, равная
1
kT
2
В случае многоатомного газа распределение энергии по степеням
свободы его молекул подчиняется закону равнораспределения энергии
по степеням свободы, который гласит:
Средняя кинетическая энергия, приходящаяся при тепловом равновесии
на одну степень свободы молекулы равна
1
kT
2
102. Основы МКТ. 10.10
Таким образом, средняя энергия молекулы должна равняться:i
Е= kT
2
где i – сумма числа поступательных, числа вращательных и удвоенного
числа колебательных степеней свободы молекулы:
i=nпост + nвращ + 2nколеб
Для молекулы с жесткой связью между атомами i совпадает с числом
степеней молекулы.
103. Лекция 11 Внутренняя энергия термодинамической системы. Теплоемкость. Работа, совершаемая газом при изменении объема
Полная энергия термодинамической системы представляет собой суммукинетической энергии движения всех тел, входящих в систему,
потенциальной энергии взаимодействия их между собой и с внешними
телами и энергии, содержащейся внутри тел системы. Если из полной
энергии вычесть кинетическую энергию, характеризующую
макроскопическое движение системы как целого, и потенциальную
энергию взаимодействия её тел с внешними макроскопическими
телами, то оставшаяся часть будет представлять собой внутреннюю
энергию термодинамической системы.
Внутренняя энергия термодинамической системы включает в себя
энергию микроскопического движения и взаимодействия частиц
системы, а так же их внутримолекулярную и внутриядерную энергии.
Вследствие того, что молекулы идеального газа на расстоянии не
взаимодействуют друг с другом внутренняя энергия такого газа будет
складываться из энергий отдельных молекул. Следовательно,
внутренняя энергия произвольной массы идеального газа m будет
равна произведению числа молекул в данной массе газа на энергию
одной молекулы
104. Термодинамика. 11.2
Um
i
mi
Na kT=
RT
2
2
Как показывают результаты экспериментов, во многих случаях
приращение температуры тела прямо пропорционально количеству
теплоты, сообщенного ему. Для количественного описания этого
соотношения вводится
коэффициент пропорциональности Стела между количеством теплоты,
сообщаемого телу, и изменением его температуры, называемый
теплоемкостью:
dQ
C тела =
dT
Этот коэффициент позволяет определить количество теплоты dQ’,
которое необходимо сообщить телу для повышения его температуры на
величину dT.
105. Термодинамика. 11.3
Очевидно, что теплоемкость термодинамической системы изменяетсяпри изменении количества вещества в ней. Для систем, находящихся
в состоянии термодинамического равновесия, их теплоемкость
пропорциональна количеству вещества. Это позволяет ввести для
описания свойств тела удельную теплоемкость:
c
Cтела
m
и, соответственно, молярную теплоемкость:
C
Cтела
Эти теплоемкости связаны между собой через молярную массу μ
следующим соотношением:
c
C
106. Термодинамика. 11.4
Теплоемкость, так же как и количество переданной телу теплоты,зависит от того, каким образом, а точнее при осуществлении какого
процесса, теплота передавалась этому телу. Обычно рассматриваются
два значения теплоемкости газов: CV – молярная теплоемкость в
изохорном процессе (V = const) и Cp – молярная теплоемкость в
изобарном процессе (p = const).
Если нагревание происходит при постоянном объеме, тело не совершает
работы над внешними телами и, следовательно, все тепло идет на
приращение внутренней энергии тела:
dQV dU
Отсюда следует, что теплоемкость любого тела при постоянном объеме
равна:
dU
CV
dT
107. Термодинамика. 11.5
Следовательно, чтобы получить теплоемкость моля идеального газа припостоянном объеме, нужно продифференцировать по температуре
выражение для моля внутренней энергии идеального газа.
U=
mi
i
RT= RT
2
2
Произведя дифференцирование, получим:
CV
i
R
2
При изменении объема газа им совершается работа и, соответственно,
подведенная теплота и изменение внутренней энергии становятся не
равными друг другу. При расширении газа часть подведенной теплоты
затрачивается на совершение им работы. Для процесса при постоянном
давлении первый закон термодинамики дает:
QP U P V CV T P V
108. Термодинамика. 11.6
Отсюда следует:CP
QP
V
CV P
T
T
Отношение ΔV / ΔT может быть найдено из уравнения состояния
идеального газа, записанного для 1 моля:
PV RT
При Р = const
V R
P V R T ,
T P
Таким образом, соотношение, выражающее связь между молярными
теплоемкостями CР и CV, имеет вид (формула Майера):
CP CV R
109. Термодинамика. 11.7
Молярная теплоемкость CР газа в процессе с постоянным давлениемвсегда больше молярной теплоемкости CV в процессе с постоянным
объемом. Из этой теоремы следует, что молярные теплоемкости газа
CР и CV и их отношение γ могут быть записаны в виде
CP i+2
i
i+2
CV R, C P CV R
R, =
2
2
CV
i
Существует зависимость количества
учитываемых при расчете степеней
свободы от температуры. Это
приводит к тому, что при
значительных изменениях
температуры теплоемкость газа
может существенно изменяться.
110. Термодинамика. 11.8
Например, для молекул водорода, при температуре порядка 50 Квращательные степени свободы как бы "вымерзают" и его молярная
3
теплоёмкость CV становится близкой к R . А при температурах
2
порядка 300 - 400 К вращательные степени свободы "включаются" и
его теплоёмкость CV приобретает значение 5 R . При дальнейшем,
2
значительном по сравнению с комнатной, повышении
температуры
начинают проявляться колебательные степени свободы. Для
двухатомного газа, например водорода, это приводит к увеличению
энергии его молекулы на величину kT, и соответственно к
возрастанию молярной теплоемкости на R. Поэтому при очень
высоких температурах молярная теплоёмкость водорода стремится к
значению 7 R .
2
111. Термодинамика. 11.9
Пусть газ заключен в цилиндрический сосуд, закрытый плотнопригнанным легко скользящим поршнем. Если вследствие каких-либо
причин газ станет расширяться, он будет перемещать поршень и
совершать над ним работу. Элементарная работа, совершаемая газом
при перемещении поршня на отрезок dh, равна
dA=fdh,
где f – сила, с которой газ действует на поршень.
Заменяя эту силу произведением давления газа P
на площадь поршня S, получаем:
dA=PSdh
Но Sdh представляет собой приращение объема
газа dV. Поэтому выражение для элементарной
работы можно записать следующим образом:
dA=PdV
112. Термодинамика. 11.10
При сжатии газа направления перемещения dh и силы f, с которой газдействует на поршень, противоположны, вследствие чего
элементарная работа dA будет отрицательна. Приращение объема dV
в этом случае также будет отрицательным. Если при изменении
объема давление не остается постоянным, работа должна вычисляться
путем интегрирования:
V2
A12 PdV
V1
Если давление газа остается постоянным,
работа, совершаемая при изменении
объема от значения V1 до значения V2,
будет равна
A12 =P(V2 -V1 )
113. Лекция 12 Распределение молекул газа по скоростям. Функция распределения Максвелла. Наиболее вероятная, средняя и средне
квадратичныескорости молекул.
В сосуде, содержащем большое число молекул, устанавливается
некоторое статистическое распределение молекул по скоростям,
зависящее от абсолютной температуры T. При этом все направления
векторов скоростей молекул оказываются равноправными
(равновероятными), а величины скоростей подчиняются определенной
закономерности. Распределение молекул газа по величине скоростей
называется распределением Максвелла.
Представим себе пространство скоростей
с прямоугольными координатными осями,
по которой будем откладывать значения
проекций vx, vy, vz отдельных молекул.
Тогда скорости каждой молекулы будет
соответствовать точка в этом
пространстве – конец вектора v.
114. Распределение Максвелла. 12.2
Плотность точек может зависеть только от модуля скорости v.Предположим, что в газе содержится N молекул. Выделим в
окрестности некоторой точки малый объем – dvxdvydvz. Относительное
число точек (молекул) в этом объеме, или другими словами,
вероятность dP того, что скорость молекулы, т.е. конец вектора v,
попадает в этот объем, можно записать так:
dP(v x ,v y ,v z )
dN(v x ,v y ,vz )
f(v)dv x dv y dv z
N
где f(v) – имеет смысл объемной плотности вероятности. Вероятности того,
что молекула имеет проекции скорости в интервалах (vx,vx+dvx), (vy,vy+dvy)
и (vz,vz+dvz) являются статистически независимыми, поэтому в
соответствии с теоремой об умножении вероятностей независимых
событий можно записать:
dP(v x ,v y ,v z )=dP(v x )dP(v y )dP(v z )
115. Распределение Максвелла. 12.3
где dРх – вероятность того, что молекула будет иметь проекции скоростив интервале (vx,vx+dvx), есть
dP(v x )=
dN(v x )
(v x )dv x
N
где φ(vx) – функция распределения по vx. С учетом, полученного
соотношения, вероятности того, что молекула имеет проекции
скорости в интервалах (vx,vx+dvx), (vy,vy+dvy) и (vz,vz+dvz) будет иметь
вид:
dP(v x ,v y ,v z )=dP(v x )dP(v y )dP(v z )= (v x ) (v y ) (v z )dv x dv ydvz
Из соображений равноправия осей vx, vy и vz ясно, что функции φ должны
одинаковым образом зависеть от соответствующих проекций скоростей.
Таким образом, функция объемной плотности вероятности может быть
представлена следующим образом:
f(v) (v x ) (v y ) (v z )
116. Распределение Максвелла. 12.4
В результате теоретических расчетов был получен аналитический видфункции распределения молекул газа по проекции скорости:
mv 2x
m
(v x )
exp
2
kT
2kT
12
Функция φ(vх) нормирована на единицу, т.е. площадь по кривой φ(vх)
(v ) dv
х
x
1
117. Распределение Максвелла. 12.5
Интегрирование в пределах от до не означает, что в газе есть молекулыс такими большими скоростями. Молекул с весьма большими
скоростями очень мало, и они практически не вносят никакого вклада в
нормировочный интеграл. Это и позволяет записывать такие пределы.
Аналогичный вид имеют функции φ(vy) и φ(vz). Тогда f(v) будет иметь
вид:
32
m(v 2x v 2y v 2z ) m 3 2
mv 2
m
f (v)
exp
exp
2
kT
2kT
2
kT
2kT
Довольно часто возникает вопрос сколько
(какая относительная часть) молекул газа
имеют скорость модуль в пределах от (v,
v+dv). Таким молекулам соответствуют все
точки, попадающие в шаровой слой с
радиусами v и v+dv .
118. Распределение Максвелла. 12.6
Объем этого слоя равен произведению этого слоя на его толщину, т.е.4πv2dv, объемная плотность вероятности f(v) во всех точках слоя
одинакова. Следовательно, согласно теореме сложения вероятностей,
попадания в этот слой:
dP=f(v) 4 v2dv
Величина dP/dv – характеризует вероятность молекуле иметь скорость
32
в пределах от (v, v+dv):
mv 2
m
2
F(v) 4
v exp
2
kT
2kT
Данное соотношение представляет собой закон распределения Максвелла
по модулю скорости. Эта функция тоже нормирована на единицу
F(v) dv 1
0
119. Распределение Максвелла. 12.7
Как и можно было ожидать, конкретный вид функции зависит от родагаза ( от массы молекул) и от параметра состояния (от температуры
Т). Необходим отметить, что давление и объем газа на распределение
молекул по скоростям не влияют.
Скорость, отвечающая максимальному
значению функции распределения, будет,
очевидно, наиболее вероятной.
Действительно, если сравнить числа молекул
ΔNv, скорости которых лежат в пределах
различным образом выбранных, но равных по
величине интервалов Δv, то наибольшим
будет ΔNv, соответствующее интервалу,
расположенному в окрестности максимума.
Таким образом, найдя максимум функции
распределения F(v), найдем наиболее
вероятную скорость vвер.
120. Распределение Максвелла. 12.8
Продифференцировав F(v) по v и приравняв полученное выражениенулю, будем иметь:
mv2
2
dF(v)
mv
2kT
Ae v 2 0
dv
kT
Удовлетворяющие этому уравнению значения v=0 и v= соответствуют
минимуму F(v). Значение v, обращающее в нуль выражение, стоящее в
скобках, представляет собой vвер:
vвер
2kT
m
Также можно найти, зная распределение молекул по скоростям,
среднее значение скорости, и v2.
vср vF(v)dv
0
8kT
m
vср.кв (v2 )ср
3kT
m
121. Распределение Максвелла. 12.9
Сопоставляя значения vвер, vср и vср.кв, можно заметить, что ониодинаковым образом зависят от температуры и массы молекулы. Если
принять vвер=1, vср=1.13 и vср.кв=1.22. Необходимо подчеркнуть, что
закон распределения молекул газа по скоростям и все вытекающие из
него следствия справедливы только для газа, находящегося в
равновесном состоянии.
Относительное количество
молекул, скорость которых
превышает некоторое
значение v0, определяется
выражением:
F (v)dv
v0
122. Распределение Максвелла. 12.10
Относительное число молекул, скорость которых превышает некотороезначение v0, сильно растет с температурой. В таблице приведены
относительные количества молекул скорости которых лежат в
определенных интервалов относительно наиболее вероятной
ΔN
скорости.
v
ΔN
v
,%
v вер
N
v вер
N
,%
0 – 0.5
8.1
2–3
4.6
0.5 – 1.5
70.7
>3
0.04
1.5 – 2
16.6
>5
8 10-9
Как видно из таблицы, более чем у 70% всех молекул скорость
отличается от наиболее вероятной не больше чем на 50%.
Скоростью, более чем в 3 раза превышающей vвер, обладает в
среднем только 0.04% молекул.
123. Лекция 13 Опыты Штерна и Ламмерта. Идеальный газ в поле силы тяжести, барометрическая формула. Распределения Больцмана.
Первое экспериментальное определение скоростей молекул былопроведено Штерном в1920 г. Прибор, использованный для этой
цели, состоял из двух коаксиальных цилиндров. По оси
цилиндров была натянута платиновая нить, покрытая серебром.
При нагревании нити электрическим током с ее поверхности
испарялись атомы серебра.
Покинув нить, атомы двигались по радиальным
направлениям. Внутренний цилиндр имел узкую
продольную щель, через которую проходил
наружу узкий пучок атомов. Весь прибор был
помещен в вакуум, за счет этого удавалось
избавиться от рассеивания
молекулярного(атомного) пучка.
Если привести прибор во вращение то произойдет размытие
полоски в результате того, что атомы обладают различными
скоростями, вследствие чего будут преодолевать расстояние
между цилиндрами за различное время.
124. Распределение Больцмана. 13.2
Смещение относительно первоначального положение равноΔs = RΔφ
R – радиус внешнего цилиндра.
Δφ – угол на который повернутся цилиндры.
В свою очередь Δφ связано с угловой скоростью относительного
вращения цилиндров
Δφ=ωt,
где t – время за которое атом серебра пролетает зазор между
цилиндрами.
t =R/v.
Радиус внутреннего цилиндра мал. Окончательно получаем:
R 2
v
s
Измерив, смещение следа Δs и скорость вращения цилиндров, можно
определить скорость атомов v. Исследование профиля следа позволяет
составить примерное представление о распределении атомов серебра по
скоростям. Результаты опыта Штерна подтвердили правильность оценки
средней скорости атомов, которая вытекает из распределения Максвелла.
125. Распределение Больцмана. 13.3
В опыте Ламмерта (1929 г.) закон распределения был проверен болееточно. Молекулярный пучок, выходящий из отверстия в сосуде, в
котором находится газ в равновесном состоянии, проходил сквозь два
вращающихся на одной оси диска. В дисках были щели вдоль
радиусов. Если щели повернуты на угол φ относительно друг друга, то
при угловой скорости ω диски повернутся на угол φ в течении
промежутка времени t=φ/ω.
Поэтому через обе щели
расстояние между которыми l,
пройдут только молекулы со
скоростью:
l
v
Меняя угловую скорость ω или угол φ между радиальными
щелями, можно выделить из пучка молекулы разных
скоростей. Улавливая детектором эти молекулы в течение
одинакового времени, можно найти их относительной
количество в пучке.
126. Распределение Больцмана. 13.4
В отсутствии внешних сил концентрация молекул газа в состояниитермодинамического равновесия всюду одинакова. Если же газ
находится во внешнем поле сил, например в поле силы тяжести, то
ситуация становится иной. При отсутствии теплового движение все
молекулы “упали” бы на поверхность Земли. Наличие же теплового
движения мешает этому. В результате совместного действия этих двух
факторов устанавливается равновесия, и концентрация молекул
становится зависящей от высоты. При тепловом равновесии
температура Т должна быть одинакова по всей толщине газа, иначе бы
возникли потоки тепла, и состояние газа не было бы равновесным, т.е.
будет рассматриваться изотермическая атмосфера.
127. Распределение Больцмана. 13.5
Атмосферное давление на какой-либо высоте hобусловлено весом вышележащих слоев газа.
Пусть Р давление газа на высоте h. Тогда
давление на высоте h+dh, будет P+dP,
причем, если dh больше нуля, то dP будет
меньше нуля, так как вес вышележащих
слоев атмосферы, а следовательно, и
давление с высотой убывают. Разность
давлений P и P+dP равна весу газа,
заключенного в объеме цилиндра с
площадью основания, равной единице, и
высотой dh:
P-(P+dP) gdh
где ρ – плотность газа на высоте h. Отсюда:
dP gdh
128. Распределение Больцмана. 13.6
Плотность газа можно выразить, через давление и температуру,используя уравнение состояния. Так как при условиях близких к
нормальным, атмосферные газы можно рассматривать как идеальные.
m P
V RT
Подставив это выражение в dP, получим:
P g
dP
gdh
RT
откуда,
dP
g
gdh
P
RT
Для случая, когда
соотношения дает:
температура
ln P
постоянна,
gh
RT
ln C
интегрирование
этого
129. Распределение Больцмана. 13.7
где С – постоянная. Произведя потенцирование этого выражения,получаем:
gh
P Ce
RT
Значение постоянной С, находим из того условия, что давление при h=0
нам известно и равно P0. Подставив h=0, получим Р0=С. Таким образом в
случае изотермической атмосферы зависимость давления от высоты
выражается формулой:
gh
P P0e
RT
Эта формула называется
барометрической. Из анализа этого
соотношения следует, что давление с
высотой убывает тем быстрее, чем
тяжелее газ и чем ниже температура.
130. Распределение Больцмана. 13.8
Заменив в барометрической формуле P через nkT, получим законизменения концентрации газа с высотой:
n=n 0 e
gh
RT
где n0 – концентрация газа на высоте равной нулю. Полученное
соотношение можно преобразовать, заменив μ/R равным ему отношением
m/k, где m – масса одной молекулы, k – постоянная Больцмана
n=n 0 e
mgh
kT
Из этого выражение следует, что с уменьшением температуры
концентрация газа на высотах отличных от нуля, убывает, обращаясь в
нуль при Т=0. При абсолютном нуле все молекулы воздуха расположились
бы на земной поверхности. При больших температурах наоборот
концентрация слабо уменьшается с высотой. Данный факт имеет простое
физическое объяснение. Действительно распределение молекул газа
получается в результате действия двух “конкурирующих” тенденций
131. Распределение Больцмана. 13.9
1) притяжение молекул газа к земле под действием силы тяжести2) тепловое движение, стремящееся распределить молекулы равномерно
по всем высотам.
На разной высоте молекула обладает разной потенциальной энергией:
E П =mgh
Следовательно, распределение молекул газа по высоте, является в то же
время распределение их по значениям потенциальной энергии. Таким
Е
образом, получим:
П
n=n 0 e
kT
Данное выражение называется распределением Больцмана. Из этого
соотношения следует, что молекулы располагаются с большей
концентрацией (плотностью) там, где их потенциальная энергия меньше,
и, наоборот, с меньшей плотностью в местах, где их потенциальная
энергия больше.
132. Распределение Больцмана. 13.10
Закон Максвелла дает распределение частиц по кинетической энергии(из распределения по v2, просто получить распределение по
кинетической энергии), распределение Больцмана зависимость от
потенциальной энергии. Эти распределения можно объединить в
один закон Максвелла-Больцмана, согласно которому содержащееся
в единице объема количество молекул, скорость которых лежит
между v и v+dv, равно:
dn ЕП ,v
m
n 0 4
2 kT
32
e
mv2
2
kT
ЕП +
2
v dv
e
E
kT
v 2dv
где n0 – число молекул в единице объема в той точке, в которой ЕП=0, а
полная энергия молекулы Е. Интегрирование этого выражения в пределах от
0 до приводит к распределению Больцмана
133. Лекция 14 Основы термодинамики. Работа газа при различных процессах. Адиабатический процесс. Круговой процесс. Тепловые
двигатели, ихКПД Цикл Карно. КПД цикла Карно.
Термодинамическая система может разными способами обмениваться
энергией с окружающей средой, поглощая или отдавая количество
теплоты и совершая работу.
Количество теплоты, поступающее в систему, считается положительным
(Q > 0).
Если система отдает количество теплоты окружающей среде, то Q < 0.
Если система совершает работу, то эта работа принимается положительной
(А > 0).
Если работа совершается внешними
источниками над системой, то A < 0.
Работа, совершаемая системой при
переходе 1 в 2, зависит от пути, т.е. от
конкретных деталей процесса, при этом
совершаемая работа будет разной. Точно
так же будут разными количества теплоты,
поступающие в систему или отдаваемые
системой при таком переходе
134. Основы термодинамики. 14.2
Многочисленные эксперименты показывают, что разность Q - A не зависитот характера протекания процесса и определяется только начальным и
конечным состояниями системы. Так как эти состояния обладают
определенной внутренней энергией U, которая для идеального газа
зависит только от температуры газа, то на основании закона
сохранения энергии, обобщенного на случай тепловых явлений, можно
записать:
Q - A = dU = U2 - U1.
В тепловом процессе, в котором количество теплоты Q поступает в
систему и сама система совершает работу A, полная энергия,
переданная системе, равна изменению внутренней энергии системы
dU. – Первое начало термодинамики
Если на РV-диаграмме отмечены две точки (два состояния) и с
помощью любой комбинации тепловых процессов осуществлен
переход из состояния 1 в состояние 2, то можно утверждать, что
внутренняя энергия системы изменилась на величину U2 - U1.
135. Основы термодинамики. 14.3
Для любого замкнутого цикла, в результате которого системавозвращается в исходное состояние, изменение внутренней энергии
равно нулю.
Но это не означает, что в замкнутом цикле не совершается работа или не
поглощается (выделяется) количество теплоты.
В формуле, выражающей содержание первого закона, знаки A и Q могут
быть разными в зависимости от характера процесса. Соответственно dU
может быть как положительной, так и отрицательной величиной.
136. Основы термодинамики. 14.4
Другая формулировка первого закона (начала) термодинамики:количество тепла, сообщенное системе идет на приращение внутренней
энергии системы и на совершение системой работы над внешними
телами:
Q U+A
В изохорном процессе (V = const) газ работы не совершает, A = 0.
Следовательно, Q = ΔU . Внутренняя энергия идеального газа зависит
только от температуры. При изохорном нагревании тепло поглощается
газом (Q > 0), и его внутренняя энергия
увеличивается. При охлаждении тепло
отдается внешним телам (Q < 0).
137. Основы термодинамики. 14.5
В изобарном процессе (Р = const) работа, совершаемая газом, выражаетсясоотношением
A = Р(V2 – V1) = РΔV.
Первый закон термодинамики для изобарного процесса
дает:
Q = U(T2) – U(T1) + Р(V2 – V1) = ΔU + РΔV
При изобарном расширении Q > 0 – тепло
поглощается газом, и газ совершает
положительную работу. При изобарном
сжатии Q < 0 – тепло отдается внешним
телам. В этом случае A < 0. Температура
газа при изобарном сжатии уменьшается,
T2 < T1; внутренняя энергия убывает,
ΔU < 0.
138. Основы термодинамики. 14.6
В изотермическом процессе температура газа не изменяется,следовательно, не изменяется и внутренняя энергия газа, ΔU = 0.
Первый закон термодинамики для изотермического процесса
выражается соотношением
Q = A.
Количество теплоты Q, полученной газом
в процессе изотермического расширения,
превращается в работу над внешними
телами. При изотермическом сжатии
работа внешних сил, произведенная над
газом, превращается в тепло, которое
передается окружающим телам.
139. Основы термодинамики. 14.7
Наряду с изохорным, изобарным и изотермическимпроцессами в термодинамике часто
рассматриваются процессы, протекающие в
отсутствие теплообмена с окружающими телами.
Сосуды с теплонепроницаемыми стенками
называются адиабатическими оболочками, а
процессы расширения или сжатия газа в
таких сосудах называются адиабатическими. В адиабатическом процессе Q = 0;
поэтому первый закон термодинамики принимает вид:
A = –ΔU
При адиабатическом расширении газ совершает положительную работу
(A > 0); поэтому его внутренняя энергия уменьшается (ΔU < 0). Это
приводит к понижению температуры газа. Вследствие этого давление газа
при адиабатическом расширении убывает быстрее, чем при
изотермическом расширении.
140. Основы термодинамики. 14.8
В термодинамике выводится уравнениеадиабатического процесса для идеального газа.
В координатах (p, V) это уравнение имеет вид
РVγ = const
Это соотношение называют уравнением Пуассона. Здесь γ = Cp / CV –
показатель адиабаты, Cp и CV – теплоемкости газа в процессах с
постоянным давлением и с постоянным объемом. Работа газа в
адиабатическом процессе просто выражается через температуры T1 и T2
начального и конечного состояний:
A = CV(T2 – T1).
Второе начало термодинамики, как и первое, может быть сформулировано
несколькими способами. В наиболее очевидной формулировке второе
начало гласит, что невозможен самопроизвольный переход тепла от тела
менее нагретого, к телу, более нагретому. Более строго, невозможны
такие процессы, единственным конечным результатом которых был бы
переход тепла от тела, менее нагретого, к телу более нагретому.
141. Основы термодинамики. 14.9
Общее свойство всех круговых процессов состоит в том, что ихневозможно провести, приводя рабочее тело в тепловой контакт только
с одним тепловым резервуаром. Их нужно, по крайней мере, два.
Тепловой резервуар с более высокой температурой называют
нагревателем, а с более низкой – холодильником. Совершая круговой
процесс, рабочее тело получает от нагревателя некоторое количество
теплоты Q1 > 0 и отдает холодильнику количество теплоты Q2 < 0.
Полное количество теплоты Q, полученное рабочим телом за цикл,
равно:
Q = Q + Q = Q – |Q |.
1
2
1
2
При обходе цикла рабочее тело возвращается в
первоначальное состояние, следовательно,
изменение его внутренней энергии равно нулю
(ΔU = 0). Согласно первому закону термодинамики,
ΔU = Q – A = 0
Отсюда следует:
A = Q = Q1 – |Q2|.
142. Основы термодинамики. 14.10
Работа A, совершаемая рабочим телом за цикл, равна полученному зацикл количеству теплоты Q. Отношение работы A к количеству
теплоты Q1, полученному рабочим телом за цикл от нагревателя,
называется коэффициентом полезного действия η тепловой машины
A Q1 -|Q 2 |
Q1
Q1
В 1824 году французский инженер
С. Карно рассмотрел круговой процесс,
состоящий из двух изотерм и двух
адиабат. Этот круговой процесс сыграл
важную роль в развитии учения о
тепловых процессах. Он называется
циклом Карно.
143. Основы термодинамики. 14.11
При изотермическом процессе внутренняя энергия идеального газаостается постоянной. Поэтому количество полученного газом тепла Q1
равно работе А12, совершаемой газом при переходе из состояния 1 в
состояние 2 (изотермический процесс при большей температуре). Эта
работа равна:
V
m
Q1 =A12 RT1 ln 2
V1
Количество отдаваемого холодильнику тепла Q2’ равно работе А34’,
затрачиваемой на сжатие газа при переводе его из состояния 3 в
состояние 4. Эта работа равна
V
m
'
Q'2 =A 34
RT2 ln 3
V4
Для того чтобы цикл был замкнутым, нужно, чтобы состояния 4 и 1
лежали на одной и той же адиабате. Отсюда вытекает условие:
T1V1 1 T2 V4 1
144. Основы термодинамики. 14.12
Аналогично, поскольку состояния 2 и 3 лежат на одной и той же адиабате,выполняется условие:
1
1
T1V2
T2 V3
Деля последние два соотношения друг на друга, приходим к условию
замкнутости цикла:
V2 V3
=
V1 V4
Подставив в определение КПД полученные нами выражения для Q1 и Q2’
получим.
V
V m
m
RT1 ln 2 RT2 ln 3
V1
V4
V
m
RT1 ln 2
V1
T1 -T2
T1
145. Лекция 15 Электрические заряды. Точечный заряд. Закон Кулона. Напряженность электрического поля. Принцип суперпозиции
электрических полей.Известно, что при определенных условиях тела приобретают
электрический заряд – электризуются. Наличие электрического заряда
проявляется в том, что заряженное тело взаимодействует с другими
заряженными телами. Электрический заряд является неотъемлемым
свойством некоторых элементарных частиц. Заряд всех элементарных
частиц одинаков по абсолютной величине (если он не равен нулю).
Обозначается он е.
Поскольку всякий заряд q образуется совокупностью элементарных
зарядов, он является целым кратным
e = 1,602177·10–19 Кл ≈ 1,6·10–19 Кл.:
q Ne
Совокупность всех известных экспериментальных фактов позволяет
сделать следующие выводы о свойствах зарядов:
146. Электростатика. 15.2
1) Существует два рода электрических зарядов, условно названныхположительными и отрицательными.
2) Заряды могут передаваться (например, при непосредственном
контакте) от одного тела к другому. В отличие от массы тела
электрический заряд не является неотъемлемой характеристикой
данного тела. Одно и то же тело в разных условиях может иметь
разный заряд.
3) Одноименные заряды отталкиваются, разноименные –
притягиваются.
Одним из фундаментальных законов природы является экспериментально
установленный закон сохранения электрического заряда
В изолированной системе алгебраическая сумма зарядов всех тел остается
постоянной:
q1 + q2 + q3 + ... +qn = const
Закон сохранения электрического заряда утверждает, что в замкнутой
системе тел не могут наблюдаться процессы рождения или исчезновения
зарядов только одного знака.
147. Электростатика. 15.3
Точечным зарядом называют заряженное тело,размерами которого в условиях данной задачи
можно пренебречь.
Впервые закон взаимодействия неподвижных
зарядов был установлен французским физиком
Ш. Кулоном (1785 г.). С помощью крутильных
весов Кулон измерял силу взаимодействия двух
заряженных шариков в зависимости от
величины зарядов на них и от расстояния между
ними. При этом Кулон исходил из того, что при
касании заряженного металлического шарика с
точно таким же, но не заряженным заряд между
ними распределится поровну.
148. Электростатика. 15.4
В результате своих опытов Кулон пришел к выводу, чтосила взаимодействия двух точечных зарядов пропорциональна
величине каждого из зарядов и обратно пропорциональна квадрату
расстояния между ними. Направление силы совпадает с проходящей
через заряды прямой. Закон кулона может быть выражен следующей
формулой
q1q2
F=k
r2
В случае одноименных зарядов, сила оказывается положительной (что
соответствует отталкиванию между зарядами). В случае разноименных
зарядов сила отрицательна (что соответствует притяжению зарядов друг к
другу). Закон Кулона можно записать в векторном виде:
qq r
F k 12 2
r
r
149. Электростатика. 15.5
По современным представлениям, электрические заряды не действуютдруг на друга непосредственно. Каждое заряженное тело создает в
окружающем пространстве электрическое поле. Это поле оказывает
силовое действие на другие заряженные тела. Главное свойство
электрического поля – действие на электрические заряды с некоторой
силой.
Для количественного определения электрического поля вводится силовая
характеристика – напряженность электрического поля.
Напряженностью электрического поля называют физическую величину,
равную отношению силы, с которой поле действует на положительный
пробный заряд, помещенный в данную точку пространства, к величине
этого заряда
F
E
q
Напряженность электрического поля – векторная физическая величина.
Направление вектора E совпадает в каждой точке пространства с
направлением силы, действующей на положительный пробный заряд.
150. Электростатика. 15.6
Как следует из закона Кулона и определения напряженности,напряженность точечного заряда пропорциональна величине заряда q
и обратно пропорциональна квадрату расстояния r от заряда до
данной точки поля:
q r
1 q r
E k
r2 r
4 0 r 2 r
Направлен вектор Е вдоль радиальной прямой, проходящей через заряд и
данную точку поля, от заряда, если он положителен, и к заряду, если он
отрицателен.
151. Электростатика. 15.7
Если с помощью пробного заряда исследуется электрическое поле,создаваемое несколькими заряженными телами, то результирующая
сила оказывается равной геометрической сумме сил, действующих на
пробный заряд со стороны каждого заряженного тела в отдельности.
Следовательно, напряженность электрического поля, создаваемого
системой зарядов в данной точке пространства, равна векторной
сумме напряженностей электрических полей, создаваемых в той же
точке зарядами в отдельности:
E E1 E2 ....
E Ei
Это свойство электрического поля означает, что
поле подчиняется принципу суперпозиции.
152. Электростатика. 15.8
Для упрощения математических расчетов во многих случаях бываетудобно игнорировать тот факт, что заряды имеют дискретную
структуру, и считать, что они “размазаны” определенным образом в
пространстве. Другими словами удобно заменить истинное дискретное
распределении зарядов фиктивным непрерывным распределением.
Такой подход позволяет существенно упростить расчеты, не внося в
тоже время значительных ошибок. При переходе к непрерывному
распределению, вводят понятие о плотности зарядов (линейной λ,
поверхностной σ или объемной ρ):
dq
dq
dq
,
, =
dV
dS
dl
С учетом эти распределений принцип суперпозиции может быть
представлен в другой форме:
E
1
4 0
rdV
r3
153. Электростатика. 15.9
Зная вектор Е в каждой точке, можнопредставить электрическое поле
наглядно с помощью линий
напряженности, или другими словами
линий вектора Е. Эти линии проводят
так, чтобы касательная к ним в каждой
точке совпадала с направлением
вектора Е, а густота линий, была бы
пропорциональна модулю вектора Е.
Кроме того этим линиям приписывают
направление, совпадающее с
направлением вектора Е.
По полученной картине можно легко судить о конфигурации данного
электрического поля – о направлении и модуле вектора Е в разных
точках поля.
154. Электростатика. 15.10
Линии Е точечного заряда, очевидно, представляют собойсовокупность радиальных прямых, направленных от заряда, если он
положителен, и к заряду, если он отрицателен. Линии одним концом
опираются на заряд, другим уходят в бесконечность. Линии нигде
кроме заряда, не начинаются и не заканчиваются; они, начавшись
на заряде (если заряд положителен), уходят в бесконечность, либо,
приходя из бесконечности, заканчиваются на заряде (если заряд
отрицателен).
155. Лекция 16 Поток вектора напряженности электрического поля. Теорема Остроградского – Гаусса
Поле Е обладает, двумя чрезвычайно важными свойствами, знаниекоторых помогает глубже проникнуть в суть понятия поля и
сформулировать его законы, а также открыло возможность решить ряд
вопросов весьма просто и изящно. Эти свойства связаны с потоком
вектора Е и его циркуляцией. Поток и циркуляция являются двумя
важнейшими характеристиками всех векторных полей.
Из принципа построения линий напряженности
следует, что густота линий Е равна модулю
вектора Е. Тогда число линий, пронизывающих
элементарную площадку dS, нормаль n которой
составляет угол α с вектором Е, определяется
как EdScosα. Эта величина и есть поток dФ
вектора Е сквозь площадку dS. В более
компактной форме
dФ=E n dS EdS
156. Электростатика. 16.2
Выбор направления вектора n условен,его можно было бы направить и в
противоположную сторону. Если
имеется некоторая произвольная
поверхность S то поток вектора Е
сквозь нее
Ф E dS
S
Эта величина алгебраическая: она зависит не только от конфигурации
поля Е, но и от выбора направления нормали. В случае замкнутой
поверхности, нормаль принято брать направленной наружу области,
области охватываемой этой поверхностью.
157. Электростатика. 16.3
Поток вектора напряженности электростатического поля через замкнутуюповерхность обладает специфическим свойством: его величина
пропорциональна электрическому заряду, расположенному внутри этой
поверхности. Это утверждение составляет физический смысл теоремы
Гаусса.
Доказательство.
1) Допустим, что в начале координат помещен точечный электрический
заряд q. Напряженность электрического поля, созданного этим
зарядом, описывается соотношением:
E
q
r
4 0 r 3
Окружим заряд q сферой радиуса r, центр которой совпадает с началом
координат. Известно, что внешняя нормаль n к элементу поверхности dS
сферы направлена по радиусу
r
n
r
158. Электростатика. 16.4
Поток вектора E через поверхность сферы равен:Ф EndS
q
4 0
S
r r
q 1
q
2
dS
4
r
r3 r
4 0 r 2
0
2)Пусть поверхность S является произвольной
достаточно гладкой замкнутой поверхностью,
причем начало координат - место расположения
заряда q - лежит внутри поверхности S.
Заметим, что
r ndS dScos
d
2
2
r r
r
где α - угол между внешней нормалью n и
радусом-вектором r точки, в окрестности
которой расположен элемент поверхности
dS; dΩ - элемент телесного угла, под которым
виден элемент поверхности dS из начала
координат.
159. Электростатика. 16.5
В этом случае прямое вычисление потока вектора E через замкнутуюповерхность S приводит к результату
q
r
q
Ф EdS
d
S
d
3
4 0 S r
4 0
S
Здесь следует иметь ввиду, что для выпуклой
замкнутой поверхности S величина d Ω>0 и
суммарное значение интеграла в данном выражении
равно 4π. Если поверхность S не является строго
выпуклой, то для части поверхности cosα>0, а для
части поверхности cosα>0, в этом случае d Ω
является алгебраической величиной, но в результате
все равно получается 4π.
Для случая, когда начало координат (т.е. точка расположения заряда q)
лежит вне замкнутой поверхности суммарное значение Ω=0, поскольку
видимая часть поверхности и невидимая из начала координат часть
поверхности приводят к одному и тому же абсолютному значению
телесного угла, но противоположных знаков.
160. Электростатика. 16.6
3) Реальное электростатическое поле обусловлено совокупностьюточечных зарядов (принцип суперпозиции), для каждого из которых
соотношение
q
Ф EndS
0
доказано для произвольной замкнутой поверхности S. Но тем самым
доказана справедливость теоремы Гаусса для произвольного
электростатического поля: поток вектора напряженности
электростатического поля через произвольную замкнутую поверхность S
равен суммарному электрическому заряду, находящемуся внутри
поверхности S, деленному на величину ε0.
Использование теоремы Гаусса в интегральной форме в отдельных
случаях, отличающихся высокой степенью симметрии расположения
электрических зарядов в пространстве, позволяет эффективно
рассчитывать характеристики электростатического поля.
161. Электростатика. 16.7
Поле равномерно заряженной плоскости.Пусть поверхностная плотность заряда равна σ. Из симметрии задачи,
очевидно, что вектор Е может быть только перпендикулярным
заряженной плоскости. Кроме того, ясно, что в симметричных
относительно этой плоскости точках вектор Е одинаков по модулю и
противоположен по направлению. Такая конфигурация поля
подсказывает, что в качестве замкнутой поверхности следует выбрать
прямой цилиндр с основаниями параллельными плоскости.
Поток сквозь боковую поверхность этого
цилиндра равен нулю, и поэтому полный поток
через всю поверхность цилиндра будет 2EΔS,
где ΔS – площадь каждого торца цилиндра.
Внутри цилиндра заключен заряд σΔS.
Согласно теореме Гаусса 2EΔS= σΔS откуда
получаем:
E
2 0
162. Электростатика. 16.8
Поле бесконечного круглого цилиндраПоле бесконечного круглого цилиндра,
заряженного равномерно по поверхности так, что
на единицу его длины приходится заряд λ. Из
соображений симметрии следует, что вектор Е в
каждой точке перпендикулярен оси цилиндра, а
модуль вектора Е зависит только от расстояния r
до оси цилиндра. Это подсказывает, что
замкнутую поверхность надо взять в форме
коаксиального прямого цилиндра.
Тогда поток вектора Е сквозь торцы этого цилиндра равен нулю, а через
боковую поверхность ЕΔS, где ΔS – площадь боковой поверхности
цилиндра ΔS=2πrh. r – радиус боковой поверхности цилиндра, h – его
высота. По теореме Гаусса для случая r>R (R – радиус бесконечного
круглого цилиндра) имеем Е2πrh= λh/ε0, откуда:
E
2 0 r
163. Электростатика. 16.9
Поле сферической поверхности, заряженной равномерно зарядом q.Это поле центрально-симметрично – направление вектора Е в любой точке
проходит через центр сферы, а модуль зависит только от расстояния до
центра сферы. При такой конфигурации поля в качестве замкнутой
поверхности надо взять концентрическую сферу. Пусть ее радиус r>R,
2
тогда по теореме Гаусса E 4 r q откуда
0
q
E
4 0 r 2
Если r<R, то замкнутая поверхность не
содержит внутри зарядов, поэтому в этой
области всюду Е=0, т.е. внутри равномерно
заряженной сферической поверхности
электрическое поле отсутствует. Вне этой
поверхности поле убывает с расстоянием
по такому же закону, как у точечного
заряда.
164. Электростатика. 16.10
Поле сферы заряженной объемной плотностью заряда ρПоле такой сферы тоже обладает центральной симметрией. Для
поля вне сферы получается тот же результат, что и в случае
поверхностно заряженной сферы. Однако для точек внутри
результат будет другой. Сферическая поверхность радиуса r (r<R)
заключает в себя заряд равный 4 r 3
3
Следовательно, теорема Гаусса для такой поверхности запишется в виде:
E 4 r 2
Откуда, заменяя ρ через 4
q
1
0
4
3
r3
R 3 получаем
3
1 q
E
r
3
4 0 R
Внутри сферы напряженность поля растет
линейно с расстоянием r от центра сферы.
Вне сферы напряженность убывает по такому
же закону, как и у точечного заряда.
165. Лекция 17 Работа сил электростатического поля. Потенциал. Эквипотенциальные поверхности. Связь между напряженностью
электрического поля ипотенциалом.
При перемещении пробного заряда q в электрическом поле электрические
силы совершают работу. Оказывается, что работа сил
электростатического поля при перемещении заряда из одной точки
поля в другую не зависит от формы траектории, а определяется только
положением начальной и конечной точек и величиной заряда. Из
механики известно, что такое поле называется консервативным. Если в
качестве пробного заряда, переносимого из точки 1 в точку 2 поля Е,
взять единичный положительный заряд, то элементарная работа сил
поля на перемещении dl равна Edl, а вся работа сил поля на пути от
точки 1 до точки 2 определяется как
2
Edl
1
Этот интеграл берется по некоторому пути (линии), поэтому его называют
линейным.
166. Электростатика. 17.2
Интеграл данного вида, взятый по замкнутому пути, называетсяциркуляцией вектора Е и обозначается
Теорема о циркуляции вектора Е гласит:
циркуляция вектора Е в любом
электростатическом поле равна нулю т.е.
2
Edl 0
1
Поле, обладающее таким свойством, называется потенциальным. Теорема
о циркуляции вектора Е позволяет сделать ряд важных выводов,
практически не прибегая к расчетам. Например, линии
электростатического поля не могут быть замкнутыми.
167. Электростатика. 17.3
Тело находящееся в потенциальном поле сил, обладает потенциальнойэнергией, за счет которой совершается работа силами поля.
Следовательно, работа сил электростатического поля может быть
представлена как разность значений потенциальной энергии, которыми
обладал заряд в точках 1 и 2 поля Е. Можно утверждать, что в
электростатическом поле существует некоторая скалярная функция
координат φ(r), убыль которой
2
1 2 Edl
1
Так определенная величина φ(r) называется потенциалом поля.
Из сопоставления данного выражения с выражением для работы сил
потенциального поля ( которая равна убыли потенциальной энергии
частицы в поле) можно сказать, что потенциал – это величина, численно
равная потенциальной энергии единичного положительного заряда в
данной точке поля.
168. Электростатика. 17.4
Потенциал какой-либо произвольной точки поля определяется сточностью до произвольной аддитивной константы.
Элементарная убыль потенциала на dl есть
d Edl
Другими словами, если известно поле E(r), то для нахождения φ надо
представить как убыль некоторой функции.
Потенциал поля неподвижного точечного заряда:
1 q
1 q
q dr
Edl
e
d
l
=
d
const
r
4 0 r 2
4 0 r 2
4
r
0
Таким образом, потенциал поля точечного заряда
1 q
4 0 r
169. Электростатика. 17.5
Если имеется система из N неподвижных точечных зарядов q1, q2, ….Согласно принципу суперпозиции в любой точке поля напряженность
Е=Е1+Е2+…, где Еi – напряженность поля создаваемого отдельно
зарядом q1 и т.д. Тогда можно записать
Edl (E1 E 2 ....)dl E1dl E2dl .... d 1 d 1 ... d
Таким образом, потенциал системы неподвижных точечных зарядов
qi
1
r
4 0
i
Если заряды, образующие системы, распределены непрерывно, то,
каждый элементарный объем dV содержит точечный заряд ρdV, где ρ –
объемная плотность заряда в месте нахождения объема dV. Тогда при
вычислении потенциала можно перейти от суммирования дискретно
распределенных в пространстве зарядов к интегрированию по
1
dV
заряженному объему:
4 0 r
170. Электростатика. 17.6
Если заряды расположены только по поверхности S то получаемследующее соотношение:
1
dS
4 0 r
Получили, что электрическое поле можно описывать как с помощью
напряженности, так и с помощью потенциала. Следовательно, раз эти две
величины описывают одно и то же физическое явление, то между ними
должна существовать однозначная связь.
Связь между φ и Е можно установить с помощью соотношения d Edl
Пусть перемещение dl параллельно оси Х, тогда dl=exdx, где ex – орт
оси Х; dx – приращение координаты х. В этом случае
Edl Ee x dx E x dx
Получим
Ex
x
171. Электростатика. 17.7
Аналогичные рассуждение, позволяют определить Ey, Ez, а зная их легконайти и вектора напряженности электрического поля Е:
E
ex
ey
ez
y
z
x
φ).
Величина, стоящая в скобках есть градиент потенциала φ (grad φ или
Окончательно связь вектора Е и потенциала φ выглядит следующим образо
E
Распределение потенциала в пространстве наглядно изображают с
помощью эквипотенциальных поверхностей – поверхностей во всех
точках, которых потенциал имеет одно и то же значение.
172. Электростатика. 17.8
Вектор Е направлен в каждой точке понормали к эквипотенциальной
поверхности в сторону уменьшения
потенциала. Эквипотенциальные
поверхности проводятся так, чтобы
разность потенциалов для двух соседних
поверхностей была бы одинаковой. Тогда
по густоте эквипотенциальных
поверхностей можно наглядно судить о
значении напряженности поля в разных
точках поля. Там где эти поверхности
расположены гуще, там напряженность
поля больше. Так как вектор Е всюду
нормален к эквипотенциальным
поверхностям, то линии вектора Е
ортогональны этим поверхностям.
173. Электростатика. 17.9
174. Электростатика. 17.10
1) Зная потенциал φ(r), можно предельно просто вычислить работусил поля приперемещении точечного заряда из точки 1 в точку 2
A12 q( 1 2 )
2) Во многих случаях оказывается, что для нахождения напряженности Е
электрического поля легче сначала подсчитать потенциал и затем взять
градиент от него, чем непосредственно вычислять Е. Действительно,
для вычисления φ нужно взять один интеграл, а для вычисления Е –
три (так как Е вектор).
175. Лекция 18 Поле В. Сила Лоренца. Закон Био – Савара. Циркуляция и поток вектора В.
Магнитные явления были известны еще вдревнем мире. Компас был изобретен более
4500 лет тому назад.
Он появился в Европе приблизительно в
XII веке новой эры. Однако только в XIX веке
была обнаружена связь между
электричеством и магнетизмом и возникло
представление о магнитном поле. Первыми
экспериментами, показавшими, что между
электрическими и магнитными явлениями
имеется глубокая связь, были опыты
датского физика Х. Эрстеда (1820 г.).
Эти опыты показали, что на магнитную
стрелку, расположенную вблизи
проводника с током, действуют силы,
которые стремятся повернуть стрелку.
176. Магнитное поле в вакууме 18.2
В том же году французский физик А. Ампер наблюдал силовоевзаимодействие двух проводников с токами и установил закон
взаимодействия токов. По современным представлениям, проводники с
током оказывают силовое действие друг на друга не непосредственно, а
через окружающие их магнитные поля. Все свойства магнитной силы
можно описать, если ввести понятие магнитного поля. Это поле
характеризуется магнитной индукцией В. Магнитное поле действует на
движущейся электрический заряд с силой
Fм q vB
Тогда полная электромагнитная сила, действующая на заряд q:
F qE q vB
ее называют силой Лоренца. Она состоит из электрической и магнитной
составляющих.
177. Магнитное поле в вакууме 18.3
Если заряженная частица движется в однородном магнитном поле поддействием силы Лоренца, а ее скорость v лежит в плоскости,
перпендикулярной вектору B то частица будет двигаться по
окружности радиуса
mv
R=
qB
Сила Лоренца в этом случае играет роль
центростремительной силы. Период обращения
частицы в однородном магнитном поле равен
2 R 2 m
T
v
qB
Это выражение показывает, что для заряженных частиц заданной
массы m период обращения не зависит от скорости v и радиуса
траектории R. Угловая скорость движения заряженной частицы по
круговой траектории:
2 qB
Называется
T
m
циклотронной частотой.
178. Магнитное поле в вакууме 18.4
Циклотронная частота не зависит от скоростичастицы. Это обстоятельство используется в
циклотронах – ускорителях тяжелых частиц.
Если частица влетает в магнитное поле не
под прямым углом, то траектория движения
будет представлять собой винтовую линию.
179. Магнитное поле в вакууме 18.5
Источниками магнитного поля являются движущиеся электрическиезаряды (токи). Магнитное поле возникает в пространстве,
окружающем проводники с током, подобно тому, как в пространстве,
окружающем неподвижные электрические заряды, возникает
электрическое поле. Магнитное поле постоянных магнитов также
создается электрическими микротоками, циркулирующими внутри
молекул вещества (гипотеза Ампера). В результате обобщения
экспериментальных данных был получен элементарный закон,
определяющий поле В точечного заряда q, движущегося с постоянной
нерелятивистской скоростью v. Этот закон записывается в виде:
0 q vr
4 r 3
μ0 – магнитная постоянная.
B
0
10 7 Гн/м
4
180. Магнитное поле в вакууме 18.6
Магнитное поле постоянных токов различной конфигурации изучалосьэкспериментально французскими учеными Ж. Био и Ф. Саваром
(1820 г.). Они пришли к выводу, что индукция магнитного поля токов,
текущих по проводнику, определяется совместным действием всех
отдельных участков проводника. Магнитное поле подчиняется
принципу суперпозиции: магнитное поле, создаваемое несколькими
движущимися зарядами или токами, равно векторной сумме магнитных
полей, создаваемых каждым зарядом или током в отдельности.
B Bi
Пусть магнитное поле создается постоянным электрическим током, тогда
выделив в этом токе точечный движущейся заряд а затем просуммировав
все эти элементарные заряды, можно найти магнитное поле В,
создаваемое данным током.
181. Магнитное поле в вакууме 18.7
Элементарный заряд q равен ρdV, где dV – элементарный объем, ρ –объемная плотность заряда, являющегося носителем тока, учтем
также, что ρv=j плотность тока. Тогда магнитное поле, создаваемое
таким зарядом равно:
jr dV
dB
0
4
r3
Магнитное поле создаваемое линейным элементом тока выглядит
следующим образом:
0 I dl,r
dB
4 r 3
Полное поле В в соответствии с принципом
суперпозиции находим интегрированием этих
выражений по всем элементам тока
dB 0
4
jr dV
r3
dB
0
4
I dl,r
r3
182. Магнитное поле в вакууме 18.8
Как и любое другое векторное поле, поле В может быть представленонаглядно с помощью лини вектора В. Их проводят обычным способом
– так, чтобы касательная к этим линиям в каждой точке совпадала с
направлением вектора В, а густота линий была бы пропорциональна
модулю вектора В в данном месте.
Магнитное поле обладает, как и электрическое поле, двумя важнейшими
свойствами – поток и циркуляция вектора В.
Поток вектора В сквозь любую замкнутую поверхность равен нулю:
BdS 0
Равенство потока вектора В нулю также является следствием того, что
в природе не существует магнитных зарядов на которых начинались
бы или заканчивались линии магнитной индукции В.
183. Магнитное поле в вакууме 18.9
Расчеты магнитного поля токов часто упрощаются при учете симметрии вконфигурации токов, создающих поле. В этом случае расчеты можно
выполнять с помощью теоремы о циркуляции вектора магнитной
индукции.
Пусть в пространстве, где создано
магнитное поле, выбран некоторый
условный замкнутый контур (не
обязательно плоский) и указано
положительное направление обхода
контура. На каждом отдельном малом
участке dl этого контура можно
определить касательную составляющую
Bl вектора B в данном месте, то есть
определить проекцию вектора B на
направление касательной к данному
участку контура. Циркуляцией вектора
В называют сумму произведений Bldl,
взятую по всему контуру L.
184. Магнитное поле в вакууме 18.10
Теорема о циркуляция вектора В: циркуляция вектора В попроизвольному контуру равна произведению μ0 на алгебраическую
сумму токов, охватываемых контуром:
Bdl I
0
k
Причем Ik – величины алгебраические. Ток считается положительным,
если его направление связано с направлением обхода по контуру
правилом правого винта. Ток противоположного направления считается
отрицательным.
185. Лекция 19 Применение теоремы о циркуляции вектора В. Поле прямого тока. Применение теоремы о циркуляции вектора В. Поле
соленоида.Магнитно поле прямого тока.
Пусть постоянный ток I течет вдоль бесконечно длинного прямого
провода, имеющего круглое сечение радиуса а. Необходимо найти
индукцию В поля снаружи и внутри провода.
Из симметрии задачи следует, что
линии вектора В в данном случае
должны иметь вид окружностей с
центром на оси провода. Причем
модуль вектора В должен быть
одинаков во всех точках на расстоянии
r от оси провода. Поэтому по теореме
о циркуляции вектора В для круглого
контура , откуда следует, что вне
провода
I
(r>a).
B 0
2 r
186. Магнитное поле в вакууме 19.2
Внутри провода из тех же соображенийсимметрии следует, что линии вектора В
являются тоже окружностями. Поэтому
выбираем контур виде окружности. По
теореме о циркуляции для контура внутри
провода
B 2 r 0 Ir
где Ir – ток, охватываемый контуром.
Он пропорционален площади охватываемой контуром.
r
I r =I
a
2
Отсюда находим, что внутри провода:
Ir
B 0 2 r a
2 a
187. Магнитное поле в вакууме 19.3
Магнитное поле соленоида.Пусть ток I течет по проводнику, намотанному по винтовой линии на
поверхность цилиндра. Такой, обтекаемый током цилиндр называется
соленоидом. Пусть на единицу длины соленоида приходится n витков
проводника. Если шаг винтовой линии достаточно мал, то каждый
виток соленоида можно приближенно заменить замкнутым витком.
Предполагается, что сечение проводника настолько мало, что можно
считать, что ток течет по поверхности соленоида.
188. Магнитное поле в вакууме 19.4
Опыт показывает на то, что в центральной части катушки магнитное полепрактически однородно и значительно сильнее, чем вне катушки. В
предельном случае бесконечно длинного соленоида однородное
магнитное поле целиком сосредоточено внутри соленоида.
Из соображений симметрии ясно, что линии вектора В внутри соленоида
направлены вдоль его оси, причем вектор В составляет с направлением
тока правовинтовую систему.
Такая конфигурация линий поля
подсказывает выбрать контур в виде
прямоугольника, две стороны которого
параллельны линиям поля, причем одна
из них находится вне соленоида. Вторые
две стороны оказываются
перпендикулярны линиям магнитной
индукции.
189. Магнитное поле в вакууме 19.5
В итоге получаем, что циркуляция по трем из четырех сторонпрямоугольника равна нулю. По стороне вне соленоида, так как там
нет поля. По сторонам перпендикулярным полю, так как проекция
линий поля на них равна нулю. Тогда согласно теореме о циркуляции
получаем
Bl 0 nlI
где l - длина стороны параллельной линиям магнитной индукции.
Окончательно получаем, поле внутри длинного соленоида имеет вид:
B 0 nI
Т.е. поле внутри длинного соленоида однородно (за исключением
областей, прилегающих к торцам соленоида).
Произведение nI называют числом ампервитков.
190. Магнитное поле в вакууме 19.6
Магнитное поле тороида.Тороид представляет собой провод, навитый на каркас, имеющий форму
тора. Предполагается, что катушка по которой течет ток I плотно, то есть
виток к витку, намотана на немагнитный тороидальный сердечник.
Из соображений симметрии можно понять, что линии вектора В должны
быть окружностями, центры которых расположены на оси тороида. Они
направлены так, что глядя вдоль них, мы увидели бы ток в витках,
циркулирующим по часовой стрелке. Поэтому ясно, что в качестве
контура следует взять одну из таких окружностей.
191. Магнитное поле в вакууме 19.7
Если контур расположен внутри тороида,то он охватывает N витков с током (N –
число витков в тороидальной катушке).
Тогда количество токов охватываемых
контуром радиуса r равно NI.
Следовательно, по теореме о
циркуляции получаем , откуда следует,
что внутри тороида
B
0 NI
2 r
Если выбранный нами круглый контур проходит вне тороида, то
токов он не охватывает, поэтому для такого контура . Это значит, что
вне тороида магнитное поле отсутствует.
192. Магнитное поле в вакууме 19.8
Магнитное поле плоскости с током.Рассмотрим безграничную проводящую плоскость,
по которой течет равномерно распределенный ток
одного направления. Введем понятие линейной
плотности тока как вектор i, направленный вдоль
линий тока. Модуль этого вектора представляет
собой ток, приходящийся на единицу длины,
которая играет роль поперечного сечения.
Разбив мысленно плоскость с током на тонкие нити с
током, нетрудно видеть, что результирующее поле В будет
направлено параллельно плоскости, причем направление с
разных сторон плоскости будет различным и определяться
по правилу правого винта.
193. Магнитное поле в вакууме 19.9
Зная, как расположены в этом случае линии вектора В, выберем контур ввиде прямоугольника. Две стороны, которого параллельны плоскости,
а две перпендикулярны. Тогда циркуляция вектора В по
перпендикулярным сторонам будет равна нулю, так как так как
проекция вектора В на них равна нулю. Следовательно по теореме о
циркуляции получаем
В итоге находим
2Bl 0il
B
1
0i
2
Магнитное поле как с одной стороны плоскости, так и с другой является
однородным. Этот результат справедлив и для ограниченной пластины с
током, но лишь на расстояниях близких к пластине и удаленных от ее
краев.
194. Магнитное поле в вакууме 19.10
BРезультаты, полученные в рассмотренных
примерах, можно было бы найти и
dB
непосредственно с помощью закона БиоdBz
Савара. Однако теорема о циркуляции
позволяет получить эти результаты
r
значительно проще и быстрее.
z
Однако теорема о циркуляции позволяет
получить эти результаты значительно проще
и быстрее. Вместе с тем надо понимать, что
R
число задач, легко решаемых с помощью
теоремы о циркуляции вектора В, небольшое.
I
Примером может служить задача о
нахождении магнитного поля на оси
кругового тока.
Прямой расчет дает следующее значение для магнитной индукции на
оси кругового тока:
0 2 R 2 I
B(z)
4 z 2 +R 2 3 2
dl
195. Магнитное поле в вакууме 19.11
В центре витка с током (z=0) и на расстоянии z>>R модуль вектора Вравен
0 2 I
0 2 R 2 I
B(z=0)
,
B(z R)
4 R
4 z 3
196. Лекция 20 Сила Ампера. Работа поля В при перемещении контура стоком.
Каждый носитель тока испытывает действие магнитной силы. Действиеэтой силы передается проводнику, по которому движутся заряды. В
результате магнитное поле действует с определенной силой на сам
проводник с током.
Пусть объемная плотность заряда, являющегося носителем тока равна ρ.
Выделим мысленно элемент объема dV проводника. В нем находится
заряд – носитель тока, равный ρdV. Тогда сила, действующая на
элемент dV проводника, может быть записана в виде:
dF dq v,B v,B dV
Так как j v
dF j,B dV
Закон Ампера
Если ток течет по тонкому проводнику, то так как jdV Idl получим
dF I dl,B Закон Ампера
197. Магнитное поле в вакууме 20.2
dF I dl,BПусть в пространстве имеется два параллельных проводника. Первый
проводник создает в пространстве магнитное поле, на второй
проводник, находящейся в поле первого будет действовать сила
Ампера. Аналогично и на первый проводник будет действовать поле
второго проводника. В результате между проводниками возникают
силы притяжения или отталкивания, обусловленные магнитным
взаимодействием токов. Можно убедиться в том, что токи, одинаково
направленные, притягиваются, а противоположно направленные –
отталкиваются.
198. Магнитное поле в вакууме 20.3
Результирующая сила Ампера, которая действует на контур с током вмагнитном поле, определяется следующим образом:
F I dl, B
Где интегрирование проводится по всему данному контуру с током. Если
магнитное поле однородно, то вектор В можно вынести из-под интеграла
и задача сводится к вычислению векторного интеграла dl
Этот интеграл представляет собой замкнутую цепочку элементарных
векторов dl, поэтому он равен нулю. Значит и F=0, т.е. результирующая
сила Ампера равна нулю в однородном магнитном поле.
Если магнитное поле неоднородно, то результирующая сила отлична
от нуля и определяется с помощью интегрирования.
199. Магнитное поле в вакууме 20.4
Поведение элементарного контура с токомудобно описывать с помощью магнитного
момента pm. По определению
pm ISn
Подробный расчет по формуле F I dl, B
с учетом малости контура приводи к следующему выражению для силы,
действующей на элементарный контур с током в неоднородном
магнитном поле:
B
F pm
n
B
n
– производная вектора В по направлению нормали n или по
направлению вектора pm.
200. Магнитное поле в вакууме 20.5
Из анализа полученной формулы можно сделать следующие выводы:B
1) как и ожидали, в однородном магнитном поле F=0, так как
0;
n
2)направление вектора F, вообще говоря, не совпадает ни с вектором
pm; вектор F совпадает лишь с направлением элементарного
приращения вектора B, взятого в направлении вектора pm в месте
расположения контура.
201. Магнитное поле в вакууме 20.6
Найдем момент сил (вращательный момент),действующий на контур с током в
однородном магнитном поле. При этом
учтем известный из механики факт, что
если результирующая сил равна нулю, то
момент сил не зависит от выбора точки,
относительно которой он вычисляется.
Рассмотрим прямоугольный контур со
сторонами a b, расположенный в
однородном магнитном поле так, что
вектор нормали n образует с вектором В
угол , и стороны контура
перпендикулярны вектору В.
202. Магнитное поле в вакууме 20.7
Обозначим силы Ампера, действующие настороны контура F1, F2, F3, F4 . Найдем
суммарный момент этих сил относительно
центра контура. Линии действия сил F2,F4
проходят через точку О, следовательно,
моменты этих сил равны нулю. Две
другие силы: F1 и F3 и радиус-векторы
точек их приложения r1 и r3 лежат в
плоскости, образованной векторами B и
n . Каждая из сил F1, F3 перпендикулярна
вектору В, а радиус-векторы r1, r3
перпендикулярны вектору n. Поэтому
силы F1, F3 образуют с радиус-векторами
r1, r3 тот же угол , что и вектор B с
нормалью n. Момент этих сил N равен
N r1 , F1 r3 , F3
203. Магнитное поле в вакууме 20.8
Слагаемые в этой сумме направлены в одну сторону. По формуле (длясилы Ампера) обе силы равны F1=F2=IaB, кроме того, r1=r2=a/2.
Поэтому слагаемые одинаковы по величине и равны
a
| r1 , F1 | | r2 , F2 | IBb sin
2
а величина результирующего момента
N=IBabsin IBSsin
Воспользовавшись определением магнитного момента контура, можно
записать величину момента сил Ампера, действующих на этот контур:
N=pm Bsin
Векторы pm, B, N составляют правую тройку векторов, поэтому в общем
виде получаем
N= pm ,B
204. Магнитное поле в вакууме 20.9
Для момента сил Ампера, существует два положения = 0 и = , вкоторых этот момент обращается в нуль. В остальных случаях
вращающий момент, действующий на контур с током, стремится
развернуть контур так, чтобы направление магнитного момента
контура совпало с направлением магнитной индукции внешнего поля,
т.е. к состоянию = 0. Поэтому при = 0 контур оказывается в
устойчивом равновесии, а при = – в неустойчивом.
Элементарная работа dА, совершаемая силой Ампера dF при
перемещении на dr в магнитном поле элемента проводника dl, равна
dA dF, dr I dl, B , dr I dr, dl , B
Векторное произведение перемещения и элемента
проводника есть вектор площадки, прочерченной
проводником при его перемещении
dS dr,dl
205. Магнитное поле в вакууме 20.10
Скалярное произведение вектора площадки и вектора магнитнойиндукции – это магнитный поток через площадку dS
dФ B,dS
поэтому для работы получаем
dA=IdФ
Если проводник, сила тока I в котором поддерживается постоянной,
совершает конечное перемещение из положения 1 в положение 2, то
работа сил Ампера при таком перемещении
2
A12 IdФ IФ
1
где Ф – магнитный поток через поверхность, прочерченную
проводником при рассматриваемом перемещении.
206. Магнитное поле в вакууме 20.11
Если в постоянном магнитном поле перемещается замкнутый контур, топоток, прочерченный всеми элементами контура, равен изменению
потока пронизывающего контур.
Предположим есть два последовательных состояния контура С1 и С2.
Поверхности S1 и S2, которые ограничивает контур в положениях С1 и
С2 и поверхность Sп, прочерченная контуром, составляют замкнутую
поверхность. По теореме Остроградского-Гаусса для магнитной
индукции суммарный поток через эту замкнутую поверхность равен
нулю. Выберем нормали n1 и n2 к поверхностям S1 и S2.
При этом поток наружу из замкнутой
поверхности складывается из потока
через S1 в направлении n1 (равен Ф1),
потока через S2 в направлении
противоположном n2 (равен Ф2) и потока
через прочерченную поверхность Sп (Ф).
Таким образом, получаем
B, dS Ф -Ф
1
S1 +S2 +SП
2
+Ф 0
207. Магнитное поле в вакууме 20.12
откуда Ф=Ф2-Ф1. Следовательно, соотношение для замкнутого контураможно записать так
A12 Ф2 -Ф1
При выводе этой формулы мы рассмотрели простое перемещение контура,
но она оказывается справедливой и при более сложных изменениях
состояния контура, например, при вращении и при деформации. В
приведенном виде она выполняется для движении не только одиночного
контура, но и катушки, состоящей из нескольких витков, в частности, для
катушки из N одинаковых витков. В последнем случае потокосцепление
равно = N м, где м – магнитный поток через один виток.
208. Лекция 21 Виды поляризации диэлектриков. Поляризованность Р. Свойства поля вектора Р. Вектор D. Условия на границе двух
диэлектриков для векторов E и DВещество, внесенное в электрическое поле, может существенно изменить
его. Это связано с тем, что вещество состоит из заряженных частиц. В
отсутствие внешнего поля частицы распределяются внутри вещества
так, что создаваемое ими электрическое поле в среднем по объемам,
включающим большое число атомов или молекул, равно нулю. В
диэлектриках нет свободных электрических зарядов. Они состоят из
нейтральных атомов или молекул. Заряженные частицы в нейтральном
атоме связаны друг с другом и не могут перемещаться под действием
электрического поля по всему объему диэлектрика.
При внесении диэлектрика во внешнее электрическое поле Е0 в нем
возникает некоторое перераспределение зарядов, входящих в состав
атомов или молекул. В результате такого перераспределения на
поверхности и, вообще говоря, и в объеме диэлектрического
образца появляются избыточные нескомпенсированные связанные
заряды.
209. Диэлектрики 21.2
Связанные заряды создают электрическое поле Е’ которое внутридиэлектрика направлено противоположно вектору напряженности Е0
внешнего поля. Этот процесс называется поляризацией диэлектрика.
Существует несколько механизмов поляризации диэлектриков. Основными
из них являются ориентационная и электронная поляризации. Первый
механизм работает при поляризации полярных диэлектриков, второй –
неполярных.
210. Диэлектрики 21.3
Каждый малый объем dV (малый по сравнению с объемомдиэлектрического тела, но большой по сравнению с объемом
молекулы, атома или элементарной ячейки кристалла) приобретает
дипольный момент
N
dp p i
pi– дипольные моменты молекул
i 1
Дипольным моментом диполя(молекулы) называется векторная
величина:
p ql
Вектор l направлен от –q к +q
Векторная величина
dp
P
n p
dV
называемая поляризованностью (численно равная дипольному моменту
единичного объема диэлектрической среды) не зависит от dV.
211. Диэлектрики 21.4
Для диэлектриков зависимость поляризованности от напряженностиэлектрического поля линейна:
P 0E
- безразмерная величина, называемая диэлектрической восприимчивостью
вещества. Эта величина не зависит от Е она характеризует свойства
самого диэлектрика.
Поле вектора Р обладает следующим свойством: поток вектора Р сквозь
произвольную замкнутую поверхность S равен взятому с обратным
знаком избыточному связанному заряду диэлектрика в объеме,
охватываемом поверхностью S
PdS q 'внутр
Это уравнение выражает теорему Гаусса для вектора Р.
212. Диэлектрики 21.5
Поскольку источниками поля Е являются все электрические заряды –сторонние и связанные, теорему Гаусса для поля Е можно записать так:
EdS (q+q')
0
внутр
Появление связанных зарядов q’ усложняет дело, и данная формула
оказывается мало применима для нахождения поля Е в диэлектрике.
Если выразить связанный заряд через поток вектора Р, тогда выражение
для потока вектора Е можно преобразовать к следующему виду:
0E + Р dS qвнутр
Величину, стоящую под интегралом в скобках, обозначают буквой D. В
итоге получили вспомогательный вектор D:
D 0E+P
213. Диэлектрики 21.6
Поток вектора D сквозь произвольную замкнутую поверхность равеналгебраической сумме сторонних зарядов, охватываемых этой
поверхностью:
DdS q
внутр
В случае изотропных диэлектриков поляризованность P 0 E
Для вектора D получим
D 0 (1 )E
D 0 E
ε – диэлектрическая проницаемость вещества:
1
Диэлектрическая проницаемость является основной электрической
характеристикой диэлектрика. Для всех веществ ε>0, для вакуума
ε=0. В изотропных диэлектриках вектор D коллинеарен вектору Е.
Поле вектора D наглядно можно изобразить с помощью линий
вектора D, направление и густота которых определяется точно так
же как и у линий вектора Е. Однако линии D могут начинаться или
заканчиваться только на сторонних заряда или на бесконечности.
214. Диэлектрики 21.7
Рассмотрим поведение векторов E и D на границе раздела двуходнородных изотропных диэлектриков. Предположим, что на
границе раздела этих диэлектриков находится поверхностный
сторонний заряд σ. Условия для E и D получим, используя теорему
о циркуляции вектора Е и о потоке D.
Edl 0, DdS q
внутр
Возьмем небольшой вытянутый прямоугольный контур, ориентировав
его следующим образом
E 2 l E1 l 0
В результате получаем граничные условия, для тангенциальной
составляющей вектора Е
E1 E2
215. Диэлектрики 21.8
Возьмем очень малой высоты цилиндр, расположив его на границераздела двух диэлектриков.
n
n
Сечение цилиндра должно быть таким,
чтобы в пределах каждого его D
торца
вектор D
1n ' D1n
был одинаков.
Тогда согласно теореме Гаусса для вектора D
S
2
1
D2 n S D1n S S
n
Взяв обе проекции вектора D на общую нормаль получим D1n ' D1n
=>
D2 n D1n
Из этого соотношения видно, что нормальная составляющая вектора
D претерпевает скачок при переходе границы раздела
Однако если сторонние заряды на границе раздела отсутствуют
=> D D
1n
2n
216. Диэлектрики 21.9
E1 E 2D2n -D1n
0 2 E 2n - 0 1E1n
D1
1
D 2
2
Если на границе раздела нет сторонних зарядов то получаем
E1 E 2
2 E 2n 1E1n
D 2n =D1n
D1
1
D 2
2
В этом случае при переходе границы, составляющие Еτ и Dn скачок
не испытывают. Составляющие же Еn и Dτ претерпевают скачок.
Полученные результаты позволяют построить линии этих векторов
при переходе из одного диэлектрика в другой.
217. Диэлектрики 21.10
Полученные результаты позволяют построить линии этих векторов припереходе из одного диэлектрика в другой.
tg
tg 2 E 2 E 2 n
tg 1 E1 E1n
2
tg 1
2
1
Это значит, что в диэлектрике с большим значением ε
линии Е и D будут составлять больший угол с нормалью к
границе раздела. На границе раздела линии Е испытывают
преломление и терпят разрыв (из-за наличия связанных
зарядов), линии же вектора D испытывают только
преломление, без разрыва (в случае если сторонних
зарядов нет).
218. Лекция 22 Намагничение вещества. Намагниченность J. Циркуляция вектора J. Вектор Н. Граничные условия для В и Н.
Экспериментальные исследования показали, что все вещества в большейили меньшей степени обладают магнитными свойствами. Если два
витка с токами поместить в какую-либо среду, то сила магнитного
взаимодействия между токами изменяется. Этот опыт показывает, что
индукция магнитного поля, создаваемого электрическими токами в
веществе, отличается от индукции магнитного поля, создаваемого теми
же токами в вакууме. Магнитные свойства веществ определяются
магнитными свойствами атомов или элементарных частиц (электронов,
протонов и нейтронов), входящих в состав атомов.
Вещества крайне разнообразны по своим магнитным свойствам. У
большинства веществ эти свойства выражены слабо.
Слабо-магнитные вещества делятся на две большие группы –
парамагнетики и диамагнетики.
Вещества, способные сильно намагничиваться в магнитном поле,
называются ферромагнетиками.
219. Магнетики 22.2
При описании магнитного поля в веществе –магнетите можно, не вдаваясь в природу
этих элементарных токов, для простоты
считать их все одинаковыми.
Пусть каждая молекула вещества
характеризуется некоторым магнитным
моментом
pm IмолSмолn
Количественной характеристикой намагниченного состояния вещества
служит векторная величина намагниченность J, равная отношению
магнитного момента pm макроскопически малого объёма V вещества к
этому объему:
p
1 N
J
m
V
p
V
i 1
mi
220. Магнетики 22.3
Аналогично тому, как это было сделано для поляризованности Р,намагниченность можно выразить как
J
dp m
n pm
dV
Намагничивание приводит к преимущественной
ориентации магнитных моментов молекул. То же
самое можно сказать и об элементарных токах.
Преимущественная ориентация элементарных
токов приводит к возникновению
макроскопических токов – токов
намагничивания. Обычные токи, связанные с
перемещением в веществе носителей тока
называются токами проводимости.
221. Магнетики 22.4
Оказывается, что для стационарного случая циркуляция намагниченностиJ по произвольному замкнутому контуру равна алгебраической сумме
токов намагничивания I’, охватываемых контуром:
Jdl I'
В магнетиках, помещенных во внешнее магнитное поле, возникают токи
намагничивания, поэтому циркуляция вектора В определяется не только
токами проводимости, но и токами намагничивания:
Bdl (I+I')
0
Однако оказывается можно найти вспомогательный вектор, циркуляция
которого определяется только токами проводимости, охватываемыми
контуром. Проведем следующие преобразования:
Bdl
0
I'
B
Jdl J dl I
0
0
Bdl
222. Магнетики 22.5
Величину, стоящую под интегралом в скобках обозначают буквойН – напряженность магнитного поля. В итоге мы нашли некоторый
вспомогательный вектор
B
H
0
J
Циркуляция которого по произвольному контуру равна алгебраической
сумме токов проводимости I, охватываемых этим контуром:
Hdl I
Эта формула выражает теорему о циркуляции вектора Н
В случае многих однородных изотропных веществ, как показывает
эксперимент, между намагниченностью и вектором Н есть прямая
пропорциональность
J H
223. Магнетики 22.6
χ – магнитная восприимчивость, безразмерная величина, характерная длякаждого данного магнетика. Магнитная восприимчивость χ бывает как
положительной, так и отрицательной. Положительной у
парамагнетиков, отрицательной у диамагнетиков. У ферромагнетиков
зависимость J от Н носит сложный характер.
Петля гистерезиса для ферромагнетиков
224.
Магнетики 22.7Почти все вещества подчиняются зависимости
могут быть разбиты на два класса:
B 0 H
1– парамагнетики, в которых намагниченность вещества
увеличивает суммарное магнитное поле; 0 J H , они
втягиваются в область сильного неоднородного магнитного поля.
1 – диамагнетики, в которых намагниченность уменьшает
суммарное поле; диамагнетики выталкиваются из области
сильного неоднородного поля. 0 J H
225. Магнетики 22.8
В результате можно получить взаимосвязь векторов В и Н.1 H B 0
μ – магнитная восприимчивость среды:
1
Найдем соотношение между магнитной
индукцией B и напряженностью H магнитного
поля в некоторой точке А на границе двух сред.
Проведем в точке А единичные векторы: – по
касательной вдоль границы раздела сред и n –
по нормали к границе, направленной от первой
среды ко второй.
Построим вблизи точки А небольшой замкнутый прямоугольный контур L,
две стороны которого параллельны вектору и равны l, а две - вектору n
и равны h. Предположим, что по границе раздела внутри контура вблизи
точки А не текут макротоки. Из теоремы о циркуляции вектора
напряженности магнитного поля следует, что
Hdl 0
226. Магнетики 22.9
Это равенство должно выполняться при любом значении h и тогда впределе при h 0 получаем
lim
h 0
H,dl (H H ) l 0
2
1
L
Здесь H1 и H2 - проекции напряженности H на направление
касательного орта в точке А. Поскольку последнее равенство в должно
выполняться при произвольном l, находим
(H 2 =H1 )
Таким образом, касательная к поверхности раздела двух сред
составляющая напряженности магнитного поля не изменяется при
переходе из одной среды в другую.
227. Магнетики 22.10
Второе условие получим с помощью теоремы Гаусса для магнитнойиндукции B. Возьмем охватывающую окрестность точки А небольшую
цилиндрическую поверхность S, основания S которой параллельны
границе раздела и лежат по разные стороны от нее, а образующая
параллельна вектору нормали n. По теореме Остроградского-Гаусса
имеем для потока В через всю поверхность S
BdS 0
S
Это равенство должно выполняться
при любом значении высоты цилиндра
h и в пределе получим
lim
h 0
B, dS (B
S
2n
-B1n ) S 0
B2n =B1n
т.е. при переходе через границу раздела двух сред,
нормальная составляющая вектора магнитной индукции
не изменяется.
228. Магнетики 22.11
Используя полученные граничные условия для векторов В и Н и связьмежду ними, найдем ход линий этих векторов при переходе границы
раздела, в случае отсутствия токов проводимости
B1 B2
Отношение тангенсов углов α1 и α2 углов
tg 2 B2 B2 n 2
tg 1 B1 B1n 1
1
2
B2n B1n
H 2n
2
=
H1n
1
H1 H 2
Линии В не терпят разрыва при переходе границы, линии же Н
терпят разрыв (из-за поверхностных токов намагничивания).
229. Лекция 23 Законы геометрической оптики. Принцип Ферма. Явление полного отражения.
Основные законы геометрической оптики были известны задолго доустановления физической природы света. Исторически эти законы были
открыты намного раньше, чем была понята электромагнитная природа
света. Первые три закона были известны Евклиду, Аристотелю. Закон
преломления был открыт в 17 в. Синелиусом и Декартом.
Границы применимости геометрической оптики
1. Когда характерные поперечные размеры пучков света достаточно
велики по сравнению с длиной волны, можно пренебречь расходимостью
пучка света и считать, что он распространяется в одном единственном
направлении: вдоль светового луча
2. Кроме отсутствия волновых эффектов, в геометрической оптике
пренебрегают также квантовыми эффектами.
3. Кроме того, как правило, не рассматриваются эффекты, связанные с откликом
среды на прохождение лучей света. Эффекты такого рода, даже формально
лежащие в рамках геометрической оптики, относят к нелинейной оптике
230. Геометрическая оптика 23.2
1. Закон прямолинейного распространения света: в оптически однороднойсреде свет распространяется прямолинейно. Опытным доказательством
этого закона могут служить резкие тени, отбрасываемые непрозрачными
телами при освещении светом источника достаточно малых размеров
(«точечный источник»).
2. Независимость световых лучей заключается в том, что они при
пересечении не возмущают друг друга. Пересечения лучей не мешают
каждому из них распространяться независимо друг от друга.
231. Геометрическая оптика 23.3
На границе раздела двух прозрачных сред свет может частично отразитьсятак, что часть световой энергии будет распространяться после
отражения по новому направлению, а частично пройти через границу и
распространяться во второй среде.
Закон отражения света: падающий и
отраженный лучи, а также перпендикуляр к
границе раздела двух сред, восстановленный в
точке падения луча, лежат в одной плоскости
(плоскость падения). Угол отражения γ равен
углу падения α.
n1 sin n 2 sin
232. Геометрическая оптика 23.4
Закон преломления света: падающий и преломленный лучи, а такжеперпендикуляр к границе раздела двух сред, восстановленный в точке
падения луча, лежат в одной плоскости. Отношение синуса угла
падения α к синусу угла преломления β есть величина, постоянная для
двух данных сред равная относительному показателю преломления.
Относительный показатель преломления
двух сред равен отношению их абсолютных
показателей преломления:
n
n=
1
n2
Физический смысл относительного
показателя преломления – это отношение
скорости распространения волн в первой
среде υ1 к скорости их распространения
v1
во второй среде υ2:
n=
v2
233. Геометрическая оптика 23.4
Абсолютный показатель преломления равен отношению скорости света cв вакууме к скорости света v в среде:
n
c
v
Закон обратимости (или взаимности) световых лучей: если навстречу
лучу, претерпевшему ряд отражений и преломлений, пустить другой луч,
то он пойдет по тому же пути, что и первый (прямой) луч, но в обратном
направлении
Ферма принцип, основной принцип геометрической оптики
234. Геометрическая оптика 23.5
Простейшая форма принципа Ферма – утверждение, что луч света всегдараспространяется в пространстве между двумя точками по тому пути, по
которому время его прохождения меньше, чем по любому из всех других
путей, соединяющих эти точки.
Свет распространяется по такому пути, для прохождения которого
ему требуется минимальное время
dt dl / v
ds
2
v c/n
dt ndl / c
v скорость света в данной
точке среды
2
1
S
ndl
c1
c
2
1
S ndl
1
- оптическая длина пути
Из принципа Ферма вытекают законы отражения и преломления света
235. Геометрическая оптика 23.6
Пусть свет падает из точки А в точку В,отказавшись от поверхности MN. Среда, в
которой проходит луч, однородна. Поэтому
минимальность оптической длины пути
сводится к минимальности его
геометрической длины. Геометрическая
длина произвольно взятого пути равна
АО’В=А’О’В (вспомогательная точка А’
является зеркальным изображением точки
А). Очевидно, что наименьшей длинно
обладает путь луча, отразившегося в точке
О, для которого угол отражения равен
углу падения.
236. Геометрическая оптика 23.7
Пусть луч распространяется из точки А в точкуВ.Эти точки находятся в средах с различными
показателями преломления. Тогда произвольная
оптическая длина между этими точками равна
L=n1S1 +n 2S2 n1 a12 +x12 +n 2 a 22 +(b-x)2
Чтобы найти экстремальное значение,
продифференцируем L по х и приравняем
полученное выражение нулю:
n1 x
n 2 (b-x)
dL
x
b-x
=
=n1 -n 2
dx
s1
s2
a12 +x 2
a 22 +(b-x) 2
Множители при n1 n2 равны соответственно sinα и sinβ. Таким образом,
мы приходим к соотношению
n1 sin n 2 sin
237. Геометрическая оптика 23.8
Среду с меньшим абсолютным показателем преломления называютоптически менее плотной. При переходе света из оптически более
плотной среды в оптически менее плотную n2 < n1 (например, из стекла
в воздух) можно наблюдать явление полного отражения, то есть
исчезновение преломленного луча. Это явление наблюдается при углах
падения, превышающих некоторый критический угол αпр, который
называется предельным углом полного внутреннего отражения . Для
угла падения α = αпр sin β = 1 значение
sinαпр = n2 / n1 < 1.
Если второй средой является воздух (n2 ≈ 1), то формулу удобно
переписать в виде
sin пр
1
n
238. Геометрическая оптика 23.9
Для границы раздела стекло–воздух (n = 1,5) критический угол равенαпр = 42°, для границы вода–воздух (n = 1,33) – αпр = 48,7°.
Явление полного внутреннего отражения
находит применение во многих оптических
устройствах. Наиболее интересным и
практически важным применением
является создание волоконных световодов,
которые представляют собой тонкие (от
нескольких микрометров до миллиметров)
произвольно изогнутые нити из оптически
прозрачного материала (стекло, кварц).
Свет, попадающий на торец световода,
может распространяться по нему на
большие расстояния за счет полного
внутреннего отражения от боковых
поверхностей.
239. Геометрическая оптика 23.10
Луч, прошедший через плоскопараллельную пластинупогруженную в другое вещество, оказывается параллельным
падающему лучу.
n1
n2
n1
sin
n12
sin
α
β
sin 1
n21
sin 1
β1
α1
1
1
n12
1
n21
240. Лекция 24 Оптическая система. Кардинальные плоскости. Формула оптической системы.
Совокупность световых лучей образует пучок.Если лучи при своем продолжении пересекаются в
одной точке, пучок называется гомоцентрическим.
Гомоцентрические пучки бывают сходящимися и
расходящимися. Частным случаем гомоцентрического
пучка является пучок параллельных световых лучей.
Всякая оптическая система осуществляет
преобразование световых пучков. Если система не
нарушает гомоцентричности пучков, то лучи
вышедшие из точки Р пересекутся в одной точке
Р’. Эта точка представляет собой оптическое
изображение точки Р.
241. Оптическая система. 24.2
Изображение называется действительным, если световые лучи в точке Рдействительно пересекаются, и мнимым, если пересекаются
продолжения световых лучей, проведенные в направлении обратном
распространению света.
Действительные изображения непосредственно
освещают соответственным образом экран.
Например, на экране будет наблюдаться
светящаяся стрела после прохождения
собирающей линзы.
Мнимое изображение такого освещения не
дает, но при использовании дополнительных
оптических приборов мнимые изображения
могут быть преобразованы в действительные.
Это происходит в человеческом глазе – на
сетчатке(экране) возникает действительное
изображение.
242. Оптическая система. 24.3
Вследствие обратимости световых лучей источниксвета Р и изображение Р’ могут поменяться местами
– точечный источник помещенный в точку Р’ будет
иметь изображение в точке Р. С помощью
оптической системы все бесконечное множество
точек Р отображается в виде бесконечного
множества точек Р’. Первое бесконечное множество
называется пространством предметов, второе –
пространством изображений.
Оптическая система представляет собой
совокупность отражающих и преломляющих
поверхностей, отделяющих друг от друга оптически
однородные среды. Оптическая система
образованная сферическими поверхностями,
называется центрированной, если центры всех
поверхностей лежат на одной прямой. Эту прямую
называют оптической осью системы.
243. Оптическая система. 24.4
Пусть на центрированную оптическую систему падает параллельный пучоклучей. Этот пучок можно рассматривать, как вышедший из точечного
источника, расположенного на бесконечности т.е. гомоцентрический
пучок. Так как система не нарушает гомоцентричности, то по выходе из
нее пучок должен остаться гомоцентричным. Следовательно, вышедший
из системы пучок должен быть либо сходящимся, либо расходящимся.
Точка F’, в которой пересекаются вышедшие из системы лучи, называется
задним или вторым фокусом системы. Задний фокус представляет собой
точку, сопряженную с точкой удаленной на бесконечность в пространстве
предметов и лежащей на оптической оси
системы. Бесконечно удаленной
плоскости в пространстве предметов
перпендикулярной оптической оси будет
соответствовать в пространстве
изображений плоскость, проходящая
через задний фокус и тоже
перпендикулярная оптической оси. Эта
плоскость называется фокальной.
244. Оптическая система. 24.5
В пространстве предметов существуетлежащая на оптической оси точка F,
обладающая тем свойством, что
вышедшие из нее или сходящиеся в
ней лучи после прохождения через
систему становятся параллельными
оптической оси. Эта точка
называется передним или первым фокусом системы, а проходящая через
нее плоскость перпендикулярная главной оптической оси называется
передней фокальной плоскостью.
Рассмотрим две произвольные сопряженные
плоскости перпендикулярные оптической оси.
Отрезок величиной длиной у, лежащей в плоскости
в пространстве предметов, будет иметь своим
изображением отрезок y’, лежащей в сопряженной
плоскости. При этом изображение y’ может быть
обращено либо в туже сторону, что и предмет либо
в обратную. В первом случае изображение
называется прямым, во втором обратным.
245. Оптическая система. 24.6
Отрезки, откладываемые от оптической оси вверх, считаютсяположительными, вниз – отрицательными.
Отношение линейных размеров изображения и предмета называется
линейным или поперечным увеличением:
y'
y
Линейное увеличение – алгебраическая величина. Оно положительное,
если изображение прямое, и отрицательное, если изображение обратное.
Оказывается существуют две сопряженные
плоскости, которые отображают друг друга с
линейным увеличением β=+1. Такая плоскость
расположенная в пространстве предметов
называется передней или первой главной плоскостью
H, расположенная же в пространстве изображений –
задней или второй главной плоскостью Н’. Точки
пересечения этих плоскостей с главной оптической
осью называются главными точками.
246. Оптическая система. 24.7
Также существуют узловые точки или узлы. Сопряженные лучи,проходящие через узлы, параллельны между собой. Перпендикулярные
к оптической оси плоскости, проходящие через узлы, называются
узловыми плоскостями
Фокальные, узловые и главные плоскости называются кардинальными
плоскостями оптической системы. Главные точки, фокусы и узлы
называются кардинальными точками.
Расстояние от передней главной точки
до переднего фокуса называется
передним фокусным расстоянием f.
Аналогично – есть заднее фокусное
расстояние f’. Фокусные расстояния –
алгебраические величины. Они являются
положительными, если фокус находится
справа от соответствующей ему главной
точки и отрицательными если слева.
247. Оптическая система. 24.8
Между фокусными расстояниями центрированной оптической системы,образованной сферическими поверхностями существует следующее
соотношение
f
n
f'
=-
n'
Отсюда следует, что если показатели преломления сред в пространстве
предметов и изображений одинаков, то одинаковы по модулю и фокусные
расстояния.
f=-f '
Величина
Ф=
n' n
=f' f
Называется оптической силой системы. Чем больше оптическая сила,
тем сильнее система преломляет световые лучи, и следовательно тем
меньше фокусное расстояние. Оптическая сила системы Ф измеряется в
СИ в диоптрях Дп.
248. Оптическая система. 24.9
Задание кардинальных плоскостей или точек полностью определяетсвойства оптической системы. В частности, зная положение
кардинальных плоскостей, можно построить оптическое изображение,
даваемое системой. Таким образом, должно существовать
соотношение, связывающее положение предмета, оптические
характеристики системы и положение изображения. Расчеты дают
следующее соотношение:
xx'=ff'
x – расстояние от предмета до
переднего фокуса, x’ – расстояние от
заднего фокуса до изображения.
Это соотношение называется
формулой Ньютона.
Если показатели преломления сред с двух сторон от системы одинаковы
то формула Ньютона принимает вид:
xx'=-f 2
249. Оптическая система. 24.10
От формулы, связывающей расстояния x и x’, можно перейти к формулесвязывающей расстояния от предмета и изображения до главных
точек s s’:
f f'
s
s'
1
Если показатели преломления сред с двух сторон от системы одинаковы то
это соотношение принимает вид:
1 1 1
s s' f
Также можно получить выражения для линейного увеличения, даваемого
центрированной оптической системы:
y'
f
f'
y
x
x'
250. Лекция 25 Тонкая линза. Формула линзы. Ход лучей в тонких линзах. Построение изображений в собирающей линзе. Построение
изображений врассеивающей линзе.
Линзой называется прозрачное тело, ограниченное двумя сферическими
поверхностями. Если толщина самой линзы мала по сравнению с
радиусами кривизны сферических поверхностей, то линзу называют
тонкой в противном случае линзу называют толстой.
Линзы бывают собирающими и рассеивающими. Собирающая линза в
середине толще, чем у краев, рассеивающая линза, наоборот, в
средней части тоньше.
251. Тонкие линзы. 25.2
В случае тонкой линзы вершины преломляющих поверхностей можносчитать находящимися в одной точке, которую называют оптическим
центром линзы. В тонкой линзе обе главные плоскости линзы
проходят через ее оптический центр. Если показатели преломления
сред, находящихся по обе стороны линзы, одинаковы, то узлы
совпадают с главными точками, т.е. помещаются также в оптическом
центре линзы. Отсюда вытекает, что любой луч, идущий через
оптический центр линзы, не изменяет своего направления... Все
прямые, проходящие через оптический центр, называются побочными
оптическими осями.
252. Тонкие линзы. 25.3
Параллельный главной оптической оси пучок лучей, падающий насобирающую линзу, после выхода из линзы собирается в точке фокуса.
Если на линзу падает пучок световых лучей который не параллелен
главной оптической оси линзы, то для того чтобы построить ход
световых лучей по выходу из линзы, необходимо провести побочную
световую ось параллельную данному пучку.
Точка пересечения побочной оптической оси
с фокальной плоскостью даст положение
побочного фокуса для этого пучка.
Следовательно, за линзой световые лучи
этого пучка пройдут через побочный фокус.
253. Тонкие линзы. 25.4
Если параллельный главной оптической оси пучок световых лучей падаетна рассеивающую линзу, то после выхода он становится расходящимся,
так что продолжения лучей собираются в переднем фокусе. Если же на
линзу падает пучок лучей не параллельный главной оптической оси, то
необходимо провести побочную ось параллельную пучку.
Точка пересечения побочной оптической оси даст
положение побочного фокуса. Пучок расходится
таким образом, что продолжения световых лучей,
проведенные против направления распространения,
должны дать проходить через побочный фокус.
Фокусное расстояние тонкой линзы определяется
радиусами сферических поверхностей, образующих
линзу, а также показателями преломления линзы и
среды в которой находится линза:
n R 1R 2
F'=-F= 0
n-n 0 R 2 -R 1
254. Тонкие линзы. 25.5
Так как главные плоскости проходят через оптический центр тонкойлинзы, то f и f’ введенные, как расстояния до главных плоскостей в
случае тонких линз в тоже время являются расстояниями от фокуса до
тонкой линзы. Как и любая оптическая система, тонкая линза может
давать изображения, которые бывают прямыми и обратными,
действительными и мнимыми, увеличенными и уменьшенными.
Можно получить частный случай формулы оптической системы
применительно к тонкой линзе. Если расстояние от предмета до линзы
обозначить через d, а расстояние от линзы до изображения через f, то
формулу тонкой линзы можно записать в виде:
1 1 1
+ = =Ф
d f F
Фокусным расстояниям линз принято приписывать определенные
знаки: для собирающей линзы F > 0, для рассеивающей F < 0.
255. Тонкие линзы. 25.6
Величины d и f также подчиняются определенному правилу знаков:d > 0 и f > 0 – для действительных предметов (то есть реальных
источников света, а не продолжений лучей, сходящихся за линзой) и
изображений;
d < 0 и f < 0 – для мнимых источников и изображений.
Для построения изображения плоского предмета, опирающегося одним
концом на оптическую ось и перпендикулярного ей, необходимо построить
изображение того конца предмета, который не опирается на оптическую
ось, а затем опустить перпендикуляр на главную оптическую ось. Чтобы
построить изображение этой точки необходимо пустить два произвольных
луча на линзу, пересечение этих световых лучей после выхода из линзы
даст положение изображения. В принципе можно пустить любые лучи,
однако проще всего пустить луч параллельный главной оптической оси и
луч, проходящий через центр оптической судьбы.
256. Тонкие линзы. 25.7
В случае построения изображения в собирающей линзе есть трихарактерных области:
1) от линзы до фокуса;
2) между фокусом и двойным фокусом;
3) за двойным фокусом.
В первой области изображения является увеличенным, прямым и мнимым
и они располагаются в пространстве предметов.
Если предмет расположен во второй области то изображение предмета
будем обратным, увеличенным и действительным. Располагаться
изображения будут за двойным задним фокусом.
257. Тонкие линзы. 25.8
Если предметы будут располагаться за двойным передним фокусом, тоизображения будут уменьшенными, обратными и действительными.
Располагаться они будут между задним фокусом и двойным задним
фокусом. Есть еще две точки на оптической оси которые изображения
которых не было описано – двойной фокус и фокус. Изображение
предмета расположенного на расстоянии равным двойному фокусному
расстоянию будет находиться в двойном заднем фокусе и иметь
линейное увеличении -1, т.е. оно будет обратным, действительным его
размеры будут такие же, как и предмета. Предмет расположенный в
фокальной плоскости будет иметь изображение на бесконечности, так
как лучи вышедшие из любой точки в фокальной плоскости после
прохождения тонкой линзы превращаются в параллельный пучок.
258. Тонкие линзы. 25.9
Если предмет или его изображение находятся в бесконечности, толинейное увеличение утрачивает смысл. Частным случаем является
телескопический ход лучей в системе из двух линз, когда и предмет,
и второе изображение находятся на бесконечно больших
расстояниях. Телескопический ход лучей реализуется в зрительных
трубах – астрономической трубе Кеплера и земной трубе Галилея.
259. Тонкие линзы. 25.10
Тонкие линзы обладают рядом недостатков, не позволяющих получатьвысококачественные изображения. Искажения, возникающие при
формировании изображения, называются аберрациями. Главные из
них – сферическая и хроматическая аберрации. Сферическая
аберрация проявляется в том, что в случае широких световых пучков
лучи, далекие от оптической оси, пересекают ее не в фокусе. Формула
тонкой линзы справедлива только для лучей, близких к оптической
оси.
260. Лекция 26 Интерференция света. Когерентные источники. Интерференция от двух когерентных источников. Бипризма Френеля.
Интерференция приотражении от тонких пленок. Кольца Ньютона.
В электромагнитной волне колеблются два вектора – напряженности
электрического и напряженности магнитного полей. Как показывает
опыт, физиологическое, фотохимическое, фотоэлектрическое и другие
действия света вызываются колебаниями электрического вектора. В
соответствии с этим под световым вектором в дальнейшем будет
подразумеваться вектора напряженности электрического поля.
261. Интерференция. 26.2
Пусть в некоторую точку пространства приходят две световые волны. Этиволны возбуждают в пространстве колебания одинакового направления.
A 1 cos( t 1 ),
A 2 cos( t 2 ).
Амплитуда суммарного колебания определяется по правилу сложения двух
колебаний одинакового направления. В результате получим:
A 2 =A12 +A 22 +2A1A 2 cos( 1 2 ).
Если разность фаз δφ=(α1-α2) возбуждаемых волнами колебаний остается
постоянной во времени. То волны называются когерентными.
В случае говорят о сложении колебаний в фазе или синфазном сложении,
для которого следует, что амплитуда суммарных колебаний равна сумме
амплитуд каждого из колебаний
A=A1 +A2
262. Интерференция. 26.3
В случае говорят о сложении колебаний с противоположными фазамиили противофазном сложении, для которого следует, что амплитуда
суммарных колебаний равна модулю разности амплитуд каждого из
колебаний:
A=|A1 -A 2 |
Квадрат амплитуды напряженности электрического поля пропорционален
интенсивности I электромагнитного поля. С учётом этого следует
выражение для интенсивности суммы колебаний электромагнитных волн:
I=I1 +I2 +2 I1I2 cos( 1 2 ).
Явление перераспределения в пространстве интенсивности
электромагнитного поля, представляющего собой сумму двух
монохроматических волн одной частоты, в зависимости от их разности фаз
называется интерференцией.
263. Интерференция. 26.4
Явление интерференции можно наблюдать, разделив (с помощьюотражений или преломлений) волну, излучаемую одним источником, на
две части. В результате получим две когерентные волны. Затем
необходимо сложить их, предварительно заставив пройти различные
оптические пути.
В общем случае полученные таким образом две световые волны пройдут
до точки сложения пути s1 и s2. Первая волна возбудит в точке
сложения колебание
s
A 1 cos (t- 1 ),
v1
А вторая волна – колебание
A 2 cos (t-
s2
),
v2
264. Интерференция. 26.5
v1 c n1скорость распространения первой и второй волны
v2 c n 2
Таким образом, разность фаз колебаний, возбуждаемых в точке сложения,
будет равна
s2 s1
v2
-
(n 2s2 -n1s1 )
v1 c
2
c/
2
0
n 2s2 -n1s1 =L2 -L1
оптическая разность хода
265. Интерференция. 26.6
Таким образом, получаем, что если оптическая разность хода равнацелому числу длин волн, то волны в точке сложения колеблются
синфазно, так, как разность фаз равна числу кратному 2π. Т.е.
получаем условие интерференционного максимума:
k 0
(k = 0, 1, 2,...) max
Если же оптическая разность хода равна полуцелому числу длин волн в
вакууме то волны в точке сложения колеблются в противофазе, так, как
разность фаз равна (k2 Т.е.
) получаем условие
интерференционного минимума:
1
(k+ ) 0 (k = 0, 1, 2,...) min
2
Рассмотрим более подробно основные свойства интерференционной
картины, создаваемой двумя источниками электромагнитных волн
одинаковой интенсивности и наблюдаемой на плоском экране,
расположенным на расстоянии l от плоскости расположения от
источников.
266. Интерференция. 26.7
В качестве таких источников могут быть, например две бесконечноузкие, параллельные друг - другу щели или два отверстиябесконечно малого диаметра, расстояние между которыми d<<l,
прорезанные в плоском непрозрачном экране. Пусть источники
электромагнитных волн располагаются в однородной среде с
показателем преломления n.
Параметрами интерференционной картины являются положение её
максимумов xmax и минимумов xmin, а также связанная с ними ширина
полос интерференционной картины Δx.
Для расчёта этих величин надо найти разность фаз излучаемых
источниками волн в точке наблюдения, расположенной на экране.
Для расчёта надо определить оптическую разность хода Δ волн от
первого и второго источников до точки наблюдения
267. Интерференция. 26.8
22 n(l2 l1 )
0
0
l12 =l2 +(x-0.5d)2 ;
l22 =l2 +(x+0.5d)2 .
l22 -l12 =(l2 -l1 )(l1 +l2 ) 2xd
xd
l
nxd
l
m 0 l
k 0
(l2 -l1 )
x max m
x
0 l
nd
nd
1
(k+ ) 0
2
x min m
(k = 0, 1, 2,...) max
(k = 0, 1, 2,...) min
(0.5 m) 0l
nd
Ширина интерференционной полосы опредемая, как
расстояние между соседними интерференционными
максимумами или минимумами, интерференционные порядки
которых отличаются на единицу.
268. Интерференция. 26.9
Бизеркала Френеля – два плоскихзеркала располагаются так, что
их отражающие поверхности
образуют угол близкий к π
0
d 2r sin 2r
a r cos r
l a b
x
r b
2ar
l r b
ширина интерференционной полосы
x 2btg 2b
x
4a 2br
N
x ( r b)
- область перекрытия волн на экране
число интерференционных полос
269. Интерференция. 26.10
Одним из наиболее часто используемых в лабораториях приборов дляполучения интерференции является бипризма Френеля изготовленные из одного куска стекла две призмы с малым
преломляющим углом θ имеющие общее основание. При освещении
бипризмы Френеля монохроматическим светом от источника,
расположенного на расстоянии а на экране будет наблюдаться картина
чередующихся светлых и темных
(n 1)
d 2a sin 2a 2a(n 1)
l a b
a b
x
2a(n 1)
ширина интерференционной полосы
4ab(n 1) 2 2
N
( a b)
число интерференционных полос
270. Интерференция. 26.11
При падении световой волны натонкую прозрачную пластинку или
пленку происходит отражение от
обеих поверхностей пластинки π В
результате возникают когерентные
световые волны, которые могут
интерферировать. Δ=nS22b
S1
S 2 2 AO
cos 2
S1 BC AC sin 1 2btg 2 sin 1
n2
n2
n sin 2 sin 1
n 2 sin 2 2
n 2 cos 2
2bn
2btg 2 sin 2 2b
n sin 2 sin 1 2b
2b
cos 2
n
cos
n
cos
n
cos
n
cos
n cos 2
2
2
2
2
2b cos 2 2b n 2 1 sin 2 2 n 2 n 2 n 2 sin 2 2 n sin 2 sin 1 2b
n
2
sin 2 1
Результирующая оптическая разность хода определяется следующим
соотношением:
2b n 2 sin 2 1 0
2
При отражении от границы раздела среды оптически более плотной,
фаза претерпевает изменение на π
271. Интерференция. 26.12
Первый эксперимент по наблюдениеинтерференции света в лабораторных
условиях принадлежит Ньютону. Он
наблюдал интерференционную картину,
возникающую при отражении света в
тонкой воздушной прослойке между
плоской стеклянной пластиной и
плосковыпуклой линзой большого
радиуса кривизны. Интерференционная
картина имела вид концентрических
колец, получивших название колец
R
r
b
Ньютона.
r
R 0
(m 1)
2
m 1, 2,3....
где R – радиус плосковыпуклой линзы. Четным m соответствуют
радиусы светлых колец, нечетным радиусы темных колец.
272. Лекция 27 Дифракция света. Принцип Гюйгенса-Френеля. Зоны Френеля. Диаграмма Френеля.
Дифракцией света называется явление отклонения света отпрямолинейного направления распространения при прохождении
вблизи препятствий. Как показывает опыт, свет при определенных
условиях может заходить в область геометрической тени. Если на пути
параллельного светового пучка расположено круглое препятствие
(круглый диск, шарик или круглое отверстие в непрозрачном экране),
то на экране, расположенном на достаточно большом расстоянии от
препятствия, появляется дифракционная картина – система
чередующихся светлых и темных колец. Если препятствие имеет
линейный характер (щель, нить, край экрана), то на экране возникает
система параллельных дифракционных полос.
Первое качественное объяснение явления дифракции на основе
волновых представлений было дано английским ученымТ.
Юнгом. Независимо от него французский ученый О. Френель
развил количественную теорию дифракционных явлений
(1818 г.).
273. Дифракция. 27.2
В основу теории Френель положил принцип Гюйгенса, дополнив егоидеей об интерференции вторичных волн.
Каждая точка, до которой доходит волновое движение, служит центром
вторичных волн; огибающая этих волн дает положение фронта волны в
следующий момент времен. Принцип Гюйгенса
Различают два вида явления дифракции в зависимости от расстояния
точки наблюдения до препятствия или неоднородности, а также от вида
волнового фронта в точке наблюдения. Если точка наблюдения
расположена достаточно далеко от препятствия и в точку наблюдения
после взаимодействия с неоднородностью приходит плоская волна, то
говорят о дифракции Фраунгофера. В остальных случаях говорят о
дифракции Френеля.
274. Дифракция. 27.3
Как следует из принципа Гюйгенса- Френеля амплитуда волны вточке наблюдения Р, создаваемая источником монохроматической
электромагнитной волны в точке О, может быть найдена как
суперпозиция амплитуд сферических волн, испускаемых вторичными
источниками на произвольной замкнутой поверхности S,
охватывающей точку O. Пусть S сферическая поверхность радиуса a c
центром в точке S. Разобьем волновую поверхность на кольцевые
зоны, зоны Френеля, таким образом, что бы расстояние от краев
каждой зоны до точки Р отличались на
Тогда расстояние от внешнего
края m-й зоны до точки Р
можно представить
следующим образом:
bm b m
2
2
275. Дифракция. 27.4
Колебания приходящие в точку Р от аналогичных точек двух соседних зон,находятся в противофазе. Поэтому и результирующее колебания,
создаваемые каждой из зон в целом будут для соседних зон
различаться по фазе на π. Для определения результирующей
амплитуды в точке Р, необходимо знать амплитуду создаваемую каждой
из зон. Очевидно, что
амплитуда каждой из зон
зависит от ее площади.
Определим площадь
произвольной зоны Френеля.
Эта площадь будет являться
разностью площадей двух
сферических сегментов,
ганицы которых
соответствуют m-ой и
(m-1)-ой зонам Френеля.
Sm =Sm -Sm-1
276. Дифракция. 27.5
Площадь сферического сегмента вычисляется по формулеSm 2 ah m
где hm – высота сегмента. Определим ее
r a (a hm ) (b m / 2) (b hm )
2
m
2
2
2
2ahm h bm m ( / 2) 2bhm h
bm m2 ( / 2) 2
hm
2(a b)
bm
h
т.к. m
b , то m 2(a b)
2
m
2
2
bm b m / 2
2
2
m
rm
S
Р
O
э
b
a
hm
Таким образом, получаем площадь сферического сегмента:
ab
Sm 2 ah m
m
a b
277. Дифракция. 27.6
В результате площадь m-й зоны ФренеляSm =Sm -Sm-1
ab
a b
Полученное выражение не зависит от m. Следовательно, при не слишком
больших m площади зон Френеля примерно одинаковы.
Радиус m-ой зоны Френеля:
rm
ab
m
a b
Если положить a=b=1 м и λ=0.5 мкм, то для радиуса первой зоны
получается значение 0.5 мм.
278. Дифракция. 27.7
Одинаковые по площади зоны должны были бы возбуждать в точкенаблюдения колебания с одинаковой амплитудой. Однако у каждой
последующей зоны угол α между лучом, проведенным в точку
наблюдения, и нормалью к волновой поверхности возрастает.
Френель высказал предположение (подтвержденное экспериментом),
что с увеличением угла α амплитуда колебаний уменьшается, хотя и
незначительно
A1 > A2 > A3 > ... > Am,
С хорошим приближением можно считать, что амплитуда колебаний,
вызываемых некоторой зоной, равна среднему арифметическому из
амплитуд колебаний, вызываемых двумя соседними зонами, т. е.
Am 1 Am 1
Am
2
279. Дифракция. 27.8
Так как расстояния от двух соседних зон до точки наблюдения отличаютсяна λ / 2, следовательно, возбуждаемые этими зонами колебания
находится в противофазе. Поэтому волны от любых двух соседних зон
почти гасят друг друга. Суммарная амплитуда в точке наблюдения есть
A = A1 – A2 + A3 – A4 + ... = A1 – (A2 – A3) – (A4 – A5) – ...
Таким образом, суммарная амплитуда колебаний в точке P всегда меньше
амплитуды колебаний, которые вызвала бы одна первая зона Френеля. В
частности, если бы были открыты все зоны Френеля, то до точки
наблюдения дошла бы невозмущенная препятствием волна с амплитудой
A0. В этом случае можно записать:
A A0
A A
A
A1 A1
A
A2 3 3 A4 5 .... 1
2 2
2 2
2
2
так как выражения, стоящие в скобках, равны нулю. Следовательно,
действие (амплитуда), вызванное всем волновым фронтом, равно
половине действия одной первой зоны.
280. Дифракция. 27.9
Если отверстие в непрозрачном экране оставляет открытой только однузону Френеля, то амплитуда колебаний в точке наблюдения возрастает
в 2 раза (а интенсивность в 4 раза) по сравнению с действием
невозмущенной волны. Если открыть две зоны, то амплитуда
колебаний обращается в нуль. Если изготовить непрозрачный экран,
который оставлял бы открытыми только несколько нечетных (или
только несколько четных) зон, то амплитуда колебаний резко
возрастает. Например, если открыты 1, 3 и 5 зоны, то
A 6 A0 , I 36I 0
281. Дифракция. 27.10
Разобьем волновую поверхность на кольцевые зоны, аналогичные зонамФренеля, но гораздо меньше по ширине ( разность хода от краев зоны
до точки Р составляет одинаковую для всех зон малую долю λ).
Колебание, создаваемое в точке Р каждой из зон, изобразим в виде
вектора, длина которого равна амплитуде колебания, а угол,
образуемый вектором с направлением принятым за начало отсчета,
дает начальную фазу колебания. В силу разбиения зон два любых
соседних вектора будут повернуты друг относительно друга на один
угол. Также амплитуда при переходе от зоны к зоне уменьшается.
Следовательно, векторная диаграмма, получаемая при сложении
колебаний возбуждаемых отдельными зонами, будет иметь вид спирали.
282. Лекция 28 Дифракция Френеля от простейших преград. Дифракция от круглого отверстия. Дифракция Френеля от простейших преград.
Дифракция отнепрозрачного круглого диска. Дифракционная решетка.
Метод расчёта с помощью зон Френеля интенсивности света в точке
наблюдения применим для анализа задач дифракции
электромагнитных волн на простых по форме препятствиях .
Пусть экран с отверстием радиуса r0 расположен так, так что центр
отверстия расположен на прямой, перпендикулярной плоскости экрана с
отверстием, соединяющей точку наблюдения P и точку источника S.
Разобьем поверхность волнового фронта, падающего на отверстие, на
зоны Френеля по отношению к точке наблюдения P. Будем называть
открытыми такие зоны Френеля, которые располагаются внутри отверстия.
Соответственно зоны Френеля, попадающие на поверхность
непрозрачного экрана, называются закрытыми.
283. Дифракция. 28.2
Если размер отверстия во много раз меньше расстояний от экрана доисточника a и от экрана до точки наблюдения b, то можно найти число
2
m открытых отверстием зон Френеля:
1 1 r0
m= +
a b
284. Дифракция. 28.3
Суммарная амплитуда в точке наблюдения естьA = A1 – A2 + A3 – A4 + ... ±Am = 0.5(A1±Am)
Амплитуды волн зон Френеля при их небольшом числе можно считать
примерно одинаковыми. По этой причине в точке Р будет либо максимум,
либо минимум интенсивности дифрагированной волны от отверстия в
зависимости соответственно от нечётности или чётности числа открытых
зон Френеля.
285. Дифракция. 28.4
m – четноеРассмотрим наблюдение интенсивности дифрагированного
отверстием света на непрозрачном экране, помещённом в
точку P, параллельно плоскости экрана с отверстием. В виду
симметрии наблюдаемое на экране распределение
интенсивности света будет иметь характер чередующихся
тёмных и светлых колец с центром в точке P. Интенсивность
света в максимумах по мере удаления от центральной точки A A1 Am
будет убывать. Убывание объясняется тем, что при
2
2
смещении точки наблюдения P из центра на периферию
открытые из точки P центральные зоны Френеля частично
закрываются и, кроме того, частично открываются новые
зоны Френеля, ослабляющие интенсивность света в точке
наблюдения.
m – нечетное
A1 Am
A
2
2
286. Дифракция. 28.5
Пусть свет из точки источника S освещает непрозрачный диск радиуса r0,за которым на прямой, перпендикулярной плоскости диска и
проведенной через его центр, располагается точка наблюдения P. Как и
выше, будем считать, что размер диска во много раз меньше
расстояний от диска до источника a и от диска до точки наблюдения b.
287. Дифракция. 28.6
Предположим, что диск из точки наблюдения P закрывает m зон Френеля. Тогдаамплитуда света A в точке наблюдения будет равна алгебраической сумме
амплитуд волн Am+1 ,Am+2 ,Am+3 ,.... открытых зон Френеля:
A=Am+1 -Am+2 +Am+3 -....=0.5Am+1 + 0.5Am+1 -0.5Am+2 +(0.5Am+3 -0.5Am+2 )+...
Учитывая, что амплитуды соседних зон Френеля примерно равны друг
другу, однотипные выражение в скобках можно положить равными нулю,
и тогда получим:
A=0.5A m+1
Отсюда следует, что в центре дифракционной картины, создаваемой
диском, всегда наблюдается светлое пятно, независимо от размеров диска.
288. Дифракция. 28.7
Дифракционная картина от диска, наблюдаемая на экране,имеет характер чередующихся тёмных и светлых колец,
в центре которых находится светлое пятно. Структура
дифракционной картины света от непрозрачного диска
имеет общие черты с дифракционной картиной света от
отверстия того же диаметра в непрозрачном экране.
Периодическая система одинаковых, расположенных на одном и том же
расстоянии друг от друга щелей, называется дифракционной решёткой.
Расстояние d между серединами соседних щелей называется периодом
дифракционной решётки. Обычно в дифракционных решётках,
используемых в оптике, щели являются узкими, т.е. их размер b во
много раз меньше периода дифракционной решётки d<<b. Размер
дифракционной решётки, состоящей из N узких щелей, называется её
шириной L и вычисляется по формуле L=Nd.
289. Дифракция. 28.8
При освещении дифракционной решётки плоской световой волной сдлинной волны λ, нормально падающей на решётку, на достаточно
большом расстоянии от решётки наблюдается дифракционная картина,
которая может наблюдаться и на конечном расстоянии с помощью
выпуклой линзы на плоском экране, помещённом в её фокусе.
290. Дифракция. 28.9
Характер распределения интенсивности представляет собой чередованиеглавных дифракционных максимумов, между которыми располагаются
побочные дифракционные максимумы и минимумы. Главные
дифракционные максимумы интенсивности располагаются в
направлениях φm, в которых волны от щелей в точке наблюдения имеют
разность хода, кратную λ, т.е.:
d sin m m
где - целые числа. Главный дифракционный максимум, соответствующий
направлению, называется дифракционным максимумом m- го порядка.
Центральный дифракционный максимум соответственно является
дифракционным максимумом нулевого порядка (m=0) и имеет
наибольшую величину.
291. Дифракция. 28.10
I6
d
2
b
5
d
4
d
3
d
b
2
d
d
0
d
2
d
3
d
b
4
d
5
d
6
d
2
b
sin
292. Лекция 29 Закономерности в атомных спектрах. Опыт по рассеянию альфа частиц. Модель атома Резерфорда. Постулаты Бора.
Элементарная боровская теория водородоподобного атома.Еще в начале XIX века были открыты дискретные спектральные линии в
излучении атома водорода в видимой области (так называемый
линейчатый спектр).
Впоследствии закономерности, которым подчиняются длины волн (или
частоты) линейчатого спектра, были хорошо изучены количественно
(И. Бальмер, 1885 г.). Совокупность спектральных линий атома
водорода в видимой части спектра была названа серией Бальмера.
Позже аналогичные серии спектральных линий были обнаружены в
ультрафиолетовой и инфракрасной частях спектра. В 1890 году
И. Ридберг получил эмпирическую формулу для частот спектральных
линий:
1
1
nm R 2 2
n
m
293. Атомная физика. 29.2
Для серии Бальмера m = 2, n = 3, 4, 5, ... . Для ультрафиолетовой серии(серия Лаймана) m = 1, n = 2, 3, 4, ... . Постоянная R в этой формуле
называется постоянной Ридберга. Ее численное значение
R = 3,29·1015 Гц.
294. Атомная физика. 29.3
Первая попытка создания модели атома на основе накопленныхэкспериментальных данных принадлежит Дж. Томсону (1903 г.). Он
считал, что атом представляет собой электронейтральную систему
шарообразной формы радиусом примерно равным 10–10 м.
Положительный заряд атома равномерно распределен по всему
объему шара, а отрицательно заряженные электроны находятся
внутри него. Для объяснения линейчатых спектров испускания атомов
Томсон пытался определить расположение электронов в атоме и
рассчитать частоты их колебаний около положений равновесия.
295. Атомная физика. 29.4
Первые прямые эксперименты по исследованию внутренней структурыатомов были выполнены Э. Резерфордом и его сотрудниками
Э. Марсденом и Х. Гейгером в 1909–1911 годах. Резерфорд предложил
применить зондирование атома с помощью α-частиц, которые
возникают при радиоактивном распаде радия и некоторых других
элементов. Масса α-частиц приблизительно в 7300 раз больше массы
электрона, а положительный заряд равен удвоенному элементарному
заряду. В своих опытах Резерфорд использовал α-частицы с
кинетической энергией около 5 МэВ (скорость таких частиц очень
велика – порядка 107 м/с, но она все же значительно меньше скорости
света). α-частицы – это полностью ионизированные атомы гелия.
296. Атомная физика. 29.5
Опыты Резерфорда и его сотрудников привели к выводу, что в центреатома находится плотное положительно заряженное ядро, диаметр
которого не превышает 10–14–10–15 м. Это ядро занимает только 10–12
часть полного объема атома, но содержит весь положительный заряд и
не менее 99,95 % его массы. Веществу, составляющему ядро атома,
следовало приписать плотность порядка ρ ≈ 1015 г/см3. Заряд ядра
должен быть равен суммарному заряду всех электронов, входящих в
состав атома. Опираясь на классические
представления о движении микрочастиц,
Резерфорд предложил планетарную модель
атома. Разработал классическую теорию
рассеяния α-частиц, и получил формулу для
распределения рассеянных частиц по значению
угла отклонения от первоначального направления:
2
Ze 2
dN
d
nd
2
4
N
m
v
sin ( / 2)
Согласно планетарной модели, в центре атома располагается
положительно заряженное ядро, в котором сосредоточена почти вся масса
атома. Атом в целом нейтрален. Вокруг ядра, подобно планетам,
вращаются под действием кулоновских сил со стороны ядра электроны.
297. Атомная физика. 29.6
По законам классической электродинамики, движущийся с ускорениемзаряд должен излучать электромагнитные волны, уносящие энергию. За
короткое время (порядка 10–8 с) все электроны в атоме Резерфорда
должны растратить всю свою энергию и упасть на ядро. То, что этого
не происходит в устойчивых состояниях атома, показывает, что
внутренние процессы в атоме не подчиняются классическим законам.
Следующий шаг в развитии представлений об устройстве атома сделал в
1913 году датский физик Н. Бор.
Первый постулат Бора (постулат стационарных состояний) гласит: атомная
система может находится только в особых стационарных или квантовых
состояниях, каждому из которых соответствует определенная энергия En.
В стационарных состояниях атом не излучает.
298. Атомная физика. 29.7
Второй постулат Бора (правило частот) формулируется следующимобразом: при переходе атома из одного стационарного состояния с
энергией En в другое стационарное состояние с энергией Em излучается
или поглощается квант, энергия которого равна разности энергий
стационарных состояний:
h nm nm En -Em
где h – постоянная Планка
h=6.626 10-34 Дж с
Третий постулат (Правило квантования). Бор предположил, что из всех
возможных орбит электрона осуществляются только те для которых
момент импульса равен целому кратному постоянной планка h, деленной
на 2π:
me vr n (n=1, 2, 3,....)
Число n – называется главным квантовым числом.
299. Атомная физика. 29.8
Применим полуклассический подход Бора к описанию движения электронав поле ядра с зарядом Ze. При Z=1 такая система соответствует атому
водорода. Произведение массы электрона на его центростремительное
ускорение должно равняться силе кулона, действующей на электрон:
v 2 Ze2
me = 2
r
r
me vr n
rn
2
me Ze
2
n2
(n=1, 2, 3,...)
(n=1, 2, 3,....)
Видно, что радиус может принимать только дискретные значения.
Внутренняя энергия атома складывается из энергии взаимодействия
электрона с ядром и кинетической электрона:
me v 2 Ze2
E=
2
r
300. Атомная физика. 29.9
Кинетическую энергию находим следующим образом:v 2 Ze2
v 2 Ze2
me = 2 me =
r
r
2
2r
Тогда внутренняя энергия атома
Окончательно, получим:
Ze2 Ze2 Ze2
E=
=2r
r
2r
m e e 4 Z2
En
(n=1, 2, 3,...)
2 2
2 n
При переходе атома водорода (Z=1) из состояния n в состояние m
излучается квант
me e 4 1 1
E n -E m 2 2 - 2
2 n m
Частота испущенного свет равна:
me e 4 1 1
2- 2
2 3 m n
301. Атомная физика. 29.10
302. Лекция 30 Гипотеза де Бройля. Принцип неопределенности. Уравнение Шредингера. Пси-функция. Ее свойства.
В 1923 году французский физик Л. де Бройль выдвинул гипотезу обуниверсальности корпускулярно-волнового дуализма. Де Бройль
утверждал, что не только фотоны, но и электроны и любые другие
частицы материи наряду с корпускулярными обладают также и
волновыми свойствами. Согласно де Бройлю, с каждым микрообъектом
связаны, с одной стороны, корпускулярные характеристики – энергия
E и импульс p, а с другой стороны, волновые характеристики – частота
ν и длина волны λ.
Корпускулярные и волновые характеристики микрообъектов связаны
такими же количественными соотношениями, как и у фотона:
E=h , p=
h h
c
Гипотеза де Бройля постулировала эти соотношения для всех
микрочастиц, в том числе и для таких, которые обладают массой m. Любой
частице, обладающей импульсом, сопоставлялся волновой процесс с
длиной волны λ = h / p. Для частиц, имеющих массу,
h
h
=
p mv
303. Элементы квантовой механики. 30.2
Первое экспериментальное подтверждениегипотезы де Бройля было получено в
1927 году американскими физиками
К. Девиссоном и Л. Джермером. Они
обнаружили, что пучок электронов,
рассеивающийся на кристалле никеля, дает
отчетливую дифракционную картину,
подобную той, которая возникает при
рассеянии на кристалле коротковолнового
рентгеновского излучения. В этих
экспериментах кристалл играл роль
естественной дифракционной решетки. По
положению дифракционных максимумов была
определена длина волны электронного пучка,
которая оказалась в полном соответствии с
формулой де Бройля.
304. Элементы квантовой механики. 30.3
В следующем 1928 году английский физик Дж. Томсон получил новоеподтверждение гипотезы де Бройля. В своих экспериментах Томсон
наблюдал дифракционную картину, возникающую при прохождении
пучка электронов через тонкую поликристаллическую фольгу из
золота. На установленной за фольгой фотопластинке отчетливо
наблюдались концентрические светлые и темные кольца, радиусы
которых изменялись с изменением скорости электронов (т. е. длины
волны) согласно де Бройлю.
305. Элементы квантовой механики. 30.4
В последующие годы опыт Дж. Томсона был многократно повторен снеизменным результатом, в том числе при условиях, когда поток
электронов был настолько слабым, что через прибор
единовременно могла проходить только одна частица
(В. А. Фабрикант, 1948 г.). Таким образом, было экспериментально
доказано, что волновые свойства присущи не только большой
совокупности электронов, но и каждому электрону в отдельности.
306. Элементы квантовой механики. 30.5
Новая теория, которая учитывает корпускулярно-волновой дуализммикрочастиц, называется волновая или квантовая механика. Основным
уравнением квантовой механики является уравнение Шредингера. Его
следует рассматривать как исходное основное предположение,
справедливость которого доказывается тем обстоятельством, что все
вытекающие из него следствия точным образом согласуются с
опытными фактами.
Состояние микрочастицы описывается в квантовой механике волновой
функцией Ψ. Она является функцией координат и времени и может быть
найдена путем решения уравнения:
U i
2m
t
Это уравнение было установлено Шредингером в 1926 г. И называется
уравнением Шредингера со временем.
В это уравнение входят следующие величины: i – мнимая единица, m –
масса частицы, - оператор Лапласа
307. Элементы квантовой механики. 30.6
2 2 22 2 2
x
y
z
U – потенциальная энергия частицы.
Как следует из уравнения Шредингера, волновая функция определяется
потенциальной энергией, т.е. видом сил действующих на частицу. Если
потенциальная энергия остается постоянной во времени, то волновая
функция распадается на два множителя, один из которых зависит только
от времени, второй только от координат.
( x, y, z, t ) e
E
i t
( x, y, z)
где Е – полная энергия частицы. Для случая стационарного поля
уравнение Шредингера преобразуется к следующему виду.
2m
2 ( E U ) 0
Это соотношение называется уравнением Шредингера для стационарных
состояний.
308. Элементы квантовой механики. 30.7
Физический смысл Ψ функции состоит в следующем: квадрат модуля Ψопределяет вероятность dP того, что частица будет обнаружена в
пределах объема dV:
dP | |2 dV * dV
Волновые функции должны всегда быть нормированы таким образом,
чтобы:
*
dV 1
Волновые функции, получаемые из решений уравнения Шредингера
должны удовлетворять следующим условиям:
1) однозначность;
2) конечность;
3) непрерывность.
Эти условия должны выполняться во всей области изменения
переменных x, y, z. Они являются следствием того факта, что волновая
функция по своему физическому смыслу определяет вероятность.
309. Элементы квантовой механики. 30.8
Уровни энергии, волновые функции, распределение плотностивероятности по координате х
310. Элементы квантовой механики. 30.9
При определенных условиях понятия положения в пространстве итраектории оказываются приближенно применимыми к движению
микрочастиц. Степень точности, с какой к частице может быть
применено представление об определенном положении ее в
пространстве, дается соотношением неопределенностей,
установленным Гайзенбергом. Наиболее важным являются два
соотношения неопределенностей.
Первое из них ограничивает точности одновременного измерения
координат и соответствующих проекций импульса частицы. Для проекции,
например на ось Х оно выглядит следующим образом:
x px
Второе соотношение устанавливает неопределенность измерения энергии,
ΔЕ, за данный промежуток времени Δt:
E t
311. Элементы квантовой механики. 30.10
312. Лекция 31 Таблица Менделеева. Состав и характеристики атомного ядра. Масса и энергия связи ядра. Радиоактивность. Виды
радиоактивности.Альфа-распад. Бета-распад.
К 20-м годам XX века физики уже не сомневались в том, что атомные ядра,
открытые Э. Резерфордом в 1911 г., также как и сами атомы, имеют
сложную структуру. В этом их убеждали многочисленные
экспериментальные факты, накопленные к этому
времени: открытие радиоактивности,
экспериментальное доказательство ядерной
модели ядра, измерение отношения e / m
для электрона, α-частицы и для так называемой
H-частицы – ядра атома водорода, открытие
искусственной радиоактивности и ядерных
реакций, измерение зарядов атомных ядер и т. д.
В настоящее время твердо установлено, что атомные ядра
различных элементов состоят из двух частиц – протонов и
нейтронов.
313. Элементы атомной физики. 31.2
По современным измерениям, положительный заряд протона в точностиравен элементарному заряду e = 1,60217733·10–19 Кл, то есть равен по
модулю отрицательному заряду электрона. В настоящее время равенство
зарядов протона и электрона проверено с точностью 10–22. Масса протона,
по современным измерениям, равна
mp = 1,67262·10–27 кг.
В ядерной физике массу частицы часто выражают в атомных единицах
массы (а. е. м.), равной 1/12 массы атома углерода с массовым числом 12
1 а.е.м.=1.66057 ·10-27 кг
mp = 1,007276 · а. е. м.
Во многих случаях массу частицы удобно выражать в эквивалентных значениях
энергии в соответствии с формулой E = mc2. Так как 1 эВ = 1,60218·10–19 Дж, в
энергетических единицах масса протона равна
938,272331 МэВ.
314. Элементы атомной физики. 31.3
Нейтрон – это нейтральная частица. По современным измерениям, массанейтрона
mn = 1,67493·10–27 кг = 1,008665 а. е. м.
В энергетических единицах масса нейтрона равна 939,56563 МэВ. Масса
нейтрона приблизительно на две электронные массы превосходит массу
протона.
Для характеристики атомных ядер вводится ряд обозначений. Число
протонов, входящих в состав атомного ядра, обозначают символом Z и
называют зарядовым числом или атомным номером (это порядковый
номер в периодической таблице Менделеева). Заряд ядра равен Ze, где e –
элементарный заряд. Число нейтронов обозначают символом N.
Общее число нуклонов (т. е. протонов и нейтронов) называют
массовым числом A:
A=Z+N
315. Элементы атомной физики. 31.4
Ядра химических элементов обозначают символомA
Z
X
где X – химический символ элемента.
Энергия связи ядра равна минимальной энергии, которую необходимо
затратить для полного расщепления ядра на отдельные частицы. Из
закона сохранения энергии следует, что энергия связи равна той энергии,
которая выделяется при образовании ядра из отдельных частиц. Энергию
связи любого ядра можно определить с помощью точного измерения его
массы. Эти измерения показывают, что масса любого ядра Mя всегда
меньше суммы масс входящих в его состав протонов и нейтронов.
Mя < Zmp + Nmn
Разность масс
ΔM = Zmp + Nmn – Mя.
называется дефектом массы.
316. Элементы атомной физики. 31.5
По дефекту массы можно определить с помощью формулыЭйнштейна E = mc2 энергию, выделившуюся при образовании данного
ядра, т. е. энергию связи ядра Eсв:
Eсв = ΔMc2 = (Zmp + Nmn – Mя)c2.
Эта энергия выделяется при образовании ядра в виде излучения γ-квантов
В таблицах принято указывать удельную энергию связи, т. е. энергию
связи на один нуклон. Удельная энергия связи нуклонов у разных атомных
ядер неодинакова.
317. Элементы атомной физики. 31.6
Уменьшение удельной энергии связи припереходе к тяжелым элементам
объясняется увеличением энергии
кулоновского отталкивания протонов. В
тяжелых ядрах связь между нуклонами
ослабевает, а сами ядра становятся менее
прочными. Наиболее устойчивыми с
энергетической точки зрения являются
ядра элементов средней части таблицы
Менделеева. Это означает, что существуют
две возможности получения
положительного энергетического выхода
при ядерных превращениях:
1) деление тяжелых ядер на более легкие;
2) слияние легких ядер в более тяжелые.
В обоих этих процессах выделяется огромное
количество энергии. В настоящее время
оба процесса осуществлены практически:
реакции деления и термоядерные реакции.
318. Элементы атомной физики. 31.7
319. Элементы атомной физики. 31.8
Почти 90 % из известных 2500 атомных ядер нестабильны. Нестабильноеядро самопроизвольно превращается в другие ядра с испусканием
частиц. Это свойство ядер называется радиоактивностью.
Так как радиоактивный распад имеет случайный характер и не зависит от
внешних условий, то закон убывания количества N(t) нераспавшихся к
данному моменту времени t ядер может служить важной статистической
характеристикой процесса радиоактивного распада.
N (t ) N 0 e t
N0 – число нераспавшихся частиц в начальный
момент времени,
λ – постоянная радиоактивного распада, которая
характеризует вероятность распада ядра в единицу
времени.
320. Элементы атомной физики. 31.9
За времяτ=1/λ
количество нераспавшихся ядер уменьшится в e ≈ 2,7 раза. Величину τ
называют средним временем жизни радиоактивного ядра. Для
практического использования закон радиоактивного распада удобно
записать в другом виде, используя в качестве основания число 2, а не e:
N (t ) N 0 2 /T
Величина T называется периодом полураспада. За время T распадается
половина первоначального количества радиоактивных ядер. Величины T и
τ связаны соотношением
1
T
ln 2 ln 2 0.693
321. Элементы атомной физики. 31.10
Альфа-распадом называется самопроизвольное превращение атомногоядра с числом протонов Z и нейтронов N в другое (дочернее) ядро,
содержащее число протонов Z – 2 и нейтронов N – 2. При этом
испускается α-частица – ядро атома гелия . Примером такого процесса
может служить α-распад радия:
226
88
222
Ra 86
Rn+ 42 He
При бета-распаде из ядра вылетает электрон. Внутри ядер электроны
существовать не могут, они возникают при β-распаде в результате
превращения нейтрона в протон. Этот процесс может происходить не
только внутри ядра, но и со свободными нейтронами. Среднее время
жизни свободного нейтрона составляет около 15 минут. При распаде
нейтрон превращается в протон и электрон . В процессе распада
нейтрона возникает частица, которая называется электронным
антинейтрино
234
90
234
Th 91
Pa 0 1 e 00 e
322. Элементы атомной физики. 31.11
В отличие от α- и β-радиоактивности γ-радиоактивность ядер несвязана с изменением внутренней структуры ядра и не сопровождается
изменением зарядового или массового чисел. Как при α-, так и при βраспаде дочернее ядро может оказаться в некотором возбужденном
состоянии и иметь избыток энергии. Переход ядра из возбужденного
состояния в основное сопровождается испусканием одного или
нескольких γ-квантов, энергия которых может достигать нескольких
МэВ.




























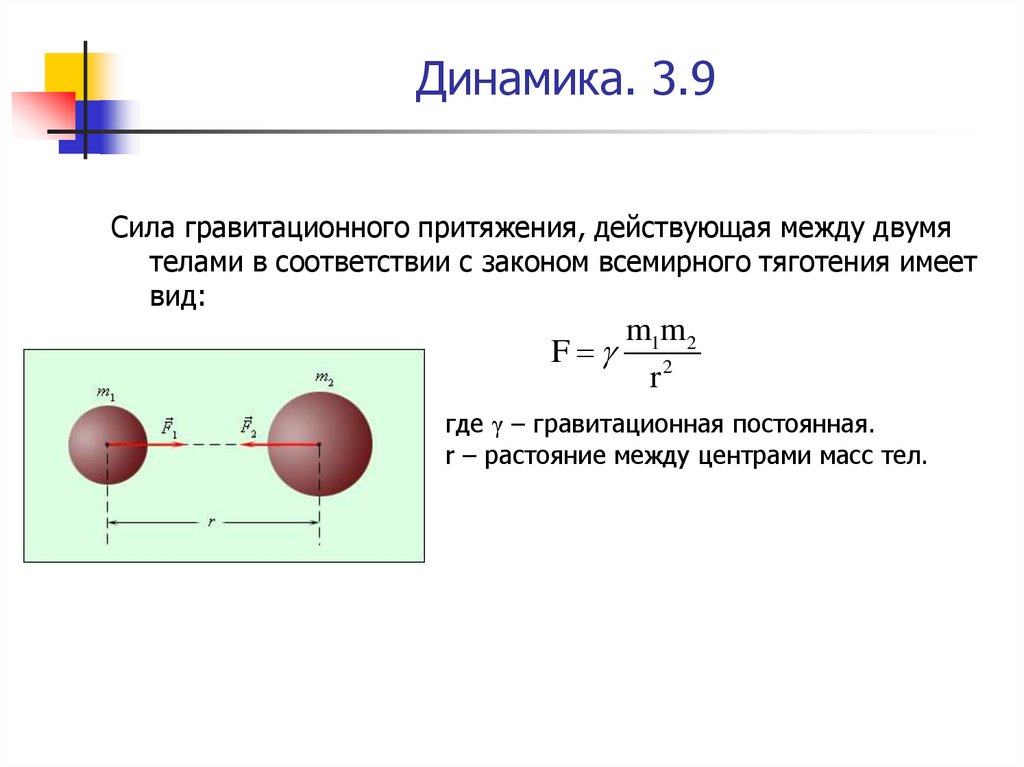































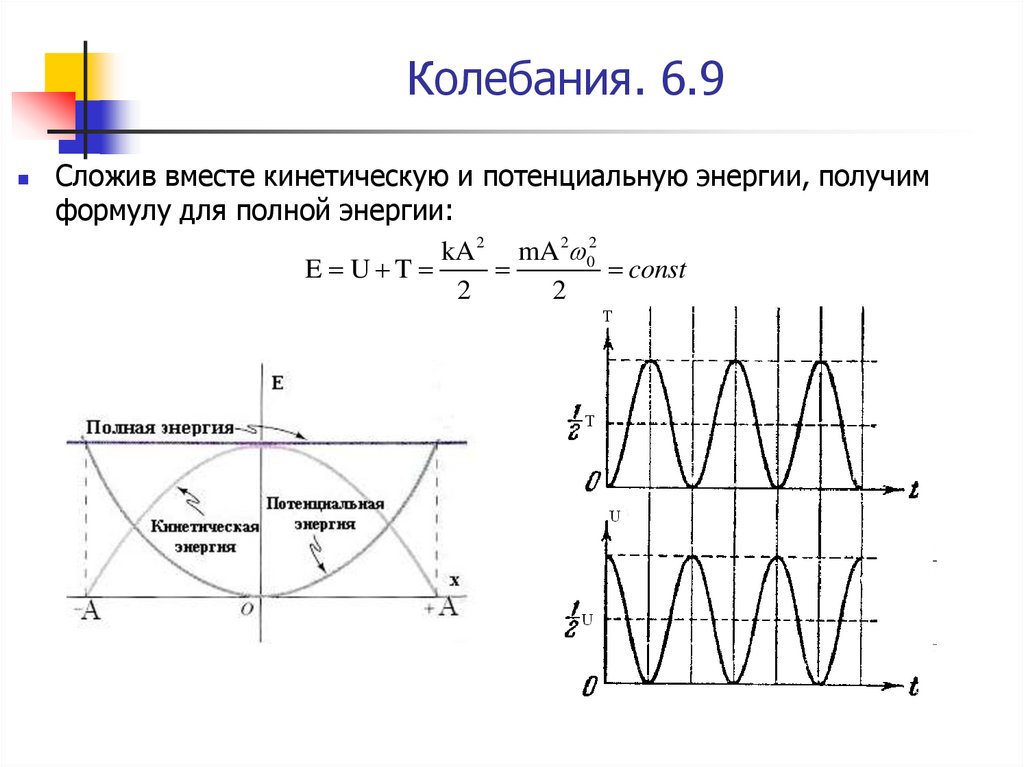
















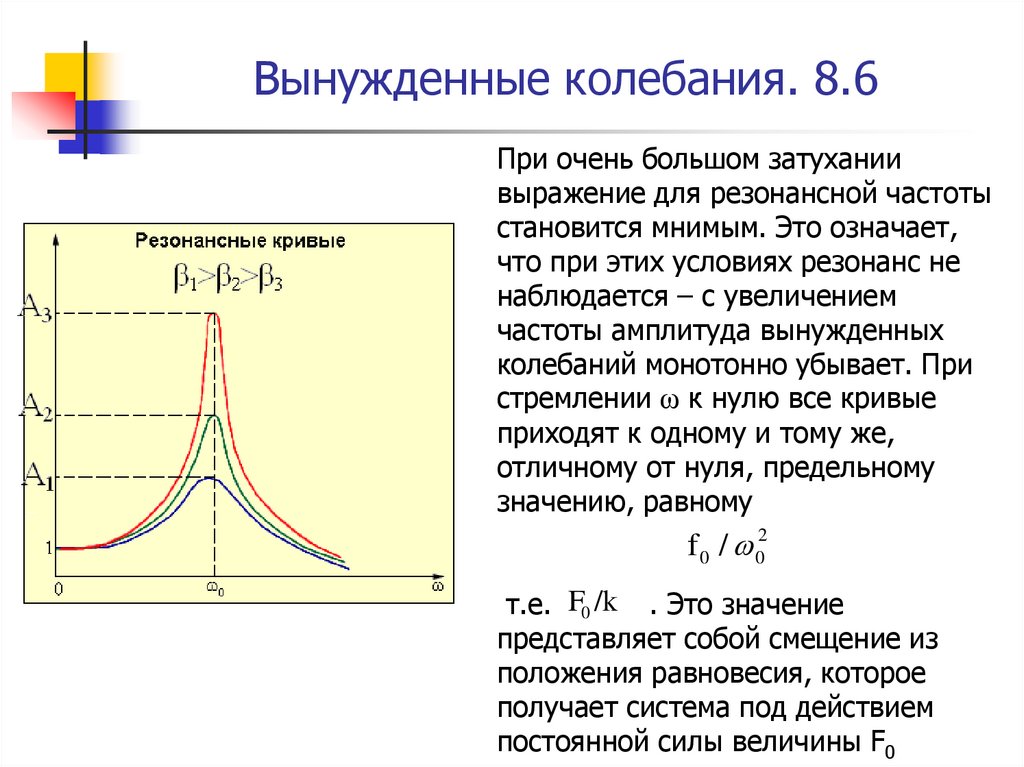










































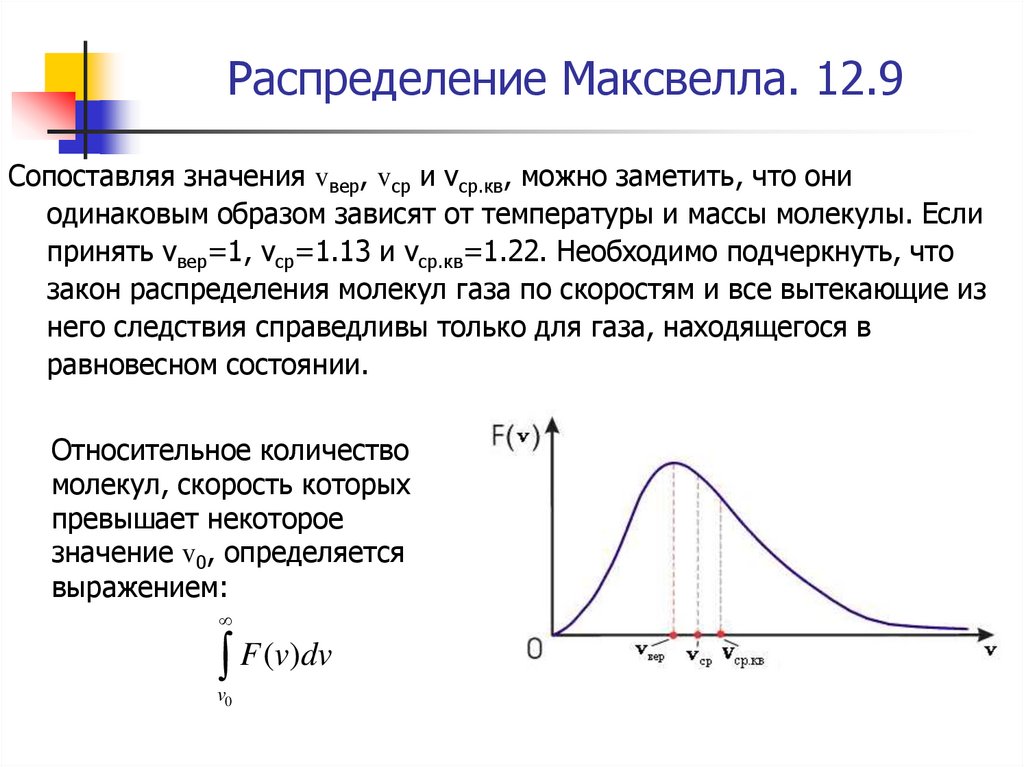
































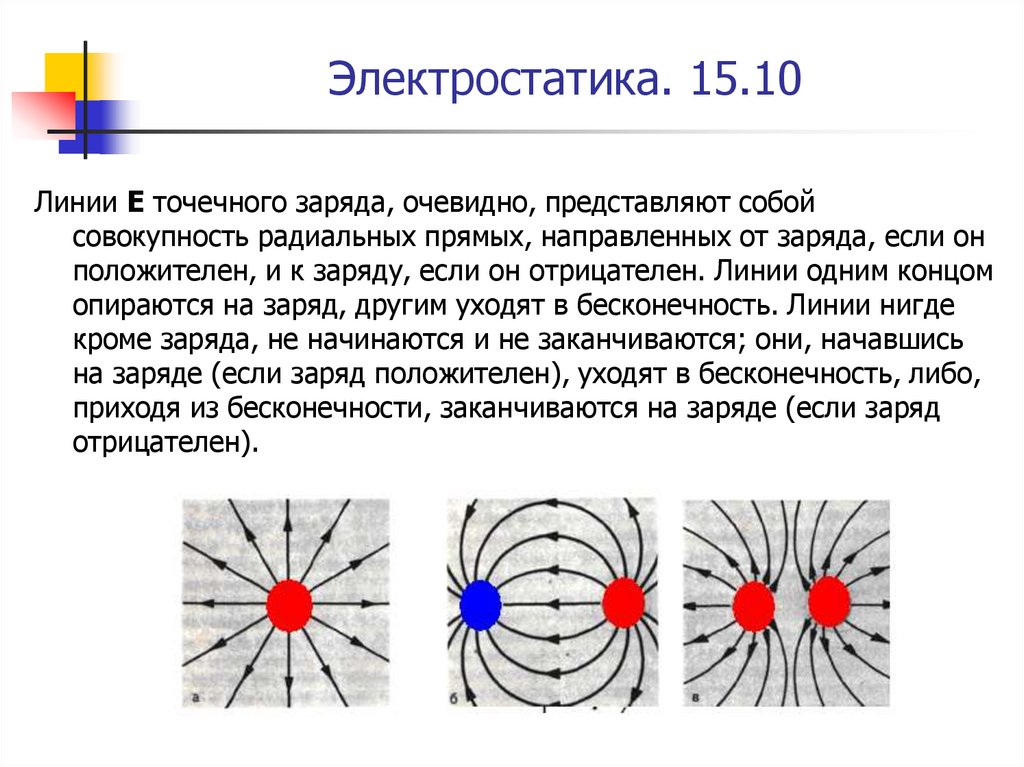







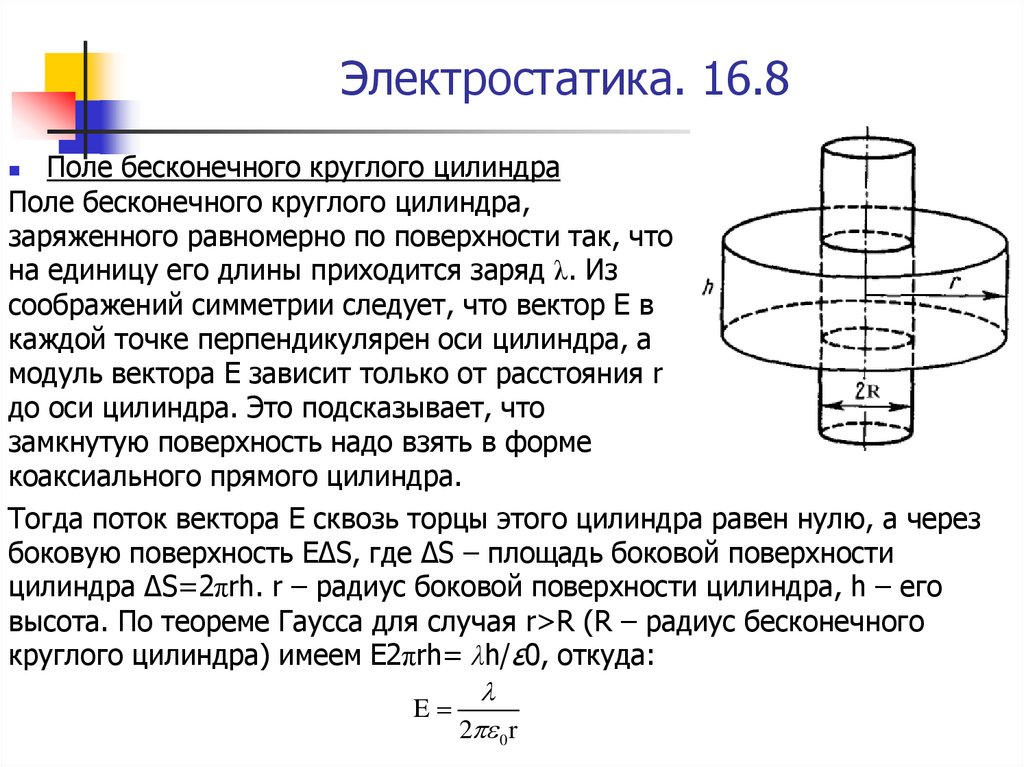









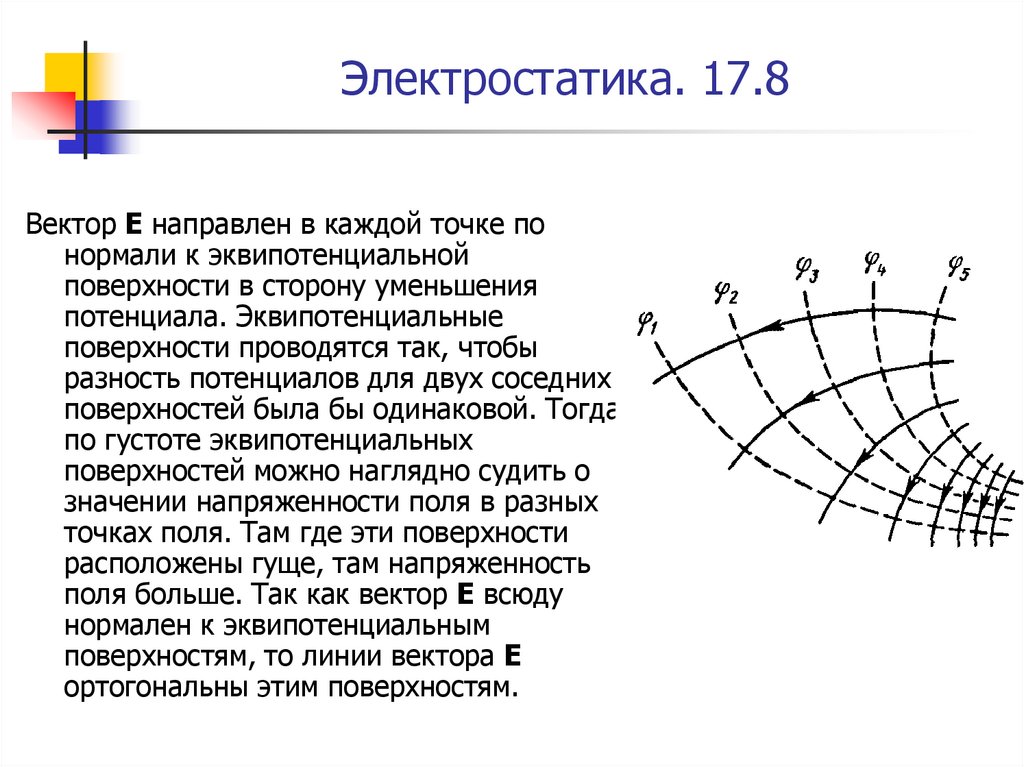


























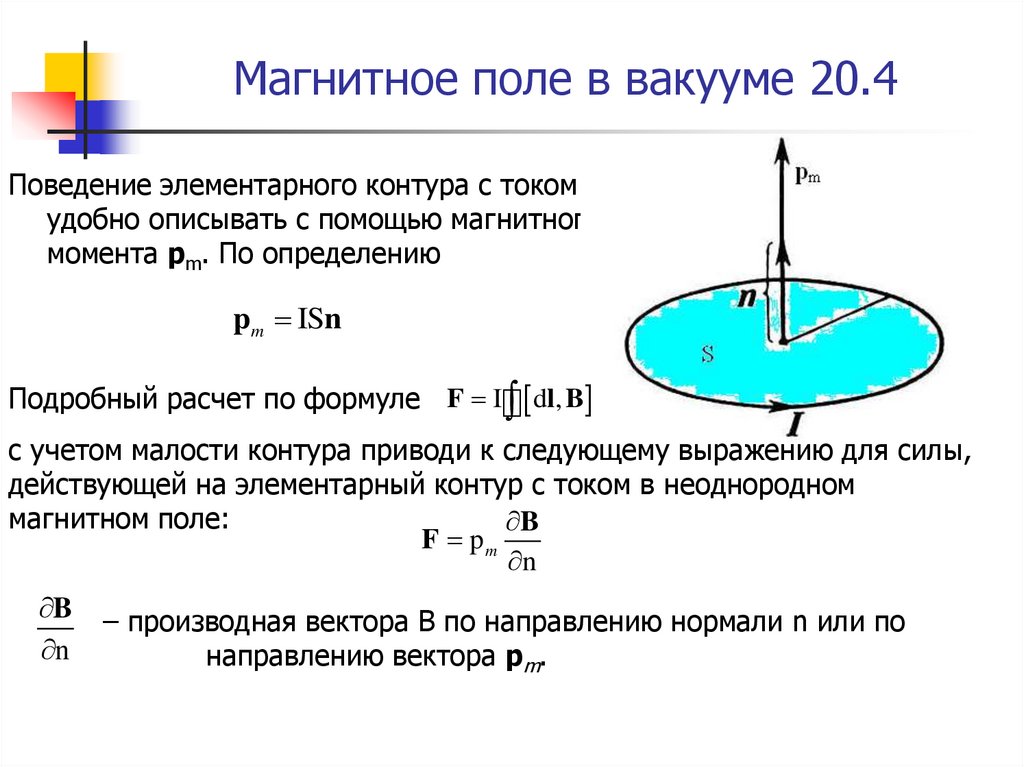









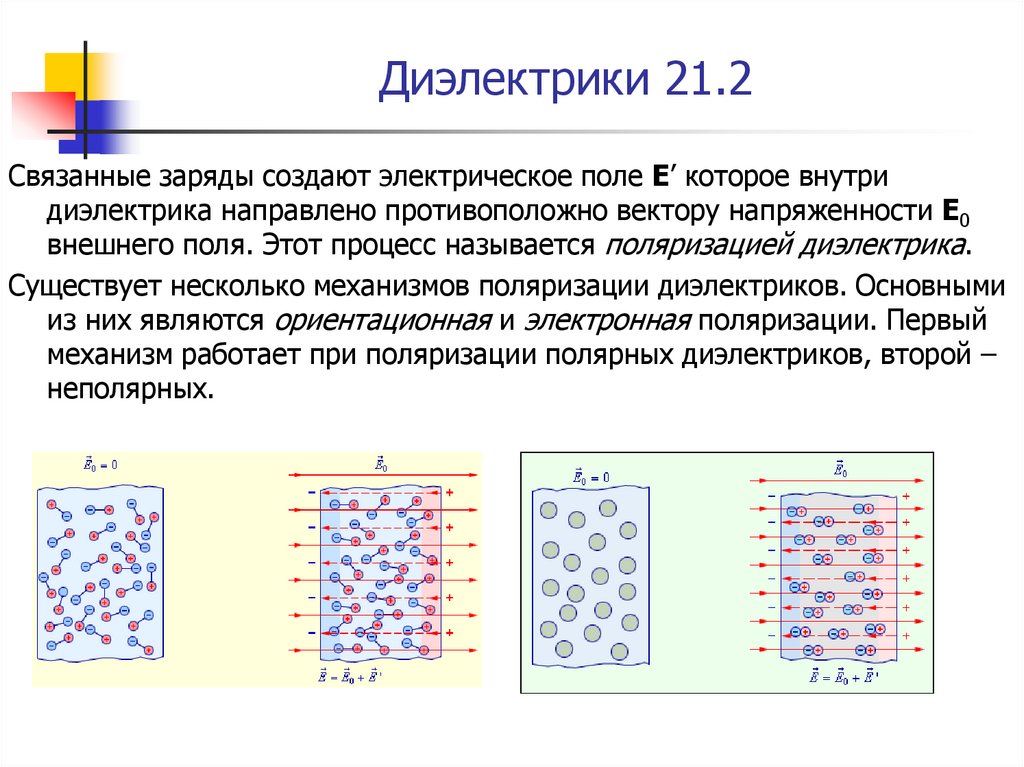
























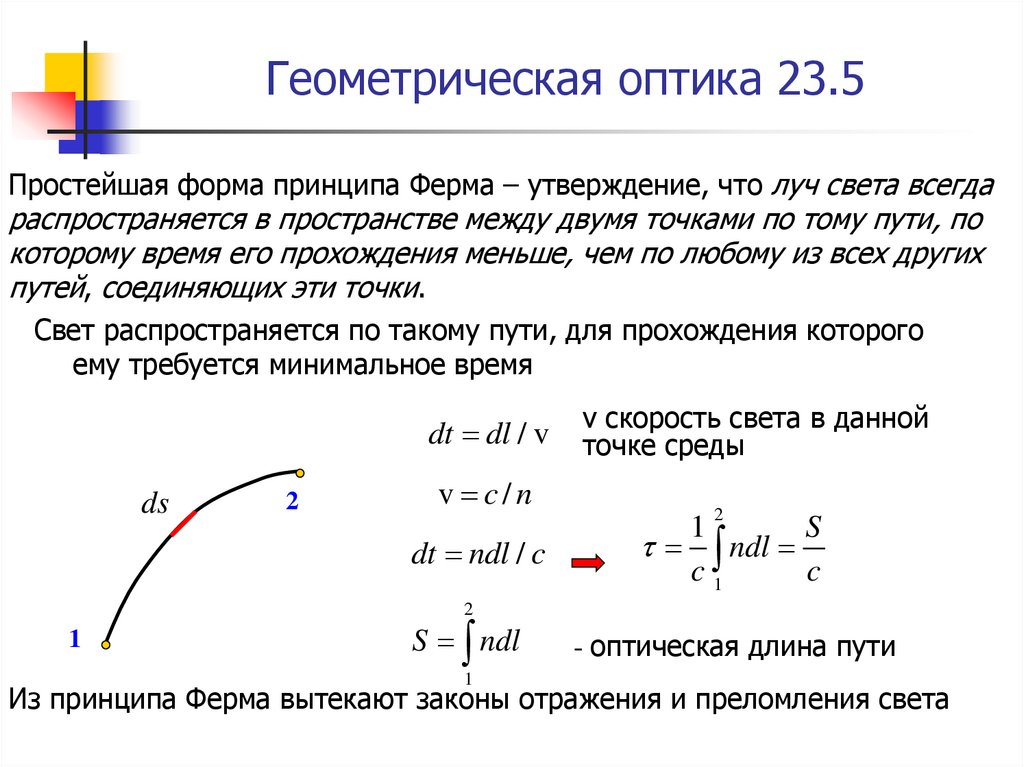

















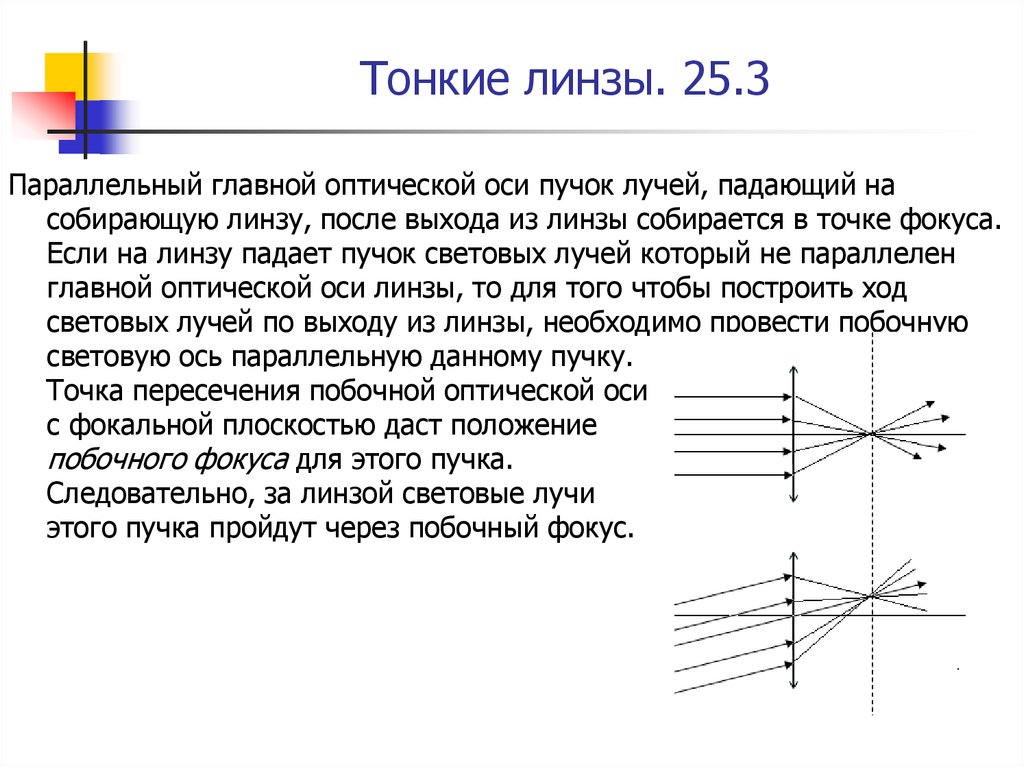















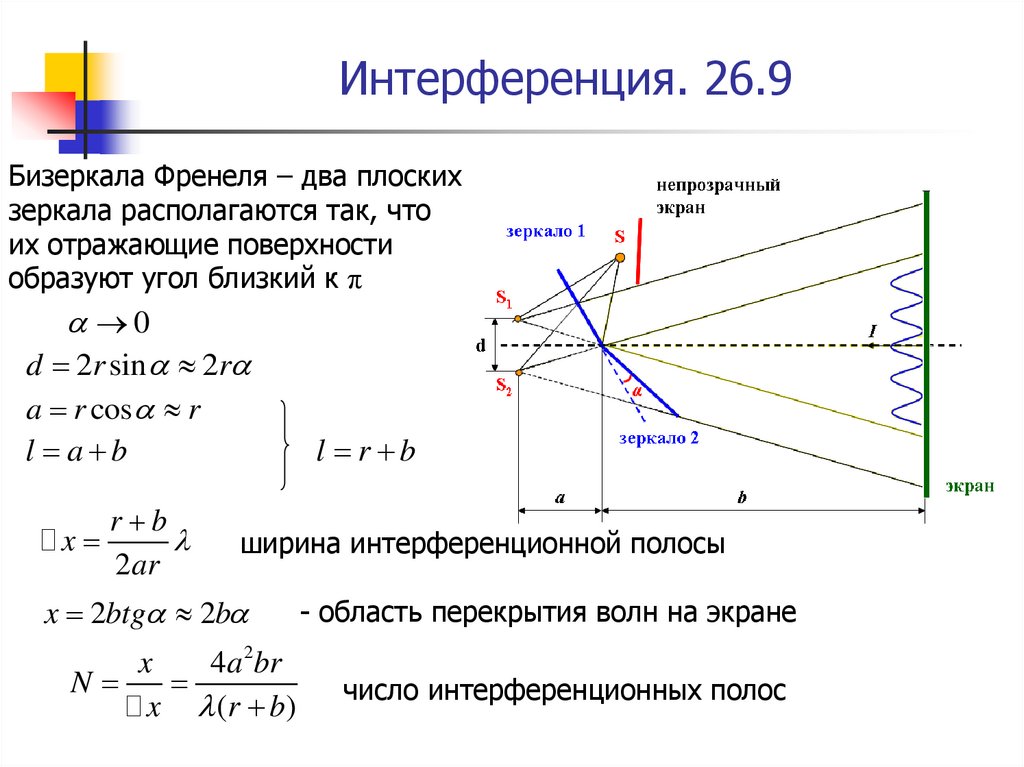
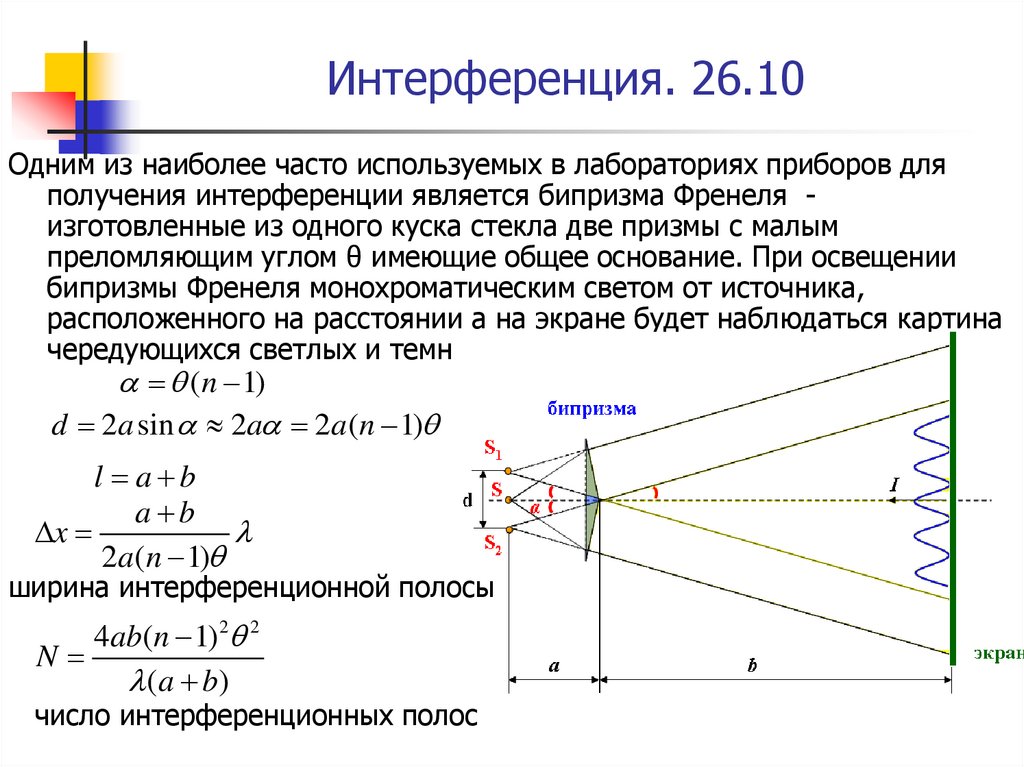

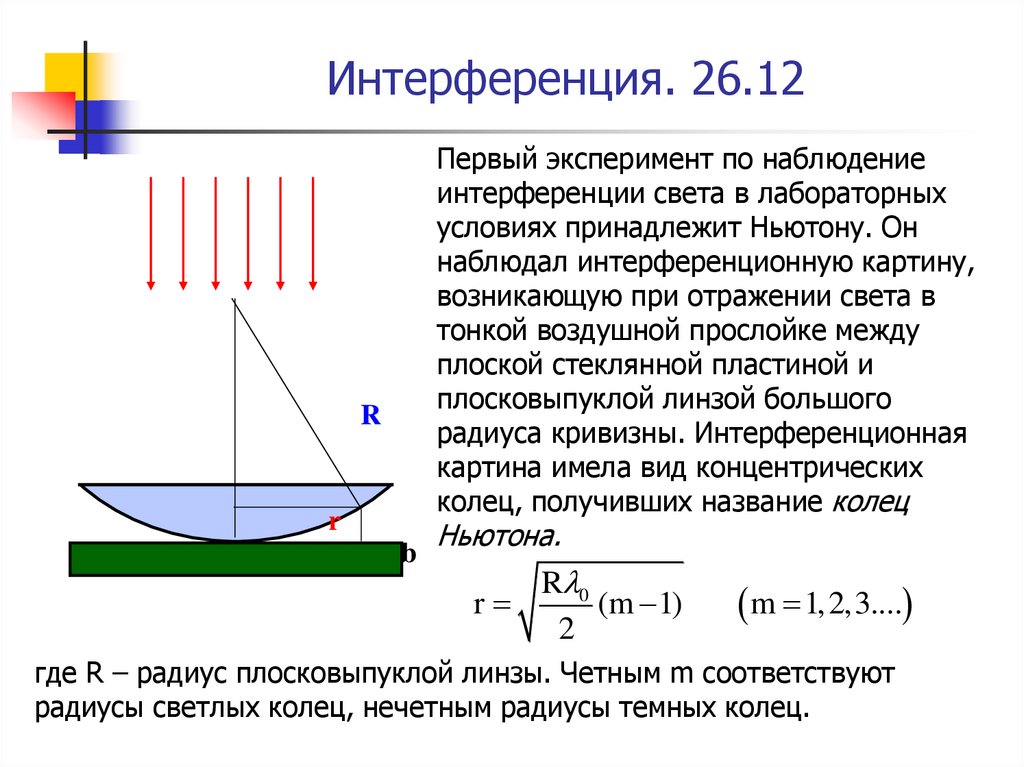





































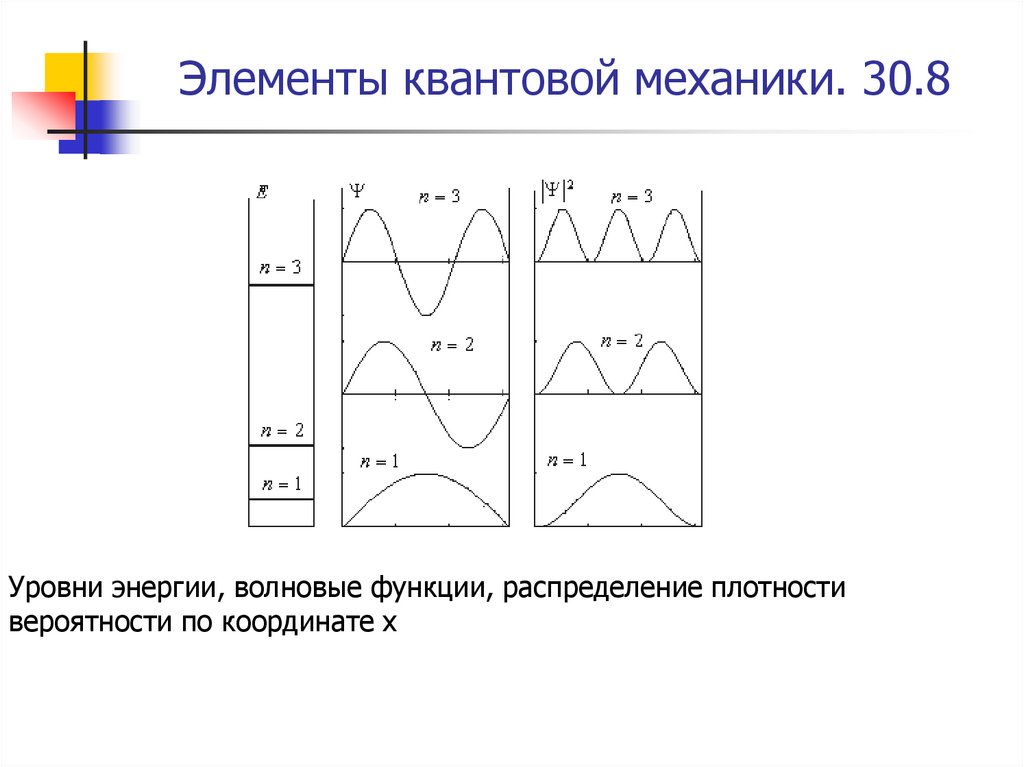













 physics
physics








