Similar presentations:
Критерии оценки лабораторных работ
1. «Все науки можно разделить на две группы − физику и собирание марок.» Э. Резерфорд
2. Курс «Физика»
Петров Никита Юрьевич3. Содержание
Критерии оценки лабораторных работКаждая лабораторная работа оценивается в 200 баллов с дискретизацией в 10 баллов:
100 баллов за ответы на вопросы по защите работы и 100 баллов за протокол. Балл,
начисляемый студенту за защиту лабораторной работы, определяется преподавателем
по качеству ответов на заданные вопросы.
Протокол оценивается по следующим критериям:
общее оформление,
таблица измерений,
обработка результатов,
графики,
вывод.
Каждый критерий оценивается в 20 баллов. Протокол считается выполненные, если
по каждому из пунктов студент набрал не менее 10 баллов.
Порядок проведения лабораторной работы:
студент допускается к лабораторной работе;
выполняет лабораторную работу;
оформляет протокол измерений;
защищает лабораторную работу
Все этапы рассчитаны на одно занятие (две пары).
Сдать протокол измерений и защитить лабораторную работу допускается до
следующего занятия, иначе студент может получить не более 70% от
максимальной оценки по каждому из видов контроля.
4. Критерии оценки лабораторных работ
Методическая литература1.
2.
3.
4.
Механика и термодинамика : методическое пособие к вводному занятию и к
лабораторным работам № 0, 1, 3, 6 по физике для студентов I курса всех факультетов /
Новосиб. гос. техн. ун-т ; [сост.: А. М. Погорельский и др.]. - Новосибирск, 2020. - 64
Электричество и магнетизм: методические указания к лабораторным работам по
физике № 10, 12, 13, 15, 16, 19 для студентов 1 и 2 курсов всех факультетов / Новосиб.
гос. техн. ун-т ; [сост.: А. В. Баранов и др.]. - Новосибирск, 2012. – 67с.
Механика и электростатика. Вопросы для защиты лабораторных работ по
физике : методические указания для выполняющих лабораторный практикум по
физике / Новосиб. гос. техн. ун-т ; [сост.: А. В. Баранов, В. В. Давыдков, В. В.
Христофоров]. - Новосибирск, 2011. - 16 с.
Электричество и магнетизм : вопросы для защиты лабораторных работ по
физике : методические указания для студентов 1-2 курсов всех факультетов / Новосиб.
гос. техн. ун-т ; [сост.: А. В. Баранов, В. В. Давыдков, В. В. Христофоров]. –
Новосибирск: Изд-во НГТУ , 2012. – 15 с.
НГТУ/ Кафедра ОФ / Учебно-методические и учебные пособия / Лабораторные
работы
НГТУ/ Кафедра ОФ / Видеоописание лабораторных работ
НГТУ/ Кафедра ОФ / Виртуальные лабораторные работы
5. Методическая литература
ЛитератураЭУМК:
• Физический практикум по механике
• Физический практикум по молекулярной физике и термодинамике
Учебные пособия
• 1. Савельев И. В. Курс общей физики. [В 3 т.]. Т. 1 : [учебное пособие для вузов по
техническим (550000) и технологическим (650000) направлениям] / И. В. Савельев. СПб. [и др.], 2011. - 432 с.
• 2. Савельев И. В. Курс общей физики. [В 3 т.]. Т. 2 : [учебное пособие для вузов по
техническим (550000) и технологическим (650000) направлениям] / И. В. Савельев. СПб. [и др.], 2011. - 496 с.
• 3. Иродов И. Е. Электромагнетизм. Основные законы : учебное пособие для вузов /
И. Е. Иродов. - М., 2006. - 319 с.
• 4. Иродов И. Е. Механика. Основные законы / И. Е. Иродов. - М., 2006. - 309 с.
• 5. Детлаф А. А. Курс физики : [учебное пособие для втузов] / А. А. Детлаф, Б. М.
Яворский. - Москва, 2009. – 719 с.
• 6. Белоусов А. П. Механика. Электростатика. Электрический ток : курс лекций / А.
П. Белоусов ; Новосиб. гос. техн. ун-т. - Новосибирск, 2007. – 146 с.
• 7. Чертов А. Г. Задачник по физике : [учебное пособие для втузов] / А. Г. Чертов, А. А.
Воробьев. - М., 2008. - 640 с.
6. Литература
• Физика (от др. греч. phýsis – природа) –наука, изучающая наиболее общие и
фундаментальные
законы
природы,
определяющие структуру и эволюцию
материального мира.
• Физика – количественная наука.
• Физика – точная наука, т.е. может
оценивать точность и надежность своих
предсказаний.
• Физика – экспериментальная наука.
• Физика – модельная наука.
7.
Зарождение физикиФилософия
(наблюдение)
Физика (научный
метод) Коперник
(гелеоцентрическая
система), Кеплер
(движение небесных
тел), Галилей
(экспериментальная
физика), Ньютон
(классическая физика)
Архимед, Демокрит
(атомизм), Герон (механика),
Эратосфен (радиус Земли),
Птолемй , физика
Аристотеля, Аль-Хазини,
Омар Хайям
Математика
Химия, биология,
медицина и т. д.
Биофизика; Физическая химия;
Математическая физика и т. д.
8. Зарождение физики
Методы физического исследованияНаблюдение – это систематическое, целенаправленное восприятие того или
иного объекта или явления без воздействия на него. Наблюдение позволяет
получить первоначальную информацию об изучаемом объекте или явлении.
Физический эксперимент – это способ познания материального мира,
заключающийся в изучении природных явлений в специально созданных
условиях. В эксперименте свойства физических явлений и объектов изучаются
с помощью измерений соответствующих физических величин. Таким
образом, провести физический эксперимент означает провести наблюдение
физического явления и измерить характеризующие его физические величины.
9. Методы физического исследования
• Физическое тело – материальный объект, характеризующийсямассой, формой, объёмом, а также рядом других параметров (в
зависимости от рассматриваемой задачи) и отделенный от других тел
границей раздела.
• Физическим явлением называется совокупность взаимосвязанных
изменений, происходящих с телами или системами тел с течением
времени. Синонимом понятия физическое явление является термин
физический процесс.
• Физический закон – общие закономерности, полученные
экспериментальным путем, которым подчиняется течение различных
процессов. Физический закон может выражаться как в словесной, так
и математической формулировке.
10.
• Научная гипотеза – это утверждение, содержащее предположениеотносительно решения стоящей перед исследователем проблемы».
Гипотеза – это главная идея решения проблемы.
• Научная теория – наиболее развитая форма организации научного
знания, дающая целостное представление о закономерностях и
существенных связях изучаемой области действительности
(например, классическая механика И. Ньютона, корпускулярная и
волновая теории света, теория биологической эволюции Ч. Дарвина)
Стоит отметить, что любая теория имеет границы применимости,
за пределами которых они перестают адекватно описывать
физический объект или явление.
• Модель – это объект любой природы, который способен замещать
изучаемый объект в интересующих исследователя свойствах. Процесс
построения моделей называется моделированием. Модели бывают
физические (натурные) и идеальные (концептуальные, физикоматематические, ментальные).
11.
Физические величины. Единицы измерения• Физическая величина – одно из свойств физического объекта
(физической системы или явления (процесса)), общее в качественном
отношении для многих физических объектов, но в количественном
отношении индивидуальное для каждого из них.
• Свойства физических объектов и процессов, которые можно прямо
или косвенно измерить, называют физическими величинами.
• При измерении физической величины ее значение Q сравнивают с
единицей измерения [Q] , т. е. с однородной величиной, принятой за
эталон.
• Число, которое получается при измерениях, называется численным
значением физической величины и обозначается {Q}.
Q {Q} [Q]
12. Физические величины. Единицы измерения
Системы единиц физических величин• 1960 г. Международная системы единиц (СИ), основанная на
Международной системе величин.
• метр (м ) – единица измерения длины;
• килограмм (кг) – единица измерения массы;
• секунда (с) – единица измерения времени;
• ампер (А) – единица измерения силы электрического тока;
• кельвин (К) – единица измерения температуры;
• моль (моль) – единица измерения количества вещества;
• кандела (кд) – единица измерения силы света.
• Единицы измерения производных физических величин связаны с
единицами измерения основных величин так же, как производные
величины связаны основными.
• Если сопоставить базовым величинам определенный символ, то связь
между величинами можно записать в виде формулы - формулы
размерности:
dim Q L 1 M 2 T 3 I 4 5 N 6 J 7
dim p dim mv MLT 1
13. Системы единиц физических величин
МеханикаМеханика – один из разделов физики, наука, изучающая относительное
движение тел в пространстве и во времени и взаимодействие между телами.
14. Механика
Основные физические модели• Материальная точка – физический объект конечной массы,
положение которого в пространстве можно описать
геометрической точкой. Материальная точка представляет
собой модель тела, характер движения которого и условия
задачи позволяют не учитывать его геометрические размеры,
внутреннюю структуру, форму и вращение.
• Возможность использования модели материальной точки к
конкретному телу в общем случае зависит не от размеров
самого тела, а от условий его движения.
• Механическая система – мысленно выделенный для анализа
объект физических исследований, совокупность
взаимосвязанных элементов, отделенная от окружающей среды
и взаимодействующая с ней как целое.
15. Основные физические модели
• Абсолютно твердое тело (твердое тело) – модельтела, расстояние между двумя произвольными точками
которого
постоянно
остается
неизменным
в
рассматриваемом процессе. Твердое тело представляет
собой частный случай механической системы.
• Неизменяемая среда – совокупность бесконечного числа
точек, расстояние между которыми неизменно.
• Сплошная среда – механическая система, в которой
вещество рассматривается как непрерывная среда. При
этом мы пренебрегаем молекулярным (атомным)
строением вещества, и считаем, что распределение в
среде всех её характеристик (плотности, напряжений,
скоростей частиц и т. д.) непрерывно.
16.
• Механическое движение – простейшая форма движения,заключающаяся в относительном изменении положения
тел или частей тела в пространстве со временем.
Относительность заключается в том, что отследить
изменение положения тела в однородном пространстве
можно только относительно других объектов.
• Механическое действие – воздействие на тело со
стороны других тел, приводящее к изменению состояния
движение этого тела или его деформации.
17.
Длинна и времяВремя характеризует длительность протекания процесса и отражает порядок
смены состояний физического объекта. Время имеет смысл, если происходит
какое-либо движение (изменение состояний системы).
Часы – система отсчета времени, основанная на периодическом процессе,
которая через равные интервалы передает сигнал доступный наблюдателю.
В классической механике принято, что в любых системах отсчета время течет
одинаково (время однородно, непрерывно и не зависит от свойств
материальных тел).
Пространство характеризует протяженность физических объектов.
Основная величина, характеризующая пространственные свойства тел,
является длина отрезка принятого за единицу.
В классической механике пространство однородно и не меняет свои свойства
в зависимости от расположения или движения тел.
Однородность заключается в одинаковости физических явлений при прочих
равных условиях в различных точках пространства.
Также пространство изотропно и непрерывно.
18. Длинна и время
Векторы. Система координатAB a
a a1i a2 j a3k
r xi yj zk
a1 a x i
a2 a y j
a3 a z k
a axi a y j azk
19. Векторы. Система координат
20.
Операции над векторамиa x ai a cos x1 x0
a y aj a cos y1 y0
az ak a cos z1 z0
a a 2x a 2y a z2
21.
Кинематика22.
Поступательное движение23. Поступательное движение
Основы кинематики. Система отсчета• Кинематика – это раздел механики, изучающий механическое
движение тел без учёта обусловливающих его причин.
• Кинематика устанавливает математические соотношения между
различными характеристиками движения, такими как перемещение,
путь, скорость, ускорение, время.
• Механическое движение не может быть задано без указания тела
отсчета
• Система отсчета – совокупность системы координат жестко
связанной с телом отсчета (абсолютно твердым телом) и часов
(системы отсчета времени), позволяющая определить положения тел
по отношению к телу отсчета в различные моменты времени.
• Инвариант – физическая величина, значение которой остается
постоянным в процессе эволюции системы, вне зависимости от
процессов происходящих внутри этой системы. Инварианты в отличие
от относительных величин не зависят от выбора системы отсчета.
Примером инварианта служит масса, время, длинна.
24. Основы кинематики. Система отсчета
Кинематика материальной точки• В кинематике движение тел рассматривается вне
связи с причинами, которые вызывают это
движение.
• В статике изучаются законы равновесия системы
тел.
• В динамике − законы движения тел и причины,
которые вызывают или изменяют движение тел.
• Материальной точкой (частицей) называют
макроскопическое тело, размерами которого в
условиях данной задачи можно пренебречь.
• Пример: Земля (RЗ ≈ 6370 км) при рассмотрении её
движения вокруг Солнца (RЗС =1,5∙108 км).
25. Кинематика материальной точки
Основные понятия кинематики точкиСистемой отсчета (СО) называют тело отсчета,
по отношению к которому рассматривается движение, вместе
с приборами для измерения расстояний и времени.
Положение частицы в СО задают с помощью радиуса− вектора
r, проведенного из начала отсчета О.
Если с СО связать декартовую систему координат,
то задание r эквивалентно заданию трех координат
x, y, z − проекций радиус-вектора на оси:
r xi yj zk .
26. Основные понятия кинематики точки
В физике применяется исключительно правая системакоординат.
27.
Движение частицы полностью описано, еслиизвестна зависимость от времени её координат
x = x(t), y = y(t), z = z(t),
( КУД )
либо её радиуса-вектора
r = r(t).
( КУД* )
Ур-ния (КУД) и (КУД*) называют кинематическими
уравнениями (законом) движения.
Линию, по которой движется частица, называют её
траекторией, а длину этой линии ∆s − путём.
Пример K: x = At, y = Bt2; A = 2 м/с, В =1 м/с2 − движение
по параболе.
Изменение р.-вектора за интервал времени ∆t = t2 − t1,
равное ∆r = r2 − r1 называют перемещением частицы
за время ∆t. Здесь r1 = r(t1), r2 = r(t2).
28.
Кинематические уравнениямядвижения
x a cos t
y b sin t
x2
a
2
y2
b
2
1, z 0 уравнение траектории движения точки
29. Кинематические уравнениямя движения
30.
3 способа описания движения• Векторный
r r (t )
• Координатный
х x (t )
y y (t )
• Естественный
S S (t )
31. 3 способа описания движения
Характеристики движения• Координаты тела
• Время движения
Скорость
32. Характеристики движения
Скорость. ПутьПод средней скоростью понимается скорость, с которой тело переместилось бы из
начальной точки в конечную за указанный промежуток времени, двигаясь
равномерно и прямолинейно в одном направлении.
r dr
мгновенная скорость
dt
t 0 t
v lim
33. Скорость. Путь
dxdy
dz
v i
j k vxi v y j vz k
dt
dt
dt
v
t2
s=
т
t1
2
2
2
vx v y vz
2
2 &2
&
&
x + y + z dt .
34.
Физический смысл производнойds( t ) s(t0 t ) s(t0 ) ( t )
s(t0 t ) s(t0 )
s
lim
t
t 0 t t 0
s lim
s v
35. Физический смысл производной
Физический смысл интегралаs
t
0
0
ds v(t )dt
36. Физический смысл интеграла
Ускорение• Ускорение – это векторная величина, равная
производной от скорости по времени
dv y
dv dv x
dv z
a
i
j
k
dt
dt
dt
dt
2
d x
dt 2
i
2
d y
dt 2
j
2
d z
dt 2
k.
2
2
ax vx x , ay vy y , a x y .
37. Ускорение
Прямая задача кинематики - зная кинематический закондвижения, легко найти скорость и ускорение частицы
v r , a r.
Обратная задача - по известному ускорению найти закон
движения. Решение этой задачи в аналитической форме
можно найти не всегда. Это возможно, например, в
случае движения с постоянным ускорением а = const.
38.
Движение с постоянным ускорениемr
r
v
r
r dv
a=
Ю т dv =
dt
r
r
r
r
r dr
r
v=
Ю т dr =
dt
r
r0
v0
t
т
0
t
т
r r
r
r
a Чdt Ю v = v0 + at
0
r 2
r
r
r r
r r
at
( v0 + at )dt Ю r - r0 є D r = v0t +
2
vx = v0 + ax t = v0 ± at
ax t 2
at 2
D x = v0t +
= v0t ±
2
2
39. Движение с постоянным ускорением
Криволинейное движение40. Криволинейное движение
Тангенциальное и нормальное ускоренияБолее удобно представить ускорение в виде векторной суммы двух компонент:
a an a
dv
a
dt
d v d
dv
a
v
dt
dt
dt
v
a an2 a 2
R
2
2
dv
dt
2
d
v2
an v n
dt
R
41. Тангенциальное и нормальное ускорения
aτ 0 v 0 v const движ.с постоянной скор.an 0 v R 0 R прямолин. движение.
2
42.
43.
Сравнение результатов вычислительного инатурного экспериментов
30º
44.
Вращательное движение45. Вращательное движение
Кинематика вращательного движениячастицы
Вращательное движ. частицы по окружности −
частный случай криволинейного движения. Смысл
специального рассмотрения этого случая в том, что
вращ. движ. − одно из наиболее распространенных
в технике. Кроме того, любое движ. твердого тела
можно представить как нало-жение (“сумму”)
поступательного и вращат. движений (пример:
движение колеса).
Для
описания вращат. движ. удобно пользоваться не
линейными характеристиками ∆r, v, …, которые
меня-ются от точки к точке тела, а угловыми ∆φ, ω,
..., которые имеют одно и то же значение для всех
точек тела.
46. Кинематика вращательного движения частицы
ВекторыПолярным (истинным) вектором называется такой вектор,
который при замене ориентации системы отсчета на
противоположную не меняется.
Аксиальным (от лат. axis – ось) вектором или псевдовектором
называется вектор, который при замене ориентации системы
отсчета на противоположную меняет свое направление на
противоположное, сохраняя свою длину.
Все вектора, полученные в результате векторного
произведения двух истинных векторов, являются аксиальными.
При векторном умножении истинного вектора на псевдовектор
получается истинный вектор.
47. Векторы
Угловые характеристики.При движении частицы по окружности её
перемещение характеризуют углом поворота ∆φ
радиуса-вектора r. Для учета направления вращения
его принято изображать направленным отрезком
∆φ, модуль которого равен углу поворота, а
направление отвечает правилу правого винта: ∆φ
направлен в ту сторону, куда будет двигаться
правый винт (ввинчиваться или вывинчиваться),
если его вращать в направлении вращения частицы.
Если ∆φ очень мал, то соответствующий dφ
обладает свойствами вектора. Его называют
вектором поворота (угловым перемещением).
48.
49.
Угловая скорость:d
d
lim
,
;
t 0 t
dt
dt
рад
с
.
Частный случай: равномерное вращение (ω = const)
можно охарактеризовать периодом вращения Т −
временем, за которое тело совершает один оборот.
2
t T , 2
.
t
T
Число оборотов за единицу времени ν равно
1
T 2
2 .
d
;
Угловое ускорение: lim
t 0 t
dt
рад
с
2
.
50.
51.
Задача• Определить предельный угол наклона
плоскости при котором тело остается
неподвижным
52. Задача
Глава 2. Динамика материальнойточки
Динамика − раздел механики, изучающий движение
тел в связи с действующими на них силами.
Динамика основана на 3х законах Ньютона.
§ 2.1. Масса тела. Импульс. Сила
П. Масса. Массой называют меру инертности тел,
которая отражает свойство тел “противиться”
попыткам изменить их скорость.
Количественно ее можно определить, если ввести
эталон m0, а массу других тел найти, сравнивая с
эталоном.
◄! напр., с помощью сжатой пружины: m=m0v0/v
Единица массы в системе СИ − килограмм (кг).
53. Глава 2. Динамика материальной точки
Инерция• Инерция – свойство тел оставаться в некоторых
системах отсчёта в состоянии покоя или
равномерного прямолинейного движения в
отсутствие или при взаимной компенсации внешних
воздействий
• Если наклон плоскости к горизонтали является
причиной ускорения тела, движущегося по ней
вниз, и замедления тела, движущегося по ней
вверх, то, при движении по горизонтальной
плоскости, у тела нет причин ускоряться или
замедляться, и оно должно пребывать в состоянии
равномерного движения или покоя.
54. Инерция
П. Импульс. Сила. Импульс: p = mv.Сила F,
действующая на тело, является мерой его
взаимодействия с другими телами.
Количественно сила
вводится с помощью импульса:
dp
F
m const ma.
dt
Единица силы в СИ − ньютон (Н):
1 Н 1кг м с 2 .
§ 2.2. Законы Ньютона
Тело, не подверженное воздействиям со стороны других
тел, называют свободным, а его движение − свободным
или движением по инерции.
1й
закон Ньютона (закон инерции): существуют такие СО,
относительно которых свободное тело либо покоится,
либо движется равномерно и прямолинейно.
◄!
СО, в которых справедлив закон инерции, называют
инерциальными (ИСО).
55.
Инерциальная система отсчета• Тела отсчета, относительно которых траектория любой
изолированной точки (одинокой во всем мире) частицы
прямолинейна
или
является
точкой,
называются
инерциальными телами отсчета.
• Часы считаются оттарированными в соответствии с
принципом Галилея, если за одинаковые по этим часам
интервалы времени изолированная частица пролетает
одинаковые
расстояния
относительно
любого
инерциального тела отсчета.
• Совокупность инерциального тела отсчета, снабженного
часами, оттарированными в соответствии с принципом
инерции Галилея, и системы координат, связанной с телом
отсчета, называется инерциальной системой отсчета.
• t → kt + t0
56. Инерциальная система отсчета
Принцип относительности Галилея• Все инерциальные системы отсчета
равноправны,
т.е.
не
существует
физических экспериментов, позволяющих
выделить какую-либо одну из них.
• Законы физики не зависят от выбора
инерциальной системы отсчета
57. Принцип относительности Галилея
Установлено, что практически инерциальной являетсягелиоцентрическая СО (система Коперника), начало
которой в центре Солнца. Ясно, что любая другая СО,
движущаяся с V = const относительно гелиоцентри-ческой,
тоже является инерциальной.
ma x Fix ,
2-й закон Ньютона: в ИСО
i
dp
F
dt
m const
ma F ( 2)
ma y Fiy ,
i
ma F .
z iz
i
Проинтегрировав (2), получим интегральную форму
2го закона:
p
t
dp Fdt p p p0 Fdt
p0
t
0
0
Величину Fdt называют импульсом силы.
t
0
( 2инт )
58.
3-й закон Ньютона: при взаимодействии двух тел сила, действующая на1-е тело со стороны 2-го, равна по величине и противоположна по
направлению силе, действующей на 2-е тело со стороны 1-го:
F12 F21.
( 3)
Это означает, что силы всегда проявляются парами: они приложены к
взаимодействующим телам, являясь силами одной физической
природы.
Пример: вз−вие электрических зарядов.
П. Принцип суперпозиции. Опыт показывает, что
если на частицу действует несколько источников сил, то
F = F1 + F2 + …, где Fi − сила, с которой на частицу действовал бы i-й
источник, когда все остальные источники удалены.
59.
§ 2.3. Силы в макроскопической механикеСила – векторная физическая величина, являющаяся мерой
взаимодействия тел. Она характеризуется направлением, модулем и
точкой приложения. [F] = Н (ньютон).
Точка приложения силы – материальная точка, на которую действует
сила.
Существование сил, возникших самостоятельно, без
взаимодействующих тел, невозможно
Всё многообразие сил в природе сводится к 4-м фундаментальным
взаимодействиям:
гравитационному, электромагнитному, ядерному и слабому.
В основе всех механических явлений лежат гравитационные и электрические силы. Т.к. детальный учет этих
сил очень сложен, то в макроскопической механике для упрощения
решения задач вводят другие, приближенные силы.
1) Сила гравитационного притяжения:
3
m1m2
м
-11
Fгр
,
где
6,67
10
2
2.
r
кг с
60. § 2.3. Силы в макроскопической механике
2) Сила тяжести (проявление гравитац. вз-вия на Земле):G mg , где g ускорение свободного падения.
3) Упругая сила (проявление
электромагн. вз-вия):
Fупр kr ,
где k − коэффициент упругости (жесткости), r − вектор
смещения частицы от положения равновесия.
Пунктиром отмечено
положение равновесия
61.
4) Сила трения (проявление электромагн. вз-вия).Различают трение покоя и трение скольжения.
Сила трения покоя автоматически принимает
значение равное внешней силе, но не превосходит
некоторую величину Fmax.
Закон Кулона: максимальная сила трения покоя Fmax
равна силе трения скольжения
Fтр m N ,
где m − коэфф. трения, N − сила нормального
давления, прижимающая трущиеся поверхности
друг к другу.
Величина m зависит от природы и состояния повстей.
Задача. Коэф. трения шин авто с дорогой m = 0,5.
Какое предельное ускорение может развить авто?
◄ 4 ведущих колеса − amax = mg = g/2;
◄ 2 ведущих колеса − amax = mg/2 = g/4.
62.
§ 2.4. Динамика криволинейного движенияУр-е ma = F решают, как правило, в скалярной форме,
спроецировав его на оси подходящей системы координат.
В случае криволин. движения, удобно использовать
связанную с телом сист. коорд., где в качестве осей
принимают направления касательной и нормали n к
траектории:
dv
: maτ m Fτ ;
dt
v2
n : man m
Fn .
R
Задача 1K. Найти первую космическую скорость v1K, т.е.
скорость движения спутника по круговой орбите с
радиусом, мало отличающимся от радиуса Земли RЗ .
◄ Сем:
v1K M З RЗ gRЗ 7,9 км с►.
63. § 2.4. Динамика криволинейного движения
Глава 3. Динамика системы частиц§ 3.1. Уравнения движения
Частицы системы могут взаимодействовать как между собой, так
и с телами, не входящими в систему.
Поэтому силы разделяют на внутренние ( Фik − сила,
действующая на i-ю частицу со стороны k-ой) и внешние
( Fi − равнодействующая всех внешних сил, действующих на i-ю
частицу).
64. Глава 3. Динамика системы частиц
Ур-я движения частиц системы имеют вид:dp1 dt Ф12 Ф13 ... Ф1N F1 ,
dp2 dt Ф21 Ф23 ... Ф2N F2 ,
(C)
Если известны все силы, то можно найти траектории ri(t) всех
частиц системы. Однако, если:
1) законы для сил неизвестны (взрыв, вз-вие элементар-ных
частиц, ...), либо
2) частиц очень много (газ),
то расчет с помощью (С) неосуществим.
В таких случаях помогают не сами эти ур-я, а их следствия,
устанавливающие ряд сохраняющихся характеристик системы.
Наиболее важными среди них (вследствие их аддитивности)
являются импульс, энергия и момент импульса системы.
65.
§ 3.2. Импульс системыИмпульсом системы Р называют сумму импульсов её частиц:
P pi mi vi .
Найдем изменение Р:
i
i
dpi
dP
Ф12 Ф13 ... F1 Ф21 Ф23 ...F2 ...
dt
i dt
Фik Фki Fi F
(2C)
i
(2С) − закон изменения импульса системы.
Здесь F − результирующая всех внешних сил, действую-щих на
частицы системы. Проинтегрировав, получим интегральную
форму закона изменения импульса:
t
P P P0 Fdt
0
(2CИНТ )
66. § 3.2. Импульс системы
§ 3.3. Центр массЦентром масс (центром инерции) системы называют такую
точку С, р.-вектор которой определяется равенством
RC
mi ri
m
, где m mi масса всей системы.
Пример: ц.м. системы двух частиц массы m.
◄!
Найдем скорость движения VC центра масс системы:
dRC
dri
1
VC
mi const mi
dt
m
dt
Следовательно, импульс системы равен
P mi vi mVC
mi vi
m
.
67. § 3.3. Центр масс
Подставим это выражение в (2С):2
dVC
d RC
in
m
m
F
( ЦМ)
2
dt
− ур-е движения
dt
ц.м.
Ур-е (ЦМ) означает, что ц.м. системы движется
так, как двигалась бы матер. точка с массой,
равной массе системы, под действием всех
внешних сил, действующих на систему.
Этот результат называют теоремой о движении
центра масс.
68.
ГЛАВА 4. ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ§ 4.1. Закон сохранения импульса
Замкнутой (изолированной) системой называют
систему, на которую не действуют внешние силы.
Согласно ур-ю (2С), импульс системы может изменяться
под действием только внешних сил Fi. Отсюда следует
закон сохранения импульса: импульс замкнутой
системы частиц остается постоянным
P pi (t ) const .
Замечание 1. Импульс может сохраняться и у
незамкнутой системы, если результирующая всех
внешних сил F =0.
Замечание 2. У незамкнутой системы может сохраняться
не сам импульс Р, а его проекция Рx на некоторое
направление x, вдоль которого Fx =0.◄Док-ва очевидны
69. Глава 4. Законы сохранения в механике
Задача Р. Из ружья М = 3 кг со скоростью v = 600 м/свылетает пуля массы m = 10 г. Найти скорость отдачи V
ружья, если оно свободно, т.е. не прижато к плечу.
mv + MV = 0 → V = −mv / M; V = 0,01•600/3 = 2 м/с.
◄ Направление скорости отдачи V↑↓v иллюстрирует
принцип действия ракетного двигателя.
70.
§ 4.2. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ И РАБОТАКинетической энергией частицы называют величину
mv 2 p 2
K
.
2
2m
П. Работа. Пусть частица, на которую действует сила F,
движется по траектории 1−2. Элементарной работой
силы F при перемещении частицы dr называют величину
dA F dr F ds cos Fv ds.
Здесь ds =|dr|−
элементарный путь,
Fv − проекция F на
направление v.
71. § 4.2. Кинетическая энергия и работа
Величина dA алгебраическая: если α острый, то dA > 0;если α тупой, то dA < 0. Работа А на конечном пути :
2
2
A 12 F dr Fv ds .
1
1
Единица работы в СИ − джоуль (Дж): 1 Дж = 1 Н•м.
Пример:
работа силы трения.
dAтр Fтр dr Fтр ds cos1800 Fтр ds mN ds
2
Aтр mNds m const ; N const mN s 0 .
1
72.
Нетрудно показать, что если F = F1 + F2 + …,то А = А1 + А2 + ...,
т.е. работа результирующей нескольких сил равна
алгебраической сумме работ, совершаемых каждой из сил
в отдельности.
Мощность − работа, совершаемая за единицу времени:
dA
dr
P
F
F v.
dt
dt
Дж
P Вт, 1Вт 1 .
с
73.
§ 4.3. ТЕОРЕМА О СВЯЗИ РАБОТЫ ИКИНЕТИЧЕСКОЙ ЭНЕРГИИ
Работа силы, действующей на частицу, определяет
изменение её кинетической энергии:
dv
2
dA F dr m vdt v v v 2v dv 2vdv
dt
mv 2
mvdv d (
) dK .
2
На конечном пути:
2
2
1 dA 1 dK
K 2 K1 A 12
(AК) - теорема о связи А и К
Следствие. Если сила направлена “по движению”, т.е.
F∙dr > 0, то А12 > 0, и кинетич. энергия тела возрастает
(разгон), и наоборот.
74. § 4.3. Теорема о связи работы и кинетической энергии
§ 4.4. КОНСЕРВАТИВНЫЕ СИЛЫПространство, в каждой точке которого на частицу
действует сила, называют силовым полем.
Пример: поле силы тяжести.
Силу называют консервативной (потенциальной),
если работа этой силы зависит только от начального (1) и
конечного (2) положений частицы и не зависит от формы
траектории между точками 1 и 2, т.е.
A 1a 2 A 1b 2 A 12.
Важное свойство: консервативные силы зависят только
от координат частиц, на которые они действуют и не
зависят от их скоростей.
Консервативными являются все 4 типа фундаментальных
сил и некоторые из макроскопических сил.
75.
1) Сила тяжести.Докажем её консервативность.
2
2
1
1
◄OY ↑↓ g
A12 mg d r mg dr mg r mg r cos mg ( y1 y2 ).
G
2) Гравитационная и кулоновская силы.
A
m1m2 гравит.
, где
r1 r2
k0 q1q2 кулон.
гр/кул
12
Здесь k0 =1/4 0 = 9∙109 Н∙м2/Кл2; r − расстояние между
взаимодействующими частицами.
2
2
3) Сила упругости.
r
r
упр
1
2
A12
2
2
,
где r − величина смещения частицы от равновесия.
76.
П. Неконсервативные силы. К ним относятсягироскопические силы (сила Лоренца; Агир = 0) и
диссипативные силы (силы трения и сопротивления
жидкости и газов).
Диссипативные силы совершают отрицательную работу
и приводят к уменьшению механич. энергии замкнутой
системы.
77.
§ 4.5. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯВведём понятие потенциальной энергии П(r), которое
служит энергетической характеристикой консервативного
силового поля.
Для этого каждой точке поля приписывают значение
П(r) такое, чтобы разность этих значений в точках 1 и 2
равнялась работе сил поля при перемещении из т.1 в т.2:
A12 F dr П1 П 2
2
(АП )
1
Ф-ла (АП) и выражения для работы консервативных сил
дают следующие выражения для потенц. энергии:
1) П mgy; 2) П
G
гр/кул
r
; 3) П
упр
r
2
2
.
78. § 4.5. Потенциальная энергия
П. Связь консервативной силы с потенц. энергией.Расчет потенц. энергии для известного силового поля
производится путем интегрирования по ф-ле (АП).
Обратная процедура расчета силы осуществляется с
помощью дифференцирования:
П
П
П
П
( АП ) Fx
, Fy
, Fz
; Fl
.
x
y
z
l
79.
§ 4.6. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙЭНЕРГИИ ЧАСТИЦЫ
Согласно теореме (АК), ΔК = А всех сил, действующих
на частицу. Кроме консервативных сил на частицу могут
действовать и иные силы. Назовем их сторонними.
Тогда
K 2 K1 A
конс
A
стор
П1 П 2 A
стор
.
Введем механическую энергию частицы Е = К + П.
Тогда полученное соотношение примет вид:
E2 E1 A
стор
.
1) Если Астор < 0, то Е2 < Е1.
2) Если Астор > 0, то Е2 > Е1.
(ЕА )
80. § 4.6. Закон сохранения механической энергии частицы
3) Если Астор = 0, тоЕ2 = Е1
( Е ) − закон сохранения мех. энергии.
Задача 2К. Найти значение 2-й космической скорости v2К ,
т.е. такой минимальной скорости, чтобы ракета смогла
преодолеть притяжение Земли (и удалиться в ∞).
◄ Сем:
2
mv2K
mM
M
км
0 v2K 2
2v1K 11,2 .
2
RЗ
RЗ
с
§ 4.7. Закон сохранения мех. энергии системы.
§ 4.8. Столкновения. Внутренняя энергия.
81.
§ 4.7. ЗАКОН СОХРАНЕНИЯ МЕХАНИЧЕСКОЙЭНЕРГИИ СИСТЕМЫ
mi vi2
Кинетич. эн-ей системы называют K K i
.
2
Найдем ур-е, описывающее изменение К.
Для каждой частицы системы ∆Кi = Ai. Просуммируем по
всем частицам:
K A
i
i
K A.
Здесь А = ∑Аi − работа всех сил, действующих на все
частицы системы. Разделим все силы на внутренние и
внешние, а внутренние − на консервативные и
диссипативные:
конс
дис
K Aвнут Aвнеш Aвнут
Aвнут
Aвнеш .
(AK C)
82. § 4.7. Закон сохранения механической энергии системы
консМожно показать, что Aвнут
можно представить в виде
убыли
собственной потенциальной энергии W системы
конс
Авнут
W1 W2 .
Потенциальная энергия системы представляет собой
энергию взаимодействия частиц, входящих в систему.
Например, потенциальная энергия гравитационного
взаимодействия системы из 3 частиц задается формулой
W
ГР
m1m2 m1m3 m2 m3
(
).
r12
r13
r23
Введем механич. энергию системы E = K + W.
Тогда (АК*С) можно записать как
E2 E1 A
дис
внут
Авнеш .
(EA C)
83.
Случай 1. Система замкнута и в ней нет диссипативных сил.Систему, в которой действуют только консервативные
силы, называют консервативной. В этом случае
дис
Aвнеш Авнут
0 E2 E1 0, т.е. Е К W const.
закон сохр. энергии замкнутой консервативной системы.
Случай 2. Система замкнутая, но не консервативная, т.е.
в ней имеются диссипативные силы. Можно показать, что
в замкнутой системе полная работа диссипативных сил
всегда отрицательна. Следовательно, в этом случае
дис
Е2 Е1 Авнут
0 E2 E1.
Резюме. Мех. энергия замкнутой неконсервативной
системы убывает.
84.
§ 4.8. СТОЛКНОВЕНИЯ. ВНУТРЕННЯЯ ЭНЕРГИЯК столкновениям (соударениям) относятся кратковременные контакты тел с Δt→0 (Δt ≤ 0,001 с).
При таких коротких взаимодействиях возникают столь
большие силы (F=Δp/Δt), что другими, постоянно действующими силами можно пренебречь. Это дает право
рассматривать сталкивающиеся тела как замкнутую
систему и применять к ним закон сохранения импульса.
Упругими называют такие столкновения, в результате
которых внутреннее состояние тел остается без изменений.
Это означает, что при упругих столкновениях сохраняется
как импульс, так и механическая энергия.
При неупругих столкновениях внутреннее состояние тел
изменяется в рез-те работы сил неупругой деформации,
которые, в отличие от упругих сил, являются диссипативными. Т.к. работа любой диссипативной силы Адис < 0,
85. § 4.8. Столкновения. Внутренняя энергия
то механич. энергия системы убывает: Е2 − Е1 = Адис < 0.Уменьшение мех. энергии означает, что она частично
преобразуется во внутреннюю (тепловую) энергию
хаотического движения молекул U, причем количество
выделяющегося тепла
Q E1 E2 U 2 U1.
Представим это соотношение в другой форме:
E1 U 1 E2 U 2 . закон сохр. полной энергии
Закон сохр. полной энергии, как и закон сохр. импульса,
выполняется при любых столкновениях.
86.
§ 4.9. УРАВНЕНИЕ МОМЕНТОВ.ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСА
П. Одна частица. Моментом импульса L частицы
относительно т. О называют векторное произведение
L = r × p. Найдем изменение L :
dL dr dp
r F M
p r
v p r F r F
dt dt
dt
dL
M
(M ) ур - е моментов частицы
dt
Здесь М = r × F − момент силы F относительно т. О.
87. § 4.9. Уравнение моментов. Закон сохранения момента импульса
П. Система частиц. Моментом импульса системычастиц L называют аддитивную величину
L Li ri pi .
Его изменение:
dL
ri ( Fi Фij) M i M ij M M .
dt
i,j
i
i,j
Можно показать, что Mij M ji M 0.
Следовательно:
dL
Mi M.
dt
(M * C) ур - е моментов для системы
Приращение L за конечный интервал времени:
t
L L L0 Mdt.
0
(M * Cинт )
88.
Получим условия, при которых сохраняется L.1) Замкнутая система. В этом случае все Fi = 0.
Fi 0 M i 0 M 0 L Li (t ) const.
NB! L замкнутой системы сохраняется относительно
любой точки О.
2) Иногда L сохраняется и для незамкнутых систем! В
этом случае проблема заключается в поиске такой точки
О, относительно которой М = 0.
◄Пример: движение планеты вокруг Солнца
3) Иногда у незамкн. систем сохраняется не сам L, а его
проекция LZ на некоторое направление Z, если MZ = 0:
dL
dLZ
MZ 0
M
M Z LZ LiZ (t ) const.
dt
dt
89.
Моментами импульса LZ и силы MZ относительнооси Z называют проекции на эту ось векторов L и М
относительно любой т. О , выбранной на данной оси.
Нетрудно показать, что выбор т. О на оси влияет на
значения моментов L и М относит. этой точки, но не
влияет на значения моментов LZ и MZ относительно оси.
dLZ dt M Z
− ур-е моментов относительно оси.
Нетрудно убедиться, что момент некоторой силы F
относительно оси Z определяется ф-лой MZ = R∙Fφ ,
где R − расстояние от точки приложения силы до оси, а
Fφ − проекция силы на орт еφ в цилиндрической системе
координат, связанной с осью Z правилом правого винта.
◄! М и MZ − характеристики вращат. способности силы
90.
Элементы динамики твердого тела91. Элементы динамики твердого тела
Задача• Что сложнее раскрутить диск или кольцо?
92. Задача
ГЛАВА 5. ДИНАМИКА ТВЕРДОГО ТЕЛАТвердое тело − тело, деформациями которого можно
пренебречь.
Любое движение тв. тела можно разложить на поступательное со скоростью V0 какой-либо произвольной точки
О (полюса) и вращение вокруг мгновенной оси, проходящей через полюс.
Можно показать, что скорость любой точки А тела равна
v V0 r ,
где r − р.-вектор, проведенный из полюса О в точку А.
Резюме: для полного описания движения тв. тела
необходимо знать V0 и .
◄! 6 степеней свободы
93. Глава 5. Динамика твердого тела
Замечание. Величина V0 зависит от выбора положенияполюса, тогда как от этого выбора не зависит.
Пример.
94.
§ 5.1. УРАВНЕНИЕ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯТВЕРДОГО ТЕЛА
Поступательным называют такое движение, при
котором любой отрезок прямой, связанный с телом, все
время остается параллельным самому себе. Для описания
поступат. движения достаточно найти
закон движения R0(t) только для полюса О.
Обычно в качестве полюса выбирают ц.м. тела С, т.к.
ур-е поступат. движения имеет самый простой вид
именно для ц.м.:
dVC
dP
P mVC m
F,
dt
dt
(F )
где F − результирующая всех внешних сил.
95. § 5.1. Уравнение поступательного движения твердого тела
§ 5.2. УРАВНЕНИЕ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯВращательным называют такое движение, при
котором все точки тела описывают окружности, центры
которых находятся на одной прямой, называемой осью
вращения.
Ур-ем вращат. движения тв. тела является ур-е моментов
dL
M,
dt
(M )
т.к. именно оно включает моменты сил, характеризующие
способность сил вращать тело.
◄Замечание. Такой простой вид (М) ур-е моментов имеет
в двух случаях: 1) относительно произвольного неподвижного начала в ИСО; 2) относит. ц. масс тела С,
при произвольном его движении.
96. § 5.2. Уравнение вращательного движения
§ 5.3. ВРАЩЕНИЕ ТЕЛА ВОКРУГ НЕПОДВИЖНОЙОСИ
Полное описание движения тв. тела достигается путем
решения ур-й (F) и (M):
dP
F,
dt
(F )
dL
M.
dt
(M )
Ур-е (М) намного сложнее, чем ур-е (F). Причина этого в
сложном (тензорном) характере связи между векторами
L и , направления которых часто не совпадают, так что
L ≠ I .
◄!Пример: вращ. стержня
В то же время, т.к. всегда P = mVС, то ур-е для VС имеет
простой вид: (F) → m∙dVС /dt = F.
Рассмотрим сравнительно простой случай вращения тела
вокруг закрепленной оси (турбина, маховик, дверь).
97. § 5.3. Вращение тела вокруг неподвижной оси
98.
Направим ось Z вдоль оси вращения и спроецируем нанее ур-е (М) :
dLZ dt M Z .
Найдем связь между LZ и Z.
Li ri mi vi ri mi vi Ri mi vi
Вектор ri mi vi перпендикулярен OZ ; вектор
2
Ri mi vi vi Ri mi Ri направлен вдоль .
Поэтому
Li z mi R i2 z ,
LZ Liz z
где
I m i R i2
так что
2
mi R i
I z ,
− момент инерции тела
относительно оси вращения.
99.
Следовательно:d ( I Z )
M Z.
dt
(M Z )
основное ур-е динамики
вращат. движения
NB! Связь LZ = IωZ выполняется для произвольной
системы частиц, движущихся с одной и той же ω.
Поэтому ур-е (MZ) справедливо для любой такой системы.
Если тело не деформируется, то I = const, так что:
d Z
I
M Z,
dt
или I z M Z .
(M T )
основное ур-е
динамики вращат.
движения тв. тела
Т.к. Z обратно пропорционально I, то момент инерции
является мерой инертности тела при его вращательном
движении.
100.
§ 5.4. МОМЕНТ ИНЕРЦИИМом. ин.
I m i r i является аддитивной величиной.
2
Если в-во в теле распределено непрерывно, то расчет I
проводится по ф-ле:
mi ri dm r
m i 0
i
I lim
2
2
V
r dV .
2
V
Пример. Момент инерции кольца (полого цилиндра)
массы m, радиуса R относительно оси, проходящей через
ц.м. кольца перпендикулярно его плоскости.
I C r dm r R R
2
V
2
dm mR .
2
V
101. § 5.4. Момент инерции
Моменты инерции IС некоторых тел относительнооси ZC, проходящей через ц.м. тела:
Твердое тело
Ось ZС
IС
Тонкий стержень длины l
Перпендикулярна
стержню
1 ml 2
12
Сплошной цилиндр (диск)
радиуса R
Совпадает с осью цилиндра
1 mR2
2
Тонкий диск радиуса R
Совпадает с диаметром
диска
1 mR2
4
Шар радиуса R
Проходит через центр шара
2 mR2
5
Полый шар радиуса R Проходит через центр
Кольцо радиуса R
2mR2/3
Совпадает с диаметром mR2/2
102.
◄ Задача. Цепью “на весу” раскручивается велосипедноеколесо. Какое требуется время, чтобы линейная скорость
обода стала равной v =10 м/с?
Радиус “звездочки” R1 = 5 см, обода R2 = 40 см, масса
обода M = 2 кг, сила натяжения цепи F = 20 Н.
I = R 1F →
= R1F/I
ω = ω0 + t = { ω0 = 0 } = tR1F/I → v = ωR2 = tR1R2F/I
Отсюда
получаем:
vMR2
vI
2
t
I MR2
8 c.
R1R2 F
R1F
103.
П. Теорема Штейнера:момент инерции I относительно произвольной оси равен
сумме момента ин. IС относительно оси, параллельной
данной и проходящей через ц.м. тела и ma2,
где а − расстояние между осями − I = IС + ma2.
Пример. Момент инерции кольца относительно оси,
проходящей через его край перпендикулярно плоскости
кольца.
I I C ma a R I C mR 2mR .
2
2
2
104.
§ 5.5. ЗАКОН СОХРАНЕНИЯ МОМЕНТА ИМПУЛЬСАОТНОСИТЕЛЬНО ОСИ
dLZ
M Z 0
M Z LZ I Z const .
dt
Пример: скамья Жуковского.
Студента с гантелями
раскручивают вместе с
платформой. Момент
импульса системы L1 = I1 1.
Если свести руки, то момент
инерции убывает I2 < I1.
Тогда из L1 = L2 следует, что
2 = I1 1 / I2 > 1.
◄Фигуристы, гимнасты
105. § 5.5. Закон сохранения момента импульса относительно оси
§ 5.6. КИНЕТИЧЕСКАЯ ЭНЕРГИЯТВЕРДОГО ТЕЛА
П. Теорема Кёнига. Найдем кинетич. энергию системы
частиц.
◄!Рис
2
mi vi2 ri RC ri 1
K
mi VC v i
2
vi VC v i 2
1
VC2
2
m
V
m
v
m
v
i
C i i
i i
2
2
mi ri mRC mi ri mi ri 0 mi v i 0
mVC2
K C ,
2
где
1
K C mi v i 2 .
2
Т. Кёнига: кинет. энергия системы частиц слагается из
энергии системы как целого mVC2/2 и энергии
относительного движения КС′ в СО, движущейся
поступательно вместе с ц.м.
◄!Пример: газ
106. § 5.6. Кинетическая энергия твердого тела
П. Кинетическая энергия вращательного движения.Кинетич. эн. тела, вращающегося вокруг неподвижной
оси равна
2
mi vi2
mi ri2 2 2
I
2
K ВР
m
r
.
i i
2
2
2
2
(К ВР )
Если ось проходит через ц.м., то
KВР,С I С 2 2 .
Тогда, в согласии с т. Кёнига, при
произвольном движении тв. тела его
кинет. энергия слагается из кинет. эн.
поступат. движения и кинет. энергии
вращения тела вокруг оси, проходящей
через ц.м.:
mVC2 I C 2
KT
.
2
2
(K T )
107.
П. Работа при вращении твердого тела.Изменение мех. энергии системы (см. § 4.7) равно
E2 E1 A
дис
внут
Авнеш .
В тв. теле частицы неподвижны относит. друг друга.
Следовательно внутренние силы работу не совершают, а
потому работа внешних сил равна приращению только
кинетической энергии тела. В случае вращат. движения
2
I
I
dAвращ dK d (
) d(
) I d
2
2
I dt I ω dt I ω M ω M ω d .
2
(dA ВР )
При повороте тела на конечный угол
A M ωd M ω const M ω .
0
(А ВР )
108.
П. Аналогия между поступат. и вращат. движением:Сопоставление ф-л для поступат. и вращат. движений
отражает аналогию между соответствующими
величинами: v ↔ ω, m ↔ I, F ↔ M, … .
109.
Неинерциальные системы отсчетаmar F Fтяг I e I к
d
dv0
I e m
m
, r m , , r
dt
dt
I к 2m vr ,
I цб m , , r
110. Неинерциальные системы отсчета
111.
ГЛАВА 6. РЕЛЯТИВИСТСКАЯ МЕХАНИКАA. Einstein, 1905
112. Глава 6. Релятивистская механика
113.
Ньютоновская классич. механика справедлива толькодля тел, движущихся со скоростями v << c,
где с − скорость света в вакууме.
Специальная теория относительности (СТО)
разработана Эйнштейном (1905) для преодоления
проблем, возникших при анализе распространения света
на основе классич. представлений о пр-ве и времени.
Ядро этих представлений составляют принцип
относительности и преобразования Галилея.
114.
§ 6.1. ПРИНЦИП ОТНОСИТЕЛЬНОСТИ ГАЛИЛЕЯП. Принцип относительности Галилея (1624):
все ИСО эквивалентны друг другу по отношению к
любым механическим явлениям.
П. Преобразования Галилея.
Поскольку мех. явления протекают одинаково во всех
ИСО, то ур-я механики должны иметь одинаковый вид
в этих СО. В ньютоновской механике при переходе от
одной ИСО − K(x,y,z,t) к другой − K′(x′,y′,z′,t′) используют преобразования Галилея. Они опираются на
аксиомы об инвариантности интервалов времени и
расстояний при переходе к другой СО.
115. § 6.1. Принцип относительности Галилея
Если в момент t = t′ = 0 начала отсчета О и О′ совпадают,то преобразования Галилея имеют вид:
r r r0 r0 Vt r Vt , t t ,
(Г)
где V − скорость системы К′ относительно К.
Обычно сходственные оси выбирают ↑↑-но друг другу.
Тогда x x Vt , y y, z z , t t.
(Г )
116.
Покажем, что пр-я Г. не изменяют вид ур-й механикипри переходе от одной ИСО к другой.
Дифференцируя (Г) по t = t′, получим закон преобразования (сложения) скоростей:
v v V ,
(V )
где v = dr/dt − скорость точки Р в системе К,
v′ = dr′/dt − скорость той же точки в К′.
Дифференцируя второй раз, получим: a a .
Сила F, действующая на частицу, тоже не зависит от
выбора СО. В самом деле, силы вз-вия частиц зависят
только от их взаимного расположения r21 = r2−r1
(упругие силы, тяготения, …) и от их относит. скорости
v21 = v2−v1 (трение): F = F(r21, v21 ). Из пр-я Г. следует,
что r21 = r21′ и v21 = v21′. Из неизменности аргументов
r21 и v21 следует неизменность ф-ций − сил, действующих
на частицу: F = F′.
117.
Наконец, т.к. m частицы не зависит от скорости, то m=m′.Поскольку все три величины: m, a и F, входящие во 2-й
и 3-й з. Ньютона, не меняются при переходе от одной ИСО
к другой, то сохраняют свой вид и сами ур-я
ma F ,
m a F ,
Fij F ji в системе К
Fij F ji в системе К .
Резюме. Ур-я движения класс. механики инвариантны
относительно пр-й Г.: при переходе к другой ИСО
“нештрихованные” величины заменяются на
“штрихованные” без изменения формы самих ур-й.
118.
§ 6.2. ПОСТУЛАТЫ ЭЙНШТЕЙНАИспользовать пр-ния Г. не только для механич., но и
для других явлений препятствовали исследования в
электродинамике.
1-е препятствие − эксперименты по измерению скорости
света.
Если прибор A, измеряющий скор.
света, покоится относительно
источника света, то он зарегистрирует скорость, равную с.
Если же прибор расположен в СО,
которая движется относительно
источника со скор. V, то следовало
бы ожидать, что c′ = c − V.
Напр., для космонавта В, движущегося от источника,
скор. света была бы равна с′ = с − V. Тогда, измерив с′,
можно найти V.
119. § 6.2. Постулаты Эйнштейна
На этой идее базировались опыты Майкельсона и Морли(M&M, 1881) по определению V движения Земли , но
оказалось, что якобы VЗ = 0. Это означает, что во всех СО,
независимо от скорости V их движения, скор. света такая
же, как и в СО, связанной с источником, т.е. с′= с′′=…= с,
что противоречит классич. закону сложения скоростей.
Опыты M&M
120.
2-е препятствие − неинвариантность ур-й электромагнитного поля относительно пр-ний Г.Означает ли это, что эл.магнитные явления происходят
по-разному в различных ИСО?
Опыты : эл.магнитные явления протекают одинаково во
всех ИСО, т.е. принцип относительности универсален.
Следовательно, переход от одной ИСО к другой должен
описываться с помощью пр-ния, которое отличается от
галилеевского.
121.
Созданная Эйнштейном СТО устранила возникшиепроблемы. В основе СТО лежит два постулата.
1й постулат − принцип относит. Э.:
все физические явления протекают одинаково во всех
ИСО, а все законы и ур-я, их описывающие, инвариантны
при переходе от одной ИСО к другой.
2й постулат − принцип постоянства скорости света:
скорость света в вакууме не зависит от движения источника и одинакова во всех направлениях и во всех ИСО.
Резюме. В отличие от всех других скоростей, скорость
света явл-ся инвариантной величиной. Это обусловлено
тем, что величина с является предельной скоростью в
природе: скорость любых частиц, сигналов и вз-вий не
может превышать с.
122.
§ 6.3. ПРЕОБРАЗОВАНИЯ ЛОРЕНЦАТ.к. пр-ния Г. противоречат опыту, то следует ревизовать
классич. представления об абсолютности пр-ва и времени,
лежащие в основе этих пр-ний.
Первый шаг − строгое определение эталонов длины и
времени. Наиболее точными сейчас являются атомные
часы, использующие эл.магн. волны, испускаемые
атомами 55Cs133, неподвижными в данной СО. С их
помощью устанавливают эталон 1 секунда
(1с = 9 192 631 770 периодов колебаний атомов Cs133)
и эталон 1 метр.
Тождественность атомов позволяет проградуировать
координатные сетки и часы во всех ИСО одинаковым
образом.
123. § 6.3. Преобразования Лоренца
П. Относительность одновременности.В классич. физике время является абсолютным. Это
означает, что если два события происходят одновременно
для наблюдателя К, то они одновременны и для любого
другого К′.
Однако, из 2-го постулата Э. следует, что истинность
утверждения об одновременности двух разнесенных в
пр-ве событий зависит от выбора СО.
Пример: поезд со вспышкой в середине вагона.
Относительность одновременности означает, что время в
разных СО течет неодинаково : в системе К′ − t′A= t′B, а
вот в системе К − tA < tB, хотя события А и В одни и те же!
Замечание. Если бы скорость с → ∞, то одновременность,
устанавливаемая таким сигналом, была бы абсолютной.
124.
П. Преобразования Лоренца следуют из постулатов Э.:x
x
x Vt
1
2
x Vt
1 2
, y y, z z , t
, y y , z z , t
t xV c 2
1
2
2
t xV c
К К
(Л)
К К
1 2
Здесь =V/c; V ↑↑ x ↑↑ x′ ;
за начало отсчета времени
принят момент t = t′ = 0,
когда О и О′ совпадают.
125.
Свойства пр-ний (Л): 1) пр-ния Л. сохраняют форму ур-йэл.магнит. поля при переходе от одной ИСО к другой;
2) при V << c пр-ния (Л) переходят в пр-ния (Г), т.е. (Г)
являются частным случаем (Л).
П. Следствия преобразований Лоренца.
1) Зависимость размера тела от выбора ИСО.
Пусть l0 x2 x1 − длина стержня, покоящегося в К′.
Длина l того же стержня в системе К равна разности
координат его концов l = x2− x1 в один и тот же момент t.
126.
Сравним l и l0 :l0 x2 x1
x2 x1
1 2
l
1 2
l l0 1
2
лоренцево сокращение
− размер тела, движущегося относит. ИСО, уменьшается
в направлении движения; но поперечные размеры
одинаковы во всех ИСО:
y2 y1 y2 y1 , ...
Размеры тела максимальны в той СО, относительно
которой тело покоится − их называют собственными
размерами.
127.
2) Зависимость промежутка времени от выбора ИСО.Пусть в К′ два события происходят в одной и той же точке
P (x′1 = x′2) в моменты t′1 и t′2, так что 0 t 2 t1 .
В системе К, относит. которой т. Р движется со скор. V, эти
события происходят в моменты t1 и t2. Из (Л) следует:
t2 t1
0
1 2
.
Резюме: промежуток времени минимален в той СО, в
которой оба события происходят в одной и той же точке.
Это свидетельствует о релятивистском эффекте
замедления хода времени: движущиеся часы идут
медленнее, чем неподвижные: 0 < .
Время, измеряемое по часам, движущимся с данным
объектом, называют собственным временем объекта.
128.
3) Релятивистский закон преобразования скорости.Пусть в плоскости x,y системы К со скор. v движется
частица. Проекции скорости этой частицы в К′-системе:
vy 1 2
dx dx dt
vx V
dy dt
v x
, v y
2
2
dt
dt dt 1 vxV c
dt dt 1 vxV c
2
2
2
(
1
v
c
)(
1
)
2
2
v v x v y c 1
.
2 2
(1 vxV c )
(VP )
При малых V << c и v << c эти ф-лы переходят в ф-лы
сложения скоростей (VΣ) классич. механики:
v x vx V , v y vy
v v V .
Из (VP) следует, что если v = c, то v′ = c, т.е. релятив.
закон преобразования скорости согласуется со 2-м
постулатом Э.
129.
4) Интервал.Ключевая задача СТО − отыскание инвариантных величин и законов. Одна из них − с. Другая важная
инвариантная величина − пространственно-временной
интервал между событиями
S12 c t l ,
2 2
12
2
12
где t12 − промежуток времени между событиями,
l12 − расстояние между точками, в которых происходят
эти события.
Инвариантность интервала следует из пр-ний (Л):
c t l .
S12 S12
2
2
12
2
12
130.
§ 6.4. ОСНОВНОЕ УРАВНЕНИЕРЕЛЯТИВИСТСКОЙ ДИНАМИКИ
Пр-ния (Л), меняют форму законов Н. при переходе к
другой СО. Поэтому ур-е динамики необходимо изменить.
1. Движение частиц с v ~ c приводит к зависимости m(v).
Её установил Кауфман (1901), экспериментируя с эл-нами
в магнитном поле:
m
m0
1
2
,
где m0 − масса покоя (при v = 0). В отличие от
релятивистской массы m, масса покоя m0 явл-ся
инвариантом, т.е. характеристикой частицы.
131. § 6.4. Основное уравнение релятивистской динамики
2. Определим релятивистский импульс какp mv
m0 v
1
2
.
Определенный таким образом импульс:
а) подчиняется закону сохр. независимо от выбора ИСО;
б) позволяет сохранить “нерелятивистскую” форму
основного ур-я динамики dp/dt = F :
m0 v
d
(
) F . (2p) основное ур. релят. динамики
dt 1 2
В таком виде основное ур-е динамики инвариантно по
отношению к пр-ниям (Л).
Ур-е (2р) позволяет найти закон движения, если
известны r0, v0 и F.
NB! В общем случае a и F неколлинеарны.
При v << c ур-е (2р) принимает “классич.” вид ma = F.
132.
§ 6.5. МАССА И ЭНЕРГИЯИзменение ф-лы для р приводит к новому выражению для
энергии. Введём кинетич. энергию, как и в ньютоновской
механике, через её изменение:
dK dA F dr F vdt v d (mv)
v dv vdv v 2 dm mvdv.
Воспользуемся рав-вом
циал
m 2 m02 (1 2 ) m 2 c 2 m02 c 2 m 2 v 2 диф
2mc dm 2mv dm 2m vdv 2mdK , т.е.
2
2
2
dK c dm ($)
2
K c (m m0 ) m0 c (
2
2
: v 0, m m0 , K 0
1
1
2
1). релят. кинет. эн.
133. § 6.5. Масса и энергия
Выражение для К при v << c принимает вид:m0 v
3
2
K m0c (1
... 1) m0c
,
2
8
2
2
2
2
4
2
2
т.е. нерелятив. форму.
Согласно ($), приращение кинет. энергии сопровождается
увеличением релят. массы. Эйнштейн понял, что масса
тела будет возрастать не только при сообщении ему кинет.
энергии, но и при любом увеличении общей энергии тела
2
Е (кинетич. + внутр.) :
dE c dm.
Интегрируя при условии Е = 0 при m = 0, получим:
E mc
2
m0c 2
1 2
m0c K . полная релят. энергия
2
134.
Следовательно, покоящееся тело (К=0) также обладаетэнергией
E0 m0c 2 ,
(E 0 )
называемой энергией покоя. Эта энергия представляет
собой внутреннюю энергию, не связанную с движением
тела как целого.
NB! В полную энергию Е не входит потенц. энергия тела
во внешнем поле.
П. Полезные формулы:
2
2 2
2 4
1) E p c m0 c инвариант;
2
2) p Ev/c ;
3) pc K ( K 2m0c ) .
2
Положив в 1) m0 = 0, получим Е = рс, которое согласуется
с 2) только если v = c. Следовательно, частица с m0 = 0
всегда движется со скор. света. К таким частицам
относятся фотоны.
135.
§ 6.6. ЗАКОНЫ СОХРАНЕНИЯВ РЕЛЯТИВИСТСКОЙ МЕХАНИКЕ
Для замкнутой системы частиц выполняется закон сохр.
релятив. импульса:
pi (t ) P const.
( P)
Кроме того, в этом случае может выполняться закон сохр.
полной релятив. энергии:
Ei (t ) mic
2
E const.
(E)
Это справедливо, в частности, для: а) системы невзаимодействующих частиц; б) при столкновениях и распадах
частиц.
Задача. Покоившаяся частица массы m0 распалась на
новую частицу и фотон с импульсом р . Найти массу
покоя новой частицы.
◄!
136. § 6.6. Законы сохранения в релятивистской механике
Специальная теорияотносительности
137. Специальная теория относительности
Постулаты Эйнштейна• Первый постулат
В любых ИСО все физические явления при
одних и тех же условиях протекают
одинаково.
• Второй постулат
Скорость света в вакууме не зависит от
движения источника света.
138. Постулаты Эйнштейна
Преобразования Лоренцаx Vt
x
1 V
2
c
x
2
y y
z z
t
1 V 2 c2
y y
z z
t Vx c 2
1 V
x Vt
2
c
t
2
t Vx c 2
1 V 2 c2
x y z c t inv
2
2
2
2 2
139. Преобразования Лоренца
Интервал времени и длинныl l0 1 v 2 c 2
0
1 v 2 c2
c 2 t12
l s12 c 2t12 2 l 2
s12
2
2
140. Интервал времени и длинны
Преобразование скоростей иускорений
v x
v y
v z
vx V
v x V
, vx
2
1 Vv x c
1 Vv x c 2
v y 1 V 2 c 2
1 Vv x c
2
v z 1 V 2 c 2
1 Vv x c 2
, vy
v y 1 V 2 c 2
1 Vv x c 2
v z 1 V 2 c 2
, vy
1 Vv x c 2
2 2
2 2
1
v
c
1
V
c
2
2
v c 1
1 Vv x c 2 2
2 c 2 1 V 2 c 2
1
v
v 2 c 2 1
1 Vv x c 2 2
141. Преобразование скоростей и ускорений
31 V 2 c 2
,
a x a x
2
1 Vv x c
Vv y 1 V 2 c 2
Vv x
a y 1 2 a y 2 a x
c
c
1 Vv x c 2
3
1 V 2 c 2
a x a x
2
1 Vv x c
Vv y 1 V 2 c 2
Vv x
, a y 1 2 a y 2 a x
3
c
c
1 Vv c 2
x
a z и a z по аналогии с a y и a y
3
142.
Кинетическая энергия, сила иускорение
1
Wк mc
1
1 v 2 c 2
2
1 v 2 c2
Fv
a
F
v
2
m
c
143. Кинетическая энергия, сила и ускорение
Массы и энергияW
mc 2
1 v 2 c 2
W0 mc 2
W m 2c 4 p 2c 2
2
W 2
W
2
2
2 2
p
p
m
c inv
2
2
c
c
144. Массы и энергия
Преобразование импульса и силыp x
W
p x VW c 2
1 V 2 c2
W Vp x
1 V 2 c2
, px
,W
Fx V ( Fv ) c 2
Fx
1 Vv x c 2
Fy
Fy 1 V 2 c 2
1 Vv x c 2
p x VW c 2
1 V 2 c2
W Vp x
1 V 2 c2
145. Преобразование импульса и силы
МКТ. Распределение Максвеллаdn n0 f (u )4 u 2du n0 F (u )du
F (u )du 1
0
m
f (u ) 0
2 kT
32
e
32
m0u 2 (2 kT )
m0
m0u 2 (2 kT )
2
dn n0
e
4
u
du
2 kT
2
dn n0
kT 3 2 e Wk ( kT ) Wk dWk
2
F (Wk )
kT 3 2 e Wk ( kT ) Wk
146. МКТ. Распределение Максвелла
Распределение Больцманаp p0e gMh
( RT )
n n0e m0 gh
( kT )
n n0e
W p ( kT )
n0e gN Am0h
( RT )
147. Распределение Больцмана
Распределение Максвелла Больцманаm0u 2
( kT )
3 2 W p
2
e
4 u 2du
m0
dn n0
2
kT
148. Распределение Максвелла - Больцмана
МОЛЕКУЛЯРНАЯ ФИЗИКАИ ТЕРМОДИНАМИКА
Савельев; Сивухин (т.2);
Иродов И. Физика макросистем;
Кикоин И., Кикоин А. Молекулярная физика.
Молекулярная физика и термодинамика −
разделы физики, изучающие строение и свойства
вещества.
Молекулярная физика базируется на
молекулярно-кинетических представлениях.
Термодинамика опирается на постулаты,
являющиеся обобщением опытных данных.
149. МОЛЕКУЛЯРНАЯ ФИЗИКА И ТЕРМОДИНАМИКА
ГЛАВА 1. КЛАССИЧЕСКАЯ СТАТИСТИКАБОЛЬЦМАНА
§ 1.1. Основные понятия физики макросистем
Макросистема − система, состоящая из очень большого
числа частиц (молекул, атомов, фотонов, ...).
Полное описание классической макросистемы достигается
путем определения микроскопических
(динамичес
ких) параметров mi , qi , ri , pi для всех ее частиц.
Состояние системы, описанное столь детально, называют
микросостоянием.
На практике для описания макросистемы используют
экспериментально измеряемые макроскопические
(термодинамич.) параметры P, ρ, V, T .., характеризующие систему в целом. Состояние, описанное с
помощью макропараметров, называют
макросостоянием.
150. Глава 1. Классическая статистика Больцмана
Опыт показывает, что если систему изолировать, то онаперейдет в равновесное состояние, когда ее макропараметры остаются неизменными, хотя микросостояние
непрерывно меняется.
Основная задача описания макросистемы − определение
ее макросостояния.
Два подхода к изучению макросистем: статистический
и термодинамический.
Термодинамика не использует представления о
строении вещества. Она основана на общих принципах
(началах), являющихся обобщением опытных фактов и
оперирует только экспериментально измеряемыми
макропараметрами.
Молекулярная (статистическая) физика, исходит
из представлений о молекулярном строении в-ва. Её
задача − объяснить свойства в-ва как результат
взаимодействия молекул.
151.
§ 1.2. МОЛЕКУЛЯРНО-КИНЕТИЧЕСКАЯ ТЕОРИЯИДЕАЛЬНОГО ГАЗА
Идеальным называют газ, у которого взаимод-вие между
молекулами и их собственный объем пренебрежимо малы.
П. Ур-е состояния идеального газа имеет вид (опыт):
PV
M
m
RT
(КМ) − ур-е Клапейрона-Менделеева.
Здесь R = 8,31 Дж/моль∙К − универс. газовая постоянная;
моль − кол-во вещества, содержащее число Авогадро
NA= 6,022∙1023 частиц. Другая форма ур-я состояния:
M
M NA R
P
T N A N nkT , ( KМ* )
m V NA
m
где n = N/V − концентрация частиц;
k = R/N = 1,38∙10−23 Дж/К − постоянная Больцмана.
152. § 1.2. Молекулярно-кинетическая теория идеального газа
П. Закон Дальтона. ◄см. семинарП. Основное ур-е кинетической теории газов.
Давление, оказываемое газом на стенки сосуда Р = F/S,
можно рассчитать, определив силу F, действующую на
элемент стенки S. Из 2-го закона Н. имеем, что F= Δp/Δt,
где Δp − величина импульса, сообщаемого молекулами
стенке S за время Δt. Можно показать, что в случае
упругого столкновения молекул со стенкой, величина Р
определяется формулой:
( УКТ ) − основное ур-ние
n
2
2
P m v n пост . кинетической теории газов.
3
3
пост m v 2 / 2
Здесь
− средняя кинетическая
энергия поступательного движения молекул;
N
− среднее значение квадрата
2
2
v vi N
скорости молекул.
i 1
153.
Ур-е ( УКТ) связывает микроскопические параметрыгаза vi, i с макроскопическим параметром Р.
Сопоставив ( УКТ ) с уравнением ( KМ* ), получим
пост
3
kT .
2
( εП )
Из ф-лы ( п) следует физический смысл макропараметра
Т: температура Т является мерой средней кинетической
энергии поступательного движения молекул.
Введем среднеквадратичную скорость
vкв
v
2
3kT / m 3RT / m .
Тогда ( УКТ ) можно записать в виде
1
1
2
2
P n m vкв vкв .
3
3
154.
§ 1.3. РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛАТ.к. макросостояние газа в равновесии не меняется, то
должно существовать - в среднем неизменное - распределение молекул по скоростям. Оно было получено
Максвеллом (1859). ◄!
Задача: найти число молекул ΔN, скорости которых лежат
в интервале [v, v + Δv]. Ясно, что это число пропорционально как полному числу молекул N, так и Δv, т.е.
N N f ( v) v,
где f(v) − ф-ция распределения молекул газа по их
скоростям. Максвелл нашел вид функции:
3/2
2
mv
m
2
f ( v) 4
2 kT
v exp(
2kT
).
(M)
155. § 1.3. Распределение Максвелла
156.
Эта ф-ция нормирована на единицу:П. Характерные скорости.
0 f (v)dv 1.
Наиболее вероятной скорости vв соответствует
максимум ф-ции f(v). Из условия df/dv = 0 получим:
vв
2kT
m
2 RT
m
.
Средняя скорость, по определению, равна:
v v vf (v)dv 8kT / m 8RT / m .
0
157.
Среднеквадратичную скорость vкв найдём из условия:v
Отсюда
2
3kT
v f ( v)dv
.
m
0
vкв
2
v
2
3kT
.
m
Значения характерных скоростей соотносятся как
vв : v : vкв 1 : 1,13 : 1,22 .
158.
§ 1.4. РАСПРЕДЕЛЕНИЕ БОЛЬЦМАНАЕсли газ находится в поле внешних сил, например, силы
тяжести, распределение его молекул по высоте сосуда
становится неоднородным.
П. Барометрическая формула. Условие равновесия
элементарного цилиндра газа с основанием S и высотой
dy имеет вид:
p2 S p1S gSdy 0.
Для идеального газа разность
давлений dp = p2 − p1 равна:
pmg
dp
dy .
RT
Если зависимость T(y) известна,
то это ур-е можно проинтегрировать и найти p(y).
159. § 1.4. Распределение Больцмана
В случае изотермической атмосферы ( T = const) получимp p0 exp(
mgy
RT
).
(БФ) − барометрич. ф-ла
Здесь р0 − давление на высоте у = 0.
160.
Т.к. p = nkT, то для изотермической атмосферы будемиметь
m gy
m gy
n n0 exp(
) n0 exp(
).
RT
kT
( БФ*)
Резюме. Падение p с высотой обусловлено уменьшением
n, вследствие действия силы тяжести. Силе тяжести
противодействует Т, т.е. кинетич. энергия молекул,
которая позволяет им подниматься вверх.
◄ Ролик
161.
П. Распределение Больцмана. Перепишем ф-лу (БФ*)в виде
n n0 exp( ) ,
kT
(Б)
где Π = mgy − потенц. энергия молекулы в поле тяжести;
n0 − концентрация молекул в той точке, где Π = 0.
Нетрудно показать, что закон (Б) справедлив также и в
поле других консервативных сил.
Закон (Б) называют распределением Больцмана.
162.
§ 1.5. РАСПРЕДЕЛЕНИЕ МАКСВЕЛЛА-БОЛЬЦМАНАОба распределения ( М ) и ( Б ) можно объединить в одно
распределение Максвелла-Больцмана, согласно
которому число молекул dN, скорости и координаты
которых лежат в интервалах [v, v+dv], [x, x+dx], …,
[z, z+dz] определяется выражением ( МБ ):
m
dN n0 4
2 kT
3/2
2
m
v
/ 2 ( x, y , z )
2
v exp(
)dvdxdydz .
kT
163. § 1.5. Распределение Максвелла-Больцмана
ГЛАВА 2. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИВ основе т/д лежат опытные законы: ур-е состояния,
I и II начала термодинамики.
§ 2.1. Квазиравновесные процессы
1-е начало т/д выражает закон сохранения энергии для
т/д процессов.
Любой процесс реализует переход системы из одного
состояния в другое, а потому приводит к нарушению
равновесия.
◄!Пример: сжатие газа поршнем
(Квази)равновесными называют процессы, которые
протекают настолько медленно, что состояние газа в
каждый момент является практически равновесным.
◄! Sand
164. Глава 2. Первое начало термодинамики
Для описания равновесного процесса требуется столькоже параметров, как и для равновесного состояния.
В случае газа таких параметров два − например, p и V.
Поэтому равновесный процесс можно изобразить
соответствующей кривой.
Для задания неравновесного состояния требуется бесконечное число параметров; неравновесные процессы
условно изображают пунктирными кривыми.
Многие реальные процессы можно считать квазиравновесными − например, процессы в цилиндрах двигателей,
поскольку скорость поршня vпорш << vмолек .
165.
П. Изопроцессы.В большинстве т/д процессов одновременно меняются все
параметры состояния.
К числу простейших относятся изопроцессы:
1) изохорный − процесс, протекающий при V = const;
2) изобарный − при р = const;
3) изотермический − при Т = const.
166.
§ 2.2. ВНУТРЕННЯЯ ЭНЕРГИЯВнутренняя (“невидимая”) энергия U включает в себя:
1) кинетич. энергию хаотического движения молекул
системы;
2) потенц. энергию взаимодействия между молекулами;
3) внутреннюю энергию самих молекул.
Основное свойство: U является однозначной ф-цией
состояния системы − например, U = U(V,T).
Поэтому приращение ΔU = U2− U1 определяется только
начальным и конечным состояниями и не зависит от вида
процесса 1 → 2.
П. Внутренняя энергия идеального газа.
В идеальном газе вз-вием молекул можно пренебречь.
Поэтому внутр. энергия равна сумме энергий отдельных
молекул U = N<
молекулы.
>, где < > − средняя энергия одной
167. § 2.2. Внутренняя энергия
Запишем выражение для средней кинет. энергиипоступательного движения в виде
пост
3
kT
kT nпост
,
2
2
где nпост = 3 − число степеней свободы поступат.
движения, kT/2 − энергия, приходящаяся на одну
степень свободы поступат. движения.
Больцман обобщил этот вывод в виде закона о равнораспределении энергии по степеням свободы: на каждую
степень свободы молекулы в среднем приходится
одинаковая кинетическая энергия, равная kT/2.
Следовательно, энергия жестких молекул :
< > = i∙kT/2, где i = nпост + nвр.
◄!Примеры
При Т ≥1500 K в молекулах активируются колебательные
степени свободы, на каждую из которых приходится
энергия < кол > = 2∙kT/2 = kT.
168.
Резюме: средняя энергия молекулы равнаkT
i , где i nпост nвр 2nкол .
2
Следовательно:
U N
M
kT M RT
NA i
i
.
m
2
m 2
169.
§ 2.3. ПЕРВОЕ НАЧАЛО ТЕРМОДИНАМИКИИзменить энергию системы можно двумя способами.
1) Механическим воздействием (сжатие, …) − изменение
определяется работой внешних сил Авнеш.
2) Путем теплообмена − энергия передается молекулам
системы путем случайных толчков, а ее количество
определяется количеством теплоты Q.
Полная энергия системы Е = К+П+U. В т/д обычно
рассматривают покоящиеся тела, мех. энергия которых
не меняется. В этом случае закон сохранения энергии
имеет вид:
E (K U) U Aвнеш Q.
Обычно вместо работы Авнеш, совершаемой внешними
силами над системой, рассматривают работу А системы
над внешними телами. В случае квазиравновесных
процессов рвнеш = р, а потому Авнеш = −А.
170. § 2.3. Первое начало термодинамики
В таком случае, закон сохр. энергии принимает вид:Q = ΔU + A.
( I ) − 1-е начало т/д
Все величины в ( I ) − алгебраические:
Q > 0 соответствует получению тепла системой.
Для элементарных процессов (когда изменения параметров малы) 1-е начало имеет вид
Q = dU + A.
( Iэл )
П. Перпетуум мобиле.
Если U2 = U1 и Q = 0, то из ( I ) следует, что А = 0.
Это означает, что невозможен перпетуум мобиле
(вечный двигатель) 1-го рода, т.е. такой периодически
действующий механизм, который совершал бы работу, не
получая энергию извне.
171.
§ 2.4. РАБОТА СИСТЕМЫВ т/д работу обычно представляют как ф-цию изменения
объема. Сделаем это на примере газа под поршнем:
A = Fг∙dh = pS∙dh = pdV.
Следовательно,
A
V2
pdV .
V1
Работа − алгебраическая величина:
а) A > 0, если V2 > V1 (расширение газа);
б) A < 0, если V2 < V1 (сжатие).
Величина А определяется не только
изменением параметров системы , но
и способом, которым происходит это
изменение.
◄! А1а2
172. § 2.4. Работа системы
Поэтому знак дифференциала в ( Iэл ) используетсятолько для прироста dU, который полностью определяется
изменением своих аргументов, независимо от способа
реализации этих изменений.
Задача А. Вычислить величину А для изопроцессов.
1) V = const:
2) p = const:
A = 0.
A
V2
pdV p(V2 V1 )
V1
V2
M
m
R(T2 T1 ) .
V2
V2
dV M
RT
RT ln .
3) T = const: A pdV
m
V
m
V1
V1
V1
M
Резюме: а) величина работы является ф-цией процесса;
б) внутренняя энергия − ф-цией состояния.
◄! U ↔ П
173.
§ 2.5. ТЕПЛОТА. ТЕПЛОЕМКОСТЬQ = dU+ A
( Iэл )
Т.к. A является функцией процесса, то из ( Iэл ) следует,
что и Q тоже является функцией процесса.
Теплоемкостью тела (системы) СТ называют
количество теплоты, которое требуется, чтобы повысить
температуру тела на 1 градус: CT = Q/dT .
Для характеристики теплоемкости вещества вводят
“единичные” теплоемкости: удельную с и молярную С.
Дж
Если масса однородного тела М, то
C
Q McdT
M
m
С = mс.
CdT .
моль К
Дж
с
кг К
Отсюда связь
Величина теплоемкости, как и Q, зависит от процесса.
174. § 2.5. Теплота. Теплоемкость
Найдем молярные теплоемкости. 1-е начало для одногомоля (индекс М):
CdT = dUМ + pdVМ.
В общем случае U зависит от двух параметров.
Например, U = U(V,T) − калорическое ур-е состояния.
Поэтому
U
U
dU
dT
dV .
T V
V T
U
dV
U
Следовательно C M M p M .
T V V T
dT
(C)
П. Теплоемкость идеального газа. Внутренняя эн.
идеального газа не зависит от объема U = U(T). Поэтому
dU M
dVM
C
p
.
dT
dT
( Cид )
а) При изохорическом процессе V = const, так что
dU M
i
i
CV
U M RT R .
dT
2
2
175.
б) Для изобарического процесса из ф-лы ( Сид ) следуетформула
dU M
VM
CP
p
pVM RT C V R . Майера
dT
T
p
Т.к. CV = iR/2, то
CP (i 2) R 2 .
в) Отношение теплоемкостей
= CP/CV.
Для идеальных газов (i 2) i .
Пример. Воздух является смесью в основном 2х-атомных
молекул. Следовательно: i = 5; = 7/5 = 1,4;
CV = 5R/2 = 20,8 Дж/(моль∙К);
CP = 7R/2 = 29,1 Дж/(моль∙К).
176.
П. Квантовая теория теплоемкости.Сравнение классической теории теплоемкости газов с
опытом показывает, что ряд опытных фактов
противоречит этой теории.
Прежде всего, это касается температурной зависимости
теплоемкости. Согласно теории, теплоемкость не зависит
от температуры. Однако из опытов следует, что это верно
только в пределах отдельных температурных интервалов.
Например, для водорода
при Т < 100 К CV = 3R/2; при 300 < T < 600 K − CV = 5R/2;
при Т > 4000 K − CV = 7R/2.
“Обрыв” кривой в т.3 соответствует диссоциации молекул.
177.
Такое поведение объясняется квантованием энергиимолекул.
В области низких температур величина теплоемкости
CV= 3R/2, что соответствует вырождению вращательных и
колебательных степеней свободы. Чтобы молекула начала
вращаться, ей необходимо сообщить энергию для
перехода на возбужденный вращательный уровень.
Минимальная энергия для такого перехода ΔEr = ħ2/I.
Возбуждение может происходить только при столкновениях c молекулами, обладающими достаточной энергией.
Т.к. средняя энергия теплового движения ~kT, то при
kT<< ΔEr этой энергии недостаточно для возбуждения
вращений. В этом случае при вычислении теплоемкости
вращения можно не учитывать. В противоположном
случае, когда kT>>ΔEr , возбуждается много вращательных уровней. Тогда дискретность уровней становится
несущественной и применима классическая теория.
178.
Характеристическая температура для вращениямолекул определяется ф-лой Тr = ħ2/kI.
Для молекулы Н2: I = 2mR2 = {m =1,67∙10−27 кг, R= 0,4Ǻ}=
5,3∙10−48 кг∙м2. → → Тr ~150 K.
Резюме При Т>>Тr справедлива классическая теория;
при Т<<Тr вращательные степени свободы “заморожены”.
Аналогично оценивается характеристич. температура
для колебаний молекул Tv=ΔEv/k=ħωv/k.
Для водорода Tv ~ 5000 K.
179.
§ 2.6. АДИАБАТИЧЕСКИЙ ПРОЦЕССАдиабатическим называют процесс, протекающий без
теплообмена с внешней средой.
Близкими к адиабатическим являются процессы в
двигателях, звуковые волны в газе и т.п.
Ур-ние адиабатического процесса для идеального газа
получим, проинтегрировав ур-е ( Iэл ):
CV dT pdV 0 .
Здесь = М/m − число молей газа. Выразив dT из ур-я
состояния pdV+Vdp = RdT , получим
dV dp
0.
V
p
Это соотношение можно записать в виде
d ( ln V ln p) 0 .
180. § 2.6. Адиабатический процесс
Отсюда следует ур-е адиабаты (ур-е Пуассона):γ
pV const , или TV γ 1 const .
П. Работу газа в адиабатическом процессе
удобно найти с помощью 1-го начала:
γ 1
V1
p1V1
M
M R
1 .
A U CV T
(T1 T2 )
m
m 1
1 V2
181.
§ 2.7. ПОЛИТРОПИЧЕСКИЕ ПРОЦЕССЫПолитропическими называют процессы, при которых
теплоемкость системы С является постоянной величиной.
Можно показать, что уравнением политропического
процесса идеального газа является уравнение
pV const .
n
Здесь n (C CP ) (C CV ) − показатель политропы.
Все рассмотренные ранее изопроцессы относятся к
категории политропических процессов. Легко видеть, что
значения n для изопроцессов равны:
процесс // изобар. изотерм. адиабат. изохор.
n
//
0
1
γ
∞.
Работу газа в политропическом процессе легче всего
вычислить с помощью 1-го начала:
R
p1V1 p2V2
A Q U (C CV ) T
(T1 T2 )
.
n 1
n 1
182. § 2.7. Политропические процессы
§ 2.8. ЦИКЛЫ. ТЕПЛОВЫЕ МАШИНЫДвигатель − механизм, который работает циклически,
преобразуя какой-либо вид энергии в механическую.
Цикл − процесс, при котором система после ряда
изменений возвращается в исходное состояние.
В зависимости от источника энергии, различают
гидро-, атомные и т.п. двигатели.
183. § 2.8. Циклы. Тепловые машины
Тепловая машина − двигатель, совершающий работу засчет тепла. Источник тепла называют нагревателем.
Основой большинства тепловых машин является цилиндр
с поршнем. В цилиндре помещается рабочее тело − газ,
или другое вещество.
Цикл машины состоит из двух этапов.
1) Цилиндр приводится в контакт с нагревателем.
Газ расширяется и совершает положительную работу
A1
1a2pdV .
Согласно 1-му началу
Q 1 = U2 − U 1 + A 1 ,
где Q1 − тепло, получаемое газом.
(1)
184.
185.
2) Газ возвращают в исходное состояние, сжимая до V1.Чтобы суммарная работа за цикл была больше нуля,
давление (а потому и Т) при сжатии должно быть меньше,
чем при расширении. Для этого цилиндр приводят в
контакт с холодильником.
В согласии с 1-м началом :
−Q2 = U1 − U2 − A2 ,
(2)
где Q2 − тепло, отдаваемое холодильнику при сжатии
газа.
Здесь, для удобства анализа, используются модули
величин Ai и Qi .
Сложив ( 1 ) и ( 2 ), получим энергетический баланс
цикла:
Q1 − Q2 = A 1 − A 2 ≡ A .
186.
Итог цикла: машина получила от нагревателя Q1,отдала холодильнику Q2 и произвела работу
A pdV A1 A 2 Q 1 Q 2 ,
т.е. не всё полученное тепло Q1 преобразуется в работу.
Принципиальная схема
тепловой машины.
Эффективность тепловой машины оценивают
коэффициентом полезного действия (к.п.д.):
A Q1 Q2
.
Q1
Q1
187.
П. Холодильная машина функционирует в обратномнаправлении: тепло Q2 отбирается у холодильника
(охлаждаемого тела), а Q1 передается телу с более
высокой Т. Но теперь работу А′ = Q1 − Q2 надо совершать
над машиной.
Холодильную машину характеризуют холодильным
коэффициентом
Q2
Q2
.
A Q1 Q2
188.
§ 2.9. ЦИКЛ КАРНОДля работы тепловой машины необходимо часть тепла,
полученного от нагревателя, передавать холодильнику.
Т.к. Q2 ≠ 0, то к.п.д. любой машины = 1 − Q2/Q1 < 1.
Циклом с максимально возможным к.п.д. является цикл
Карно, состоящий из двух изотерм и двух адиабат.
189. § 2.9. Цикл Карно
Реализация цикла Карно:Цикл Карно является единственным циклом, который
можно осуществить квазиравновесно при наличии только
двух термостатов − нагревателя и холодильника.
Нетрудно показать, что к.п.д. идеального (работающего
без потерь) цикла Карно равен
◄! самост.
K
T1 T2
.
T1
(K )
190.
П. Теоремы Карно.1-я теорема Карно: к.п.д. двигателей, работающих по
циклу Карно, зависит только от Т1 и Т2, но не зависит от
устройства двигателя и рода рабочего вещества.
2-я теорема Карно: к.п.д. любой тепловой машины не
может превосходить к.п.д. идеальной машины Карно,
работающей при тех же экстремальных температурах
рабочего вещества Т1max и T2min.
◄ Ролик
191.
ГЛАВА 3. ВТОРОЕ НАЧАЛО ТЕРМОДИНАМИКИ§ 3.1. Постулат 2-го начала термодинамики
1-е начало накладывает запрет на производство работы
из ничего − к машине необходимо подвести Q1.
Возможен ли более скромный запрос:
можно ли сконструировать тепловую машину полностью
преобразующую подведенное тепло в работу, т.е. машину
с = А/Q1 =1?
Такую машину называют перпетуум мобиле 2-го рода.
Опыты отрицают возможность построения такой машины.
Этот факт называют постулатом 2-го начала т/д.
Существует несколько эквивалентных формулировок
2-го начала. Приведем две из них.
192. Глава 3. Второе начало термодинамики
1. Формулировка Томсона (лорд Кельвин), 1851:“невозможен круговой процесс, единственным
результатом которого было бы производство работы за
счет охлаждения теплового резервуара.”
Формулировка Томсона накладывает запрет на вечный
двигатель 2-го рода.
Пример перпетуум мобиле 2-го рода.
193.
2. Формулировка Клаузиуса, 1850: “теплота не можетсамопроизвольно переходить от тела менее нагретого к
телу более нагретому.”
◄! Пример: 20+40
Резюме. 2-е начало отражает наличие асимметрии в
природе: разрешается полное преобразование механич.
энергии в тепловую , а также самопроизвольный переход
тепла от горячего тела к холодному, но не наоборот.
194.
§ 3.2. ОБРАТИМЫЕ И НЕОБРАТИМЫЕ ПРОЦЕССЫЕще одна формулировка 2-го начала −математическая −
оперирует понятиями обратимых и необратимых процессов.
Процесс называют обратимым, если после его завершения систему можно возвратить в начальное состояние
таким образом, чтобы в окружающих телах не осталось
никаких изменений. Если это сделать невозможно, то
процесс необратимый.
Нетрудно понять, что обратимыми являются квазиравновесные процессы. Другой пример обратимых процессов −
мех. движение в отсутствие диссипативных сил. Пример:
абсолютно упругое отражение шарика от пола.
195. § 3.2. Обратимые и необратимые процессы
Любой реальный процесс необратим. Однако, хотяидеального возврата в прежнее состояние достичь нельзя,
существует множество процессов, очень близких к
обратимым. Например, это все изопроцессы.
Вместе с тем имеются процессы, которые всегда протекают
только в одном направлении, а потому в принципе
являются необратимыми. Это:
1) самопроизвольное расширение газа;
2) самопроизвольный переход тепла от горячего тела
к холодному;
3) переход кинетической энергии макроскопического
движения во внутреннюю энергию в результате трения.
Необратимость прочих процессов связана с тем, что в них
реализуется хотя бы один из этих 3-х односторонних
процессов.
196.
§ 3.3. ЭНТРОПИЯЭнтропия − характеристика, которая указывает
направление протекания реальных процессов.
Оказывается, если система при элементарном обратимом
переходе из одного состояния в другое при тем-ре Т
получает теплоту δQ, то отношение δQ/Т является
полным дифференциалом некоторой функции S.
Эта ф-ция и есть энтропия, определяемая одним из
двух эквивалентных равенств:
Q
dS
,
T равн
Q
S2 S1
.
T равн
1
2
(S)
Факт существования ф-ции, дифференциал которой
равен δQ/Т, называют принципом существования
энтропии.
197. § 3.3. Энтропия
Из определения ( S ) следует, что можно вычислитьтолько разность энтропий. Значит, энтропия определяется
с точностью до произвольной постоянной.
Пример 1. Адиабатический процесс. δQ = 0 → dS = 0, т.е.
энтропия системы не меняется. Поэтому адиабатический
процесс называют также изэнтропическим.
Пример 2. Изотермический процесс.
2
S
1
Q
2
1
Q
Q .
T
T1
T
Например, при таянии m=1 кг льда энтропия в-ва возрастает на ∆S = m∙ l/T = 1230 Дж/К, где l − уд. теплота
плавления льда; Т = 273 К − тем-ра плавления.
NB! Увеличение S соответствует увеличению хаоса:
упорядоченное расположение молекул Н2О в кристалле
льда сменилось их беспорядком в жидком состоянии.
198.
Пример 3. Энтропия идеального газа.Если известны термическое и калорическое ур-ния
состояния, то ∆S вычисляется просто:
Q
dU pdV
dS
.
T
T
Для идеального газа dU = CVdT , pV = RT.
Следовательно,
1
RT
dS CV dT
dV .
T
V
Проинтегрировав, получим
T2
V2
p2
V2
S CV ln R ln CV ln
CP ln .
T1
V1
p1
V1
199.
§ 3.4. ПРИНЦИП ВОЗРАСТАНИЯ ЭНТРОПИИФундаментальное свойство энтропии − во всех
самопроизвольных, односторонних процессах её значение
всегда возрастает.
Докажем это свойство на примере теплообмена между
двумя телами. В этом случае изменение энтропии всей
системы равно
S S1 S2 Q1 T1 Q2 T2 .
Если, например, Т2 > T1, то Q1 = −Q2 > 0. Поэтому
1 1
S Q1 0 ,
T1 T2
т.е. общая энтропия системы, в которой происходит
теплообмен, возрастает.
Аналогично доказывается, что энтропия возрастает и
в других самопроизвольных процессах.
200. § 3.4. Принцип возрастания энтропии
Т.к. всякий реальный процесс сопровождается односторонними явлениями, идущими с повышением S,то прирост энтропии в реальном процессе будет больше
изменения S в идеализированном обратимом процессе.
Пусть δQ − тепло, полученное системой в некотором
элементарном процессе. Если бы этот процесс был
обратимым, то изменение S равнялось бы δQ/Т.
Однако в реальном процессе изменение S будет
превышать это значение, т.е. dS > δQ/T.
Если вместо знака > ввести знак ≥ , то получим общий
закон изменения энтропии как для обратимых
(знак =), так и для необратимых процессов:
dS
Q
T
. ( II )
− “математическая формулировка”
2−го начала термодинамики
201.
Для решения практических задач удобно объединитьоба начала т/д одной формулой:
dU pdV
dS
.
T
( I II )
Для замкнутой (т.е. теплоизолированной) системы
δQ = 0, так что 2-е начало сводится к утверждению:
dS 0.
(II З )
Энтропия любой изолированной системы растет до тех
пор (и достигает своего max) пока система не достигнет
т/д равновесия, т.е. когда в ней прекратятся все
необратимые процессы.
Принцип возрастания энтропии ( IIз ) относится к закрытым системам. Если же система является открытой, т.е.
обменивается с внешней средой массой и энергией, то
её энтропия может и убывать. Пример: живой организм.
202.
§ 3.5. ЭНТРОПИЯ И ВЕРОЯТНОСТЬУстановим связь между макроскопической формулировкой 2-го начала dS ≥ δQ/T и статистической теорией.
С молекулярно-кинетической точки зрения любое макросостояние системы (характеризуемое через p, V, T,…)
может быть реализовано различными способами (микросостояниями), характеризуемыми состоянием каждой из
входящих в систему молекул (их координат и скоростей).
Число различных микросостояний, соответствующих
данному макросостоянию, называют статистическим
весом G макросостояния. Эргодическая гипотеза
утверждает, что все микросостояния равновероятны.
Отсюда следует пропорциональность вероятности реализации некоторого состояния системы Р его статистическому весу: P = G∙w,
где w − вероятность каждого из микросостояний данного
макросостояния.
203. § 3.5. Энтропия и вероятность
Если система находится в неравновесном состоянии, тоона самопроизвольно (спонтанно) будет переходить в
более вероятное, равновесное состояние.
Пример. Пусть V2 − объем всего сосуда, а V1 − объем его
части, в которой находятся все молекулы, отделенные от
остальной части сосуда перегородкой. После удаления
перегородки, газ оказывается в неравновесном состоянии
и, расширяясь, переходит в новое равновесное состояние.
204.
Вместе с тем, согласно 2-му началу, все самопроизвольныепроцессы в замкнутых макросистемах сопровождаются
увеличением энтропии. Поэтому логично предположить
(идея Больцмана), что между энтропией S макросистемы
в некотором состоянии и вероятностью Р того же состояния
должна существовать связь. Установим её.
Рассмотрим необратимый процесс расширения идеального газа в пустоту в теплоизолированном сосуде от объёма V1 до
объёма V2. Т.к. при теплоизолированном
расширении в вакуум ∆U = 0, то тем-ра
идеального газа остаётся без изменений.
Поскольку S − функция состояния, то её приращение в
этом необратимом процессе можно вычислить с помощью
некоторого обратимого процесса, который переводил бы
газ в то же самое конечное состояние.
205.
Здесь в качестве такого процесса можно использоватьизотермическое квазиравновесное расширение
Qобр
Aобр
RT
V2
V2
S
ln
kN ln ,
T
T
T
V1
V1
где N = NA − число молекул в газе.
Теперь рассмотрим возможности реализации каждого из
состояний. В рассмотренном процессе распределение по
скоростям в начальном и конечном состояниях одинаково,
т.к. оно зависит только от тем-ры Т, которая не изменилась. Пространственные же возможности распределения
молекул увеличились. Т.к. молекулы беспорядочно движутся, то каждая из них с одинаковой вероятностью
бывает во всех частях сосуда. Поэтому число возможных
положений, а потому и число различных состояний некоторой молекулы увеличилось в V2/V1 раз.
206.
Т.к. положение некоторой другой молекулы не зависитот того, где находится 1-я, то число её микросостояний
также возрастает в V2/V1 раз.
Следовательно, число различных микросостояний
системы из двух молекул возрастёт в (V2/V1)2 раз. Для
всех же N молекул число возможных микросостояний
увеличится в G2/G1 = (V2/V1)N раз.
Поэтому приращение энтропии можно записать как
N
V2
V2
G2
S 2 S1 kN ln
k ln k ln
, или S k ln G .
V1
G1
V1
( Б)
Полученное соотношение называют ф-лой Больцмана.
Строгий вывод ф-лы (Б) даётся в теор. физике.
Анализ принципа возрастания энтропии ( IIЗ) со статистической точки зрения приводит к фундаментальному
выводу: все замкнутые макросистемы стремятся переходить от состояний менее вероятных к более вероятным.
207.
Переход к более вероятному состоянию с бóльшим значением энтропии представляет собой переход к болеебеспорядочному состоянию. Действительно, увеличение
энтропии системы dS = δQ/T соответствует сообщению
системе теплоты δQ, которое увеличивает степень
беспорядка (хаоса) в системе. Равновесному, наиболее
вероятному состоянию, в котором энтропия достигает
максимума S=max, отвечает достижение максимального
“хаоса” в системе.
Резюме. Энтропия является мерой степени беспорядка в
системе.
П. Флуктуации. По законам статистики возможны, хотя
и маловероятны, и противоположные процессы, в рез-те
которых энтропия убывает. Причиной таких процессов
являются флуктуации − хаотические отклонения тех
или иных величин от их средних значений.
208.
Например, в состоянии равновесия число молекул, находящихся в объёме V1 сосуда, обычно близко к среднемузначению N1=N∙V1/V2. Наличие флуктуаций приводит к
отклонению от среднего значения. Но чем больше отклонение, тем менее вероятна такая флуктуация. В принципе, может случиться, что все молекулы соберутся в
объёме V1. Однако вероятность Р=(V1/V2)N такого события
необыкновенно мала. Например, пусть V2=2V1, N=NA.
Тогда
1
3 6 102 2
P
2
NA
10
,
что соответствует практически невероятному событию.
Резюме. Статистический смысл 2-го начала заключается в том, что за каким-либо состоянием системы в
подавляющем большинстве случаев следуют еще более
вероятные состояния.
209.
§ 3.6. ТЕОРЕМА НЕРНСТАТеорема Нернста утверждает: при приближении температуры к абсолютному нулю энтропия стремится к
определенному конечному пределу S0.
Действительно, при абсолютном нуле температур энергия
системы минимальна. Число G0 допустимых квантовых
состояний системы при этом также достигает минимума.
Оно равно G0 =1, либо какому-то целому числу, равному
кратности вырождения состояния с минимальной энергией. Поэтому для энтропии также получается конечное
значение S0 k ln G0 .
Если условиться считать, что S0=0, то всякая неоднозначность в определении энтропии исчезнет. Энтропию,
определенную таким образом, называют абсолютной
энтропией. Теорему Нернста нельзя вывести из первых
двух начал т/д, поэтому её часто называют 3-им началом
термодинамики.
210. § 3.6. Теорема Нернста
ГЛАВА 4. ТВЕРДЫЕ ТЕЛА§ 4.1. Типы кристаллов
Под твердыми телами здесь понимаются кристаллические в-ва. Другой тип твердых тел − аморфные в-ва −
можно отнести к твердым только по признаку сохранения
формы. По всем остальным они (стекло, смолы, пластмассы) ведут себя как жидкости с аномально высокой
вязкостью.
◄!энергетика структурирования
Устойчивая структура кристаллов обусловлена взаимодействием между их структурными частицами. В
зависимости от природы частиц в узлах решетки и от
характера вз-вия различают 4 типа кристаллов:
ионные, атомные, молекулярные и металлические.
211. Глава 4. Твердые тела
1. Ионные кристаллы. В узлах находятся ионы противоположных знаков; вз-вие в основном электростатическое.Такую связь называют ионной (гетерополярной).
Пример: кубическая решетка с чередующимися Na+ и Cl−.
2. Атомные кристаллы. В узлах нейтральные атомы;
взаимодействие посредством обобщенных электронных
пар.
Такую связь называют ковалентной (гомеополярной).
Пример: алмаз и графит; оба состоят из 6С12, но отличаются строением решетки.
212.
3. Молекулярные кристаллы. В узлах молекулы сориентированными в направлении соседей дипольными
моментами. Такое взаимодействие между молекулами
называют вандерваальсовым. Эта связь слабая; поэтому
молекулярные кристаллы легко летучи.
Пример: нафталин.
4. Металлические кристаллы. В узлах положительные
ионы. Пр-во между ними заполнено свободными электронами. Такую связь называют металлической.
Наличием свободных электронов объясняется высокая
проводимость металлов.
213.
§ 4.2. ТЕПЛОЕМКОСТЬ ТВЕРДЫХ ТЕЛП. Классическая теория. Простейшая модель тв. тела −
кристаллич. решетка, в узлах которой расположены тождественные атомы, совершающие тепловые колебания. Расстояние
между атомами ~1,5÷2Å, амплитуда колебаний ~0,1Å. Энергия
этих колебаний составляет основную часть внутренней
энергии твердого тела.
Каждый атом обладает 3-мя колебат. степенями свободы.
Следовательно, внутренняя энергия одного моля твердого тела
U = NA∙3kT = 3RT. Отсюда получаем молярную теплоёмкость
твердого тела:
U
CV
3R ( C ДП )
T
− закон Дюлонга и Пти
Опыт (Рис. CV) показывает, что для многих твердых тел закон
(СДП) выполняется лишь при весьма высокой Т, а при обычной
температуре CV < 3R. При низкой же Т теплоёмкость всех
веществ быстро убывает, стремясь к нулю по закону С ~ Т3.
214. § 4.2. Теплоемкость твердых тел
Рис. CVЗдесь ТD − характеристическая температура
Дебая, которая указывает для каждого в-ва область
температур (при Т > TD), где применим закон (СДП).
Например: для Al − ТD=396 K; для Cu − ТD=309 K.
Теория теплоемкости твердых тел, учитывающая квантование энергии, создана Эйнштейном и Дебаем. Эта
теория хорошо согласуется с опытными данными; для
высоких Т она приводит к ф-ле (СДП).
215.
ЭЛЕКТРОДИНАМИКА216. Электродинамика
ЭЛЕКТРОМАГНЕТИЗМСавельев И.В. Курс общей физики
Детлаф А.А., Яворский Курс физики
Калашников С.Г. Электричество
Иродов И.Е.
Сивухин Д.В.
Волькенштейн В.С. Сборник задач по общему курсу физики.
2010
*****
Электромагнетизм − раздел физики,
изучающий явления, в основе которых лежат
электрические силы вз−вия между частицами,
обладающими электрическим зарядом.
Часть электрич. вз−вия, обусловленную
движением зарядов, называют магнитной силой.
Отсюда другое название этого вз-вия −
электромагнитное.
217. Электромагнетизм
ГЛАВА 1. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ В ВАКУУМЕ§ 1.1. Электрические заряды
Понятие эл. заряда является первичным.
П.Свойства зарядов.
1. Заряды бывают двух типов: положительные и
отрицательные. Знак проявляется через взаимодействие:
одноименные заряды отталкиваются, разноименные −
притягиваются.
218. Глава 1. Электрическое поле в вакууме
2. Эл. заряд передается только порциями, кратнымиэлементарному заряду е.
Носителями отрицат. элем. заряда являются электроны
(me = 0,91∙10−30 кг), положительного − протоны
(mр = 1,67∙10−27 кг = 1836me).
3. Закон сохранения эл. заряда: “алгебраическая
сумма эл. зарядов в электрически изолированной системе
остается неизменной при любых процессах,
происходящих в системе.”
4. Величина заряда является релятивистским
инвариантом.
219.
П. Распределение зарядов.Единицей заряда в СИ является кулон (Кл):
1 Кл = 1 А∙с; 1 Кл = 6,25∙1018е → е = 1,6 ∙10−19 Кл.
Для упрощения расчетов, в тех случаях, когда зарядов
очень много, удобно считать, что они распределены в
пр-ве непрерывно. С этой целью вводят понятия
объёмной = dq/dV, поверхностной s = dq/dS и
линейной
l = dq/dl
плотности зарядов.
Пример. Пусть на площадке S =1 см2 находится N =106
эл-нов. Тогда
q 106 ( 1,6 10 19 )
9 Кл
s
1,6 10
4
2.
S
10
м
220.
◄!§ 1.2. ЗАКОН КУЛОНА
Раздел эл.магнетизма, изучающий вз-вие неподвижных
зарядов, называют электростатикой.
Закон вз-вия двух покоящихся точечных зарядов, находящихся в вакууме, установлен Кулоном (1785):
сила, действующая на заряд q′ со стороны q
Fq k 3 r ,
r
(K )
где r − радиус−вектор заряда q′ относительно заряда q.
В СИ k = 1/4 0 = 9∙109 Н∙м2/Кл2,
где 0 = 1/4 k = 8,85∙10−12 Кл2/Н∙м2 − электрическая
постоянная.
Задача: сила эл. вз-вия между двумя студентами.
221. ◄!► § 1.2. Закон Кулона
Если заряды помещены в среду (диэлектрик), то вз-виеослабевает
qq r
Fq
,
3
4 0 r
( Kε )
где
− диэлектрическая проницаемость среды:
возд =1,0006, стекл = 6, вода = 81.
NB! Ф-ла (К ) справедлива только для жидких и
газообразных диэлектриков.
П. Принцип суперпозиции. Сила F, действующая на
заряд q со стороны системы зарядов qi:
qqi
F Fi , причем каждая Fi k 3 ri
ri
не зависит от наличия других зарядов. Пр. суперпозиции
явл-ся опытным законом.
◄! В+М+П
222.
§ 1.3. ЭЛЕКТРИЧЕСКОЕ ПОЛЕ◄!
Электр. вз-вие осуществляется через электр. поле,
порождаемое зарядами в окружающем пр-ве.
Характеристикой поля служит напряженность поля
E Fq / q , где Fq
сила, действующая на заряд q′,
помещенный в поле.
Пример. Напряженность поля точечного заряда q
(K ε ) E
q r
,
3
4 0 r
( E1 )
П. Принцип суперпозиции полей следует из
суперпозиции сил :
◄Рис!
qE qE1 qE2 ... E E1 E2 ...
223. § 1.3. Электрическое поле ◄!►
Например, напряженность поля, порожденного системойточечных зарядов
q
1
E
4 i r
0
i
r
3 i
(E Σ )
i
Если заряды распределены в пр-ве непрерывно, то Σ-ние
заменяется ∫-нием
dq
E k
V
r
3
r.
Задача. Найти напряженность поля, порожденного
отрезком нити, заряженной с линейной плотностью l.
l
l
Ex
(sin 2 sin 1 ), Ey
(cos 1 cos 2 ).
4 0 a
4 0 a
Здесь а − удаление от нити до точки поля; 1 и 2 − углы,
под которыми точка видна из концов отрезка.
Частный случай: поле бесконечной прямолинейной нити.
l
1 0, 2 Ex 0, Ey E
.
2 0 a
(E H )
224.
§ 1.4. СИЛОВЫЕ ЛИНИИСиловые линии − линии, касательные к которым в
каждой точке совпадают с направлением Е.
Густоту линий , т.е. число линий, пронизывающих
перпендикулярную линиям единичную площадку,
выбирают равной
модулю Е, т.е.
N / S E.
225. § 1.4. Силовые линии
Пример 1. Силовые линии точечного заряда.Общее св-во линий Е для электростатических полей :
силовые линии могут начинаться или заканчиваться
только на зарядах, либо уходить в ∞.
226.
Пример 2. Силовые линии диполя.Диполь − система из двух одинаковых по величине, но
противоположных по знаку зарядов.
Характеристикой диполя явл-ся величина дипольного
момента p = ql, где вектор l направлен от отрицат.
заряда к положительному.
Силовые линии − сплошные;
эквипотенциальные − пунктир.
227.
§ 1.5. ТЕОРЕМА ГАУССАПотоком Е через малую ΔS называют скалярное
произведение Ф = E ∙ ΔS = E ∙ nΔS =E∙ΔS∙cos .
Ф − алгебраическая величина; её знак зависит от , т.е.
от направления нормали n к ΔS. Поток Е через
произвольную пов-сть:
Ф E dS .
228. § 1.5. Теорема Гаусса
Теорема Гаусса: поток Е через произвольную замкнутуюпов-сть S равен алгебраической сумме зарядов внутри
этой пов-сти, деленной на 0.
1-е фундаментальное
qin
E dS
. (1)
ур-е электростатики.
0
NB! В случае замкнутых пов-стей за нормаль к пов-сти
принято брать нормаль, направленную наружу.
Докажем теорему для простейшего случая сферической
пов-сти радиуса r, окружающей единственный заряд q,
расположенный в центре сферы:
qr dS
q
S E dS S 4 0 r 3 dS ndS 4 0
qS 4 0 r q 0 .
rdS
S r 3
2
◄Обобщение док-ва − самост.
229.
П. Применение теоремы Гаусса эффективно длярасчета полей, обладающих симметрией.
Пример 1: поле бесконечной заряженной плоскости.
Поле обладает плоской симметрией: вектор Е перпендикулярен к плоскости.
◄!
Ф Фбок Фосн 0 2 E dS 2E S 2 En S
осн
sS
2 En S
0
s
En
.
2 0
Знак Еn совпадает со знаком
заряда σ.
230.
Пример 2: поле двух параллельных плоскостей, заряженных разноименными зарядами с плотностями и − .Это поле является суперпозицией полей, создаваемых
плоскостями по отдельности Е = Е+ + Е−.
◄!
Напряженность поля между плоскостями равна
s
E
,
0
(Eконд )
а вне этой области поле равно 0.
Этот рез-т приближенно справедлив и для пластин
конечных размеров, т.е. для конденсатора.
231.
Пример 3: поле заряженной сферы (сферическаясимметрия):
En
q
4 0 r
2
, r R;
и заряженного цилиндра (осевая симметрия):
l
En
, r R.
2 0 r
Внутри сферы и цилиндра (r < R) поле отсутствует: Е = 0.
232.
§ 1.6. РАБОТА СИЛ ЭЛЕКТРОСТАТИЧЕСКОГО ПОЛЯРассмотрим перемещение q′ из т. 1 в т. 2 в поле неподвижного заряда q. Найдем работу сил поля.
Для удобства поместим начало отсчета О в т. расположе
ния заряда q.
2
2
q q
A12 q E dr
4 0
1
r dr r dr
q q
dr
q q
2
4 0 1 r
4 0
2
r dr
1 r 3
1 1
.
r1 r2
( A)
NB! А12 не зависит от формы пути.
Следовательно, электростат. поле
точечного заряда явл-ся потенциальным.
233. § 1.6. Работа сил электростатического поля
Из пр. суперпозиции следует, что электростат. полелюбой системы зарядов является потенциальным.
П. Теорема о циркуляции вектора Е.
При перемещении по замкнутому пути т.1 ≡ т.2, и А12=0.
E
d
r
.
Если q′ =1, то работа сводится к интегралу
Следовательно:
2-е фундаментальное
E dr 0. ( 2ст ) ур-е электростатики
Интеграл E dr
называют циркуляцией вектора Е,
а потому ур-е (2ст) называют теоремой о циркуляции
вектора Е.
Из (2ст) следует, что силовые линии электростат. поля не
могут быть замкнутыми.
◄! Примеры эл.стат. полей
234.
§ 1.7. ПОТЕНЦИАЛПотенциал является второй характеристикой электростат.
поля: Е − силовая характеристика, потенциал −
энергетическая.
Потенциалом называют такую ф-цию , убыль которой
1− 2 между точками 1 и 2 равна
1 2 E dr .
2
(Δ )
1
Тогда работа поля при перемещении заряда q′ равна:
2
A12 q E dr q ( 1 2 ).
( A )
1
Дж
.
Единица потенциала в СИ − вольт (В): 1 В 1
Кл
235. § 1.7. Потенциал
П. Потенциал точечного заряда и системы зарядов.Формула (∆ ) в случае элементарного перемещения dr
имеет вид:
d E dr .
( d )
Для неподвижного точечного заряда
E dr
q
dr
q
2 d (
const ).
4 0 r
4 0 r
Следовательно, потенциал поля точечного заряда
q
4 0 r
const .
Значение const выбирают так, чтобы упростить выражение
для . Обычно принимают, что ∞ = 0. При таком выборе
потенциал точечного заряда
q
4 0 r
.
( 1 )
◄! Рис
236.
Для системы точечных зарядов из (d ) следует, чтоd ( E1 E2 ...) dr E1 dr E2 dr ... d 1 d 2 ...
i, т.е. пр. суперпозиции
Следовательно
справедлив и для потенциала.
Поэтому потенциал системы точечных зарядов
qi
P
,
4 0
ri
1
(
)
где ri − расстояние от заряда qi до интересующей точки
поля Р.
Пример* q1(0,3см)=5нКл, q2(9,0)=−10нКл → (0,0)=500В.
Если заряды распределены непрерывно, то суммирование
заменяется интегрированием:
1
dq
.
4 0 r
( )
237.
П. Потенциальная энергия заряда в электростатическом поле.Работу консервативного электростат. поля можно
представить как убыль потенциальной энергии:
A12 W1 W2 ,
( AW )
где W1 и W2 − потенц. энергия заряда в начальной и
конечной точках траектории.
Сопоставив формулы (A ) и (AW), получим выражение
для потенциальной энергии заряда q' во внешнем
электростатическом поле:
W q .
( W )
Пример* Q(0,0)=10мкКл→WQ=Q =5мДж; A0∞=5мДж.
238.
§ 1.8. СВЯЗЬ МЕЖДУ ПОТЕНЦИАЛОМИ ВЕКТОРОМ Е
Если известна Е, то вычисление сводится к ∫-нию по
ф-ле (∆ ). Получим обратную ф-лу для расчета Е по
известному (х,y,z). Для этого совершим перемещение dl
в произвольном направлении l. Тогда Е∙dl = El∙dl.
С другой стороны, Е∙dl = −d .
Следовательно, E l.
(El )
l
В частности,
Ex x, Ey y, Ez z.
Следовательно: E (
i
j
k ) .
x
y
z
(E )
Пример: точ. заряда →Ex= −∂ /∂x =qx/4 0r3, Ey=…
Преимущества : 1) − скаляр;
2) простота измерений Δ .
239. § 1.8. Связь между потенциалом и вектором Е
П. Эквипотенциальные поверхности.Пов-сть, все точки которой имеют одно и то же значение
потенциала, называют эквипотенциальной.
◄При перемещении dl вдоль эквипот. пов-сти (dl║ )
изменение d = 0. Тогда, согласно ф-ле (Еl), El = 0.
Следовательно: 1) вектор Е перпендикулярен
к эквипот. пов-сти.
Теперь совершим перемещ. dl
по нормали к эквипот. пов-сти в
сторону уменьшения (dl║n).
Тогда d < 0 и
El l 0.
Следовательно: 2) вектор Е
направлен в сторону уменьшения .
Резюме. Силовые линии перпендикулярны эквипот.
пов-стям, причем вектор Е направлен в сторону
уменьшения .
240.
◄! График (r) + вектор E для точечных + и − зарядовПример: и Е точечного заряда (сферы).
Пример. Электрическое поле Земли. Земля заряжена
отрицательно; возле пов-сти Е≈130 В/м →QЗ =−6∙105 Кл.
241.
242.
ГЛАВА 2. ПРОВОДНИКИ В ЭЛЕКТРИЧЕСКОМПОЛЕ
§ 2.1. Поле в веществе
В любом теле, помещенном в поле Е0, происходит разделение зарядов. Эл-ны смещаются против поля, а ядра− по
полю. Поэтому на теле возникают нескомпенсированные
заряды разного знака. Это явление называют электрич.
индукцией, а нескомпенс. заряды − индуцированными.
Индуцир. заряды создают собственное поле Е′, которое
вместе с Е0 образует результирующее поле
◄! Рис
E E0 E .
Расчет Е′ сводится к определению индуцир. зарядов.
Их распределение зависит от свойств тела. По электрич.
св-вам тела делятся на проводники и диэлектрики.
243. Глава 2. Проводники в электрическом поле
§ 2.2. ПОЛЕ ВНУТРИ И СНАРУЖИ ПРОВОДНИКАПроводники − тела, в которых имеются свободные эл.
заряды. Пример − металлы; роль свободных зарядов
играют эл-ны проводимости.
П.1. Поле внутри проводника. Если зарядить пров-к
или поместить во внешнее поле, то в пров-ке установится
такое распределение зарядов, при котором суммарное
поле внутри пр-ка
E E0 E 0.
◄ Пунктиром показаны
силовые линии внешнего поля;
сплошными − суммарного.
244. § 2.2. Поле внутри и снаружи проводника
Отсюда идея электростатич. защиты: для ограждения эл.приборов от внешних полей, их помещают в металлич.
корпус. Внешнее поле компенсируется внутри корпуса
полем индуцированных на его пов-сти зарядов.
245.
П.2. Избыточные и индуцированные зарядырасполагаются только на пов-сти пров-ка. Этот вывод
следует из т. Гаусса:
Ein 0
E dS 0 qin 0.
П.3. Т.к. внутри пров-ка Е = 0, то во всех его точках
= const, т.е. пров-к является эквипотенциальной
областью:
пр
E dr .
пров
Пример1. Потенциал заряженного шара радиуса R.
Поле вне шара совпадает с полем заряда q, помещенного
в центр шара. Поэтому вне шара = q/4 0r, где r −
расстояние от центра шара. Следовательно, потенциал
пов-сти шара (r=R), а потому и всего шара Ш = q/4 0R.
Пример 2. Потенциал незаряж. шара, на расстоянии
r от центра которого расположен точечный заряд q. ◄!
246.
П.4. Внутри заряженного пр-ка Е = 0, но снаружи Е ≠ 0.Пов-сть пров-ка является эквипотенциальной; поэтому
вне пров-ка Е перпендикулярен к его пов-сти, т.е. Е=Еn.
Величину поля вблизи от пов-сти пров-ка можно найти с
помощью т. Гаусса: En = / 0.
Величина различна в разных точках пров-ка; она
больше на остриях. В этих местах велика и величина Е.
247.
Примеры.◄!Пробой
248.
§ 2.3. ЭЛЕКТРОЕМКОСТЬ УЕДИНЕННОГОПРОВОДНИКА
Увеличение заряда уединенного пр-ка приводит к прямо
пропорциональному увеличению Е во всем пр-ве, а потому
и потенциала пр-ка
пр
E dr .
пров
Следовательно,
заряду
уединенного пр-ка пропорционален его
q C .
( C1 )
Коэф. пропорциональности С называют емкостью пр-ка.
Пример. Емкость шара:
q 4 0 R C q 4 0 R.
249. § 2.3. Электроемкость уединенного проводника
§ 2.4. КОНДЕНСАТОРЫКонденсаторы − устройства, способные накапливать
на обкладках большие заряды. Хар-кой конденсатора
является емкость C = q/U, где q − заряд обкладки,
U − разность потенциалов (напряжение) между
обкладками. Ёмкость зависит от геометрии конденсатора
и среды между обкладками.
Пример. Плоский конденсатор: ◄! ССФ и СЦИЛ −самост.
s
qd
q 0 S
E
U Ed
C
0
0 S
U
d
(C ПЛ )
П. Соединение конденсаторов может быть параллельным или последовательным. Эквивалентная емкость
таких соединений (батарей) определяется из формул:
CПАР Ci ;
1
CПОСЛ
1
.
Сi
◄! самост.
250. § 2.4. Конденсаторы
ГЛАВА 3. ДИЭЛЕКТРИКИ◄Л. 14+
§ 3.1. Поляризация диэлектриков
Диэлектрики − в-ва, которые практически не проводят
эл. ток. Заряды, входящие в состав молекул диэл-ка,
называют связанными, т.к. их перемещение ограничено
пределами молекулы.
При внесении во внешнее поле происходит поляризация
диэл-ка. Это означает, что в нем возникает результирующий дипольный момент, а на пов-сти появляются
нескомпенсированные поляризационные заряды.
251. Глава 3. Диэлектрики ◄л. 14+►
П. Механизмы поляризации.1) У молекул неполярного диэл-ка “центры тяжести”
+ и − зарядов совпадают, а потому дипольные моменты
молекул равны нулю. Таковы неполярные молекулы H2,
N2, О2, CCl4, ...
Под действием внешнего поля Е0 молекулы превращаются
в диполи, моменты которых p=ql ориентированы вдоль
Е0, а диэл-к в целом − в макродиполь, заряды которого
расположены на противоположных концах диэл-ка.
252.
2) Молекулы полярных диэл-ков (CO, H2O, HCl, …)обладают собственным дипольным моментом.
Под действием Е0 молекулы ориентируются своими дип.
моментами вдоль Е0, в рез-те чего диэл-к поляризуется.
253.
3) В ионных кристаллах (NaCl) поле вызывает смещение+ и − ионов, расположенных в узлах кристаллической
решетки, в противоположные стороны, что и приводит к
поляризации кристалла.
Резюме. В рез-те поляризации на противоположных
концах диэл-ка возникают поляриз. заряды q′, которые
порождают собственное поле Е′, направленное против Е0.
Поэтому суммарное поле Е=Е0 + Е′ внутри диэл-ка всегда
слабее, чем вне его.
П. Поляризованность. Характеристикой поляризации
диэл-ка служит дип. момент единицы объема:
1
P
V
pi
поляризованность диэл - ка ,
ΔV
где рi − дип. момент одной молекулы.
254.
Установлено, что у изотропных диэл-ков (жидкости, газы,аморфные тв.тела, порошки) Р= c 0Е, где c − диэлектр.
восприимчивость (c − безразмерн. величина; c ≥ 0).
◄!В анизотропн. диэл-ках (монокрист-лы) направления Р
и Е не совпадают; у них связь между P и E − тензорная.
Величина Р связана с плотностью поляризац. зарядов.
Например, в случае однородной поляризации:
s P cos Pn ,
(s )
где − угол между направлением нормали к пов-сти
диэл-ка и вектором Е.
В случае неоднородной поляризации в диэл-ке могут
возникнуть ещё и объемные поляриз. заряды, плотность
которых определяется ф-лой
div P.
( )
255.
§ 3.2. ВЕКТОР ЭЛЕКТРИЧЕСКОГО СМЕЩЕНИЯ DЭл. поле порождается как сторонними зарядами q,
которые не входят в состав молекул диэл-ка, так и связанными q′. Следовательно, т. Гаусса имеет вид:
(q q ) in
.
E dS
0
( 1 )
Использование (1′) осложняется тем, что распределение
зарядов q' заранее неизвестно. Чтобы обойти это
затруднение вводят вспомогательный вектор электрического смещения (эл. индукции) D = 0E + P.
Ур-е для D получим, использовав для определения q'
интегральную форму ур-я (ρ'):
q dV P dS .
V
S
( q )
256. § 3.2. Вектор электрического смещения D
В итоге т. Гаусса для поля в диэл-ках приобретает видD dS qin .
( 1D )
Важно, что (1D) не содержит заряды q'. Зная D и зависимость Р(Е), можно затем рассчитать искомое Е.
Например, для изотропных диэл-ков Р= c 0Е, а потому
D 0 E c 0 E 0 (1 c ) E 0 E
(DE)
где =1+ c − диэлектрическая проницаемость в-ва.
В вакууме Р=0, поэтому =1, D0= 0E0.
П. Сегнетоэлектрики − кристаллич.
в-ва, которые могут обладать спонтанной
поляризованностью в отсутствие Е0.
Особенностями сегнетоэл-ков являются
их большая (до 104) и
явление гистерезиса.
257.
§ 3.3. РАСЧЕТ ПОЛЯ В ДИЭЛЕКТРИКАХВ общем случае расчет сложен. Исключением явл-ся
случай, когда всё пр-во, где имеется поле Е0, заполнено
однородным изотроп. диэл-ком.
В качестве примера рассмотрим
расчет поля в плоском конденсаторе, между обкладками которого
помещена пластина из диэл-ка.
1 способ. Воспользуемся пр-пом
суперпозиции: Е=Е0+E'.
Напряженность поля Е0, создаваемого обкладками равна Е0= / 0.
Напряж. поля E', созданного
поляризационными зарядами,
равна E'= '/ 0 внутри пластины
и E'=0 − вне диэл-ка. Оба поля
направлены навстречу друг другу.
258. § 3.3. Расчет поля в диэлектриках
Поэтому внутри диэл-ка:Е=Е0 − E' = Е0 − '/ 0;
вне диэл-ка:
Е=Е0 = / 0.
Выразим ' через поляризованность Р:
1
P
V
1
q
pi S d q d S s ,
! сравни (s )
где q′∙d − дипольный момент пластины диэл-ка.
Поэтому, для поля внутри диэл-ка:
E E0
P
0
P c 0 E E0 c E.
Отсюда следует, что
E0
E0
E
1 c
,
1 c
т.е. поле Е в диэл-ке ослабляется в раз.
Отметим также, что
D 0 E 0 E0 D0 ,
т.е. поле вектора D не меняется.
259.
2 способ. Применим (1D) к гауссовой пов-сти S, одна изсторон которой расположена в обкладке, другая в диэл-ке:
DS sS
E0
s
E
.
0 0
D
D s
Замечание. Наличие диэл-ка внутри конд-ра приводит
к уменьшению U=E∙d и увеличению C=q/U в раз.
Можно показать, что аналогичным образом происходит
ослабление поля сферы и точечного заряда, погруженных
в однородный изотропный диэл-к:
E
E0
q
4 0 r
2
.
Эти рез-ты иллюстрируют общее правило:
если однородный и изотроп. диэл-к полностью заполняет
объем, ограниченный эквипотенциальными пов-стями
поля сторонних зарядов, то напряженность поля внутри
диэл-ка в раз меньше, чем напряженность поля сторонних зарядов: E = E0/ , D= 0 Е= 0Е0=D0.
260.
Замечание. Если эти условия не выполняются, то D≠ 0Е0.Например, в пластине диэл-ка, перекошенной относительно обкладок со сторонними зарядами , вектор Е╫Е0,
так что D= 0 Е ≠ 0Е0.
Резюме. В общем случае поле D, как и Е, зависит не
только от сторонних зарядов q, но (косвенно) и от
поляризац-х q′. Об этом свидетельствует
ф-ла D= 0 Е.
Удобство D в том, что его поток D dS зависит только
от q, т.е. источниками D явл-ся только сторонние заряды.
261.
§ 3.4. УСЛОВИЯ НА ГРАНИЦЕ ДИЭЛЕКТРИКОВСвязь между Е1 и Е2 по разные стороны границы, разделяющей два диэлектрика, устанавливают с помощью
теоремы о циркуляции (2ст), применив её к узкому h<<l
прямоугольнику на границе раздела: Е1 = Е2 .
Связь между D1 и D2 находят, использовав теорему Гаусса
(1D) для малого цилиндра. При отсутствии сторонних
зарядов на границе получим: D1n = D2n.
Из полученных соотношений следует, что линии D
преломляются на границе раздела. Действительно, из
Е1 = Е2 и 1Е1n = 2Е2n следует,
что
tg 2 2
.
tg 1 1
Закон преломл. силовых линий
в изотропных диэлектриках,
очевидно, такой же (т.к. E↑↑D).
262. § 3.4. Условия на границе диэлектриков
Пример: эллипсоидные тела. Можно показать, что эллипсоиды “сохраняют” однородность поля. Преломлениелиний D приводит к следующим картинам:
1 < 2
(стекло в воздухе)
Число линий D не
меняется, но из-за
их преломления
величина D внутри
диэл-ка возрастает.
1 > 2
(воздух в стекле)
Задача: С. 3.108.
263.
ГЛАВА 4. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯ§ 4.1 Энергия системы зарядов
Система зарядов обладает потенциальной энергией W.
Найдем сначала W двух зарядов. Энергия их вз-вия (как
и любая эн.) зависит только от состояния системы.
Поэтому зафиксируем q1 и найдем работу его поля при
перемещении q2 из ∞ в конечное положение
A = − q1q2/4 0 r12.
◄!Рис
Эта работа равна убыли потенц. энергии A12 = W1 −W2.
Отсюда, полагая W1≡W∞=0, получим для эн. двух зарядов
q1q2
q2
q1 1
W
1
, 2
(q1 1 q2 2 ).
4 0 r12
4 0 r12
4 0 r12 2
Здесь 1 − потенциал 2-го заряда в точке расположения
1-го, 2 − потенциал 1-го заряда в точке располож. 2-го.
264. Глава 4. Энергия электрического поля
Энергию системы зарядов найдем добавляя к исходнойсистеме из ∞ заряды q3, затем q4,... В итоге получим,
что энергия вз-вия системы точечных зарядов равна
qi q j
1
W
qi i ,
2 i
все пары 4 0 ri j
где
i
qj
j (j i)
4 0 ri j
( W)
− потенциал поля в точке
расположения i-го заряда, создаваемый всеми другими
зарядами. В случае непрерывного распределения зарядов
∑-е заменяется ∫-ем:
1
W dq,
2
(W )
где − потенциал, создаваемый всеми зарядами системы
в месте расположения заряда dq.
265.
П. Энергия заряженного проводника.Wпров
1
q C 2 q 2
dq пров dq
.
2
2
2
2
2C
Пример: энергия заряженного шара.
ш
q
4 0 R
Wш
q
2
8 0 R
.
П. Энергия конденсатора. Согласно ф-ле (W∫), интеграл
можно разбить на две части − для каждой из обкладок:
1
Wконд ( q q ) q q q
2
q
qU CU 2
( )
.
( WK )
2
2
2
266.
§ 4.2. ЭНЕРГИЯ ЭЛЕКТРИЧЕСКОГО ПОЛЯФ-ла (W∫) определяет электр. энергию системы через
ее заряды. На примере плоского конденсатора покажем,
что W можно выразить через хар-ку самого поля −
вектор Е:
ED
CU 2 0 S d 2 0 V 2
W
U
E D 0 E
V.
2
2d d
2
2
Здесь V = d∙S − объем конденсатора. Если считать, что
энергия содержится непосредственно в электр. поле, то
ее плотность будет равна
W ED E D
w
.
V
2
2
(w )
267. § 4.2. Энергия электрического поля
Т.к. (w) не зависит от геометрии системы, то энергиюполя в общем случае можно представить в виде
E D
W
dV .
2
Задача. Рассчитать энергию эл. поля заряженного шара,
погруженного в диэлектрик с проницаемостью .
W w dV
R
0
0
2
R E
2
dV
4 r 2 dr
q2
.
2
4
2 (4 0 ) R r
8 0 R
q
2
268.
ГЛАВА 5. ПОСТОЯННЫЙ ТОК§ 5.1. Сила тока
Эл. ток − упорядоченное движение электрич. зарядов.
В отсутствие эл. поля заряды движутся хаотически, а
потому ток отсутствует.
При включении поля на хаотич.
движение зарядов со скоростью
v накладывается упорядоченное
движение со скоростью u.
Поэтому скорость зарядов будет
v + u. Т.к. <v> = 0, то средняя
скорость зарядов равна:
<v + u> = <v> + <u> = u.
269. Глава 5. Постоянный ток
Сила тока − величина заряда, переносимого черезрассматриваемую пов-сть S (напр., через поперечное
сечение пров-ка) за единицу времени: I = dq/dt.
Ток, не изменяющийся со временем, называют постоянным: I = ∆q/∆t. В системе СИ: [ I ]=A, 1A =1 Кл/с.
Вектор плотности тока − j = u, где − объемная
плотность носителей тока. Если носителями являются
как положит., так и отрицат. заряды, то
j u u , где u E u .
Направление j совпадает с направлением упорядоченного
движения положительных зарядов, т.е. направление
тока совпадает с направлением Е.
270.
Величина j равна силе тока через единичную площадку,перпендикулярную направлению u. Следовательно
I j dS .
S
Для пост. тока в однородном проводнике j=const. В этом
случае, I = j·S = uS = neuS, где n – концентрация
носителей тока (в металлах – свободных электронов),
S − поперечное сечение пров-ка, .
Пример. Оценим скорости v и u.
8kT
8 1,38 10 23 300
км
5 м
1. v
10
100
!
31
m
9,1 10
с
с
кг
г
2. I 1 A; S 1 мм ; Cu : m 8900 3 , m 63,5
.
м
моль
m
I
мм
28 1
5 м
n
N A 8,4 10
7,4 10
~ 0,1
3 u
m
м
neS
с
с
2
271.
§ 5.2. ЗАКОН ОМА ДЛЯ УЧАСТКА ЦЕПИЭл. ток в проводниках обеспечивается эл. полем. Т.к. в
пров-ке Е ≠ 0, то пров-к не эквипотенциален. Потенциал
убывает в направлении Е, т.е. в направлении тока.
Для любого пров-ка (твердого, жидкого или газообр-го)
существует зависимость I от разности потенциалов на
концах проводника; её называют вольт−амперной
характеристикой пров-ка.
Вид ВАХ для однородного металлического пр-ка
установил Ом:
I ( 1 2 ) / R U / R.
(O)
Здесь R − сопротивление пров-ка; [R]=Ом, 1 Ом=1В/А.
Для цилиндрического пров-ка R = l/S, где l − длина
пр-ка, S − площадь его поперечного сечения,
− удельное электрическое сопротивление.
272. § 5.2. Закон Ома для участка цепи
П. Дифференциальная форма з. Ома устанавливаетсвязь между векторами j и E:
1
j E s E.
(Od )
Здесь s = 1/ − удельная электрич. проводимость.
Вывод. Рассмотрим малый цилиндр с образующими,
параллельными E ↑↑ j.
I j dS , 1 2 E dl , R (dl / dS ) (O) j
1
В векторном виде : j E.
1
E.
273.
§ 5.3. ЭЛЕКТРОДВИЖУЩАЯ СИЛАЕсли ток в замкнутой цепи течет в направлении АВС, то
1 > 2. Тогда на участке СА положительные заряды
должны двигаться в направлении возрастания , т.е.
против сил электрич. поля. Это возможно только если на
заряды, кроме сил поля, будут действовать в направлении
СА другие силы неэлектростатического происхождения.
Такие силы называют сторонними, а устройство,
в котором они действуют, − источником тока.
Источник тока играет
роль насоса в эл. цепи.
274. § 5.3. Электродвижущая сила
Для хар-ки сторонних сил вводят напряженность сторонних сил Е*=F*/q, где F* − сторонняя сила.Работу сторонних сил над единичным положит. зарядом
q = +1 на участке цепи 1-2 называют электродвижущей
силой (э.д.с.)
2
E 12 E dl .
1
П. Напряжение. Кроме сторонних сил, на заряд
действуют силы электростатического поля. Работу
результирующей силы при перемещении заряда q = +1
на участке 1-2 называют напряжением U:
2
U E dl E dl 1 2 E 12.
2
1
1
275.
§ 5.4. ЗАКОН ОМА ДЛЯ ПОЛНОЙ ЦЕПИНа неоднородном участке цепи на заряды действуют
как электростатические, так и сторонние силы, так что
j = s(Е+Е*).
(Oнd)
Рассмотрим случай тонких проводов, когда j везде
параллелен оси провода.
Умножим ур-е (Oнd) скалярно на dl/ , а затем проинтегрируем вдоль участка. Здесь dl − элемент оси, направленный от сечения 1 к 2.
j dl
jl dl
I
1 s 1 E dl 1 E dl s s S dl
RI 1 2 E 12.
(O Н ) з. Ома для неодн. уч - ка цепи
2
j dl
2
2
dl
R
Здесь
1 S
2
− сопротивление участка цепи 1-2.
276. § 5.4. Закон Ома для полной цепи
NB! Все величины в (ОН) алгебраические. А именно:1. jl > 0 и I = jl·S > 0, если j↑↑dl, т.е. если ток течет в
направлении 1-2.
2. E12 > 0, если Е*↑↑dl, т.е. если э.д.с. способствует движению положительных зарядов в направлении 1-2.
◄Направление действия э.д.с. совпадает с направлением
Е* внутри источника, т.е. от отрицательного полюса к
положительному. !Рис
Пример ЗОНУЦ. Найти 2 − 1 на зажимах источника
E = 4 В, r = 0,5 Ом, если |I|=2 А.
◄Семинар
Для замкнутой цепи 1 = 2. Следовательно, (Он) →
RI E.
(OЗ )
П. Правила Кирхгофа упрощают расчет разветвленных
цепей.
◄! Самостоят.
277.
§ 5.5. РАБОТА И МОЩНОСТЬ ТОКАРабота, совершаемая электростатическими и сторонними
силами, действующими на участке цепи
A U q U It.
Мощность тока, т.е. работа в единицу времени, равна
P dA dt UI ( 1 2 E 12 ) I .
Эта мощность может расходоваться на совершение работы,
на протекание хим. реакций, либо на нагрев участка.
П. Закон Джоуля – Ленца. Если проводник покоится и
в нем не происходят хим. р-ции, то работа тока полностью
превращается в тепло
Q UIt RI t.
2
( Д Л)
278. § 5.5. Работа и мощность тока
Мощность тепловыделения:dQ
P
RI 2 .
dt
( Д Л)
П. Дифференциальная форма з. Джоуля-Ленца.
Выделим малый цилиндр с образующими, параллельными j. За время dt в этом объеме выделится тепло
dQ RI dt
2
dl
dS
( j dS ) 2 dt dS dl dV j 2 dVdt.
Следовательно, удельная мощность тепловыделения
PУД = dQ/(dV·dt) определяется ф-лой
PУД j 2 sE 2 .
П. Характеристики источника тока.
( Д Лd )
◄л.р.13
279.
ГЛАВА 6. ЭЛЕКТРОПРОВОДНОСТЬ МЕТАЛЛОВ◄Л. 16+
§ 6.1. Проводимость веществ
По способности проводить ток все в-ва делят на пров-ки,
полупров-ки и диэлектрики (изоляторы).
Проводники. Пров-ками явл-ся металлы, электролиты,
ионизованный газ (плазма). Общее св-во проводников −
наличие в них свободно движущихся заряж. частиц.
В металлах это свободные эл-ны, концентрация которых
n очень велика. Для меди n ~ 8·1028 м−3, а s=6·107 1/Ом·м.
Для других металлов s = 6·105 ÷ 6·107 1/Ом·м.
В изоляторах эл-ны прочно связаны с атомами. Поэтому
n очень мало и s = 10−18 ÷ 10−8 1/Ом·м.
В полупр-ках s = 10−8 ÷ 6·105 1/Ом·м. У п/п-ков свободно
могут перемещаться только те из валентных эл-нов, энергия которых больше энергии активации . Число таких
эл-нов, а потому и s растут при повышении тем-ры:
s=s ·exp(− /kT). У Ge − =0,72 эВ; алмаза (диэл.) − =7 эВ.
280. Глава 6. Электропроводность металлов ◄л. 16+►
§ 6.2. КЛАССИЧЕСКАЯ ТЕОРИЯЭЛЕКТРОПРОВОДНОСТИ МЕТАЛЛОВ
В классической теории Друде − Лоренца эл-ны рассматриваются как электронный газ, обладающий свойствами
идеального газа. В промежутках между соударениями с
ионами решетки эл-ны движутся свободно, пробегая в
среднем путь l.
Предполагается, что при соударениях с ионами эл-ны
(поскольку me << M+) полностью теряют упорядоченную
составляющую скорости движения, т.е. в рез-те столкновения достигается хаотизация движения эл-нов.
После столкновения эл-н движется с ускорением a=eE/m,
так что u=umax/2 = a /2, где − среднее время свободного
пробега. Т.к. v >> u, то ≈ l/v. Тогда
ne l
j enu
E
2mv
2
ne l
s
.
2mv
2
( Od )
281. § 6.2. Классическая теория электропроводности металлов
Если бы столкновений с решеткой не было, то l и s → ∞,а → 0.
Резюме. Согласно классич. теории, сопротивление металлов обусловлено соударениями эл-нов с ионами решетки.
П. Локальный закон Джоуля-Ленца.
К концу свободного пробега эл-н приобретает дополнительную кинетич. энергию
2
mumax
m eE l 2 e 2l2 2
K
(
)
E .
2
2
2 m v
2mv
Столкнувшись с ионом, эл-н полностью передает её
решетке. Эта энергия идет на увеличение внутр. энергии
металла, т.е. на его нагрев. Каждый эл-н в среднем ежесекундно испытывает 1/ = v/l соударений. Следовательно,
в 1-це объема за 1-цу времени выделится тепло
PУД
nv e l
ne l 2
2
2
n
E
E
s
E
.
2
l 2mv
2mv
K
2 2
2
(Д Лd )
282.
Резюме. Классич. теория позволяет получить законыОма и Дж.-Ленца.
НО !
Из этой теории следует, что, поскольку n и l не должны
зависеть от Т, то
v
~
~ T.
s nl
1
Этот вывод противоречит опытным данным, согласно
которым
~ T.
Объяснение несоответствия дает квантовая теория.
283.
МАГНИТНОЕ ПОЛЕ КРУГОВОГО ТОКАm
I 2 R 2
- на оси,
B m0
3
4
[ R 2 d 2 ]2
B m0
m I
- в центре круга.
2 R
284. Магнитное поле кругового тока
МАГНИТНОЕ ПОЛЕ СОЛЕНОИДАМагнитная индукция на оси соленоида:
B m0
m
N
I n, n
4
l
- число витков на единицу длины соленоида.
285. Магнитное поле соленоида
ДВИЖЕНИЕЗАРЯЖЕННОЙ ЧАСТИЦЫ В ПОСТОЯННОМ
МАГНИТНОМ И ЭЛЕКТРИЧЕСКОМ ПОЛЯХ
Сила, действующая на
поле
заряд в магнитном
V Vx i
arc cos V B
T 2 m
B q
V B
R
- сила Лоренца
- вектор скорости,
B B (cos cos i sin cos j sin k )
F q V B sin - модуль силы,
F q V B
- вектор магнитной индукции
mV
qB sin
- радиус кривизны траектории,
- угол между вектором скорости и вектором магнитной индукции,
- период обращения,
E Ex i - вектор напряженности электрического поля.
Уравнения движения
2x
d
m
q V y Bz Vz B y E x ,
dt 2
2y
d
m
q Vz Bx V x Bz ,
dt 2
2z
d
m
q V x B y V y Bx .
dt 2
286. Движение заряженной частицы в постоянном магнитном и электрическом полях
ДВИЖЕНИЕ ЗАРЯЖЕННОЙ ЧАСТИЦЫ В ПОСТОЯННОМ МАГНИТНОМ ПОЛЕ( E 0 )
б
а
Траектория заряженной частицы
а - α=-90º, β=0;
б – α=-45º, β=45º:
в – 1 - α=90º, β=0; 2 – α=80º, β=0º.
в
287. Движение заряженной частицы в постоянном магнитном поле ( )
ДВИЖЕНИЕ ЗАРЯЖЕННОЙЧАСТИЦЫ В
МАГНИТНОМ И ЭЛЕКТРИЧЕСКОМ ПОЛЯХ
F q V B E
- сила действующая на заряд
Компоненты вектора напряженности магнитной индукции
Bx B cos cos , B y B sin cos , Bz B sin .
90 , 0.
90 , 0.
288. Движение заряженной частицы в магнитном и электрическом полях
ПЕРЕМЕННОЕ ЭЛЕКТРИЧЕСКОЕB const,
ПОЛЕ
б
а
-
Ex E0 (t ), (t) 1 приt n T ,
при t n T .
б (t ) 0
в
в - δ-функция
E0 1000 в / м
а - V 20 м / сек; б - V0 40 м / сек;
0
289. Переменное электрическое поле
МОДЕЛЬ ЦИКЛОТРОНАδ-функция
1
Ex E0 (t ), (nT ) 1, [(n )T ] 1. E 1000 в / м
0
2
290. Модель циклотрона
МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКАЗакон Био-Савара-Лапласа
Вектор магнитной индукции поля
m I
dB m 0
[dl r ],
3
4 r
m I
B m0
[dl r ].
3
4 r
m0 1.26 10 6
Гн - магнитная постоянная
м
m - относительная магнитная проницаемость
[ I ] 1А,[dl ] 1м,[ r ] 1м, [ B] 1Тл(Тесла).
R
Магнитная индукция прямолинейного
бесконечного проводника с током
B m0
m I
.
4 R
291. Магнитное поле постоянного тока
ДВИЖЕНИЕ ЗАРЯЖЕННОЙ ЧАСТИЦЫ В МАГНИТНОМПОЛЕ ПРЯМОЛИНЕЙНОГО ПРОВОДНИКА С ТОКОМ
m I
B m0
[dl r ]. Bx 0,
3
4 r
2
R
By
m0 I z
2 ,
4 R
Bz
m0 I y
2 ,
4 R
y z2 .
Уравнения движения
d2x
m 2 q V y Bz Vz B y ,
dt
d2y
d 2z
m 2 q Vx Bz , m 2 q Vx B y .
dt
dt






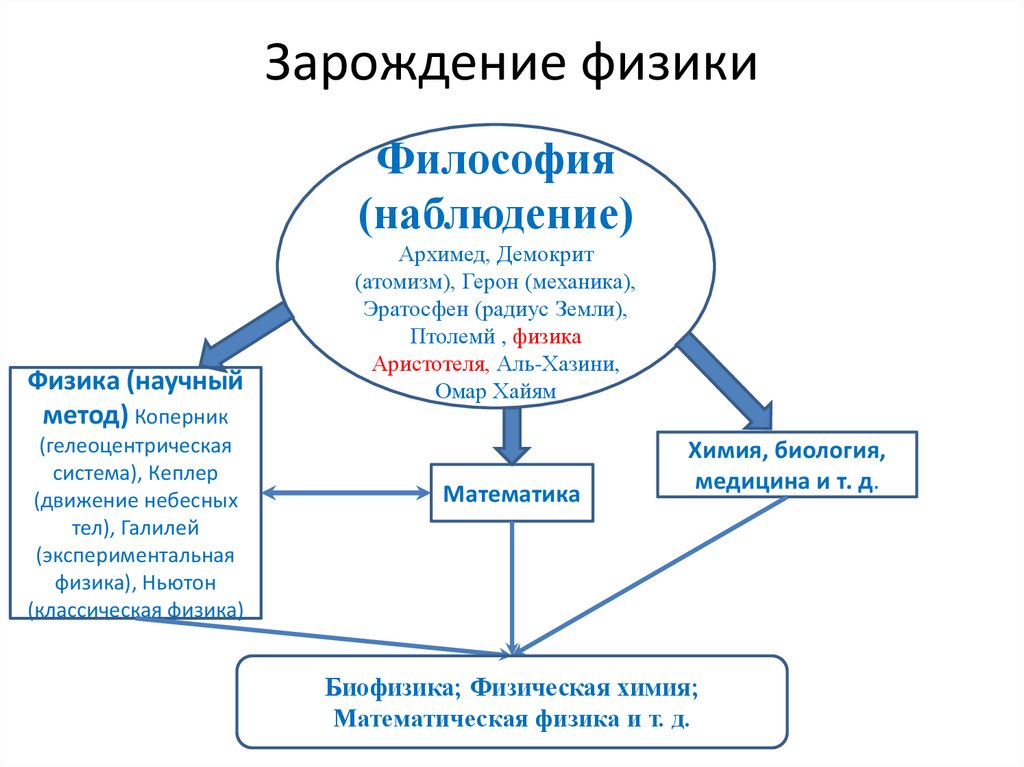
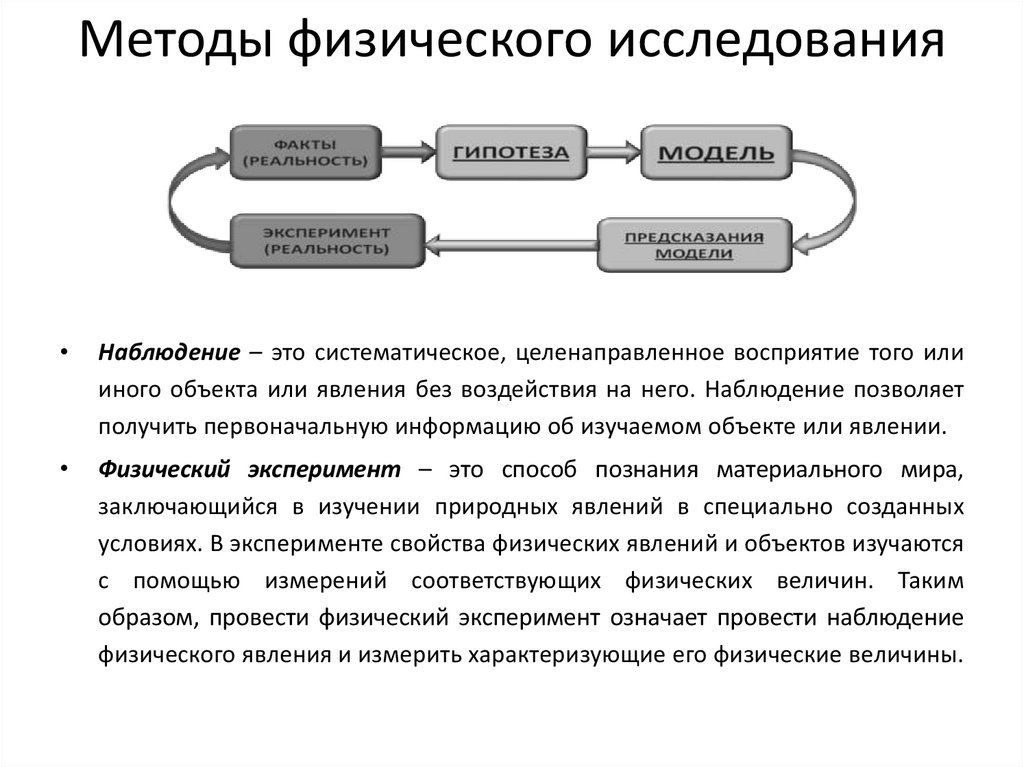




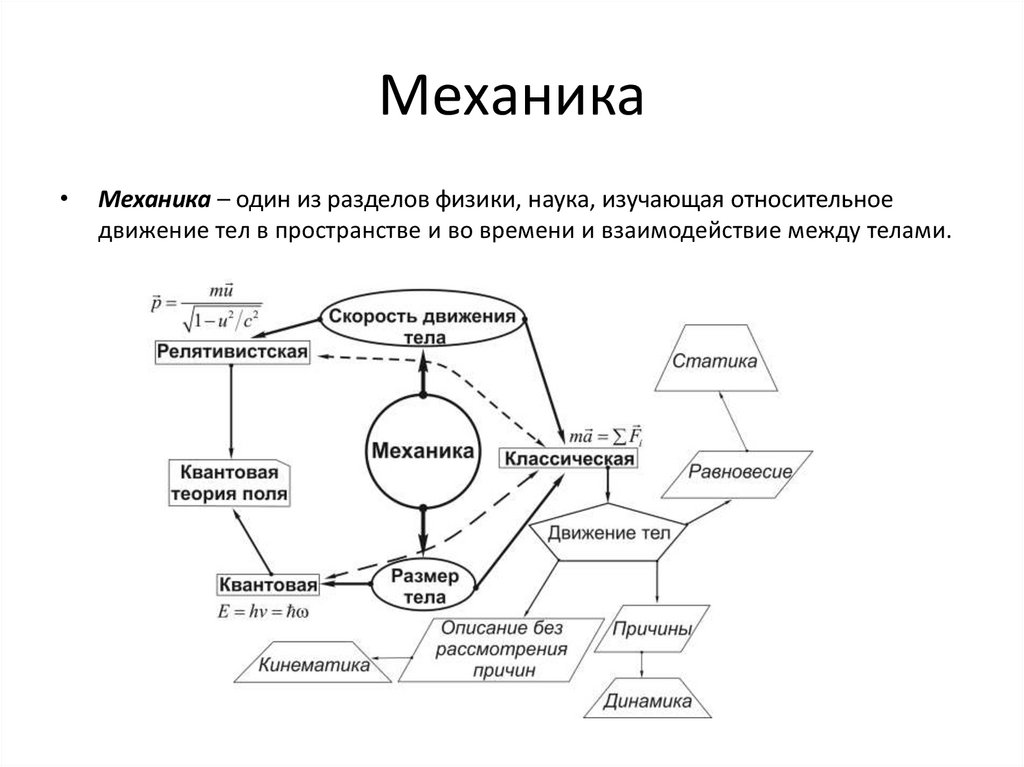




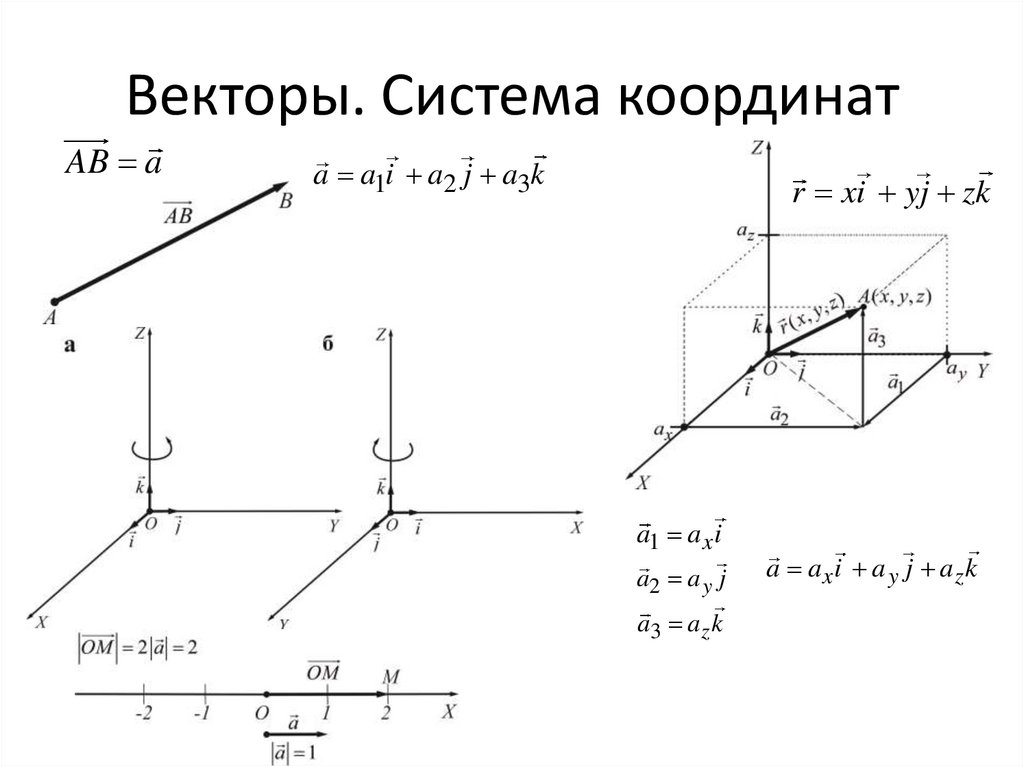
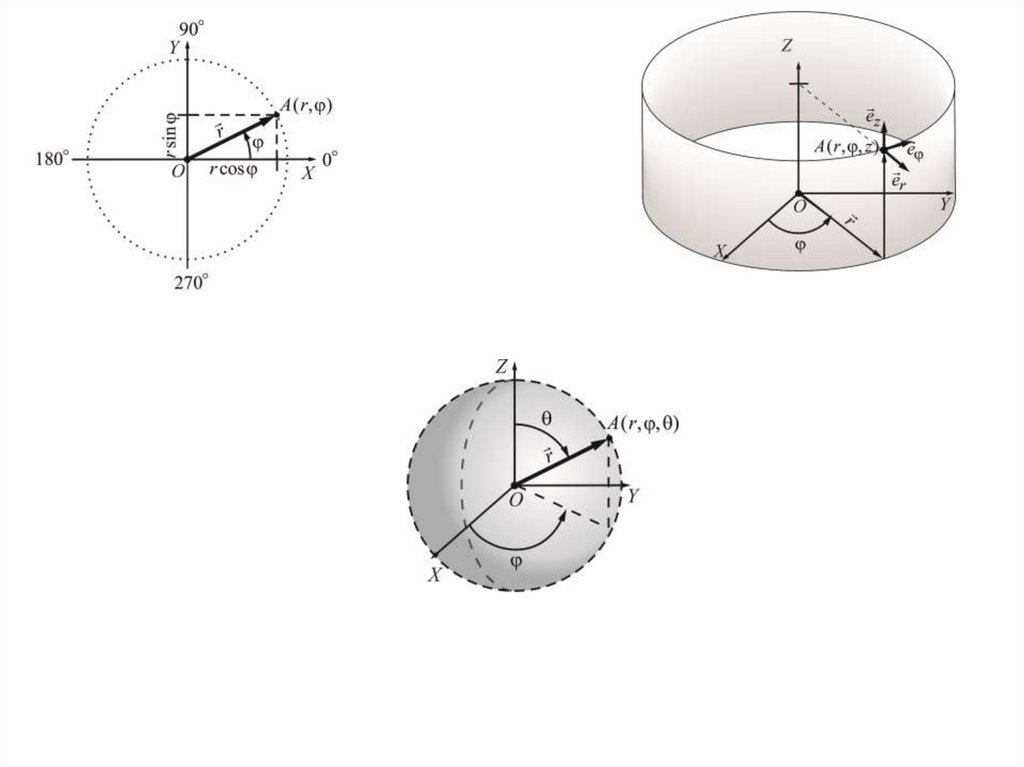
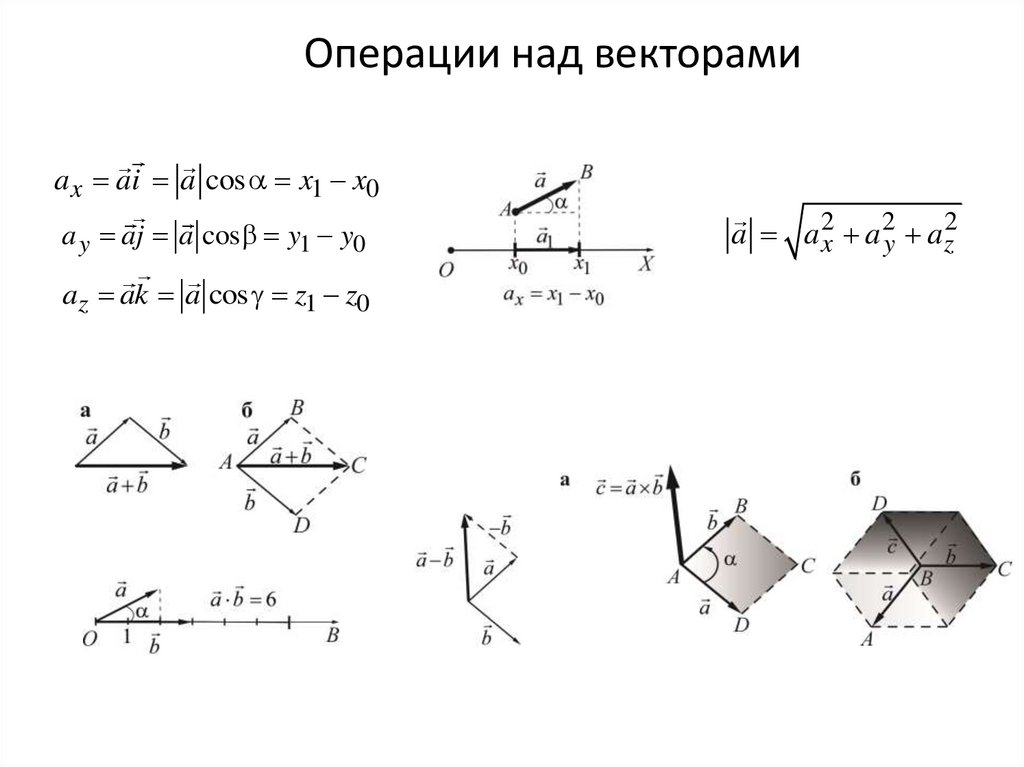




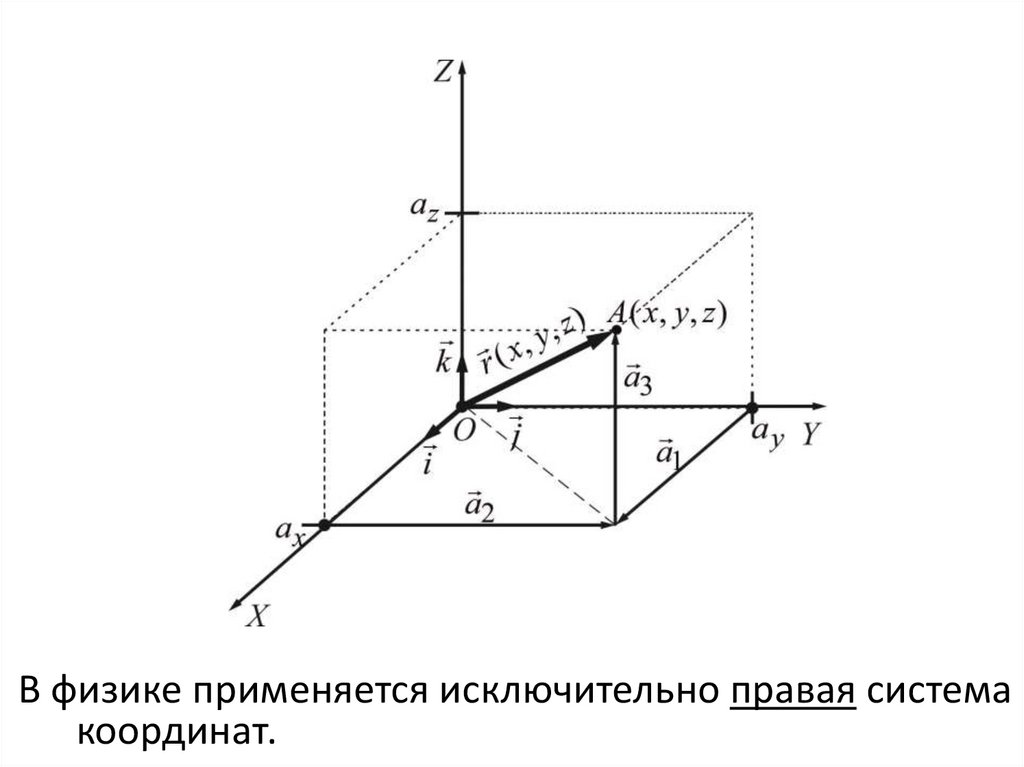


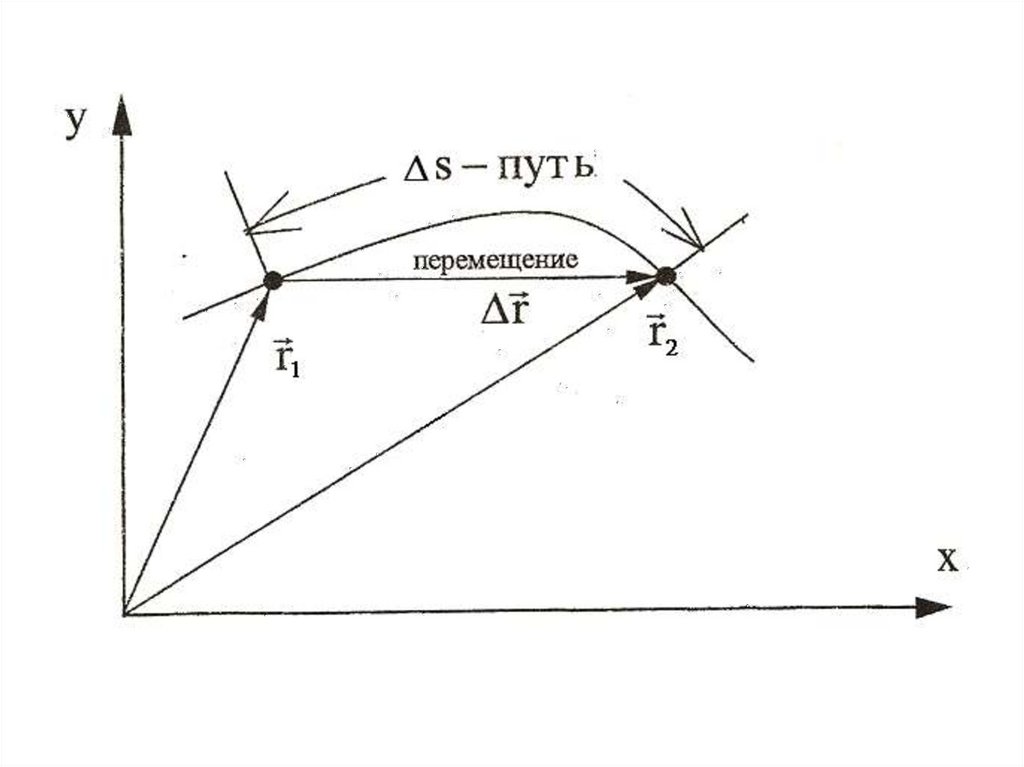


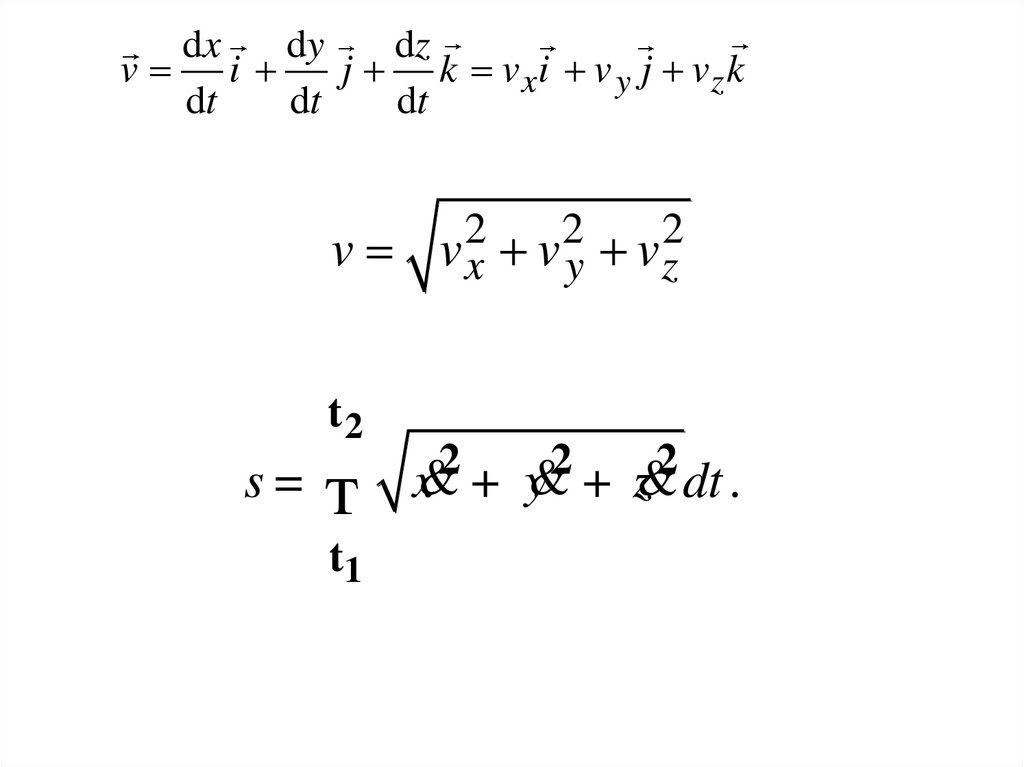
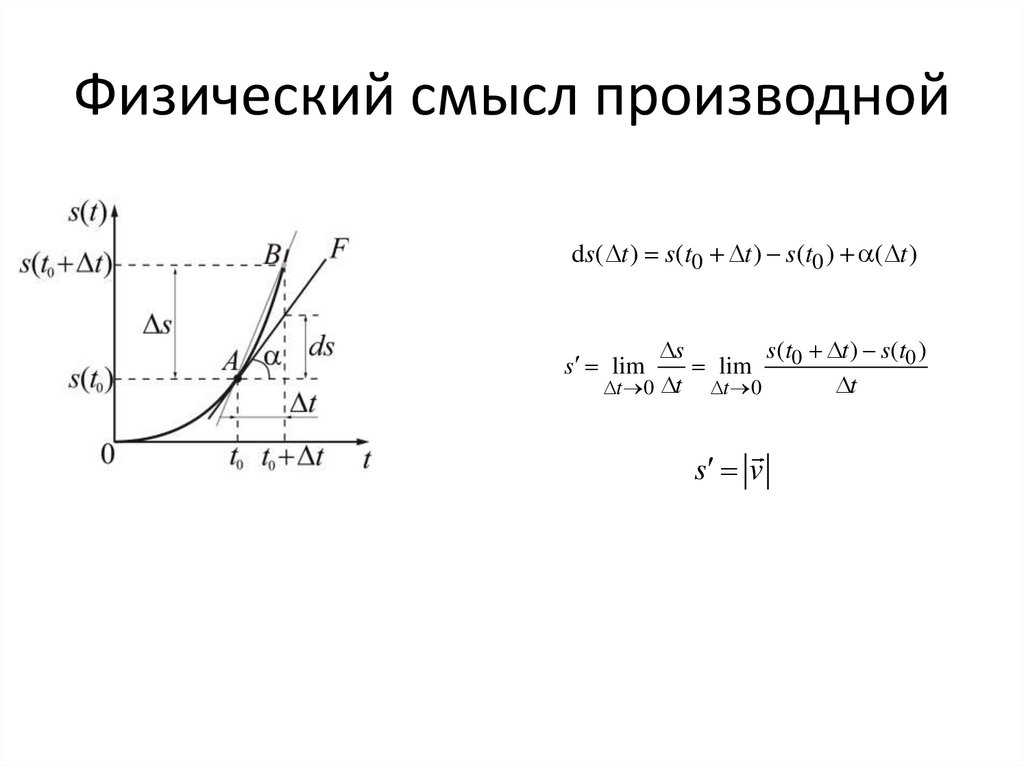
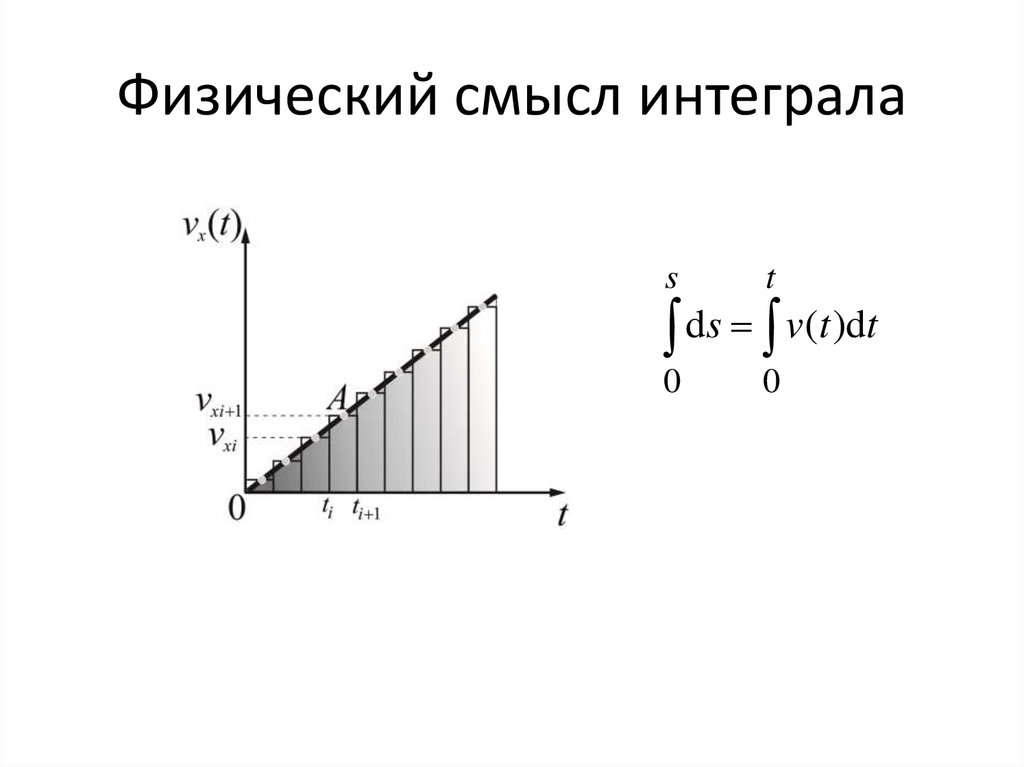



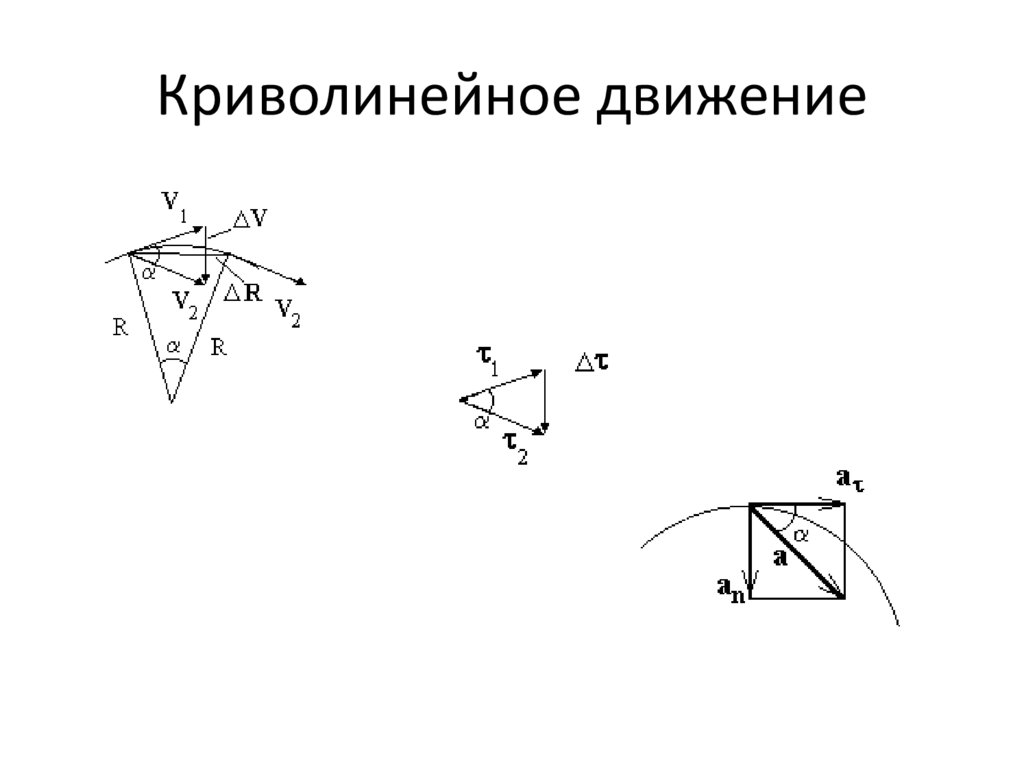


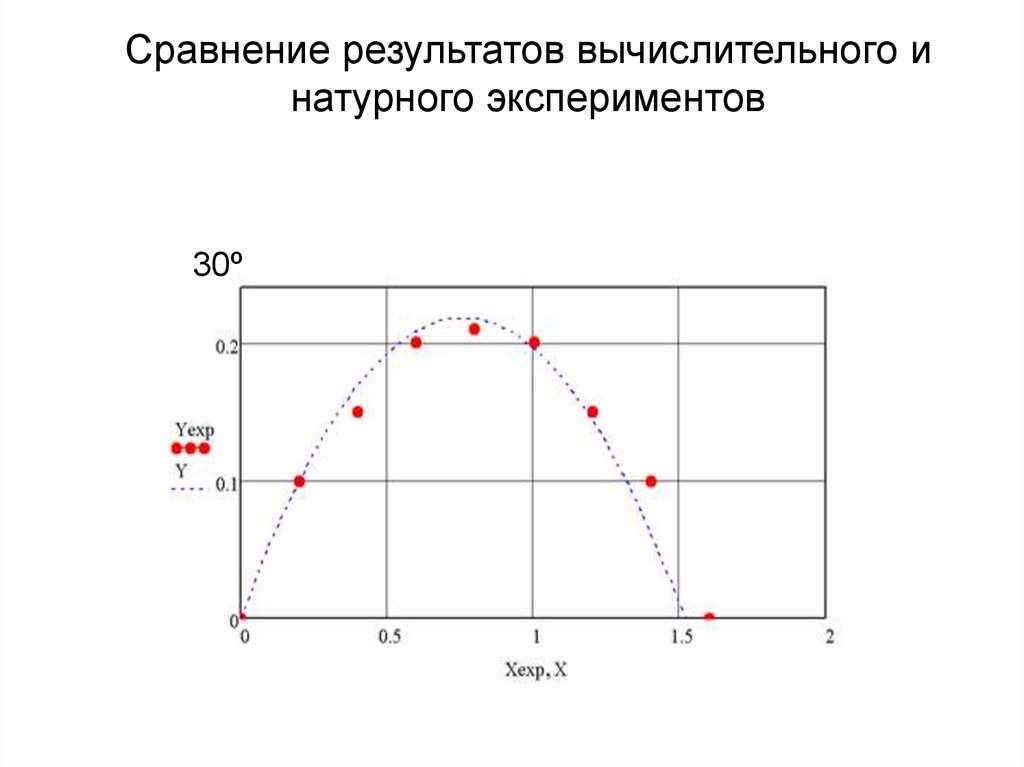



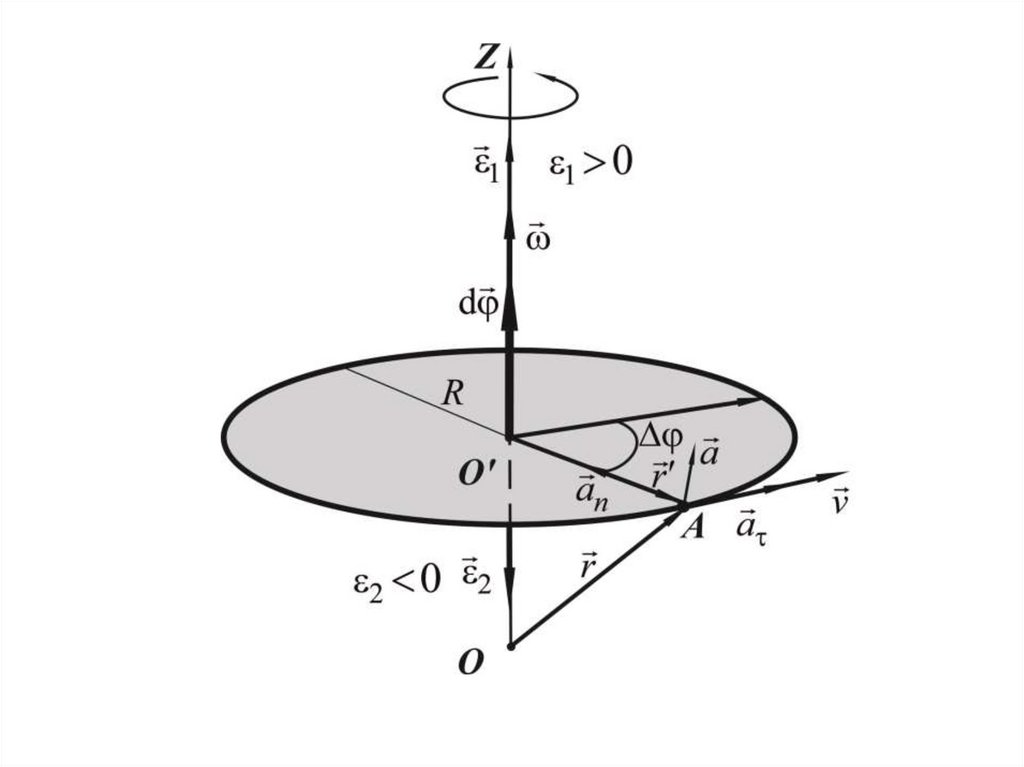


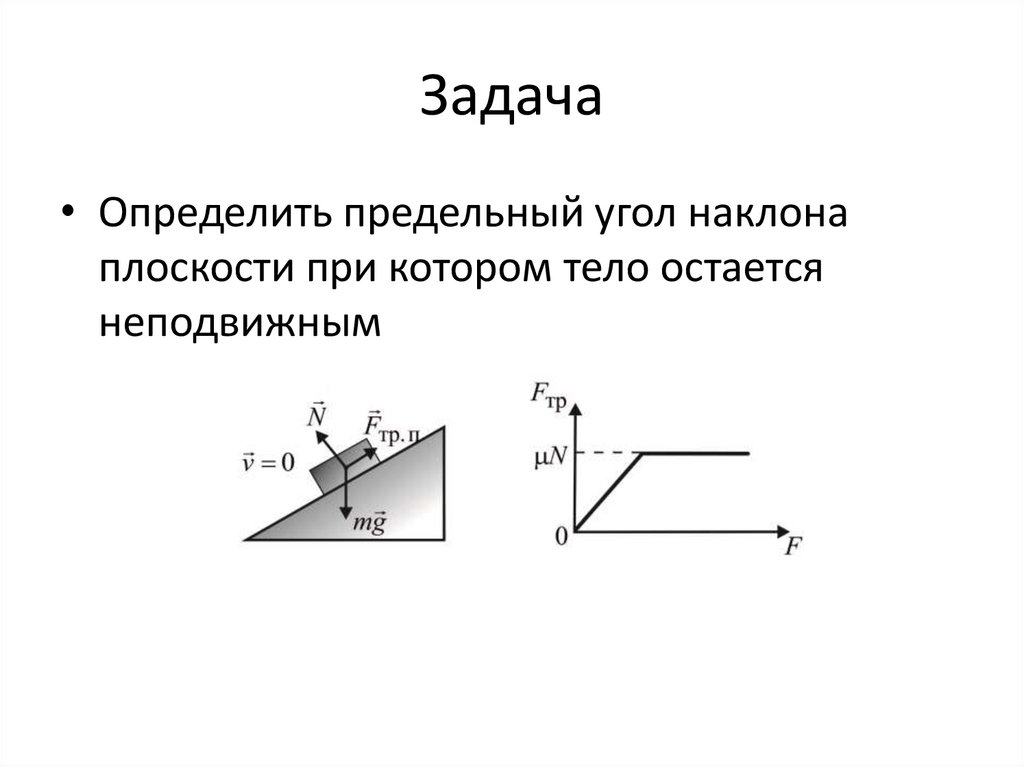








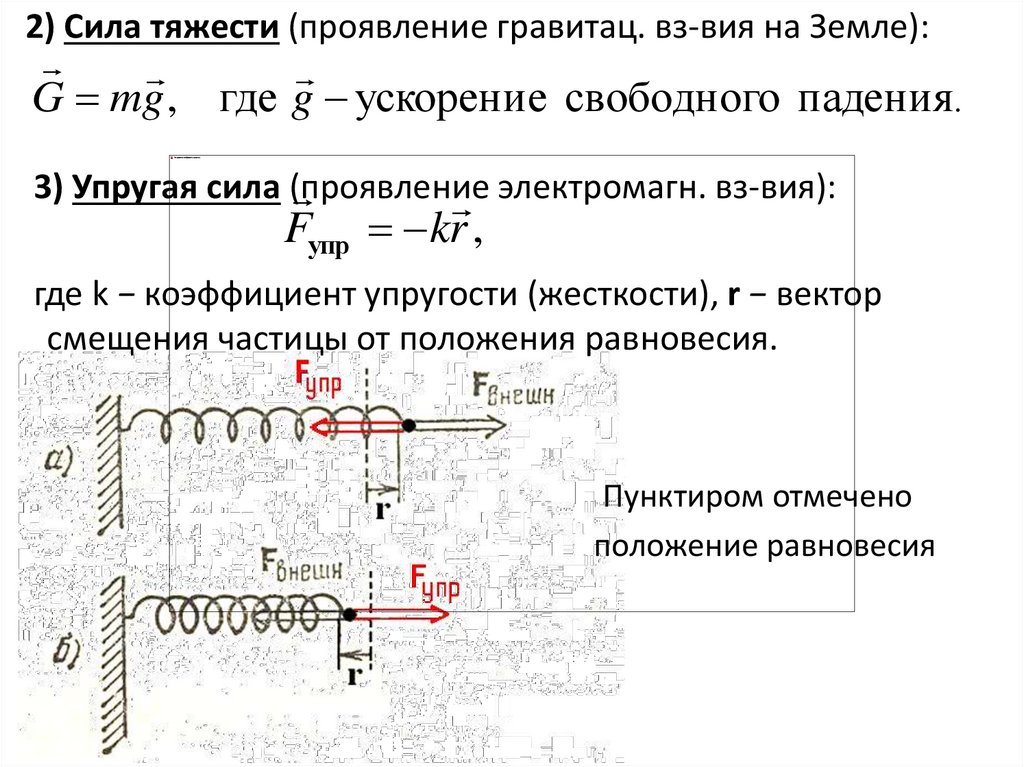


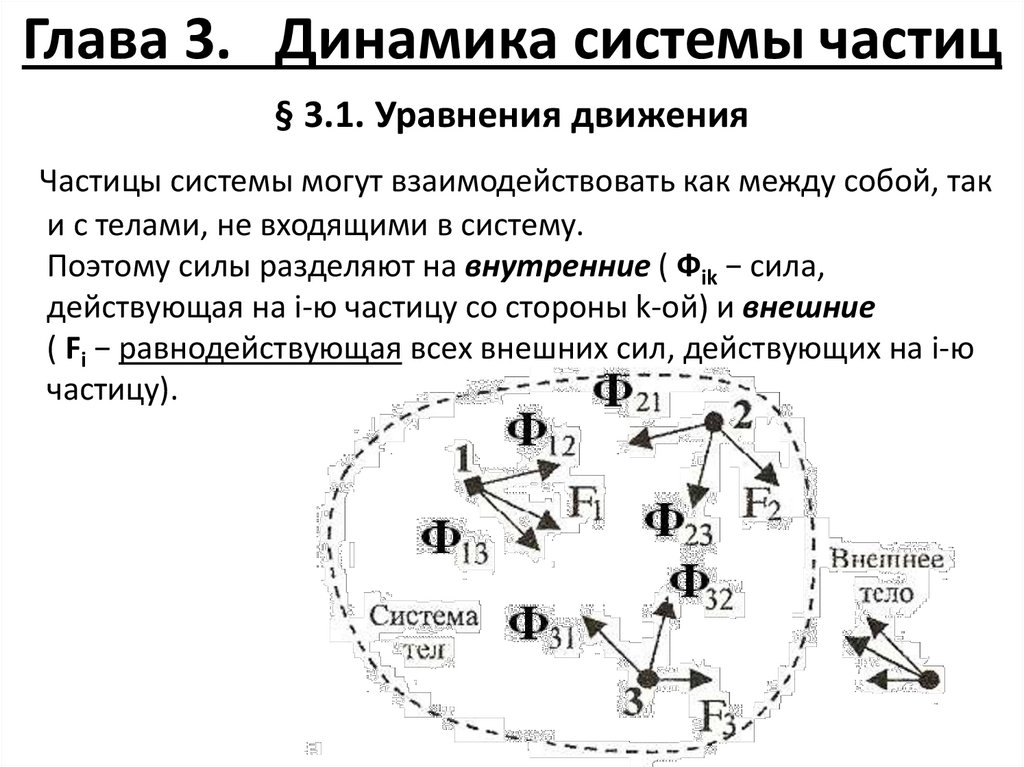





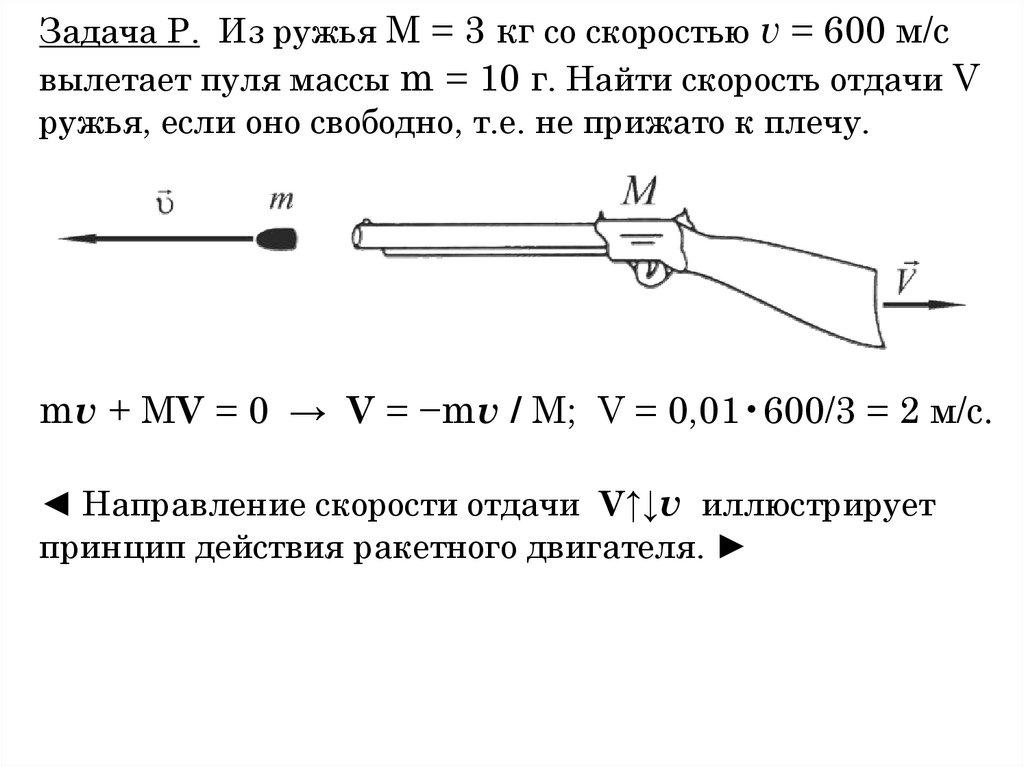
















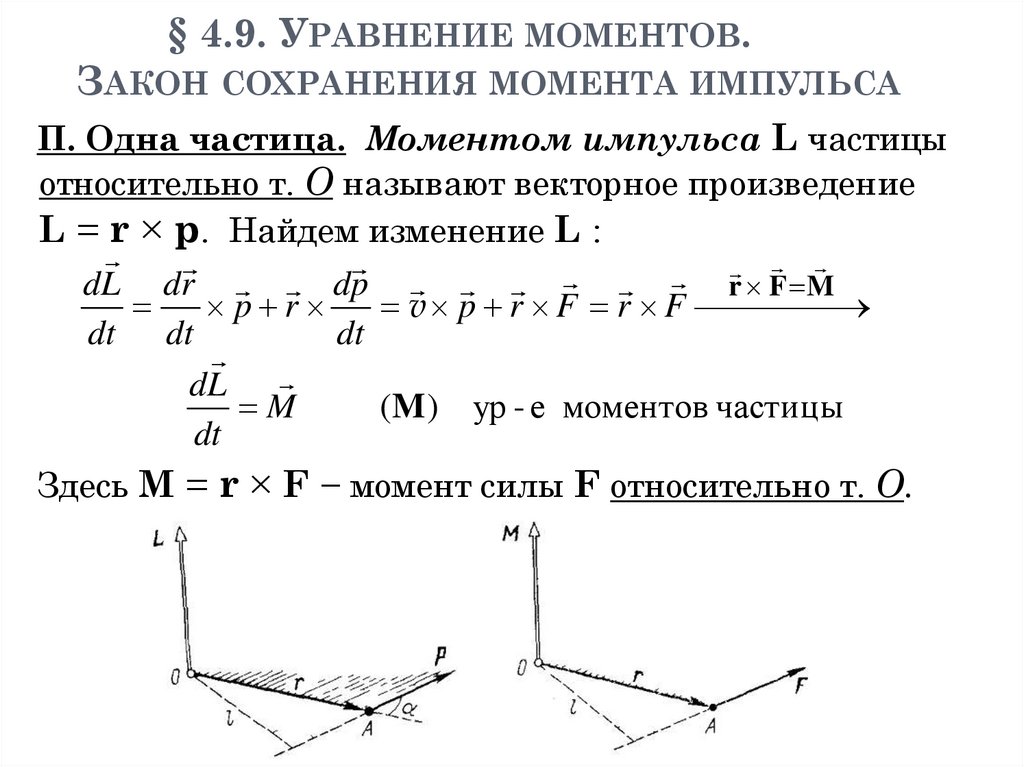





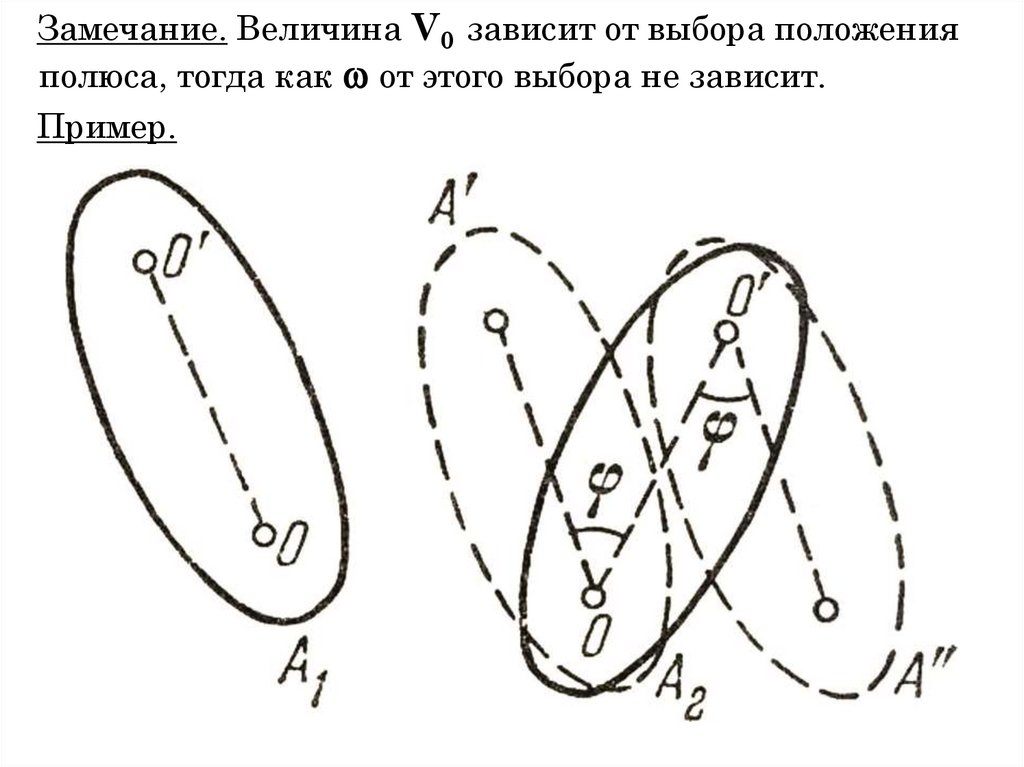



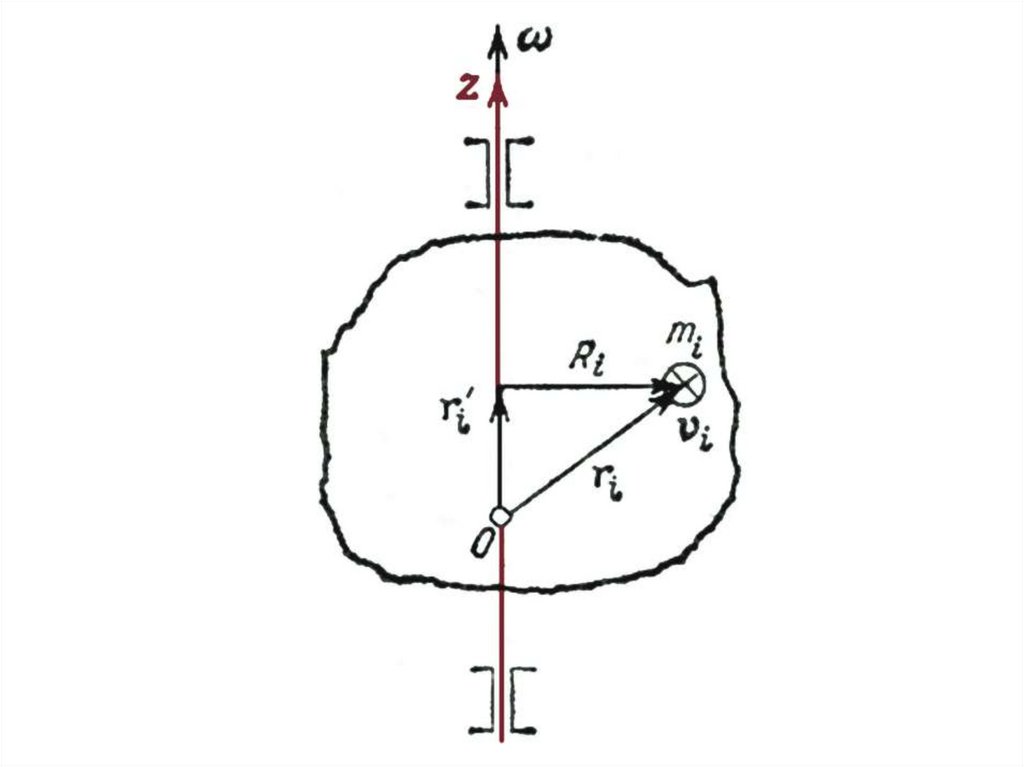



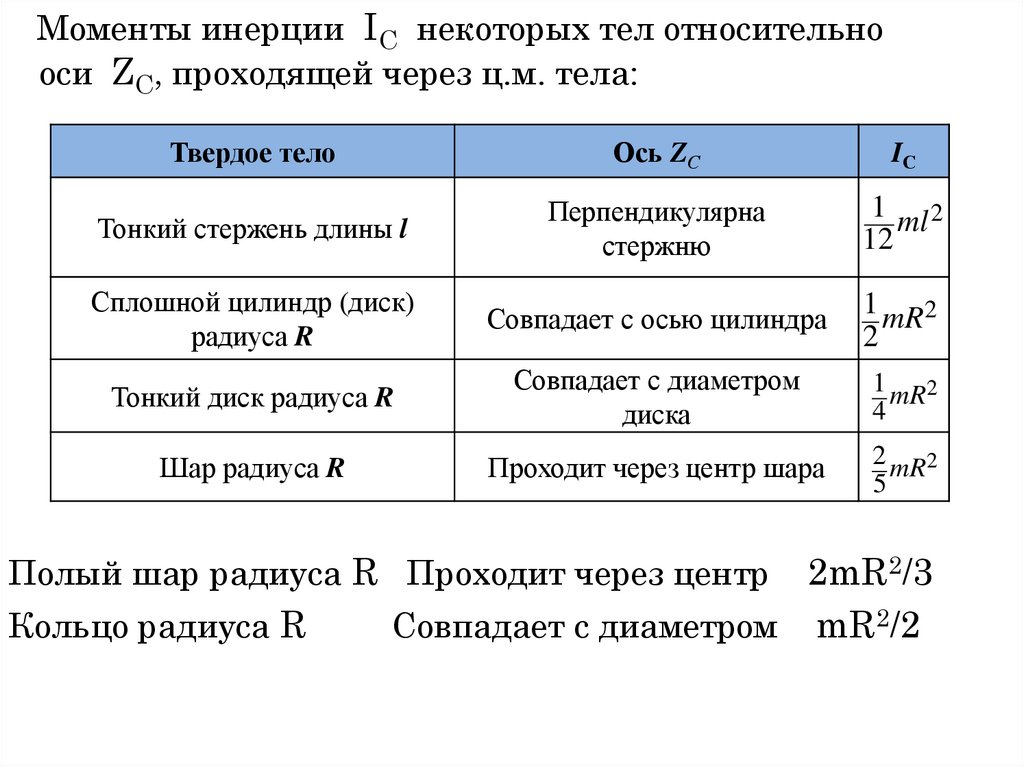

















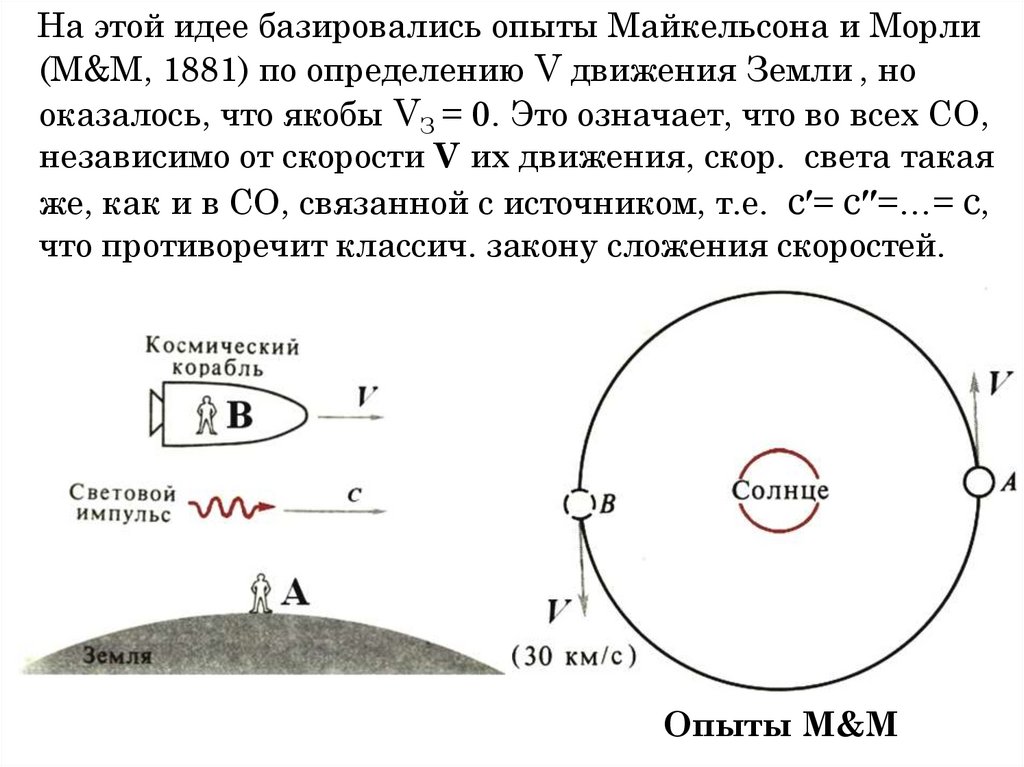





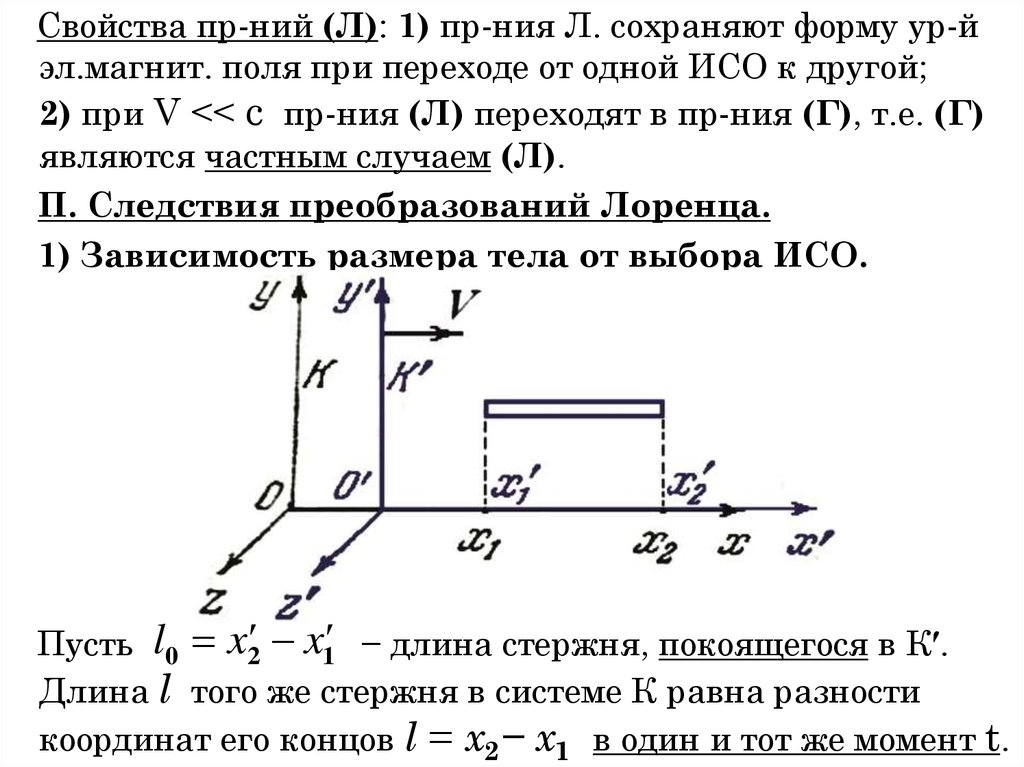





























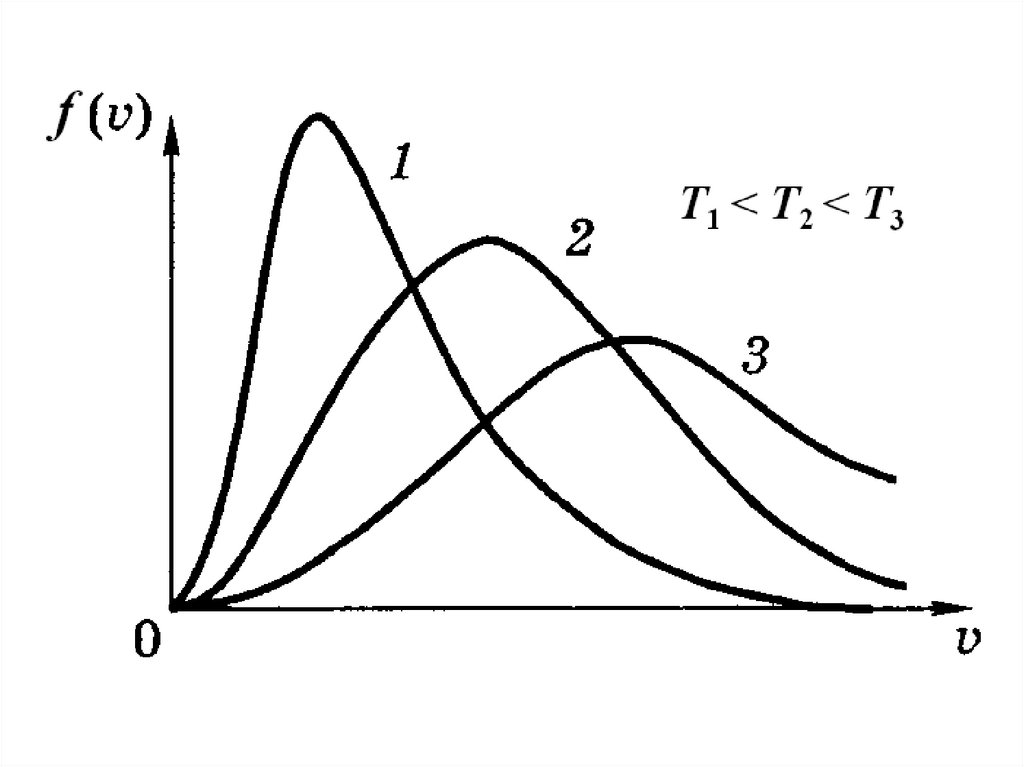



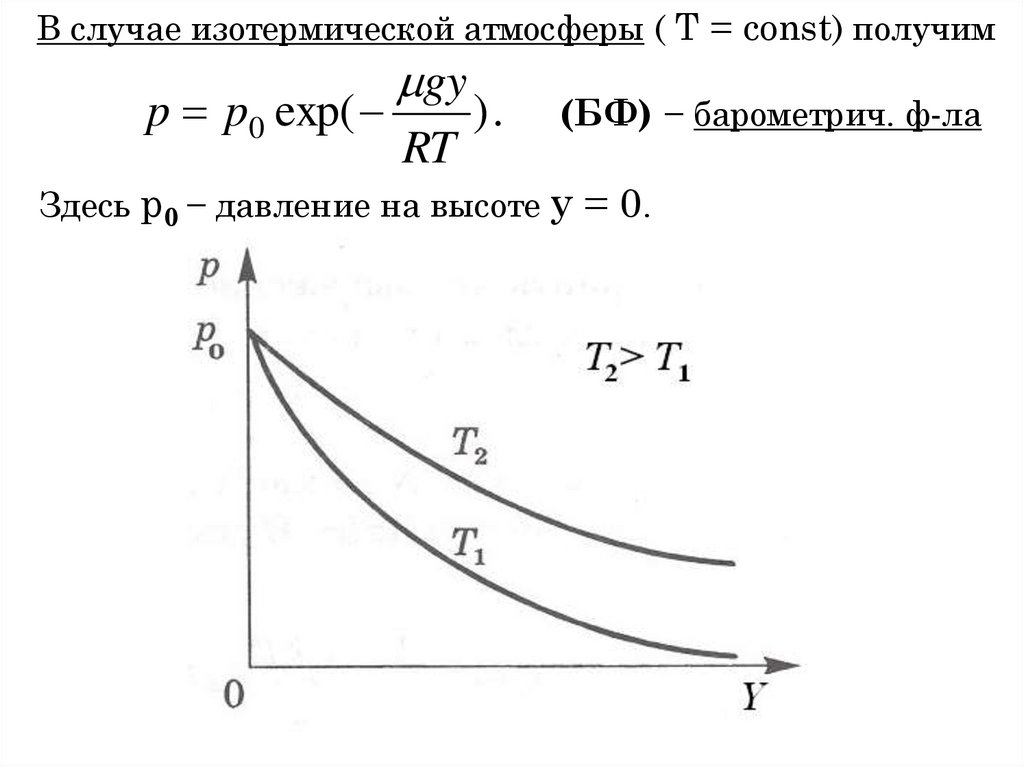




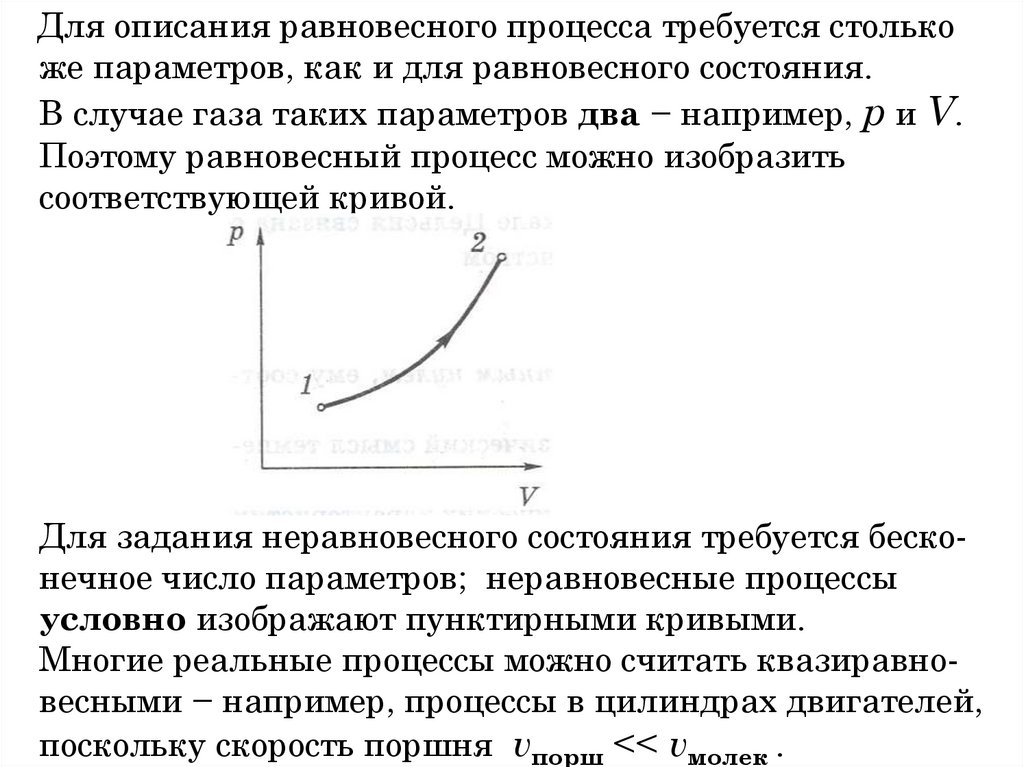











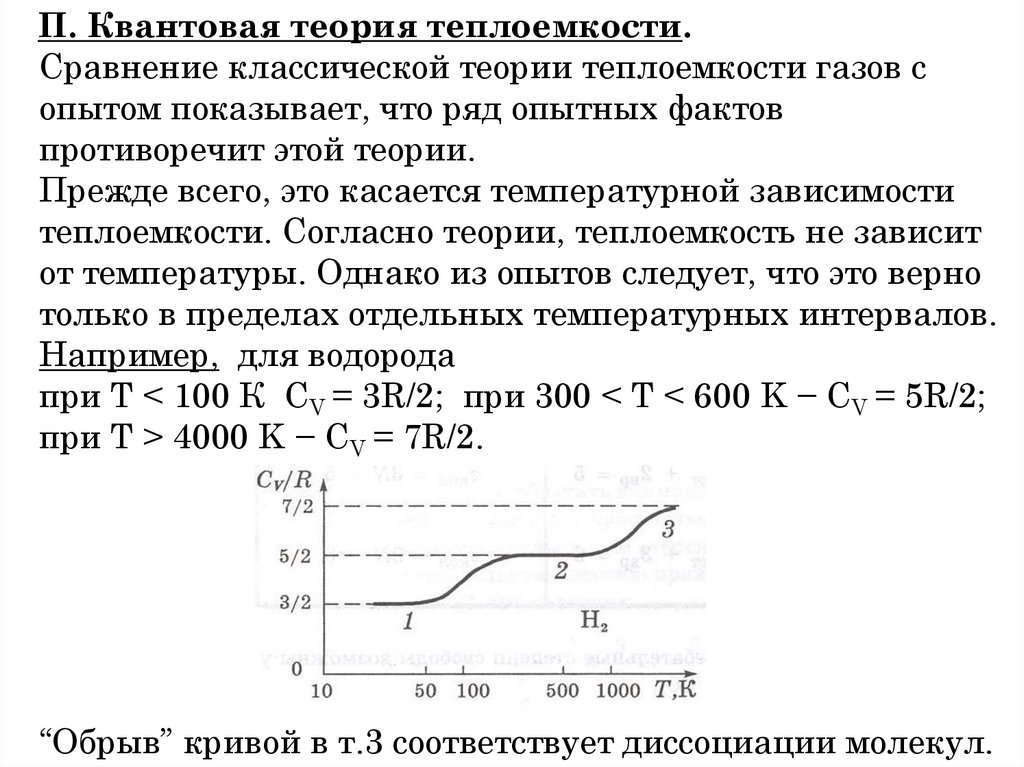



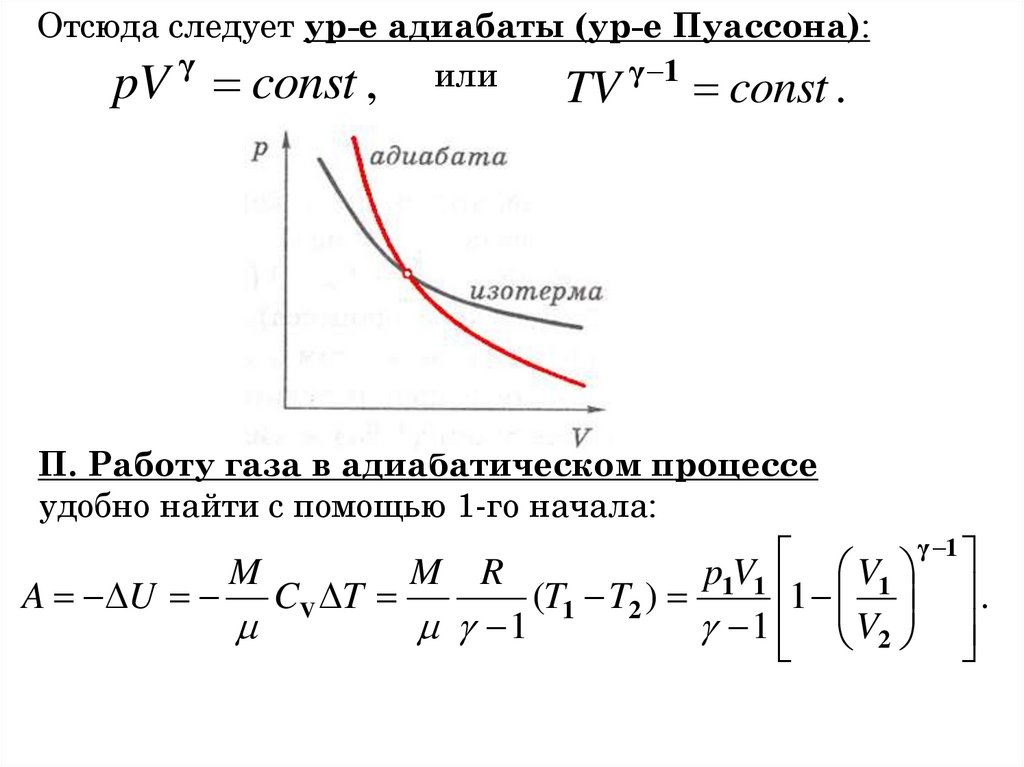

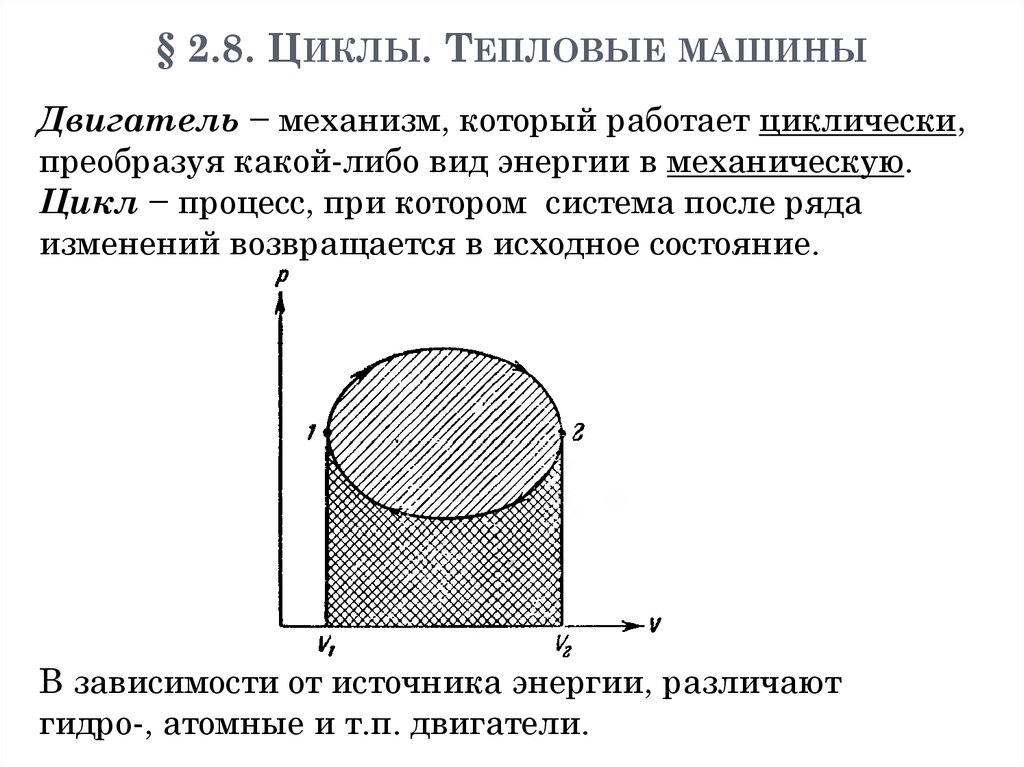

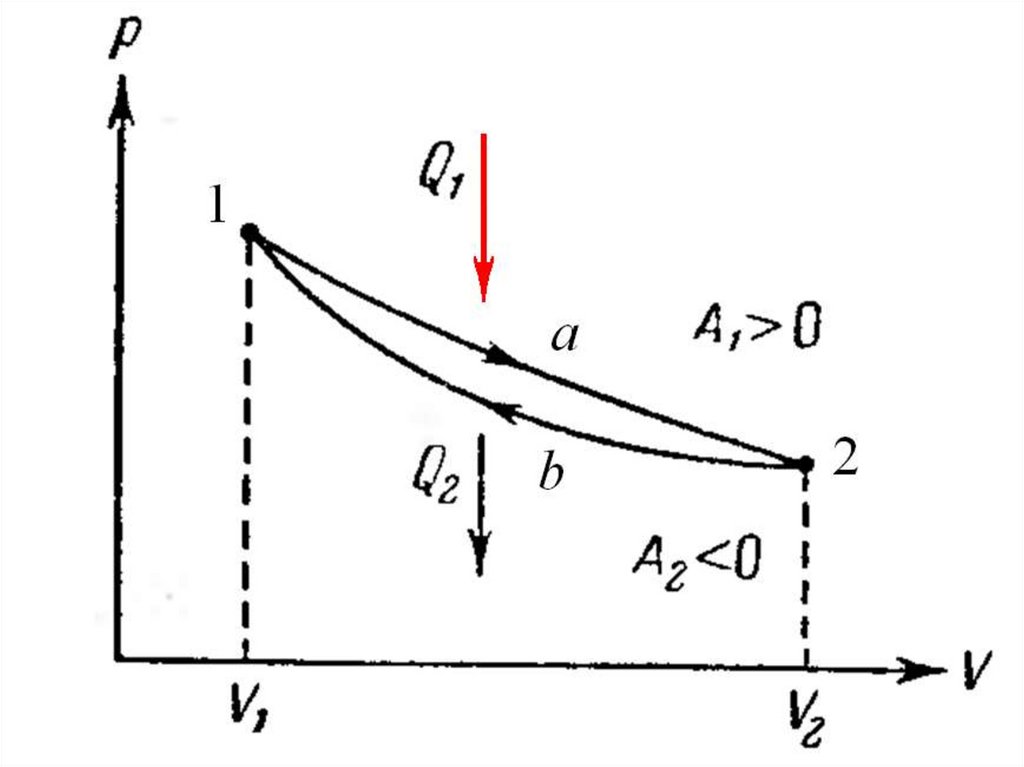



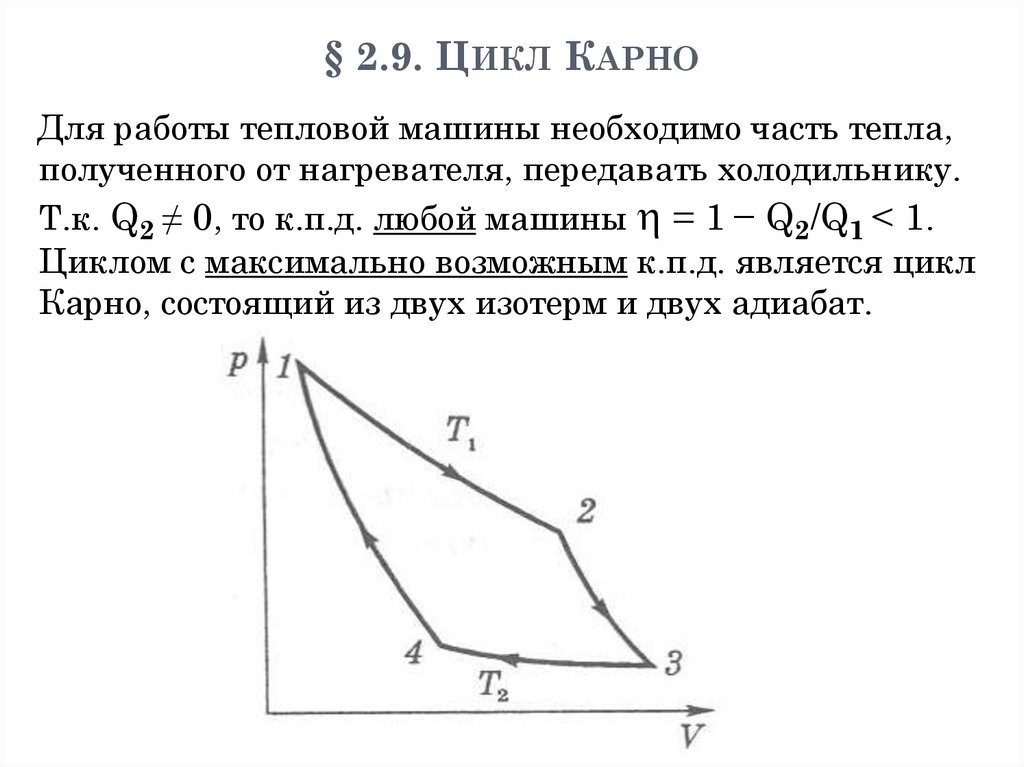
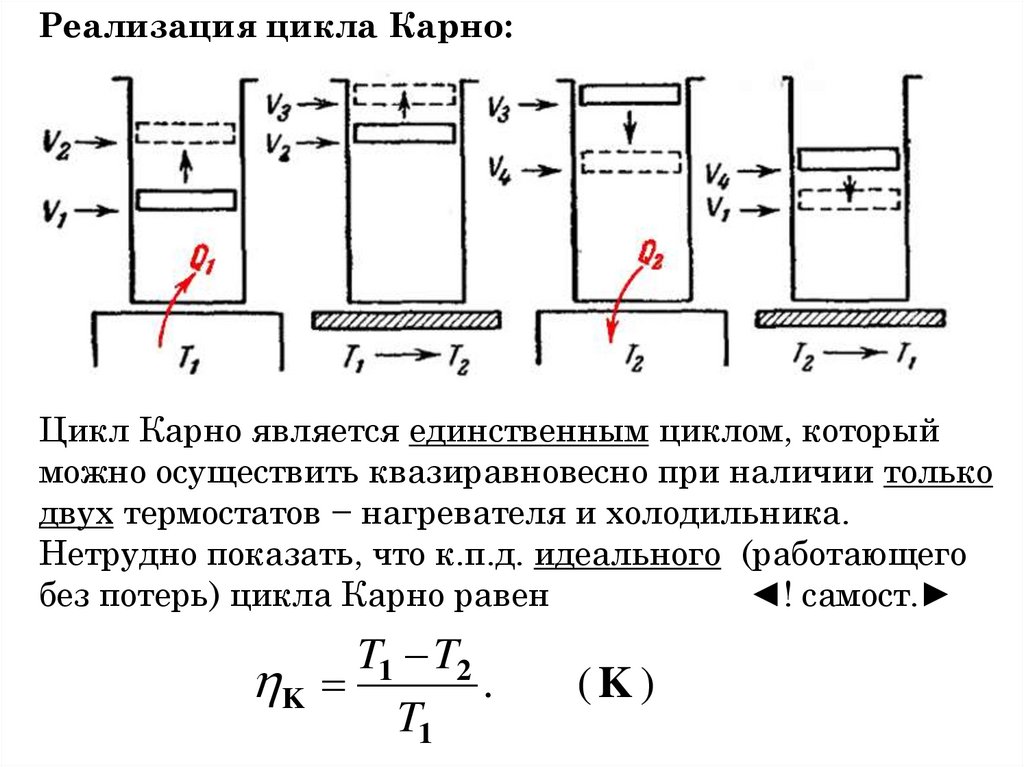













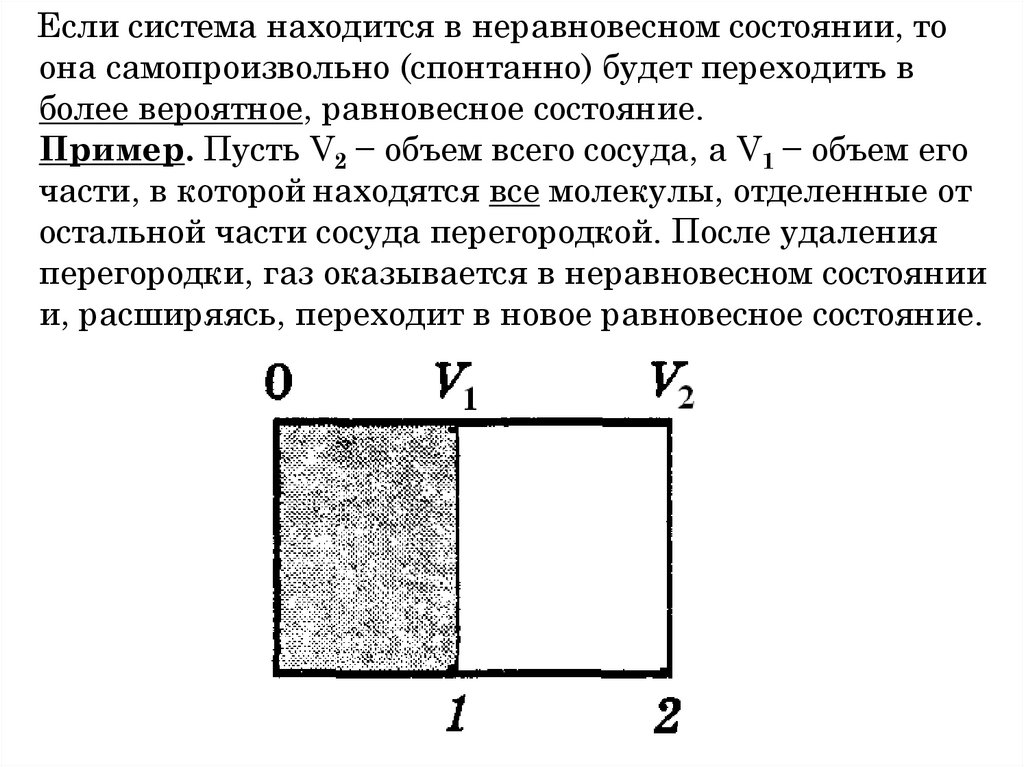







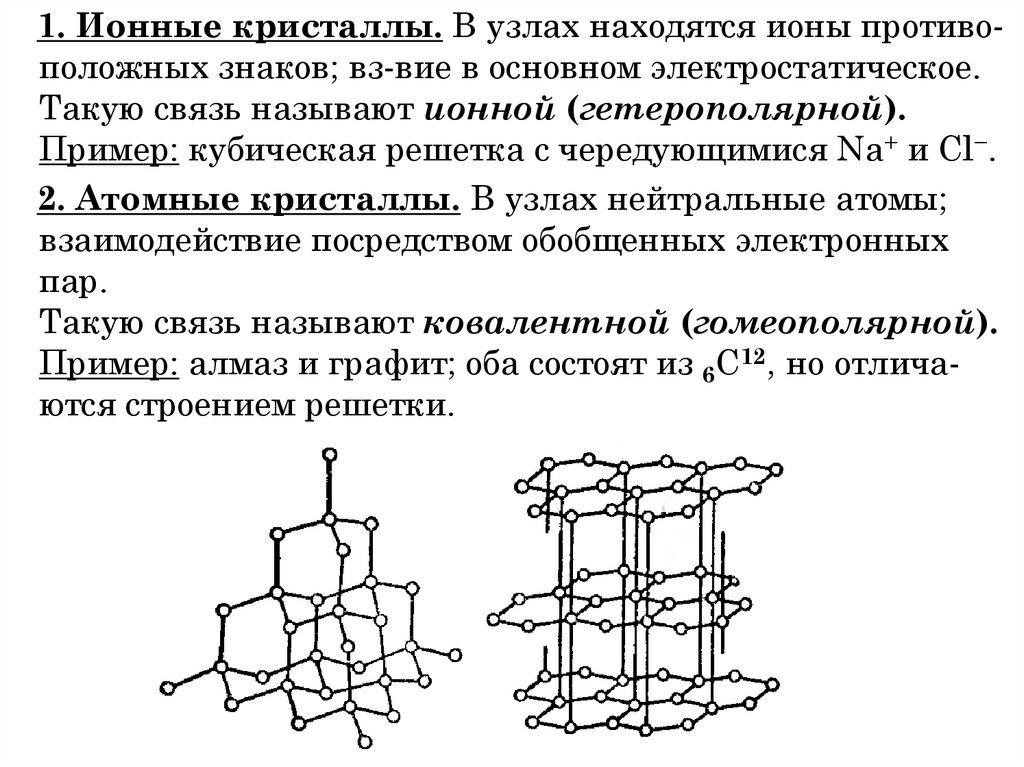


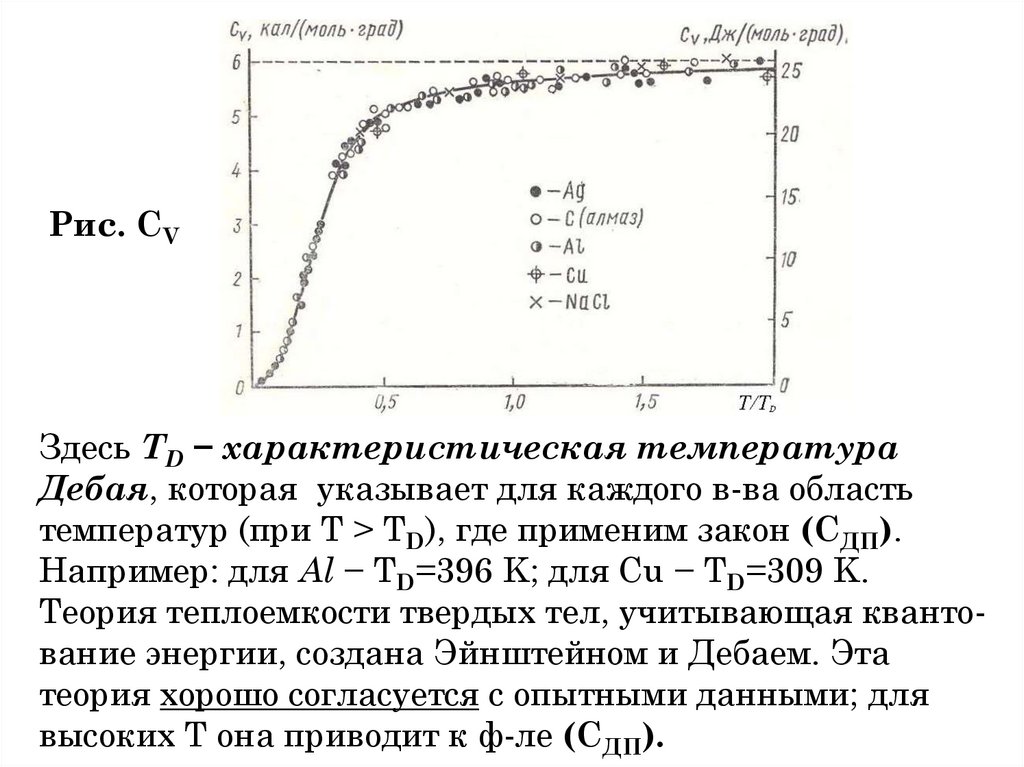


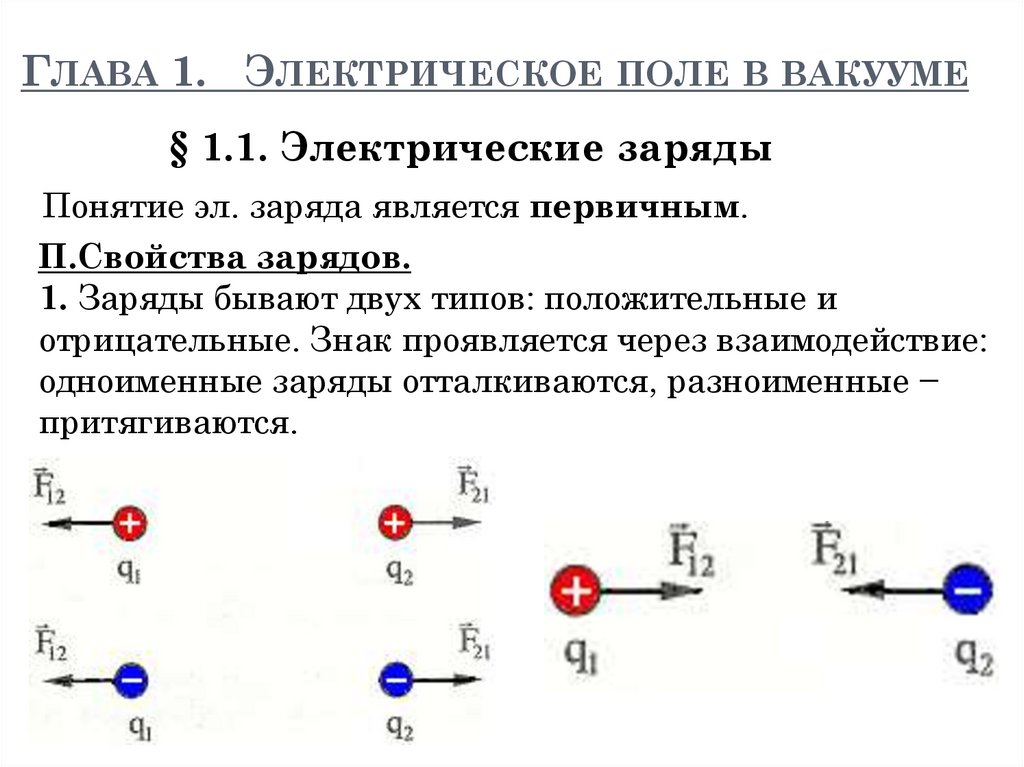






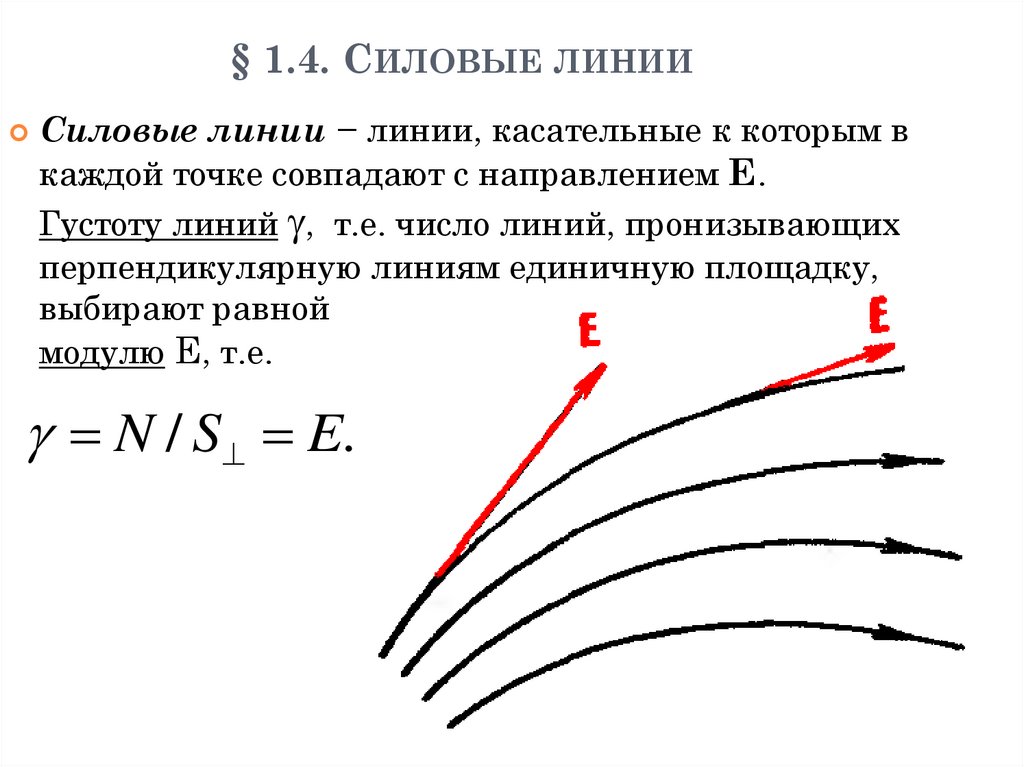
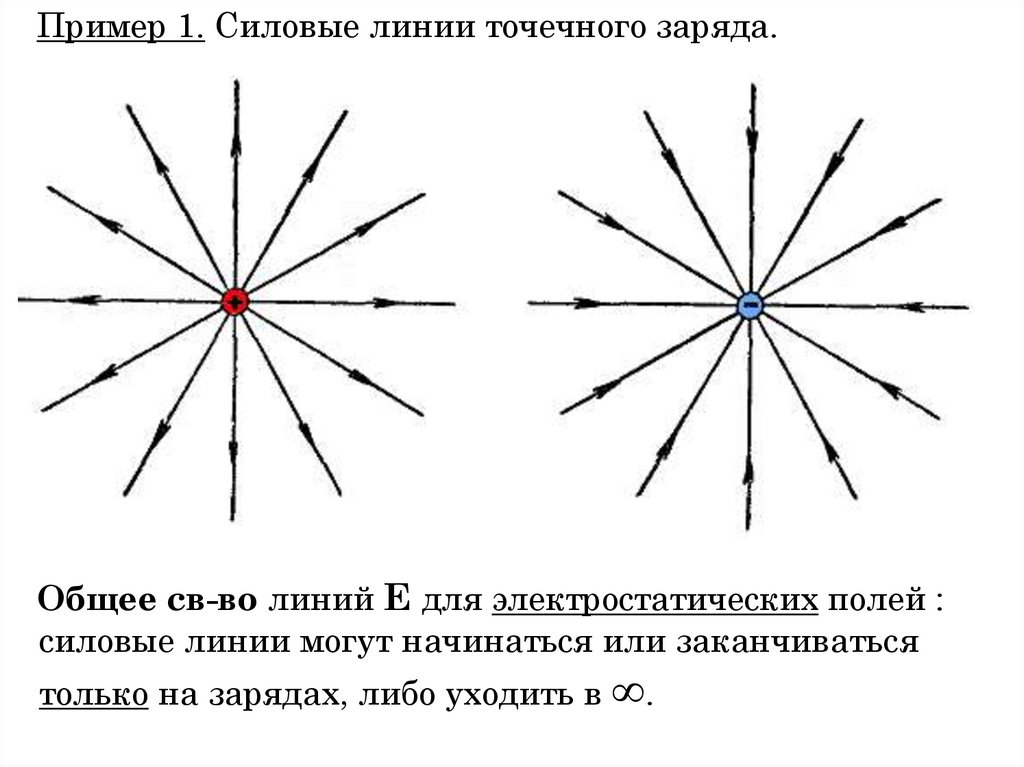
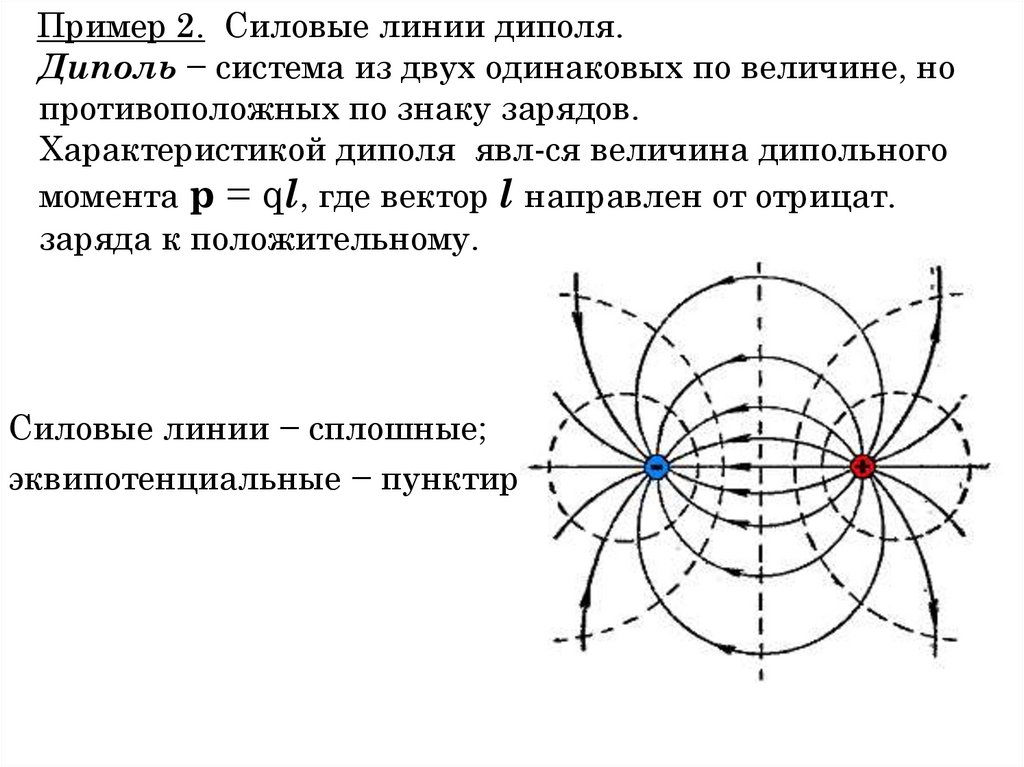
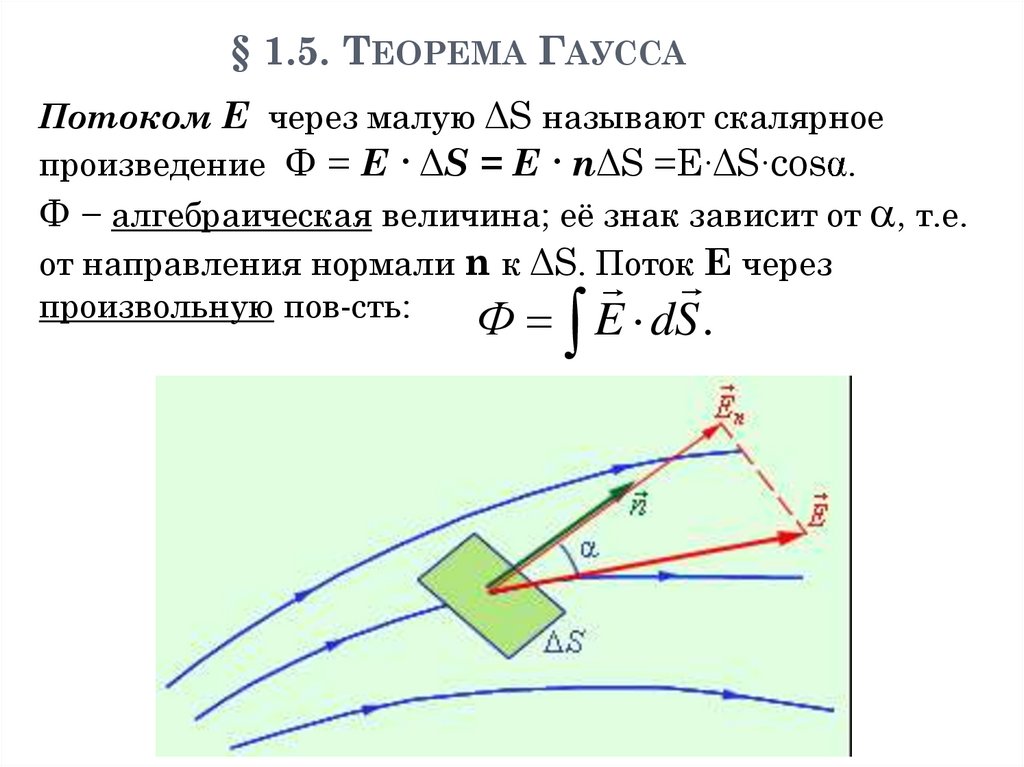












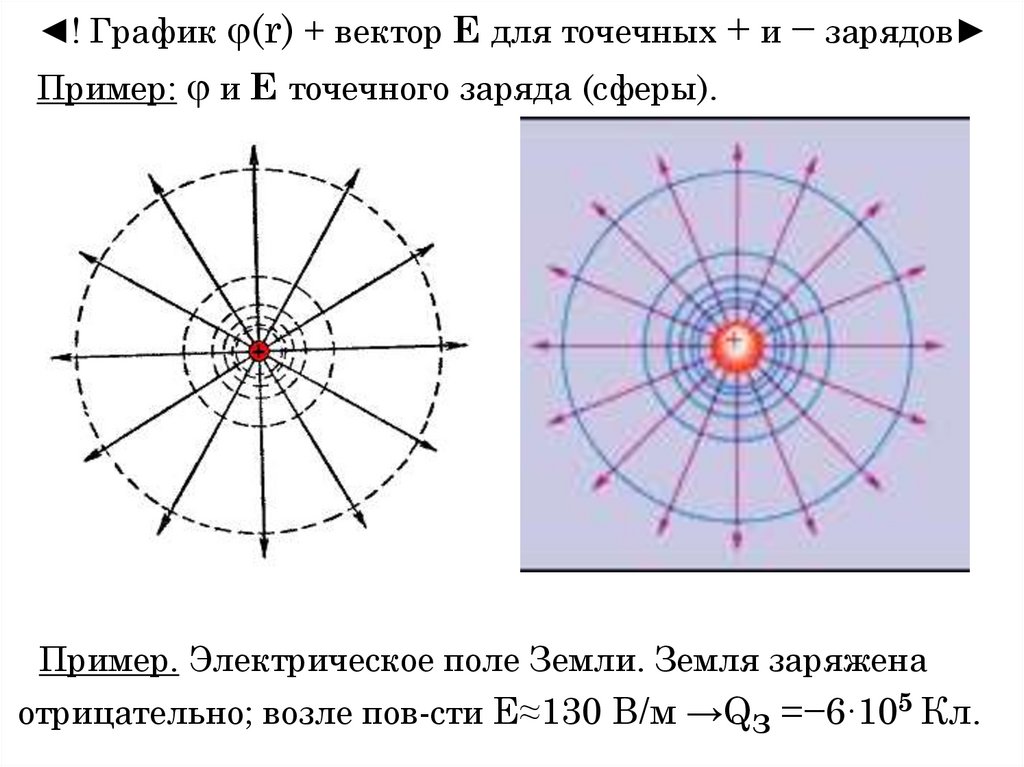
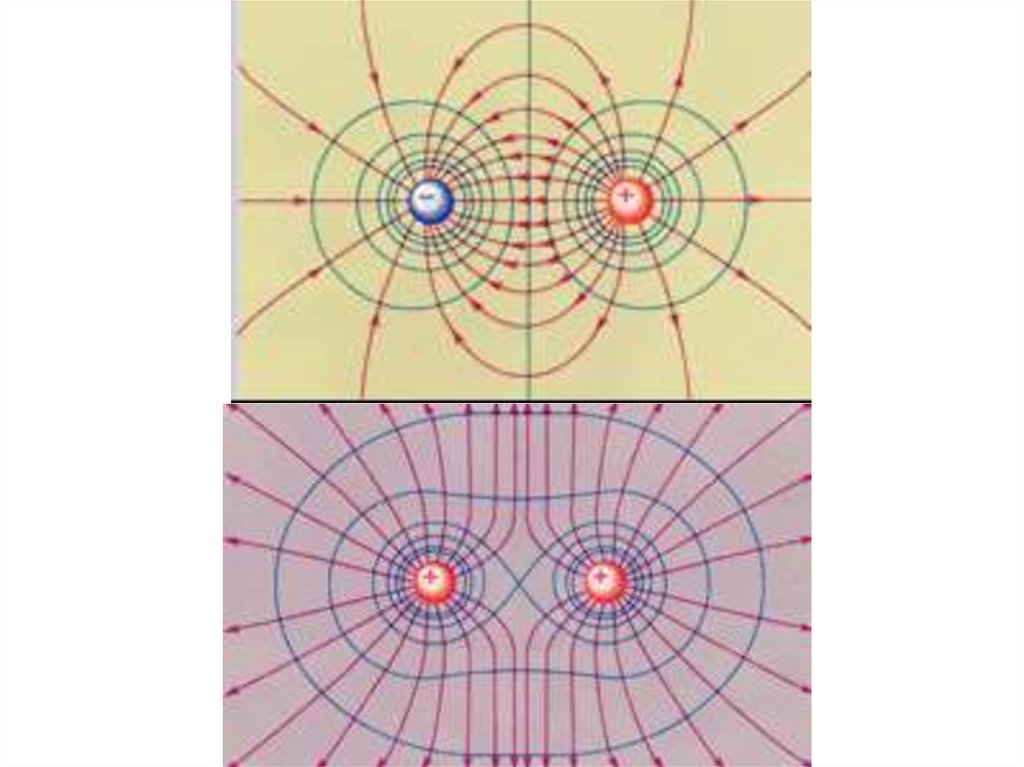

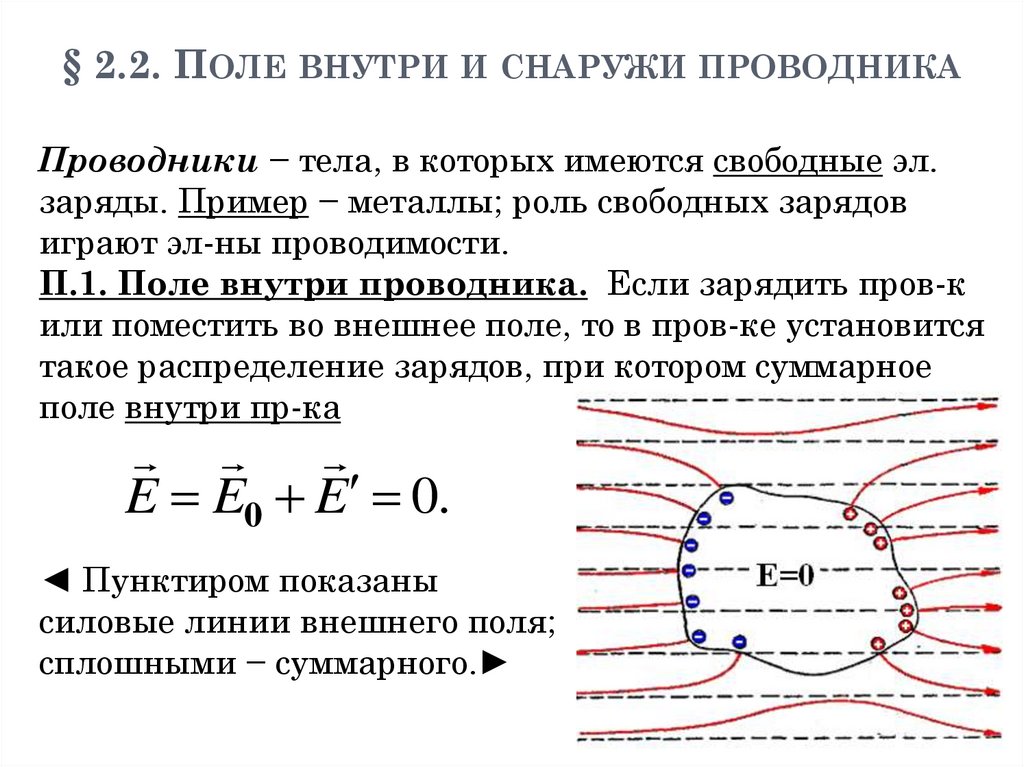
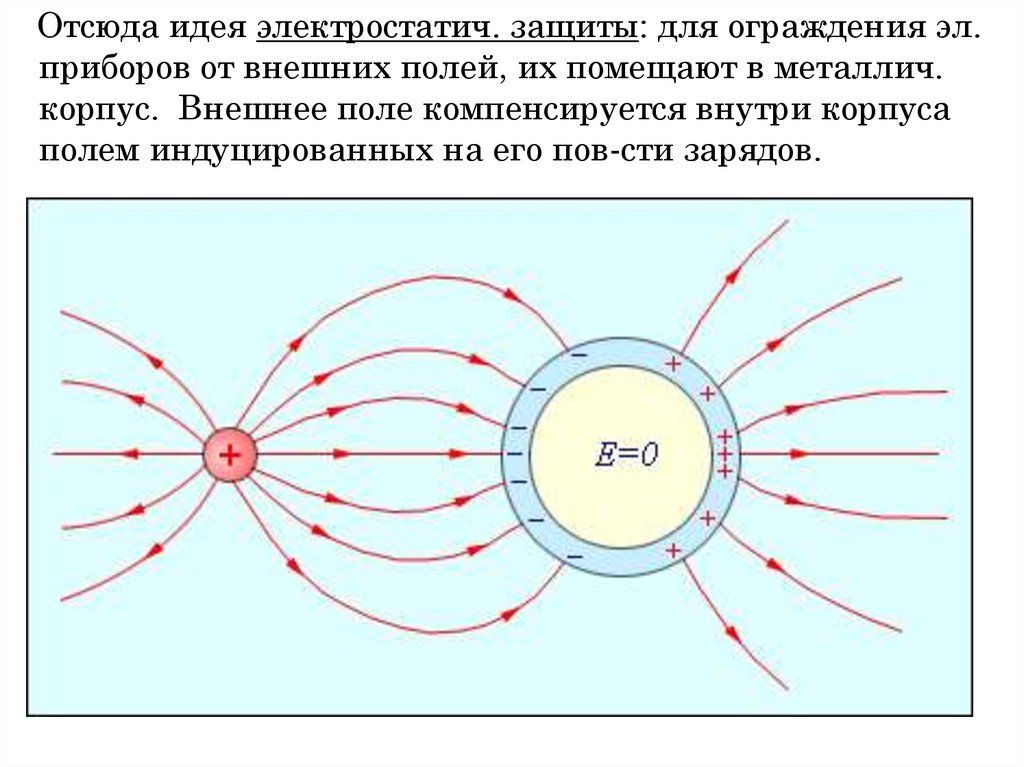

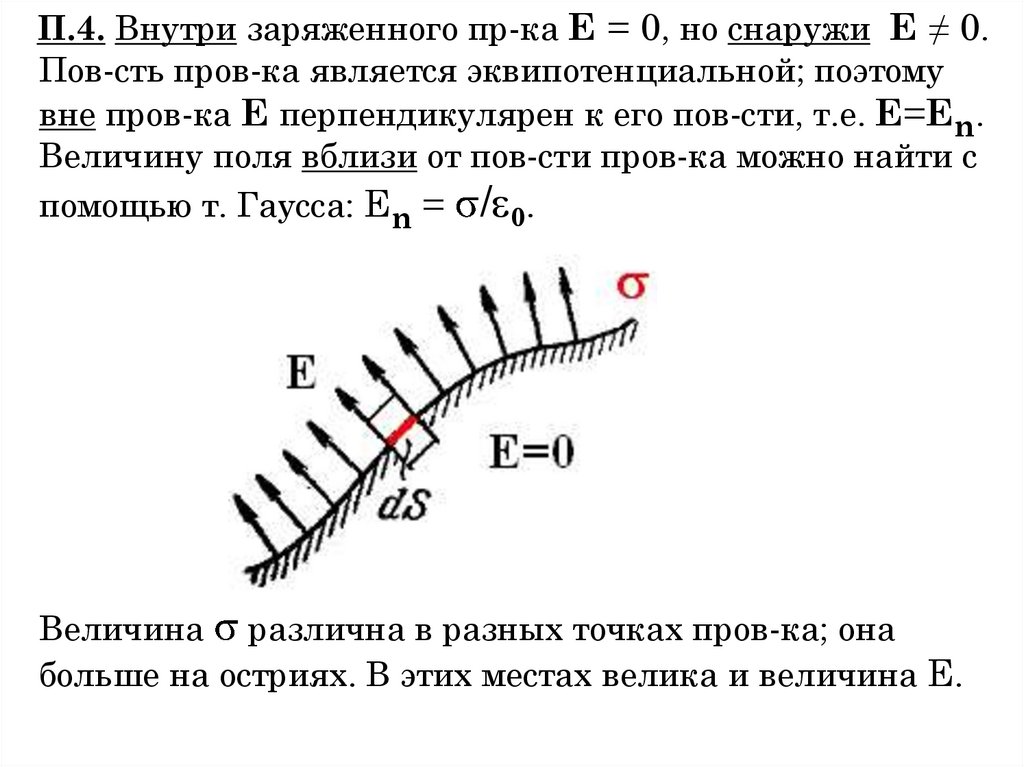
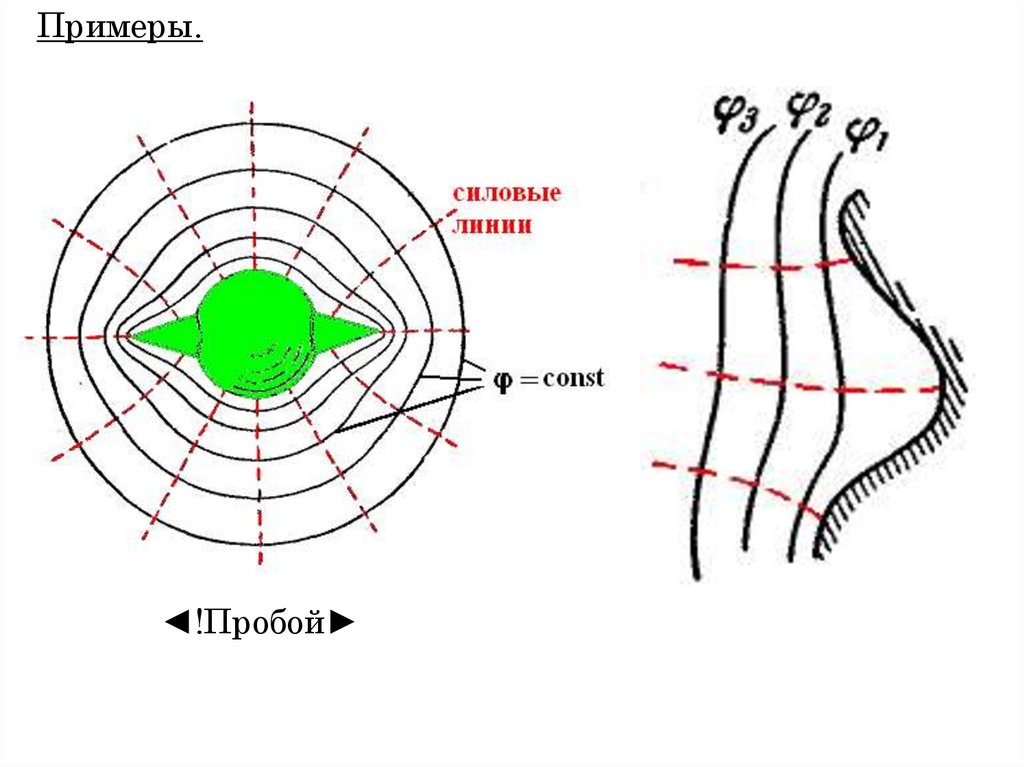




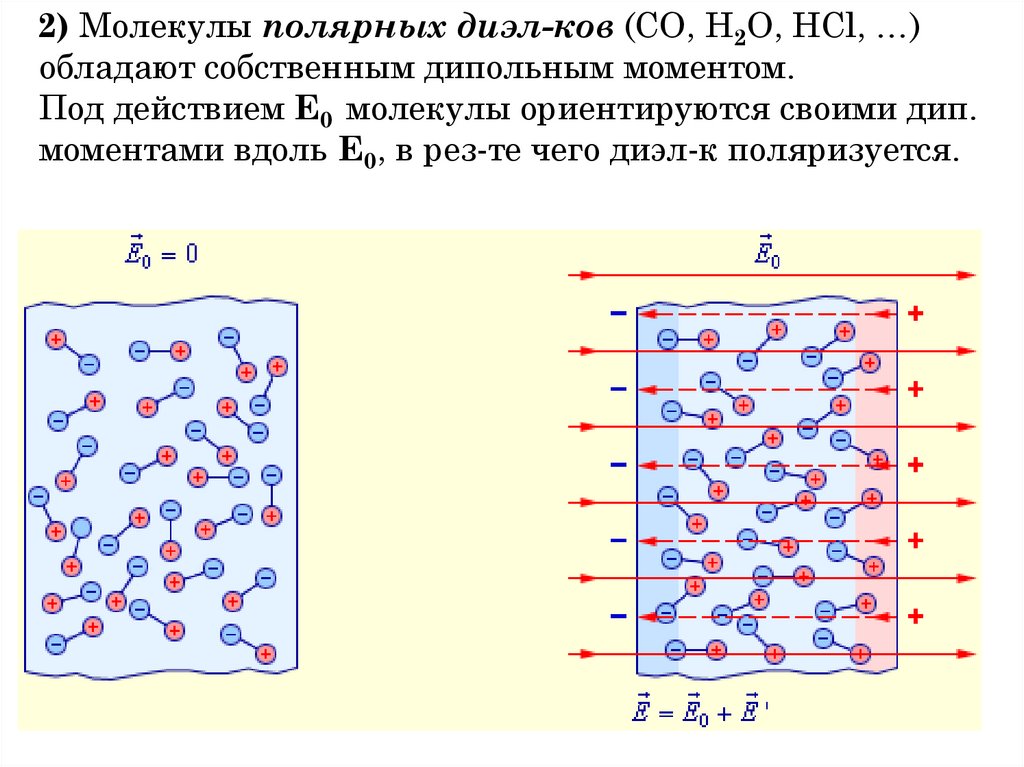




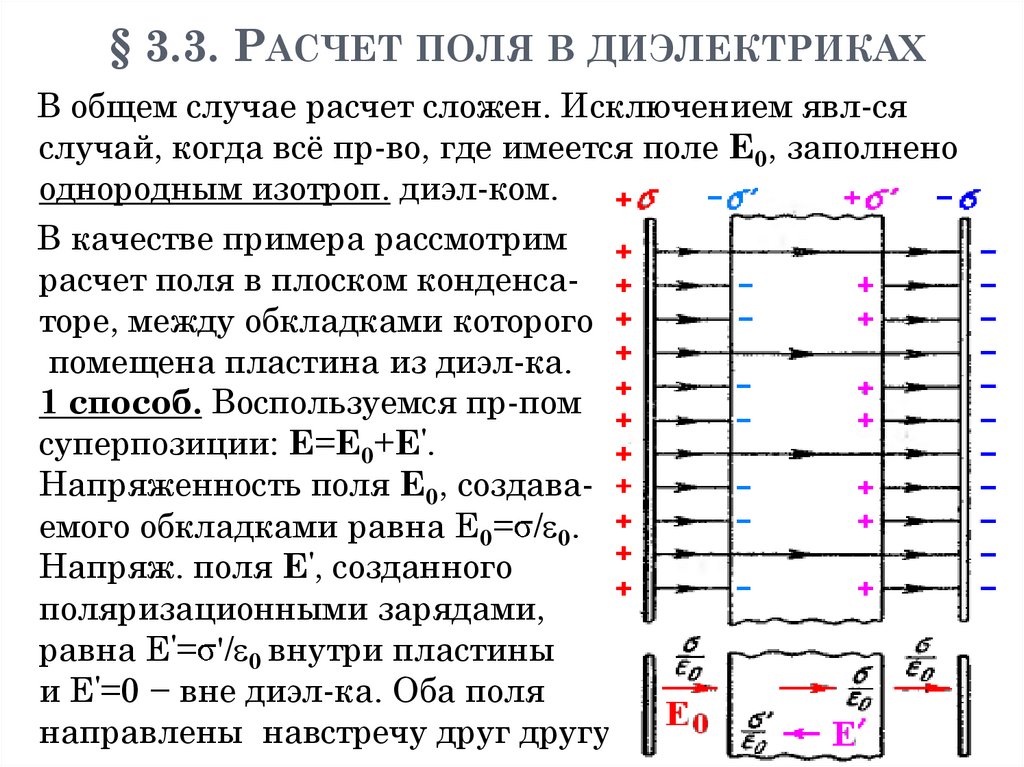


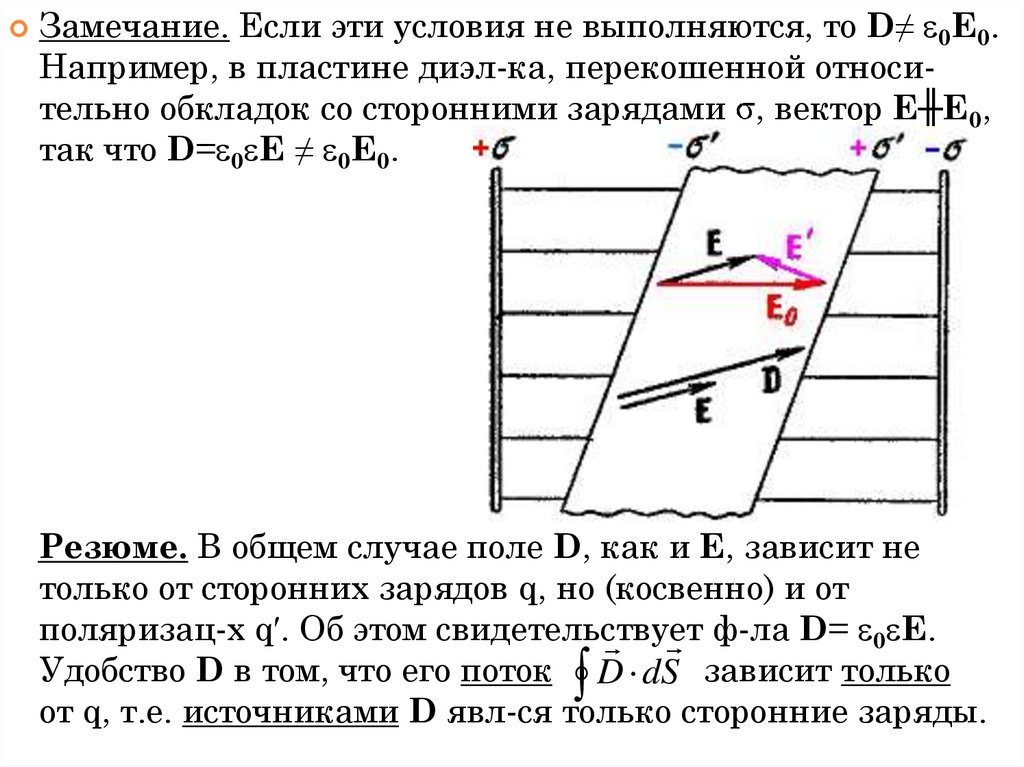

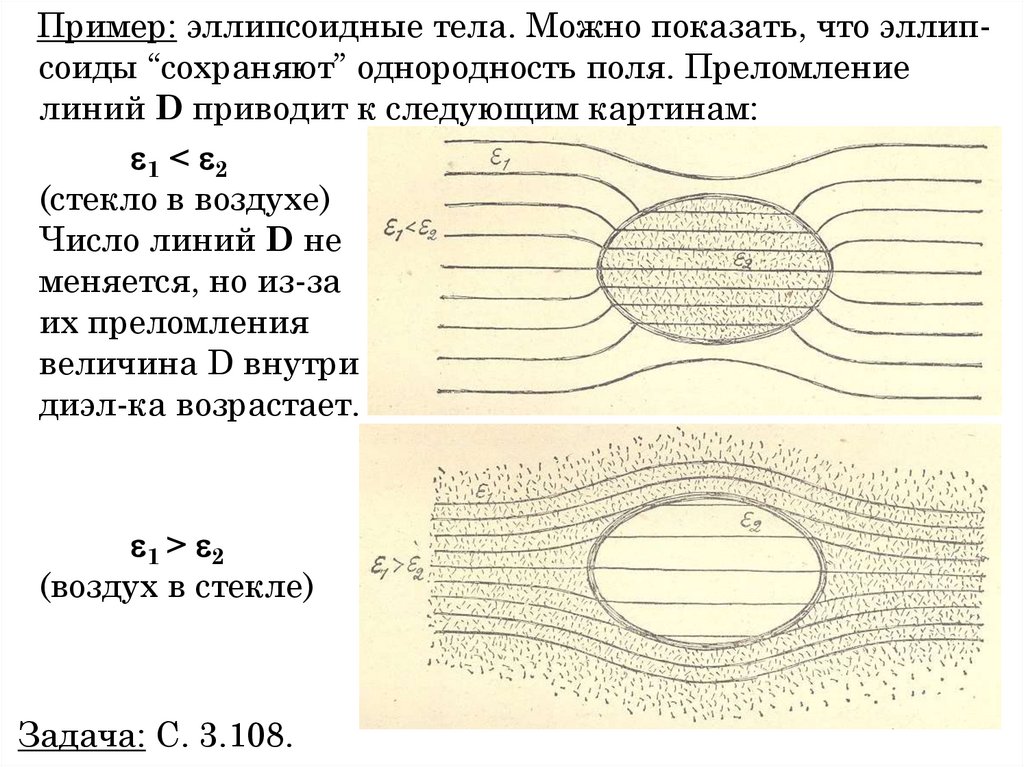










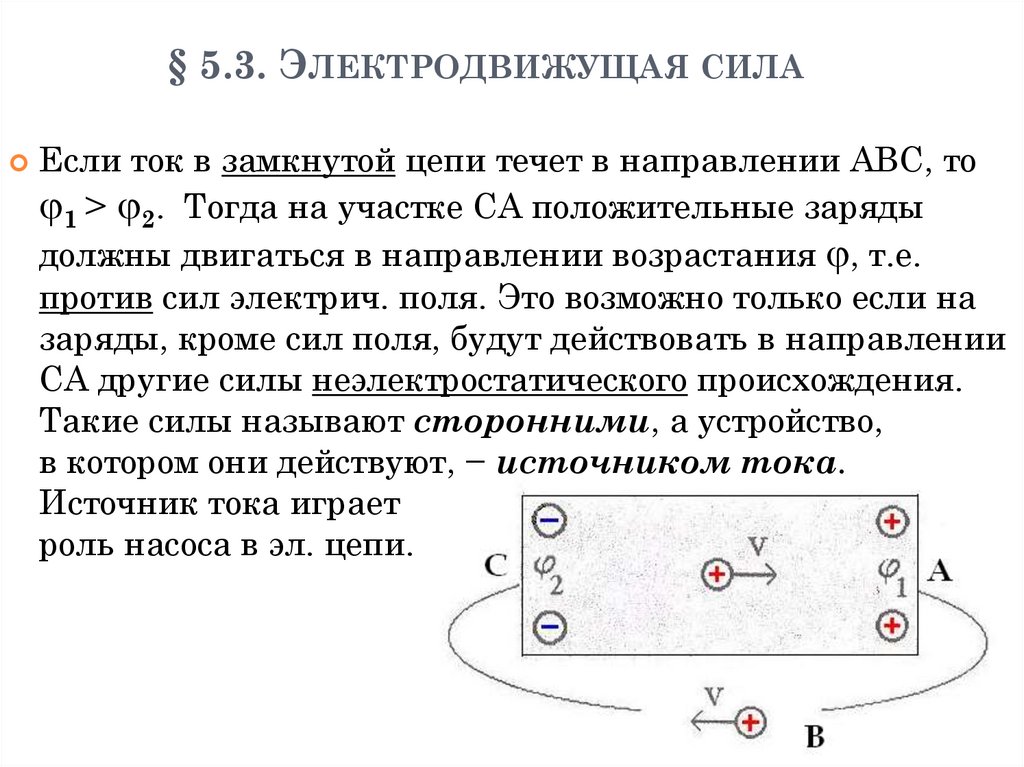









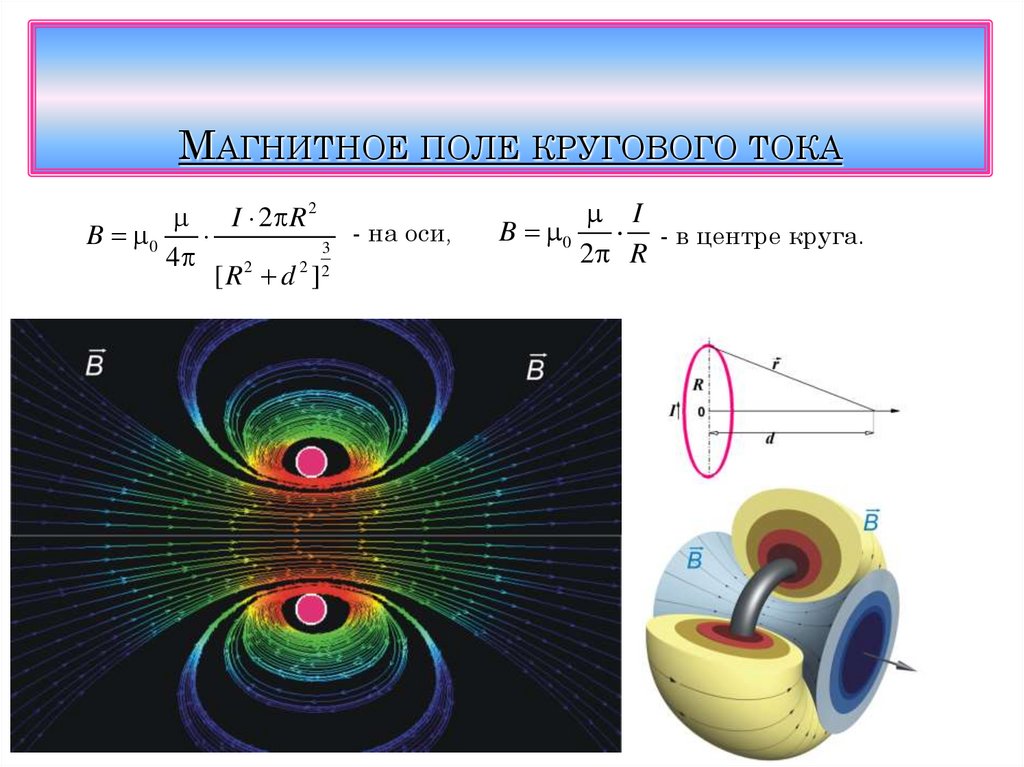
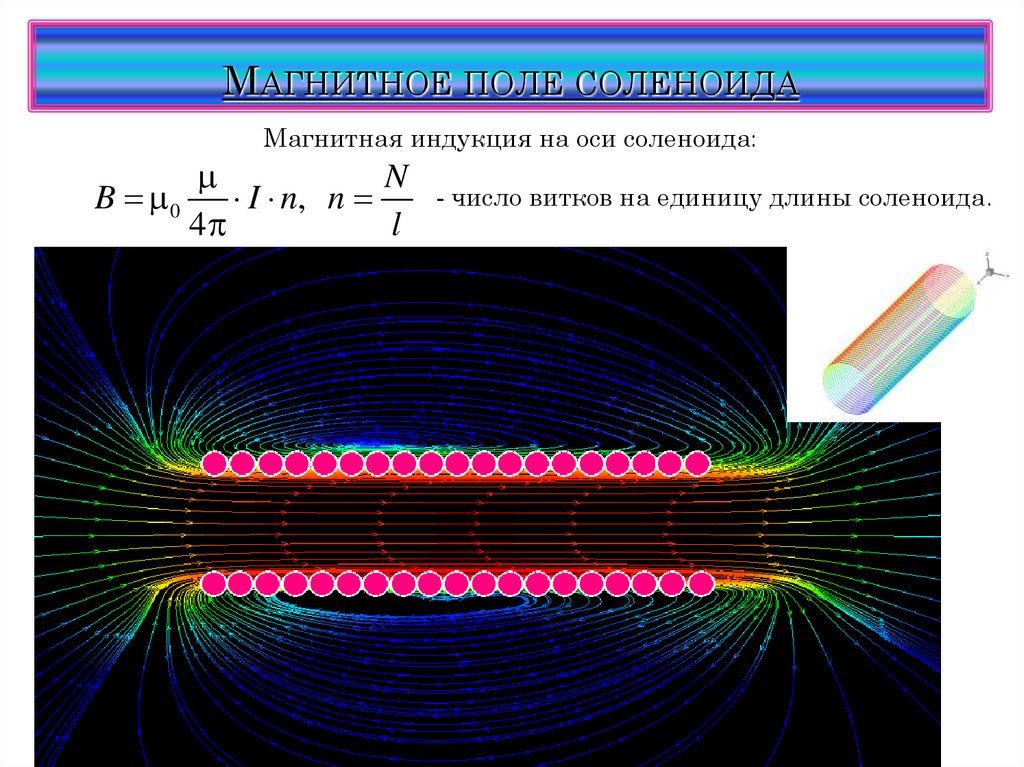

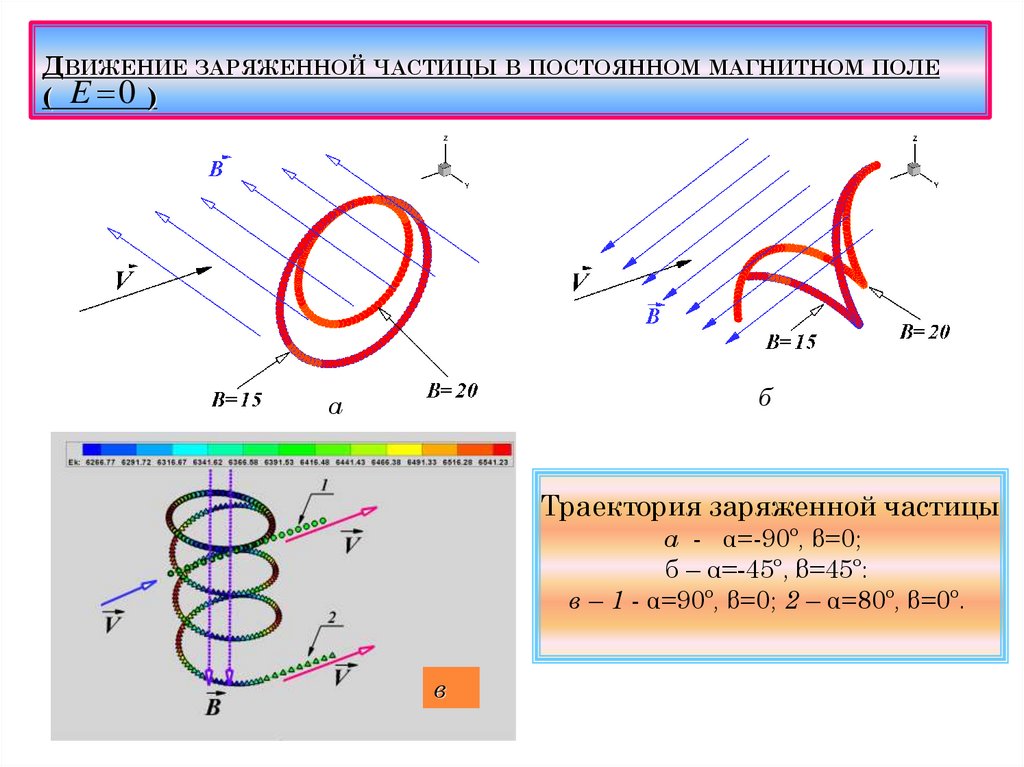

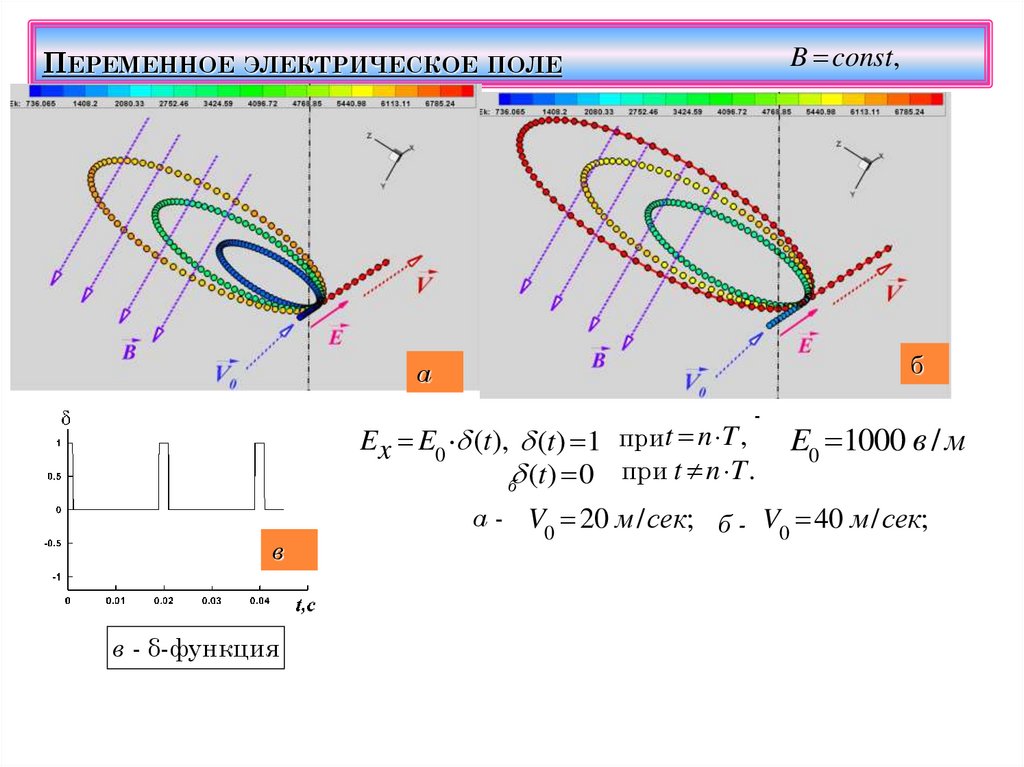
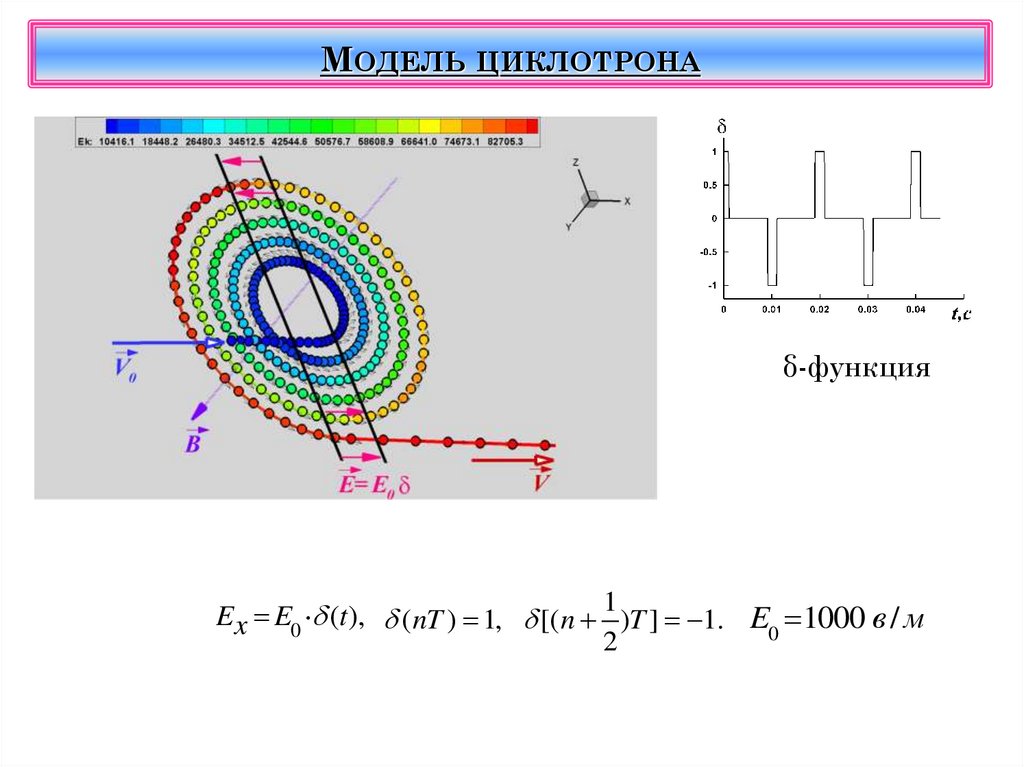

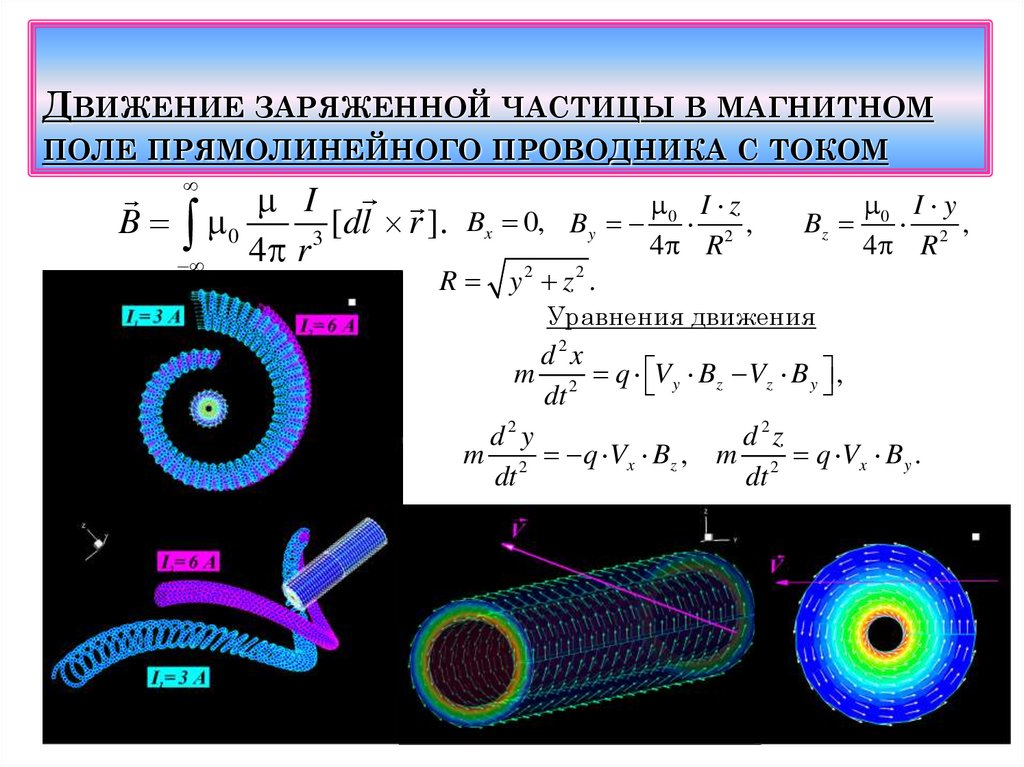
 physics
physics








