Введение в кинематику. Кинематика точки (лекция 7)

1.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра строительная механика
Теоретическая механика
Тема 9.
Введение в кинематику.
Кинематика точки
Лукашевич Надежда Кимовна
к.т.н., доцент
Сойту Наталья Юрьевна
к.т.н., доцент

2. Лекция 7.

Тема 9. КИНЕМАТИКА ТОЧКИ
9.1. Введение в кинематику.
9.2. Векторный способ задания движения точки.
9.3. Координатный способ задания движения точки.
9.4. Естественный способ задания движения точки.
9.5. Некоторые частные случаи движения точки.
2

3.

Тема 9. КИНЕМАТИКА ТОЧКИ
3
9.1. Введение в кинематику
Кинематика – раздел теоретической механики, в котором изучают геометрические свойства
движения материальных тел.
Система отсчета – какая-нибудь система координат, связанная с телом, относительно которой
рассматривается движение данного тела.
Систему отсчета можно связать с любым телом. Система отсчета может быть как движущейся,
так и условно неподвижной.
Движение тел происходит в пространстве с течением времени.
Пространство в теоретической механике рассматривается
пространство. За единицу длины принимается 1 метр.
как
трехмерное
евклидово
Время является универсальным, т. е. одинаковым во всех системах отсчета. Время – скалярная,
непрерывно изменяющаяся величина. За единицу времени принимается 1 секунда. Время
считается независимой переменной, все остальные переменные рассматриваются как функции
времени.
Начальный момент времени – условно выбранный момент времени t0 0 , от которого ведется
отсчет времени.

4.

Траектория точки – непрерывная линия, которую описывает движущаяся точка относительно
данной системы отсчета.
По виду траектории движение точки делится на прямолинейное и криволинейное.
Прямолинейным называется движение точки, траекторией которого является прямая линия.
Криволинейным называется движение точки, траектория которого любая кривая.
Для решения задач кинематики необходимо, чтобы движение было каким-либо образом задано.
Кинематически задать движение – это значит определить положение тела относительно данной
системы отсчета в любой момент времени.
Основные задачи кинематики
1. Установление математических способов задания движения.
2. Определение кинематических величин, характеризующие данное движение по известному
закону движения точки.
Способы задания движения точки:
1. Векторный
2. Координатный
3. Естественный.
4

5.

9.2. Векторный способ задания движения точки
5
Закон движения
Точка М движется относительно системы отсчета OXYZ.
Положение точки однозначно задается радиус-вектором r .
Движение задается вектор-функцией r r (t ) или
где x rx
r xi yj zk ,
y ry z rz проекции радиус-вектора на оси X, Y, Z.
Закон движения позволяет определить положение движущейся
точки в любой момент времени.
Скорость точки при векторном способе задания движения
За промежуток времени t t1 t радиус-вектор получает приращение
Средняя скорость за t
Vcp
r
t
r r1 r
r dr
t 0
t 0 t
dt
Вектор скорости точки в любой момент времени равен
первой производной от радиуса-вектора по времени:
Вектор скорости в каждый момент времени направлен по
касательной к траектории точки в сторону движения.
Скорость точки в момент времени t V limVcp lim
dr
V
dt

6.

Ускорение точки при векторном способе задания движения
За промежуток времени t t1 t
скорость получает приращение V V1 V
Среднее ускорение за промежуток времени t
acp
V
t
V dV
t 0 t
dt
Ускорение точки в момент времени t a lim acp lim
t 0
Вектор ускорения в данный момент времени равен первой производной от скорости или
2
d
V
d
r
второй производной от радиуса-вектора по времени: a
2
dt
dt
.
При прямолинейном движении вектор ускорения направлен вдоль прямой, по которой движется
точка.
Если траектория точки плоская кривая, то вектор ускорения лежит в плоскости этой кривой и
направлен в сторону вогнутости траектории.
Если траектория точки пространственная кривая, то вектор ускорения лежит в соприкасающейся
плоскости и направлен в сторону вогнутости траектории.
Соприкасающаяся плоскость – это плоскость, в которой происходит бесконечно малый поворот
касательной к траектории при элементарном перемещении движущейся точки.
6

7.

9.3. Координатный способ задания движения точки
Закон движения
Точка М движется относительно системы отсчета OXYZ. Положение
точки в любой момент времени однозначно определяется тремя
координатами X, Y, Z .
Уравнения движения точки в декартовых координатах имеют вид
X X (t ) Y Y (t ) Z Z (t )
Если точка движется в плоскости OXY , ее движение описывается
двумя уравнениями
X X (t ) Y Y (t )
Если точка движется вдоль оси, ее движение описывается одним
уравнением
X X (t )
7

8.

Скорость точки при координатном способе задания движения
dr , где
r xi yj zk
dt
d (i x jy k z )
dx
dy
dz
Взяв производную, получим V
i
j k
dt
dt
dt
dt
Определим скорость точки по формуле
V
Запишем вектор скорости через проекции V i Vx jV y k Vz
Приравняв коэффициенты при одноименных единичных векторах, получим
Vx
dx
dt
Vy
dy
dt
Vz
dz
dt
Проекции скоростей точек на координатные оси равны первым производным
от соответствующих координат по времени.
Модуль скорости
V Vx2 V y2 Vz2
Направление вектора скорости задается направляющими косинусами
cos
Vx
V
cos
Vy
V
Vz
cos
V
8

9.

Ускорение точки при координатном способе задания движения
Определим ускорение точки по формуле a
Взяв производную, получим a
dV
, где V i Vx jV y k Vz
dt
d (i Vx jV y k Vz )
dt
Запишем вектор ускорения через проекции
i
dV
dVx
dV
j y k z
dt
dt
dt
a i a x ja y k a z
Приравняв коэффициенты при одноименных единичных векторах, получим
dVx d 2 x
ax
2
dt
dt
d2y
ay
2
dt
dt
dV y
dVz d 2 z
az
2
dt
dt
Проекции ускорения точек на координатные оси равны первым производным
от соответствующих проекций скоростей или вторым производным от координат
по времени
2
2
2
Модуль ускорения a a x a y a z
Направление вектора ускорения задается направляющими косинусами
cos 1
.
ax
a
cos 1
ay
a
cos 1
az
a
9

10.

9.4. Естественный способ задания движения точки
10
Закон движения
Естественный способ задания движения точки применяется, если точка
движется по известной траектории.
Положение точки однозначно определяется криволинейной координатой
S, которая откладывается от точки О вдоль траектории.
Уравнение движения S S (t )
.
Скорость точки при естественном способе задания движения
За промежуток времени t t1 t криволинейная координата получает приращение S S1 S
Средняя скорость за промежуток времени t Vcp
S
t
S dS
t 0 t
dt
Скорость точки в момент времени t V limVcp lim
t 0
Модуль скорости точки в данный момент времени равен
первой производной от криволинейной координаты по времени:
V
Вектор скорости в каждый момент времени направлен по касательной к траектории точки
в сторону движения.
.
dS
dt

11.

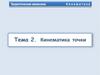
Ускорение точки при естественном способе задания движения
МƬnb – естественная система координат.
Ось Ƭ – касательная; n – нормаль; b – бинормаль.
Вектор ускорения лежит в плоскости МƬn.
Ускорение раскладывается на две составляющие a an a
Проекция ускорения на бинормаль всегда равна нулю
ab 0
Приращение скорости dV за бесконечно
малый промежуток времени dt dV V1 V
Проекции ускорений на координатные оси:
a
где
dV AC DB MB MA V1 V
и
dV
dt
an
dVn
dt
(1)
dVn AD MA d V d
Подставим в формулы для проекций ускорений (1):
dV dV
a
dt
dt
.
и
dVn Vd Vd dS
d V 2
an
V V
, где
dt
dt
dt dS
dS
dV
Окончательно получим a
dt
an
V2
ab 0
d
k
dS
1
k
– радиус кривизны траектории.
11

12.

a – тангенциальное ускорение, характеризует изменение скорости по модулю.
Вектор тангенциального ускорения направлен по касательной к траектории: при ускоренном
движении так же, как вектор скорости, при замедленном – в противоположную сторону.
an – нормальное ускорение, характеризует изменение скорости по направлению.
Вектор нормального ускорения направлен по нормали внутрь траектории.
Модуль полного ускорения
a (an ) 2 (a ) 2
.
Связь естественного способа задания движения с координатным
При координатном способе задания движения модуль скорости V Vx2 V y2 Vz2
Подставив в формулу для тангенциального ускорения, получим
d V V V
dV d V V V
a
dt
dt
dt
2
x
2
y
2
z
Тангенциальное ускорение a
2
x
2Vx
dV
dVx
dV
2V y y 2Vz z V a V a V a
y y
z z
dt
dt
dt x x
V
2 Vx2 V y2 Vz2
Vx a x V y a y Vz a z
При движении точки в плоскости: a
.
1
2 2
z
2
y
V
Vx a x V y a y
V
; an
a 2 a 2 ;
V2
.
an
12

13.

13
Пример:
Точка М движется по закону
x 4t 2 1 (м), y 3t (м).
Определить и построить: траекторию точки, скорость, полное, тангенциальное и нормальное
ускорения и радиус кривизны траектории в момент времени t = t1 = 1 с.
Решение
1) Определим траекторию.
Для определения траектории исключим время из уравнений координат (выразим время из
второго уравнения и подставим в первое).
2
4
y
Точка движется по параболе x
1 .
9
Для построения траектории составим таблицу значений координат
2) Определим положение точки в заданный момент времени (при t = t1 = 1 с).
Подставив время t = t1 = 1 с в уравнения движения, получим координаты точки:
x1 4 12 1 3 (м), y1 3 1 3 (м).
В заданный момент времени движущаяся точка М находится в точке с координатами (– 3, 3).
Построим траекторию и покажем точку в заданный момент времени.

14.

14
3) Определим скорость.
Определим две составляющие скорости:
При t = t1 = 1 с
dx
dy
Vx
8t V y
3
Vx 8 м/с; V y 3 м/с.
dt
dt
Модуль скорости V Vx2 V y2
8 2 32 73 8,54
Построим скорости: составляющие скоростей параллельны
соответствующим осям и, если знак «+», направлены так же,
как ось, «-» – в противоположную сторону.
4) Определим ускорения.
dVx
8
Определим две составляющие ускорения: a x
dt
Модуль ускорения a
ay
dV y
dt
0
a x2 a y2 ( 8) 2 0 2 8
Определим тангенциальное и нормальное ускорения
V a V y a y 8 8 3 0
2
a x x
7,49
an a 2 a 2 82 7,49
V
8,54
7,84 2,80
Построим ускорения: a x параллельна оси X, направлена в противоположную сторону (знак «-»);
a y 0 ; a – по скорости (движение ускоренное); a n – перпендикулярно a внутрь траектории.
5) Определим радиус кривизны траектории.
V 2 8,54 2 73
26,01
an
2,8
2,8

15.

9.5. Некоторые частные случаи движения точки
1) Если a 0 , a n 0 – движение равномерное прямолинейное. Точка движется по прямой с
постоянной скоростью. Закон равномерного прямолинейного движения имеет вид x x0 Vt .
2) Если a 0 , a n 0 скорость меняется только по модулю, при этом точка движется по прямой
с ускорением a a .
а) при a const – движение равнопеременное прямолинейное. Если знаки скорости и ускорения
совпадают, движение равноускоренное, если не совпадают – равнозамедленное.
at 2
Закон равнопеременного прямолинейного движения имеет вид x x0 V0t
.
2
б) при a const – движение неравномерное прямолинейное. Если знаки скорости и ускорения
совпадают, движение называется ускоренным, если не совпадают – замедленным.
3) Если a 0 , a n 0 – движение равномерное криволинейное. Скорость меняется только по
направлению, точка движется по кривой с постоянной по модулю скоростью.
Закон равномерного криволинейного движения имеет вид S S 0 Vt .
4) Если a 0 , a n 0 скорость меняется по модулю и по направлению, то есть точка движется
по кривой с ускорением a (an ) 2 (a ) 2 .
а) при a const – движение равнопеременное криволинейное.
a t 2
Закон равнопеременного криволинейного движения имеет вид S S0 V0t
.
б) при a const – движение неравномерное криволинейное.
2
15

16.

Санкт-Петербургский государственный
архитектурно-строительный университет
кафедра строительная механика
Авторы:
Лукашевич Надежда Кимовна
Сойту Наталья Юрьевна
tehmeh@spbgasu.ru