Педагогические, теоретические и практические аспекты проблемы ЕГЭ. Решение задания 13 ЕГЭ - 2016

1. Педагогические, теоретические и практические аспекты проблемы ЕГЭ

Решение задания 13
ЕГЭ - 2016

2. Задание 13демонстрационного варианта ЕГЭ - 2016

• а) Решите уравнение
• б) Найдите все корни этого уравнения,
принадлежащие промежутку

3. Типовые задания 13

Уравнения, содержащие показательные выражения.
Уравнения, содержащие логарифмические выражения.
Уравнения, содержащие иррациональные выражения.
Уравнения, содержащие дробные выражения.
Уравнения, содержащие модули.
Уравнения, содержащие корни.
Уравнения, содержащие обратные тригонометрические
функции.
• Комбинированные уравнения.
• Серия тригонометрических уравнений.

4. Типовые задания 13

• Уравнения, содержащие показательные выражения.
.
Решите уравнение
Найдите все корни этого уравнения, принадлежащие отрезку
Решите уравнение
Найдите все корни этого уравнения, принадлежащие отрезку
Решите уравнение
Найдите все корни этого уравнения, принадлежащие отрезку

5. Типовые задания 13

• Уравнения, содержащие логарифмические выражения.
Решите уравнение
Найдите все корни этого уравнения, принадлежащие отрезку
Решите уравнение

6. Типовые задания С1

• Комбинированные уравнения.
Решите уравнение
Решите уравнение

7. Типовые задания 13

• Уравнения, содержащие дробные выражения.
Решите уравнение
Решите уравнение

8. Типовые задания 13

• Уравнения, содержащие корни.
Решите уравнение
Решите уравнение

9. Типовые задания 13

10. Типичные ошибки в решении задания 13 ЕГЭ по математике (потеря корней, появление «посторонних» корней)

11.

Первое задание:
а) Решите уравнение:
б) Найдите все корни на промежутке [
При решении уравнения попытаемся
представить тангенс суммы двух углов по
формуле
Получилось:
И – внимание! – потеря корня!
]

12.

Смотрите внимательно: после этого
преобразования мы получили отдельно
стоящий tgx. Но tgx не определен при
. А в исходном уравнении x вполне
мог быть равен
.
То есть, выполняя это невинное
преобразование, мы сузили ОДЗ. Поэтому,
выполняя преобразование нужно
следить за тем, что происходит с
областью допустимых значений.

13.

Итак, мы идем другим путем.
Запишем tgx и ctgx через sin и cos:
Используем формулы синуса и косинуса
суммы:

14.

Вынесем за скобку общий множитель:
Приведем выражение в скобках к общему
знаменателю:
Знаменатель дроби не равен нулю, то есть
и

15.

Произведение двух множителей равно нулю, если
хотя бы один из них равен нулю:
или
1.
вот он, потерянный корень!
2.
Раскроем скобки, приведем подобные члены:

16.

Итак, мы получили два решения:

17.

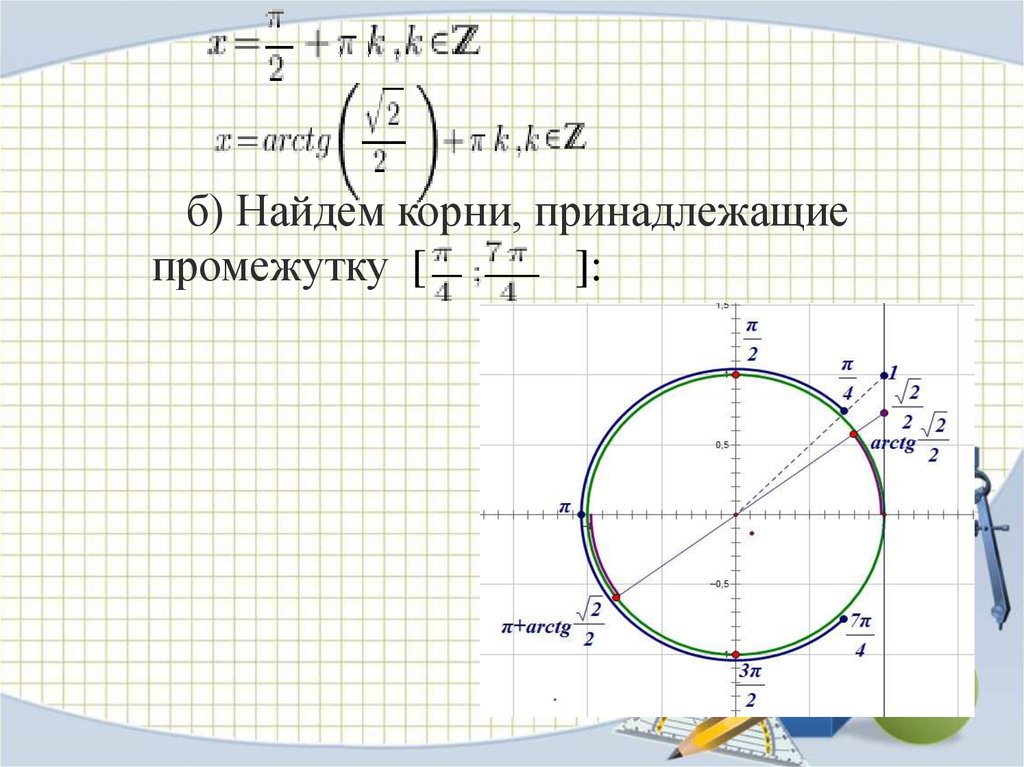
б) Найдем корни, принадлежащие
промежутку [
]:

18.

На рисунке красными точками обозначены
решения уравнения;
синей дугой обозначен промежуток, которому
принадлежат корни;
угловая величина сиреневой
дуги равна дуги равна
Двигаясь из точки , мы
встречаем на пути
,
Это и есть корни уравнения, принадлежащие
промежутку [
].

19.

Мы видим, что
корень
не
заданному промежутку.
Ответ: а)
б)
,
принадлежит
,

20. Способы отбора корней в тригонометрических уравнениях

Арифметический
Геометрический
Алгебраический
Функциональнографический

21.

Арифметический способ
перебор значений
целочисленного параметра
и вычисление корней.

22.

Найдите все корни уравнения sin 2 x cos x,
3
принадлежащие промежутку ; .
sin 2 x cos x;
cos x (2 sin x 1) 0;
cos x 0,
1
sin x ;
2
1) cos x 0
x n; n Z .
2
4
Если n=0,то
3
x ,
;
2 2
4
.
Если n=1,то
3 3
3
x
,
;
2
2
4
Если n=-1,то
x
2
,
3
;
2
4
.
.
Если n=-2,то
3
3
3
x
,
;
.
2
2
4

23.

1
2) sin x ,
2
x
6
2 n
или
5
x
2 n, n Z .
6
Если n=-1, то
11
11
3 или
x
,
;
6
6
4
x
7
7
3
,
;
.
6
6
4
Если n=0, то
x
6
,
3
;
6
4
5 5
3
x
,
; .
6
6
4
или
Если n=1, то
17 17
3
x
,
;
.
6
6
4
13 13
3 или
x
,
;
6
6
4
Ответ :
,
,
2 2 6
.

24.

Алгебраический способ
а) решение неравенства
относительно неизвестного
целочисленного параметра и
вычисление корней;
б) исследование уравнения с
двумя целочисленными
параметрами.

25. Решить уравнение

2 sin x 3 cos x 3 0.
2
Укажите корни,
принадлежащие отрезку 4 ;5 .

26.

2 sin x 3 cos x 3 0;
2
2 ( 1 c o s x ) 3 cos x 3 0;
2
2 2 cos x 3 cos x 3 0;
2
2 cos x 3 cos x 1 0;
2
2 cos x 3 cos x 1 0;
2

27.

2 cos x 3 cos x 1 0;
, ,n
n
22 ,nnn
n ZZ
Z.
32))1xx) x 2
1
33
2
cos x 2 ,
cos x 1;
x 3 2 n,
x 2 n, n Z .
13
x
.
3
x 4 .
n=2
2 5n , n5
,Zn; Z ;
4 4 1
2
n
54 , n; Z ;
43) x 32 n
3
1
, n5
Z ; Z ;
1 4 2 n 2 n5
4
,
n
4 23n 13
5, n Z ;
. Z;
32 xn 5 , n
1
1
3
2
1
1
, nZ ; Z ;
4 4 32 n2 n5 5 , n3
3 2 n 2 1 3, n Z ;
24 1 2n 2521 , n Z ;
3 32n 4 ,3n Z ;
3 n 2. 3
513 n 116 , n Z ;
1 6 n 2 6, n Z ;
6
3
1
2
n2 6 2.n 2 3 , n Z ;
нет значений.
Ответ :
2 n,
3
13
2 n, n Z ;
; 4 .
3

28.

Геометрический способ:
а) изображение корней на
тригонометрической окружности
с последующим их отбором на
заданном промежутке;
б) изображение корней на
координатной прямой с
последующим отбором с учетом
имеющихся ограничений.

29.

2 cos x 3 cos x 1 0;
2
Выполним отбор корней в
уравнении по
предыдущем
x
2
n
,
n
Z
;
4
другому
!
3
x 2 k , k Z .
Ответ :
53
y
1
7
13
3 3
3
04
2рад
-1
2 n , n Z ;
3
13
2 k , k Z ;
; 4 .
3
;5
0
0,5
1
5
11
333

30. Решить уравнение

2 sin x sin x cos x 3 cos x 0.
2
Укажите корни,
принадлежащие отрезку
2
3
;
2 2
.

31.

2 sin x sin x cos x 3 cos x 0.
2
2
2tg x tgx 3 0;
2
tgx 1,
О
д
н
о
р
о
д
н
о
е
у
р
а
в
н
е
н
и
е
Разделим
на
3
tgx ; cos x; cos x≠0.
2
2
2
x
n
,
n
Z
;
4
x arctg 3 k , k Z .
2

32.

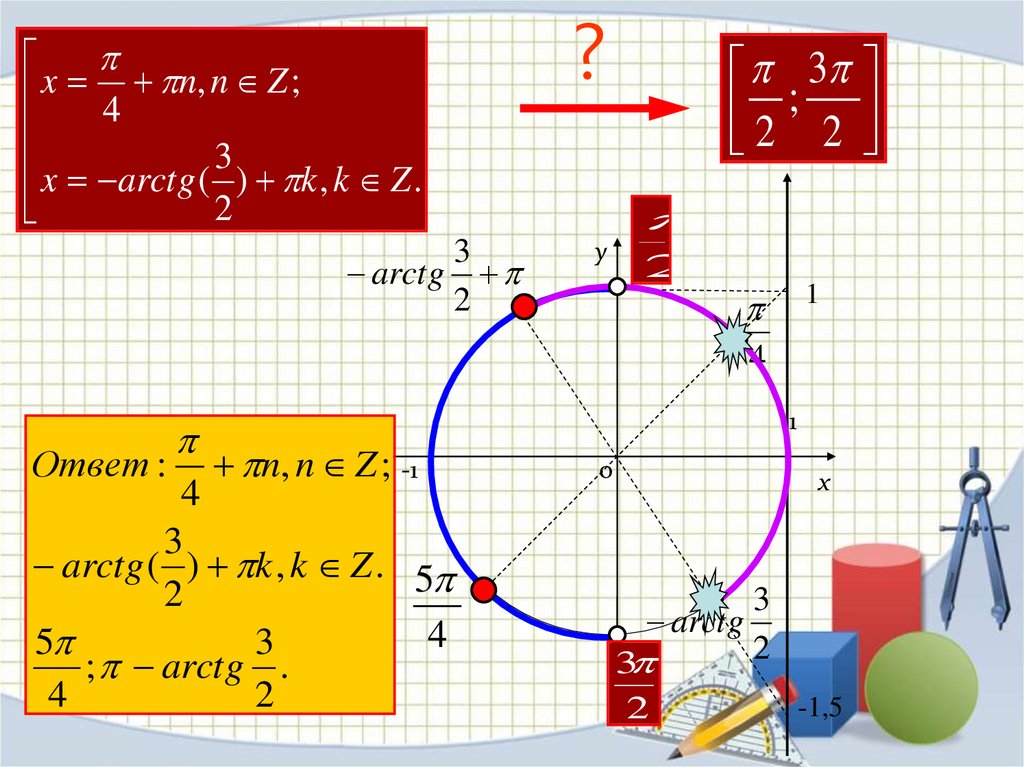
x 4 n, n Z ;
x arctg ( 3 ) k , k Z .
2
3
arctg
2
Ответ :
?
y
3
2 ; 2
2
4
1
1
n, n Z ; -1
4
3
arctg ( ) k , k Z . 5
2
4
5
3
; arctg .
4
2
0
x
3
arctg
2
3
2
-1,5

33. Отбор корней на координатной прямой.

x
cos
2 0.
x
sin
3
Решение :
x
cos 2 0,
sin x 0;
3
0
x 2 k , k Z ,
x 3 n, n Z .
3
5
x
T (cos ) 4 ,
2
x
T (sin ) 6 .
3
Наим. общий период :
Т общ 12 .
7
Ответ :
6 т, 6 т, т Z .
9
1 1
х

34.

Функционально-графический
способ
выбор корней с использованием
графика простейшей
тригонометрической функции.

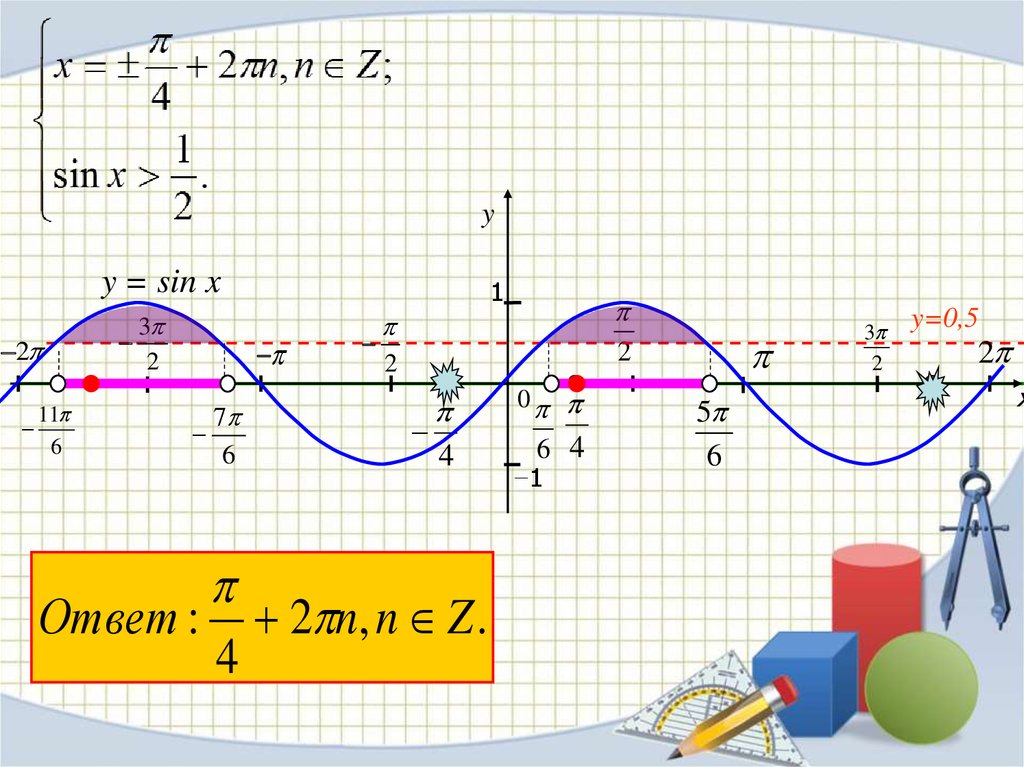
35. Решите уравнение

2
cos
x
,
2
1
sin x ;
2
2
1
2 sin x cos x 2 sin x cos x
2 0; sin x 2 ;
2 sin x 1
x
2 n, n Z ;
4
2
sin x 1 .
(cos x
) (2 sin x 1)
2
2
2
sin 2 x 2 sin x cos x
2 0;
2 sin x 1
2 sin x 1
0;

36.

y
y = sin x
2
11
6
3
2
1
7
6
2
2
4
Ответ : 2 n, n Z .
4
6 4
0
−1
5
6
3
2
y=0,5
2
x

37. Для успешного решения задач типа 13 необходимо знать и уметь:

• 1. Понимать, уметь "читать" числовую окружность. При
этом использовать не только градусную меру углов, но и
радианную.
• 2. Знать определения синуса, косинуса, тангенса и
котангенса.
• 3. Знать таблицу значений тригонометрических функций
основных аргументов и аргументов первой четверти.
Применяя числовую окружность, уметь находить значения
тригонометрических функций аргументов других четвертей.
• 4. Используя числовую окружность, уметь читать и
применять свойства тригонометрических функций (знаки,
четность, периодичность, формулы симметричных точек).

38. Для успешного решения задач типа 13 необходимо знать и уметь:

• 5. Уметь решать простейшие тригонометрические уравнения
по формулам и с использованием числовой окружности.
• 6. Уметь решать простейшие тригонометрические
неравенства, используя числовую окружность.
• 7. Уметь выбирать корни согласно условию задачи или по
виду уравнения, для чего уметь находить области
определения различных функций, заданных формулой.
• 8. Знать основные тригонометрические формулы, формулы
двойных аргументов.
• 9. Знать основные методы решения тригонометрических
уравнений (замена, разложение на множители).

39. Работать над темой рекомендуется в соответствии со следующим планом:

Числовая окружность.
Числовая окружность в координатной плоскости.
Градусная и радианная мера угла.
Определение, значения и свойства синуса, косинуса, тангенса и
котангенса.
Обратные тригонометрические функции и их свойства.
Простейшие тригонометрические уравнения.
Простейшие тригонометрические неравенства.
Выбор корней при решении тригонометрических уравнений.
Методы решения тригонометрических уравнений.
Системы тригонометрических уравнений.
Примеры решения задания 13 из экзаменационных вариантов.