Дифференциальное уравнение энергии трехмерной нестационарной теплопроводности твердых тел

1. ТЕПЛОМАССООБМЕН

Дифференциальное уравнение
энергии трехмерной
нестационарной
теплопроводности твердых тел
Вопрос 1
2016 год

2.

• Для определения количества теплоты, проходящее за время dτ
через изотермическую поверхность dF твердого тела
конечных размеров, необходимо интегрировать уравнение
Фурье (1) по площади F и времени τ, т.е. знать температурное
поле внутри рассматриваемого тела.
t
QT dF d .
n
(1)
– закон Фурье
• Для решения этой задачи выводится дифференциальное
уравнение теплопроводности при следующих допущениях:
тело однородно;
изотропно;
физические параметры его постоянны.

3.

• Для определения количества теплоты, проходящее за время dτ
через изотермическую поверхность dF твердого тела
конечных размеров, необходимо интегрировать уравнение
Фурье (1) по площади F и времени τ, т.е. знать температурное
поле внутри рассматриваемого тела.
t
QT dF d .
n
(1)
– закон Фурье
• Для решения этой задачи выводится дифференциальное
уравнение теплопроводности при следующих допущениях:
тело однородно;
изотропно;
физические параметры его постоянны.

4.

• В соответствии с законом сохранения энергии количество
теплоты dQT1, введенный в элементарный объем тела извне за
время dτ путем теплопроводности, плюс количество теплоты,
выделяемое внутренними источниками dQT2, равно
изменению внутренней энергии вещества dQT = dU:
dQT dQT 1 dQT 2 .
Для определения членов этого уравнения в
декартовой системе координат выделим
элементарный параллелепипед со сторонами
dx, dy, dz.
Подводимая теплота – dQx, dQy, dQz;
отводимая теплота – dQx+dx, dQy+dy,
dQz+dz.
(2)

5.

Тогда для грани dy dz, по закону Фурье
(1), запишем:
t
dQx dy dz d .
x
dQx dx
t t
dx
x x x
t 2t
dy dz d 2 dx
x x
dy dz d .
Разность этих величин представляет собой количество теплоты,
оставшейся в параллелепипеде:
dQTx1 dQx dQx dx
2t
2 dx dy dz d .
x

6.

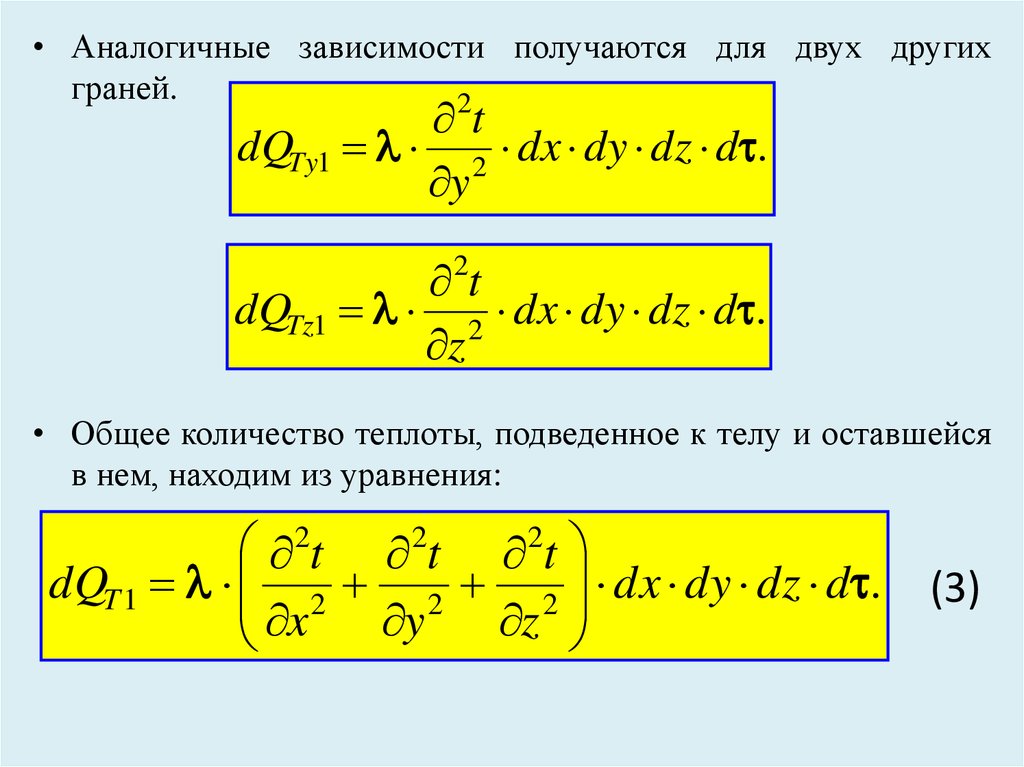
• Аналогичные зависимости получаются для двух других
граней.
2
t
dQTy1 2 dx dy dz d .
y
t
dQTz1 2 dx dy dz d .
z
2
• Общее количество теплоты, подведенное к телу и оставшейся
в нем, находим из уравнения:
2t 2t 2t
dQT 1 2 2 2 dx dy dz d .
y
z
x
(3)

7.

• Обозначим через qυ удельное количество выделяемой теплоты
в единице объема в единицу времени (мощность внутренних
источников теплоты), Вт/м3, то можно записать
dQT 2 q dx dy dz d .
(4)
• Изменение внутренней энергии тела за время dτ
t
dQT c dx dy dz d .
(5)
• Подставим выражения (3), (4) и (5) в уравнение (2), после
преобразований получим следующее выражение:
2
2
2
t
t t t
c 2 2 2 q .
y
z
x

8.

• Величина
a
c
называется коэффициентом
температуропроводности.
• Общее дифференциальное уравнение теплопроводности
Фурье в декартовой системе координат
2
2
2
t
t t t q
q
2
a 2 2 2
a t , (6)
c
y
z c
x
где дифференциальный оператор Лапласа равен
2
2
2
t t t
2
t 2 2 2 .
y
z
x
(7)

9.

• Уравнение (6) устанавливает связь между временным и
пространственным изменением температуры в любой точке
тела, в которой происходит процесс теплопроводности.