Similar presentations:
Графический способ решения систем уравнений
1.
Открытый урок по математике и информатике.Авторы:
Сиверенко Елена Васильевна – учитель математики
Левоник Светлана Викторовна – учитель математики
и информатики
2.
• Обобщить графический способрешения систем уравнений;
• Сформировать умения графически решать системы уравнений второй степени, привлекая
известные учащимся графики;
• Дать наглядные представления,
что система двух уравнений с
двумя переменными второй
степени может иметь от одного
до четырех решений, или не
иметь решений.
3.
Элементарные функции и их графики:• Линейная функция: y=kx+b,
график – прямая.
• Прямая пропорциональность: y=kx,
график – прямая, проходящая через начало координат.
• Постоянная функция: y=b,
график – прямая, проходящая через точку с координатами
(0;b), параллельно оси абсцисс.
• Обратная пропорциональность: y=k/x,
график – гипербола.
• Квадратичная функция: y=ax2+bx+c,
график – парабола.
• Функция вида: y=x3,
график – кубическая парабола.
• Функция вида: y=√x,
график – «ветвь» параболы, расположенная в I четверти.
Уравнение с двумя переменными:
• Уравнение окружности: (x - xo)2+(y - yo)2=R2,
график – окружность с центром в точке (xo; yo) и
радиусом R.
4.
1. Выразите переменную у через переменную х иопределите, что представляет собой график
уравнения:
у х 0;
6 х 2 у 8;
5 х у 2;
ху 3;
х 2 у 4 0;
2
2
х у 1;
у 4 0.
у х;
у 3 х 4;
у 5 х 2;
у 3 ;
х
у х 2 4;
у 1 х ;
2
у 4.
5.
2. Определите координаты центра и радиусаокружности:
0;0 R 4;
2
2
х 7 у 2 3; 7;2 R 3;
2
2
х 2 х у 0.
1;0 R 1.
х у 16;
2
2
6.
Графическое решение системы уравнений с двумяпеременными сводится к отысканию координат общих
точек графиков уравнений.
Графиком уравнения с двумя переменными
называется множество точек координатной
плоскости, координаты которых обращают
уравнение в верное равенство.
Этапы решения:
• Постройте графики каждого уравнения системы в
координатной плоскости.
• Найдите координаты общих точек этих графиков.
• Запишите ответ.
Замечание. Графический способ позволяет
решить систему лишь приближенно,
поэтому для получения точного ответа
полученные решения следует проверить
подстановкой в условие, или выбрать
другой способ решения.
7.
Решите графически систему уравнений:x у 2;
2
2
x y 4.
1. x+y=2 y=2–x - линейная
функция, график – прямая;
2. x2+y2=4 – уравнение
окружности, с центром в
(0;0) и R=2;
y
3. А(0;2) и В(2;0) – точки
пересечения графиков.
4
A(0;2)
2
B(2;0)
-5
5
x
-2
-4
-6
Ответ: (0;2), (0;2).
8.
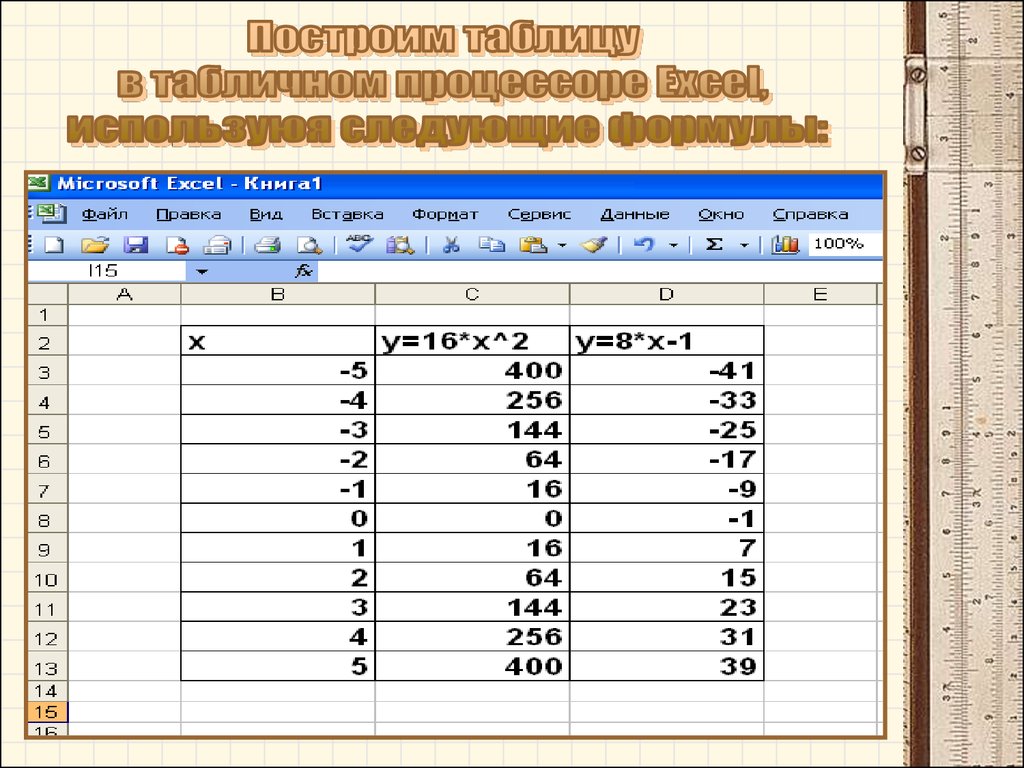
Рассмотрим решениеследующей системы уравнений:
y 16 x 0
y 16 x
y
8
x
1
y
8
x
1
2
2
9.
10.
Решение ситемы уравнений-6
-4
-2
450
400
350
300
250
200
150
100
50
0
-50 0
-100
y=16*x^2
y=8*x-1
2
4
6
Ответ: (0;0).
11.
y xxy 4
y x 2
2.
y x
3
1.
y x 4
xy 2
2
3.
12.
y x31.
xy 4
x
Решение системы уравнений
150
100
50
0
-6
-4
-2
-50
0
2
4
6
-100
-150
y=x^3
y=-4/x
Ответ: решений нет.
y=x^3
y=-4/x
-5
-125
0,8
-4
-64
1
-3
-27
1,333333333
-2
-8
2
-1
-1
4
-0,5
-0,125
8
-0,2
-0,008
20
0
0
0,2
0,008
-20
0,5
0,125
-8
1
1
-4
2
8
-2
3
27
1,333333333
4
64
-1
5
125
-0,8
13.
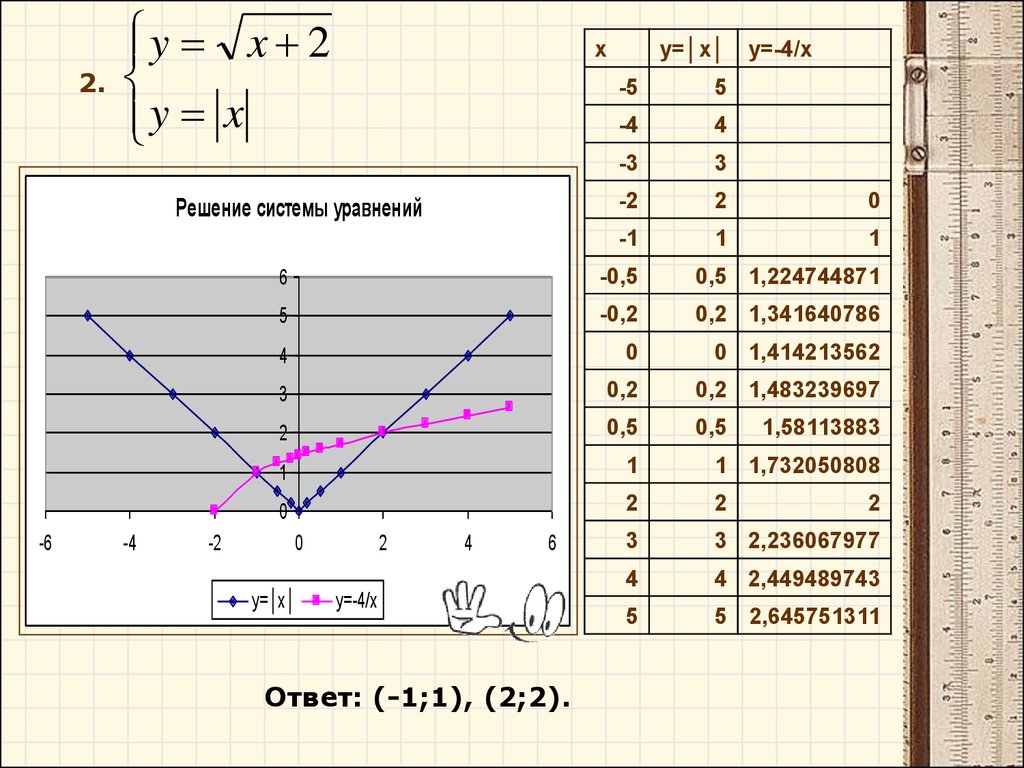
2.y x 2
y x
x
Решение системы уравнений
-6
-4
-2
y=│x│ y=-4/x
-5
5
-4
4
-3
3
-2
2
0
-1
1
1
6
-0,5
0,5 1,224744871
5
-0,2
0,2 1,341640786
4
0
0 1,414213562
3
0,2
0,2 1,483239697
2
0,5
0,5
1
1
1 1,732050808
0
2
2
3
3 2,236067977
4
4 2,449489743
5
5 2,645751311
0
y=│x│
2
4
6
y=-4/x
Ответ: (-1;1), (2;2).
1,58113883
2
14.
3.y x2 4
xy 2
x
y=-x^2+4
-5
-21
-0,4
-4
-12
-0,5
-3
Решение системы уравнений
0
-1
-1
3
-2
-0,5
3,75
-4
-0,2
3,96
-10
0
4
0,2
3,96
10
-10
0,5
3,75
4
-15
1
3
2
-20
2
0
1
-25
3
-5
0,666666667
4
-12
0,5
5
-21
0,4
10
5
0
-4
-2
-5 -0,666666667
-2
15
-6
y=2/x
-5 0
y=-x^2+4
2
y=2/x
4
6
Ответ: (-2,2;-0,9), (0,5;3,7), (1,8;1,1).
15.
П. 12 учебника;№238,
№241(а), До скорой
встречи на
№242(а), следующем
уроке!
№243.













 mathematics
mathematics informatics
informatics








