Calculus++. Find the radius of convergence for 3n

1.

Calculus++ Light

2.

Question 3. Find the radius of convergence for
3n
3
2 (n!) n
the power series
x .
1
(3n)!
a)
n 1
an
27
Solution: We have to find R lim
3
n a
n 1
b)
3n
3
2 (n!)
(3(n 1))!
2
lim
c) 1
n (3n)! 23( n 1) (( n 1)! ) 3
27
1 (3n 3)!
d)
lim
8
3
3
n (3n)! 2 ( n 1)
1
e
)
(3n 1)(3n 2)(3n 3) 27
8
lim
.
3
3
n
8
2 (n 1)

3.

Answers to Questions from Light #8:
Infinite Series II
Question 1: S1 and S4 are convergent
L1 0, L4 ;
S2 and S3 are divergent L2 43 , L3 2.
Question 2: c ) 53
2
3
Question 4: b) III only

4.

Calculus++
Infinite Series

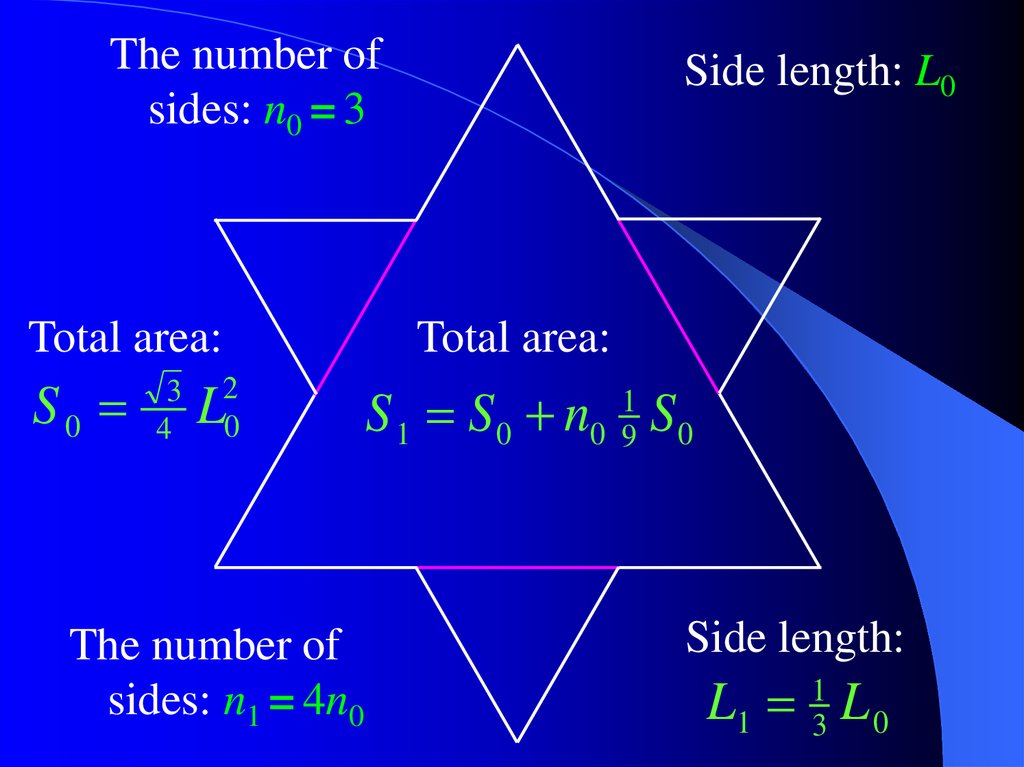
5. Picture of the Week

Snowflake Curve
We construct a snowflake curve step by step,
starting from an equilateral triangle.
At each step we count:
a) the number of straight-line segments in
the curve,
b) the total length of all segments (perimeter
of the curve),
c) the total area bounded by the curve.

6.

The number of
sides: n0 = 3
Total area:
S0
3
4
Side length: L0
Total area:
2
0
L
The number of
sides: n1 = 4n0
S 1 S 0 n0 19 S 0
Side length:
L1 L 0
1
3

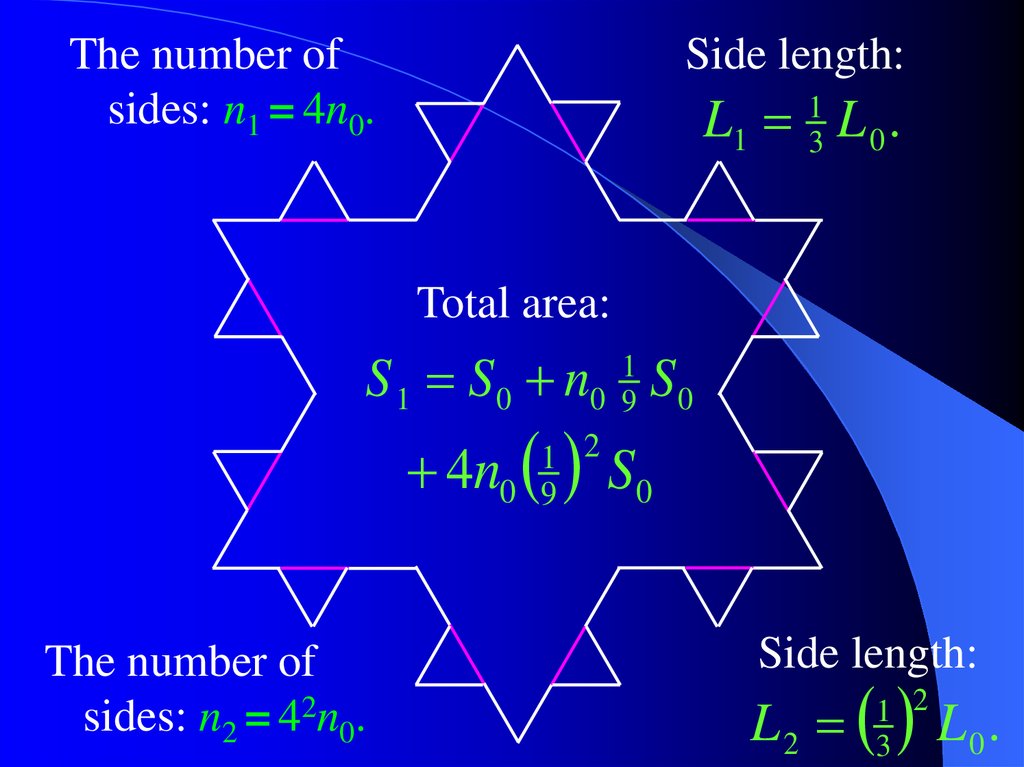
7.

The number of
sides: n1 = 4n0.
Side length:
L1 L 0 .
1
3
Total area:
S 1 S 0 n0 19 S 0
4n
1 2
0 9
The number of
sides: n2 = 42n0.
S0
Side length:
L2
L0.
1 2
3

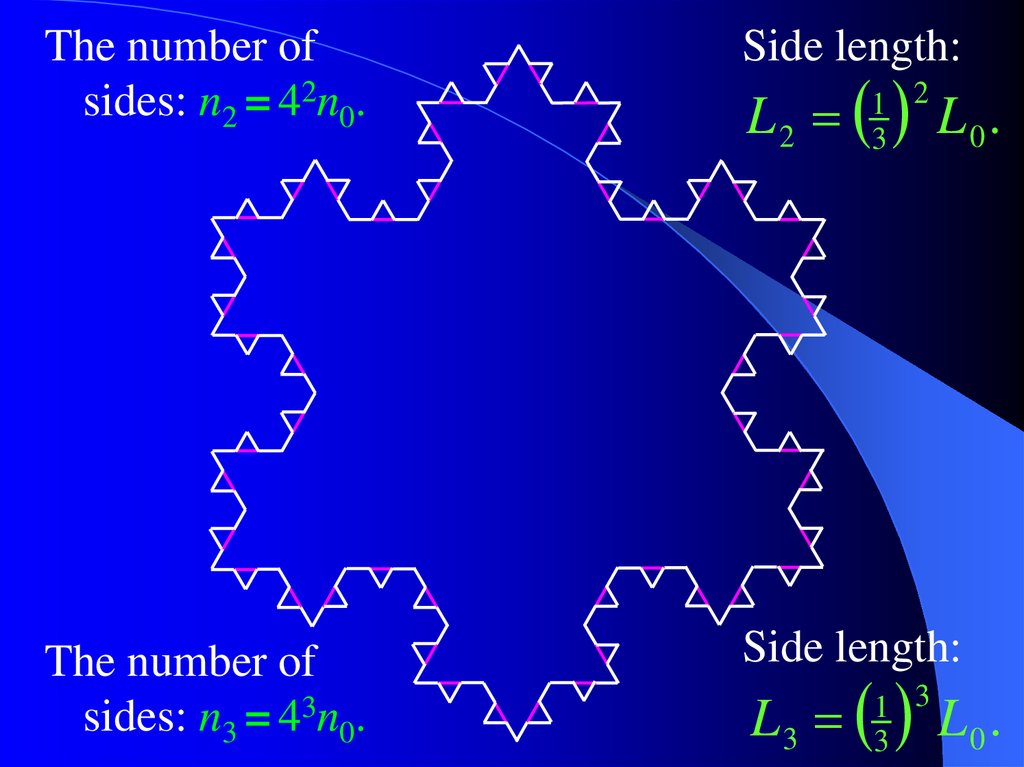
8.

The number of
sides: n2 = 42n0.
Side length:
The number of
sides: n3 = 43n0.
Side length:
L2
1 2
3
L3
1 3
3
L0.
L0.

9.

Total Perimeter after n steps
n
4
Pn L0 as n
3
Total Area after n steps
2
n
1 4 4
4
S n S0 n0 S0 1
9 9 9
9
1
1
8
lim Sn S0 n0 S0
S
0
4
n
9 1 9 5

10.

Question 1 (December 2011 Exam, Q9).
Determine the convergence set for the series
n
x
.
2n
n 1 1 x
a) ( 1,1) b) ( , 1) and (1, )
c) ( , 1), ( 1,1) and (1, )
d ) ( , ) e) [ 1,1]
Solution: Let’s try your favourite values x 0
and x 1. For x 0 we have
n
x
Converges.
0
0
.
2n
n 1 1 x
n 1

11.

n
x
1
For x 1 we obtain
.
2n
2
1
x
n
1
n
1
Diverges.
a) ( 1,1) b) ( , 1) and (1, )
c) ( , 1), ( 1,1) and (1, )
Converges
d ) ( , ) e) [ 1,1]
n
n
x
2
Let’s try x = 2 now.
.
2n
n
n 1 1 x
n 1 1 4
n
1
2
Limit comparison test: an
, bn n
n
n
n
2
1 4
an
2 2
lim
lim
1. Answer : c).
n
n b
n 1 4
n

12.

The limit comparison test.
a
n 1
n
and
b
n 1
n
Suppose that
are series with positive terms.
an
If lim
c where c is a finite positive
n b
n
number, then either both series converge, or
both diverge.
If
b
n 1
n
converges and c = 0, then
converges as well.
a
n 1
n
an
If bn diverges and lim
then an
n b
n
n 1
n 1
diverges as well.

13.

Question 2. Which of the following series are
convergent?
1
1
III.
I. sin k II. 2
3k 1
2
k 1
k 1
k 1 k 4k 5
a. I only b. II only c. III only
d. I and II only e. II and III only
1
Solution: For series III ak
.
3k 1
ak
k
1
1
Consider bk . Then lim
lim
.
k b
k 3k 1
k
3
k
1
Since diverges, series III diverges as well.
k
k 1

14.

1
For series II ak 2
.
k 4k 5
1
Consider bk 2 .
2
k
ak
k
lim 2
Then lim
1
.
k b
k k 4 k 5
k
1
Since the series 2 converges,
k 1 k
1
the series 2
converges as well.
k 1 k 4k 5
a. I only b. II only c. III only
d. I and II only e. II and III only

15.

For series I ak sin k .
2
1
Consider bk k . sin( y ) y, if y is small
k
2
ak
sin 2
Then lim
lim
.
k
k
bk
k
2
1
Since the geometric series k converges
k 1 2
the series sin k converges as well.
2
k 1
a. I only b. II only c. III only
d. I and II only e. II and III only

16.

For any series
a
n 1
n
with positive and
negative terms we can obtain a positive
series by taking absolute values:
a
n 1
n
n
.
( 1)
For example, for the series
and
n
n 1
cos n
the
series
of
absolute
values
are
2
n 1 n
| cos n |
1
given by
and
.
2
n
n
n 1
n 1

17.

If the series of absolute value converges, then
an converges
we say that the series
n 1
absolutely.
Using the Cauchy criterion for convergence of
partial sums Sn one can show that if the
series
a
n 1
n
converges, then the series
converges as well.
a
n 1
n

18.

( 1)
Example. 2 .
n 1 n
n
1
The series of absolute values 2
n 1 n
converges.
n
( 1)
Therefore the series 2
n 1 n
converges absolutely.
If
a
a diverges,
then we say that the series a
n 1
n
converges, but
n 1
converges conditionally.
n
n 1
n

19.

A test for convergence of alternating series
where
(
1
)
b
,
n
n
bn 0.
n 1
If 1) lim bn 0,
n
2) the sequence bn is non-increasing,
then the series
( 1) b
n
n 1
n
converges.

20.

Question 3. Which of the following series is
conditionally convergent?
n 1
I. ( 1)
n 2
n 1
n 1
II. ( 1) 2
n 2
n 1
n n 1
III. ( 1) 3
n 2
n 1
n
n
a. I only b. II only c. III only
d. II and III only
e. I and III only
n 1
Solution: For series I: an ( 1)
,
n 2
n
and the sequence an does not converge to 0.
Thus, the necessary condition of convergence
is not satisfied. Hence, series I diverges.

21.

n 1
For series III: an ( 1) 3
,
n 2
n 1
and an 3
.
Answer : b) II only.
n 2
1
Let’s compare |an| with bn 2 .
2
n
an
( n 1)n
lim
lim 3
1.
n b
n n 2
n
1
The series bn 2 converges.
n 1
n 1 n
n
Hence, series III converges absolutely.
a. I only b. II only c. III only
d. II and III only
e. I and III only

22.

n 1
For series II: an ( 1) 2
,
n 2
n 1
and an 2
.
n 2
1
Let’s compare |an| with bn .
n
an
(n 1)n
lim
lim 2
1
.
n b
n n 2
n
1
The series bn
diverges.
n
n 1
n
1
Hence, the series an diverges as well.
n
n 1

23.

To show that series II converges we have to
show that:
n 1
1) lim 2
0,
n n 2
correct
n 1
3) The sequence 2
is non-increasing,
n 2 for n = 1,2,3…
x 1
Consider the function f ( x ) 2
.
2
x
2
2 2x x
f ( x)
.
2
2
Solutions:
( x 2)
x1 1 3
2
f ( x ) 0 2 2 x x 0
x 2 1 3
f ( x) 0
for
x 1 3.

24.

x 1
The function f ( x ) 2
x 2
decreases on the interval ( 1 3 ; ).
n 1
Hence, the sequence
decreases for n =
2
n 2 1,2,3…
n 1
3) The sequence 2
is non-increasing,
n 2 for n = 1,2,3…
correct
n 1
Thus, the series ( 1) 2
n 2
n 1
n
converges conditionally.