Similar presentations:
算法设计与分
1.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
Ž{ O†©Û
101ù Ž{Vã
O•{
˜‡«~
‘ g
éX‡"
4öÅ
Ç
Œë°¯ŒÆ <óœUÆ
January 26, 2021
2.
Y擌
䕏嚎
摿
呀
Y
8¹
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
1
¯K¦)
2
Ž{Ä:
3
Ž{ O
4
˜‡«~
5
‘ g
6
éX‡"
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Ä •{
3.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
¯K¦)†OŽÅŽ{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
k¯KÒI‡¦)
4.
Y擌
䕏嚎
摿
呀
Y
¯K¦)†OŽÅŽ{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
k¯KÒI‡¦)
OŽÅŽ{
OŽÅŽ{ O†©Û
•¯K¦)Jø˜«k
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
[2]
廜
5.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
OŽÅŽ{¦)¯K Ú½
– 1. £ã¯K
I5¿µ
™²\ó
¯K
©Lˆ´Ä²(º
Jø = &Eº
Ž{Ä:
´Äkd3 &Eº
O•{
ù &EkŸo^º
˜‡«~
‘ g
éX‡"
‡¦
Ÿo(Jº
®²Š = b½º„I= b½º
¥m(Jk=
¹º
º=
•ª(JXÛµdº
¥m(JI‡P¹§=
ÃIP
6.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
OŽÅŽ{¦)¯K Ú½
– 1. £ã¯K
I5¿µ
™²\ó
¯K
©Lˆ´Ä²(º
Jø = &Eº
Ž{Ä:
´Äkd3 &Eº
O•{
ù &EkŸo^º
˜‡«~
‘ g
éX‡"
‡¦
Ÿo(Jº
®²Š = b½º„I= b½º
¥m(Jk=
¹º
º=
•ª(JXÛµdº
¥m(JI‡P¹§=
ÃIP
7.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
OŽÅŽ{¦)¯K Ú½
– 1. £ã¯K
I5¿µ
™²\ó
¯K
©Lˆ´Ä²(º
Jø = &Eº
Ž{Ä:
´Äkd3 &Eº
O•{
ù &EkŸo^º
˜‡«~
‘ g
éX‡"
‡¦
Ÿo(Jº
®²Š = b½º„I= b½º
¥m(Jk=
¹º
º=
•ª(JXÛµdº
¥m(JI‡P¹§=
ÃIP
8.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
OŽÅŽ{¦)¯K Ú½
– 1. £ã¯K
I5¿µ
™²\ó
¯K
©Lˆ´Ä²(º
Jø = &Eº
Ž{Ä:
´Äkd3 &Eº
O•{
ù &EkŸo^º
˜‡«~
‘ g
éX‡"
‡¦
Ÿo(Jº
®²Š = b½º„I= b½º
¥m(Jk=
¹º
º=
•ª(JXÛµdº
¥m(JI‡P¹§=
ÃIP
9.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
OŽÅŽ{¦)¯K Ú½
– 1. £ã¯K
I5¿µ
™²\ó
¯K
©Lˆ´Ä²(º
Jø = &Eº
Ž{Ä:
´Äkd3 &Eº
O•{
ù &EkŸo^º
˜‡«~
‘ g
éX‡"
‡¦
Ÿo(Jº
®²Š = b½º„I= b½º
¥m(Jk=
¹º
º=
•ª(JXÛµdº
¥m(JI‡P¹§=
ÃIP
10.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
OŽÅŽ{¦)¯K Ú½
– 1. £ã¯K
I5¿µ
™²\ó
¯K
©Lˆ´Ä²(º
Jø = &Eº
Ž{Ä:
´Äkd3 &Eº
O•{
ù &EkŸo^º
˜‡«~
‘ g
éX‡"
‡¦
Ÿo(Jº
®²Š = b½º„I= b½º
¥m(Jk=
¹º
º=
•ª(JXÛµdº
¥m(JI‡P¹§=
ÃIP
11.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
OŽÅŽ{¦)¯K Ú½
– 1. £ã¯K
I5¿µ
™²\ó
¯K
©Lˆ´Ä²(º
Jø = &Eº
Ž{Ä:
´Äkd3 &Eº
O•{
ù &EkŸo^º
˜‡«~
‘ g
éX‡"
‡¦
Ÿo(Jº
®²Š = b½º„I= b½º
¥m(Jk=
¹º
º=
•ª(JXÛµdº
¥m(JI‡P¹§=
ÃIP
12.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
OŽÅŽ{¦)¯K Ú½
– 1. £ã¯K
I5¿µ
™²\ó
¯K
©Lˆ´Ä²(º
Jø = &Eº
Ž{Ä:
´Äkd3 &Eº
O•{
ù &EkŸo^º
˜‡«~
‘ g
éX‡"
‡¦
Ÿo(Jº
®²Š = b½º„I= b½º
¥m(Jk=
¹º
º=
•ª(JXÛµdº
¥m(JI‡P¹§=
ÃIP
13.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 2. ïáêÆ .
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
I5¿µ
¯K¦)
•·Üud¯K êÆ .´Ÿoº
Ž{Ä:
´Äk®²)û
O•{
aq¯KŒ/•º
˜‡«~
.¥ ÎҴIJ(½Âº
‘ g
.´ÄŒ±=†!{zº
éX‡"
.´Ä « Ÿo5ÆÚá5º
14.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 2. ïáêÆ .
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
I5¿µ
¯K¦)
•·Üud¯K êÆ .´Ÿoº
Ž{Ä:
´Äk®²)û
O•{
aq¯KŒ/•º
˜‡«~
.¥ ÎҴIJ(½Âº
‘ g
.´ÄŒ±=†!{zº
éX‡"
.´Ä « Ÿo5ÆÚá5º
15.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 2. ïáêÆ .
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
I5¿µ
¯K¦)
•·Üud¯K êÆ .´Ÿoº
Ž{Ä:
´Äk®²)û
O•{
aq¯KŒ/•º
˜‡«~
.¥ ÎҴIJ(½Âº
‘ g
.´ÄŒ±=†!{zº
éX‡"
.´Ä « Ÿo5ÆÚá5º
16.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 2. ïáêÆ .
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
I5¿µ
¯K¦)
•·Üud¯K êÆ .´Ÿoº
Ž{Ä:
´Äk®²)û
O•{
aq¯KŒ/•º
˜‡«~
.¥ ÎҴIJ(½Âº
‘ g
.´ÄŒ±=†!{zº
éX‡"
.´Ä « Ÿo5ÆÚá5º
17.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 2. ïáêÆ .
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
I5¿µ
¯K¦)
•·Üud¯K êÆ .´Ÿoº
Ž{Ä:
´Äk®²)û
O•{
aq¯KŒ/•º
˜‡«~
.¥ ÎҴIJ(½Âº
‘ g
.´ÄŒ±=†!{zº
éX‡"
.´Ä « Ÿo5ÆÚá5º
18.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 3. Ž{ O Ä ( †E|
Ä ( kµ
^S
Ì‚
^‡
üÑ̇kµ
S“
öå
%
©£
Ä 5y
‘Å
ã|¢
g,éu
OŽÅŽ{
Ä ( †E|
‘§ -:œ
òÏLäN«~5©Où)"
19.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 3. Ž{ O Ä ( †E|
Ä ( kµ
^S
Ì‚
^‡
üÑ̇kµ
S“
öå
%
©£
Ä 5y
‘Å
ã|¢
g,éu
OŽÅŽ{
Ä ( †E|
‘§ -:œ
òÏLäN«~5©Où)"
20.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 3. Ž{ O Ä ( †E|
Ä ( kµ
^S
Ì‚
^‡
üÑ̇kµ
S“
öå
%
©£
Ä 5y
‘Å
ã|¢
g,éu
OŽÅŽ{
Ä ( †E|
‘§ -:œ
òÏLäN«~5©Où)"
21.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 3. Ž{ O Ä ( †E|
Ä ( kµ
^S
Ì‚
^‡
üÑ̇kµ
S“
öå
%
©£
Ä 5y
‘Å
ã|¢
g,éu
OŽÅŽ{
Ä ( †E|
‘§ -:œ
òÏLäN«~5©Où)"
22.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 3. Ž{ O Ä ( †E|
Ä ( kµ
^S
Ì‚
^‡
üÑ̇kµ
S“
öå
%
©£
Ä 5y
‘Å
ã|¢
g,éu
OŽÅŽ{
Ä ( †E|
‘§ -:œ
òÏLäN«~5©Où)"
23.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 3. Ž{ O Ä ( †E|
Ä ( kµ
^S
Ì‚
^‡
üÑ̇kµ
S“
öå
%
©£
Ä 5y
‘Å
ã|¢
g,éu
OŽÅŽ{
Ä ( †E|
‘§ -:œ
òÏLäN«~5©Où)"
24.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 3. Ž{ O Ä ( †E|
Ä ( kµ
^S
Ì‚
^‡
üÑ̇kµ
S“
öå
%
©£
Ä 5y
‘Å
ã|¢
g,éu
OŽÅŽ{
Ä ( †E|
‘§ -:œ
òÏLäN«~5©Où)"
25.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 3. Ž{ O Ä ( †E|
Ä ( kµ
^S
Ì‚
^‡
üÑ̇kµ
S“
öå
%
©£
Ä 5y
‘Å
ã|¢
g,éu
OŽÅŽ{
Ä ( †E|
‘§ -:œ
òÏLäN«~5©Où)"
26.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 3. Ž{ O Ä ( †E|
Ä ( kµ
^S
Ì‚
^‡
üÑ̇kµ
S“
öå
%
©£
Ä 5y
‘Å
ã|¢
g,éu
OŽÅŽ{
Ä ( †E|
‘§ -:œ
òÏLäN«~5©Où)"
27.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 3. Ž{ O Ä ( †E|
Ä ( kµ
^S
Ì‚
^‡
üÑ̇kµ
S“
öå
%
©£
Ä 5y
‘Å
ã|¢
g,éu
OŽÅŽ{
Ä ( †E|
‘§ -:œ
òÏLäN«~5©Où)"
28.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 3. Ž{ O Ä ( †E|
Ä ( kµ
^S
Ì‚
^‡
üÑ̇kµ
S“
öå
%
©£
Ä 5y
‘Å
ã|¢
g,éu
OŽÅŽ{
Ä ( †E|
‘§ -:œ
òÏLäN«~5©Où)"
29.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 4. Ž{©Û
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
̇kµ
Ž{Ä:
(5
O•{
Âñ5
˜‡«~
‘ g
éX‡"
-½5
E,Ý
30.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 4. Ž{©Û
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
̇kµ
Ž{Ä:
(5
O•{
Âñ5
˜‡«~
‘ g
éX‡"
-½5
E,Ý
31.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 4. Ž{©Û
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
̇kµ
Ž{Ä:
(5
O•{
Âñ5
˜‡«~
‘ g
éX‡"
-½5
E,Ý
32.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 4. Ž{©Û
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
̇kµ
Ž{Ä:
(5
O•{
Âñ5
˜‡«~
‘ g
éX‡"
-½5
E,Ý
33.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
̇kµ
6§ã
Ýã(I.NassiÚB.Sneidermanu² 6§ã– N-Sã)
PADã(Problem Analysis Diagram)
–è
34.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
̇kµ
6§ã
Ýã(I.NassiÚB.Sneidermanu² 6§ã– N-Sã)
PADã(Problem Analysis Diagram)
–è
35.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
̇kµ
6§ã
Ýã(I.NassiÚB.Sneidermanu² 6§ã– N-Sã)
PADã(Problem Analysis Diagram)
–è
36.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
̇kµ
6§ã
Ýã(I.NassiÚB.Sneidermanu² 6§ã– N-Sã)
PADã(Problem Analysis Diagram)
–è
37.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ6§ã
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
m©
M = 0, N = 0, i = 1
)0 ∼ 1ƒm ü‡‘Åê©OD‰xi , yi
Ž{Ä:
x2 + y 2 ≤ 1
O•{
Ä
´
˜‡«~
M =M +1
‘ g
éX‡"
i=i+1
Ä
i > 1000
ÑÑM, N
(å
N =N +1
38.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ6§ã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
Bu•ÄŽ{
››6§"
":µ
¬y©Ø²w¶
êâ( ز("
39.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ6§ã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
Bu•ÄŽ{
››6§"
":µ
¬y©Ø²w¶
êâ( ز("
40.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ6§ã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
Bu•ÄŽ{
››6§"
":µ
¬y©Ø²w¶
êâ( ز("
41.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ6§ã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
Bu•ÄŽ{
››6§"
":µ
¬y©Ø²w¶
êâ( ز("
42.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ6§ã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
Bu•ÄŽ{
››6§"
":µ
¬y©Ø²w¶
êâ( ز("
43.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µÝã
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
第一任务
第二任务
¹
¯K¦)
第三任务
Ž{Ä:
顺序
条件
F
ELSE
部分
T
THEN
部分
条件
O•{
˜‡«~
循环条件
‘ g
éX‡"
DO-WHILE
部分
REPEAT
-UNTIL
值1
值2
...
值n
部分
CASE
CASE
部分
...
CASE
部分
循环条件
循环
选择
部分
44.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µÝã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
gar¶
i@²("
":µ
Ø´*¿"
45.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µÝã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
gar¶
i@²("
":µ
Ø´*¿"
46.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µÝã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
gar¶
i@²("
":µ
Ø´*¿"
47.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µÝã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
gar¶
i@²("
":µ
Ø´*¿"
48.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µÝã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
gar¶
i@²("
":µ
Ø´*¿"
49.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µPADã
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
P1
P2
P1
while
条件
P
C
P2
¯K¦)
Ž{Ä:
(a) 顺序
(b) while循环
(c) if选择
O•{
P1
˜‡«~
‘ g
éX‡"
(d) 语句标号
until
条件
L1
P
X=
P2
L2
Ln
def
(e) 定义
Pn
(f) until循环
(g) case多分支
50.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µPADã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
gar¶
i@²(¶
6§˜ß"
":µ
Ø´±›"
51.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µPADã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
gar¶
i@²(¶
6§˜ß"
":µ
Ø´±›"
52.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µPADã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
gar¶
i@²(¶
6§˜ß"
":µ
Ø´±›"
53.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µPADã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
gar¶
i@²(¶
6§˜ß"
":µ
Ø´±›"
54.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µPADã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
gar¶
i@²(¶
6§˜ß"
":µ
Ø´±›"
55.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µPADã `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
gar¶
i@²(¶
6§˜ß"
":µ
Ø´±›"
56.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è
Algorithm 1 Power algorithm
Input: n ≥ 0 {// Ñ\˜‡Œu0
Output: y = xn
1: y ← 1
2: X ← x
3: N ← n
4: while N 6= 0 do
5:
if N is even then
6:
X ←X ×X
7:
N ← N/2
8:
else {N is odd}
9:
y ←y×X
10:
N ←N −1
11:
end if
12: end while
ê}
57.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è
Algorithm 2 Power algorithm
Input: n ≥ 0 {// Ñ\˜‡Œu0
Output: y = xn
1: y ← 1
2: X ← x
3: N ← n
4: while N 6= 0 do
5:
if N is even then
6:
X ←X ×X
7:
N ← N/2
8:
else {N is odd}
9:
y ←y×X
10:
N ←N −1
11:
end if
12: end while
ê}
58.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è
Algorithm 3 Power algorithm
Input: n ≥ 0 {// Ñ\˜‡Œu0
Output: y = xn
1: y ← 1
2: X ← x
3: N ← n
4: while N 6= 0 do
5:
if N is even then
6:
X ←X ×X
7:
N ← N/2
8:
else {N is odd}
9:
y ←y×X
10:
N ←N −1
11:
end if
12: end while
ê}
59.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è
Algorithm 4 Power algorithm
Input: n ≥ 0 {// Ñ\˜‡Œu0
Output: y = xn
1: y ← 1
2: X ← x
3: N ← n
4: while N 6= 0 do
5:
if N is even then
6:
X ←X ×X
7:
N ← N/2
8:
else {N is odd}
9:
y ←y×X
10:
N ←N −1
11:
end if
12: end while
ê}
60.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è
Algorithm 5 Power algorithm
Input: n ≥ 0 {// Ñ\˜‡Œu0
Output: y = xn
1: y ← 1
2: X ← x
3: N ← n
4: while N 6= 0 do
5:
if N is even then
6:
X ←X ×X
7:
N ← N/2
8:
else {N is odd}
9:
y ←y×X
10:
N ←N −1
11:
end if
12: end while
ê}
61.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è
Algorithm 6 Power algorithm
Input: n ≥ 0 {// Ñ\˜‡Œu0
Output: y = xn
1: y ← 1
2: X ← x
3: N ← n
4: while N 6= 0 do
5:
if N is even then
6:
X ←X ×X
7:
N ← N/2
8:
else {N is odd}
9:
y ←y×X
10:
N ←N −1
11:
end if
12: end while
ê}
62.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è
Algorithm 7 Power algorithm
Input: n ≥ 0 {// Ñ\˜‡Œu0
Output: y = xn
1: y ← 1
2: X ← x
3: N ← n
4: while N 6= 0 do
5:
if N is even then
6:
X ←X ×X
7:
N ← N/2
8:
else {N is odd}
9:
y ←y×X
10:
N ←N −1
11:
end if
12: end while
ê}
63.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
Ö •B¶
‚ª;n¶
êâ˜ß"
":µ
ŒÀz§Ý$"
64.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
Ö •B¶
‚ª;n¶
êâ˜ß"
":µ
ŒÀz§Ý$"
65.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
Ö •B¶
‚ª;n¶
êâ˜ß"
":µ
ŒÀz§Ý$"
66.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
Ö •B¶
‚ª;n¶
êâ˜ß"
":µ
ŒÀz§Ý$"
67.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
Ö •B¶
‚ª;n¶
êâ˜ß"
":µ
ŒÀz§Ý$"
68.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 5. Ž{L«µ–è `":
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
`:µ
Ö •B¶
‚ª;n¶
êâ˜ß"
":µ
ŒÀz§Ý$"
69.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 6. Ž{¢y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
I5¿Ö 5‰§‰7‡5º§¿g•µ
8
¹
¯K¦)
k= Cþ§§‚´Ÿoa.º
Ž{Ä:
ÑÑ gSÚ‚ª´Ÿoº
O•{
˜‡«~
‘ g
éX‡"
I‡õ ê|§5
kõŒº
^Ÿo( 5|„êâº
¤IS•Nþº
$Ž„ÝXÛº
70.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 6. Ž{¢y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
I5¿Ö 5‰§‰7‡5º§¿g•µ
8
¹
¯K¦)
k= Cþ§§‚´Ÿoa.º
Ž{Ä:
ÑÑ gSÚ‚ª´Ÿoº
O•{
˜‡«~
‘ g
éX‡"
I‡õ ê|§5
kõŒº
^Ÿo( 5|„êâº
¤IS•Nþº
$Ž„ÝXÛº
71.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 6. Ž{¢y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
I5¿Ö 5‰§‰7‡5º§¿g•µ
8
¹
¯K¦)
k= Cþ§§‚´Ÿoa.º
Ž{Ä:
ÑÑ gSÚ‚ª´Ÿoº
O•{
˜‡«~
‘ g
éX‡"
I‡õ ê|§5
kõŒº
^Ÿo( 5|„êâº
¤IS•Nþº
$Ž„ÝXÛº
72.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 6. Ž{¢y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
I5¿Ö 5‰§‰7‡5º§¿g•µ
8
¹
¯K¦)
k= Cþ§§‚´Ÿoa.º
Ž{Ä:
ÑÑ gSÚ‚ª´Ÿoº
O•{
˜‡«~
‘ g
éX‡"
I‡õ ê|§5
kõŒº
^Ÿo( 5|„êâº
¤IS•Nþº
$Ž„ÝXÛº
73.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 6. Ž{¢y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
I5¿Ö 5‰§‰7‡5º§¿g•µ
8
¹
¯K¦)
k= Cþ§§‚´Ÿoa.º
Ž{Ä:
ÑÑ gSÚ‚ª´Ÿoº
O•{
˜‡«~
‘ g
éX‡"
I‡õ ê|§5
kõŒº
^Ÿo( 5|„êâº
¤IS•Nþº
$Ž„ÝXÛº
74.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 6. Ž{¢y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
I5¿Ö 5‰§‰7‡5º§¿g•µ
8
¹
¯K¦)
k= Cþ§§‚´Ÿoa.º
Ž{Ä:
ÑÑ gSÚ‚ª´Ÿoº
O•{
˜‡«~
‘ g
éX‡"
I‡õ ê|§5
kõŒº
^Ÿo( 5|„êâº
¤IS•Nþº
$Ž„ÝXÛº
75.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 7. §SNÁ
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
̇kµ
xÝÿÁµéŽ{
ˆ‡©|?1ÿÁ¶
çÝÿÁµu 鉽 Ñ\´Äk•½ÑÑ"
76.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
OŽÅŽ{¦)¯K Ú½
– 7. §SNÁ
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
̇kµ
xÝÿÁµéŽ{
ˆ‡©|?1ÿÁ¶
çÝÿÁµu 鉽 Ñ\´Äk•½ÑÑ"
77.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
OŽÅŽ{¦)¯K Ú½
– 8. © ?›
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
̇kµ
¹
¯K£ã¶
¯K¦)
.`²¶
8
Ž{Ä:
O•{
Ž{L«¶
˜‡«~
Ž{©Û¶
‘ g
5‰“è¶
éX‡"
ÿÁ(J¶
¦^•H"
78.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
OŽÅŽ{¦)¯K Ú½
– 8. © ?›
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
̇kµ
¹
¯K£ã¶
¯K¦)
.`²¶
8
Ž{Ä:
O•{
Ž{L«¶
˜‡«~
Ž{©Û¶
‘ g
5‰“è¶
éX‡"
ÿÁ(J¶
¦^•H"
79.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
OŽÅŽ{¦)¯K Ú½
– 8. © ?›
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
̇kµ
¹
¯K£ã¶
¯K¦)
.`²¶
8
Ž{Ä:
O•{
Ž{L«¶
˜‡«~
Ž{©Û¶
‘ g
5‰“è¶
éX‡"
ÿÁ(J¶
¦^•H"
80.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
OŽÅŽ{¦)¯K Ú½
– 8. © ?›
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
̇kµ
¹
¯K£ã¶
¯K¦)
.`²¶
8
Ž{Ä:
O•{
Ž{L«¶
˜‡«~
Ž{©Û¶
‘ g
5‰“è¶
éX‡"
ÿÁ(J¶
¦^•H"
81.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
OŽÅŽ{¦)¯K Ú½
– 8. © ?›
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
̇kµ
¹
¯K£ã¶
¯K¦)
.`²¶
8
Ž{Ä:
O•{
Ž{L«¶
˜‡«~
Ž{©Û¶
‘ g
5‰“è¶
éX‡"
ÿÁ(J¶
¦^•H"
82.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
OŽÅŽ{¦)¯K Ú½
– 8. © ?›
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
̇kµ
¹
¯K£ã¶
¯K¦)
.`²¶
8
Ž{Ä:
O•{
Ž{L«¶
˜‡«~
Ž{©Û¶
‘ g
5‰“è¶
éX‡"
ÿÁ(J¶
¦^•H"
83.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
OŽÅŽ{¦)¯K Ú½
– 8. © ?›
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
̇kµ
¹
¯K£ã¶
¯K¦)
.`²¶
8
Ž{Ä:
O•{
Ž{L«¶
˜‡«~
Ž{©Û¶
‘ g
5‰“è¶
éX‡"
ÿÁ(J¶
¦^•H"
84.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ ½Â
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Ž{Ò´é)û8I¯K
•{ÚÚ½9Ù£ã"
85.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ ‡ƒ
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
Ž{döŠ!››( !êâ( n‡ƒ|¤§
Ù¥öŠÌ‡kµ
Žâ$Žµ\!~!¦!ض
˜‡«~
'X' µŒu!
u! u!Ø u¶
‘ g
Ü6$Žµ†!½!š¶
éX‡"
êâDxµÑ\!ÑÑ!DŠ"
86.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ ‡ƒ
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
Ž{döŠ!››( !êâ( n‡ƒ|¤§
Ù¥öŠÌ‡kµ
Žâ$Žµ\!~!¦!ض
˜‡«~
'X' µŒu!
u! u!Ø u¶
‘ g
Ü6$Žµ†!½!š¶
éX‡"
êâDxµÑ\!ÑÑ!DŠ"
87.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ ‡ƒ
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
Ž{döŠ!››( !êâ( n‡ƒ|¤§
Ù¥öŠÌ‡kµ
Žâ$Žµ\!~!¦!ض
˜‡«~
'X' µŒu!
u! u!Ø u¶
‘ g
Ü6$Žµ†!½!š¶
éX‡"
êâDxµÑ\!ÑÑ!DŠ"
88.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ ‡ƒ
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
Ž{döŠ!››( !êâ( n‡ƒ|¤§
Ù¥öŠÌ‡kµ
Žâ$Žµ\!~!¦!ض
˜‡«~
'X' µŒu!
u! u!Ø u¶
‘ g
Ü6$Žµ†!½!š¶
éX‡"
êâDxµÑ\!ÑÑ!DŠ"
89.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ ‡ƒ
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
Ž{döŠ!››( !êâ( n‡ƒ|¤§
Ù¥öŠÌ‡kµ
Žâ$Žµ\!~!¦!ض
˜‡«~
'X' µŒu!
u! u!Ø u¶
‘ g
Ü6$Žµ†!½!š¶
éX‡"
êâDxµÑ\!ÑÑ!DŠ"
90.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ ‡ƒ
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
Ž{döŠ!››( !êâ( n‡ƒ|¤§
Ù¥öŠÌ‡kµ
Žâ$Žµ\!~!¦!ض
˜‡«~
'X' µŒu!
u! u!Ø u¶
‘ g
Ü6$Žµ†!½!š¶
éX‡"
êâDxµÑ\!ÑÑ!DŠ"
91.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ /
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Ž{´OŽÅƉ¥•äk•{Ø5Ÿ Ø%Vg§
• ™•OŽÅƉ (µ"
92.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ A
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
̇kµ
¯K¦)
Ñ\¶
Ž{Ä:
ÑѶ
O•{
˜‡«~
k¡5¶
‘ g
(½5¶
éX‡"
Œ15"
93.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ A
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
̇kµ
¯K¦)
Ñ\¶
Ž{Ä:
ÑѶ
O•{
˜‡«~
k¡5¶
‘ g
(½5¶
éX‡"
Œ15"
94.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ A
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
̇kµ
¯K¦)
Ñ\¶
Ž{Ä:
ÑѶ
O•{
˜‡«~
k¡5¶
‘ g
(½5¶
éX‡"
Œ15"
95.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ A
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
̇kµ
¯K¦)
Ñ\¶
Ž{Ä:
ÑѶ
O•{
˜‡«~
k¡5¶
‘ g
(½5¶
éX‡"
Œ15"
96.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ A
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
̇kµ
¯K¦)
Ñ\¶
Ž{Ä:
ÑѶ
O•{
˜‡«~
k¡5¶
‘ g
(½5¶
éX‡"
Œ15"
97.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
•{
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ O Ä
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
̇kµ
( z•{¶
¡•é–•{¶
Zy{"
98.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
•{
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ O Ä
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
̇kµ
( z•{¶
¡•é–•{¶
Zy{"
99.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
•{
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{ O Ä
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
̇kµ
( z•{¶
¡•é–•{¶
Zy{"
100.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Ž{ O Ä •{
– 1. ( z•{
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
• gŽ´gº•e!ÅÚ¦°§¦¯K©)†õU
z"
¹
gº•eµòE,…Œ
K '…Ú-:¶
¯K¦)
Ž{Ä:
˜‡«~
éX‡"
¯K§éѯ
ÅÚ¦°µòE,¯K²eZÚ°z?n§
^/n«Ä ( 09Ä öŠ £ãŽ{"
O•{
‘ g
¯Ky©
`
5µ
ÎÜg‘S.¶
g( ˜ß¶
¬ëêD4"
¬
[z
101.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Ž{ O Ä •{
– 1. ( z•{
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
• gŽ´gº•e!ÅÚ¦°§¦¯K©)†õU
z"
¹
gº•eµòE,…Œ
K '…Ú-:¶
¯K¦)
Ž{Ä:
˜‡«~
éX‡"
¯K§éѯ
ÅÚ¦°µòE,¯K²eZÚ°z?n§
^/n«Ä ( 09Ä öŠ £ãŽ{"
O•{
‘ g
¯Ky©
`
5µ
ÎÜg‘S.¶
g( ˜ß¶
¬ëêD4"
¬
[z
102.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Ž{ O Ä •{
– 1. ( z•{
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
• gŽ´gº•e!ÅÚ¦°§¦¯K©)†õU
z"
¹
gº•eµòE,…Œ
K '…Ú-:¶
¯K¦)
Ž{Ä:
˜‡«~
éX‡"
¯K§éѯ
ÅÚ¦°µòE,¯K²eZÚ°z?n§
^/n«Ä ( 09Ä öŠ £ãŽ{"
O•{
‘ g
¯Ky©
`
5µ
ÎÜg‘S.¶
g( ˜ß¶
¬ëêD4"
¬
[z
103.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Ž{ O Ä •{
– 1. ( z•{
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
• gŽ´gº•e!ÅÚ¦°§¦¯K©)†õU
z"
¹
gº•eµòE,…Œ
K '…Ú-:¶
¯K¦)
Ž{Ä:
˜‡«~
éX‡"
¯K§éѯ
ÅÚ¦°µòE,¯K²eZÚ°z?n§
^/n«Ä ( 09Ä öŠ £ãŽ{"
O•{
‘ g
¯Ky©
`
5µ
ÎÜg‘S.¶
g( ˜ß¶
¬ëêD4"
¬
[z
104.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Ž{ O Ä •{
– 1. ( z•{
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
• gŽ´gº•e!ÅÚ¦°§¦¯K©)†õU
z"
¹
gº•eµòE,…Œ
K '…Ú-:¶
¯K¦)
Ž{Ä:
˜‡«~
éX‡"
¯K§éѯ
ÅÚ¦°µòE,¯K²eZÚ°z?n§
^/n«Ä ( 09Ä öŠ £ãŽ{"
O•{
‘ g
¯Ky©
`
5µ
ÎÜg‘S.¶
g( ˜ß¶
¬ëêD4"
¬
[z
105.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Ž{ O Ä •{
– 1. ( z•{
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
• gŽ´gº•e!ÅÚ¦°§¦¯K©)†õU
z"
¹
gº•eµòE,…Œ
K '…Ú-:¶
¯K¦)
Ž{Ä:
˜‡«~
éX‡"
¯K§éѯ
ÅÚ¦°µòE,¯K²eZÚ°z?n§
^/n«Ä ( 09Ä öŠ £ãŽ{"
O•{
‘ g
¯Ky©
`
5µ
ÎÜg‘S.¶
g( ˜ß¶
¬ëêD4"
¬
[z
106.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Ž{ O Ä •{
– 1. ( z•{
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
• gŽ´gº•e!ÅÚ¦°§¦¯K©)†õU
z"
¹
gº•eµòE,…Œ
K '…Ú-:¶
¯K¦)
Ž{Ä:
˜‡«~
éX‡"
¯K§éѯ
ÅÚ¦°µòE,¯K²eZÚ°z?n§
^/n«Ä ( 09Ä öŠ £ãŽ{"
O•{
‘ g
¯Ky©
`
5µ
ÎÜg‘S.¶
g( ˜ß¶
¬ëêD4"
¬
[z
107.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
Ž{ O Ä •{
– 2. ¡•é–•{
̇ڽµ
3‰½ Ä– gþ£OaÚé–¶
¹
£Où é–Úa
ŠÂ¶
¯K¦)
£OaÚé–ƒm
'X¶
Ž{Ä:
¢yaÚé–"
8
O•{
˜‡«~
` 5µ
‘ g
Ä–z
éX‡"
µC5
õ 5
U«5
-^5
108.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
Ž{ O Ä •{
– 2. ¡•é–•{
̇ڽµ
3‰½ Ä– gþ£OaÚé–¶
¹
£Où é–Úa
ŠÂ¶
¯K¦)
£OaÚé–ƒm
'X¶
Ž{Ä:
¢yaÚé–"
8
O•{
˜‡«~
` 5µ
‘ g
Ä–z
éX‡"
µC5
õ 5
U«5
-^5
109.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
Ž{ O Ä •{
– 2. ¡•é–•{
̇ڽµ
3‰½ Ä– gþ£OaÚé–¶
¹
£Où é–Úa
ŠÂ¶
¯K¦)
£OaÚé–ƒm
'X¶
Ž{Ä:
¢yaÚé–"
8
O•{
˜‡«~
` 5µ
‘ g
Ä–z
éX‡"
µC5
õ 5
U«5
-^5
110.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
Ž{ O Ä •{
– 2. ¡•é–•{
̇ڽµ
3‰½ Ä– gþ£OaÚé–¶
¹
£Où é–Úa
ŠÂ¶
¯K¦)
£OaÚé–ƒm
'X¶
Ž{Ä:
¢yaÚé–"
8
O•{
˜‡«~
` 5µ
‘ g
Ä–z
éX‡"
µC5
õ 5
U«5
-^5
111.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
Ž{ O Ä •{
– 2. ¡•é–•{
̇ڽµ
3‰½ Ä– gþ£OaÚé–¶
¹
£Où é–Úa
ŠÂ¶
¯K¦)
£OaÚé–ƒm
'X¶
Ž{Ä:
¢yaÚé–"
8
O•{
˜‡«~
` 5µ
‘ g
Ä–z
éX‡"
µC5
õ 5
U«5
-^5
112.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
Ž{ O Ä •{
– 2. ¡•é–•{
̇ڽµ
3‰½ Ä– gþ£OaÚé–¶
¹
£Où é–Úa
ŠÂ¶
¯K¦)
£OaÚé–ƒm
'X¶
Ž{Ä:
¢yaÚé–"
8
O•{
˜‡«~
` 5µ
‘ g
Ä–z
éX‡"
µC5
õ 5
U«5
-^5
113.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
Ž{ O Ä •{
– 2. ¡•é–•{
̇ڽµ
3‰½ Ä– gþ£OaÚé–¶
¹
£Où é–Úa
ŠÂ¶
¯K¦)
£OaÚé–ƒm
'X¶
Ž{Ä:
¢yaÚé–"
8
O•{
˜‡«~
` 5µ
‘ g
Ä–z
éX‡"
µC5
õ 5
U«5
-^5
114.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
Ž{ O Ä •{
– 2. ¡•é–•{
̇ڽµ
3‰½ Ä– gþ£OaÚé–¶
¹
£Où é–Úa
ŠÂ¶
¯K¦)
£OaÚé–ƒm
'X¶
Ž{Ä:
¢yaÚé–"
8
O•{
˜‡«~
` 5µ
‘ g
Ä–z
éX‡"
µC5
õ 5
U«5
-^5
115.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
Ž{ O Ä •{
– 2. ¡•é–•{
̇ڽµ
3‰½ Ä– gþ£OaÚé–¶
¹
£Où é–Úa
ŠÂ¶
¯K¦)
£OaÚé–ƒm
'X¶
Ž{Ä:
¢yaÚé–"
8
O•{
˜‡«~
` 5µ
‘ g
Ä–z
éX‡"
µC5
õ 5
U«5
-^5
116.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
Ž{ O Ä •{
– 2. ¡•é–•{
̇ڽµ
3‰½ Ä– gþ£OaÚé–¶
¹
£Où é–Úa
ŠÂ¶
¯K¦)
£OaÚé–ƒm
'X¶
Ž{Ä:
¢yaÚé–"
8
O•{
˜‡«~
` 5µ
‘ g
Ä–z
éX‡"
µC5
õ 5
U«5
-^5
117.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Ž{ O Ä
– 3. Zy{
•{
̇ڽµ
O{ü‡N¶
‰Dƒ{üá5ÚpÄ5K¶
{ü‡NpÄ¥&¢¯K)§¿‰Ñ·AŠ"
118.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
Ž{ O Ä
– 3. Zy{
•{
̇ڽµ
O{ü‡N¶
‰Dƒ{üá5ÚpÄ5K¶
{ü‡NpÄ¥&¢¯K)§¿‰Ñ·AŠ"
¹
¯K¦)
Ž{Ä:
O•{
Zy5
{ü‡N•U¢y{ü ?Ö§
õ‡‡N%U ¤E, ?Ö"
˜‡«~
‘ g
` 5µ
éX‡"
¢y{ü¶
¥%z"
[4]
119.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
Ž{ O Ä
– 3. Zy{
•{
̇ڽµ
O{ü‡N¶
‰Dƒ{üá5ÚpÄ5K¶
{ü‡NpÄ¥&¢¯K)§¿‰Ñ·AŠ"
¹
¯K¦)
Ž{Ä:
O•{
Zy5
{ü‡N•U¢y{ü ?Ö§
õ‡‡N%U ¤E, ?Ö"
˜‡«~
‘ g
` 5µ
éX‡"
¢y{ü¶
¥%z"
[4]
120.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
Ž{ O Ä
– 3. Zy{
•{
̇ڽµ
O{ü‡N¶
‰Dƒ{üá5ÚpÄ5K¶
{ü‡NpÄ¥&¢¯K)§¿‰Ñ·AŠ"
¹
¯K¦)
Ž{Ä:
O•{
Zy5
{ü‡N•U¢y{ü ?Ö§
õ‡‡N%U ¤E, ?Ö"
˜‡«~
‘ g
` 5µ
éX‡"
¢y{ü¶
¥%z"
[4]
121.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
Ž{ O Ä
– 3. Zy{
•{
̇ڽµ
O{ü‡N¶
‰Dƒ{üá5ÚpÄ5K¶
{ü‡NpÄ¥&¢¯K)§¿‰Ñ·AŠ"
¹
¯K¦)
Ž{Ä:
O•{
Zy5
{ü‡N•U¢y{ü ?Ö§
õ‡‡N%U ¤E, ?Ö"
˜‡«~
‘ g
` 5µ
éX‡"
¢y{ü¶
¥%z"
[4]
122.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
Ž{ O Ä
– 3. Zy{
•{
̇ڽµ
O{ü‡N¶
‰Dƒ{üá5ÚpÄ5K¶
{ü‡NpÄ¥&¢¯K)§¿‰Ñ·AŠ"
¹
¯K¦)
Ž{Ä:
O•{
Zy5
{ü‡N•U¢y{ü ?Ö§
õ‡‡N%U ¤E, ?Ö"
˜‡«~
‘ g
` 5µ
éX‡"
¢y{ü¶
¥%z"
[4]
123.
Y擌
䕏嚎
摿
呀
Y
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
Ž{ O Ä
– 3. Zy{
•{
̇ڽµ
O{ü‡N¶
‰Dƒ{üá5ÚpÄ5K¶
{ü‡NpÄ¥&¢¯K)§¿‰Ñ·AŠ"
¹
¯K¦)
Ž{Ä:
O•{
Zy5
{ü‡N•U¢y{ü ?Ö§
õ‡‡N%U ¤E, ?Ö"
˜‡«~
‘ g
` 5µ
éX‡"
¢y{ü¶
¥%z"
[4]
124.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
˜‡¯K¦)
Ž{«~
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
¦ü‡
ê •Œú ê
¯K©Ûµü‡
êÆ .µa, b > 0
†b/c pŸ¶
꧕Œú ê¶
ꧦc§cU
Øa, b§…a/c
Ž{ Oµn)<ó¦)üê •Œú êL§§ÏL
/qÞ}Á0Œ±/ÁÑ0a, bk= ú ꧿òù
ú ê/\¦0§ÒU
•Œú ê;
äN Oµ
^forÌ‚qÞŒU Ï꧿^Cþ\¦¦Ñ Ïê¶
5¿ Ïê23/4§80ü‡êâ¥Ñyüg§¤±§ÿ
Á,Ïê´Ä¤‰êâ ÏꞧAT^Ì‚Šé Ø
´^‡Šé"
125.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
˜‡¯K¦)
Ž{«~
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
¦ü‡
ê •Œú ê
¯K©Ûµü‡
êÆ .µa, b > 0
†b/c pŸ¶
꧕Œú ê¶
ꧦc§cU
Øa, b§…a/c
Ž{ Oµn)<ó¦)üê •Œú êL§§ÏL
/qÞ}Á0Œ±/ÁÑ0a, bk= ú ꧿òù
ú ê/\¦0§ÒU
•Œú ê;
äN Oµ
^forÌ‚qÞŒU Ï꧿^Cþ\¦¦Ñ Ïê¶
5¿ Ïê23/4§80ü‡êâ¥Ñyüg§¤±§ÿ
Á,Ïê´Ä¤‰êâ ÏꞧAT^Ì‚Šé Ø
´^‡Šé"
126.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
˜‡¯K¦)
Ž{«~
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
¦ü‡
ê •Œú ê
¯K©Ûµü‡
êÆ .µa, b > 0
†b/c pŸ¶
꧕Œú ê¶
ꧦc§cU
Øa, b§…a/c
Ž{ Oµn)<ó¦)üê •Œú êL§§ÏL
/qÞ}Á0Œ±/ÁÑ0a, bk= ú ꧿òù
ú ê/\¦0§ÒU
•Œú ê;
äN Oµ
^forÌ‚qÞŒU Ï꧿^Cþ\¦¦Ñ Ïê¶
5¿ Ïê23/4§80ü‡êâ¥Ñyüg§¤±§ÿ
Á,Ïê´Ä¤‰êâ ÏꞧAT^Ì‚Šé Ø
´^‡Šé"
127.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
˜‡¯K¦)
Ž{«~
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
¦ü‡
ê •Œú ê
¯K©Ûµü‡
êÆ .µa, b > 0
†b/c pŸ¶
꧕Œú ê¶
ꧦc§cU
Øa, b§…a/c
Ž{ Oµn)<ó¦)üê •Œú êL§§ÏL
/qÞ}Á0Œ±/ÁÑ0a, bk= ú ꧿òù
ú ê/\¦0§ÒU
•Œú ê;
äN Oµ
^forÌ‚qÞŒU Ï꧿^Cþ\¦¦Ñ Ïê¶
5¿ Ïê23/4§80ü‡êâ¥Ñyüg§¤±§ÿ
Á,Ïê´Ä¤‰êâ ÏꞧAT^Ì‚Šé Ø
´^‡Šé"
128.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
˜‡¯K¦)
Ž{«~
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
¦ü‡
ê •Œú ê
¯K©Ûµü‡
êÆ .µa, b > 0
†b/c pŸ¶
꧕Œú ê¶
ꧦc§cU
Øa, b§…a/c
Ž{ Oµn)<ó¦)üê •Œú êL§§ÏL
/qÞ}Á0Œ±/ÁÑ0a, bk= ú ꧿òù
ú ê/\¦0§ÒU
•Œú ê;
äN Oµ
^forÌ‚qÞŒU Ï꧿^Cþ\¦¦Ñ Ïê¶
5¿ Ïê23/4§80ü‡êâ¥Ñyüg§¤±§ÿ
Á,Ïê´Ä¤‰êâ ÏꞧAT^Ì‚Šé Ø
´^‡Šé"
129.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
˜‡¯K¦)
Ž{«~
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
¦ü‡
ê •Œú ê
¯K©Ûµü‡
êÆ .µa, b > 0
†b/c pŸ¶
꧕Œú ê¶
ꧦc§cU
Øa, b§…a/c
Ž{ Oµn)<ó¦)üê •Œú êL§§ÏL
/qÞ}Á0Œ±/ÁÑ0a, bk= ú ꧿òù
ú ê/\¦0§ÒU
•Œú ê;
äN Oµ
^forÌ‚qÞŒU Ï꧿^Cþ\¦¦Ñ Ïê¶
5¿ Ïê23/4§80ü‡êâ¥Ñyüg§¤±§ÿ
Á,Ïê´Ä¤‰êâ ÏꞧAT^Ì‚Šé Ø
´^‡Šé"
130.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
•Œú ê¦) Ž{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Algorithm 8 greatest common divisor
Input: int a, b
Output: c
1: c ← 1
2: for (i = 2; i <= a and i <= b; i + +) do
3:
while a mod i = 0 and b mod i = 0 do
4:
c←c∗i
5:
a ← a/i
6:
b ← b/i
7:
end while
8: end for
9: return c
131.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
•Œú ê¦) Ž{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Algorithm 9 greatest common divisor
Input: int a, b
Output: c
1: c ← 1
2: for (i = 2; i <= a and i <= b; i + +) do
3:
while a mod i = 0 and b mod i = 0 do
4:
c←c∗i
5:
a ← a/i
6:
b ← b/i
7:
end while
8: end for
9: return c
132.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
•Œú ê¦) Ž{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Algorithm 10 greatest common divisor
Input: int a, b
Output: c
1: c ← 1
2: for (i = 2; i <= a and i <= b; i + +) do
3:
while a mod i = 0 and b mod i = 0 do
4:
c←c∗i
5:
a ← a/i
6:
b ← b/i
7:
end while
8: end for
9: return c
133.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
•Œú ê¦) Ž{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Algorithm 11 greatest common divisor
Input: int a, b
Output: c
1: c ← 1
2: for (i = 2; i <= a and i <= b; i + +) do
3:
while a mod i = 0 and b mod i = 0 do
4:
c←c∗i
5:
a ← a/i
6:
b ← b/i
7:
end while
8: end for
9: return c
134.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
•Œú ê¦) Ž{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Algorithm 12 greatest common divisor
Input: int a, b
Output: c
1: c ← 1
2: for (i = 2; i <= a and i <= b; i + +) do
3:
while a mod i = 0 and b mod i = 0 do
4:
c←c∗i
5:
a ← a/i
6:
b ← b/i
7:
end while
8: end for
9: return c
135.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
•Œú ê¦) Ž{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Algorithm 13 greatest common divisor
Input: int a, b
Output: c
1: c ← 1
2: for (i = 2; i <= a and i <= b; i + +) do
3:
while a mod i = 0 and b mod i = 0 do
4:
c←c∗i
5:
a ← a/i
6:
b ← b/i
7:
end while
8: end for
9: return c
136.
Y擌
䕏嚎
摿
呀
Y
Euclid•Œú
ê½n
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
½nµØ”˜„5§b a > b > 0,
Kkgcd(a, b) = gcd(b, a mod b)"
y²µ
∵ a > b > 0, ∴ a = kb + r, ùpk, r
ê§Kr =
a mod b"
b d´a, b ˜‡ú ê§Kkd|a, d|b§ r = a − kb§
kd|r§Ïdd´(b, a mod b) ú ê"
Ó /§b d´(b, a mod b) ú ê§Kd|b, d|r§d
ua = kb + r§Ïdd•´(a, b) ú ê"
Ïd(a, b)Ú((b, a mod b) ú ê´˜
§Ù•Œú
ê•7,ƒ § y"
137.
Y擌
䕏嚎
摿
呀
Y
EuclidŽ{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Algorithm 14 Euclid algorithm for greatest common divisor
(Î=ƒØ{)
Input: int a, b
Output: a
1: while b ! = 0 do
2:
r←b
3:
b ← a%b
4:
a←r
5: end while
6: return a
138.
Y擌
䕏嚎
摿
呀
Y
EuclidŽ{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Algorithm 15 Euclid algorithm for greatest common divisor
(Î=ƒØ{)
Input: int a, b
Output: a
1: while b ! = 0 do
2:
r←b
3:
b ← a%b
4:
a←r
5: end while
6: return a
139.
Y擌
䕏嚎
摿
呀
Y
EuclidŽ{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Algorithm 16 Euclid algorithm for greatest common divisor
(Î=ƒØ{)
Input: int a, b
Output: a
1: while b ! = 0 do
2:
r←b
3:
b ← a%b
4:
a←r
5: end while
6: return a
140.
Y擌
䕏嚎
摿
呀
Y
EuclidŽ{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Algorithm 17 Euclid algorithm for greatest common divisor
(Î=ƒØ{)
Input: int a, b
Output: a
1: while b ! = 0 do
2:
r←b
3:
b ← a%b
4:
a←r
5: end while
6: return a
141.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Stein•Œú ê n
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
gcd(a, a) = a¶
gcd(ka, kb) = k · gcd(a, b)§•Ò´•Œú ê$ŽÚ ¦
$ŽŒ± †§AÏ § k = 2ž§`²ü‡óê •Œú
ê7,U 2 Ø"
k þã5ÆÒŒ±‰ÑSteinŽ{Xeµ
˜a1 = a, b1 = bÚc1 = 1¶
XJai Úbi Ñ´óê, Kai+1 = an /2, bn+1 = bn /2, cn+1 =
2cn (5¿§¦2•‡r ꆣ˜ =Œ§Ø2•‡r êm
£˜ =Œ)¶
XJai ´óê§bi Ø´óê§Kai+1 = ai /2, bi+1 = bi ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJbi ´óê§ai Ø´óê§Kbi+1 = bi /2, ai+1 = ai ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJai Úbi ÑØ´óê§Kai+1 = |ai −bi |, bi+1 = min(ai , bi ),
ci+1 = ci "
XJa = 0§b´•Œú ꧎{(å¶
XJb = 0§a´•Œú ꧎{(å¶
142.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Stein•Œú ê n
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
gcd(a, a) = a¶
gcd(ka, kb) = k · gcd(a, b)§•Ò´•Œú ê$ŽÚ ¦
$ŽŒ± †§AÏ § k = 2ž§`²ü‡óê •Œú
ê7,U 2 Ø"
k þã5ÆÒŒ±‰ÑSteinŽ{Xeµ
˜a1 = a, b1 = bÚc1 = 1¶
XJai Úbi Ñ´óê, Kai+1 = an /2, bn+1 = bn /2, cn+1 =
2cn (5¿§¦2•‡r ꆣ˜ =Œ§Ø2•‡r êm
£˜ =Œ)¶
XJai ´óê§bi Ø´óê§Kai+1 = ai /2, bi+1 = bi ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJbi ´óê§ai Ø´óê§Kbi+1 = bi /2, ai+1 = ai ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJai Úbi ÑØ´óê§Kai+1 = |ai −bi |, bi+1 = min(ai , bi ),
ci+1 = ci "
XJa = 0§b´•Œú ꧎{(å¶
XJb = 0§a´•Œú ꧎{(å¶
143.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Stein•Œú ê n
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
gcd(a, a) = a¶
gcd(ka, kb) = k · gcd(a, b)§•Ò´•Œú ê$ŽÚ ¦
$ŽŒ± †§AÏ § k = 2ž§`²ü‡óê •Œú
ê7,U 2 Ø"
k þã5ÆÒŒ±‰ÑSteinŽ{Xeµ
˜a1 = a, b1 = bÚc1 = 1¶
XJai Úbi Ñ´óê, Kai+1 = an /2, bn+1 = bn /2, cn+1 =
2cn (5¿§¦2•‡r ꆣ˜ =Œ§Ø2•‡r êm
£˜ =Œ)¶
XJai ´óê§bi Ø´óê§Kai+1 = ai /2, bi+1 = bi ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJbi ´óê§ai Ø´óê§Kbi+1 = bi /2, ai+1 = ai ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJai Úbi ÑØ´óê§Kai+1 = |ai −bi |, bi+1 = min(ai , bi ),
ci+1 = ci "
XJa = 0§b´•Œú ꧎{(å¶
XJb = 0§a´•Œú ꧎{(å¶
144.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Stein•Œú ê n
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
gcd(a, a) = a¶
gcd(ka, kb) = k · gcd(a, b)§•Ò´•Œú ê$ŽÚ ¦
$ŽŒ± †§AÏ § k = 2ž§`²ü‡óê •Œú
ê7,U 2 Ø"
k þã5ÆÒŒ±‰ÑSteinŽ{Xeµ
˜a1 = a, b1 = bÚc1 = 1¶
XJai Úbi Ñ´óê, Kai+1 = an /2, bn+1 = bn /2, cn+1 =
2cn (5¿§¦2•‡r ꆣ˜ =Œ§Ø2•‡r êm
£˜ =Œ)¶
XJai ´óê§bi Ø´óê§Kai+1 = ai /2, bi+1 = bi ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJbi ´óê§ai Ø´óê§Kbi+1 = bi /2, ai+1 = ai ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJai Úbi ÑØ´óê§Kai+1 = |ai −bi |, bi+1 = min(ai , bi ),
ci+1 = ci "
XJa = 0§b´•Œú ꧎{(å¶
XJb = 0§a´•Œú ꧎{(å¶
145.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Stein•Œú ê n
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
gcd(a, a) = a¶
gcd(ka, kb) = k · gcd(a, b)§•Ò´•Œú ê$ŽÚ ¦
$ŽŒ± †§AÏ § k = 2ž§`²ü‡óê •Œú
ê7,U 2 Ø"
k þã5ÆÒŒ±‰ÑSteinŽ{Xeµ
˜a1 = a, b1 = bÚc1 = 1¶
XJai Úbi Ñ´óê, Kai+1 = an /2, bn+1 = bn /2, cn+1 =
2cn (5¿§¦2•‡r ꆣ˜ =Œ§Ø2•‡r êm
£˜ =Œ)¶
XJai ´óê§bi Ø´óê§Kai+1 = ai /2, bi+1 = bi ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJbi ´óê§ai Ø´óê§Kbi+1 = bi /2, ai+1 = ai ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJai Úbi ÑØ´óê§Kai+1 = |ai −bi |, bi+1 = min(ai , bi ),
ci+1 = ci "
XJa = 0§b´•Œú ꧎{(å¶
XJb = 0§a´•Œú ꧎{(å¶
146.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Stein•Œú ê n
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
gcd(a, a) = a¶
gcd(ka, kb) = k · gcd(a, b)§•Ò´•Œú ê$ŽÚ ¦
$ŽŒ± †§AÏ § k = 2ž§`²ü‡óê •Œú
ê7,U 2 Ø"
k þã5ÆÒŒ±‰ÑSteinŽ{Xeµ
˜a1 = a, b1 = bÚc1 = 1¶
XJai Úbi Ñ´óê, Kai+1 = an /2, bn+1 = bn /2, cn+1 =
2cn (5¿§¦2•‡r ꆣ˜ =Œ§Ø2•‡r êm
£˜ =Œ)¶
XJai ´óê§bi Ø´óê§Kai+1 = ai /2, bi+1 = bi ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJbi ´óê§ai Ø´óê§Kbi+1 = bi /2, ai+1 = ai ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJai Úbi ÑØ´óê§Kai+1 = |ai −bi |, bi+1 = min(ai , bi ),
ci+1 = ci "
XJa = 0§b´•Œú ꧎{(å¶
XJb = 0§a´•Œú ꧎{(å¶
147.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Stein•Œú ê n
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
gcd(a, a) = a¶
gcd(ka, kb) = k · gcd(a, b)§•Ò´•Œú ê$ŽÚ ¦
$ŽŒ± †§AÏ § k = 2ž§`²ü‡óê •Œú
ê7,U 2 Ø"
k þã5ÆÒŒ±‰ÑSteinŽ{Xeµ
˜a1 = a, b1 = bÚc1 = 1¶
XJai Úbi Ñ´óê, Kai+1 = an /2, bn+1 = bn /2, cn+1 =
2cn (5¿§¦2•‡r ꆣ˜ =Œ§Ø2•‡r êm
£˜ =Œ)¶
XJai ´óê§bi Ø´óê§Kai+1 = ai /2, bi+1 = bi ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJbi ´óê§ai Ø´óê§Kbi+1 = bi /2, ai+1 = ai ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJai Úbi ÑØ´óê§Kai+1 = |ai −bi |, bi+1 = min(ai , bi ),
ci+1 = ci "
XJa = 0§b´•Œú ꧎{(å¶
XJb = 0§a´•Œú ꧎{(å¶
148.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Stein•Œú ê n
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
gcd(a, a) = a¶
gcd(ka, kb) = k · gcd(a, b)§•Ò´•Œú ê$ŽÚ ¦
$ŽŒ± †§AÏ § k = 2ž§`²ü‡óê •Œú
ê7,U 2 Ø"
k þã5ÆÒŒ±‰ÑSteinŽ{Xeµ
˜a1 = a, b1 = bÚc1 = 1¶
XJai Úbi Ñ´óê, Kai+1 = an /2, bn+1 = bn /2, cn+1 =
2cn (5¿§¦2•‡r ꆣ˜ =Œ§Ø2•‡r êm
£˜ =Œ)¶
XJai ´óê§bi Ø´óê§Kai+1 = ai /2, bi+1 = bi ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJbi ´óê§ai Ø´óê§Kbi+1 = bi /2, ai+1 = ai ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJai Úbi ÑØ´óê§Kai+1 = |ai −bi |, bi+1 = min(ai , bi ),
ci+1 = ci "
XJa = 0§b´•Œú ꧎{(å¶
XJb = 0§a´•Œú ꧎{(å¶
149.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Stein•Œú ê n
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
gcd(a, a) = a¶
gcd(ka, kb) = k · gcd(a, b)§•Ò´•Œú ê$ŽÚ ¦
$ŽŒ± †§AÏ § k = 2ž§`²ü‡óê •Œú
ê7,U 2 Ø"
k þã5ÆÒŒ±‰ÑSteinŽ{Xeµ
˜a1 = a, b1 = bÚc1 = 1¶
XJai Úbi Ñ´óê, Kai+1 = an /2, bn+1 = bn /2, cn+1 =
2cn (5¿§¦2•‡r ꆣ˜ =Œ§Ø2•‡r êm
£˜ =Œ)¶
XJai ´óê§bi Ø´óê§Kai+1 = ai /2, bi+1 = bi ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJbi ´óê§ai Ø´óê§Kbi+1 = bi /2, ai+1 = ai ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJai Úbi ÑØ´óê§Kai+1 = |ai −bi |, bi+1 = min(ai , bi ),
ci+1 = ci "
XJa = 0§b´•Œú ꧎{(å¶
XJb = 0§a´•Œú ꧎{(å¶
150.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Stein•Œú ê n
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
gcd(a, a) = a¶
gcd(ka, kb) = k · gcd(a, b)§•Ò´•Œú ê$ŽÚ ¦
$ŽŒ± †§AÏ § k = 2ž§`²ü‡óê •Œú
ê7,U 2 Ø"
k þã5ÆÒŒ±‰ÑSteinŽ{Xeµ
˜a1 = a, b1 = bÚc1 = 1¶
XJai Úbi Ñ´óê, Kai+1 = an /2, bn+1 = bn /2, cn+1 =
2cn (5¿§¦2•‡r ꆣ˜ =Œ§Ø2•‡r êm
£˜ =Œ)¶
XJai ´óê§bi Ø´óê§Kai+1 = ai /2, bi+1 = bi ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJbi ´óê§ai Ø´óê§Kbi+1 = bi /2, ai+1 = ai ,
ci+1 = ci (w,¤á§Ï•2Ø´Ûê
ê)¶
XJai Úbi ÑØ´óê§Kai+1 = |ai −bi |, bi+1 = min(ai , bi ),
ci+1 = ci "
XJa = 0§b´•Œú ꧎{(å¶
XJb = 0§a´•Œú ꧎{(å¶
151.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
SteinŽ{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Algorithm 18 Stein algorithm for greatest common divisor
1: int gcd(int a, int b) {
2: if a == 0 then
3:
return b;
4: end if
5: if b == 0 then
6:
return a;
7: end if
8: if a%2 == 0 && b%2 == 0 then
9:
return 2gcd(a >> 1, b >> 1);
10: else if a%2 == 0 then
11:
return gcd(a >> 1, b);
12: else if b%2 == 0 then
13:
return gcd(a, b >> 1);
14: else
15:
return gcd(abs(a − b), min(a, b));
16: end if }
152.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
SteinŽ{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Algorithm 19 Stein algorithm for greatest common divisor
1: int gcd(int a, int b) {
2: if a == 0 then
3:
return b;
4: end if
5: if b == 0 then
6:
return a;
7: end if
8: if a%2 == 0 && b%2 == 0 then
9:
return 2gcd(a >> 1, b >> 1);
10: else if a%2 == 0 then
11:
return gcd(a >> 1, b);
12: else if b%2 == 0 then
13:
return gcd(a, b >> 1);
14: else
15:
return gcd(abs(a − b), min(a, b));
16: end if }
153.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
SteinŽ{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Algorithm 20 Stein algorithm for greatest common divisor
1: int gcd(int a, int b) {
2: if a == 0 then
3:
return b;
4: end if
5: if b == 0 then
6:
return a;
7: end if
8: if a%2 == 0 && b%2 == 0 then
9:
return 2gcd(a >> 1, b >> 1);
10: else if a%2 == 0 then
11:
return gcd(a >> 1, b);
12: else if b%2 == 0 then
13:
return gcd(a, b >> 1);
14: else
15:
return gcd(abs(a − b), min(a, b));
16: end if }
154.
Y擌
䕏嚎
摿
呀
Y
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
SteinŽ{
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
Algorithm 21 Stein algorithm for greatest common divisor
1: int gcd(int a, int b) {
2: if a == 0 then
3:
return b;
4: end if
5: if b == 0 then
6:
return a;
7: end if
8: if a%2 == 0 && b%2 == 0 then
9:
return 2gcd(a >> 1, b >> 1);
10: else if a%2 == 0 then
11:
return gcd(a >> 1, b);
12: else if b%2 == 0 then
13:
return gcd(a, b >> 1);
14: else
15:
return gcd(abs(a − b), min(a, b));
16: end if }
155.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
Ž{©Û
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
EuclidŽ{†SteinŽ{§•ŒS“gêA ´ƒ
"
´§I‡5¿ ´§éuŒƒê§Euclid¦ Áû •ª
ò¦zgS“Ñ•E,§éuŒƒêSteinò•k`³§Ï
TŽ{ ïØ{Ú
§•k ê £ Ú\~{"
156.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
g
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
‘
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
1
OŽÅŽ{¦)¯K̇k= Ú½º
2
Ž{üÑ̇k=
˜‡«~
3
Ž{d=n‡ƒ|¤º
‘ g
[1, 3]
¯K¦)
Ž{Ä:
O•{
éX‡"
º
157.
Y擌
䕏嚎
摿
呀
Y
̇땩z I
A
ng
Y 䞌怦 吼 䋳撜兕
sted Artificial In
tel
Tru
lig
e
敧
Y
α COT A I
Y
e
nc
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
4öÅ, •œ, ÜÆ, and qxx.
OŽÅŽ{.
Œë°¯ŒÆч , Œë, 2020.08.
“Ê.
<aå ƒ•))5g²LÆ yâ.
MOOC, 2017.
Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford
Stein.
Introduction to Algorithms.
MIT Press, MA, 2009.07.
Joao Fabiano.
Emergence’s Devil Haunts the Moral Enhancer’s Kingdom Come.
Practical Ethics, 2013.
158.
Y敧
擌
䕏嚎
摿
呀
sted Artificial In
tel
Tru
lig
e
α COT A I
Y
e
nc
A
ng
Y
Y
Y 䞌怦 吼 䋳撜兕
éX‡"
ognitive C
ous C
om
om
pu
on
ti
ut
Ž{ O†©
Û
101ù Ž{
Vã
4öÅ
8
¹
¯K¦)
Ž{Ä:
O•{
˜‡«~
‘ g
éX‡"
Email: liu.hongbo@foxmail.com
Homepage: www.scholat.com/liuhongbo



































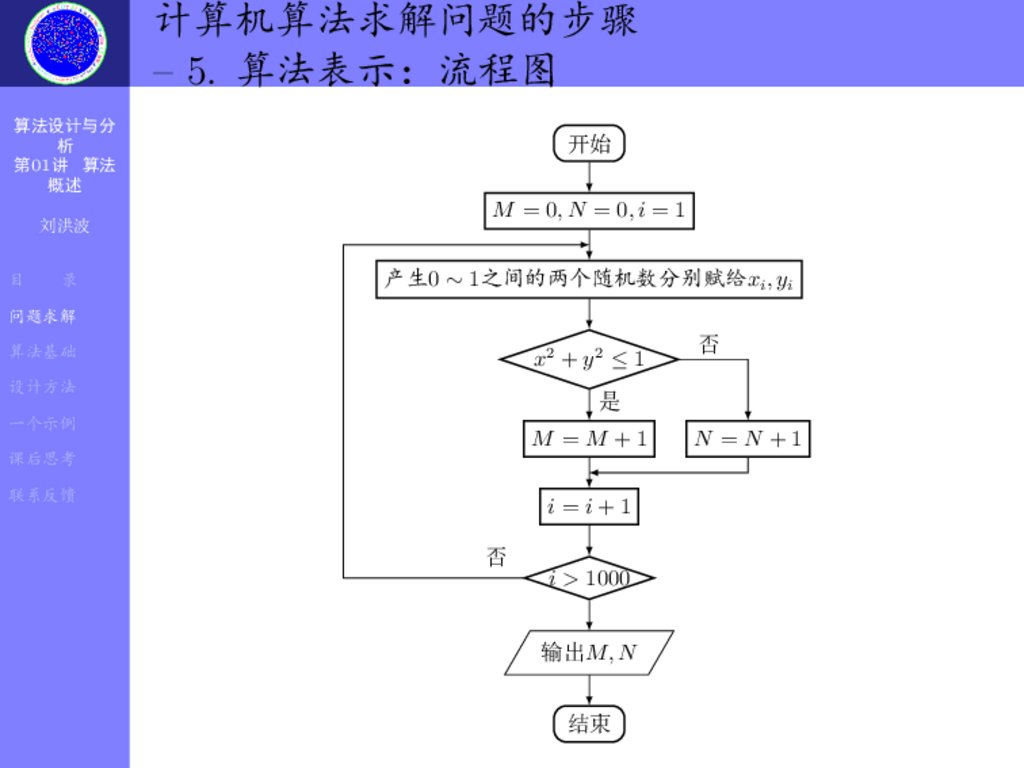





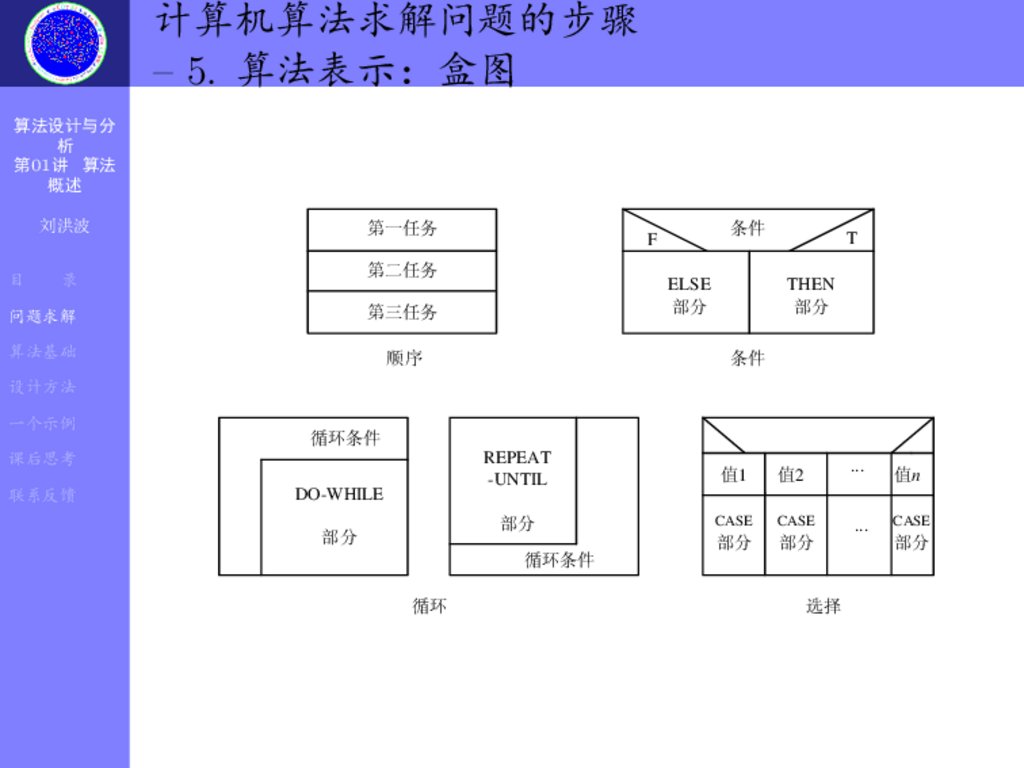





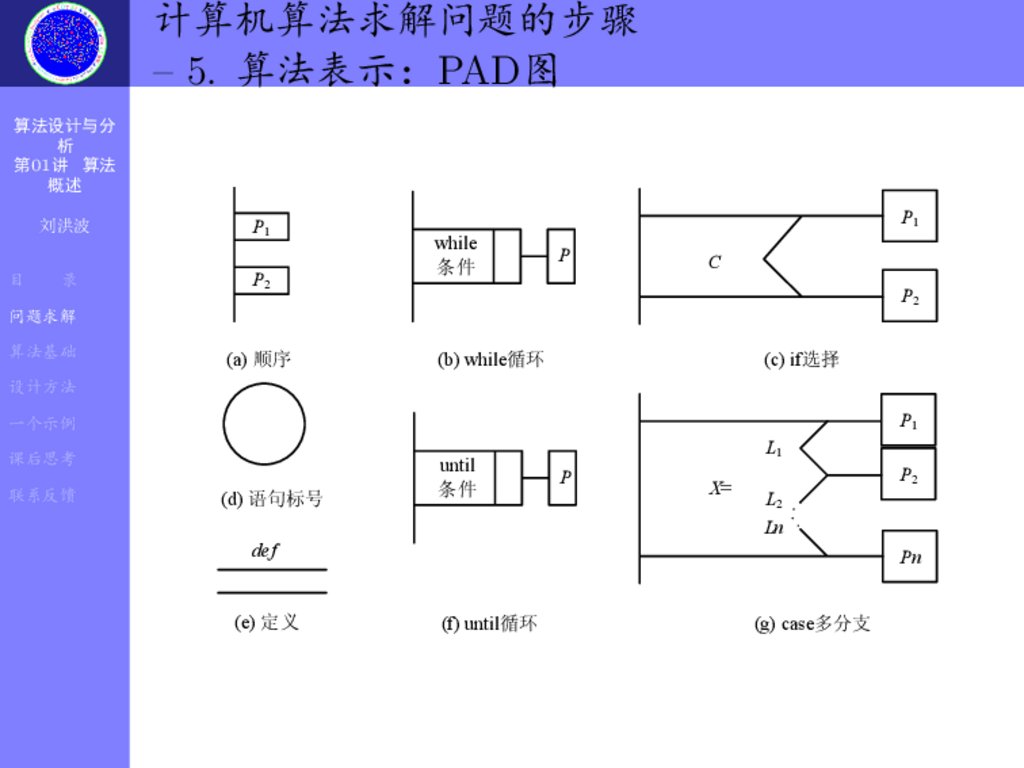













































































































 informatics
informatics








