Similar presentations:
Mode analysis of the tree-like networks of nonlinear oscillators
1. Mode analysis of the tree-like networks of nonlinear oscillators
O. Katkova (MA-student)1, A. Safin1, M. Kapranov1, E. Surovyatkina2,3, J. Kurths31National
Research University "MPEI", Moscow, Russia
2Space Research Institute, Russian Academy of Sciences, Moscow, Russia
3Potsdam Institute for Climate Impact Research, Potsdam, Germany
22 May 2017
1
2. OUTLINE
• IntroductionTree-like networks in nature and mathematics
Tree-like networks in complex artificial systems
• Theoretical analysis
Problem of normal modes
Quasi-Hamiltonian approach and truncated equations
• Application of the Quasi-Hamiltonian approach
Complex network analysis. Synchronization
Topological properties of the complex network organization
• Conclusions
2
3. TREE-LIKE NETWORKS IN NATURE
Tree rootsEgypt map
Vascular
system
R. Rammal, et al. 1986.
T. Nakayama, et al. 1994
3
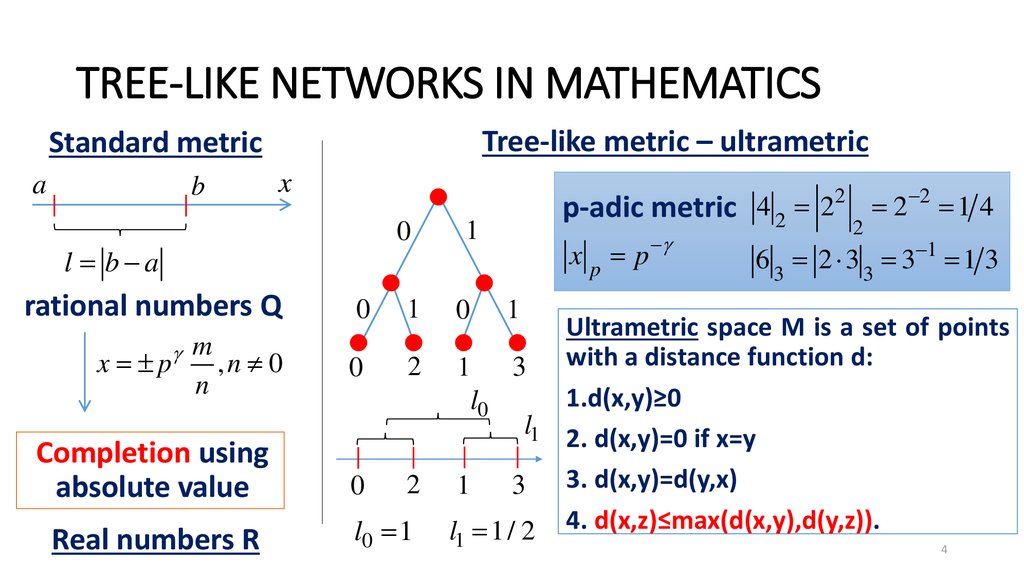
4. TREE-LIKE NETWORKS IN MATHEMATICS
Tree-like metric – ultrametricStandard metric
a
b
x
0
l b a
2
2
4
2
2
1 4
p-adic metric 2
1
x p p
rational numbers Q
0
1
0
m
x p
,n 0
n
0
2
1
3
l0
l1
0
2
1
Completion using
absolute value
Real numbers R
l0 1
1
3
l1 1 / 2
2
6 3 2 3 3 3 1 1 3
Ultrametric space M is a set of points
with a distance function d:
1.d(x,y)≥0
2. d(x,y)=0 if x=y
3. d(x,y)=d(y,x)
4. d(x,z)≤max(d(x,y),d(y,z)).
4
5. ARTIFICIAL NEURAL NETWORKS
Silicon-basedneural networks
B. Benjamin, 2014
Spintronic-based
neural networks
J. Grollier, 2016
5
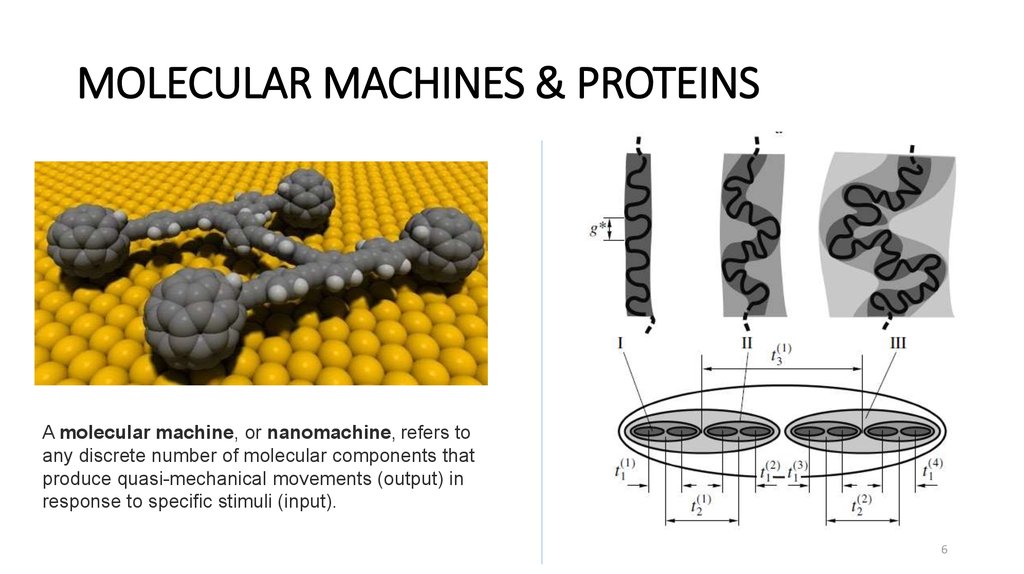
6. MOLECULAR MACHINES & PROTEINS
MOLECULAR MACHINES & PROTEINSA molecular machine, or nanomachine, refers to
any discrete number of molecular components that
produce quasi-mechanical movements (output) in
response to specific stimuli (input).
6
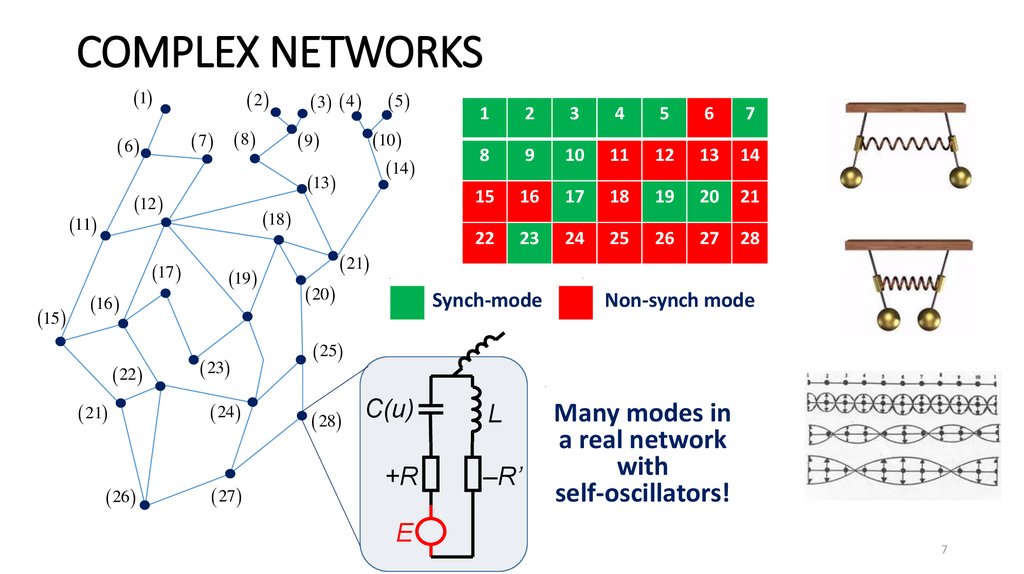
7. COMPLEX NETWORKS
17 8
6
17
16
22
21
26
5
3 4
10
14
9
13
12
11
15
2
18
19
23
21
20
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
.
.
Synch-mode
Non-synch mode
25
.
24
27
28
C(u)
+R
E
L
–R’
Many modes in
a real network
with
self-oscillators!
7
8. MATHEMATICAL MODEL
Kuramoto modelN
d i
i K Aij sin j i
dt
j 1
Ui const , f U
Network of Landau-Stuart oscillators
dzi
K
zi 1 i i q 1 iq zi zi*
N
dt
zi zi* zi - cubic nonlinear term
i
N
zi z j
j 1
Landau, 1944. Stuart, 1960.
- given normal mode
?
Structure of normal modes is unknown
Different types of nonlinearity
8
9. QUASI-HAMILTONIAN APPROACH
Equations of motionc j
t
cj
H
Fc j
i
H
c*j
Fc j , H H c1,..., cN
- complex amplitude of j-th oscillator,
- Hamiltonian of all system
- perturbation term (~ small parameter)
General and simple way to write truncated equations (for slowly varying amplitudes and phases)
General structure of Hamiltonian
N
H A jk c j ck* 0.5 B*jk c j ck B jk c*j ck* H 3 H 4 ...
j 1
H2
9
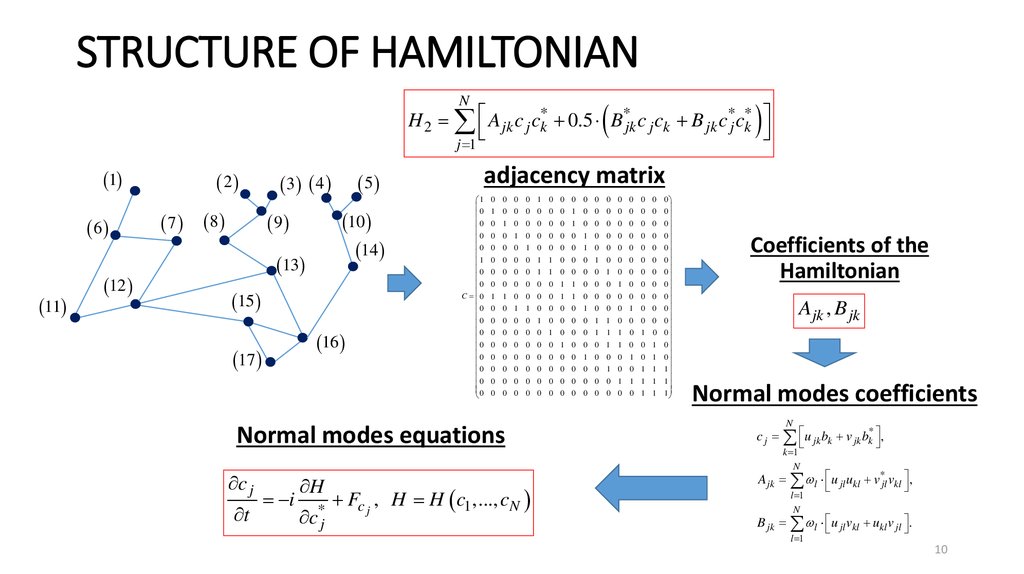
10. STRUCTURE OF HAMILTONIAN
NH 2 A jk c j ck* 0.5 B*jk c j ck B jk c*j ck*
j 1
1
6
11
12
2
7 8
10
14
9
13
15
16
17
adjacency matrix
5
3 4
1
0
0
0
0
1
0
0
C 0
0
0
0
0
0
0
0
0
0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 1 0 0 0 0 0 0 0 0
0 0 1 0 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 1 0 0 0 0 0 0
0 0 0 0 1 1 0 0 0 0 1 0 0 0 0 0
0 0 0 0 0 0 1 1 0 0 0 1 0 0 0 0
1 1 0 0 0 0 1 1 0 0 0 0 0 0 0 0
0 0 1 1 0 0 0 0 1 0 0 0 1 0 0 0
0 0 0 0 1 0 0 0 0 1 1 0 0 0 0 0
0 0 0 0 0 1 0 0 0 1 1 1 0 1 0 0
0 0 0 0 0 0 1 0 0 0 1 1 0 0 1 0
0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0
0 0 0 0 0 0 0 0 0 0 1 0 0 1 1 1
0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1
0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1
Normal modes equations
c j
t
i
H
c*j
Fc j , H H c1,..., cN
Coefficients of the
Hamiltonian
Ajk , B jk
Normal modes coefficients
N
c j u jk bk v jk bk* ,
k 1
N
A jk l u jl ukl v*jl vkl ,
l 1
N
B jk l u jl vkl ukl v jl .
l 1
10
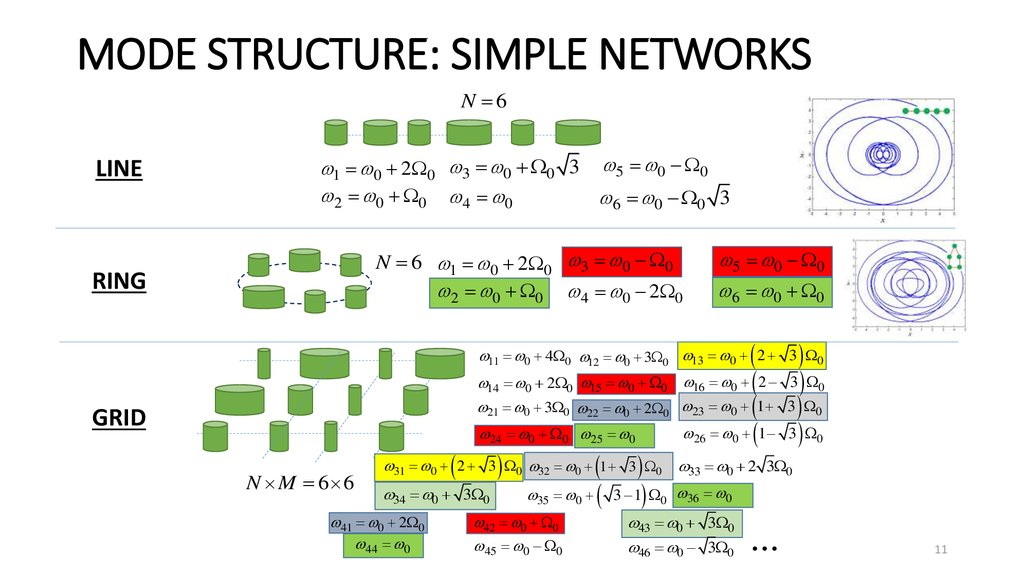
11. MODE STRUCTURE: SIMPLE NETWORKS
N 6LINE
1 0 2 0 3 0 0 3 5 0 0
2 0 0 4 0
6 0 0 3
N 6 1 0 2 0 3 0 0
2 0 0 4 0 2 0
RING
5 0 0
6 0 0
16 0 2
23 0 1
26 0 1
3 0
3 0
3 0
11 0 4 0 12 0 3 0 13 0 2 3 0
14 0 2 0 15 0 0
21 0 3 0 22 0 2 0
GRID
24 0 0 25 0
N M 6 6
31 0 2 3 0 32 0 1 3 0
34 0 3 0
41 0 2 0
44 0
35 0
42 0 0
45 0 0
33 0 2 3 0
3 1 0 36 0
43 0 3 0
46 0 3 0
...
11
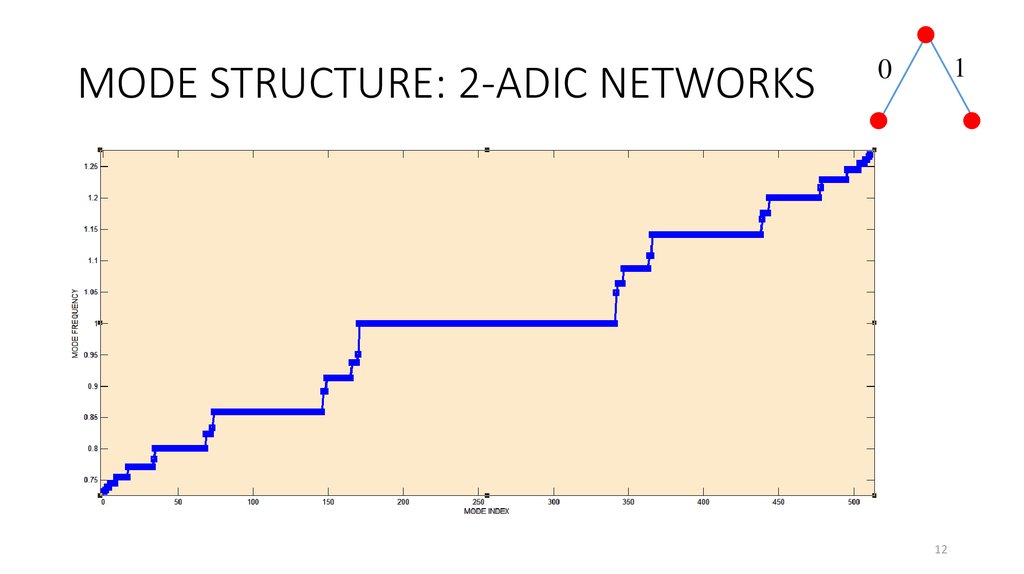
12. MODE STRUCTURE: 2-ADIC NETWORKS
10
12
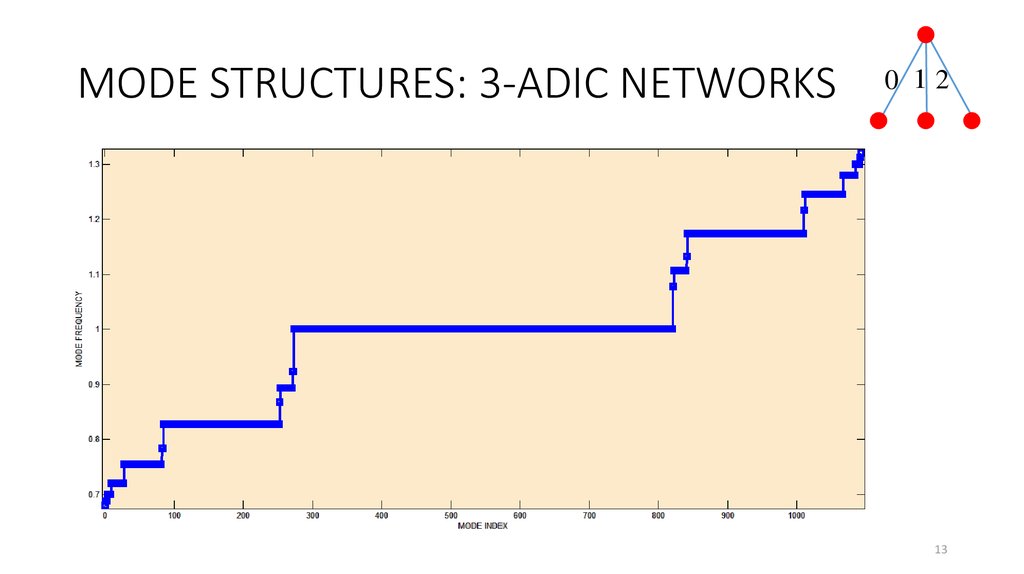
13. MODE STRUCTURES: 3-ADIC NETWORKS
0 1213
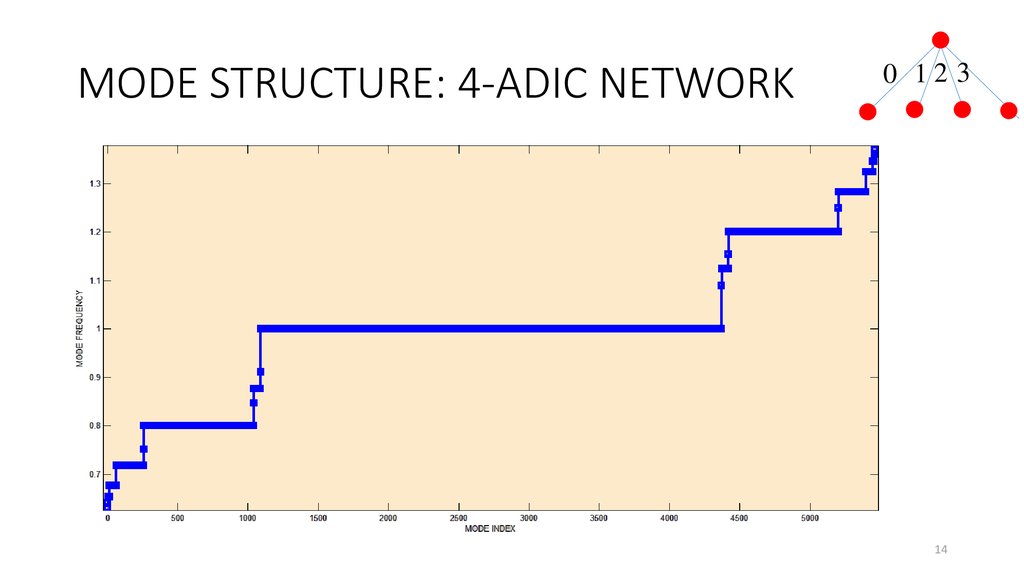
14. MODE STRUCTURE: 4-ADIC NETWORK
0 12 314
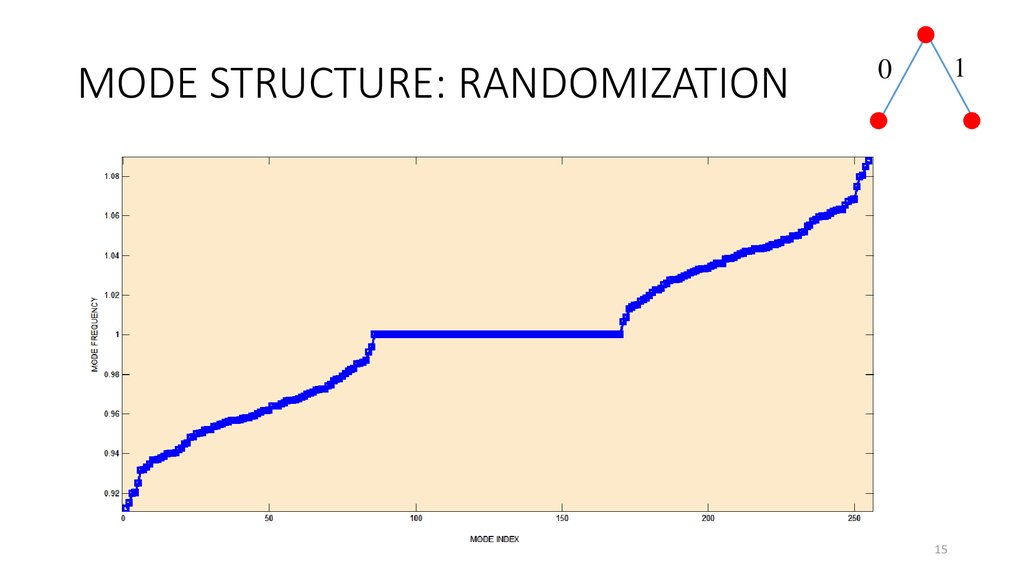
15. MODE STRUCTURE: RANDOMIZATION
10
15
16. MODE STABILITY & SYNCHRONIZATION
MODE STABILITY & SYNCHRONIZATIONDegenerate mode
Nondegenerate duplets
(identical case)
(nonidentical case)
Two
frequencies
born
from
degenerate mode, can synchronize if
they are close enough, but they lose
synchronization when they are
separated to some extent.
Non-isochronous
of
oscillators
increase
the
phase
locking
bandwidth between two modes in
noidentical case
Phase locking area at the parameter
plane becomes asymmetric
16
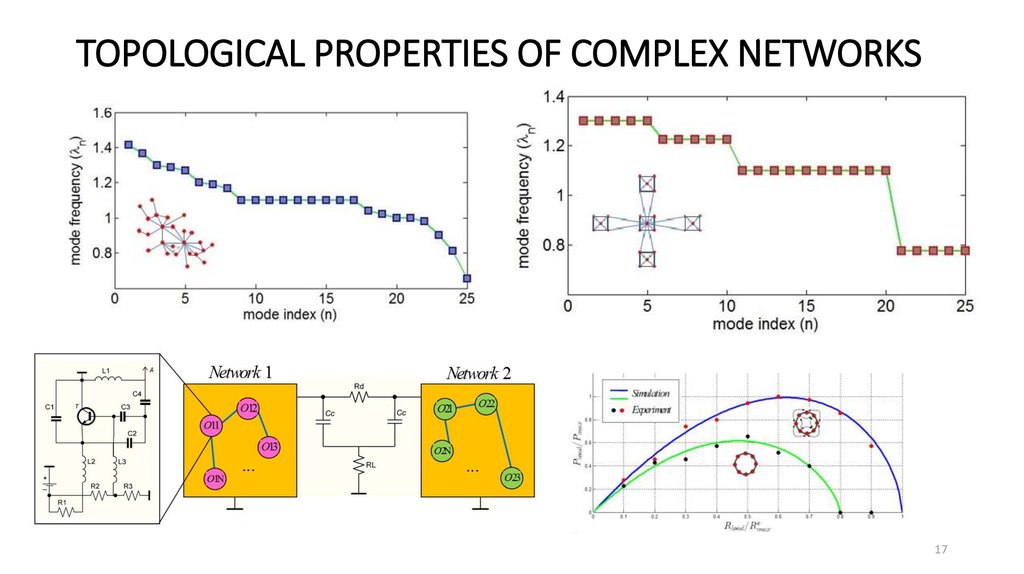
17. TOPOLOGICAL PROPERTIES OF COMPLEX NETWORKS
1718. CONCLUSION
The structure of normal modes of tree-like (ultrametric) networks isfractal (“devil’s staircase”).
Increasing of p (number of branches) leads to the increasing of
degenerate modes
We propose to apply the quasi-Hamiltonian approach to derive
normal modes using priori knowledge of the network topology only.
We find that hierarchical networks are characterized by a smaller
number of stable nontrivial modes than randomly organized.
Our analysis gives rise to an approach to specify topological
transformations of networks that can enhance synchronization.
Randomization of the coupling frequencies leads to the modes nondegeneracy and difficulties with synchronization.
18








 biology
biology informatics
informatics








