The Taylor Formula

1.

Calculus++ Light

2. The Taylor Formula

f (c)
2
f ( x ) f (c) f (c)( x c)
( x c)
2!
(n)
( n 1)
f (c)
f
( )
n
n 1
( x c)
( x c) ,
n!
(n 1)!
where c ( x c), (0,1).
For instance,
0
0
e
e
2
3
e e e ( x 0) ( x 0) ( x 0)
2
!
3
!
0
e
e
n
n 1
( x 0)
( x 0) , where
n!
(n 1)!
x.
x
0
0

3.

Question 1. If
x 3 x 1 a0 a1 ( x 2) a2 ( x 2) 2 a3 ( x 2)3 ,
for all real numbers x, then
a) a0 1, a1 12 , a2 0, a3 18
b) a0 1, a1 1, a2 0, a3 1
c) a0 7, a1 6, a2 10, a3 1
d ) a0 7, a1 11, a2 12, a3 6
e) a0 7, a1 11, a2 6, a3 1
Solution: Taylor’s formula tells us
0
f ( x) f (2) f (2)( x 2)
( 4)
f (2)
f (2)
f ( )
2
3
4
( x 2)
( x 2)
( x 2) .
2!
3!
4!

4.

x x 1 a0 a1 ( x 2) a2 ( x 2) a3 ( x 2) ,
3
2
Therefore x x 1 7 (3x 1)
2
3
x 2
3
( x 2)
11
6
3
12 6 x x 2 ( x 2) ( x 2)
3!
6
2
a) a0 1, a1 12 , a2 0, a3 18
b) a0 1, a1 1, a2 0, a3 1
c) a0 7, a1 6, a2 10, a3 1
d ) a0 7, a1 11, a2 12, a3 6
e) a0 7, a1 11, a2 6, a3 1

5.

Answers to Questions from Light #7:
Taylor’s Formula & Infinite Series
Question 2: e)
Question 3: L e
1
2
2
Question 4: S ln 2

6.

Calculus++
Infinite Series

7.

Question 1. What is the greatest value of b for
which any function f that satisfies the
properties (i), (ii), and (iii) must also satisfy
f (1) < 5?
(i) f (x) is infinitely differentiable for all x;
(ii) f (0) = 1, f (0) 1, and f (0) 2;
(iii) | f ( x) | b, for all x [0,1].
a) 1 b) 3 c) 6 d ) 12 e) 24
Solution: Taylor’s formula tells us
f (1) f (0) f (0)(1 0)
f (0)
f ( )
2
3
(1 0)
(1 0) .
2!
3!

8.

Using the properties (ii) and (iii) we obtain
b
f ( )
3 .
f (1) 1 1 1
3!
3!
b
Solve the equation 3 5 to obtain b = 12.
3!
Therefore, the greatest value of b for which
f (1) < 5 is 12.
a) 1 b) 3 c) 6 d ) 12 e) 24

9.

e 1 x x x x
x
1
2!
2
1
3!
3
1
n!
n
1
( n 1)!
n 1
e x .
In particular,
e 1 1
1
2!
1
3!
1
n!
1
( n 1)!
e ,
where (0,1).
That is
1 1 21! 31! n1! ( n 11)! e
1 1 21! 31! n1! ( n 11)! e
1 1 21! 31! n1! ( n 11)! 3.

10.

Question 2. Use the Taylor formula to show
that e is irrational.
k
Solution. Let us assume that e is rational, e .
m
Then the Taylor formula tells us that for any n:
k
1 1
m
1 1 21! 31! n1! ( n 11)! 3.
Take n max( m,3), and multiply both sides
1
2!
1
3!
1
n!
1
( n 1)!
of the double inequality by n! to obtain
k
2 n! 1
n!
m
2 n! n2!! n3!! 1 3 ( nn !1)! .
n!
2!
n!
3!
n!
( n 1)!

11.

Therefore
k
n!
n!
3
n! 2 n! 2! 3! 1 n 1
m
k
0 n! 2 n! n2!! n3!! 1 1
m
1
n 1
an integer number
Contradiction!
Thus, our assumption that e is a rational
number leads to a contradiction.
Therefore, e is an irrational number.

12.

Question 3. Find lim n sin( 2 e n!).
n
Solution. The Taylor formula tells us that for
1
1
1
1
1
any n: e 2 2! 3! n! ( n 1)! ( n 2)! e ,
where is a number between 0 and 1.
Multiply by 2 n! to obtain
2 e n! 2 (2n! 1)
n!
2!
n!
3!
2
n 1
2 n!
( n 2 )!
e.
= M, an integer number
Therefore
sin( 2 e n!) sin 2 M
sin
2
n 1
2
n 1
2
( n 1)( n 2 )
2 n!
( n 2 )!
e
e

13.

Hence, lim n sin( 2 e n!)
n
lim n sin
n
2
n 1
2
( n 1)( n 2 )
e .
Since sin x is equivalent to x, when x is small,
we obtain
lim n sin( 2 e n!) lim
n
n
2 n
n 1
2 n
( n 1)( n 2 )
e 2 .
0

14.

Consider an infinite sequence
a1 , a2 , a3 , a4 , , ak ,
If we add all the terms of this sequence we
obtain an infinite series
a1 a2 a3 ak
n
For example, consider the sequence an ( 1) :
1, 1, 1, 1, 1, 1, 1, 1,
The corresponding infinite series is
0
0
0
0
1 1 1 1 1 1 1 1 0 or ?! 1?
0
0
0
0
What is the value of this infinite series?
This infinite series does not have a value.

15.

The sum of the first n terms of an infinite series,
Sn, is called the n-th partial sum of the series
Sn a1 a2 an .
An infinite series converges, if converges the
sequence of its partial sums:
lim Sn S .
n
The limit, S, of the sequence of partial sums is
the sum of the infinite series.

16.

Example. The geometric series
ab .
k
k 1
The n-th partial sum of the geometric series is
given by n
n 1
n
b b
.
S n ab a b a
1 b
k 1
k 1
k
k
If a = 0, the sequence Sn converges to 0.
If a 0 and |b| > 1, the sequence of partial sums
Sn diverges.
If |b| < 1, the sequence Sn converges.
n 1
ab
b b
.
lim a b lim a
n
n
1 b
1 b
k 1
n
k

17.

If b = 1, the sequence of partial sums Sn diverges
(unless a = 0).
n
n
S n ab a 1 an sgn a .
k
k 1
k 1
If b = –1, the sequence of partial sums Sn also
diverges (again, unless a = 0).
a, if n is odd,
S n ab a ( 1) 0, if n is even.
k 1
k 1
n
n
k
k

18.

A necessary condition for convergence.
If a series
a
k 1
k
converges, then lim ak 0.
k
Indeed, if the sequence of partial sums
n
S n ak converges, then (Cauchy criterion)
k 1
, N , n N and m 0 : | Sn m Sn | .
Set m = 1, then , N , n N : | an 1 | .
Therefore lim ak lim an 1 0.
k
n

19.

Question 5. Which of the following series
converge?
k
2
e ln k
I.
k!
k 1
III.
cos k
II. k
k
k 1
log
k 2
k
k
a. I only b. II only c. III only
d. I and II only e. II and III only
ln k
Solution: For series III: ak log k k
1.
ln k
lim ak 1 0. Hence, series III diverges.
k

20.

In series II: lim
k
k
k lim exp ln k
k
k
ln k
ln k
lim exp
exp lim
exp 0 1.
k
k
k k
The sequence cos(k) diverges as k .
cos k
Hence, the sequence ak k
k
does not converge to 0 as k .
Therefore, series II diverges.
a. I only b. II only c. III only
d. I and II only e. II and III only

21.

Important series.
1 1
1
1
1 q q q q .
2 3
n
n 1 n
This series converges if q > 1, and it diverges if
q 1.

22.

Question 5. A certain ball has the property
that each time it falls from a height h onto a
hard, level surface, it rebounds to a height
rh, where 0 < r < 1.
Suppose that the ball is dropped from an
initial height of H meters.
a) Assuming that the ball continues to bounce
indefinitely, find the total distance that it
travels.
Solution:

23.

A bouncing ball – total distance travelled
d H 2rH 2r H 2r H
n
4
2r H H 2 H r
r
1 r n 1
H 2H
H
.
1 r
1 r
1 r
Answer : d H
1 r
2
h
H
rH
2
r H
3
r4 H
r H
3
«Ацкок»
1
2

24.

Question 7. A certain ball has the property
that each time it falls from a height h onto a
hard, level surface, it rebounds to a height
r h, where 0 < r < 1.
Suppose that the ball is dropped from an
initial height of H meters.
b) Calculate the total time that the ball spends
bouncing.
Hint: A ball having zero velocity falls ½ gt2
meters in t seconds.
Solution: Actually, philosophers might find it
obvious that the ball never stop bouncing.

25.

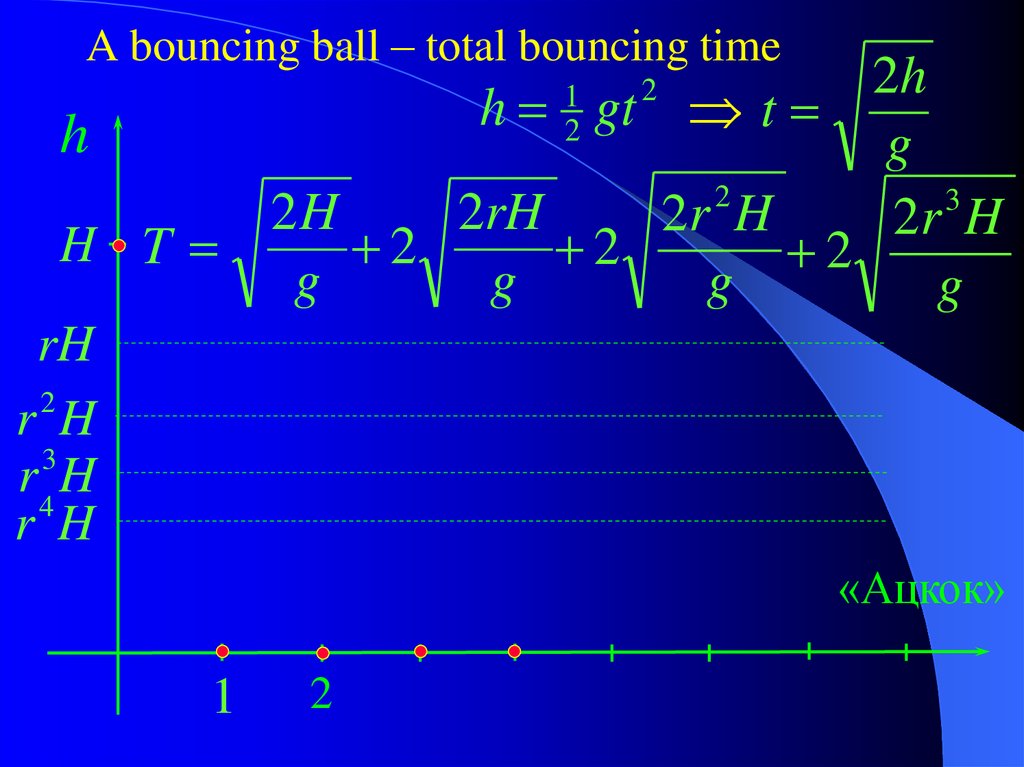
A bouncing ball – total bouncing time
2h
h gt t
h
g
2
3
2H
2rH
2r H
2r H
H T
2
2
2
g
g
g
g
rH
2
r H
3
r4 H
r H
1
2
2
«Ацкок»
1
2

26.

2
3
2H
2rH
2r H
2r H
T
2
2
2
g
g
g
g
2H
2H
2
g
g
r r r
2
3
2H
2H 1 r
2H
r
.
2
g
g 1 r
g 1 r
2H 1 r
Answer : T
g 1 r

27.

Question 7. c) Suppose that each time the ball
strikes the surface with velocity v, it
rebounds with velocity – kv, where 0 < k < 1.
How long will it take for the ball to come to
rest?
Solution:
The velocity of the ball when it hits the
ground for the first time is given by
2H
v gt , where t
, v 2Hg .
g

28.

Hence, the ball that rebounds with velocity v1
will reach the height
2
v1
H1
.
2g
2 2
k v
2
In our case v1 kv. Hence H 1
k H.
2g
Therefore r k 2 ,
2H 1 k
2H 1 r
.
and T
g 1 k
g 1 r
2H 1 k
Answer : T
g 1 k