Mathematical Induction

1.

Calculus++ Light

2. Mathematical Induction

Let Sn, n = 1,2,3,… be statements involving
positive integer numbers n.
Suppose that
1. S1 is true.
2. If Sk is true, then Sk +1 is also true.
Then Sn is true for all positive integer numbers n.

3.

Question 1. Let x1 = 1 and xn 1 7 6 xn
for all positive integers n. If it is assumed
that the sequence {xn} converges, then a ) 1
lim xn
b) 0
Solution. First, we find fixed points of the
c ) 13
relationship xn 1 7 6 xn .
That is, we find solutions of the equation d ) e
e) 7
x 7 6x.
n
x 7 6 x x1 1, x2 7.
2
Next, we calculate a few terms of the
sequence. x2 7 6 1 13 3 x2 7
x3 7 6 x2 7 6 3 x3 7 6 7
5 x3 7.

4.

x4 7 6 x3 7 6 5 x4 7 6 7
6 x4 7
a) 1
Our first statement S1: 6 x4 7.
b) 0
The general statement Sn: 6 xn 3 7.
The first statement S1 is correct.
Let us assume that a statement Sk :
6 xk 3 7 is also correct. Then
c ) 13
d) e
e) 7
xk 4 7 6 xk 3 7 6 6 xk 4 7 6 7
6 xk 4 7
Therefore, the principle of mathematical
induction tells us that 6 xn 3 7 for any
positive integer n.

5.

Since we know that the sequence xn converges
6 lim xn 3 7
n
But, what if this is a free-response
question?
Then we can pass to the limit n
in both parts of the relationship
xn 1 7 6 xn .
L lim xn 1 lim 7 6 xn .
n
a) 1
b) 0
c ) 13
d) e
e) 7
n
Since f ( x) 7 6 x is a continuous function
for x 76 , we obtain
L 7 6 lim xn 7 6 L . L 7.
n

6.

Answers to Questions from Light #2:
Sequences and Limits
1 ( 1)
Question 1: An
, Bn n
2
Question 2: d ) b1 36
n
Question 3a: N min 17
Question 3b: N min Integer part of
1
5
Question 4: 2
Question 5: 4
k
You have to show that k 2
k 1 2
5 8

7.

Calculus++
Also known as
Hysterical Calculus

8.

Question 1b. Find the limit of the sequence
n
n a n b
.
yn
2
n
n a n b
Solution. We have
2
n
n a n b
n
n
a
b
n ln
exp ln
exp
2
2
Using the equivalence n a ~ 1 1n ln a we obtain
n
n a n b
1 ln a ln b
~ exp n ln 1
n
2
2

9.

Using now the equivalence ln 1 1n c ~ 1n c,
we obtain
n
a b
1 ln a ln b
~ exp n
exp ln ab
n
2
2
ab
.
n
n a n b
ab .
Therefore, lim
n
2
n
n

10.

Question 2b. Find the following limit
17
20
L lim
.
20
17
x 1 1 x
1 x
Solution. Actually, the equivalence
x (1 ( x 1)) ~ 1 m( x 1),
m
m
gives an incorrect result for this limit.
20
17
L lim
x 1 1 1 20( x 1)
1 1 17( x 1)
1
1
lim
lim 0 0. Incorrect!
x 1
x 1 x 1 x 1
To obtain a correct result we have to use
x ~ 1 m( x 1) m(m 1)( x 1) .
m
1
2
2

11.

The last equivalence yields
20
L lim
2
x 1 1 1 20( x 1) 1 20 19( x 1)
2
17
2
1
1 1 17( x 1) 2 17 16( x 1)
1
1
lim
2
1
x 1 ( x 1) 1 19( x 1) 2
( x 1) 2 16( x 1)
2
2
2
1
1
( x 1) 2 16( x 1) ( x 1) 2 19( x 1)
lim
x 1 ( x 1) 1 16( x 1) 2 ( x 1) 1 19( x 1) 2
2
2
2
1
3
2 (19 16)( x 1)
lim
2
2
1
x 1 ( x 1) 1 16( x 1)
(
x
1
)
2
2
2 19( x 1)

12.

Question 3. Find the following limit
sin tan x tan sin x
lim
.
x 0 arcsin arctan x arctan arcsin x
Solution. We have to find precise equivalent
functions for each term at x = 0
sin tan x 0 x 0 x x 0 x 4 ( 3) 51! x 5
2
1
6
3
0 x ( 275) x
6
1
7!
7
tan sin x 0 x 0 x x 0 x ( 3) x
2
1
6
0 x ( 107) x
6
4
3
1
7!
7
Therefore, sin tan x tan sin x 168 71! x 7 .
1
5!
5

13.

A similar (but even more difficult) calculation
yields
arcsin(arc tan x) x x 13 x 341 x
3
5
arctan(arc sin x) x x 13 x 173 x
1
3!
1
3!
3
1
5!
1
5!
5
1 7
7!
1 7
7!
Therefore
arcsin arctan x arctan arcsin x 168 x .
1
7!
7
sin tan x tan sin x
and lim
1.
x 0 arcsin arctan x arctan arcsin x

14. Picture of the Week

15.

Question 8. The initial location of a snail is
the point S1 = (0,0).
The first 3 turning points, keeping the snail
confined inside a unit square, are given by
S2 = (½, 1), S3 = (1, ½), and S4 = (½, 0).
After that the snail always heads towards the
midpoint of the next path segment that it
sees, without crossing its own path.
That is, the coordinates (xn, yn) of the turning
points Sn are given by
xn 3 xn 4
yn 3 yn 4
and yn
xn
,
2
2
for n = 5,6,7,…

16.

a) Show that xn+3 + xn+2 + xn+1 + ½ xn = 2,
and find a similar relationship for the ycoordinates.
b) Find the x and y coordinates of the limiting
point S of the snail path.
c) Repeat parts a) and b) for a snail confined
inside an isosceles triangle.
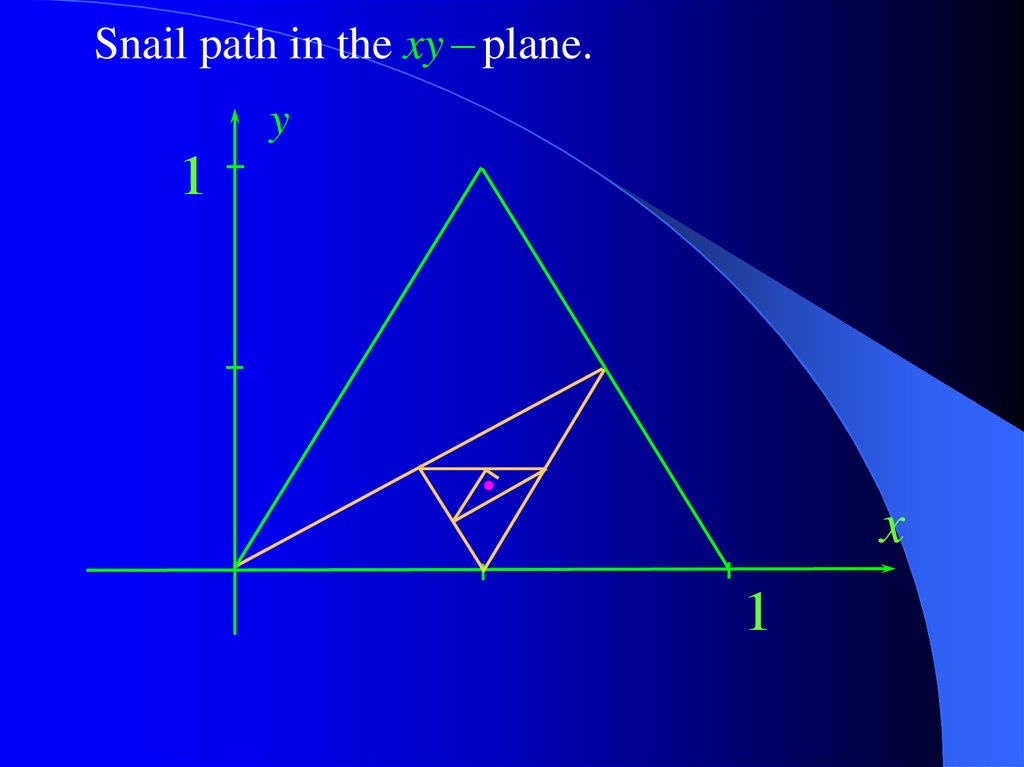
The initial location of the snail is S1 = (0,0).
The first 2 turning points are S2 = (¾, ½) and
S3 = (½, 0).

17.

Snail path in the xy – plane.
y
1
x
1

18.

Solution. Write down the characteristic
equation for the formula
xn 3 xn 4
xn
.
2
xn 1 xn
4
xn 4
0 12 12 0.
2
Unfortunately, this equation has only two real
solutions, but it definitely has a solution 1 1.
Divide the characteristic polynomial by 1.
( 1)( 12 ).
Denote z n xn 3 xn 2 xn 1 12 xn ,
then z n 1 z n xn 4 xn 3 xn 2 12 xn 1
xn 3 xn 2 xn 1 12 xn xn 4 12 ( xn 1 xn ) 0.
4
1
2
1
2
3
2
1

19.

Therefore z n 1 z n z n 1 z n 2 z1.
z n xn 3 xn 2 xn 1 12 xn
x4 x3 x2 12 x1
12 1 12 12 0 2.
If the sequence xn converges to x , then
lim xn 3 lim xn 2 lim xn 1 lim xn x .
Thus
n
n
n
n
Passing to the limit n in the relationship
xn 3 xn 2 xn 1 12 xn 2
we obtain x x x 12 x 2.
4
Hence x .
7

20.

Snail path in the xy – plane.
y
1
x
1

21.

Answers to Questions from Seminar 2.
1
3
Questions 1b and 1c: lim yn , lim zn .
n
2
2 n
Question 8: n = 20182 – 1.