Stolz-Cesaro Theorem

1.

Calculus++ Light

2.

Question 4. Find the limit of the sequence
2, 2 2 , 2 2 2 , 2 2 2 2 ,
Solution. Our sequence can be written down
as follows
1
2
2 ,2
1 ( 1 )2
2
2
,2
1 ( 1 ) 2 ( 1 )3
2
2
2
,2
1 ( 1 ) 2 ( 1 )3 ( 1 ) 4
2
2
2
2
,
Therefore the nth term of the sequence is given
1 ( 1 ) 2 ( 1 ) 3 ( 1 ) 4 ( 1 ) n
2
by
an 2 2 2 2 2
.
Using the formula for the sum of a geometric
series we obtain
1
1 n 1
(2)
( ) ( ) ( )
1
1
2
1 )n
n
lim
1
(
1
2
1 ( 2 )
n
2.
lim an lim 2 2
1
2
n
1 2
2
1 3
2
n
1 n
2
2
1 ( ) .
1 n
2

3. Stolz-Cesaro Theorem

Let an and bn be two sequences of real numbers.
Assume that:
I. bn as n ,
II. bn is increasing for sufficiently large n,
an 1 an
III. lim
L.
n b
n 1 bn
an
Then lim
L.
n b
n
an
Question 1. an ln n, bn n, lim
?
n b
n
Solution. The conditions I and II of the StolzCesaro theorem are satisfied.

4.

an 1 an
ln( n 1) ln n
lim
lim
n b
n
b
n 1 n
n 1
n
n 1
1
lim ln 1
lim ln
n
n
n
n
1
ln lim 1 ln 1 0.
n n
Thus, the Stolz-Cesaro Theorem tells us that
an
ln n
lim
lim
0.
n b
n n
n
2
n
To find the limit lim n
n 2
either apply the Stolz-Cesaro Theorem
twice,

5.

or write it down as a product
lim
n
n
2
n
n
2
n
,
apply the Stolz-Cesaro Theorem to lim
n
and then use the product rule
lim xn yn lim xn lim yn .
n
n
n
n
2
n

6.

Answers to Questions from Light #1:
Sequences and Limits
1
1
1
Question 0: an
n(n 1) n n 1
17
Question 1:
a650 Question 2: nmin 11
20
Question 4: 10
3
Question 5: x log 2
2018
1 2
A 3, B 2, C 2018, D 2

7.

Calculus++
Also known as
Hysterical Calculus

8.

Question 1a. Find the following limit
1
1
1
1
1
2
3
n
lim
.
n
n
Solution. Use the Stolz-Cesaro theorem.
In this case bn n .
The sequence bn is infinitely large and
increasing. Hence, the conditions I and II of
the Stolz-Cesaro theorem are satisfied.
1
an
1
1
an 1
1
1
2
1
2
1
1
an 1 an
n
n 1
1
1
n
n 1

9.

an 1 an
1
1
bn 1 bn
n 1 n 1 n
1
n 1 n
1
n 1 n 1 n n 1 n
1
n 1 n
1
n 1
an 1 an
n
2.
lim 1
Hence lim
n b
n
b
n
1
n 1
n
The Stolz-Cesaro Theorem tells us that
1
1
1
1
an
1
2
3
n
2.
lim
lim
n
n b
n
n

10. Cauchy Criterion

A sequence xn, n = 1,2,3,… is called a
fundamental sequence (or Cauchy
sequence) if for any 0 we can find a
number N such that, for any n > N and any
m > 0:
x x .
n m
n
Theorem (Cauchy Criterion). A sequence xn,
n = 1,2,3,…, converges if and only if it is a
Cauchy sequence.

11.

Definition (of non-fundamental sequences).
A sequence xn, n = 1,2,3,… is not a Cauchy
sequence if we can find 0 such that, for
any number N, we can find n > N and m > 0,
such that xn m xn .

12.

Question 3. The sequence –1, +1, –1, +1,… is
not a Cauchy sequence (and, hence, it
diverges).
Solution. Let 1, and let N be any natural
number. Take n = 2N + 1, m = 1.
Since n is odd and n + m is even, we have
xn= –1 and xn+m = +1.
Hence xn m xn 1 ( 1) 2 .
Therefore, the sequence
{xn} = –1, +1, –1, +1, …
is not a Cauchy sequence.

13.

Question 4. Use the Cauchy criterion to show
that the sequence
n
1
xn , n 1,2,3, ,
k 1 k
diverges.
Solution: According to the Cauchy criterion it
is sufficient to show that {xn} is not a
fundamental sequence:
0, N , n N , m 0 : xn m xn .
We have
n m
1
xn m xn
k n 1 k
n m
m
1
.
n m
k n 1 n m

14.

Choosing m = n we obtain
m
n
1
xn m xn
.
n m n n 2
Thus, 0 (for instance, 14 ), N
n N (for instance, n N 1),
1
(we
set
m
=
n):
x
x
m 0
n m
n
4.
1
2
Therefore, our sequence {xn} is not
fundamental, and the Cauchy criterion tells
us that {xn} diverges.

15.

Question 5. Use the Cauchy criterion to show
n
1
that the sequence xn 2 , n 1,2, ,
k 1 k
converges.
Solution: It is sufficient to show that the
sequence xn is fundamental:
0, N , n N , m 0 : xn m xn .
n m
n m
1
1
We have xn m xn 2
k n 1 k
k n 1 ( k 1) k
n m
1 1
1
1
1
1
k n n 1 n 1 n 2
k n 1 k 1
1
1
1
1
n m 1 n m
n 2 n 3

16.

m
1
1
1
.
n n m n ( n m) n
1
Thus xn m xn .
n
1
Therefore 0, N , we set N
,
n N , m 0 :
1 1
1
xn m xn 1 .
n N
Thus, the sequence xn is fundamental, and
therefore it converges to some limit L.
In fact, L
2
6
.

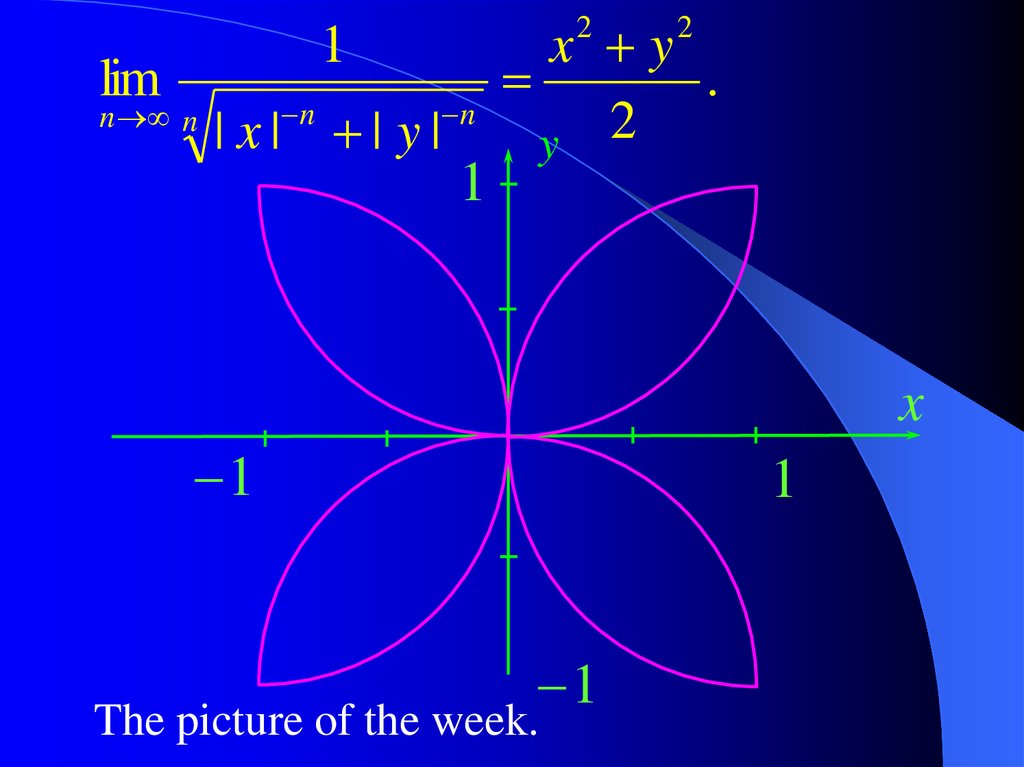
17. Picture of the Week

18.

Question 8. Draw the curve defined by the
1
equation lim
n n
n
| x| | y|
x y
.
2
2
n
2
Solution. We already know that
lim | x | | y | max(| x |, | y |).
n
1
Therefore lim
n
n
n
| x| | y|
n
n
n
| x| | y|
| x || y |
| x || y |
lim
n
n
n n
max(| x |, | y |)
| x| | y|
min(| x |, | y |).
n
n
n

19.

Thus, we have to draw the curve defined by
the equation
2
2
x y
min(| x |, | y |)
.
2

20.

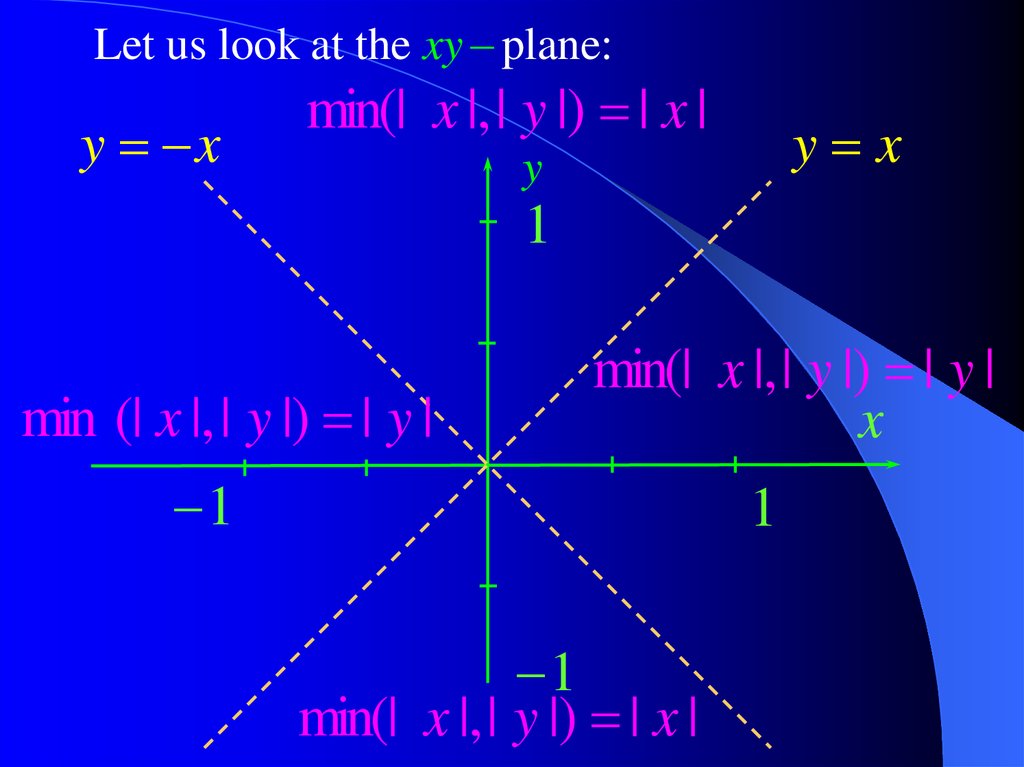
Let us look at the xy – plane:
y x
min(| x |, | y |) | x |
y x
y
1
min (| x |, | y |) | y |
min(| x |, | y |) | y |
x
1
1
1
min(| x |, | y |) | x |

21.

x y
The curve defined by the equation y
2
2
2
is the circle with the radius 1, centred at the
point (0,1).
2
2
Indeed,
x y 2y 0
x y 2 y 1 1
2
2
x ( y 1) 1.
2
2
x y
The curve defined by the equation x
2
2
is the circle with the radius 1, centred at the
point (1,0):
2
2
( x 1) y 1.
2

22.

The equations of our curve.
( x 1) y 1 ( x 1) y 1
y
y x
1
y x
2
2
2
x ( y 1) 1
x
2
x ( y 1) 1
2
2
2
1
2
2
x ( y 1) 1
2
1
2
2
x ( y 1) 1
( x 1) y 11
2
2
( x 1) y 1
2
2

23.

lim
1
n n
n
| x| | y|
x y
.
y 2
2
n
1
2
x
1
1
1
The picture of the week.

24.

Answers to Questions from Seminar 1.
Question 2: 13 .
n
n
5
1
Question 3: an 6 2 3 ( 1)
a100 a99 5 2
Question 8b:
98
lim sin n n 1.
2
n
2
2 n
Question 8c: lim sin
0.
n
3n 1
1, for 0 x 1;
Question 9: y x, for 1 x 2;
1 x 2 , for 2 x.
2
n