Similar presentations:
Calculus
1. Calculus
Патрик Анатолий ЕвгеньевичPatrick Anatoly
Urgent messages (from 9:00 till 21:00)
patrick.anatoly.icef@gmail.com
Send non-urgent messages (at any time) to
apatrik@hse.ru
2.
SpringExam
18 %
The Final Calculus
Exam
42 %
December
Exam 24 %
Autumn
Exam
The battles we
must win
in 2022-23
16 %
3.
Exam FormatsPart I: 30 Multiple Choice questions: choose
ONE correct answer from FIVE.
Duration: 90 minutes
Part II: 4 (Autumn), 5 (Winter), or 6 (Spring
and Summer) free-response questions.
Duration: 80, 90, or 100 minutes.
2019, 2020, 2021 Calculus Autumn Exam
papers will be available before the end of
September.
4.
Functions: bad, good, and funnyBasic elementary functions f (x) are: constants c,
1
n where n is a
n
n
n
x natural number
x , x x,
(inverse)
(reciprocal)
x
a ,
sin x,
cos x ,
tan x,
log a x,
a
x
where a > 0
1
arcsin x, csc x
sin x
1
arccos x , sec x
cos x
1
arctan x, cot x
tan x
5.
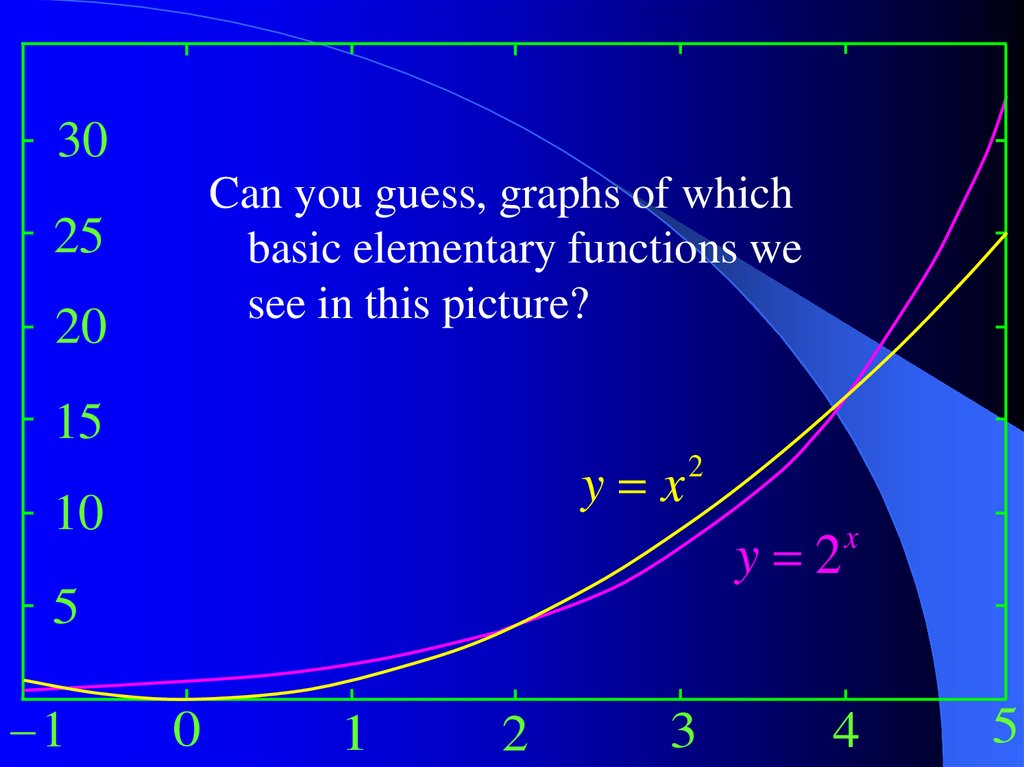
30Can you guess, graphs of which
basic elementary functions we
see in this picture?
25
20
15
y x
10
2
y 2
x
5
1
0
1
2
3
4
5
6.
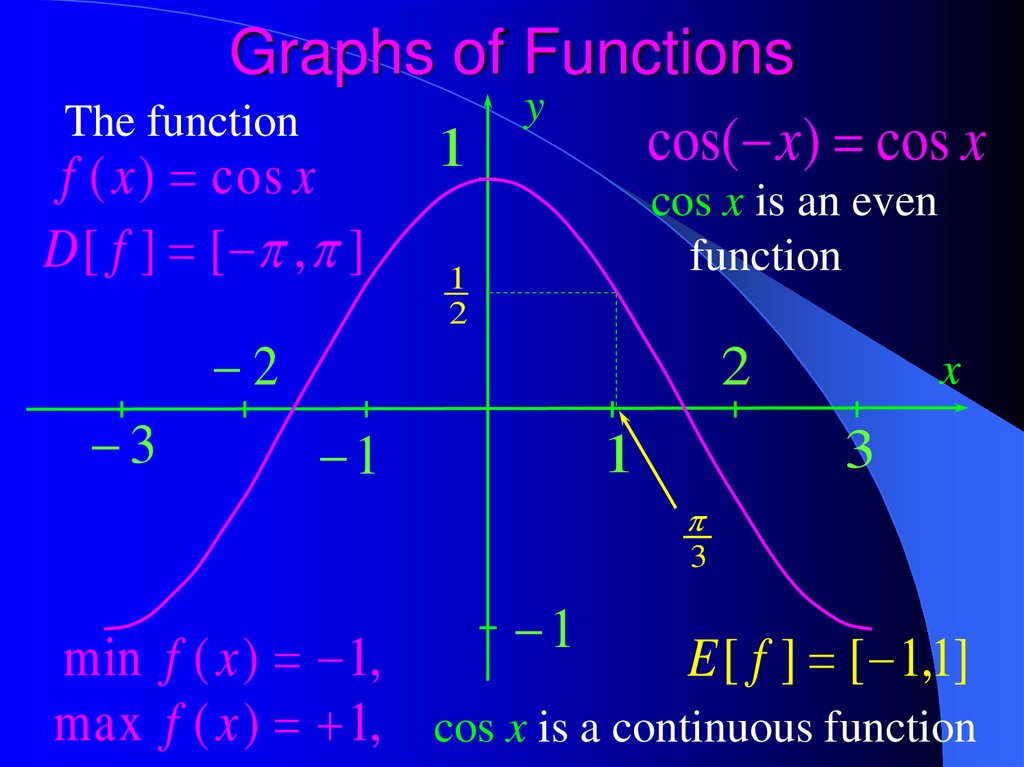
Graphs of Functionsy
The function
cos( x) cos x
1
f ( x ) cos x
D [ f ] [ , ]
2
3
cos x is an even
function
1
2
2
1
x
3
1
3
1
min f ( x ) 1,
E [ f ] [ 1,1]
max f ( x ) 1, cos x is a continuous function
7.
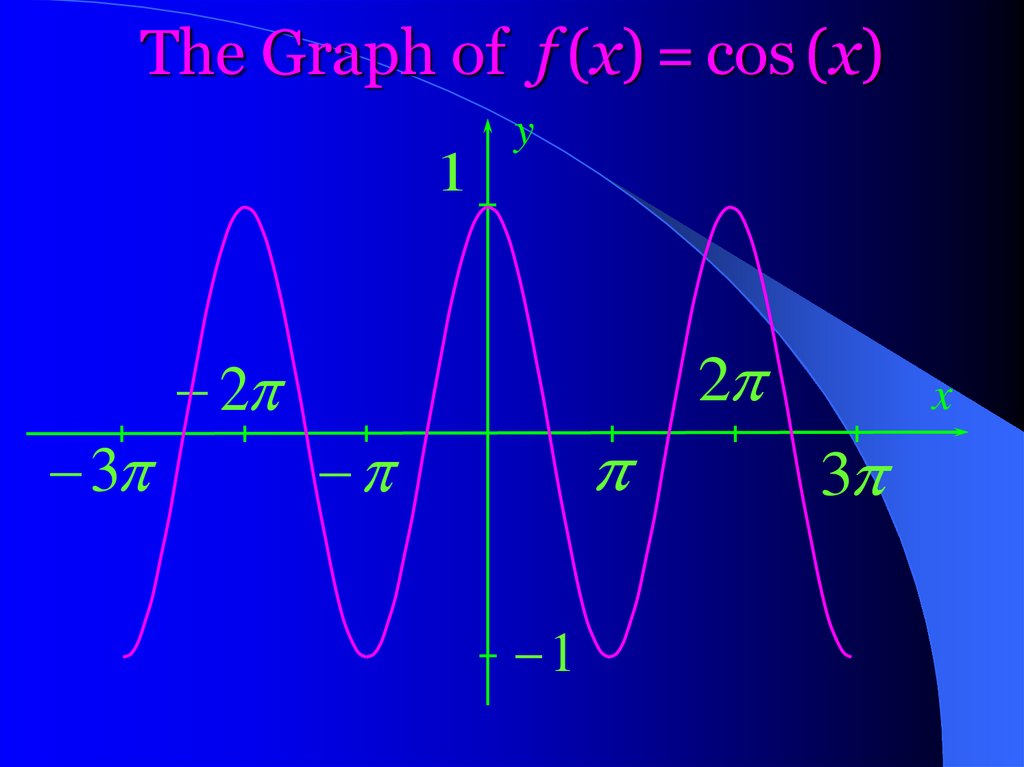
The Graph of f (x) = cos (x)1
3
2
y
2
1
x
3
8.
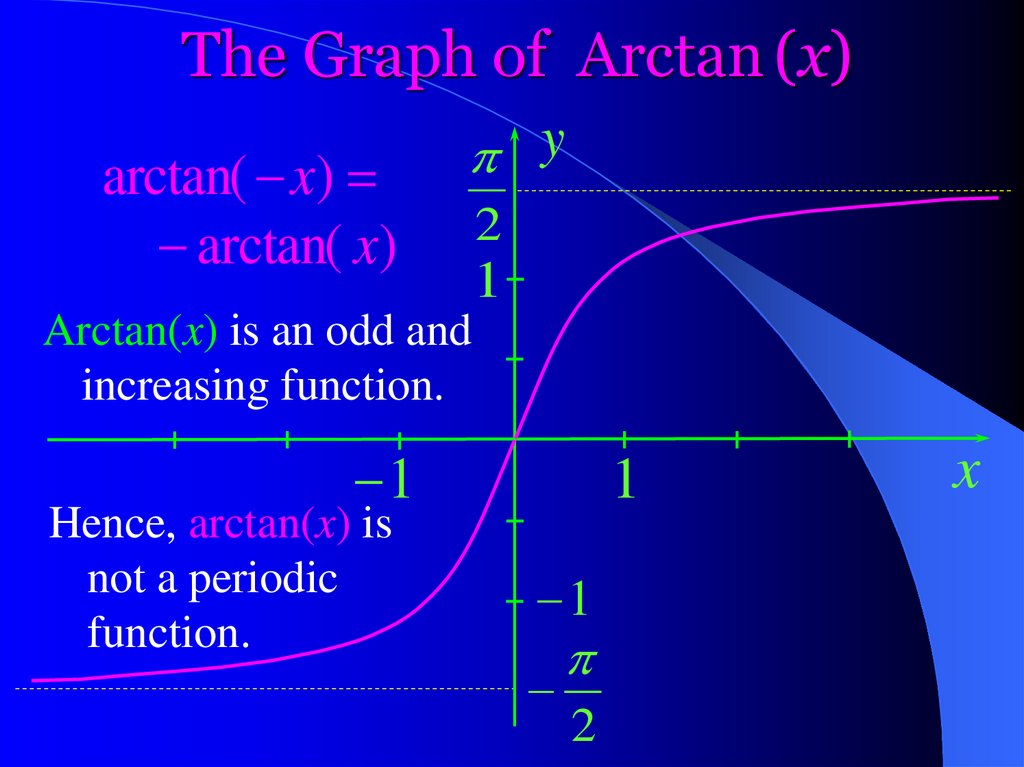
The Graph of Arctan (x)arctan( x)
arctan( x)
y
2
1
Arctan(x) is an odd and
increasing function.
1
Hence, arctan(x) is
not a periodic
function.
1
1
2
x
9.
Inverse FunctionsA function g (x) is called inverse to the
function f (x) if g ( f (x)) = x for all x D ( f ).
Often, the function inverse to f (x) is denoted
f –1(x).
To find the inverse function f –1(x), we have to
solve the equation x = f (y) for y.
Not every function f (x) is invertible.
In order to be invertible, a function f (x) must
obtain every value from its range exactly
once.
Functions like that are called “one-to-one”.
10.
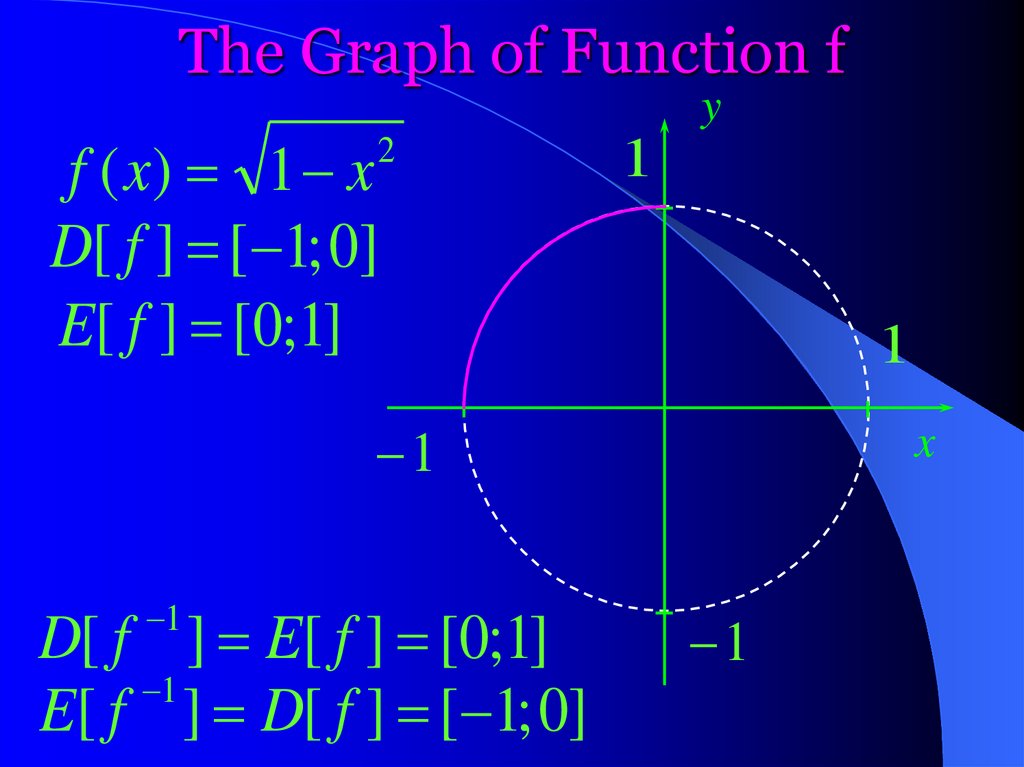
Question 1. The function f is defined byf ( x) 1 x , where 1 x 0.
Find the inverse function f 1 ( x ).
2
Solution. First we draw the graph of the
function f.
y 1 x
2
y 1 x x y 1
2
2
2
2
Therefore the graph of the function f is a part
of the circle with radius 1 centred at (0;0).
11.
The Graph of Function ff ( x) 1 x
D[ f ] [ 1; 0]
E[ f ] [0;1]
2
y
1
1
1
1
D[ f ] E[ f ] [0;1]
1
E[ f ] D[ f ] [ 1; 0]
x
1
12.
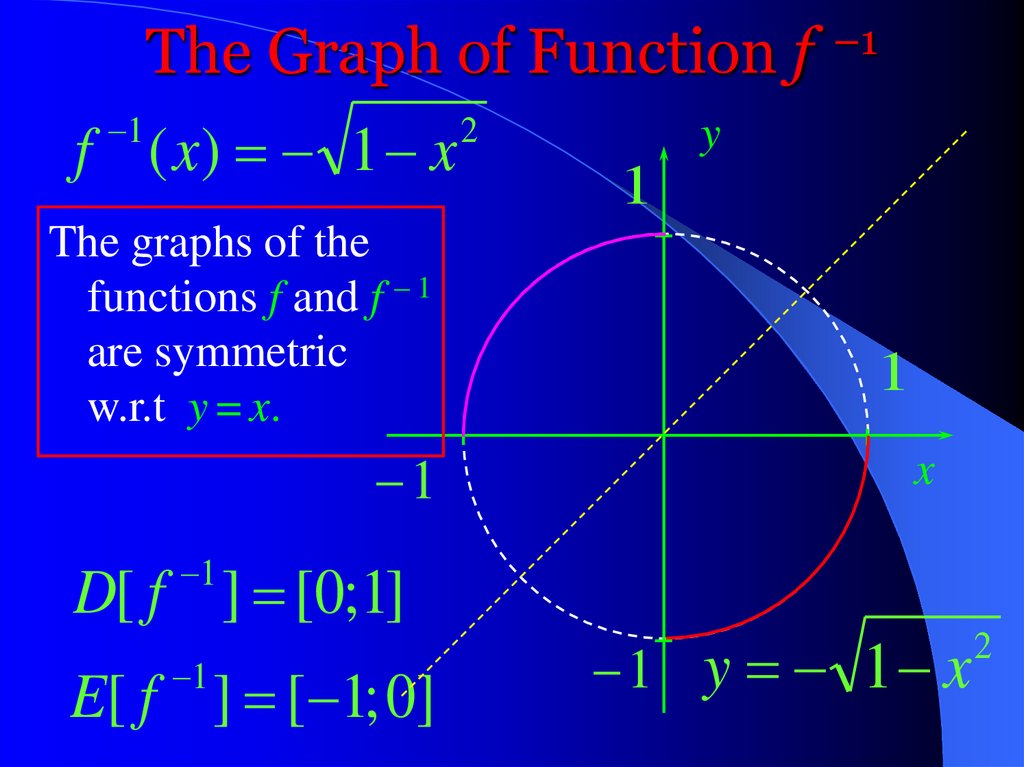
Solution (continues). To find the formula forthe inverse function f –1 we have to solve the
equation x 1 y 2 for y.
x 1 y
2
x 1 y y 1 x
y 1 x
2
2
2
2
The range of the inverse function f –1 is the
interval [ – 1; 0], therefore we take the
negative solution y 1 x .
Therefore the inverse function f –1 is also a
part of the unit circle and it is given by
2
f ( x) 1 x , where 0 x 1.
1
2
2
13.
–1The Graph of Function f
1
f ( x) 1 x
The graphs of the
functions f and f – 1
are symmetric
w.r.t y = x.
1
y
2
1
1
x
1
D[ f ] [0;1]
1
E[ f ] [ 1; 0]
1 y 1 x
2
14.
New Functions from OldWe can add, divide, and multiply basic
elementary functions.
If we apply those operations a finite number
of times, then the obtained result will be an
elementary function.
Example 1 (Polynomials).
Linear functions: P1(x) = a x + b,
g1(x) = 20 x + 22, g1(x) has exactly one root.
Quadratic polynomials: P2(x) = a x2 + b x + c,
g2(x) = x2 + 20 x + 23, g2(x) has exactly two
roots.
15.
New Functions from OldExample 1 (Polynomials).
A polynomial of degree n:
Pn(x) = an x n + an – 1 x n – 1 + an – 2 x n – 2 + … +
+ a2 x 2 + a1 x + a0
Every polynomial of positive degree n has at
most n real roots.
16.
New Functions from OldHowever, if we add and/or multiply c and x
infinitely many times, the result is not
necessarily an elementary function.
x x x x ln( 1 x ),
if 1 x 1.
n
1 2
1 3
1
x 4 x 9 x n 2 x Li 2 ( x),
if 1 x 1.
1
2
2
1
3
3
1
n
n
Li2(x) is called dilogarithm.
It is not an elementary function, but the shape
of its graph is very similar to the shape of
the graph of – ln(1 – x).
17.
Question 0 (GRE Mathematics). Suppose thatf (1 + x) = f (x) for all real x.
If f is a polynomial and f (5) = 22, then f (15/2)
is
a) 22 b) 0 c) 22 d ) 332
e) not uniquely determined by the given info
Solution: If f (1 + x) = f (x) for all real x, then
the polynomial equation f (x) = 22 has
infinitely many roots: x1 = 5, x2 = 6, x3 = 7,
x4 = 8, ….
That is possible only if f (x) is actually a
constant function f (x) = 22.
Therefore f (15/2) = 22.
18.
New Functions from OldAlso, we can combine elementary functions.
If f (x) and g(x) are elementary functions, then
h(x) = f (g(x)) is another elementary functions
called the composition of f and g .
x
Example 2. Let f ( x )
, g ( x ) sin( 3 x ).
1 x
a) Find the functions f (g(x)) and g( f (x)).
g ( x)
sin( 3 x)
Solution.
f ( g ( x))
1 g ( x)
.
1 sin( 3 x)
3x
g ( f ( x )) sin( 3 f ( x)) sin
.
1 x
19.
xExample 2. Let f ( x )
, g ( x ) sin( 3 x ).
1 x
b) Find the domains of f (g(x)) and g( f (x)).
Solution. g(x) is defined for any x.
g ( x)
f ( g ( x))
1 g ( x)
Therefore, f (g(x)) is defined if sin( 3 x ) 1.
That is, if 3 x arcsin( 1) 2 n, n Z .
D[ f g ] {x R : x 6 23 n, n Z }
3x
Since g ( f ( x )) sin
, it is defined if
1 x
1 x 0.
D[ g f ] {x R : x 1}













 mathematics
mathematics








