Similar presentations:
Irrational Numbers
1.
Calculus++ Light2. Irrational Numbers
3.
Question 1. The Dirichlet function is defined1, if x is rational
as follows f ( x )
0, if x is irrational
Is this function even or odd or neither?
Is this function periodic? If yes, find a period
of this function.
Solution. If x is a rational number, so is – x.
k k
.
n
n
If x is a irrational number, so is – x.
Hence f (– x) = f (x), and therefore the Dirichlet
function is even.
4.
The sum of two rational numbers is a rationalk
k
k
n
k
n
1
2
1
2
2
1
number:
.
n1 n2
n1n2
The sum of a rational and an irrational number
is an irrational number.
Let x be a rational number, let y be an
irrational number, and let us assume that
z = x + y is a rational number.
Then y = z + (– x) is also a rational number.
Contradiction!
Hence, the sum of a rational and an irrational
number is an irrational number.
5.
Therefore f (x + y) = f (x) for any rationalnumber y.
Thus, the Dirichlet function is periodic.
Any rational number is a period of this
function.
However, unlike trigonometric functions
sin(x) or cos(x), the Dirichlet function does
not have minimal (or principal) period T.
6.
Question 2. The numbers 2 and 3 areirrational. Show that the number 2 3
is irrational too.
Solution. We have 2 3
3 2 3 2
3 2
1
.
3 2
3 2
3 2
If 2 3 is a rational number, then
1
m
n
2 3
3 2
m
2 3 n
1
1 n m
3 2 3 2
2
2
2 m n
7.
n mis a rational number.
2
2m n
2
2
Contradiction!!!
Therefore our assumption was incorrect and
2 3 is an irrational number.
8.
Question 3. Letf ( x) x x x x x ,
and denote g ( x) f 1 ( x).
1
2
2
1
3
3
1
4
4
1
5
5
Find a general formula for the second
derivative of inverse function, g (x), and
calculate g (0).
1
Solution. We know that g ( x)
.
The chain rule yields
f ( g ( x))
1
g ( x)
f ( g ( x)) g ( x).
2
( f ( g ( x)))
f ( g ( x))
.
g ( x)
3
( f ( g ( x)))
9.
f ( x) x x x x xf ( g ( x))
g ( x)
.
3
( f ( g ( x)))
1
2
2
1
3
3
1
4
4
1
5
5
Since f (0) = 0, we have g (0) = 0.
f ( x) 1 x x x x f ( g (0)) 1
2
3
f ( x) 1 2 x 3x 4 x f ( g (0)) 1
2
g (0) 1.
3
4
10.
Question. Which of the following conditionsimply that a real number x is rational?
I. x is rational
II. x2 and x5 are rational
III. x2 and x4 are rational
a) I only b) II only c) I and II only
d) I and III only e) II and III only
m
Solution: If x is rational, then x .
2
n
m
Therefore x 2 is also rational.
n
Counterexample to III: 2 is irrational, but
2
2
2 and
2
4
2 4 are rational.
2
11.
Let now x2 and x5 be rational:k
m
5
2
and x .
x
l
n
If m = 0, then x2 = 0, x5 = 0, and x = 0 is a
rational number.
x5
k n2
.
In all other cases x 2 2
2
(x )
l m
Therefore x is a rational number.
a) I only b) II only c) I and II only
d) I and III only e) II and III only
12.
Calculus++Also known as
Hysterical Calculus
13.
Question 1. Show that 2 is irrational.Solution. Any integer number n is either even,
n = 2k, or odd, n = 2k + 1, where k is another
integer number.
The square of an odd number is odd
(2k 1) 4k 4k 1 2(2k 2k ) 1.
2
2
2
Hence n2 can be even only if n is even.
Analogously, the square of an even number is
even: (2k)2 = 4 k2 = 2(2 k2).
Hence n2 can be odd only if n is odd.
That is n2 is even (odd), if and only if n is
even (odd).
14.
Let us now assume that2 is a rational
k
number, that is 2 , where, k and n, do
n
not have common factors.
In particular, either both k and n are odd, or
only one of them is even.
2
k
Then 2 2
n
k 2n .
2
2
That is, k2 is even, and hence k is also even:
k = 2m, where m is another integer number.
2
2
2
2
But then 2n 4m n 2m .
That is, n2 is even, and hence n is also even.
Contradiction!
15.
Thus, our assumption that 2 is a rationalnumber leads to a contradiction, and hence
this number is irrational.
Remark. Using a similar argument one can
show that 3 2 is an irrational number.
To show that 3 is an irrational number, note
that any integer number n is either divisible
by 3: n = 3k,
or n = 3k +1,
or n = 3k +2.
16. Higher derivatives
Notations for n-th order derivatives:n
d
f (x) or
n
dx
f
(n)
( x).
The following properties are often useful for
calculating high-order derivatives:
n
n
n
d f ( x) d g ( x)
d
( f ( x) g ( x))
n
n
n
dx n n dx
dx n k
d x
d x
if
k
<
n,
0
,
n!,
n
n
dx
dx
n k
d x
k!
k n
if
k
>
n.
and
x
,
k
dx
(k n)!
17.
Question 5. Find the n-th derivative of then
function
x
f ( x)
1 x
.
Solution. Recall the formula for the sum of a
geometrical series
n
1 x
1 x x x
.
1 x
n
n
x 1 1
1 1 x
Hence f ( x)
1 x
1 x 1 x
1
2
n 1
(1 x x x ).
1 x
2
n 1
18.
Thereforen
n
n
d
d
1
d
2
n 1
f ( x) n
n (1 x x x )
n
dx
dx 1 x dx
1
d 1
0
2
dx 1 x (1 x)
2
d
1
2
d
1
2
3
2
dx 1 x dx (1 x) (1 x)
3
2 3
d
2
d 1
4
3
3
dx 1 x dx (1 x) (1 x)
4
2 3 4
d 2 3
d
1
5
4
4
(1 x)
dx 1 x dx (1 x)
19.
nd
n!
Thus
f ( x)
.
n
n 1
dx
(1 x)








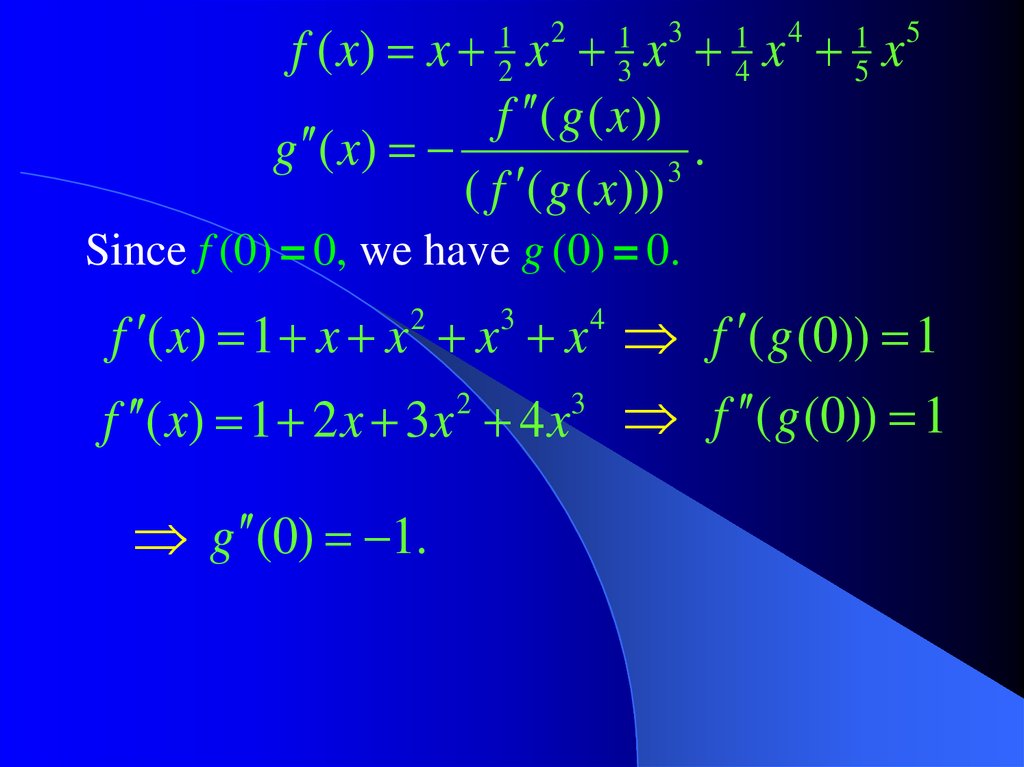










 mathematics
mathematics








