Data Structures and Algorithms

1. Snímek 1

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
Data Structures and Algorithms
Petr Felkel
[email protected]
DSA
Marko Genyk-Berezovskyj
[email protected]
http://service.felk.cvut.cz/courses/X36DSA
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
0/1

2. Snímek 2

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
INTRO
Různé algoritmy
mají
různou složitost
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
1/1

3. Snímek 3

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
INTRO
The complexity
of different algorithms
varies
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
2/ 1

4. Snímek 4

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
The speed...
One algorithm (program, method…)
is faster than another one.
Jeden algoritmus (program, metoda…)
je rychlejší než druhý.
What does it this sentence mean ??
Co ta věta znamená ??
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
3/1

5. Snímek 5

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
4/1
Asymptotic complexity
y
y
x
x
Každému algoritmu lze jednoznačně přiřadit rostoucí funkci,
zvanou asymptotická složitost,
která charakterizuje počet operací algoritmu.
Čím pomaleji tato funkce roste, tím je algoritmus rychlejší.
Each algorithm can be unambiguously assigned a growing function
referred to as asymptotic complexity
which characterizes the number of operations of the algorithm.
The slower the is growth of this function the faster is the algorithm.
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

6. Snímek 6

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
5/1
INTRO
Find min and
maxand
in min
the in
array
— STANDARD
Find max
the array
min
max
3
3
min
max
3
3
3
2
7
10
0
5 –10 4
6
3
2
7
10
0
5 –10 4
6
if (a[i] < min) min = a[i];
if (a[i] > max) max = a[i];
min
max
2
3
3
2
7
10
0
5 –10 4
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
6

7. Snímek 7

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
6/1
INTRO
Find min and max in the array — STANDARD
min
max
2
7
3
2
7
10
0
5 –10 4
6
etc...
finished
code
min
max
–10
10
3
2
7
10
0
5 –10 4
min = a[0]; max = a[0];
for ( i = 1; i < a.length; i++) {
if (a[i] < min) min = a[i];
if (a[i] > max) max = a[i]; }
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
6

8. Snímek 8

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
7/1
INTRO
Find minFind
andmax
max
inmin
theinarray
— FASTER!
and
the array
min
max
3
3
min
max
3
3
3
2
7
10
0
5 –10 4
6
3
2
7
10
0
5 –10 4
6
if (a[i] < a[i+1]) {
if ( a[i] < min) min = a[i];
if (a[i+1] > max) max = a[i+1];}
min
max
2
7
3
2
7
10
0
5 –10 4
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
6

9. Snímek 9

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
8/1
INTRO
and
the array
Find minFind
andmax
max
inmin
theinarray
— FASTER!
min
max
3
3
3
2
7
10
0
5 –10 4
6
if (a[i] < a[i+1]) {
if ( a[i] < min) min = a[i];
if (a[i+1] > max) max = a[i+1];}
else {
if ( a[i] > max) max = a[i];
if (a[i+1] < min) min = a[i+1];}
min
max
0
10
3
2
7
10
0
5 –10 4
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
6

10. Snímek 10

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
9/1
INTRO
Find min and max in the array — FASTER!
finished
code
min
max
–10
10
3
2
7
10
0
5 –10 4
6
min = a[0]; max = a[0];
for (i=1; i < a.length-1; i=i+2 ) {
if (a[i] < a[i+1]) {
if ( a[i] < min) min = a[i];
if (a[i+1] > max) max = a[i+1];}
else {
if ( a[i] > max) max = a[i];
if (a[i+1] < min) min = a[i+1];}}
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

11. Snímek 11

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
INTRO
Elementary operation
compare two numbers
or
arithmetic operation or
move one number
A
Complexity
total number of elementary operations
Složitost
celkový počet elementárních operací
simplification
zjednodušení
B
Complexity
total number of elementary operations on the data
Složitost
celkový počet elementárních operací nad daty
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
10 / 1

12. Snímek 12

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
INTRO
B
Complexity
total number of elementary operations on the data
Složitost
celkový počet elementárních operací nad daty
further
simplification
další
zjednodušení
C
Complexity
total number of number (character) comparisons
in the data
Složitost
celkový počet porovnání čísel (znaků)
.v datech
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
11 / 1

13. Snímek 13

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
12 / 1
INTRO
Find min and max in the array — STANDARD
complexity
A
All
operations
1
a.length = N
1
min = a[0]; max = a[0];
1
N
N–1
for ( i = 1; i < a.length; i++){
N–1
0...N–1
if (a[i] < min) min = a[i];
N–1
0...N–1
if (a[i] > max) max = a[i]; }
Best
1 + 1 + 1 + N + N–1 + N–1 +0 + N–1 + 0 = 4N+4 ops
Worst
1 + 1 + 1 + N + N–1 + N–1 +N–1 + N–1 + N–1 = 6N–2 ops
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

14. Snímek 14

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
13 / 1
INTRO
Find min and max in the array — STANDARD
complexity
B
operations
on data
1
a.length = N
1
min = a[0]; max = a[0];
for ( i = 1; i < a.length; i++){
N–1
0...N–1
if (a[i] < min) min = a[i];
N–1
0...N–1
if (a[i] > max) max = a[i]; }
Best
Worst
1 + 1 + N–1 +0 + N–1 + 0 = 2N ops
1 + 1 + N–1 + N–1 + N–1 + N–1 = 4N–2
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
ops

15. Snímek 15

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
14 / 1
INTRO
Find min and max in the array — STANDARD
complexity
C
tests only
on data
a.length = N
min = a[0]; max = a[0];
for ( i = 1; i < a.length; i++){
N–1
if (a[i] < min) min = a[i];
N–1
if (a[i] > max) max = a[i]; }
always
N–1 + N–1 = 2N–2 tests
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

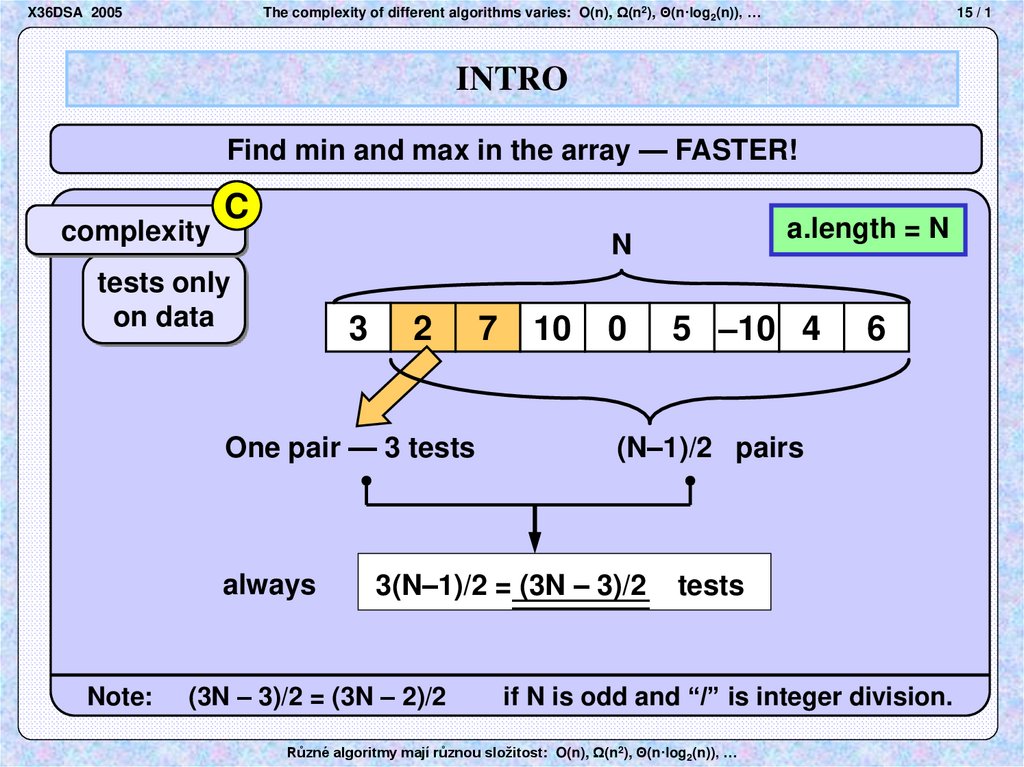
16. Snímek 16

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
15 / 1
INTRO
Find min and max in the array — FASTER!
complexity
C
tests only
on data
3
2
One pair — 3 tests
always
Note:
a.length = N
N
7
10
0
6
(N–1)/2 pairs
3(N–1)/2 = (3N – 3)/2
(3N – 3)/2 = (3N – 2)/2
5 –10 4
tests
if N is odd and “/” is integer division.
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

17. Snímek 17

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
16/ 1
INTRO
Array size N
STD method
comparisons
2 (N – 1)
10
18
14
1.29
20
38
29
1.31
50
98
74
1.32
100
198
149
1.33
200
398
299
1.33
500
998
749
1.33
1 000
1 998
1 499
1.33
2 000
3 998
2 999
1.33
5 000
9 998
7 499
1.33
1 000 000
1 999 998
1 499 999
1.33
Tab. 1
FAST method ratio STD/FAST
comparisons
(3N – 2)/2 *)
*) integer division
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

18. Snímek 18

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
INTRO
data
problem
array a:
4
2
4
3
4
2
7
array b:
1
–1
0
–2
5
1
0
Kolik prvků pole a je rovno součtu prvků pole b?
How many elements of array a are equal to the sum of array b?
soution
array a:
4
2
4
3
4
2
7
array b:
1
–1
0
–2
5
1
0
Result == 3
sum of b == 4
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
17 / 1

19. Snímek 19

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
INTRO
function
SLOW
method
FAST
method
int sumArr(int[] arr) {.../*easy*/}
count = 0;
for (int i = 0; i < a.length; i++)
if (a[i]==sumArr(b)) count++;
return count;
count = 0;
sumOf_b = sumArr(b);
for (int i = 0; i < a.length; i++)
if (a[i]==sumOf_b) count++;
return count;
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
18/ 1

20. Snímek 20

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
19 / 1
INTRO
array a:
4
2
4
3
4
2
7
SLOW
method
array b:
array a:
FAST
method
array b:
size of a ≈ n
size of b ≈ n
≈nxn
operations
1
4
–1
2
0
4
sum of b:
1
–1
–2
3
5
4
1
2
0
7
≈2xn
operations
4
0
–2
size of a ≈ n
size of b ≈ n
5
1
0
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

21. Snímek 21

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
20 / 1
INTRO
Array size N
SLOW method
operations
N2
FAST method
operations 2N
ratio
SLOW/FAST
10
100
20
5
20
400
40
10
50
2 500
100
25
100
10 000
200
50
200
40 000
400
100
500
250 000
1 000
250
1 000
1 000 000
2 000
500
2 000
4 000 000
4 000
1 000
5 000
25 000 000
10 000
2 500
2 000 000 4 000 000 000 000
4 000 000
1 000 000
Tab. 2
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

22. Snímek 22

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
21 / 1
INTRO
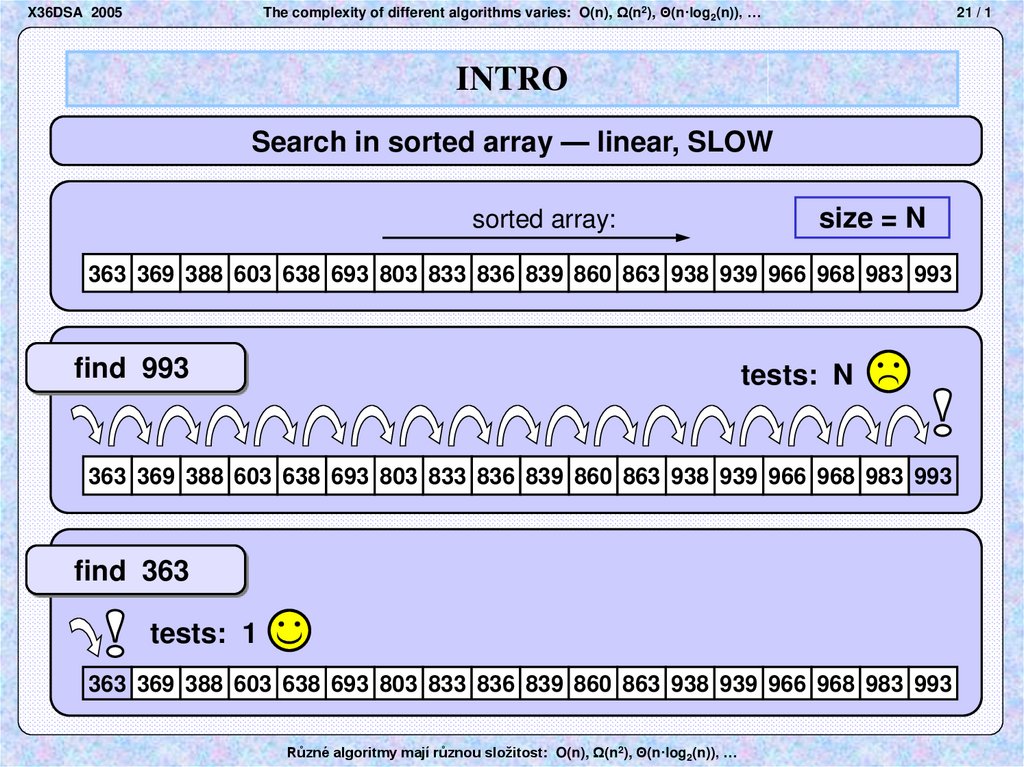
Search in sorted array — linear, SLOW
sorted array:
size = N
363 369 388 603 638 693 803 833 836 839 860 863 938 939 966 968 983 993
find 993
tests: N
363 369 388 603 638 693 803 833 836 839 860 863 938 939 966 968 983 993
find 363
tests: 1
363 369 388 603 638 693 803 833 836 839 860 863 938 939 966 968 983 993
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

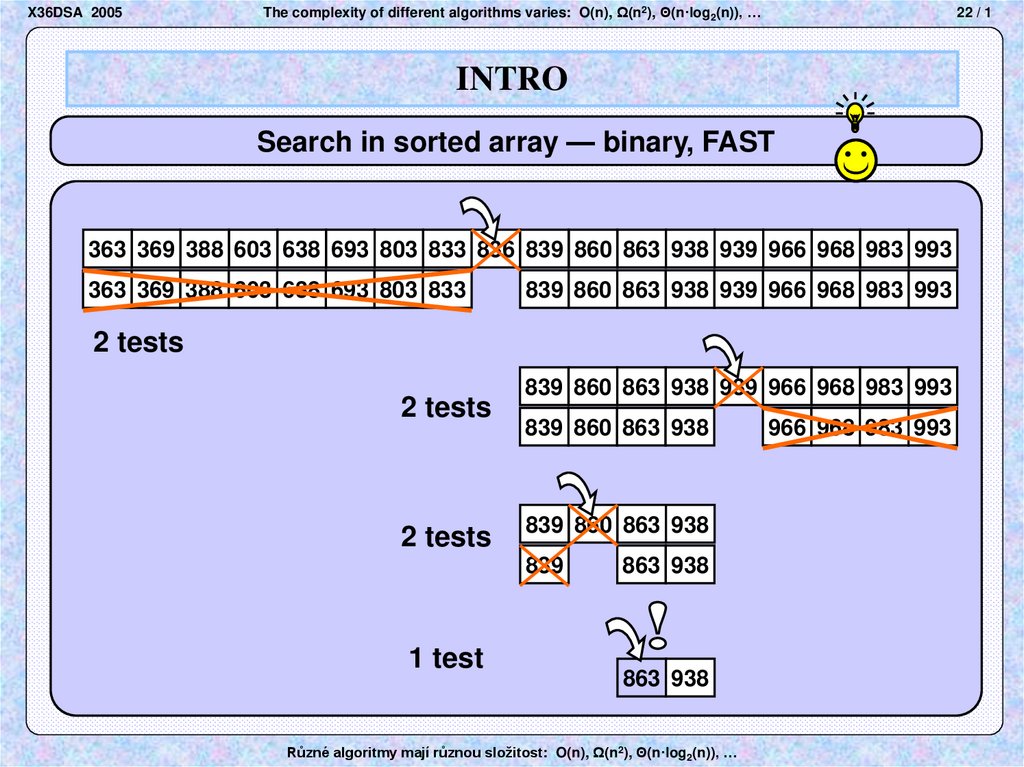
23. Snímek 23

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
22 / 1
INTRO
Search in sorted array — binary, FAST
363 369 388 603 638 693 803 833 836 839 860 863 938 939 966 968 983 993
363 369 388 603 638 693 803 833
839 860 863 938 939 966 968 983 993
2 tests
2 tests
2 tests
839 860 863 938 939 966 968 983 993
839 860 863 938
839 860 863 938
839
1 test
863 938
863 938
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
966 968 983 993

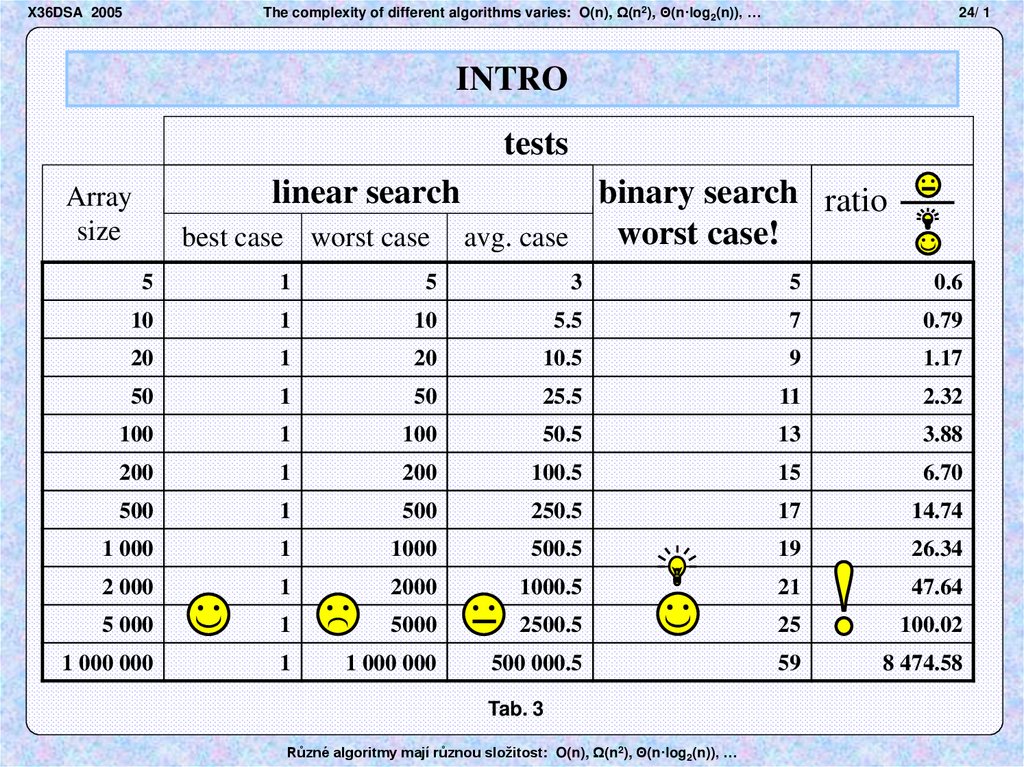
24. Snímek 24

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
23 / 1
INTRO
N
…
k
…
. . .
8
8 =23
3
4
4 =22
2
2
1
0
N =2k
2 =21
1
1 =20
N = 2k =>
k = log2(N)
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

25. Snímek 25

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
24/ 1
INTRO
tests
linear search
binary search ratio
worst case!
best case worst case avg. case
Array
size
5
1
5
3
5
0.6
10
1
10
5.5
7
0.79
20
1
20
10.5
9
1.17
50
1
50
25.5
11
2.32
100
1
100
50.5
13
3.88
200
1
200
100.5
15
6.70
500
1
500
250.5
17
14.74
1 000
1
1000
500.5
19
26.34
2 000
1
2000
1000.5
21
47.64
5 000
1
5000
2500.5
25
100.02
1 000 000
1
1 000 000
500 000.5
59
8 474.58
Tab. 3
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

26. Snímek 26

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
25/ 1
Order of growth
The computation time
for various time complexities
assuming that 1 operation takes 1 s (10-6 sec)
10
20
40
60
500
1000
log2 n
3,3 s
4,3 s
5 s
5,8 s
9 s
10 s
n
10 s
20 s
40 s
60 s
0,5ms
1ms
n log2 n
33 s
86 s
0,2ms
0,35ms
4,5ms
10ms
n2
0,1ms
0,4ms
1,6ms
3,6ms
0,25s
1s
n3
1ms
8ms
64ms
0,2s
125s
17min
n4
10ms
160ms
2,56s
13s
17h
11,6days
2n
1ms
1s
n!
3,6s
77000 yrs
12,7 days 36000 yrs 10137 yrs 10287yrs
1034 yrs
1068yrs
101110yrs 102554yrs
Tab. 4
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

27. Snímek 27

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
Order of growth
Order of growth of functions
Řád růstu funkcí
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
26 / 1

28. Snímek 28

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
Order of growth
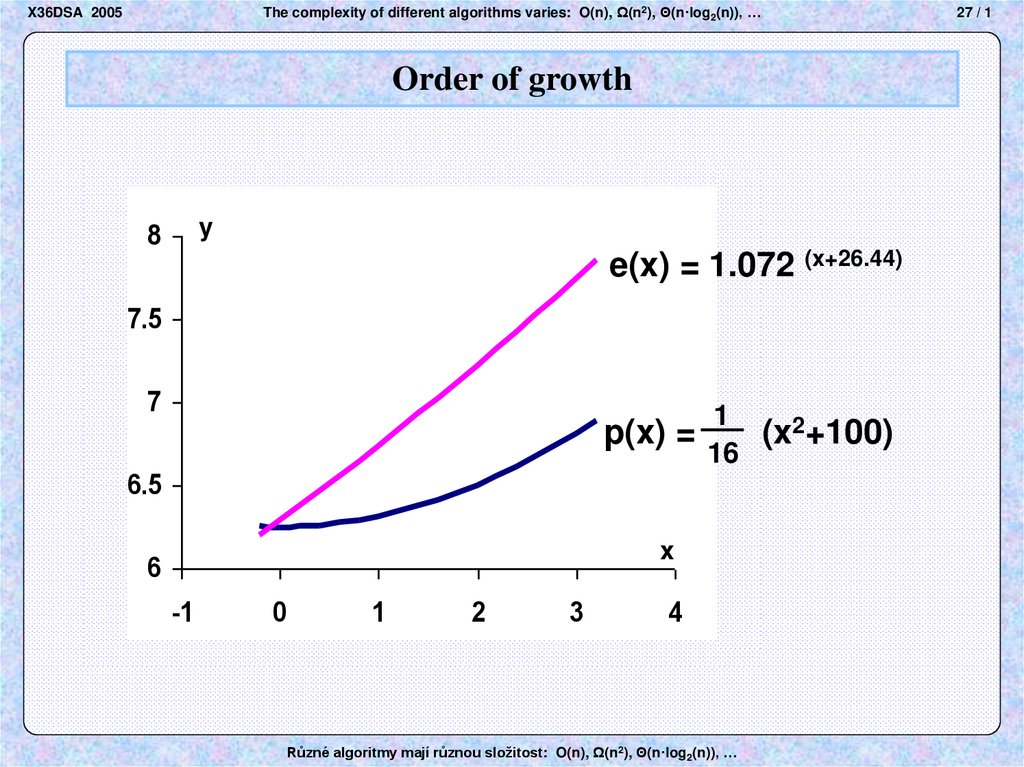
y
8
e(x) = 1.072 (x+26.44)
7.5
7
1
p(x) =
(x2+100)
16
6.5
x
6
-1
0
1
2
3
4
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
27 / 1

29. Snímek 29

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
Order of growth
Zoom out! :
25
y
p(x) =
1
(x2+100)
16
20
e(x) = 1.072 (x+26.44)
15
10
5
x
0
-5
0
5
10
15
20
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
28 / 1

30. Snímek 30

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
Order of growth
Zoom out! :
e(x) = 1.072 (x+26.44)
350 y
300
250
200
p(x) =
150
100
50
x
0
0
10
20
30
40
50
60
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
1
(x2+100)
16
29 / 1

31. Snímek 31

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
Order of growth
Zoom out! :
10000
y
e(x) = 1.072 (x+26.44)
8000
6000
4000
2000
p(x) =
0
0
20
40
60
80
100
1
(x2+100)
16
x
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
30 / 1

32. Snímek 32

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
21 / 1
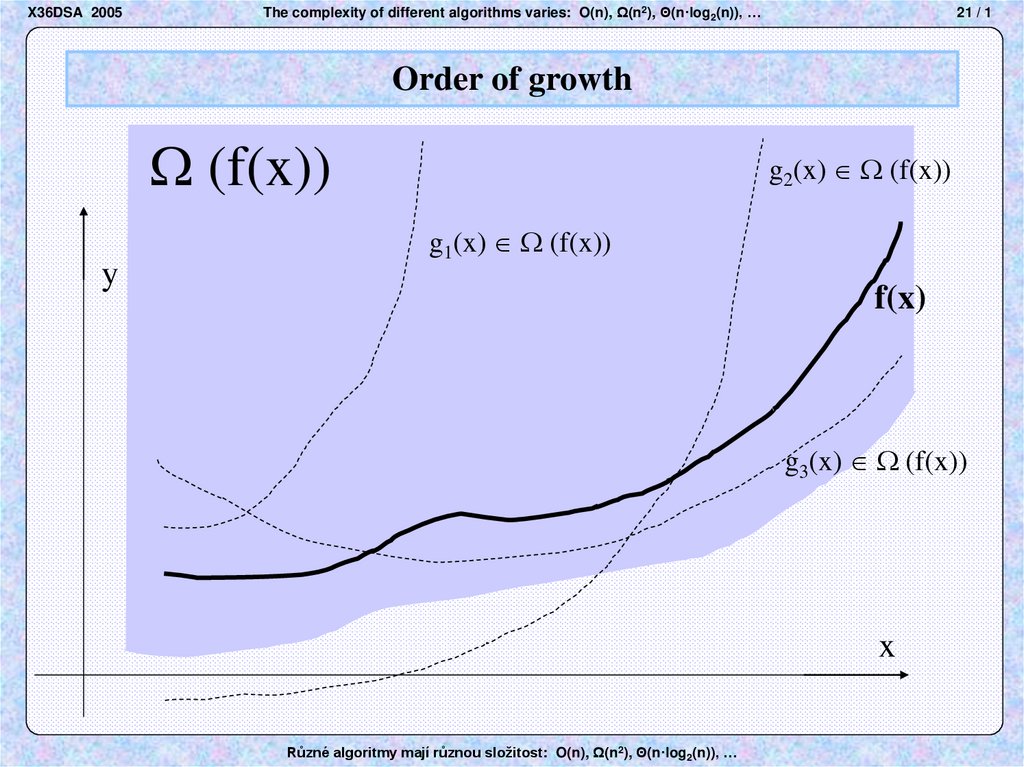
Order of growth
(f(x))
y
g2(x) (f(x))
g1(x) (f(x))
f(x)
g3(x) (f(x))
x
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

33. Snímek 33

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
Order of growth
(f(x))
Omega
V množině (f(x))
se octne každá funkce g(x), která od určitého bodu x0
(není nijak předem předepsáno, kde by x0 měl být)
a) – je už vždy větší než funkce f(x)
b) – sice větší než f(x) není, ale po vynásobení
nějakou kladnou konstantou
(hodnota konstanty také není nijak předepsána)
je už vždy větší než funkce f(x).
Takže: pokud najdeme nějaké x0 a c>0 takové, že
c·g(x) > f(x) všude napravo od x0, (někdy stačí c=1)
je jisto, že g(x) (f(x))
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
32 / 1

34. Snímek 34

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
33 / 1
Order of growth
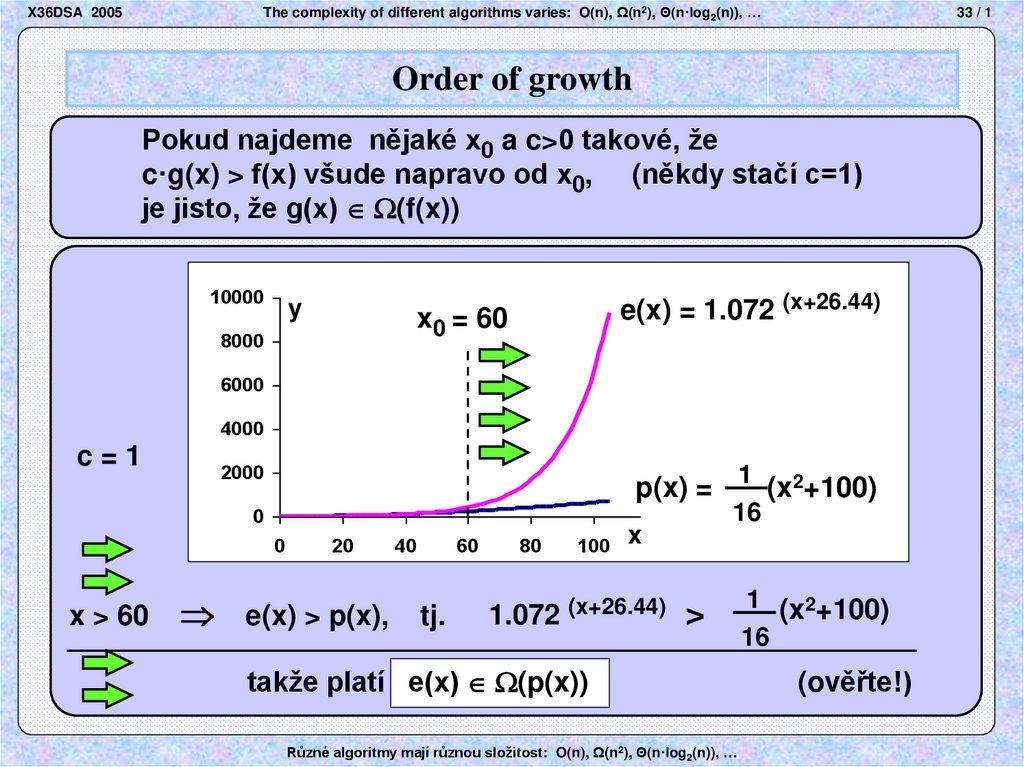
Pokud najdeme nějaké x0 a c>0 takové, že
c·g(x) > f(x) všude napravo od x0, (někdy stačí c=1)
je jisto, že g(x) (f(x))
10000
y
e(x) = 1.072 (x+26.44)
x0 = 60
8000
6000
4000
c=1
2000
p(x) = 1 (x2+100)
0
0
x > 60
20
40
e(x) > p(x), tj.
60
80
100
x
16
1.072 (x+26.44) >
takže platí e(x) (p(x))
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
1 (x2+100)
16
(ověřte!)

35. Snímek 35

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
34 / 1
Order of growth
Pokud najdeme nějaké x0 a c>0 takové, že
c·g(x) > f(x) všude napravo od x0,
je jisto, že g(x) (f(x))
b(x) = x + 3 x
r(x) = x–1
c=4
20 y
15
x0 = 3.1
4·r(x) = 4(x–1)
b(x) = x + 3 x
10
5
r(x) = x–1
0
-5 0
x > 3.1
x
1
2
4·r(x) > b(x), tj.
3
4
5
6
7
4(x-1) > x + 3 x
takže platí r(x) (b(x))
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
(ověřte!)

36. Snímek 36

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
Order of growth
Typické ukázky
x2 Ω(x)
x3 Ω(x2)
xn+1 Ω(xn)
2x Ω(x2)
2x Ω(x3)
2x Ω(x5000)
x Ω(log(x))
x log(x) Ω(x)
x2 Ω(x log(x) )
2x Ω(x20000)
x20000 Ω(x)
x Ω(1)
always
hard to believe
f(x) > 1
200000
f(x) Ω(1)
x Ω(log(x)20000)
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
35 / 1

37. Snímek 37

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
36 / 1
Order of growth
y
g2(x) O(f(x))
f(x)
g1(x) O(f(x))
g3(x) O(f(x))
O(f(x))
x
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

38. Snímek 38

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
Order of growth
O(f(x))
O Omikron
V množině O(f(x))
se octne každá funkce g(x), která od určitého bodu x0
(není nijak předem předepsáno, kde by x0 měl být)
a) – je už vždy menší než funkce f(x)
b) – sice menší než f(x) není, ale po vynásobení
nějakou kladnou konstantou ( asi < 1 )
(hodnota konstanty také není nijak předepsána)
je už vždy menší než funkce f(x).
Takže: pokud najdeme nějaké x0 a c>0 takové, že
c·g(x) < f(x) všude napravo od x0, (někdy stačí c=1)
je jisto, že g(x) O(f(x))
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
37 / 1

39. Snímek 39

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
38 / 1
Order of growth
Pokud najdeme nějaké x0 a c>0 takové, že
c·g(x) < f(x) všude napravo od x0, (někdy stačí c=1)
je jisto, že g(x) O(f(x))
10000
y
e(x) = 1.072 (x+26.44)
x0 = 60
8000
6000
c=1
4000
2000
p(x) = 1 (x2+100)
0
0
x > 60
20
40
p(x) < e(x), tj.
60
80
100
x
16
1 (x2+100)
< 1.072 (x+26.44)
16
takže platí p(x) O(e(x))
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
(ověřte!)

40. Snímek 40

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
39 / 1
Order of growth
Pokud najdeme nějaké x0 a c>0 takové, že
c·g(x) < f(x) všude napravo od x0, (někdy stačí c=1)
je jisto, že g(x) O(f(x))
b(x) = x + 3 x
r(x) = x–1
20 y
15
x0 = 1
b(x) = x + 3 x
10
5
r(x) = x–1
0
-5 0
x>1
x
1
r(x) < b(x), tj.
2
3
4
x–1 <
5
6
7
x+3 x
takže platí r(x) O(b(x))
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

41. Snímek 41

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
Order of growth
f Ω(g) <==> g O(f)
x O(x2)
x2 O(x3)
xn O(xn+1)
x2 O(2x)
x3 O(2x)
x5000 O(2x)
log(x) O(x)
x O(x log(x))
x log(x) O(x2)
x20000 O(2x)
x O(x20000)
1 O(x)
always
hard to believe
f(x) > 1
1 O(f(x))
log(x)20000 O( 200000 x )
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
40 / 1

42. Snímek 42

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
41 / 1
Order of growth
g2(x) (f(x))
f(x)
y
(f(x))
g1(x) (f(x))
g3(x) (f(x))
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
x

43. Snímek 43

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
Order of growth
Theta
(f(x)) = Ω(f(x)) O(f(x))
V množině (f(x)) se octne každá funkce g(x),
která spadá jak do Ω(f(x)) tak do O(f(x)).
f(x) (g(x))
g(x) (f(x))
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
42 / 1

44. Snímek 44

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
43 / 1
Order of growth
f(x) (g(x))
b(x) = x + 3 x
r(x) = x–1
e(x) (p(x))
r(x) O(b(x))
g(x) (f(x))
20 y
15
b(x) = x + 3 x
10
5
r(x) = x–1
0
-5 0
x
1
r(x) (b(x))
2
3
4
5
6
r(x) (b(x))
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
7

45. Snímek 45

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
Order of growth
Rules
(a > 0) (f(x)) = (a f(x))
g(x) O(f(x)) (f(x)) = (f(x) + g(x))
Examples
1.8x + 600 log2(x) (x)
x3 + 7x1/2 + 5(log2(x))4 (x3)
13 3x + 9x12 + 42x-4 + 29 (3x)
4 2n + 3 2n-1 + 5 2n/2 (2n)
0.1x5 + 200x4 + 7x2 + x - 3 (x5)
–’’– O(x5)
–’’– (x5)
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
44 / 1

46. Snímek 46

The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
X36DSA 2005
45 / 1
Order of growth
(f(x)) = { g(x) ; x0>0,c>0 x>x0: c·f(x) < g(x) }
(f(x)) = { g(x) ; x0>0,c>0 x>x0: g(x) < c·f(x) }
(f(x)) = { g(x) ; x0>0,c1>0, c2>0 x>x0: c1·f(x) < g(x) < c2·f(x)
}
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …

47. Snímek 47

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
Order of growth
Řád růstu funkce
Řád růstu funkce f
je taková “co nejjednodušší” funkce g,
pro kterou platí
g(x) f(x)
ff(x) = 4 2n + 3 2n-1 + 5 2n/2 (2n)
Řád růstu ff(x) je 2n
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
46 / 1

48. Snímek 48

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
Asymptotic complexity
Asymptotická složitost
Asymptotická složitost algoritmu A
je řád růstu funkce f(n), která charakterizuje
počet elementárních operací algoritmu A
při zpracování dat o rozsahu n.
(rozsah dat = celkový počet čísel a znaků v nich)
Ve většině případů nehraje roli, zda uvažujeme
A) počet všech elementárních operací
B) počet všech elementárních operací nad daty
C) počet testů nad daty
Asymptotická složitost vycházívá táž.
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
47 / 1

49. Snímek 49

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
Asymptotic complexity
Asymptotická složitost
Asymptotická složitost hledání minima v poli o n prvcích je n.
V obou uvedených případech.
Asymptotická složitost pomalého zjišťování, kolik čísel v poli je
rovno součtu jiného pole je n2.
Asymptotická složitost rychlého zjišťování, kolik čísel v poli je
rovno součtu jiného pole je n.
Za předpokladu, že obě pole mají délku n.
Asymptotická složitost lineárního hledání prvku v poli je n.
Asymptotická složitost hledání prvku uspořádaném poli
pomocí půlení intervalu je log(n).
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
48 / 1

50. Snímek 50

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
Order of growth
Funkce f(x) roste asymptoticky rychleji než funkce g(x), když
f(x) Ω(g(x)) & f(x) (g(x))
Algoritmus A je asymptoticky rychlejší než algoritmus B, když
fA(n) Ω(fB(n)) & fA(n) (fB(n)),
kde fA(n), resp. fB(n) je funkce určující počet operací,
které provede algoritmus A, resp. B,
při zpracování dat o rozsahu n.
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
49 / 1

51. Snímek 51

X36DSA 2005
The complexity of different algorithms varies: O(n), Ω(n2), Θ(n·log2(n)), …
Order of growth
Function f(x) grows asymptotically faster then function g(x) if
f(x) Ω(g(x)) & f(x) (g(x))
Algorithm A is asymptotically faster then algorithm B when
fA(n) Ω(fB(n)) & fA(n) (fB(n))
where fA(n) resp. fB(n) is the function specifying the number of
operations performed by algorithm A resp. B
during processing the data of size n.
Různé algoritmy mají různou složitost: O(n), Ω(n2), Θ(n·log2(n)), …
50 / 1