2.89M

Category: $mathematics$ mathematics

Combinational logic design

1.

COMBINATIONAL LOGIC DESIGN
Chapter 2
Digital Design and Computer Architecture, 2nd Edition
David Money Harris and Sarah L. Harris
Chapter 2 <1>

COMBINATIONAL LOGIC DESIGN
Chapter 2 :: Topics
Introduction
Boolean Equations
Boolean Algebra
From Logic to Gates
Multilevel Combinational Logic
X’s and Z’s, Oh My
Karnaugh Maps
Combinational Building Blocks
Timing
Chapter 2 <2>

3.

COMBINATIONAL LOGIC DESIGN
Introduction
A logic circuit is composed of:
• Inputs
• Outputs
• Functional specification
• Timing specification
functional spec
inputs
outputs
timing spec
Chapter 2 <3>

4.

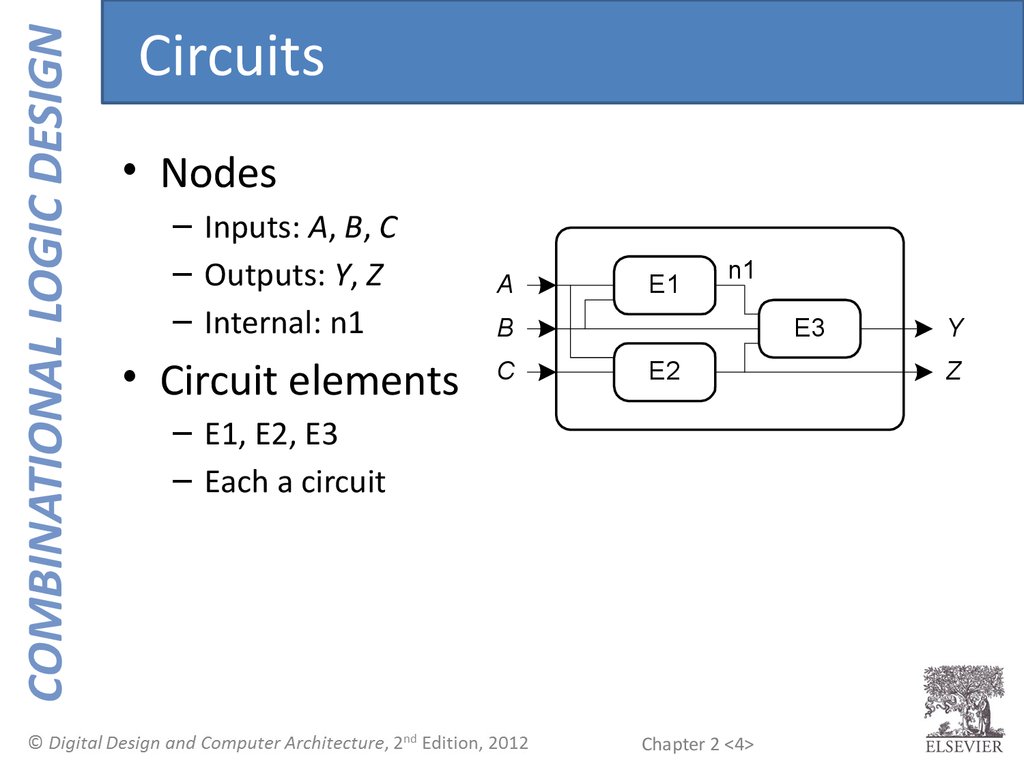
COMBINATIONAL LOGIC DESIGN
Circuits
• Nodes
– Inputs: A, B, C
– Outputs: Y, Z
– Internal: n1
A
• Circuit elements
C
E1
n1
B
E3
E2
– E1, E2, E3
– Each a circuit
Chapter 2 <4>
Y
Z

5.

COMBINATIONAL LOGIC DESIGN
Types of Logic Circuits
• Combinational Logic
– Memoryless
– Outputs determined by current values of inputs
• Sequential Logic
– Has memory
– Outputs determined by previous and current values
of inputs
functional spec
inputs
outputs
timing spec
Chapter 2 <5>

6.

COMBINATIONAL LOGIC DESIGN
Rules of Combinational Composition
• Every element is combinational
• Every node is either an input or connects
to exactly one output
• The circuit contains no cyclic paths
• Example:
Chapter 2 <6>

7.

COMBINATIONAL LOGIC DESIGN
Boolean Equations
• Functional specification of outputs in terms
of inputs
• Example: S = F(A, B, Cin)
Cout = F(A, B, Cin)
A
B
Cin
C
L
S
Cout
S
= A B Cin
Cout = AB + ACin + BCin
Chapter 2 <7>

8.

COMBINATIONAL LOGIC DESIGN
Some Definitions
• Complement: variable with a bar over it
A, B, C
• Literal: variable or its complement
A, A, B, B, C, C
• Implicant: product of literals
ABC, AC, BC
• Minterm: product that includes all input variables
ABC, ABC, ABC
• Maxterm: sum that includes all input variables
(A+B+C), (A+B+C), (A+B+C)
Chapter 2 <8>

9.

COMBINATIONAL LOGIC DESIGN
Sum-of-Products (SOP) Form
All equations can be written in SOP form
Each row has a minterm
A minterm is a product (AND) of literals
Each minterm is TRUE for that row (and only that row)
Form function by ORing minterms where the output is TRUE
Thus, a sum (OR) of products (AND terms)
A
0
0
1
1
B
0
1
0
1
Y
0
1
0
1
minterm
minterm name
A B
m0
m1
A B
m2
A B
m3
A B
Y = F(A, B) =
Chapter 2 <9>

10. Sum-of-Products Form

COMBINATIONAL LOGIC DESIGN
Sum-of-Products (SOP) Form
Sum-of-Products Form
All equations can be written in SOP form
Each row has a minterm
A minterm is a product (AND) of literals
Each minterm is TRUE for that row (and only that row)
Form function by ORing minterms where the output is TRUE
Thus, a sum (OR) of products (AND terms)
A
0
0
1
1
B
0
1
0
1
Y
0
1
0
1
minterm
minterm name
A B
m0
m1
A B
m2
A B
m3
A B
Y = F(A, B) =
Chapter 2 <10>

11. Sum-of-Products Form

12.

COMBINATIONAL LOGIC DESIGN
Product-of-Sums (POS) Form
All Boolean equations can be written in POS form
Each row has a maxterm
A maxterm is a sum (OR) of literals
Each maxterm is FALSE for that row (and only that row)
Form function by ANDing the maxterms for which the
output is FALSE
• Thus, a product (AND) of sums (OR terms)
A
0
0
1
1
B
0
1
0
1
Y
0
1
0
1
maxterm
maxterm name
A
A
A
A
+
+
+
+
B
B
B
B
M0
M1
M2
M3
Y = F(A, B) = (A + B)(A + B) = Π(0, 2)
Chapter 2 <12>

13.

COMBINATIONAL LOGIC DESIGN
Boolean Equations Example
• You are going to the cafeteria for lunch
– You won’t eat lunch (E)
– If it’s not open (O) or
– If they only serve corndogs (C)
• Write a truth table for determining if you
will eat lunch (E).
O
0
0
1
1
C
0
1
0
1
E
Chapter 2 <13>

14. 15. SOP & POS Form

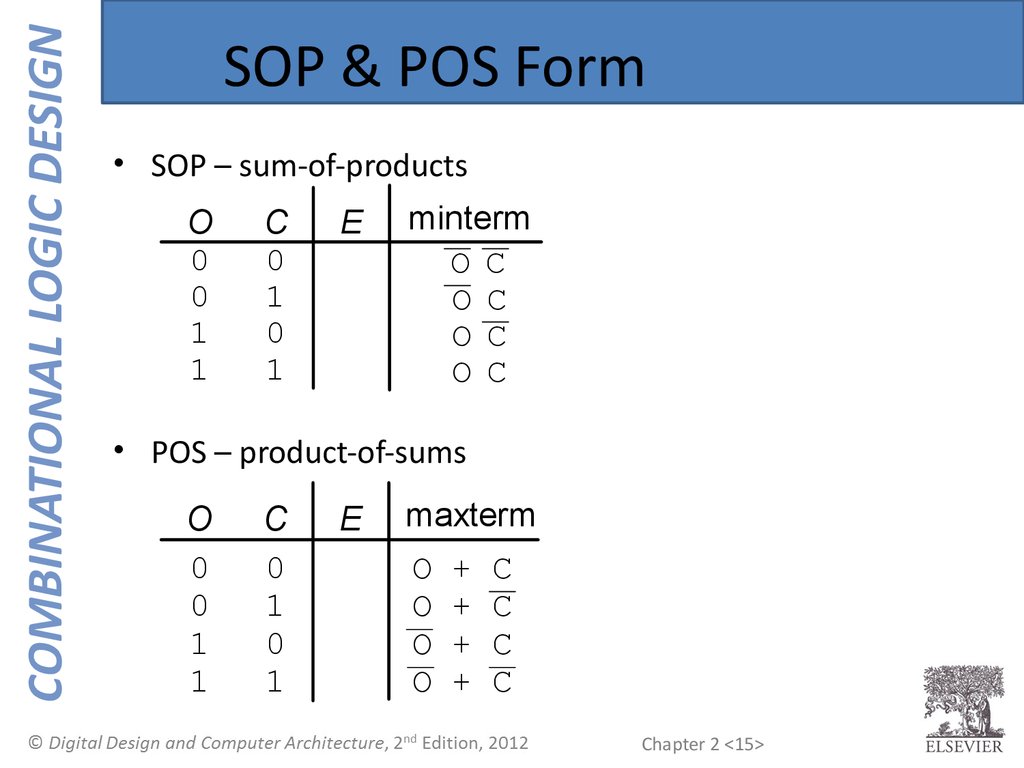
COMBINATIONAL LOGIC DESIGN
SOP & POS Form
• SOP – sum-of-products
O
0
0
1
1
C
0
1
0
1
E
minterm
O C
O C
O C
O C
• POS – product-of-sums
O
0
0
1
1
C
0
1
0
1
E
maxterm
O
O
O
O
+
+
+
+
C
C
C
C
Chapter 2 <15>

16.

COMBINATIONAL LOGIC DESIGN
SOP & POS Form
• SOP – sum-of-products
O
0
0
1
1
C
0
1
0
1
E
0
0
1
0
minterm
O C
O C
O C
O C
E = OC
= Σ(2)
• POS – product-of-sums
O
0
0
1
1
C
0
1
0
1
E
0
0
1
0
maxterm
O
O
O
O
+
+
+
+
C
C
C
C
E = (O + C)(O + C)(O + C)
= Π(0, 1, 3)
Chapter 2 <16>

17.

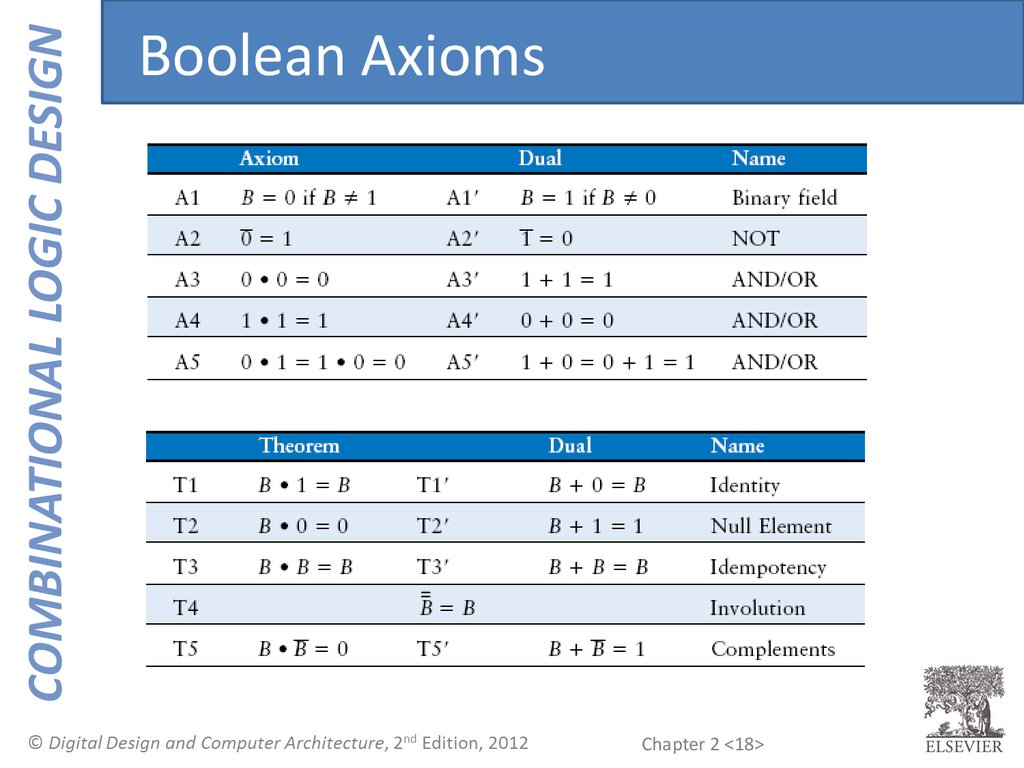
COMBINATIONAL LOGIC DESIGN
Boolean Algebra
• Axioms and theorems to simplify Boolean
equations
• Like regular algebra, but simpler: variables
have only two values (1 or 0)
• Duality in axioms and theorems:
– ANDs and ORs, 0’s and 1’s interchanged
Chapter 2 <17>

18.

COMBINATIONAL LOGIC DESIGN
Boolean Axioms
Chapter 2 <18>

19.

COMBINATIONAL LOGIC DESIGN
T1: Identity Theorem
• B 1=B
• B+0=B
Chapter 2 <19>

20.

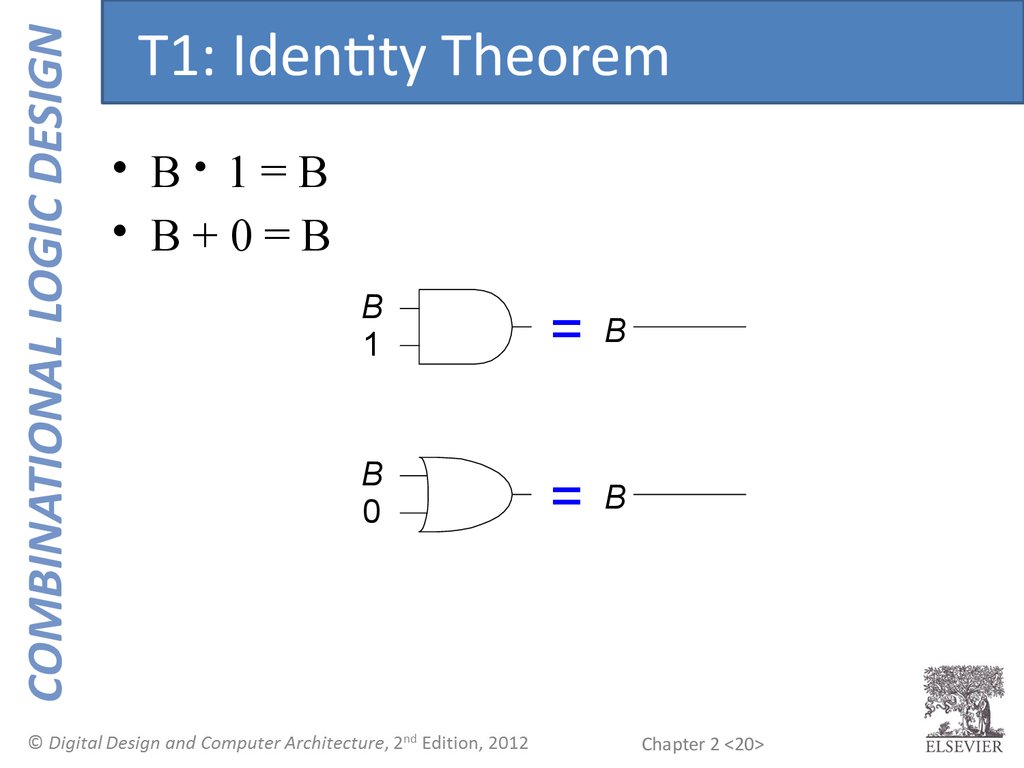
COMBINATIONAL LOGIC DESIGN
T1: Identity Theorem
• B 1=B
• B+0=B
B
1
=
B
B
0
=
B
Chapter 2 <20>

21.

COMBINATIONAL LOGIC DESIGN
T2: Null Element Theorem
• B 0=0
• B+1=1
Chapter 2 <21>

22.

COMBINATIONAL LOGIC DESIGN
T2: Null Element Theorem
• B 0=0
• B+1=1
B
0
=
0
B
1
=
1
Chapter 2 <22>

23.

COMBINATIONAL LOGIC DESIGN
T3: Idempotency Theorem
• B B=B
• B+B=B
Chapter 2 <23>

24.

COMBINATIONAL LOGIC DESIGN
T3: Idempotency Theorem
• B B=B
• B+B=B
B
B
=
B
B
B
=
B
Chapter 2 <24>

25.

COMBINATIONAL LOGIC DESIGN
T4: Identity Theorem
• B=B
Chapter 2 <25>

26.

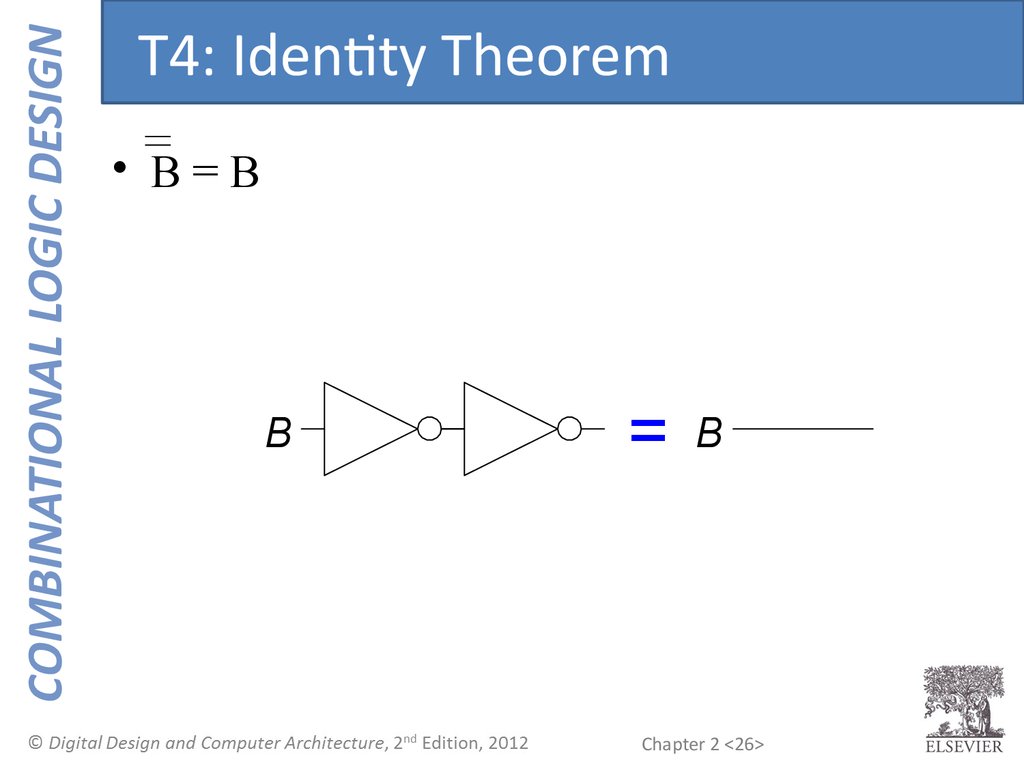
COMBINATIONAL LOGIC DESIGN
T4: Identity Theorem
• B=B
B
=
B
Chapter 2 <26>

27.

COMBINATIONAL LOGIC DESIGN
T5: Complement Theorem
• B B=0
• B+B=1
Chapter 2 <27>

28.

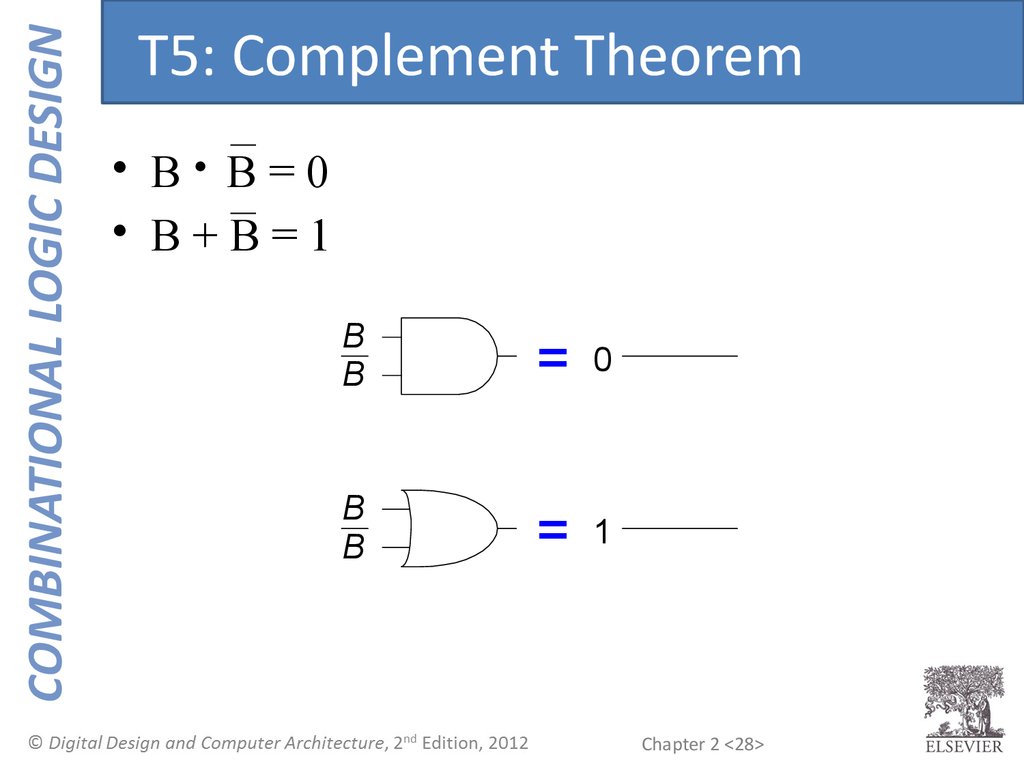
COMBINATIONAL LOGIC DESIGN
T5: Complement Theorem
• B B=0
• B+B=1
B
B
=
0
B
B
=
1
Chapter 2 <28>

29.

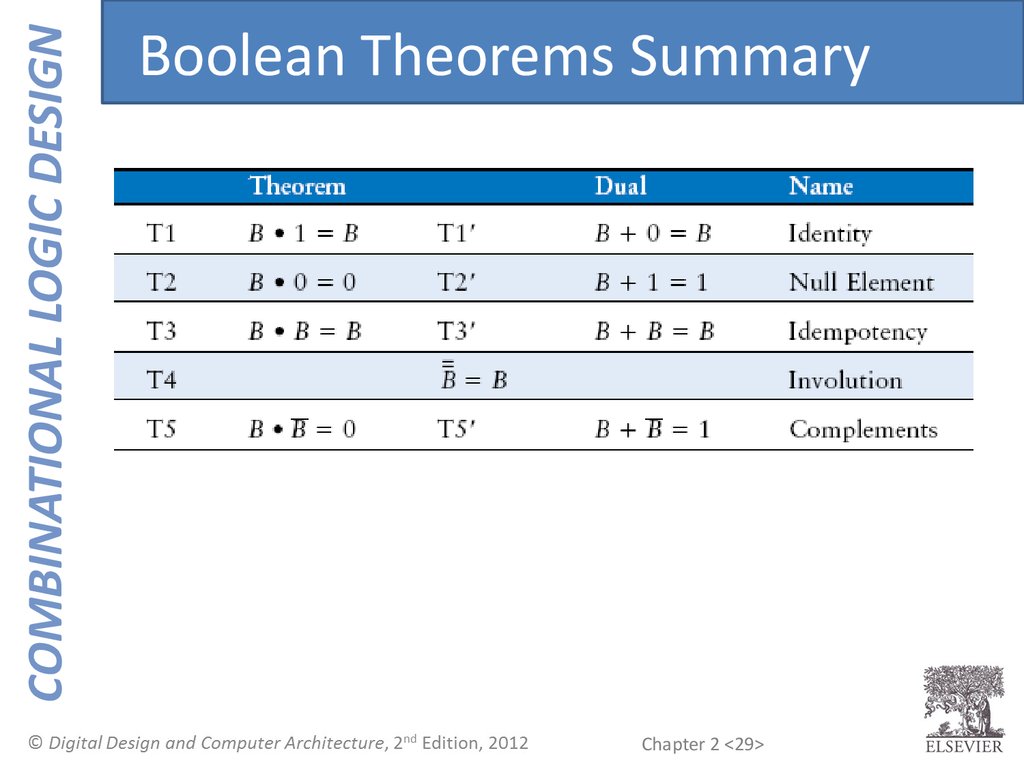
COMBINATIONAL LOGIC DESIGN
Boolean Theorems Summary
Chapter 2 <29>

30.

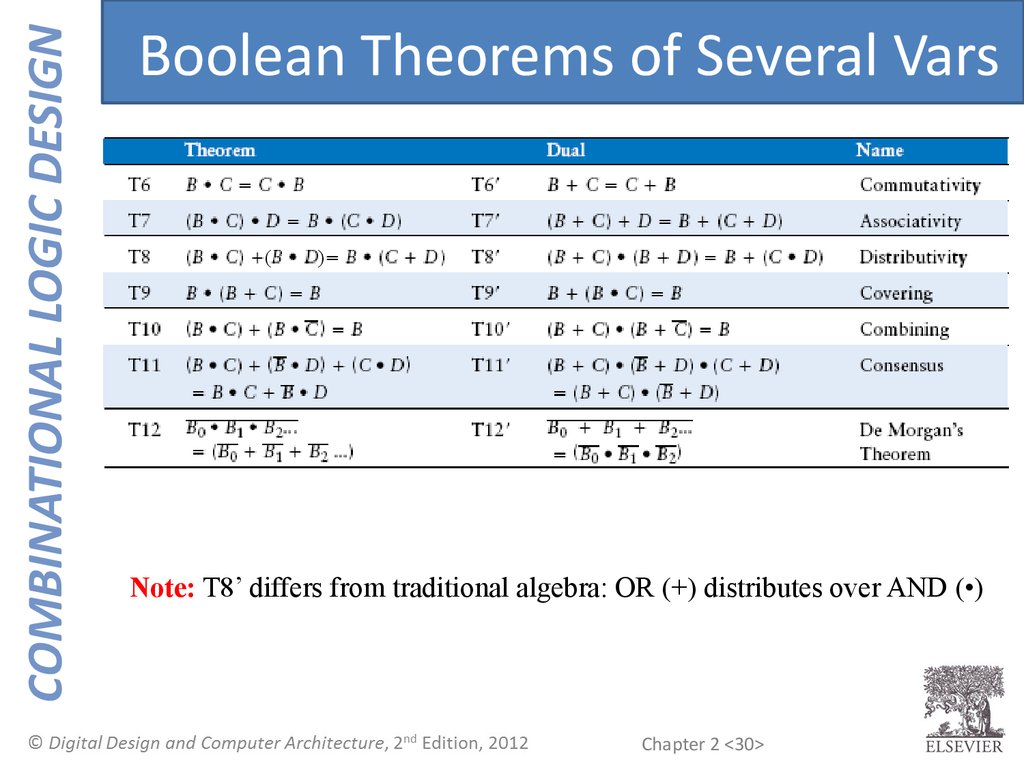
COMBINATIONAL LOGIC DESIGN
Boolean Theorems of Several Vars
(
)
Note: T8’ differs from traditional algebra: OR (+) distributes over AND (•)
Chapter 2 <30>

31.

COMBINATIONAL LOGIC DESIGN
Simplifying Boolean Equations
Example 1:
Y = AB + AB
Chapter 2 <31>

32.

COMBINATIONAL LOGIC DESIGN
Simplifying Boolean Equations
Example 1:
Y = AB + AB
= B(A + A) T8
= B(1) T5’
= B T1
Chapter 2 <32>

33.

COMBINATIONAL LOGIC DESIGN
Simplifying Boolean Equations
Example 2:
Y = A(AB + ABC)
Chapter 2 <33>

34.

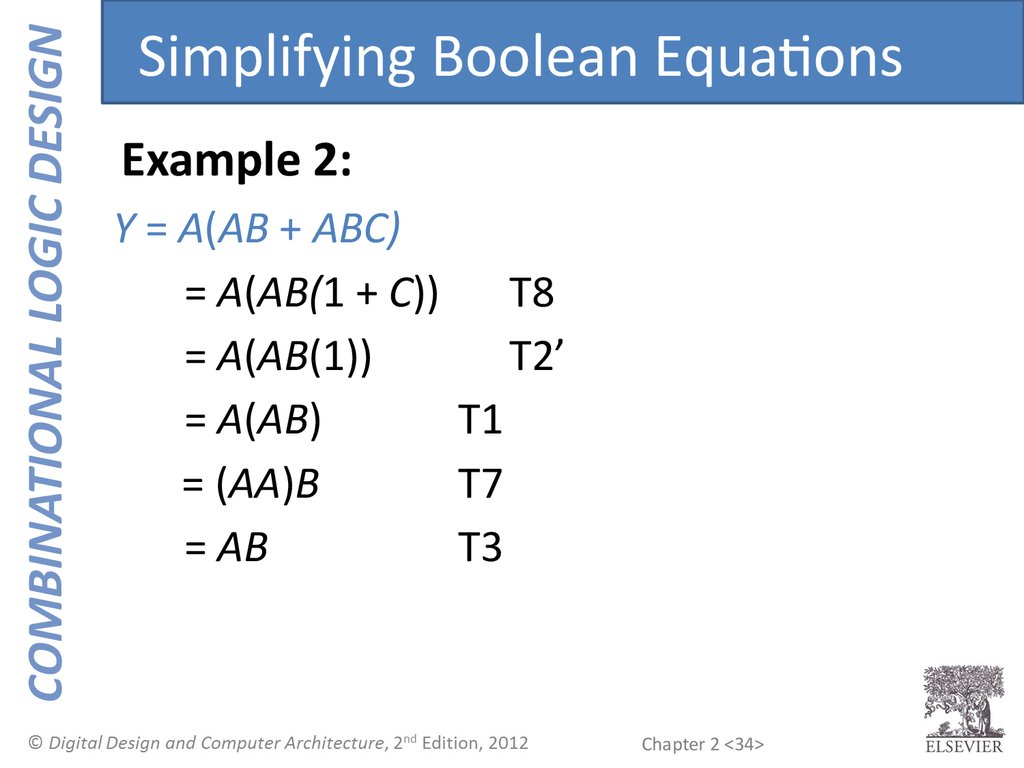
COMBINATIONAL LOGIC DESIGN
Simplifying Boolean Equations
Example 2:
Y = A(AB + ABC)
= A(AB(1 + C))
T8
= A(AB(1))
T2’
= A(AB)
T1
= (AA)B
T7
= AB
T3
Chapter 2 <34>

35.

COMBINATIONAL LOGIC DESIGN
DeMorgan’s Theorem
• Y = AB = A + B
• Y=A+B=A B
A
B
Y
A
B
Y
A
B
Y
A
B
Y
Chapter 2 <35>

36.

COMBINATIONAL LOGIC DESIGN
Bubble Pushing
• Backward:
– Body changes
– Adds bubbles to inputs
A
B
Y
A
B
Y
Y
A
B
Y
• Forward:
– Body changes
– Adds bubble to output
A
B
Chapter 2 <36>

37.

COMBINATIONAL LOGIC DESIGN
Bubble Pushing
• What is the Boolean expression for this
circuit?
A
B
C
D
Y
Chapter 2 <37>

38.

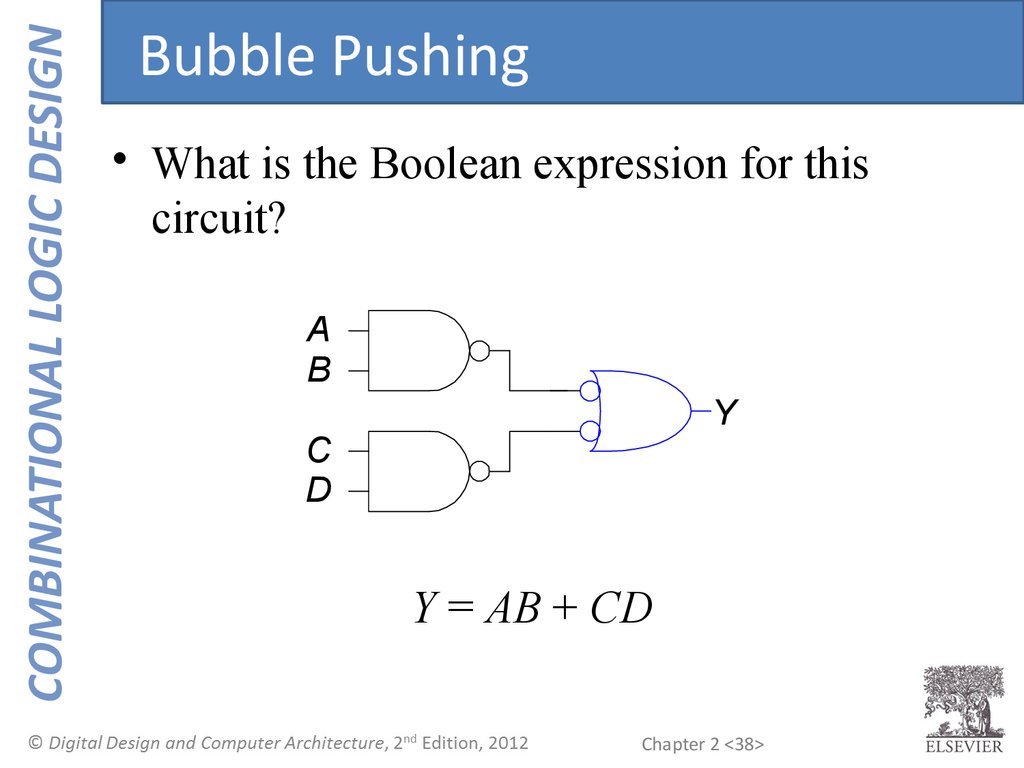
COMBINATIONAL LOGIC DESIGN
Bubble Pushing
• What is the Boolean expression for this
circuit?
A
B
Y
C
D
Y = AB + CD
Chapter 2 <38>

39.

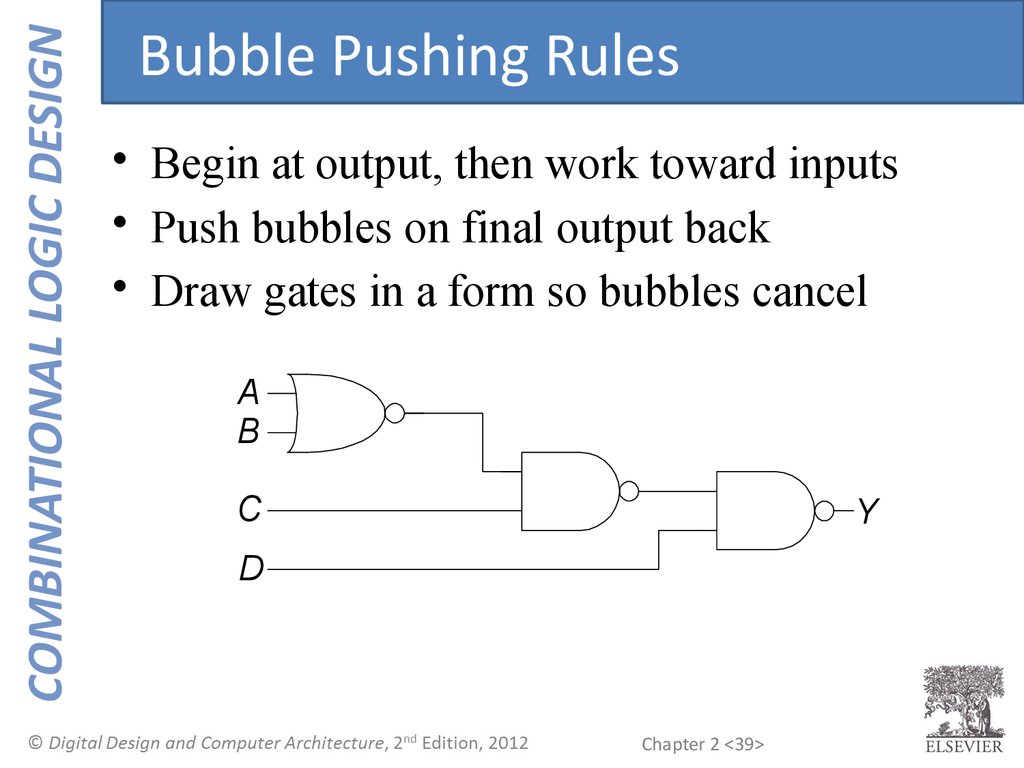
COMBINATIONAL LOGIC DESIGN
Bubble Pushing Rules
• Begin at output, then work toward inputs
• Push bubbles on final output back
• Draw gates in a form so bubbles cancel
A
B
C
Y
D
Chapter 2 <39>

40.

COMBINATIONAL LOGIC DESIGN
Bubble Pushing Example
A
B
C
Y
D
Chapter 2 <40>

41.

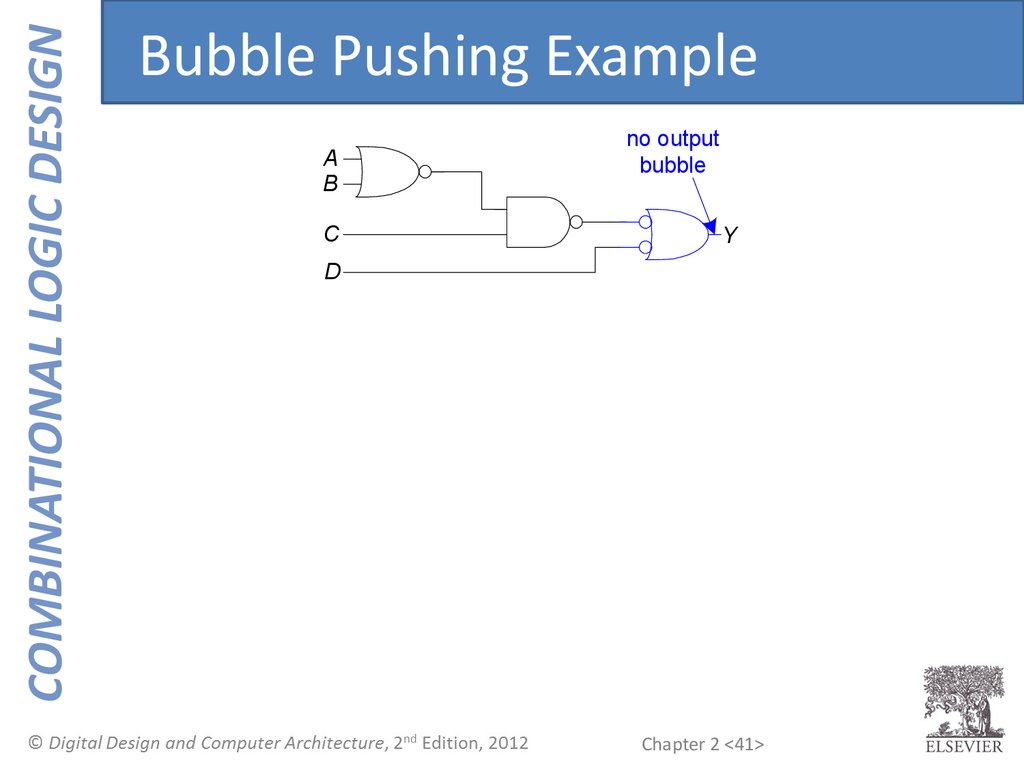
COMBINATIONAL LOGIC DESIGN
Bubble Pushing Example
A
B
C
no output
bubble
Y
D
Chapter 2 <41>

42.

COMBINATIONAL LOGIC DESIGN
Bubble Pushing Example
A
B
no output
bubble
C
Y
D
A
B
C
bubble on
input and output
Y
D
Chapter 2 <42>

43.

COMBINATIONAL LOGIC DESIGN
Bubble Pushing Example
no output
bubble
A
B
C
Y
D
A
B
bubble on
input and output
C
Y
D
A
B
no bubble on
input and output
C
Y
D
Y = ABC + D
Chapter 2 <43>

44.

COMBINATIONAL LOGIC DESIGN
From Logic to Gates
• Two-level logic: ANDs followed by ORs
• Example: Y = ABC + ABC + ABC
A
B
A
C
B
C
minterm: ABC
minterm: ABC
minterm: ABC
Y
Chapter 2 <44>

45.

COMBINATIONAL LOGIC DESIGN
Circuit Schematics Rules
Inputs on the left (or top)
Outputs on right (or bottom)
Gates flow from left to right
Straight wires are best
Chapter 2 <45>

46.

COMBINATIONAL LOGIC DESIGN
Circuit Schematic Rules (cont.)
• Wires always connect at a T junction
• A dot where wires cross indicates a
connection between the wires
• Wires crossing without a dot make no
connection
wires connect
at a T junction
wires connect
at a dot
wires crossing
without a dot do
not connect
Chapter 2 <46>

47.

COMBINATIONAL LOGIC DESIGN
Multiple-Output Circuits
• Example: Priority Circuit
Output asserted
corresponding to
most significant
TRUE input
A3
Y3
A2
Y2
A1
Y1
A0
Y0
PRIORITY
CiIRCUIT
A3
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
A2
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
A1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
A0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y3
Chapter 2 <47>
Y2
Y1
Y0

48.

49.

COMBINATIONAL LOGIC DESIGN
Priority Circuit Hardware
A3
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
A2
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
A1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
A0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y3
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
Y2
0
0
0
0
1
1
1
1
0
0
0
0
0
0
0
0
Y1
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
Y0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
A3 A 2 A1 A 0
Y3
Y2
Y1
Y0
Chapter 2 <49>

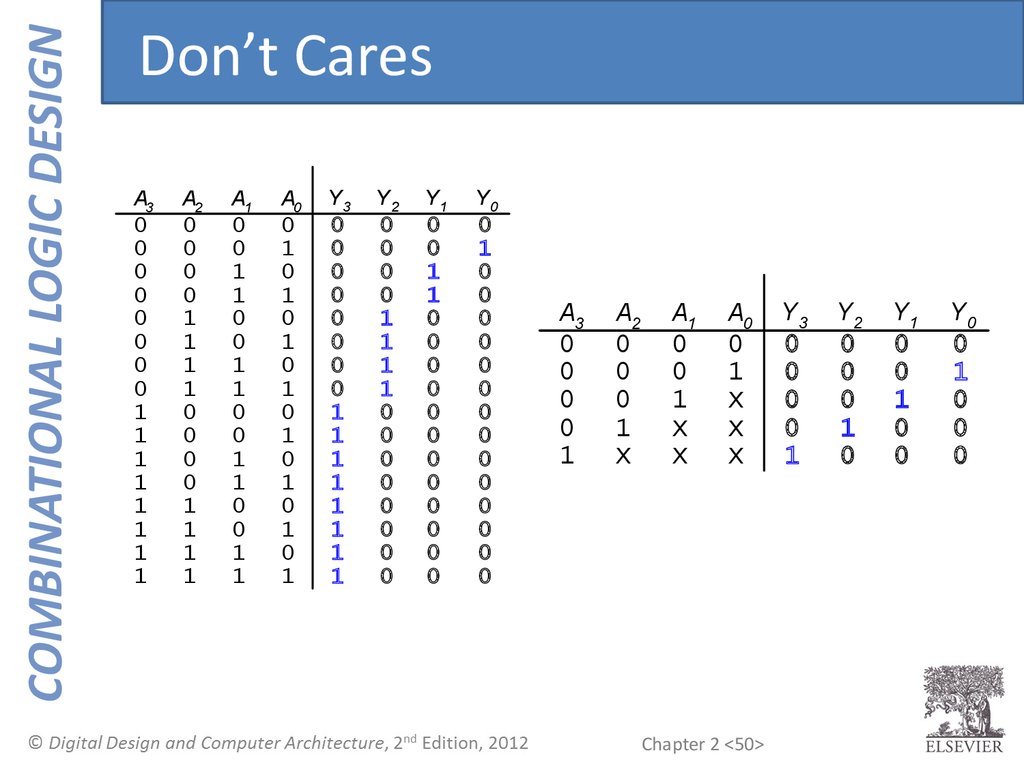
50.

COMBINATIONAL LOGIC DESIGN
Don’t Cares
A3
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
A2
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
A1
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
A0
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y3
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
Y2
0
0
0
0
1
1
1
1
0
0
0
0
0
0
0
0
Y1
0
0
1
1
0
0
0
0
0
0
0
0
0
0
0
0
Y0
0
1
0
0
0
0
0
0
0
0
0
0
0
0
0
0
A3
0
0
0
0
1
A2
0
0
0
1
X
A1
0
0
1
X
X
A0
0
1
X
X
X
Chapter 2 <50>
Y3
0
0
0
0
1
Y2
0
0
0
1
0
Y1
0
0
1
0
0
Y0
0
1
0
0
0

51.

COMBINATIONAL LOGIC DESIGN
Contention: X
• Contention: circuit tries to drive output to 1 and 0
–
–
–
–
Actual value somewhere in between
Could be 0, 1, or in forbidden zone
Might change with voltage, temperature, time, noise
Often causes excessive power dissipation
A=1
Y=X
• Warnings:
B=0
– Contention usually indicates a bug.
– X is used for “don’t care” and contention - look at the context
to tell them apart
Chapter 2 <51>

52.

COMBINATIONAL LOGIC DESIGN
Floating: Z
• Floating, high impedance, open, high Z
• Floating output might be 0, 1, or
somewhere in between
– A voltmeter won’t indicate whether a node is floating
Tristate Buffer
E
Y
A
E
0
0
1
1
A
0
1
0
1
Y
Z
Z
0
1
Chapter 2 <52>

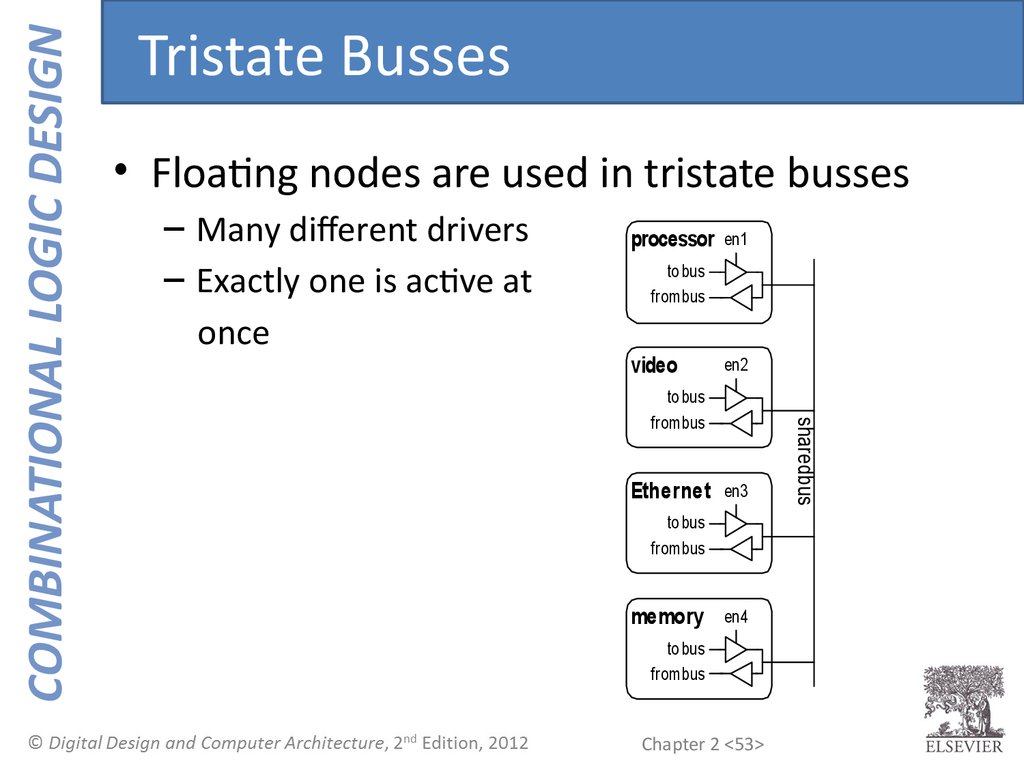
53.

• Floating nodes are used in tristate busses
– Many different drivers
– Exactly one is active at
once
processor
en1
to bus
from bus
video
en2
to bus
from bus
Ethernet
en3
to bus
from bus
memory
en4
to bus
from bus
Chapter 2 <53>
sharedbus
COMBINATIONAL LOGIC DESIGN
Tristate Busses

54.

COMBINATIONAL LOGIC DESIGN
Karnaugh Maps (K-Maps)
• Boolean expressions can be minimized by
combining terms
• K-maps minimize equations graphically
• PA + PA = P
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C
0
1
0
1
0
1
0
1
Y
1
1
0
0
0
0
0
0
Y
Y
AB
00
01
11
10
0
1
0
0
0
1
1
0
0
0
C
AB
C
00
01
11
10
0 ABC
ABC
ABC
ABC
1 ABC
ABC
ABC
ABC
Chapter 2 <54>

55.

COMBINATIONAL LOGIC DESIGN
K-Map
• Circle 1’s in adjacent squares
• In Boolean expression, include only
literals whose true and complement form
are not in the circle
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C
0
1
0
1
0
1
0
1
Y
1
1
0
0
0
0
0
0
Y
AB
00
01
11
10
0
1
0
0
0
1
1
0
0
0
C
Y = AB
Chapter 2 <55>

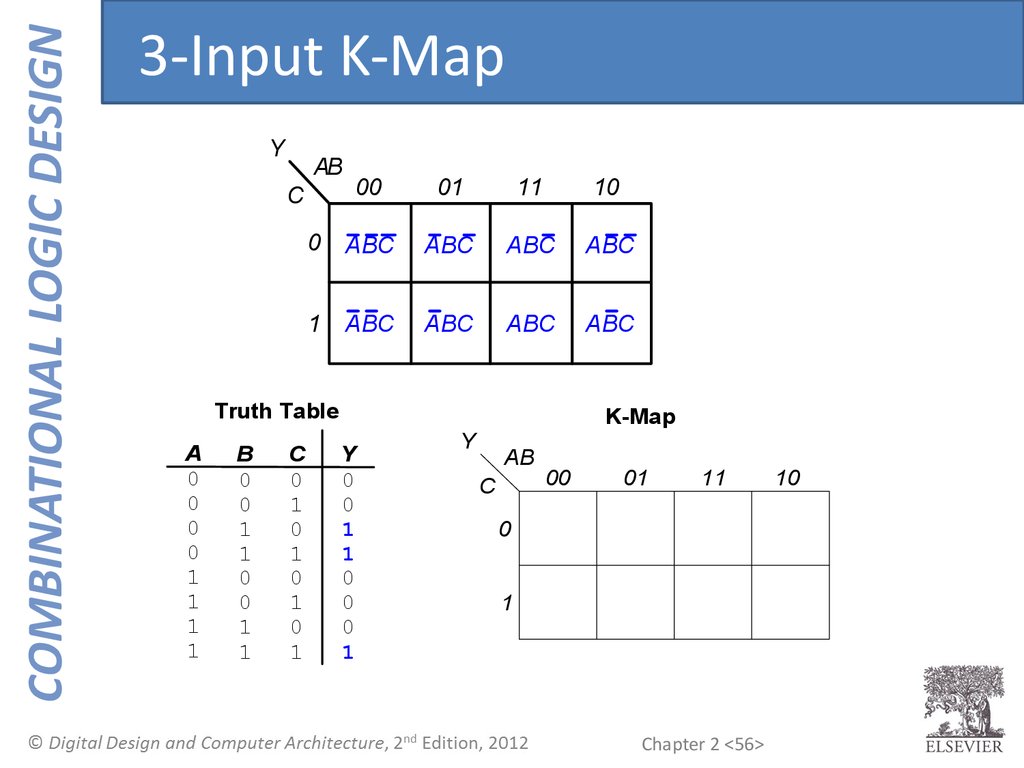
56.

COMBINATIONAL LOGIC DESIGN
3-Input K-Map
Y
AB
00
01
11
10
0
ABC
ABC
ABC
ABC
1
ABC
ABC
ABC
ABC
C
Truth Table
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C
0
1
0
1
0
1
0
1
K-Map
Y
0
0
1
1
0
0
0
1
Y
AB
C
00
01
11
0
1
Chapter 2 <56>
10

57.

COMBINATIONAL LOGIC DESIGN
3-Input K-Map
Y
AB
00
01
11
10
0
ABC
ABC
ABC
ABC
1
ABC
ABC
ABC
ABC
C
Truth Table
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C
0
1
0
1
0
1
0
1
K-Map
Y
0
0
1
1
0
0
0
1
Y
AB
C
00
01
11
10
0
0 1 1 0
1
0 1 0 0
Y = AB + BC
Chapter 2 <57>

58.

COMBINATIONAL LOGIC DESIGN
K-Map Definitions
• Complement: variable with a bar over it
A, B, C
• Literal: variable or its complement
A, A, B, B, C, C
• Implicant: product of literals
ABC, AC, BC
• Prime implicant: implicant corresponding
to the largest circle in a K-map
Chapter 2 <58>

59.

COMBINATIONAL LOGIC DESIGN
K-Map Rules
• Every 1 must be circled at least once
• Each circle must span a power of 2 (i.e. 1, 2,
4) squares in each direction
• Each circle must be as large as possible
• A circle may wrap around the edges
• A “don't care” (X) is circled only if it helps
minimize the equation
Chapter 2 <59>

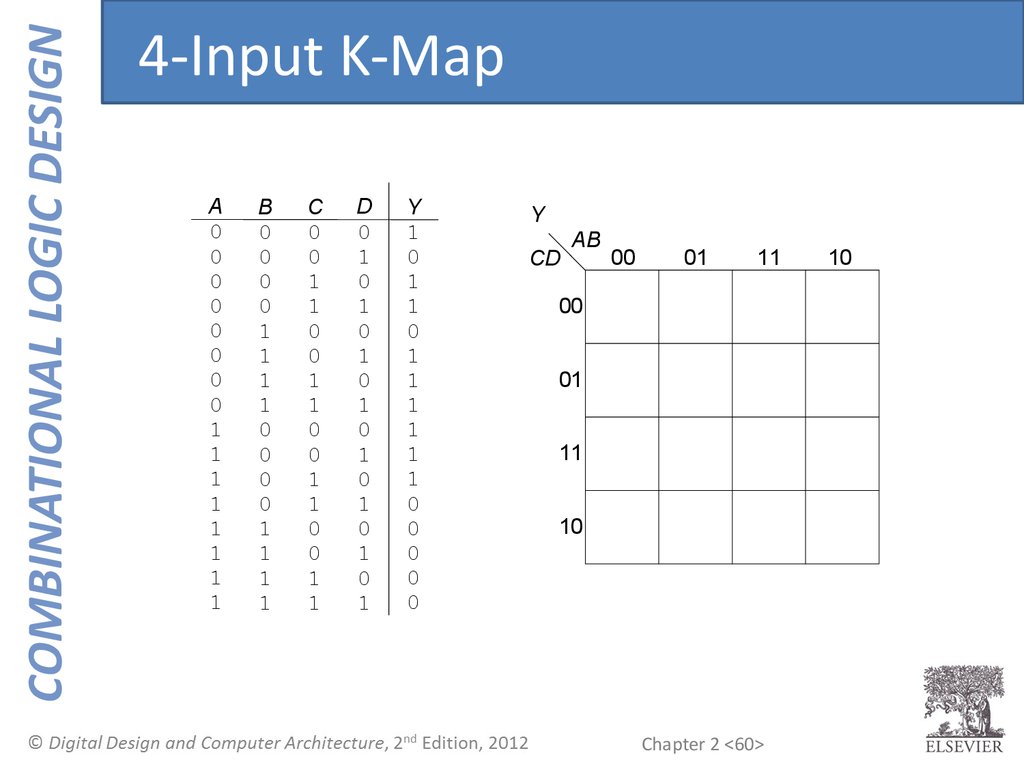
60.

COMBINATIONAL LOGIC DESIGN
4-Input K-Map
A
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
1
0
1
1
0
1
1
1
1
1
1
0
0
0
0
0
Y
CD
AB
00
01
11
00
01
11
10
Chapter 2 <60>
10

61.

COMBINATIONAL LOGIC DESIGN
4-Input K-Map
A
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
1
0
1
1
0
1
1
1
1
1
1
0
0
0
0
0
Y
AB
00
01
11
10
00
1
0
0
1
01
0
1
0
1
11
1
1
0
0
10
1
1
0
1
CD
Chapter 2 <61>

62.

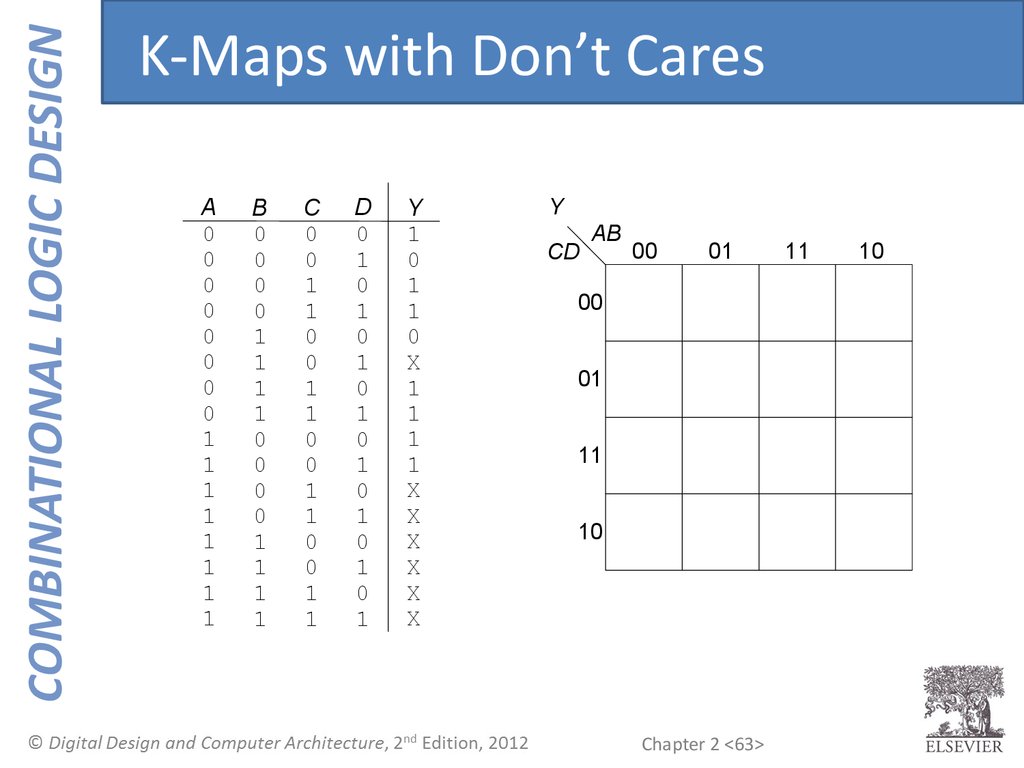
63.

COMBINATIONAL LOGIC DESIGN
K-Maps with Don’t Cares
A
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
1
0
1
1
0
X
1
1
1
1
X
X
X
X
X
X
Y
CD
AB
00
01
00
01
11
10
Chapter 2 <63>
11
10

64.

COMBINATIONAL LOGIC DESIGN
K-Maps with Don’t Cares
A
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
C
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
D
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Y
1
0
1
1
0
X
1
1
1
1
X
X
X
X
X
X
Y
AB
00
01
11
10
00
1
0
X
1
01
0
X
X
1
11
1
1
X
X
10
1
1
X
X
CD
Chapter 2 <64>

65.

66.

COMBINATIONAL LOGIC DESIGN
Combinational Building Blocks
• Multiplexers
• Decoders
Chapter 2 <66>

67.

COMBINATIONAL LOGIC DESIGN
Multiplexer (Mux)
• Selects between one of N inputs to connect
to output
• log2N-bit select input – control input
• Example:
2:1 Mux
S
S
0
0
0
0
1
1
1
1
D1
0
0
1
1
0
0
1
1
D0
0
D1
1
D0
0
1
0
1
0
1
0
1
Y
0
1
0
1
0
0
1
1
Y
S
0
1
Y
D0
D1
Chapter 2 <67>

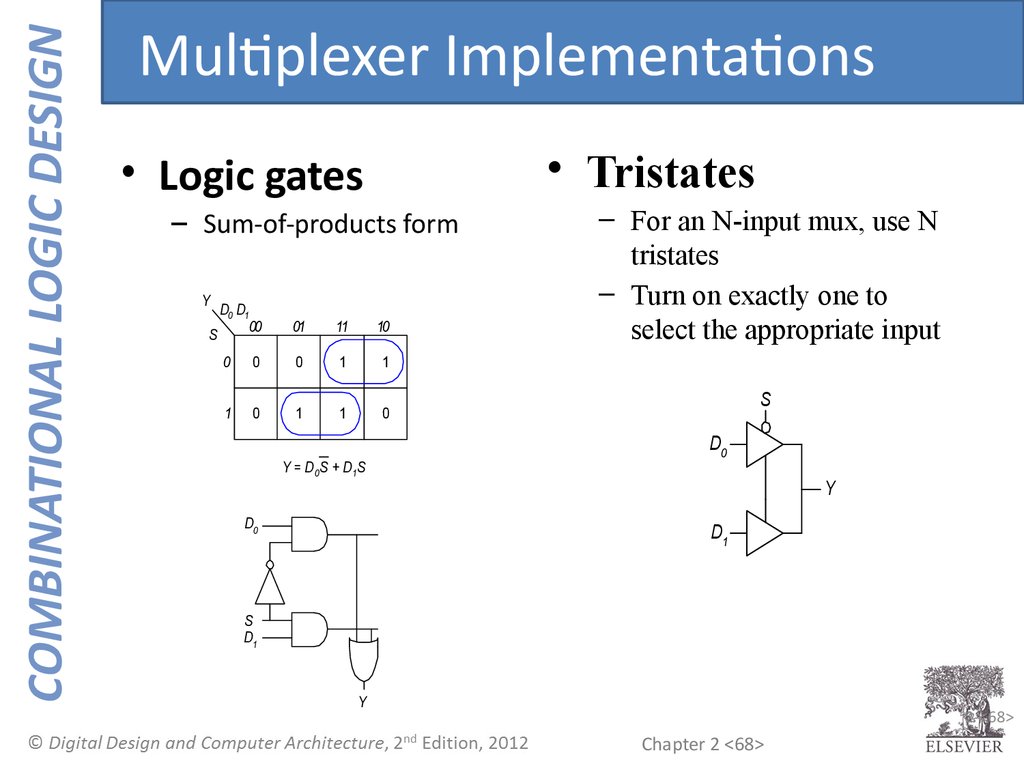
68.

COMBINATIONAL LOGIC DESIGN
Multiplexer Implementations
• Logic gates
• Tristates
– Sum-of-products form
Y
D0 D1
00
S
01
11
10
0
0
0
1
1
1
0
1
1
0
Y = D 0S + D1S
D0
– For an N-input mux, use N
tristates
– Turn on exactly one to
select the appropriate input
S
D0
Y
D1
S
D1
Y
2-<68>
Chapter 2 <68>

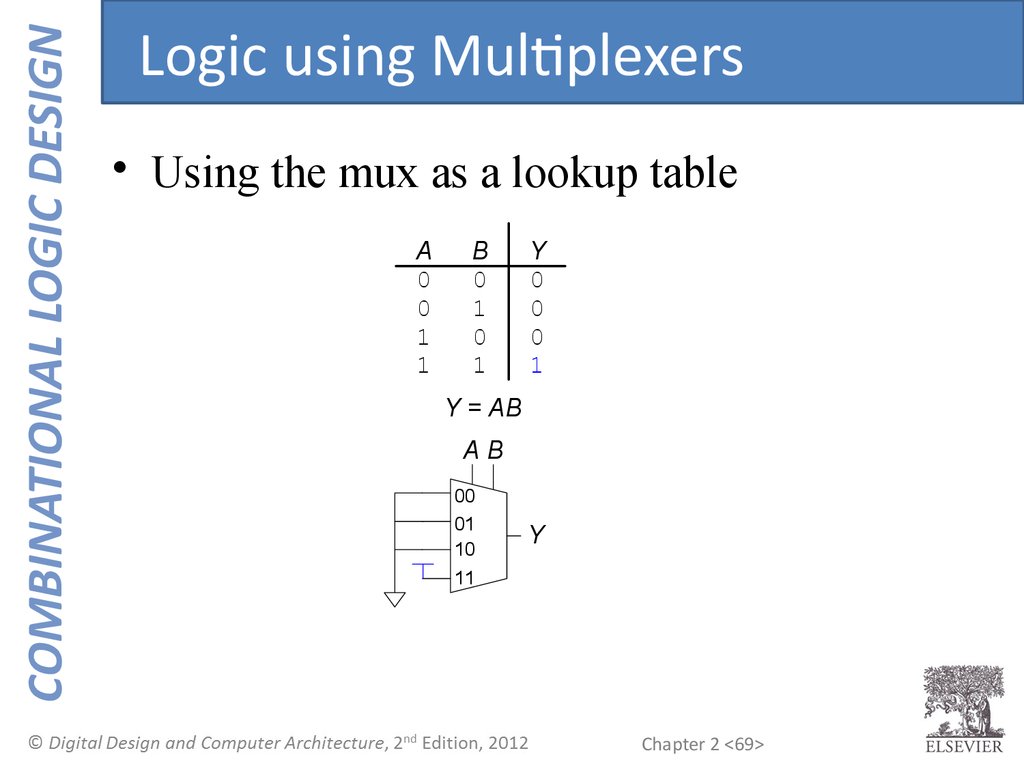
69.

COMBINATIONAL LOGIC DESIGN
Logic using Multiplexers
• Using the mux as a lookup table
A
0
0
1
1
B
0
1
0
1
Y
0
0
0
1
Y = AB
AB
00
01
10
Y
11
Chapter 2 <69>

70.

COMBINATIONAL LOGIC DESIGN
Logic using Multiplexers
• Reducing the size of the mux
Y = AB
A
0
0
1
1
B
0
1
0
1
Y
0
0
0
1
A
Y
0
0
1
B
A
0
B
Chapter 2 <70>
1
Y

71.

COMBINATIONAL LOGIC DESIGN
Decoders
• N inputs, 2N outputs
• One-hot outputs: only one output HIGH at
2:4
once
Decoder
A1
A0
A1
0
0
1
1
A0
0
1
0
1
Y3
0
0
0
1
11
10
01
00
Y3
Y2
Y1
Y0
Y2
0
0
1
0
Y1
0
1
0
0
Y0
1
0
0
0
Chapter 2 <71>

72.

COMBINATIONAL LOGIC DESIGN
Decoder Implementation
A1
A0
Y3
Y2
Y1
Y0
Chapter 2 <72>

73.

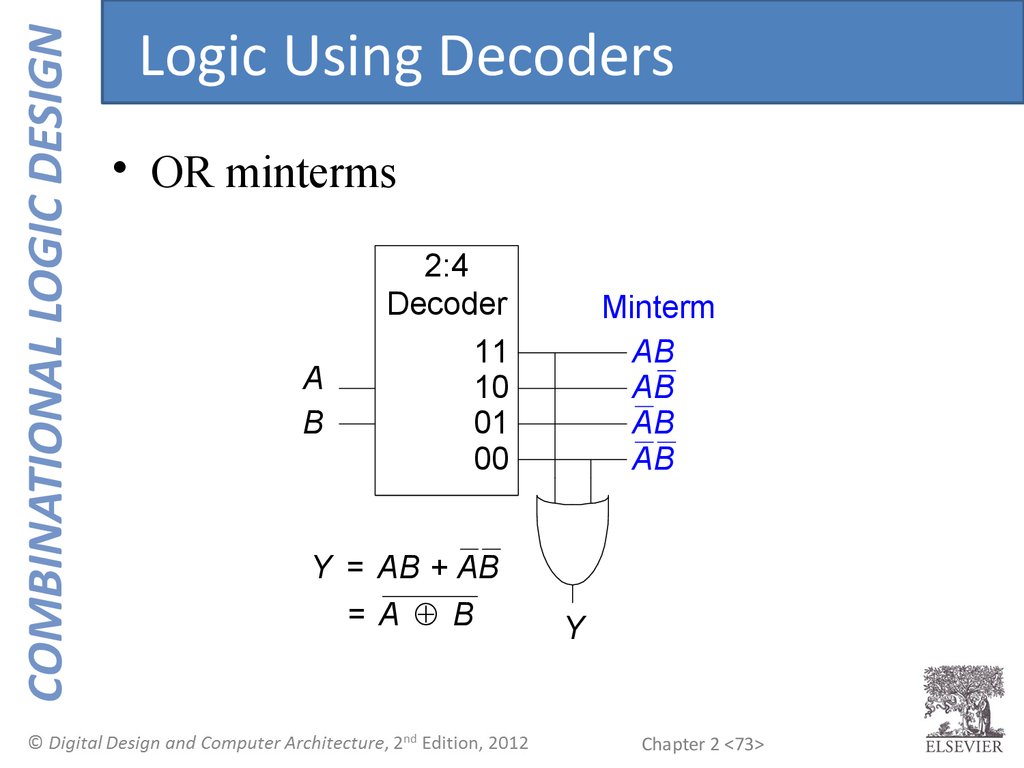
COMBINATIONAL LOGIC DESIGN
Logic Using Decoders
• OR minterms
A
B
2:4
Decoder
11
10
01
00
Y = AB + AB
= A B
Minterm
AB
AB
AB
AB
Y
Chapter 2 <73>

74.

COMBINATIONAL LOGIC DESIGN
ENOUGH FOR TODAY!
Chapter 2 <74>

75.

COMBINATIONAL LOGIC DESIGN
Timing
• Delay between input change and output
changing
• How to build fast circuits?
A
Y
delay
A
Y
Time
Chapter 2 <75>

76.

COMBINATIONAL LOGIC DESIGN
Propagation & Contamination Delay
• Propagation delay: tpd = max delay from input to output
• Contamination delay: tcd = min delay from input to
output
A
Y
tpd
A
Y
tcd
Time
Chapter 2 <76>

77.

COMBINATIONAL LOGIC DESIGN
Propagation & Contamination Delay
• Delay is caused by
– Capacitance and resistance in a circuit
– Speed of light limitation
• Reasons why tpd and tcd may be different:
– Different rising and falling delays
– Multiple inputs and outputs, some of which are
faster than others
– Circuits slow down when hot and speed up when
cold
Chapter 2 <77>

78.

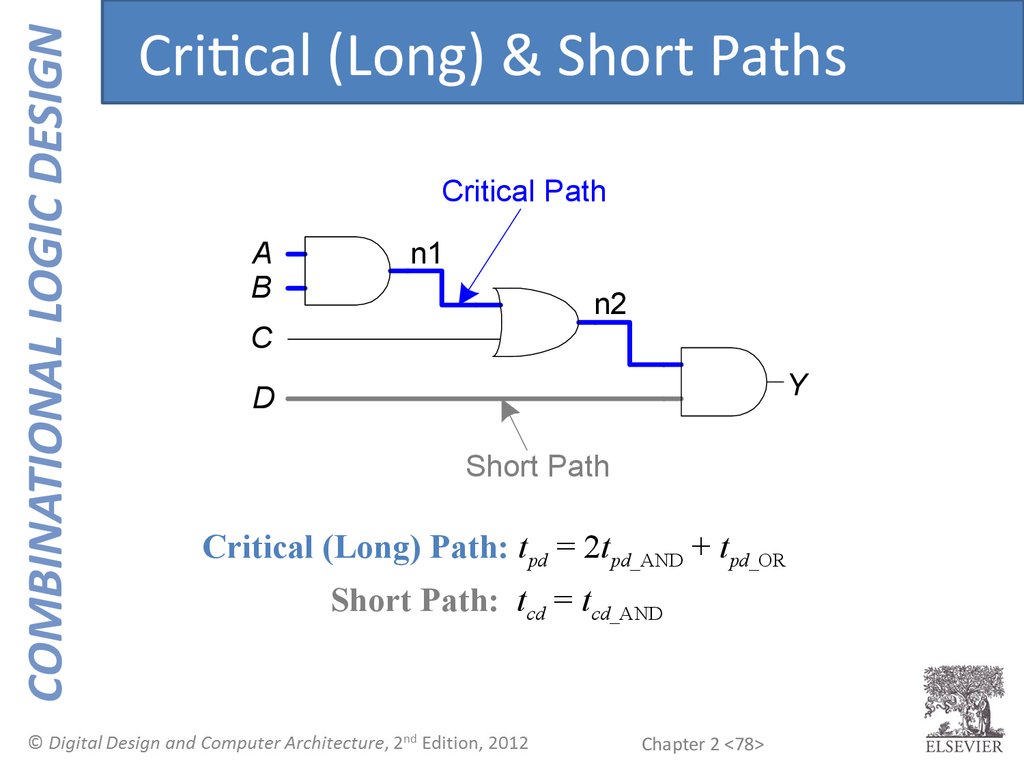
COMBINATIONAL LOGIC DESIGN
Critical (Long) & Short Paths
Critical Path
A
B
n1
n2
C
Y
D
Short Path
Critical (Long) Path: tpd = 2tpd_AND + tpd_OR
Short Path: tcd = tcd_AND
Chapter 2 <78>

79.

COMBINATIONAL LOGIC DESIGN
Glitches
• When a single input change causes an output
to change multiple times
Chapter 2 <79>

80.

COMBINATIONAL LOGIC DESIGN
Glitch Example
• What happens when A = 0, C = 1, B falls?
A
B
Y
C
Y
AB
00
01
11
10
0
1
0
0
0
1
1
1
1
0
C
Y = AB + BC
Chapter 2 <80>

81.

COMBINATIONAL LOGIC DESIGN
Glitch Example (cont.)
A=0
B=1 0
0
Critical Path
1
n1
Y=1
0
n2
C=1
1
0
Short Path
B
n2
n1
Y
glitch
Time
Chapter 2 <81>
1

82.

COMBINATIONAL LOGIC DESIGN
Fixing the Glitch
Y
AB
00
01
11
10
0
1
0
0
0
1
1
1
1
0
C
AC
Y = AB + BC + AC
A=0
B=1 0
Y=1
C=1
Chapter 2 <82>

83.

COMBINATIONAL LOGIC DESIGN
Why Understand Glitches?
• Glitches don’t cause problems because of
synchronous design conventions (see
Chapter 3)
• It’s important to recognize a glitch: in
simulations or on oscilloscope
• Can’t get rid of all glitches – simultaneous
transitions on multiple inputs can also
cause glitches
Chapter 2 <83>

English Русский Rules