Similar presentations:
Digital Logic Design
1.
Digital Logic DesignLecture – 3:
Combining Logic Gates
Konakbayev Olzhas, senior-lecturer,
2.
Lecture baseDigital Electronics: Principles & Applications, 9th edition by Roger
Tokheim & Patrick E. Hoppe:
• Chapter 4
2
3.
Topics to cover• Constructing Circuits from Boolean Expressions
• Minterm and Maxterm Boolean Expressions
• Boolean Expression from a Truth Table
• Truth Tables and Boolean Expressions
• Simplifying Boolean Expressions
• Karnaugh Maps
• Using NAND Logic
• Using DeMorgan’s Theorem
3
4.
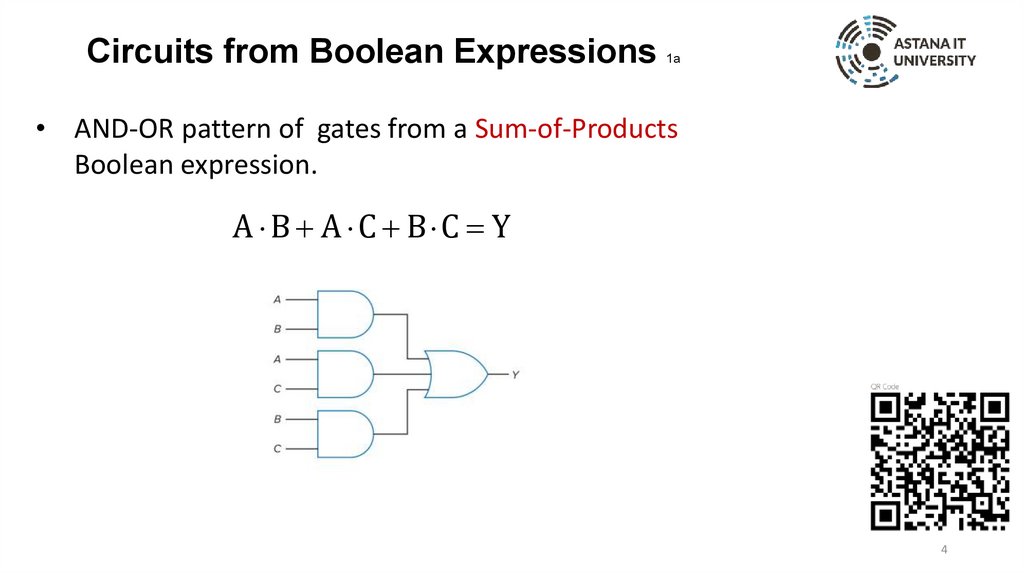
Circuits from Boolean Expressions1a
• AND-OR pattern of gates from a Sum-of-Products
Boolean expression.
A B A C B C Y
4
5.
Circuits from Boolean Expressions2
• OR-AND pattern of gates from a Product-of-Sums
Boolean expression.
(A B) (A B C) Y
5
6.
Circuits from Boolean Expressions3
• Step 1: Identify pattern of operation
6
7.
Circuits from Boolean Expressions4
• Step 2: Add the first OR gate with inputs
7
8.
Circuits from Boolean Expressions5
• Step 3: Add the second OR gate with inputs
8
9.
Minterm and Maxterm Boolean Expressions1
• Maxterm Boolean Expression
C+B+A C+B+A C+B+A =Y
(Product-of-Sum Expression)
9
10.
Minterm and Maxterm Boolean Expressions2
• Minterm Boolean Expression
C B A C B A C B A Y
(Sum-of-Product Expression)
10
11.
Boolean Expression from a Truth Table• Step 1: Write an AND
expression for each
instance Y = 1.
• Step 2: OR the
expressions together
to form a Boolean
expression.
11
12.
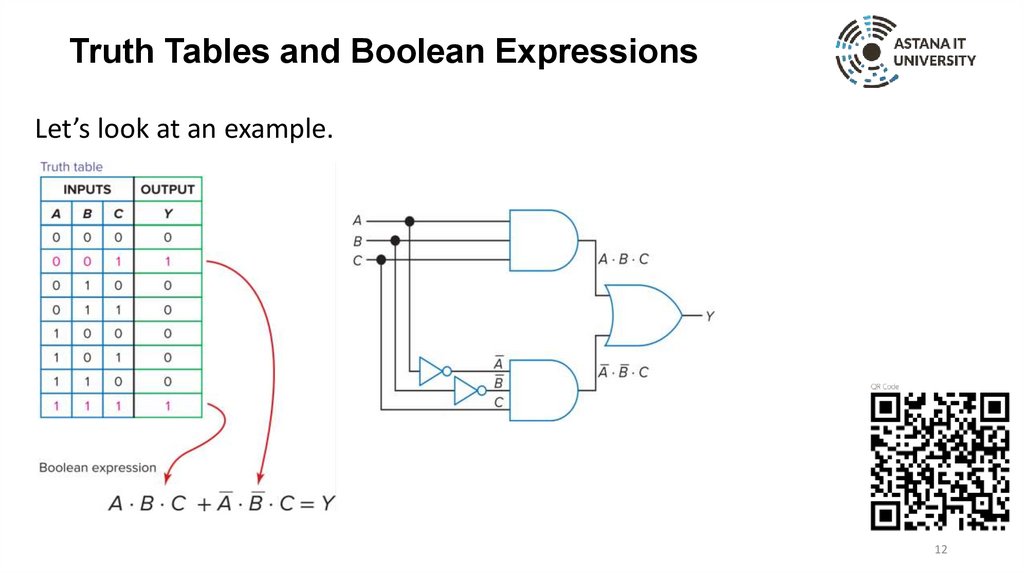
Truth Tables and Boolean ExpressionsLet’s look at an example.
12
13.
Simplifying Boolean Expressions1
• Original Boolean Expression
13
14.
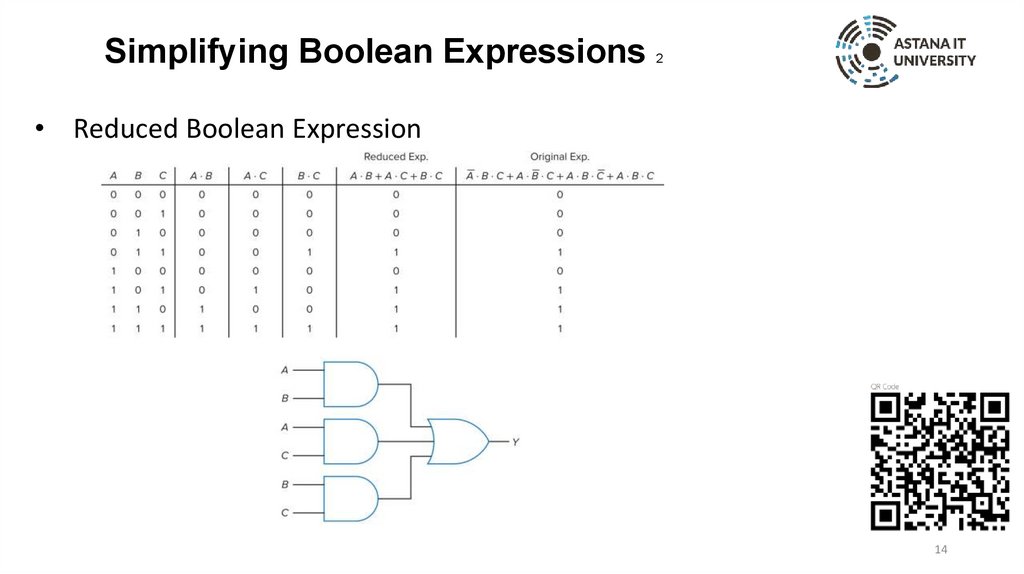
Simplifying Boolean Expressions2
• Reduced Boolean Expression
14
15.
Single-variable Boolean Theorems1
• The first Boolean theorem states that X ANDed with
0 is 0.
X 0 0
15
16.
Single-variable Boolean Theorems2
• The second Boolean theorem states that X ANDed
with 1 is X.
X 1 X
16
17.
Single-variable Boolean Theorems3
• The third Boolean theorem states that X ANDed with
X is X.
X X X
17
18.
Single-variable Boolean Theorems4
• The fourth Boolean theorem states that X ANDed
with ഥ
X is 0.
X X 0
X
18
19.
Single-variable Boolean Theorems5
The fifth Boolean theorem states that X ORed with 0 is X.
X+0=0
19
20.
Single-variable Boolean Theorems6
• The sixth Boolean theorem states that X ORed with 1
is 1.
X+1=1
20
21.
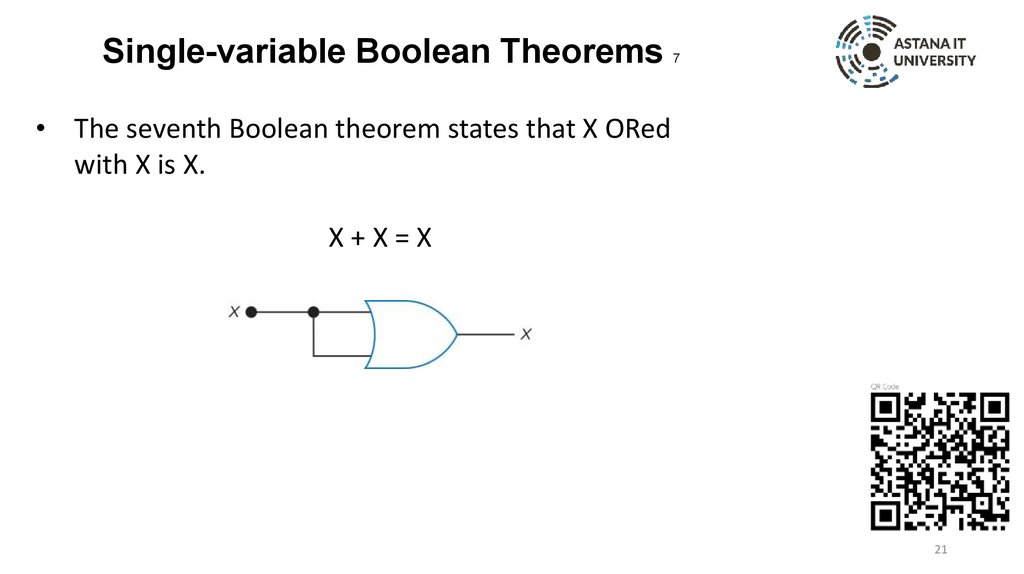
Single-variable Boolean Theorems7
• The seventh Boolean theorem states that X ORed
with X is X.
X+X=X
21
22.
Single-variable Boolean Theorems8
• The eighth Boolean theorem states that X ORed with
ഥ
X is 1
X X 1
22
23.
Single-Variable Boolean Theorems9
23
24.
Multivariable Boolean Theorems1
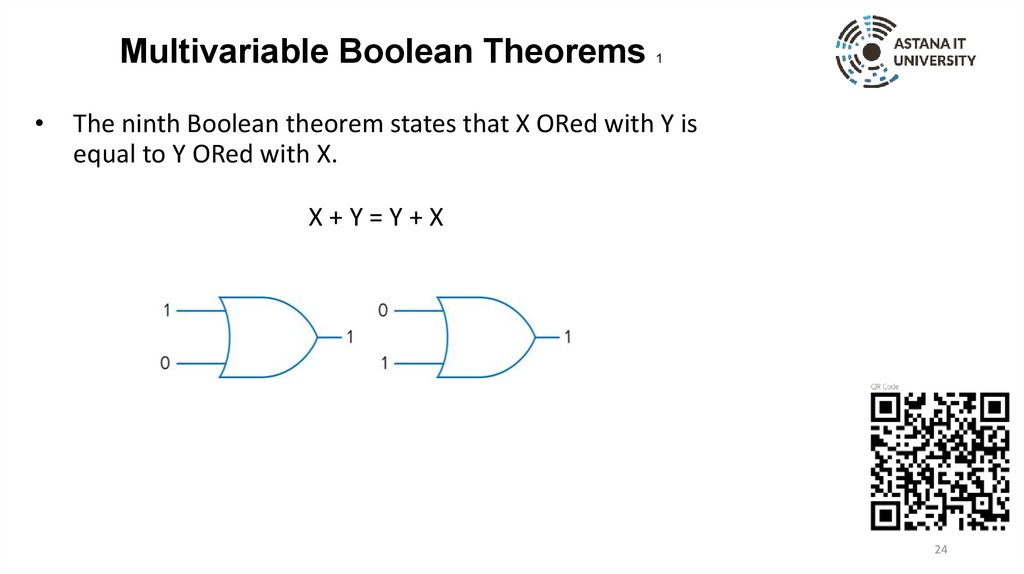
The ninth Boolean theorem states that X ORed with Y is
equal to Y ORed with X.
X+Y=Y+X
24
25.
Multivariable Boolean Theorems2
• The tenth Boolean theorem states that X ANDed with
Y is equal to Y ANDed with X.
X Y Y X
25
26.
Multivariable Boolean Theorems3
• The eleventh Boolean theorem demonstrates when
ORing multiple inputs, the order of operation does
not matter.
X Y Z X Y Z X Y Z
26
27.
Multivariable Boolean Theorems4
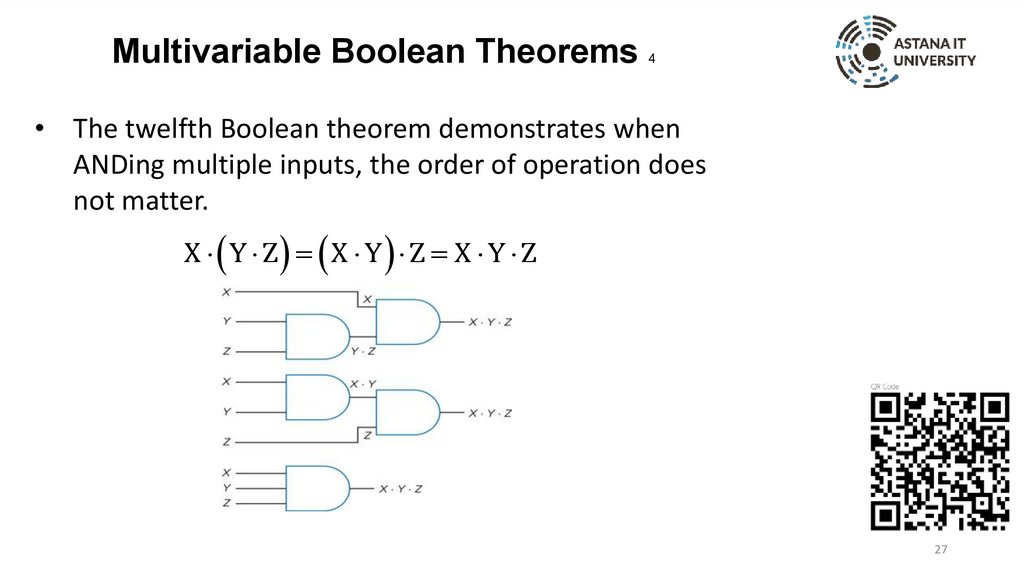
• The twelfth Boolean theorem demonstrates when
ANDing multiple inputs, the order of operation does
not matter.
X Y Z X Y Z X Y Z
27
28.
Multivariable Boolean Theorems5
• The thirteenth Boolean theorem is sometimes called
the distributive theorem.
X Y Z X Y X Z
28
29.
Multivariable Boolean Theorems6
• The fourteenth Boolean theorem states X ORed with
X ANDed with Y is equal to X.
X X Y X
29
30.
Multivariable Boolean Theorems7
• The fifteenth Boolean theorem states X ORed with ഥ
X
ANDed with Y is equal to X ORed with Y.
X X Y X Y
Access the text alternative for slide images.
30
30
31.
Multivariable Boolean Theorems8
31
32.
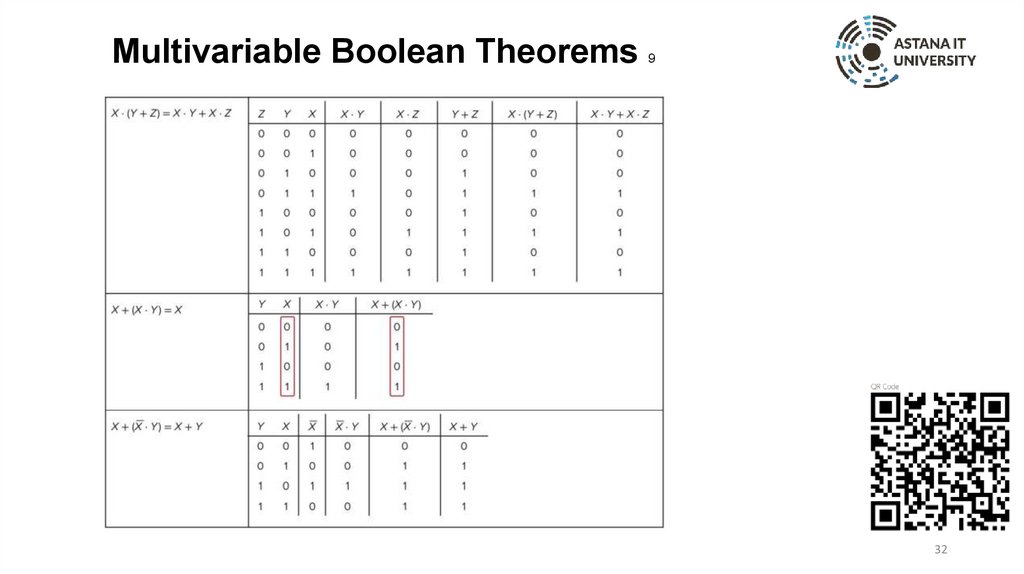
Multivariable Boolean Theorems9
32
33.
Boolean Reduction with Two Variables1
33
34.
Boolean Reduction with Two Variables2
• Let’s check our answer.
34
35.
Boolean Reduction with Three Variables1
35
36.
Boolean Reduction with Three Variables2
• Let’s check our answer.
36
37.
Karnaugh Maps• The columns and rows of the two and three input
Karnaugh maps must be laid out in this manner.
37
38.
Karnaugh Maps with Three Variables1
Step 1: Write the minterm for each input
combination that produces a 1 on the
output.
38
39.
Karnaugh Maps with Three Variables2
Step 2: Write the Sum of Product expression
using the minterms.
39
40.
Karnaugh Maps with Three Variables3
Step 3: Fill in the 1’s for each minterm in
The Sum of Product expression
40
41.
Karnaugh Maps with Three Variables4
Step 4: Loop adjacent 1’s in groups of
two, four, or eight.
41
42.
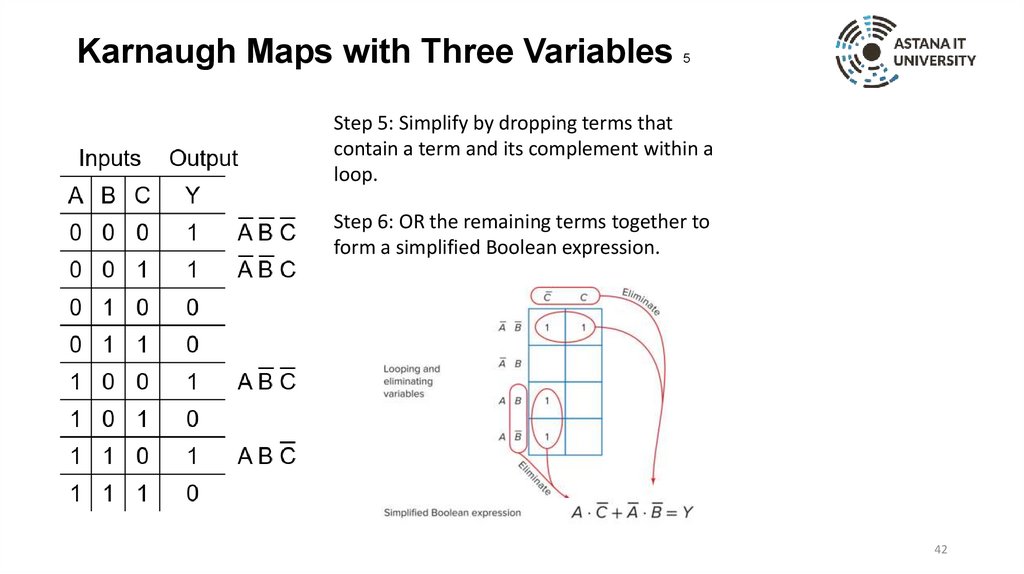
Karnaugh Maps with Three Variables5
Step 5: Simplify by dropping terms that
contain a term and its complement within a
loop.
Step 6: OR the remaining terms together to
form a simplified Boolean expression.
42
43.
Karnaugh Maps with Three Variables6
43
44.
Boolean Reduction with Three Variables• Let’s check our answer.
44
45.
Karnaugh Maps with Four Variables1
45
46.
Karnaugh Maps with Four Variables2
46
47.
Other Looping Possibilities1
• Consider the Karnaugh map as a vertical cylinder.
47
48.
Other Looping Possibilities2
• Consider the Karnaugh map as a horizontal cylinder.
48
49.
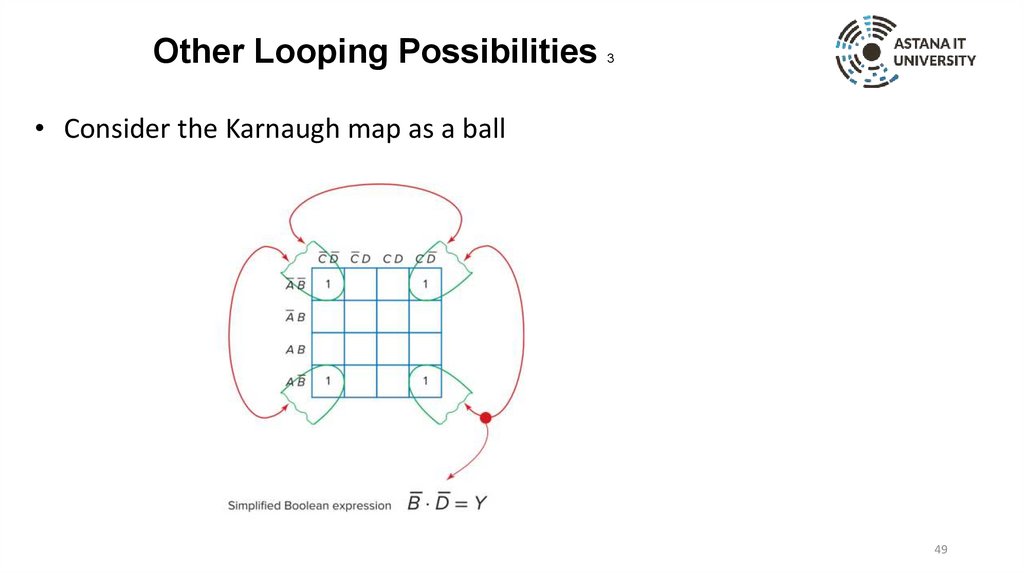
Other Looping Possibilities3
• Consider the Karnaugh map as a ball
49
50.
Using NAND Logic1
• Start with a minterm (sum-of-products) Boolean
expression.
• Draw the AND-OR logic diagram using AND, OR, and
NOT symbols.
• Substitute NAND symbols for each AND and OR
symbol, keeping all connections the same.
• Substitute NAND symbols with all inputs tied
together for each inverter.
• Test the logic circuit containing all NAND gates to
determine if generates the proper truth table.
50
51.
Using NAND Logic2
• Start with a minterm (sum-of-products) Boolean
expression.
• Draw the AND-OR logic diagram using AND, OR, and
NOT symbols.
51
52.
Using NAND Logic3
• Substitute NAND symbols for each AND and OR
symbol, keeping all connections the same.
• Substitute NAND symbols with all inputs tied together
for each inverter.
52
53.
De Morgan’s Theorem1
• First Theorem
53
54.
De Morgan’s Theorem2
Change OR to AND
Compliment each individual
variable
• Compliment the entire
function
• Eliminate all groups of
double overbars.
• Final expression
54
55.
De Morgan’s Theorem3
• Second Theorem
55
56.
De Morgan’s Theorem4
Change AND to OR
Compliment each
individual variable
Compliment the entire
function
Eliminate all groups of
double overbars.
• Final expression
56
57.
De Morgan’s Theorem 5Break the line, change the sign
A B A gB
A gB A B
57
58.
De Morgan’s Theorem6
Let’s do an example
58
59.
Review1
• Draw the circuit for the Boolean expression shown.
A B A C B C Y
59
60.
Review2
• Draw the circuit for the Boolean expression shown.
A gB A gC BgC Y
60
61.
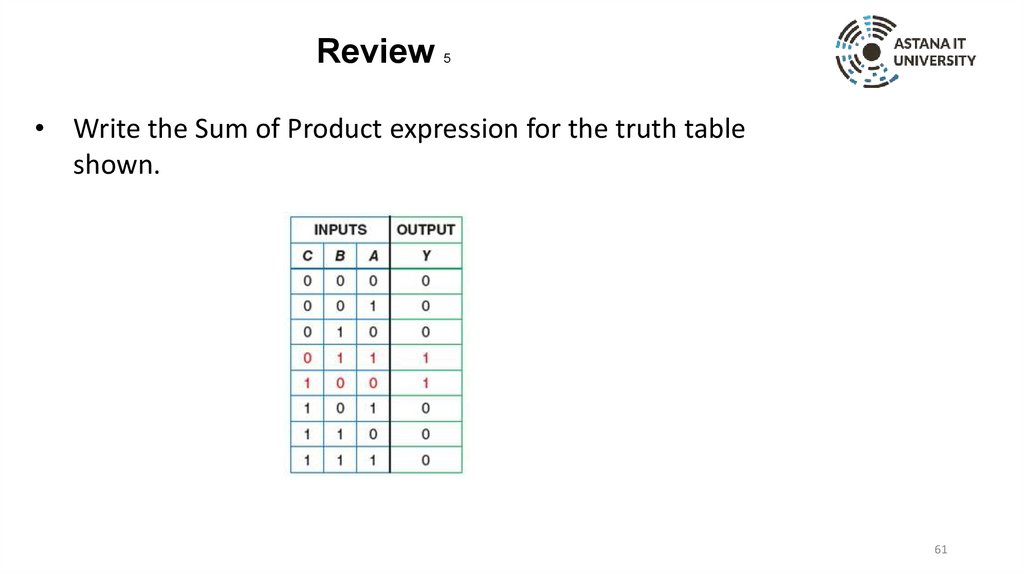
Review5
• Write the Sum of Product expression for the truth table
shown.
61
62.
Review 6• Write the Sum of Product expression for the truth
table shown.
62
63.
Review11
• Label the rows and columns of the Karnaugh maps.
63
64.
Review12
• Label the rows and columns of the Karnaugh maps.
64
65.
Review13
• Use the Karnaugh mapping to determine the reduced
Sum of Product expression.
65
66.
Review14
• Use the Karnaugh mapping to determine the reduced
Sum of Product expression.
66
67.
Review21
• Use De Morgan’s Theorem to simplify this Boolean
expression.
A B C A B C Y
67
68.
Review22
• Use De Morgan’s Theorem to simplify this Boolean
expression.
A B C A B C Y
A B C A B C Y
68
69.
Thank you!69



























































 mathematics
mathematics