Площадь треугольника. (8 класс)

1.

2.

Перпендикуляр, проведенный из вершины треугольника к прямой,
содержащей противоположную сторону, называется высотой
треугольника.
В
Ы
С
О
Т
А
1
В
Ы
С
О
Т
А
1
В
Ы
С
О
Т
А
Высота в прямоугольном
треугольнике, проведенная из
вершины острого угла,
совпадает с катетом.
1
Высота в тупоугольном
треугольнике, проведенная из
вершины острого угла,
проходит во внешней области
треугольника.

3.

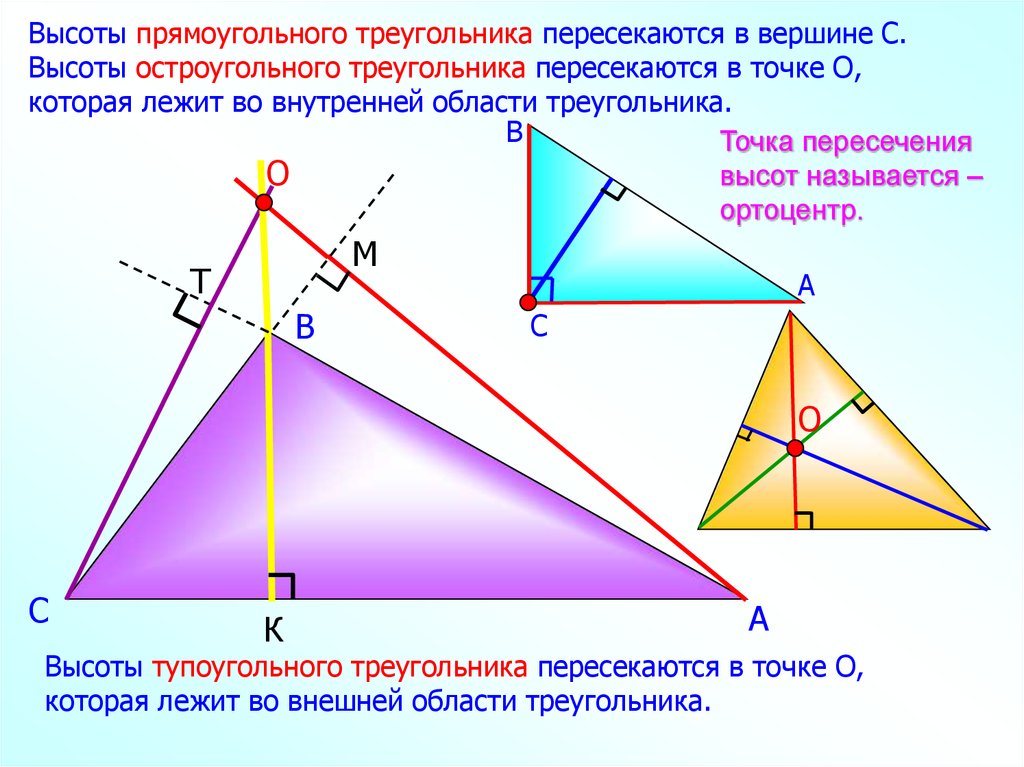
Высоты прямоугольного треугольника пересекаются в вершине С.
Высоты остроугольного треугольника пересекаются в точке О,
которая лежит во внутренней области треугольника.
В
Точка пересечения
O
высот называется –
ортоцентр.
М
Т
В
А
С
O
С
К
А
Высоты тупоугольного треугольника пересекаются в точке О,
которая лежит во внешней области треугольника.

4.

Свойства площадей
10. Равные многоугольники имеют равные площади.
20. Если многоугольник составлен из нескольких
многоугольников, то его площадь равна сумме
площадей этих многоугольников.
Эти свойства помогут нам получить формулу для
вычисления площади параллелограмма.

5.

Площадь треугольника равна половине произведения
его основания на высоту.
С
D
Докажем, что
1
S AB CH
2
А
В
H
ABС DCВ, по трем сторонам
SABC = SBCD
S АВС
1
S
2
1
AB CH
ABDС
2

6.

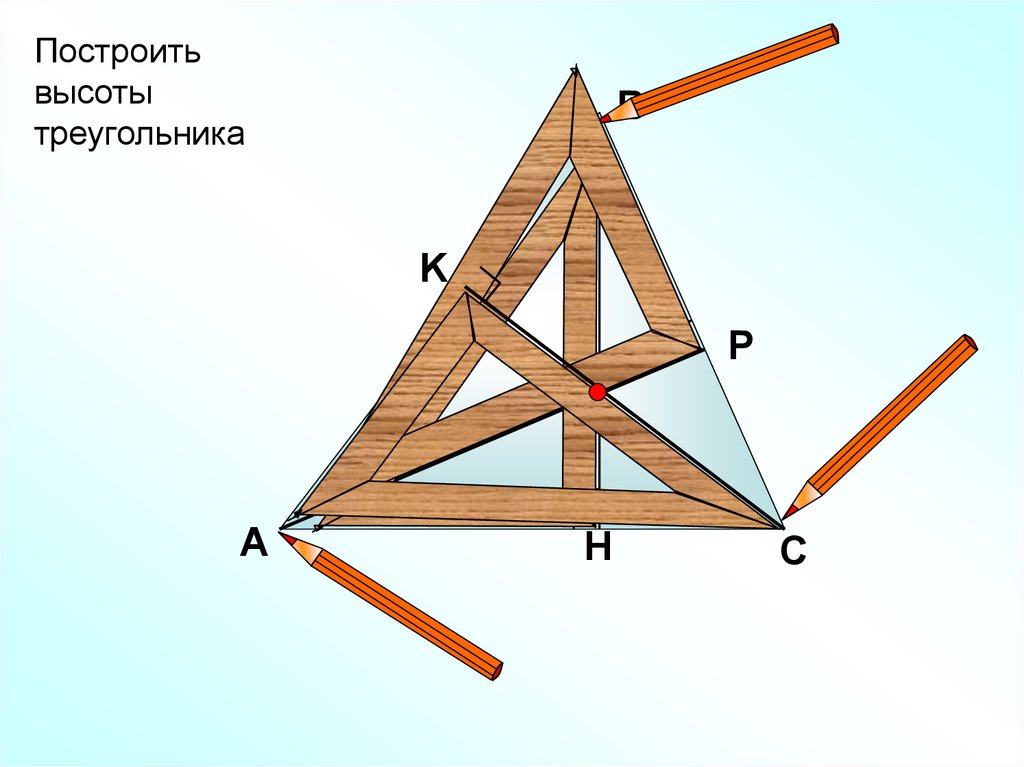
Построить
высоты
треугольника
В
K
Р
А
H
С

7.

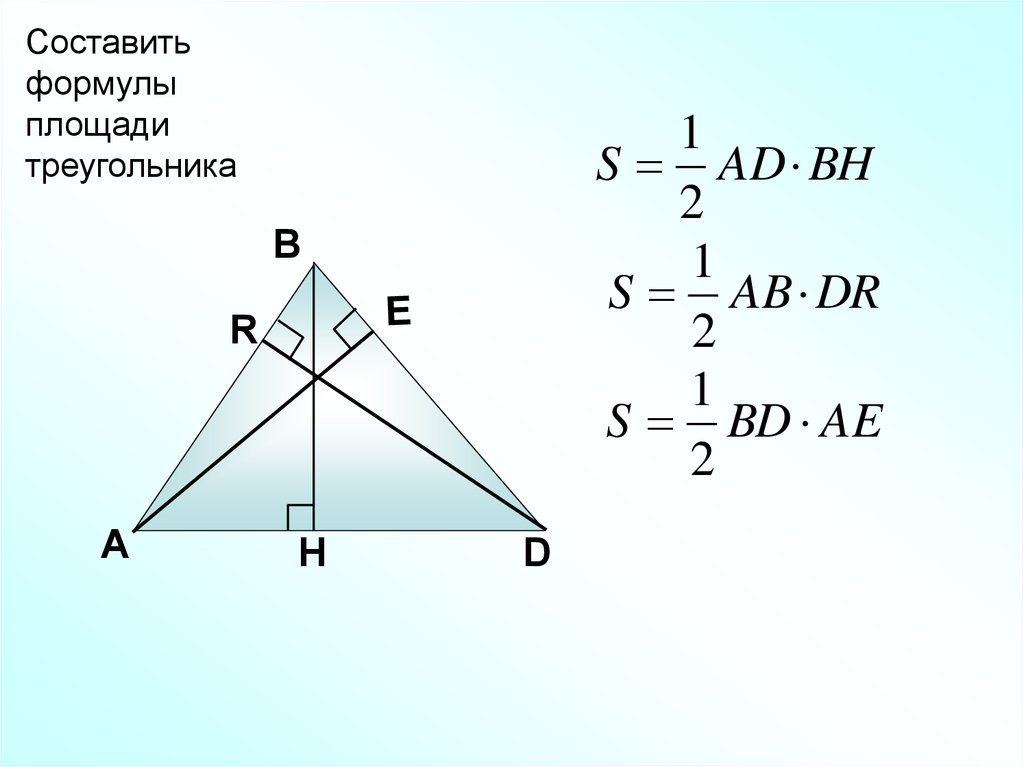
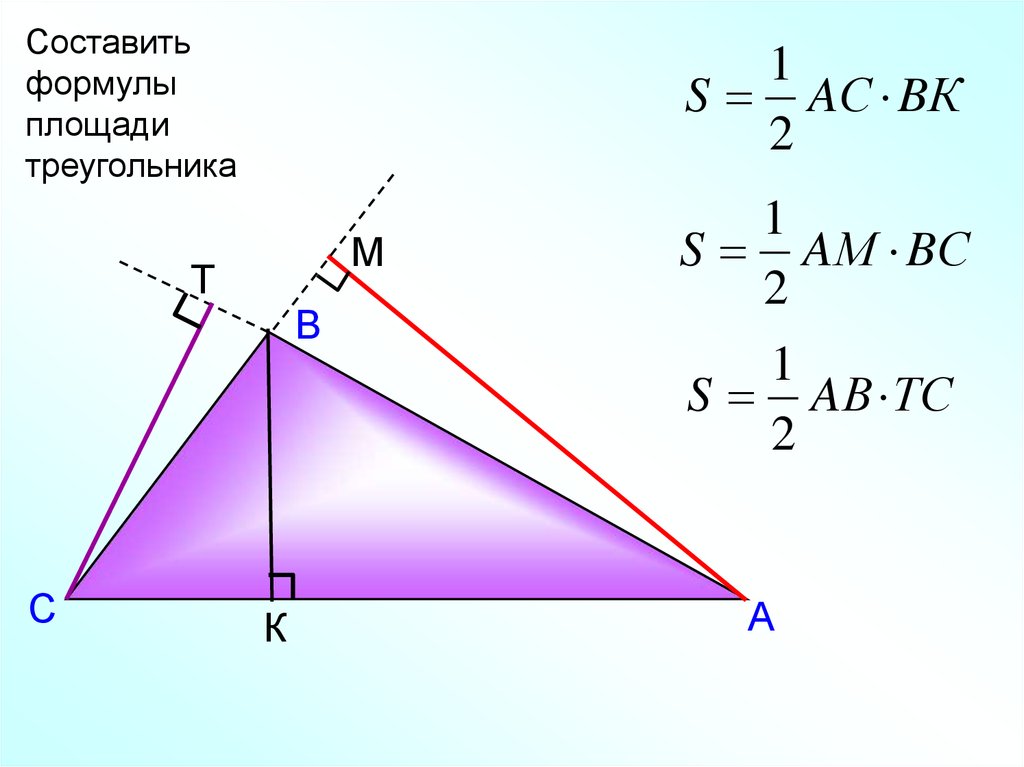
Составить
формулы
площади
треугольника
1
S AD BH
2
1
S AB DR
2
1
S BD AE
2
В
R
А
H
D

8.

Составить формулы площади треугольника
1
S СD АB
2
В
1
S СА СB
2
D
a
С
b
А
SABC =
1
2
Следствие 1.
Площадь прямоугольного треугольника равна
половине произведения катетов.
ab

9.

Составить
формулы
площади
треугольника
1
S AС BК
2
М
Т
В
С
К
1
S AМ BС
2
1
S AВ ТС
2
А

10.

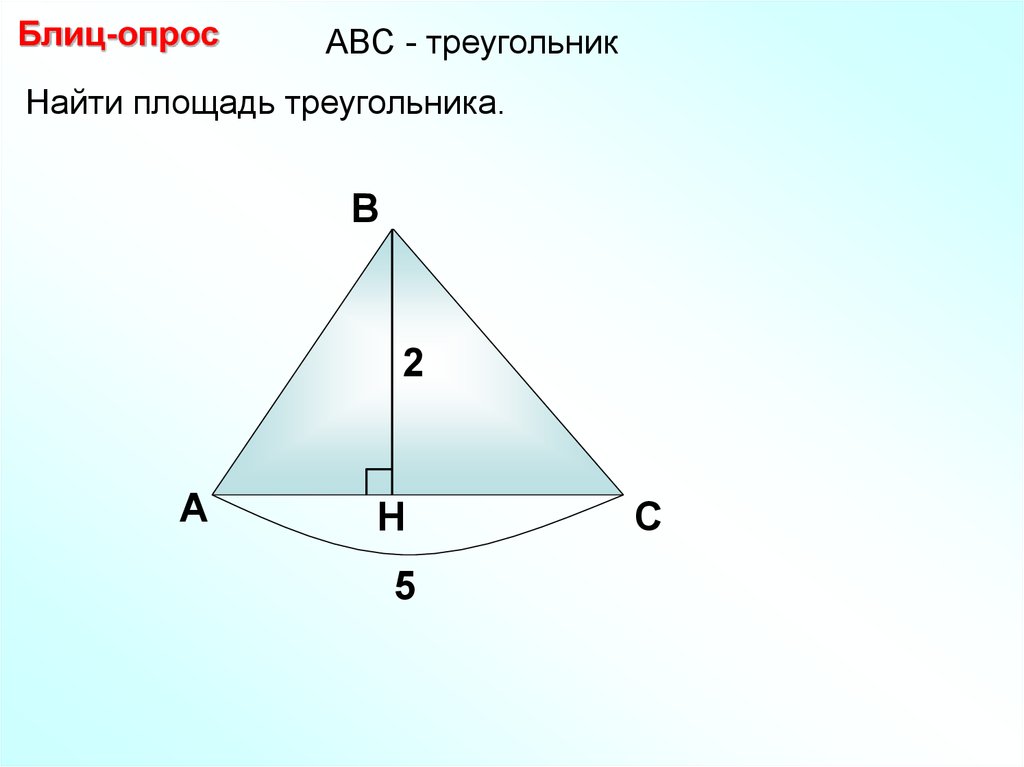
Блиц-опрос
АBC - треугольник
Найти площадь треугольника.
В
2
А
H
5
С

11.

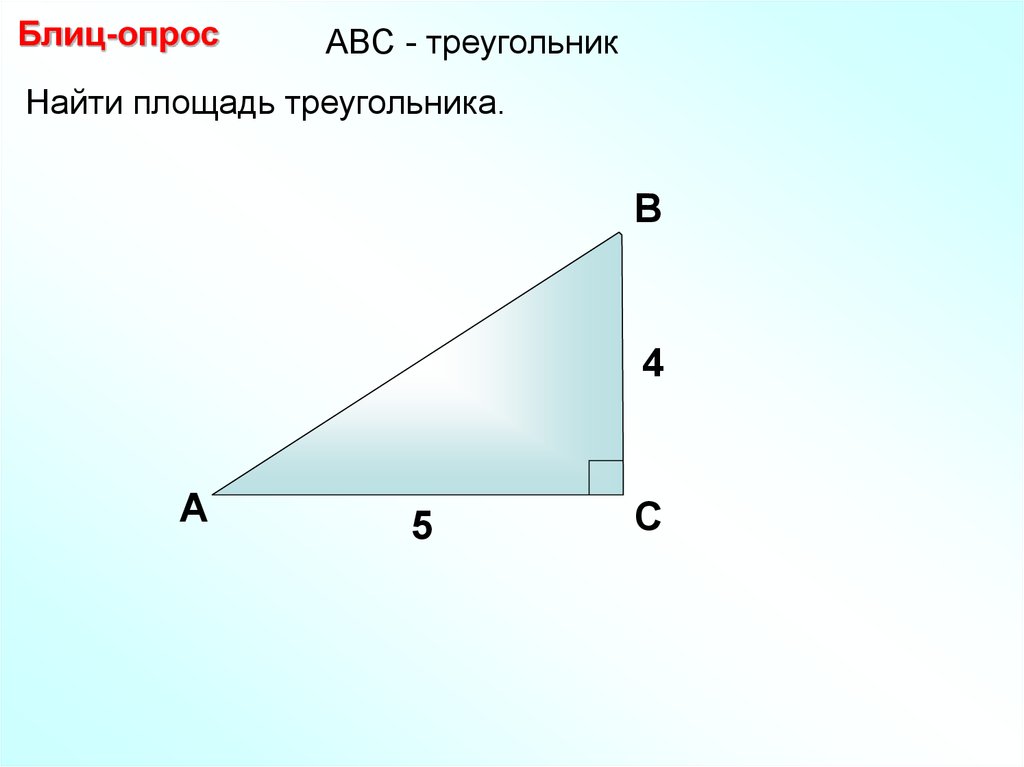
Блиц-опрос
АBC - треугольник
Найти площадь треугольника.
В
4
А
5
С

12.

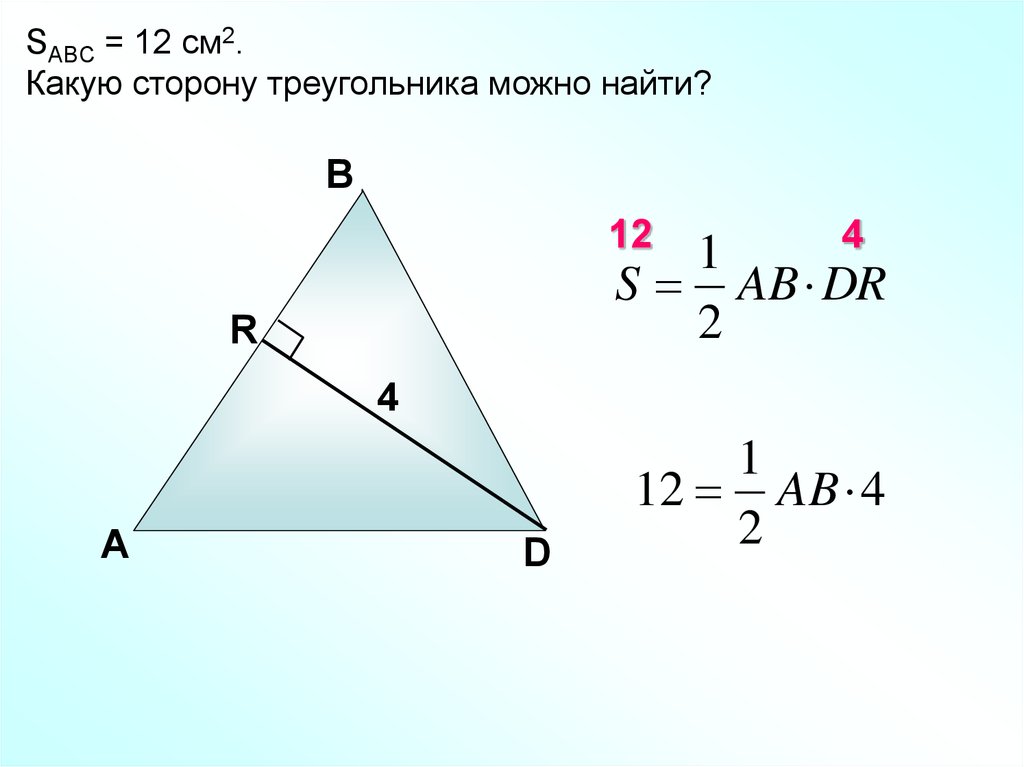
SABC = 12 см2.
Какую сторону треугольника можно найти?
В
12
4
1
S AB DR
2
R
4
А
D
1
12 AB 4
2

13.

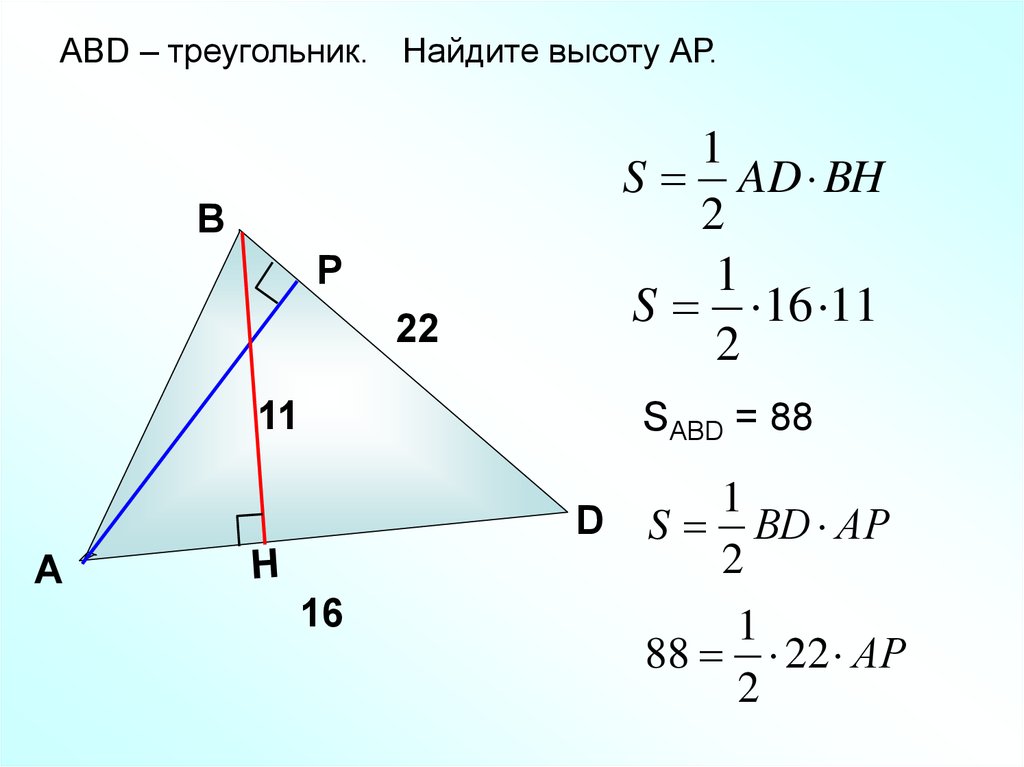
АBD – треугольник. Найдите высоту АР.
1
S AD BH
2
В
Р
22
11
1
S 16 11
2
SABD = 88
1
D S ВD АР
2
А
16
1
88 22 АР
2

14.

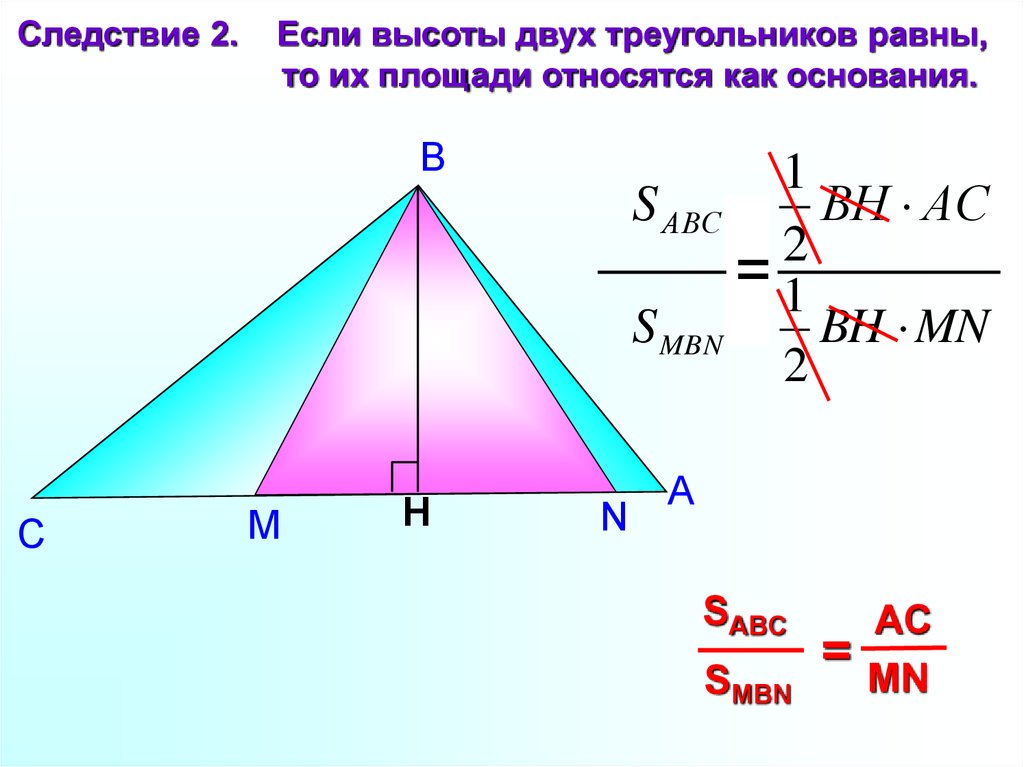
Следствие 2.
Если высоты двух треугольников равны,
то их площади относятся как основания.
В
С
М
H
1
S АВС ВH АC
2
=1
S MBN BH MN
2
N
А
SABC
SMBN
=
AC
MN

15.

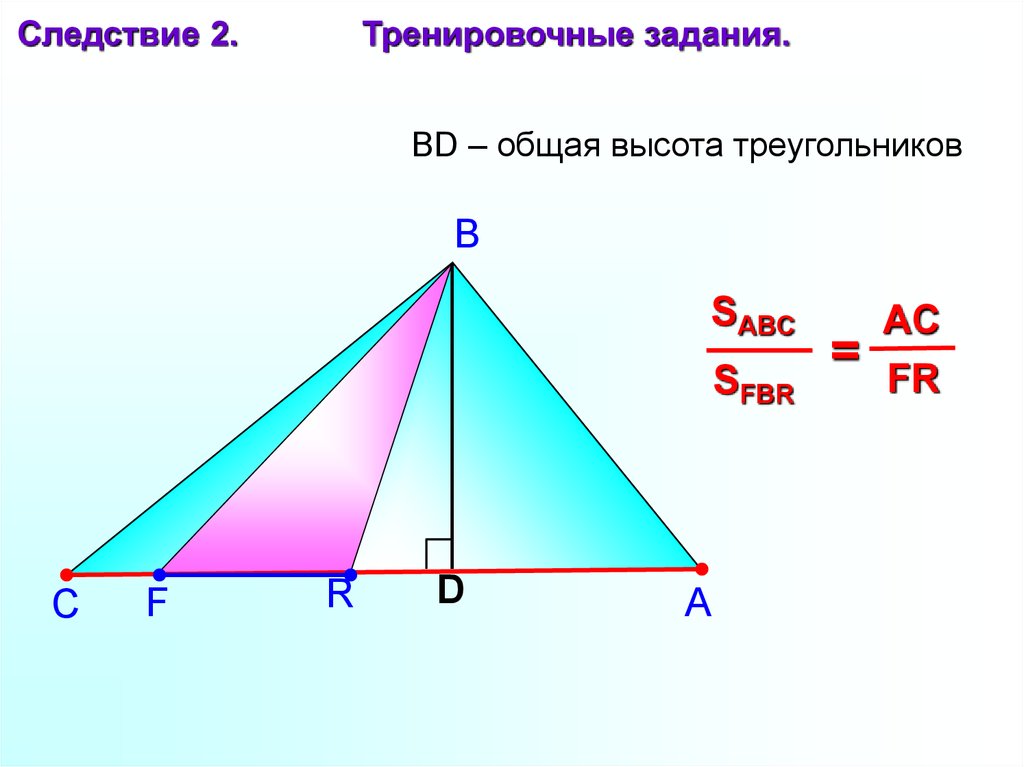
Следствие 2.
Тренировочные задания.
BD – общая высота треугольников
В
SABC
SFBR
С
F
R
D
А
=
AC
FR

16.

Следствие 2.
Тренировочные задания.
В
SCBF
SCBR
SCBR
SABR
С
F
R
D
А
=
CF
CR
=
CR
AR

17.

Тренировочные задания.
Сравните площади двух треугольников, на которые
разделяется данный треугольник его медианой.
BH – общая высота треугольников
В
SCBD
SDBA
С
D
H
А
=
CD
DA
=1

18.

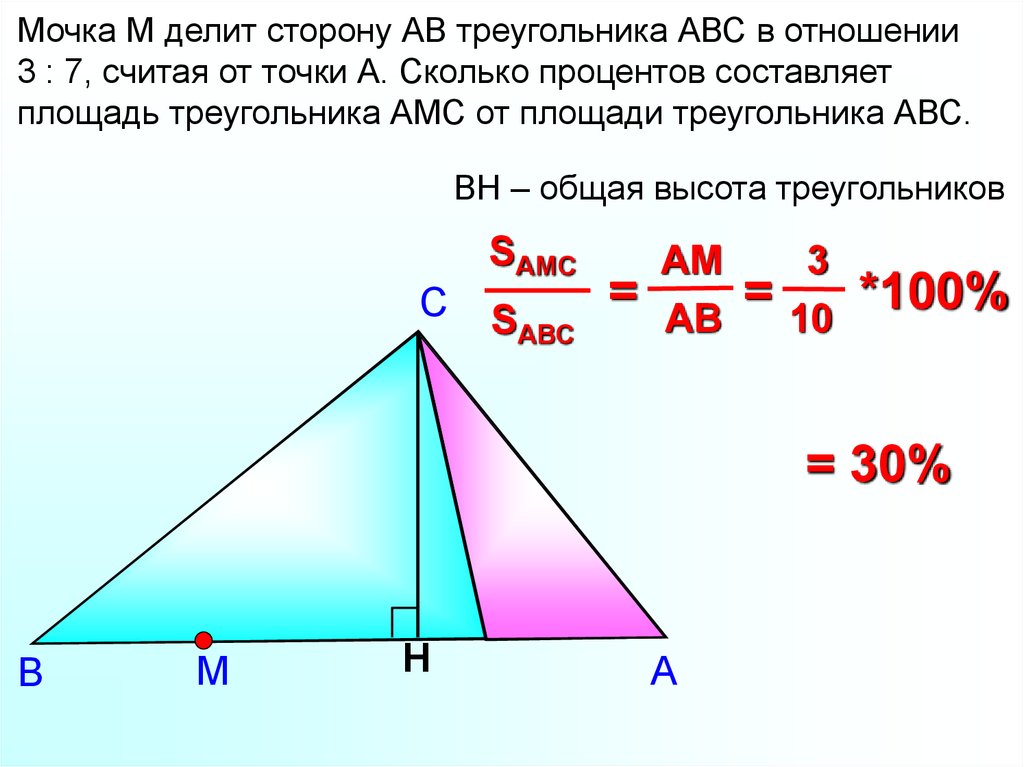
Мочка М делит сторону АВ треугольника АВС в отношении
3 : 7, считая от точки А. Сколько процентов составляет
площадь треугольника АМС от площади треугольника АВС.
BH – общая высота треугольников
С
SАМC
SAВС
=
АМ
АВ
=
3
10
*100%
= 30%
В
М
H
А

19.

Докажите что площадь ромба
равна половине произведения его диагоналей.
1
1
S АВСD 2S ABC 2 AC OB AC BD
2
2
В
А
О
D
С
SABCD =
1
2
AC BD
SABCD =
1
2
d1 d2

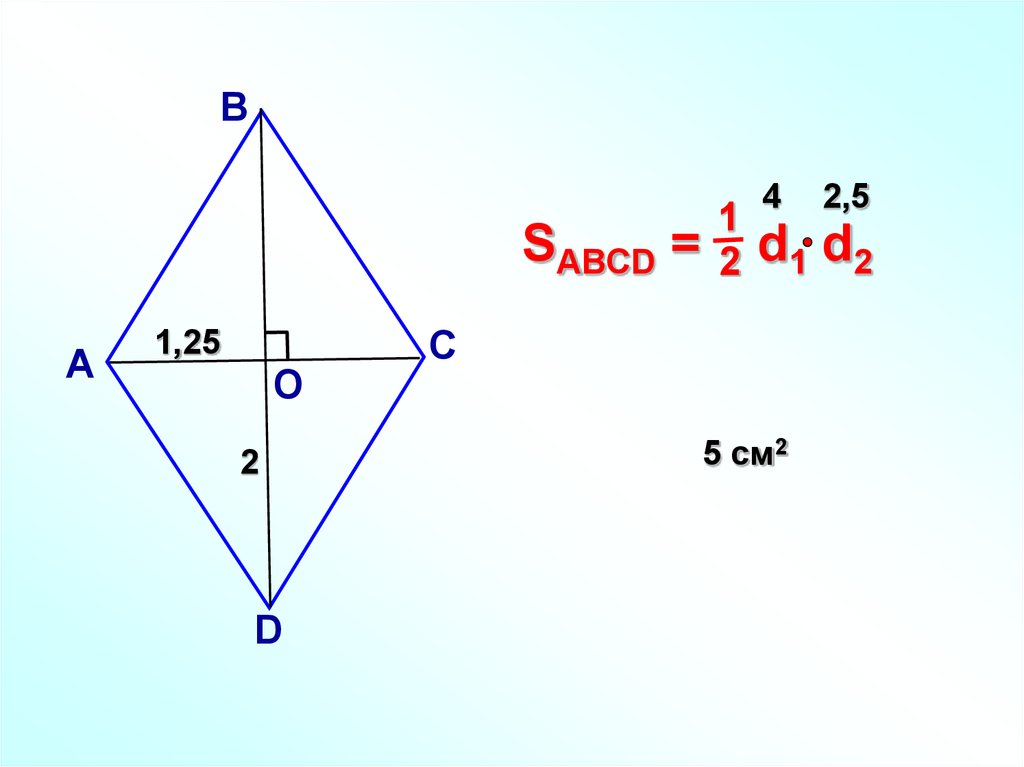
20.

В
SABCD =
А
1,25
О
2
D
1
2
4
2,5
d1 d2
С
5 см2

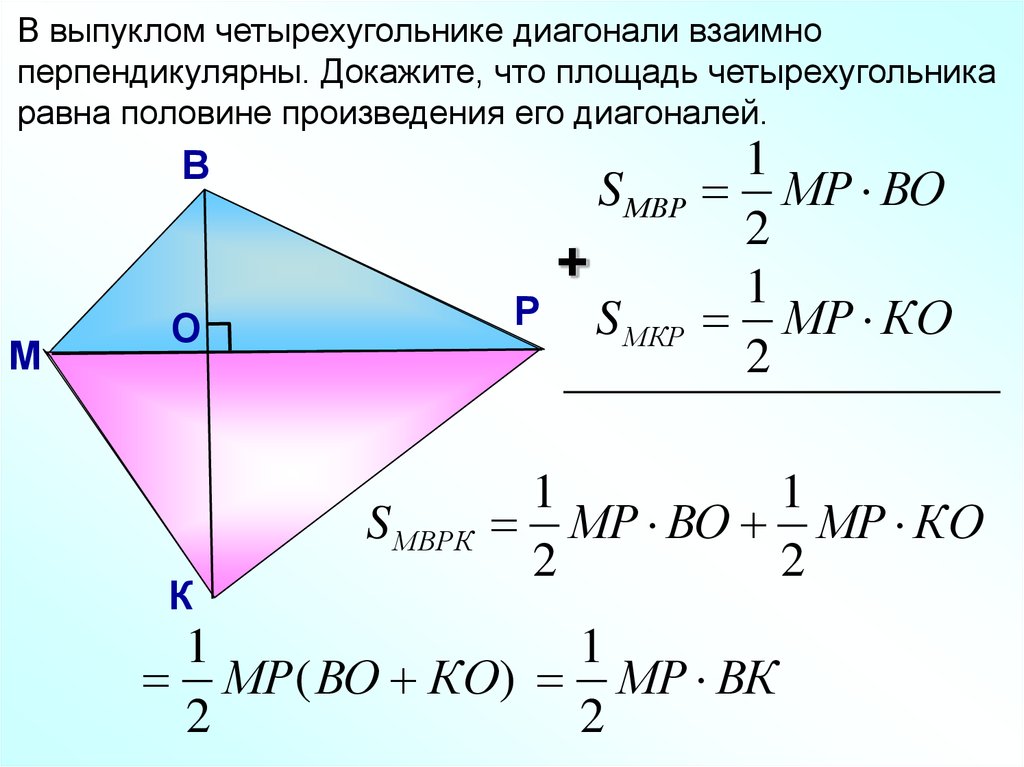
21.

В выпуклом четырехугольнике диагонали взаимно
перпендикулярны. Докажите, что площадь четырехугольника
равна половине произведения его диагоналей.
В
М
S МВР
Р
О
S МВРК
К
+
S МКР
1
МР ВО
2
1
МР КО
2
1
1
МР ВО МР КО
2
2
1
1
МР ( ВО КО) МР ВК
2
2

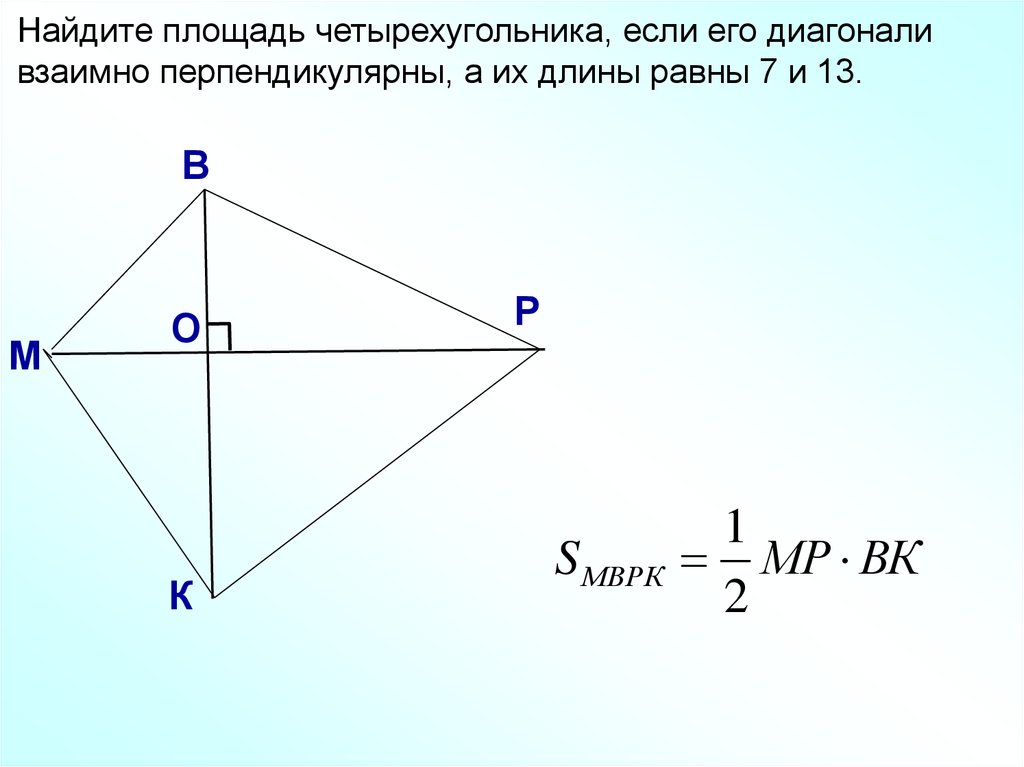
22.

Найдите площадь четырехугольника, если его диагонали
взаимно перпендикулярны, а их длины равны 7 и 13.
В
М
О
К
Р
S МВРК
1
МР ВК
2

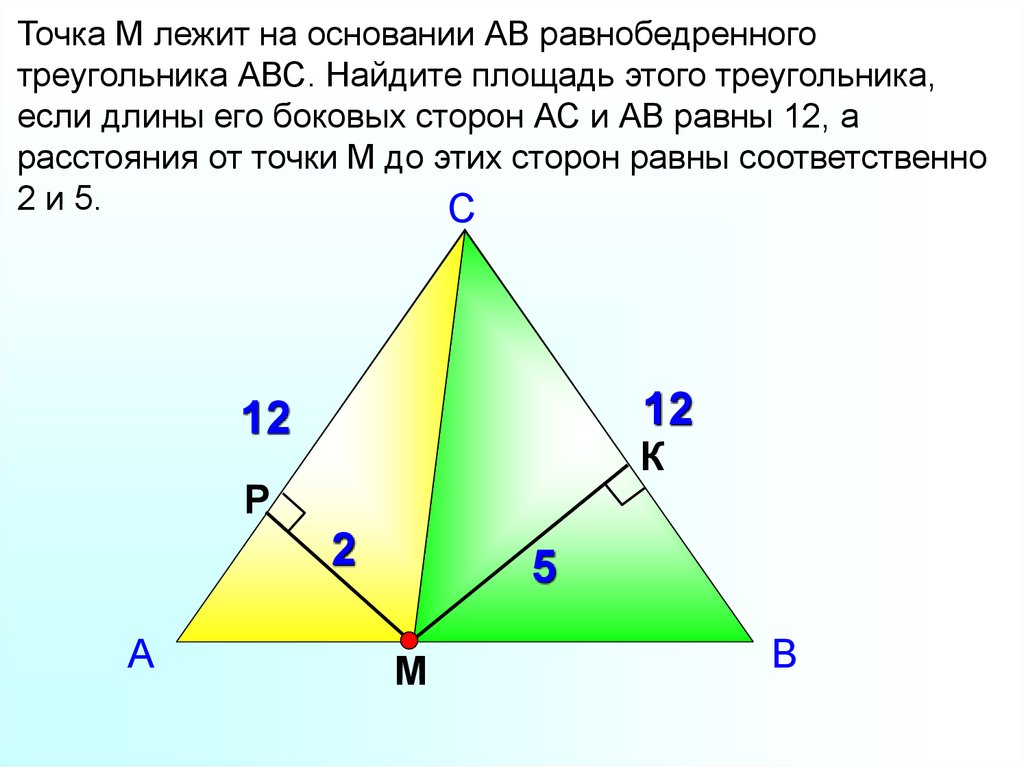
23.

Точка М лежит на основании АВ равнобедренного
треугольника АВС. Найдите площадь этого треугольника,
если длины его боковых сторон АС и АВ равны 12, а
расстояния от точки М до этих сторон равны соответственно
2 и 5.
С
12
12
К
Р
2
А
5
М
В

24.

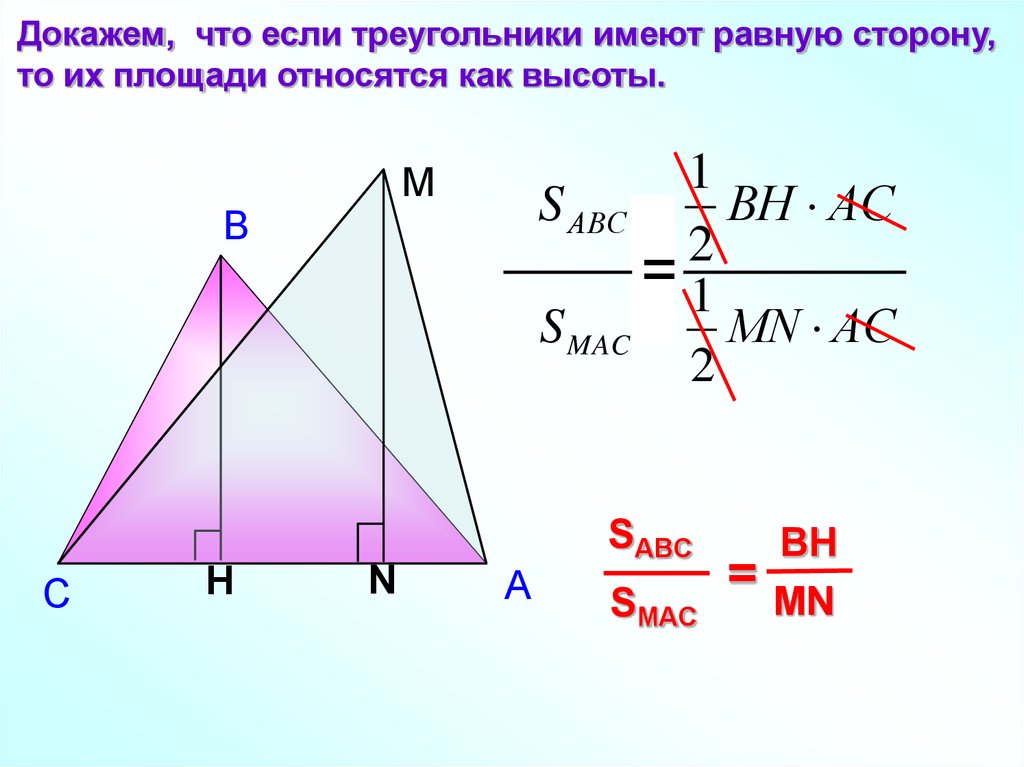
Докажем, что если треугольники имеют равную сторону,
то их площади относятся как высоты.
1
S АВС ВH АC
2
=1
S MAC МN АС
2
М
В
SABC
С
H
N
A
SMAC
=
BH
MN

25.

Высоты треугольников АВС и КВС, опущенные на сторону
ВС, относятся как 7 : 6.
Найдите площадь треугольника АВС, если она на 15 больше
площади треугольника КВС.
А
К
х+15
х
SABC
SКВC
Х + 15
Х
В
H
N
С
=
АH
КN
=
7
6